Introduction

Traditional villages are inextricably linked to the local natural environment, and their integration represents an important historical experience in Chinese architectural culture. These villages, which have developed within the local environment, have long integrated natural factors and cultural contexts. Over the course of history, they have evolved their own unique path structures and architectural textures1. This historical accumulation has extremely high research value. The planning that maintains the internal structure of traditional villages helps to protect the structure of traditional villages, so that people can appreciate their original style even if they have been eroded by time. It also helps to maintain the identity and cultural continuity of the villagers. In recent years, rapid urbanization and rural reconstruction have altered people’s residential structures and living styles2. As material carriers of rural life, traditional villages have been significantly impacted by these changes. The number of traditional Chinese villages is decreasing annually, and both tangible and intangible heritage face the risk of disappearing due to urbanization3. Many traditional villages, originally in a state of natural growth, have been disrupted by various external factors. The imposition of urban-style planning has hindered their development according to their original growth models. What’s more, some traditional villages have shown few signs of natural growth and have transformed entirely into modern-style villages. This situation poses a significant challenge to the historical continuity of spatial forms in traditional villages. Recently, various measures to protect traditional villages have been actively implemented. For instance, driven by digital technologies (e.g., 3D modeling and GIS) and community participation models, an organic integration of cultural heritage preservation and rural revitalization has been progressively realized. However, these measures primarily focus on post-damage restoration rather than the sustainable continuity of the original village.

Due to the conflict between development and conservation in traditional villages, there is an urgent demand to develop a novel planning approach that minimizes human subjectivity, enhances objective constraints, and maximizes the restoration original characteristics of the target village. Based on the self-similarity of traditional villages, “fractal iteration” can provide suitable theoretical support. We generate multiple planning schemes by extracting “fractal units”, iterating them conditionally, and then performing appropriate manual adjustments. After evaluating the degree of disorder at three levels: “point”, “line”, and “plane”—the best scheme is finally selected. The characteristic of this new planning model is that it begins at the origin of villages and ultimately returns to the villages themselves. In this process, human involvement is minimal, and the original intent of building traditional villages is preserved as much as possible. This research holds great significance for protecting the historical and cultural heritage of traditional Chinese villages4.

Methods

Basic concepts and related theories

Fractal theory

Fractal theory is a nonlinear research method that utilizes fractal geometry to study complex phenomena5. The word “fractal” first appeared in the paper titled “How Long is the British Coastline?”6 by Benoit B. Mandelbrot in 1967. The term derives from the Latin word “fractus”, which means irregular and broken7. It refers to a type of shape composed of parts that are similar to the whole in some way. The most basic characteristic of fractal theory is its use of fractional dimensions and mathematical methods to describe and study objective phenomena. Compared with traditional Euclidean geometry, fractal theory encompasses the study of non-smooth and irregular geometric shapes found in nature and nonlinear systems, as well as the disordered and self-similar systems prevalent in social activities8.

In the process of being applied to various disciplines, fractal theory has gradually become a method for re-analyzing and understanding the structure of things. In the field of architecture, it has developed into an effective means of quantifying urban spaces and village forms9. The research directions of fractal theory in architecture are divided into two major areas:

One area involves using fractal theory to quantitatively analyze urban spaces in order to study their fractal characteristics and developmental forms. In 1991, Batty published “The City as Fractal: Modeling Growth and Form”, which marked the beginning of fractal studies in urban morphology. Fractal in Geography, edited by Lam and Cola, is considered a theoretical work that guides the fractal study of urban forms10. In China, the study of fractal theory started relatively late, but it has played an indispensable role in quantifying village morphology. For example, Xincheng Pu’s monograph, Quantitative Research Methods of Traditional Rural Village Plane Morphology, proposes dividing the analysis of plane morphology in traditional villages into three levels: boundary (line), space (plane), and building (group). In his quantitative research at the spatial (plane) level, Pu used the area-perimeter method and the box-counting dimension method to calculate the fractal dimensions of 22 traditional villages in Zhejiang Province. He then used these fractal dimensions to define the degree of village structure and the spatial characteristics of the villages.

The second area involves architectural design research using fractal concepts combined with computer-aided parametric design. In 1996, Bovill. C published the book Fractal Geometry in Architectural Design, in which he argued that the facades and shapes of many buildings exhibit fractal characteristics. Wolfgang E. Lorenz and other researchers have used fractal theory to characterize the multi-layered complexity of architectural designs and proposed a method to evaluate their self-similarity and complexity11. Yalong Mao proposed several methods for combining fractal theory with parametric design in his article “Fractal Iteration Parametric Architectural Design”. The combination of these two approaches can effectively realize fractal iteration in parametric architectural design and achieve a fusion of complexity science and architecture.

Fractal iteration

Fractal iteration is derived from the concepts of “self-similarity” and “fractal unit” in fractal theory. Self-similarity means that a certain structure of a research object is similar when observed from different spatial scales. To put it simply, it can be understood that the structure of the whole and its parts has a certain similarity12. Over the past few decades, complexity science has shown that many natural systems have similar geometric patterns that recur at different scales of observation13. This recurring simplest basic graphic unit is called a “fractal unit”. The graphics generated by repeating and iterating with its fractal characteristics also have the same fractal characteristics. This is the process of fractal iteration using self-similarity. The mathematical formula to express this process is F(n + 1) = F(Fn)14.

Parametric design

The concept of parametric design

Parametric design refers to the process of quantifying important parameters that affect design results, establishing constraints between parameters and results, and achieving the goal of changing the final result by modifying some parameters. In the process of parametric design, the model becomes a part of the design process in a dynamic form, rather than being the final result15. This concept originated from a philosophical proposal that there is a conversion relationship between diagrams and functions, which deepens the understanding of the concept of diagrams16. In 1971, Moretti defined parametric architecture as the study of relationships between dimensions of a design based on parameters. Kalay expanded on Moretti’s definition in 1989, considering parametric modeling as the computational representation of geometric relationships that were automatically updated and visualized when parameters were changed17. This development prompted architects to begin thinking about the relationship between architectural form and mathematics, especially mathematical functions.

The rise of parametric design corresponds with the development of computer technology. In the 1960s, the application of computers in the architectural design industry was primarily limited to data processing. By the 1980s, CAD drawing had become popular in the design industry, and a trend of computer drawing replacing manual drawing gradually emerged. Parametric design also began to surface around this time and was initially applied in the field of building construction. Frank Gehry was a pioneer in this field. In the mid-1990s, a team specialized in the development of digital technologies for architecture was formed within the design industry. This move subsequently sparked a trend of researching digital design in the field of architecture, with parametric design being one of the key areas. In 2013, Ulrich Fleming wrote in his article “The Logic of Architecture: Design, Computation, and Cognition” that architects had been freed from the analytical calculations of basic geometric shapes, and had begun to master more complex theories of architectural form generation18.

Research on parametric design started relatively late in China. Professor Weiguo Xu’s team from Tsinghua University pioneered relevant teaching and research activities in 2003 and subsequently organized ten digital architecture exhibitions. Following these developments, parametric design rapidly advanced in the field of architecture and achieved significant practical results. Notably, during the 2008 Beijing Olympics and the 2010 Shanghai World Expo, several digitally designed buildings were implemented in China. Additionally, more parametric designs have been executed, such as the Guangzhou Opera House designed by Zaha Hadid, the Beijing Phoenix International Media Center by BIADUFO, and excellent parametric buildings designed by Gensler19. The advancement of parametric design is closely linked to computer technology. With the rapid development of this technology, parametric design is expected to have a more comprehensive application system and broader development prospects in the future.

Parametric design has emerged as a new design paradigm capable of addressing environmental and social issues through the integration of form and function20. Similar to fractal theory, parametric design begins with rational mathematical thinking but also faces certain limitations, such as limited flexibility, design complexity, irreducibility of physical models, and marginalization of emotions21. Therefore, it is necessary to continuously explore ways to mitigate these limitations during the design process in order to make fully use of its benefits.

Parametric software introduction

Table 1 lists five parametric design software. We briefly introduce their iteration principles and their respective advantages and disadvantages.

Table 1 Introduction and illustration of parametric software (Figures source: Drawn by the authors)
Full size table

Village disorder

The concept of village disorder

From a fractal perspective, it is believed that the internal structure of traditional villages consists of building units, streets, and other elements that continuously self-replicate and iterate. This iterative process, influenced by various factors such as terrain, precipitation, temperature, water sources, transportation, religion, and agricultural production methods, forms a unique traditional village. This is reflected in the specific structure of the village, where the buildings, streets, and local environment form various combinations. Some of these combinations are disordered and some are ordered. The “disorder” and “order” revealed by their random growth do not exist independently. The two are mutually inclusive and interdependent, and together constitute the inherent laws of traditional villages. Quantitative analysis of this “disorder” is the core content of disorder evaluation. Specifically, it is to choose appropriate quantitative methods to evaluate the order of the target villages at three levels: “point—building unit”, “line—street”, and “plane—local environment”.

Western countries experienced an earlier urbanization process; research and development of spatial order evaluation began much earlier, and the corresponding theories became more complete. Edgar Rubin first proposed the figure-ground relationship theory in his doctoral thesis in 1915. This theory is one of the foundations of Gestalt psychology and is used to describe the relationship between “figure” and “ground” in visual perception. In his 1986 monograph, Finding Lost Space: Theories of Urban Design, Roger Transik explored the common “lost space” problem in modern cities. Transik emphasized a variety of urban design principles, such as connectivity, boundaries, form, and function. The study of urban texture is also used as a method to evaluate spatial order. In the 1960s, Colin Rowe analyzed the morphological changes and generation principles of urban texture. He proposed that the entity and its texture provide energy for the corresponding specific space. Kevin Lynch also used texture to describe the morphological characteristics of settlements, asserting that urban texture is a combination of different elements in space formed over many years of urban development, which can be used to grasp the characteristics of the city. These factors that reflect urban order are integrated to improve the urban environment.

China started late in evaluating spatial order, which is divided into three parts: First, some researches are based on regional division. China has a large land area, covering a variety of landforms and climates, where in-depth analysis has been conducted. For example, Wang Haibo took the traditional village architecture in Southern Shaanxi as his research object and selected 30 representative traditional villages in three cities of Southern Shaanxi to explore the influence of regional factors such as culture, psychology, environmental timing, and defense on the order of traditional villages. Second, some researches are based on morphological structure. Zhao Di and Zhang Xiaoli applied the research method of mutual verification of pictures and texts, along with elements of spatial morphological structure, to analyze the spatial order of different types of villages before and after the “Japanese Pirates” war in the Ming Dynasty and summarized their development laws. Third, other researches are based on humanities and religion. Xiong Jian divided the space of the Wuchuan Gelao village into three elements: point, line, and plane, and conducted a quantitative study on the spatial morphology. By dividing the internal virtual and real space to establish a village topology map, he verified the correlation between the internal social order and spatial structure of the village and revealed the universal characteristics of the spatial layout of the traditional village morphology of the Wuchuan Gelao people.

Spatial order evaluation is not only a mathematical representation of spatial form but also serves as a “gatekeeper” of authenticity and functionality. If changes exceed a reasonable threshold, it may cause the village to become a “symbolic setting” or an “inefficient spatial container”. Accordingly, through scientific quantification and multi-dimensional calibration, the protection and renewal of traditional villages, maintaining “both form and spirit”, can be achieved in modern planning.

Quantification method of village disorder

Point dimensions: “Points” correspond to building units. Buildings in a traditional village can be abstracted as “points”. Their representation is based on the coordinate information of specific buildings in the village. Quantifying the order of building units involves determining the degree of association between each “point” and others. This process employs the Delaunay triangulation algorithm as the quantification method. The centroids of the buildings are connected to form a Delaunay triangulation network diagram. The angular relationships between adjacent points in the triangulation network are measured, and the standard deviations are calculated.

Considering the relationship between buildings abstracted as “points”, we focus on analyzing the angle relationship between adjacent buildings, rather than the orientation angle of the buildings themselves. If the line connecting the centroids of two buildings is vertical (90°) or parallel (0°), it is regarded as having the lowest disorder. If the centroid line forms an angle of 45°, it is regarded as having the highest disorder.

Therefore, we need to measure the angles between all adjacent buildings that influence each other. Then calculate the average deviation between the angle α of all adjacent buildings and 45°. Mathematically, this is expressed as:

$$A=\overline{\left|\alpha -45^\circ \right|}$$
(1)

In Eq. (1), the larger the A value, the greater the average difference between the building angles and the disorder angle of 45°. The lower the disorder of the building angles in the village, the stronger the perceived order22.

Line dimensions: “Lines” correspond to streets. Streets in traditional villages can be represented as “lines”. They are expressed by the direction and position of specific streets in the villages. Determining the degree of chaos for each “line” quantifies the street. The quantification method is street direction entropy. Street direction and length data is counted and converted into a visual polar coordinate histogram using Python programming. This statistical data is used to calculate direction entropy.

$$H(X)=-\mathop{\sum }\limits_{x}^{n}P\,(x)\,{\log }_{2}\left[P(x)\right]$$
(2)

In Eq. (2), H(X) represents the directional entropy value of the village streets, while P(x) indicates the frequency of streets in the x direction. To aid calculations and align with the CAD plan, the 360° plane is divided into 36 equal sectors, each covering 10°. To minimize edge effects near common angles such as 0° and 90°, each sector is shifted 5° counterclockwise, ensuring that it centers within the group rather than at the boundary23. The frequency of each directional data path within these sectors is counted to determine the directional entropy value. Generally, the more orderly the distribution, the lower the entropy value24.

Plane dimensions: “Planes” correspond to the local environments. In traditional villages, the local environments can form planes of various shapes and locations. There are similarities between different local environments, and there are also similarities between the local environment and the overall environment. The method used to describe the degree of this similarity is also the method used to measure the disorder of the “plane”. The quantitative method employed is the spatial syntax comprehensibility calculation. To perform this, the village road axis map is drawn and imported into the Depthmap software, where parameters are debugged to obtain the comprehensibility scatter plot. The data obtained from calculating comprehensibility can reflect the correlation between environmental perception and the street network. To put it simply, the higher the comprehensibility of a traditional village, the closer it is to being a single-core space and the simpler the space configuration. Conversely, the lower the comprehensibility, the easier it is to get lost25. Comprehensibility is a numerical value that measures the similarity between the local environment and the overall environment. The calculation formula is as follows:

$${R}^{2}=\frac{{\left[\sum \left({Ci}-\bar{C}\right)\left({Ii}-\bar{I}\right)\right]}^{2}}{{\sum \left({Ci}-\bar{C}\right)}^{2}{\sum \left({Ii}-\bar{I}\right)}^{2}}$$
(3)

In Eq. (3), it can be seen that R2, a measure of comprehensibility, is a function of both local and overall connectivity and integration26. When R2 is less than 0.5, spatial comprehensibility is poor, overall spatial similarity is low, the spatial structure appears more chaotic, and both local and overall self-similarity are low, indicating high disorder. When R2 is between 0.5 and 0.7, spatial comprehensibility is moderate. When R2 is 0.7 or higher, there is a significant correlation between the horizontal and vertical axes, indicating high spatial comprehensibility. In this scenario, people can predict a larger range of space through their local spatial experiences, and the level of disorder is low.

Research area

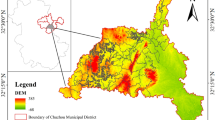
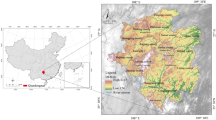
Dawangbang Village, located in Jingxing County, Shijiazhuang City, Hebei Province, is famous for its unique geographical ___location, historical background, and traditional architecture. It is an important window for studying the history and culture of northern rural areas. Located at the southern foot of the Taihang Mountains, it has a relatively flat terrain and is surrounded by hills and mountains. This geographical environment provides a natural barrier for the village and also gives it rich natural resources, such as fertile land and abundant water sources, which are important conditions for agricultural production. Moreover, historically, Jingxing was one of the Eight “Xings” (mountain pass) of Taihang. It was a place of contention for military strategists. Dawangbang Village is located near a major transportation route, so it may be a subsidiary village resulting from ancient military farming or defense of mountain passes.

During the investigation, we learned through communication with the local officials that the area of Dawangbang Village is 13,791.7 acres, with 225 households and 620 people. There are three major clans in the village, namely Wang, Du, and Lv. At present, there are only 70 to 80 permanent households, and the permanent population is 170 due to the serious issue of aging. The main source of income is agriculture, with cash crops such as corn and sweet potatoes. Additionally, a small number of villagers engage in small-scale livestock breeding as a supplementary income. Although there are many wells in the village, most remain unused. Currently, tap water is the primary water supply, and winter heating relies on coal burning. The ancient tree on the east side of the village, which is a famous scenic spot, has a history of over 2000 years.

As shown in Fig. 1, mountains border the north side of Dawangbang Village, while farmland stretches along the south side. The roads and buildings within the village are closely integrated, with a main road running east to west through the center. Numerous secondary roads branch off from this main artery to both the north and south, giving the village a distinctive finger-like layout.

Fig. 1
figure 1

Satellite picture of Dawangbang Village (Figures source: Drawn by the authors).

Full size image

During our field research in Dawangbang Village, we gathered detailed information on the local human geography through field visits, as shown in Fig. 2. The primary task involved creating a 3D model of the village using drone modeling technology, which facilitated the production of a detailed floor plan. The architectural protection status in Dawangbang Village is well-maintained, the road layout is complex, and there is an observable trend towards expansion and renewal. Additionally, as one of the villages in the fifth batch of the List of Traditional Chinese Villages, Dawangbang Village retains complete traditional characteristics. In summary, the authors believe that Dawangbang Village is an ideal subject for research on simulating the expansion of the original village form.

Fig. 2
figure 2

Dawangbang Village survey situation (Figures source: Google Earth).

Full size image

Feasibility of applying fractal iteration and parametric design to village planning

Fractals are ubiquitous in nature. Since the advent of fractal theory, it has been widely used in the field of architecture. Its quantitative methods and results have also played a role in the study of traditional villages. From the perspective of pure morphological analysis and complexity science, fractal theory provides scholars with mathematical tools to express, study, and measure the fractal characteristics of the spatial morphology of villages27. It also offers a quantitative basis for understanding the self-organizing mechanisms and complex order of village forms. As the study of village morphology deepens, scholars have discovered that the layout of roads, buildings, and vegetation in most traditional villages is intricate. This seemingly chaotic appearance actually conceals a structural mechanism that has been guiding the evolution of villages for thousands of years.

The formation process of traditional villages is lengthy, with natural and human factors intertwined. The transformation of villages is mostly in response to changes in the natural environment28. In this process, all things develop and change together29. For example, buildings and roads are built according to the terrain and direction of rivers. These characteristics demonstrate that the development of traditional villages is a process of gradual artificial adaptation to changes in the natural environment. When describing the laws of a phenomenon, studying it in isolation may result in perceptions of chaos and disorder. However, by observing it at different scales, we find that similarities and self-similarity prevail in nature.

The development of traditional villages is not a top-down overall plan, but rather a bottom-up construction. Its formation often lacks clear planning and predictability, instead reflecting a degree of collective consciousness. This collective consciousness includes social cognition, class division, blood identity, construction inheritance, and Feng Shui theory. Naturally, residences built under a similar collective consciousness exhibit common characteristics. The road network, as a unique structure, illustrates this point well. Based on this, we can conclude that the road network structure within the village is a manifestation of the village’s unique self-similarity characteristics.

Because the “fractal unit” represents the smallest unit of self-similarity in fractal graphics, we can use the self-similarity of lines to extract the “fractal unit” for the target village. After extracting and comparing “fractal units” from 12 traditional villages in Jingxing (Table 2), we found that similar natural environmental conditions lead to similar spatial layouts in different villages30. Generally, the “self-similarity of lines” provides the basic theoretical foundation for applying “fractal iteration” to original village planning.

Table 2 Comparison between fractal units and local planar similarity of villages (Figures source: Drawn by the authors)
Full size table

We can take advantage of the “self-similarity of lines” to integrate the iterative system with the village planning process. The iterative system is a mechanism that continuously loops feedback through each cycle. Each operation cycle is called an iteration, and the output of one iteration is fed back as the input for the next cycle’s data. If a fractal figure is used as the initial value of the iteration, the resulting outputs will also exhibit a high degree of self-similarity. Parametric software is a system that allows for real-time modeling of desired spatial changes31. Using this software as a carrier for the iterative system can effectively enhance design efficiency and generate multiple selectable solutions within a controllable range of variables. In addition, introducing “iteration” into the quantitative methods of fractal theory can predict the development trends of villages. Using the self-similarity of traditional villages, we can observe traces of development in each period as a whole. We found that various functions and spaces within the village are nested and compatible with each other, and the combination of units at different scales in traditional villages constitutes a self-similar whole. The dynamic principle of this combination is self-similarity and self-organization. These are natural fractals, embodying the village characteristic of “harmony between man and nature”32. Therefore, using the self-similarity feature for village planning is only one option among the many functions of self-similarity.

Technical route overview

Figure 3 is the technical route chart of this study. Fractal algorithms, when combined with visual digital software, can effectively implement fractal iterative parametric architectural design and facilitate the integration of complexity science with architecture33. This paper takes the self-similarity of traditional villages as the basis for integrating fractal theory with parametric design. This process provides research ideas and technical guidance for village planning. Finally, the paper employs disorder assessment as a quantitative method to evaluate the feasibility of the planning scheme.

Fig. 3
figure 3

Technical route chart (Figures source: Drawn by the authors).

Full size image

Taking Dawangbang Village as the target, this paper introduces the parameterized iteration process and disorder evaluation by taking one of the planning schemes generated based on the above process as an example. A total of five planning schemes were generated, and the most suitable one among them was selected based on the disorder evaluation standard.

Parameterized iterative process

Extract the fractal unit

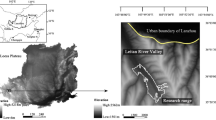
When using parametric software for iteration, the first step is to determine the “fractal unit” to be used. The basic characteristics of fractal units should be generalization and simplicity. A previous article explained that the self-similarity of lines forms the basis of original village planning. Therefore, we will extract the “fractal unit” from the village road network. As is well known, the space syntax road axis diagram summarizes road relationships in a very simple form. Therefore, it is used as the basis for extracting the “fractal unit”.

Figure 4 shows the space syntax road axis diagram of Dawangbang Village. We use its core area as an example, simplifying it to obtain a combination of lines that is as simple as possible. By properly splitting the connecting nodes, we can obtain several minimal units with independent characteristics that make up the road network. Most of these smallest units are shaped like the letter “T”, so the “T” shape is identified as the “fractal unit” of the road network in Dawangbang Village.

Fig. 4
figure 4

Road axis map to extract fractal unit (Figures source: Drawn by the authors using CAD and Photoshop).

Full size image

Parameterized iteration

Considering the parametric software mentioned above, we believe that the combination of VB6 and Grasshopper best meets the requirements of original village planning. The compiled graphics generation function in VB6 can satisfy the requirements of fractal iteration. Grasshopper also supports programming languages such as C#, VBS, and Python (Fig. 5). Programs compiled in VB6 can be integrated into Grasshopper using these languages to form a new program. This new program can be integrated with Grasshopper’s existing basic programs that control parameters such as angle, length, and number of iterations. Together, they form a complete parametric iteration system. This system conveniently controls the shapes of fractal units and the settings of various iterative parameters. Consequently, the “fractal unit” can be gradually iterated with the self-similar parts and the special vertices of each cycle34. Thus, a self-similar and continuously iterative product is formed, simulating the village path generation pattern.

Fig. 5
figure 5

Grasshopper’s built-in programming language (Figures source: Rhino).

Full size image

The specific combination process is as follows:

We established a coordinate system and mathematical functions in VB6, creating an iterative system with the “T” shape as the “fractal unit”. This function was set to randomly select the iteration size and rotation angle within a certain range. The generation logic of this program follows the iterative logic of the L-system. Each endpoint of the “fractal unit” serves as the starting point for the next iterative graph, performing calculations similar to those in a nuclear fission chain reaction. In this way, a new “T” shape is generated at the endpoint of each existing “T” shape. Through parameter control, the size and rotation angle of the “T” shapes generated in each iteration are randomly selected within a specified range. Repeated iterations result in multiple “T” shapes connected end to end (Figs. 6 and 7). Since the parameter values are set randomly, the graphics generated by each iteration differ. This feature also reflects the diversity of random fractal iterations.

Fig. 6
figure 6

Results of 15 iterations (Figures source: Drawn by the authors using VB6).

Full size image
Fig. 7
figure 7

Results of 30 iterations (Figures source: Drawn by the authors using VB6).

Full size image

The program that generates the “T” shape in VB6 is converted into a format compatible with Grasshopper, creating a new operator. This operator is then integrated with another one that controls the random point selection on the existing path, together forming a complete parametric iteration process. In this design process, numerous variables are controllable. The parametric iteration allows these variables to be set as several controllable parameters, thereby enabling the real-time control of the generated products35.

Based on the actual situation analysis of Dawangbang Village, there is no large-scale idle land in the village reserved for expansion planning; only some smaller vacant lands are available. This area accounts for about 14.38% of the residential area of Dawangbang Village (since the main body used in this experiment is the road network of Dawangbang Village; the residential area represented by the road network serves as the reference for the renovation area). In early iterative experiments, we found that expanding along existing paths is more controllable and stable. The expected implementation is the iterative model shown in Fig. 8. We drew the main path of the expansion area in Rhino (Fig. 9) and set five random points on the curve in Grasshopper. We then set the “fractal unit” (“T” shape) to randomly iterate between 3 and 6 times using these five random points as the starting points. The iteration size of the graph is randomly generated within the range of 300 to 1500. The iteration angle of the graph is randomly generated within the range of 0 to 360 degrees. In this way, we obtain the final fractal iteration result (Fig. 10).

Fig. 8
figure 8

Expected iteration model (Figures source: Drawn by the authors using Photoshop).

Full size image
Fig. 9
figure 9

Randomized point taking for existing paths (Figures source: Drawn by the authors using Rhino).

Full size image
Fig. 10
figure 10

Iteration results of path randomized point taking (Figures source: Drawn by the authors using Rhino).

Full size image

Throughout the process, the angle between the long and short arms of each “T” shape was always maintained at 90°, without random iteration. This approach was to ensure that each “fractal unit” maintained its basic structural independence. Randomly iterating the angles between the long and short arms of the “T” shape would result in an overly chaotic overall shape. Such a chaotic pattern would lose its unique self-similarity and devolve into a jumble of disorganized and meaningless lines. This outcome would significantly deviate from the original village planning concept and is therefore undesirable. After the parametric iteration generates the preliminary graphics (Fig. 10), we will further debug the results in subsequent stages. We will make appropriate adjustments to the original village road layout based on local slopes, elevation differences, and other conditions, rather than mechanically replicating the iterative results.

Application and optimization

The essence of parametric iteration lies in rapidly generating multiple outputs based on predefined criteria. However, not all iterations can perfectly align with the target village’s actual conditions. Thus, selecting and adapting the results according to contextual environmental factors is essential. As shown in Fig. 11, the blue frame represents the expansion area; the results mentioned above are obtained by inputting the iterative results into it. However, this simple combination is too mechanical, and there are some differences in details compared with the flexible and changeable road system in traditional villages. Therefore, selecting and optimizing these elements is necessary to achieve a village planning form that aligns with the origins of Dawangbang Village. These elements include road shape, road width, road spacing, houses, other buildings, orientation of new buildings, building density, building size, and other factors.

Fig. 11
figure 11

Expansion area of Dawangbang Village (Figures source: Drawn by the authors using CAD).

Full size image

Optimization process:

  1. (1)

    Dawangbang Village is located in a mountainous area, so there are inevitably some height differences in the village. When dealing with the impact of height differences on roads, we give priority to iterating results in which the road direction conforms to the site contour as much as possible. We introduce terrain slope thresholds (such as limiting road slopes to less than or equal to 15%) during the optimization process, and refer to the circuitous layout pattern of traditional village roads (such as zigzag roads) to ensure that the generated plan is coordinated with the terrain.

  2. (2)

    As shown in Fig. 12, the average path distance, average house spacing, average house size, and contour line trends are first calculated based on the Dawangbang Village plan. Using this data, we select the generated roads and place them in the planned expansion area. By eliminating paths outside the expansion area, we obtain the preliminary road distribution shown in Fig. 13.

  3. (3)

    Additionally, the newly added road corners appear overly mechanical, necessitating optimization through chamfering, topological deformation, and other techniques. Roads treated in this manner align more closely with the characteristics of traditional village roads. After processing the roads, we place houses and buildings according to the previously calculated data, positioning their gates near the roads and orienting them north-south as much as possible. During the building placement process, fractal geometry is employed to create rich scale levels and complex rhythms, integrating the buildings with the surrounding environment organically36. The model obtained after the above processing is shown in Fig. 14.

Fig. 12
figure 12

Iteration results combined with the original village (Figures source: Drawn by the authors using CAD).

Full size image
Fig. 13
figure 13

Road optimization (Figures source: Drawn by the authors using CAD).

Full size image
Fig. 14
figure 14

Optimization results (Figures source: Drawn by the authors using CAD).

Full size image

After the above optimization processes, the final results of the parametric iterative planning of Dawangbang Village were completed (Fig. 15).

Fig. 15
figure 15

Final results of parametric iterative planning in Dawangbang Village (Figures source: Drawn by the authors using CAD).

Full size image

Results

Fractal iteration is essentially a method for analyzing the developmental characteristics of objects in their natural state. Combining fractal iteration with parametric design and applying these methods to traditional village planning represents a highly innovative approach. However, this method inevitably has certain limitations. For example, concerns exist regarding the validity of the process for establishing fractal units based on topology, the appropriateness of iteration rules, and the impact of uncontrollable variables on the outcomes of random fractal iterations. Traditional village planning, however, is not a mechanized project but rather an exploratory process that integrates characteristics from disciplines such as architecture, planning, and fractal geometry. Therefore, solutions tailored to the village planning of a specific region are not singular. To identify the most reasonable solution, it is necessary to develop a quantitative evaluation standard. Disorder assessment provides an objective and quantitative means to assess the internal order and degree of chaos at various levels, including buildings, paths, and the local environment within the village. Using disorder assessment as an evaluation criterion is a more logical and appropriate choice.

Results of village disorder assessment

To calculate the building disorder, we must first represent the buildings in Dawangbang Village. The effective information of each building is represented as “points”. This process involves using AutoCAD to determine and depict the centroids of the buildings, which are then used as “points” for the disorder calculation. The centroid coordinates of the buildings before and after expansion in Fig. 16 are imported into MATLAB to generate the Delaunay triangulation of the building coordinate points in Dawangbang Village (Figs. 17 and 18). Then, using AutoCAD, we depict each line segment, extract its adjacent angles and lengths for the calculation, and obtain the following data:

Fig. 16
figure 16

Dawangbang Village centroid (Left: original, right: new) (Figures source: Drawn by the authors using CAD).

Full size image
Fig. 17
figure 17

Delaunay triangle network diagram of Dawangbang Village buildings (Before expansion) (Figures source: Drawn by the authors using Matlab).

Full size image
Fig. 18
figure 18

Delaunay triangle network diagram of Dawangbang Village buildings (After expansion) (Figures source: Drawn by the authors using Matlab).

Full size image

The angles of the connecting lines between the building centroids were measured and compared with 45° to calculate their mean, denoted as A=\(\overline{\left|{\rm{\alpha }}-45^\circ \right|}\). Before the expansion of Dawangbang Village, A was found to be 22.90°, and it increased slightly to 23.28° after the expansion. Comparing these two sets of data, the increase in A value suggests a decrease in disorder. The reason for this change is that, although the expansion was designed through parameterized iteration, the placement of buildings was still primarily based on manual and subjective selection, which reduced the disorder to some extent. The difference in A before and after the expansion was minor (0.38°), indicating that both sets of data were close to the median of the disorder. Thus, the expansion plan had little effect on the disorder of the original village.

The information required to calculate the street direction entropy includes the length and angle of the street. The centerline of the road (Fig. 19) effectively represents these two types of information. Therefore, we extract the length and angle data from the road centerline map of Dawangbang Village, both before and after its expansion. The data is grouped into 10° intervals, and the frequency of line lengths within each group is counted. The change in street disorder before and after the expansion is assessed based on the calculated P(x) value. Simultaneously, the data is imported into Python for processing to generate a polar coordinate histogram of the streets. This approach allows us to analyze the impact of the expansion plan on the disorder of the original village streets more intuitively and specifically.

Fig. 19
figure 19

Map of Dawangbang Village Road center (Left: original, right: new) (Figures source: Drawn by the authors using CAD).

Full size image

The calculation results for Dawangbang Village are as follows: before the expansion, the unweighted entropy was 2.83 and the weighted entropy was 2.75; after the expansion, these values increased to 2.85 and 2.78, respectively. This comparison shows a slight increase in both unweighted and weighted entropy. Although the street disorder has increased slightly, the change is not significant. Therefore, the expansion plan is considered reasonable. The increase in entropy is attributed to the disorder-shaped iteration process, which does not limit the iteration angle. Allowed to iterate freely within (0,360°), the generated iteration lines (streets) are not completely controllable, leading to an increase in the angles of newly added streets and, consequently, the entropy value. As shown in Fig. 20, the frequency of street directions in Dawangbang Village within the interval (356°, 5°) is relatively high. Increasing the frequency of iteration angles in the (356°, 5°) and (176°, 185°) intervals during the iteration process can align the street disorder of the expansion plan more closely with that of the original village.

Fig. 20
figure 20

Histogram of polar coordinates of streets before and after the expansion of the of Dawangbang Village (Figures source: Drawn by the authors using Phyton).

Full size image

Space Syntax—Comprehensibility reflects the difficulty of people’s actions in the environment. This concept is quantified in the graphical data by the regression coefficient R2 of the scatter plot. Specifically, a higher R2 indicates greater comprehensibility, higher self-similarity, and lower environmental disorder. Conversely, a lower R2 suggests lower comprehensibility, lower self-similarity, and higher environmental disorder.

Draw the axis diagrams (Figs. 21 and 22) of Dawangbang Village before and after the expansion in AutoCAD, and import them into the spatial syntax software, Depthmap, for calculation. Then, draw the comprehensibility scatter plot, setting the X coordinate to Integration [HH] and the Y coordinate to Integration [HH] R = 3. The comprehensibility scatter plots of Dawangbang Village before and after the expansion are obtained (Figs. 23 and 24).

Fig. 21
figure 21

Axis map of Dawangbang Village (Original) (Figures source: Drawn by the authors using CAD).

Full size image
Fig. 22
figure 22

Axis map of Dawangbang Village (New) (Figures source: Drawn by the authors using CAD).

Full size image
Fig. 23
figure 23

Scatterplot of comprehensibility before the expansion of Dawangbang Village (R = 3) (Figures source: Drawn by the authors using DepthmapX).

Full size image
Fig. 24
figure 24

Scatterplot of comprehensibility after the expansion of Dawangbang Village (R = 3) (Figures source: Drawn by the authors using DepthmapX).

Full size image

The data is calculated as follows: Before the expansion of Dawangbang Village, the regression coefficient R2 is 0.500 (Fig. 23). The comprehensibility is moderate, self-similarity is average, and people can moderately understand the overall feeling from the local environment, with moderate disorder. After the expansion, the regression coefficient R2 is 0.373 (Fig. 24). The comprehensibility is low, self-similarity is low, and people poorly understand the overall feeling from the local environment, with high disorder.

Comparing the above two sets of data, it is evident that R2 decreases significantly after the transformation, primarily due to the limited expansion area available in traditional villages. Parametric iterative planning aims to create a village planning model that maintains self-similarity on a global scale. However, planning only local areas might result in the formation of a “new core area”, as shown in Fig. 25, which can significantly affect the overall understandability and integration of the village. This phenomenon is an inevitable part of village expansion. As long as the new plan minimally impacts the overall integration, it can be considered reasonable.

Fig. 25
figure 25

Comparison of the integration degree R = 3 before (left) and (right) after the expansion of Dawangbang Village (Figures source: Drawn by the authors using CAD).

Full size image

The results of disorder assessment of various expansion schemes of Dawangbang Village

Through parametric iteration, a variety of original expansion planning schemes suitable for Dawangbang Village can be generated. The village disorder degree is tested for each scheme, and the optimal result is obtained through data analysis. The expansion scheme mentioned above is defined as Expansion Scheme 1. Then, different expansion schemes, numbered 2 to 5, are generated using the same process (Fig. 26). After evaluating the village disorder degree of each scheme, the best scheme is selected.

Fig. 26
figure 26

Dawangbang Village parametric iteration Scheme 1–5 (Figures source: Drawn by the authors using CAD, Rhino and Photoshop).

Full size image

As shown in Fig. 27, there is no significant difference between iterative expansion schemes 2 to 5 and the original village disorder degree mentioned above. This preliminarily confirms the rationality of using parametric iteration in original village planning. When comparing the data for “point”, “line”, and “plane”, it is important to note that the core of parametric iteration applied to village planning is the “self-similarity of line”. Therefore, the evaluation data for “line-street direction entropy” is the priority measurement object, followed by “point” and “plane”.

Fig. 27
figure 27

Diagram of the village disturbance assessment of 1–5 expansion schemes of Dawangbang Village (Figures source: Drawn by the authors using Matlab, Phyton and DepthmapX).

Full size image

According to the data in Table 3: the weighted entropy of “Scheme 2” is 2.7469, which is closest to that of the original village. Additionally, the angle deviation A(|α−45°|) and comprehensibility R2 are also within a reasonable range. Therefore, “Scheme 2” is recommended as the optimal choice among the five expansion schemes.

Table 3 The results of the disorder assessment for the expansion schemes 1 to 5 of Dawangbang Village (Data source: Calculated by the authors)
Full size table

The comprehensive analysis of the expansion scheme priority ranking is as follows: Scheme 2 is the highest priority, followed by Scheme 3, Scheme 4, Scheme 5, and finally Scheme 1.

Results of the disorder assessment of Dawangbang Village

The new scheme at the “building unit” level has little difference from the original village data. The mean of the new scheme A is 23.2238, and the original village data is 22.896, with a difference of only 1.431%. The renovation area accounts for 14.38% of the residential area, which is very small in comparison, so we can exclude the influence of the renovation area ratio on the disorder detection. Therefore, the expansion plan is considered to be more reasonable.

The new scheme at the “street” level has little difference from the original village data. The mean of the street direction entropy of the new scheme is 2.8365, and the original village data is 2.8332, with a difference of only 0.12%. The renovation area accounts for 14.38% of the residential area, which is very small in comparison, so we can exclude the influence of the renovation area ratio on the disorder detection. Therefore, the expansion plan is considered to be more reasonable.

From the data comparison at the “local environment” level, the disorder of the Dawangbang Village expansion plan at the “local environment” level is far less close to the original village data than the “building unit” and “street” levels. The average R² of the new plan with intelligibility R = 3 is 0.4178, while the original village data is 0.500, and the difference accounts for 16.44%. The definition of intelligibility is the ability of people to perceive the overall environment of the local environment. Based on this definition and our choice of expansion area, it can be inferred that the reason for this large data difference is the limitation of the expansion area. Parametric iterative planning is committed to creating a village planning model with self-similarity in the whole range. Local expansion has changed the overall shape of the village to a certain extent, which may cause a large difference in intelligibility data. If the entire village is expanded in all directions, the data error will be extremely small. However, the area available for expansion in traditional villages is limited, which is also an unavoidable realistic factor in village expansion.

In addition to comparing with the original village data, we also started to compare with the disorder data of traditional villages in Jingxing. In the previous preparation of the paper, we analyzed and counted the disorder detection data of 48 traditional villages in Jingxing, Hebei, and obtained the following range of disorder data:

The architectural angle disorder value of traditional villages in Jingxing showed a relatively stable but slightly fluctuating trend, with a value range of 21.078 to 27.939. A comprehensive analysis of its causes shows that villages with A-values below 21.940 have high architectural disorder, A-values between 21.940 and 24.767 have moderate architectural disorder, and A-values above 24.767 have low architectural disorder.

The unweighted directional entropy of traditional villages in Jingxing County ranges from 2.2236 to 2.8692. After comprehensive analysis of its causes, it can be considered that villages with unweighted directional entropy values higher than 2.8658 have high street disorder, those with entropy values between 2.6608 and 2.8658 have moderate street disorder, and those with entropy values lower than 2.6608 have low street disorder.

The comprehensibility of traditional villages in Jingxing County ranges from 0.0705 to 0.7284. After comprehensive analysis of its causes, it can be determined that villages with comprehensibility values between 0.2321 and 0.5635 have relatively moderate local environment disorder, and villages with comprehensibility values higher than 0.5635 have low local environment disorder.

In summary, the disorder data of “building units”, “streets”, and “local environment” from the five expansion plans of Dawangbang Village fall within the data range of 48 traditional villages in Jingxing, so the planning scheme has been verified as relatively reasonable.

Discussion

Based on the background of the decreasing number of traditional villages in contemporary times and the fact that current planning methods are generally unable to inherit the unique structure of traditional villages, we combined fractal iteration with parametric design to form a new planning process for traditional villages. The core of this process is that traditional villages exhibit self-similarity. We utilize their unique self-similarity and adjustable parametric software to quickly and efficiently generate a variety of new planning schemes that have similar self-similarity to the original villages. This model can restore the unique internal structure of the target village as much as possible and better preserve its original style.

The specific steps of this process are: extracting fractal units, parametric iteration, application and optimization, and disorder detection. First, we extracted the “T” shaped fractal unit from the road network of Dawangbang Village, then wrote the fractal unit iteration rule in VB6 (Visual Basic 6.0) and combined it with Grasshopper. Parametric software can generate several results with different characteristics by adjusting various parameters in the production process (angle, length, number of iterations, etc.). Combined with the situation of Dawangbang Village (topography, road shape, road width, residential size, etc.), these results were selected and optimized. Finally, the generated planning scheme was tested for village disorder at the three levels of “building unit,” “street,” and “local environment” to verify the rationality of its planning model.

In this experiment, we generated five new planning schemes for Dawangbang Village. Then we tested the disorder of the village and compared it with the original one. The results showed that the disorder data of “building unit”, “street”, and “local environment” after the update were slightly different from the original village data, and they were all within the range of the disorder data of 48 traditional villages in Jingxing. Therefore, it was preliminarily confirmed that the new planning scheme generated in this experiment can be considered to restore the original structural characteristics of Dawangbang Village.

There are still some challenging issues to be solved in the current research progress. For example, the parametric iteration experiment conducted in this paper is still based on two-dimensional graphics, and the preliminary results of the fractal iteration output are also two-dimensional plane graphics. Even though we can perfectly absorb the two-dimensional new planning path graphics into the 3D village model in modeling software (such as SketchUp, Rhino) and get a three-dimensional planning scheme, this approach is somewhat unsatisfactory. It only forces the output results to fit the terrain to a certain extent, rather than incorporating the terrain as part of the parameters into the fractal iteration from the beginning. Similarly, there are similar drawbacks in culture. At present, we can only copy the culturally representative buildings and nodes that have been statistically well-documented in the “application and optimization” stage into the planning area appropriately. This approach still has a lot of subjective factors and does not incorporate the culture that can represent the vitality of the village into the fractal iteration process.

There are very few cases where fractal iteration combined with parametric design has been applied to village planning in current academic research. This undoubtedly represents a new type of planning approach. Combining fractal algorithms with parameterized architectural design is a trend in the development of digital technology. It also facilitates a multidisciplinary integration and a natural expression in the field of architecture37. By incorporating the idea of analyzing growth laws in natural states from fractal theory, and using parametric software as a tool along with scientific testing methods, this approach forms a complete and rigorous planning system. In this process, there is interaction among multiple disciplines including fractal geometry, architecture, planning, and computer programming, shedding light on the field of ontogenetic planning in traditional village. At the same time, it also provides new research ideas for various fields, such as: Cultural heritage protection and management. Such experiments can help researchers and planners understand how to effectively protect and maintain the cultural characteristics of traditional villages while ensuring that they adapt to modern living needs. Studying how to modernize without destroying the original cultural characteristics is an important topic in this field. Sustainable development and rural revitalization. Exploring how to use the planning and design principles of traditional villages to promote sustainable development, as well as the combination of traditional knowledge and modern technology, can provide new ideas for rural revitalization. Urban and rural planning and spatial design. By studying the spatial layout and community structure of traditional villages, researchers can provide inspiration for modern urban and rural planning, especially in creating more inclusive, accessible, and humane urban environments. Environmental psychology. Studying the spatial use and psychological feelings of residents in traditional villages can provide insights into how humans interact with their living environments, which is instructive for designing living and working spaces that are more in line with human needs. Historical geography and sociology. A deep understanding of the historical evolution, social structure, and cultural heritage of traditional villages can help reveal the historical background and social dynamics of regional development and provide rich cases and data for related social science research. Exploring how to develop tourism by protecting and rationally utilizing the historical and cultural resources of traditional villages, especially in the fields of ecotourism and cultural tourism, can bring new growth points to the local economy.