Accelerated proton dissociation in an excited state induces superacidic microenvironments around graphene quantum dots

Proton transport in interfaces is vital across a broad range from cell membranes in biology^1,2, fuel cells^3,4, to metallic and oxide surfaces for catalysis^5,6. Many efforts have been made to observe the proton transport using electrical^7,8 and optical^9,10,11 signals. Proton transport behaviors also govern the chemical and physical properties in the interfaces of carbon nanostructures, which are fundamental in carbon nanostructures-related catalytic and diagnostic applications. Graphene quantum dots (GQDs) are representative carbon nanostructures with a large proportion of surface atoms or functional groups^12,13. This enables them to attract research interests in (i) interfacial chemical and physical adsorption (e.g., applications in disease diagnosis/treatment)^14,15 and (ii) interfacial energy transfer (e.g., applications in photo/electro-catalysis^16,17, or photovoltaic conversion^18,19). For example, the photoluminescence of GQDs can be enhanced by the adsorption of nicotinamide adenine dinucleotide, which makes GQDs the differentiator between non-cancerous and cancer cells²⁰. The GQDs can also transfer the energy from light into the generation of protons, which enables GQDs to be the controllable acidic catalyst²¹. Additionally, electron-hole pairs can be created and then separated at the surface of GQDs by light absorption, making GQDs photodetectors²².

It is worth noting that studies based on interfacial adsorption and energy transfer cannot explain proton-based photo-catalytic mechanisms²¹. Kang et al. have uncovered the light-generated 31.62-fold acidity enhancement of carbon quantum dots (CQDs, similar to the sp²–sp³ hybrid structures of GQDs) in aqueous dispersion, which elevates the catalytic performance of CQDs and supplements understanding of the interfacial properties of carbon nanostructures²¹. However, the enhanced proton concentration cannot explain the 10-fold elevation (corresponding to 200–1000-fold acidity enhancement) of CQDs’ catalytic activity. We have also proved that the abundant oxygen-containing groups (–COOH) on GQD surfaces can generate a superacidic microenvironment around GQDs, accelerating the proton exchange near the GQDs²³. Precisely describing the microenvironment change of carbon nanostructures with light induction can facilitate studying the interfaces of carbon nanostructures^24,25,26. Meanwhile, developing microenvironmental characterizations is notable in interfacial chemistry/physics mechanism studies.

Here, a light-induced superacidic microenvironment of GQDs was proposed and elucidated based on the excitation and deactivation processes in fluorescent response and photo-catalysis processes of GQDs. Ultra-low-field (ULF) nuclear magnetic resonance (NMR)²⁷ compatible with a light source was used to in-situ study the proton transport of GQDs in the excited state. The change in acidity originating from the dissociated protons in the interfaces of GQDs can be reflected as the change in NMR relaxation time. It is worth noting that high-field NMR relaxometry with an embedded light source can also be used to study the interfacial changes of GQDs or other materials. The –OH groups are considered the key functional group to bring the light-induced proton dissociation and superacidity to the microenvironment of GQDs (Hammett acidity function, H₀ = –13.40). The thermodynamic calculation result shows that the –OH groups of GQDs have the most considerable acidity enhancement in their microenvironment with light induction (\({{\mathrm{p}}}{K}_{{\text{a}}}^{*}\) = –4.62, which is stronger than that of H₂SO₄). Density functional theory (DFT) simulations also show that the –OH at the edge and the –OH binding to sp² carbon of the GQDs primarily dissociate protons, generating a superacidic microenvironment around GQDs in the excited state. The H₀ associated with the GQD microenvironment is stronger than that of H₂SO₄ (H₀ = –11.93), explaining the high catalytic activity of the sp²–sp³ hybrid carbon nanostructure. Indeed, with light induction, the GQDs’ microenvironment with enhanced acidity in the aqueous phase can be adopted to bind antibodies or polyethylene glycol via the amide or ester bonds, respectively. The mild operation in the aqueous phase also allows for the effective functionalization of GQDs with environment-susceptible biomolecules. Apart from this, selective organo-catalysis with high yield was realized by the light-induced superacidity of the microenvironment of GQDs based on the Friedel-Crafts alkylation/acylation.

Characterization of GQDs

As zero-dimensional graphene fragments, GQDs were prepared from graphene using a modified Staudenmaier method²⁸. The resulting GQDs were highly oxidized, causing them to be well-dispersed in water (Suppl. Figs. 1–3) and possess abundant –OH groups (65.71%) and –COOH groups (Suppl. Fig. 3). The spherical aberration-corrected high-angle annular dark-field (HAADF) scanning transmission electron microscope (STEM) image of GQDs (Fig. 1a) shows the typical honeycomb sp² carbon nanostructure of GQDs. It is worth noting that, due to the presence of –OH and –COOH groups, the sp³ carbon nanostructure is also present in GQDs. Indeed, the signal intensity of the dashed line in Fig. 1a demonstrates the existence of –OH groups (Fig. 1b). Thus, the GQDs are sp²–sp³ hybrid nanostructures. Additionally, the optical band gap of GQDs is 2.57 eV (Suppl. Fig. 4).

a The HAADF-STEM image of GQDs. Scale bar: 0.5 nm. A full HAADF-STEM image can be found in Suppl. Fig. 2. b The integral of the signal intensity for the area indicated by the dashed line in (a). c Illustration of ULF NMR system with the compatibility of the light source. The ULF NMR relaxometry works in an aluminum-shielded chamber. It consists of two coil pairs for generating the static 0.1 mT B₀ field and the excitation field (B₁), the pre-polarization field (B_p) coil, the second-order gradiometer for NMR signal readout inductively coupled to the superconducting quantum interference device (SQUID) in liquid helium cryostat, as well as the data acquisition module and the console (not shown here). During the measurement, 10 mL of the sample is placed beneath the cryostat at room temperature. Light is introduced to the sample through optical fiber. The pulse sequence for measuring T₁ can be found in Suppl. Fig. 5. Illustrations of transiting light-induced interface change of GQDs into the relaxation time change in (d) the ground state and (e) excited state. Hexagons filled with aqua and red represent GQDs in the ground and excited states, respectively. To shorten the T₁ and enlarge the ΔT₁, Gd³⁺ was used throughout the experiments (Suppl. Figs. 6, 7). The Gd³⁺ dissolved in water can accelerate the relaxation of protons. The Gd³⁺ first forms coordinate bonds with oxygen in water, and then protons in the coordinated water exchange with the protons in bulk water. In the ground state, proton exchange occurs between the coordinated and the bulk water. In the excited state, the proton exchange occurs between the GQDs and the bulk water, reducing the relaxation time. The data for T₁ fittings shown here are Test 1 of GQDs aqueous dispersion without and with light induction. Full data are included in Suppl. Fig. 8. Source data are provided as a Source Data file.

Full size image

Evidencing light-induced superacidity of GQDs using ULF NMR

In ref. ²¹. the acidity of carbon nanostructure interfaces was indirectly investigated by measuring the macroscopic changes, which is inadequate to observe the properties of the interfacial structures. Fortunately, the NMR relaxation theory²⁹ provides a route to study the interfacial properties of nanomaterials, which can reflect proton transport and changes in NMR relaxation times. More importantly, the ULF NMR system is compatible with the light source (Fig. 1c), which makes the in-situ study of interfacial properties via the NMR relaxation time under light induction possible. This work uses the longitudinal relaxation time (T₁) of ULF NMR relaxometry to evaluate the change in the acidic microenvironment of interfaces of GQDs (Suppl. Figs. 6 and 7, detailed description in the Methods section). As portrayed in Fig. 1d, e, the interfacial acidity of GQDs in the excited state increases the proton exchange rate and thus shortens the T₁. With the induction of the corresponding UV light (365 nm), the aqueous dispersion of GQDs shows a ΔT₁ [ΔT₁ = (T₁ in ground state, \({T}_{1}^{{\text{Ground}}}\)) – (T₁ in excited state, \({T}_{1}^{{\text{Excited}}}\))] of 345.87 ± 15.23 ms (Suppl. Fig. 8), indicating the acidity changes in the microenvironment of GQDs in the excited state. Such an acidity change can also be evaluated by thermodynamic computing as follows^30,31,32:

where \({{\mathrm{p}}}{K}_{{\text{a}}}^{*}\) and \({{\mathrm{p}}}{K}_{{\text{a}}}^{0}\) (8.60) are the acid dissociation constants of GQDs in the excited and ground states, respectively, ∆E_GQDs–O^– (2.57 eV, Suppl. Fig. 4a, b) is the energy difference between GQDs–OH and GQDs–OH^* (excitation state), ∆E_GQDs–OH (2.91 eV, Suppl. Fig. 4c, d) is the energy difference between GQDs–OH and GQDs–O^* (excitation state), R is the gas constant with a value of 8.31 J mol^–1 K^–1, T is the temperature (298.15 K). Therefore, the \({{\rm{p}}}{K}_{{{\rm{a}}}}^{*}\) of GQDs is calculated to be –4.62, which is stronger than that of H₂SO₄ (pK_a = –3) and is consistent with the NMR relaxometry result (Suppl. Fig. 9).

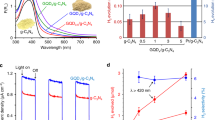
Due to the complexity of the interfacial functional groups of GQDs, the light-induced acidity in the excited state of GQDs needs to be clarified. Therefore, GQDs with similar band gaps but different surface structures were synthesized to evaluate the light-induced super-acidity of GQDs interfaces. As the type of functional groups of GQDs is the basis for generating a response under light induction, GQDs with different functional groups (–OH, –COOH, –C–O–C–, –CHO, –NH₂, –N(C)₃, and –NH–C–, Suppl. Figs. 10 and 11, Suppl. Tables 1 to 4) are used to clarify the functions of surface structure in the acidity of excitation state of GQDs. Those GQDs with different functional groups show distinct T₁ changes when excited by light induction (Fig. 2a). The ΔT₁ values of –OH, –COOH, –C–O–C–, –CHO, –NH₂, –N(C)₃, and –NH–C– functionalized GQDs are 345.87 ± 15.23, 205.60 ± 19.43, 131.65 ± 35.96, 78.17 ± 6.29, 43.39 ± 14.12, –5.78 ± 8.23, and 4.23 ± 7.96 ms, respectively. Among the GQDs, –OH functionalized GQDs show the largest ΔT₁ with light induction, indicating that the presence of –OH in the GQD surface structure is one potential factor to enhance the acidity with light induction. To prove this point further, GQDs with different amounts (9.91%–86.21%) of –OH were prepared (Suppl. Figs. 11 and 12, Suppl. Tables 1 and 2). With the increasing proportion of –OH in oxygen-containing groups of GQDs and the I_D/I_G value, ΔT₁ tends to increase, reaching saturation at 361.62 ms (Fig. 2b). Such a result indicates a high proportion of –OH in oxygen-containing groups of GQDs as well as the high defect of GQDs bring high acidity in the microenvironment of GQDs with light induction, leading to a large ΔT₁.

a Difference between T₁ values (ΔT₁) of GQDs with different functional groups without and with light induction. ΔT₁ = (T₁ in the ground state, \({T}_{1}^{{\text{Ground}}}\)) – (T₁ in the excited state, \({T}_{1}^{{\text{Excited}}}\)). b The ΔT₁ values and I_D/I_G values (ratios of D peak and G peak intensities acquired from Raman spectra) of GQDs with different hydroxy contents without and with light induction. c The relation between K of GQDs aqueous dispersion and D₂O concentration in the solvent. K = (\({T}_{1}^{{\text{Ground}}}\) – \({T}_{1}^{{\text{Excited}}}\)) / \({T}_{1}^{{\text{Ground}}}\). d The H₀ comparison of different superacids. e The influence of temperature on Gd³⁺ aqueous solution without light induction as well as GQDs with and without light induction. f The influence of light intensity on the ΔT₁ of GQDs. g The influence of KCl concentrations on ΔT₁ of GQDs. h The influences of ions and anions (1 mmol L^–1) on T₁ of GQDs without and with light induction. The concentrations of GQDs and Gd³⁺ used in these experiments were 10 mg L^–1 and 0.05 mmol L^–1, respectively. The hydroxy-functionalized GQDs were used in (c–h). Error bars indicate the standard deviation (SD) of three replicates of each test. The lines connecting the dots represent trends in the data. Source data are provided as a Source Data file.

Full size image

To clarify the origins of the change in T₁ of aqueous dispersion of GQDs with light induction, GQDs were dispersed in a solvent consisting of H₂O and D₂O. As shown in Suppl. Fig. 13, T₁ values increased with the concentration of D₂O in the solvent, regardless of light induction. This increase derives from the reduced number of exchangeable protons, which transmits the NMR relaxation of Gd³⁺ to the solvent, resulting in a decreased proton-exchange rate. To distinguish the T₁ increase caused by D₂O in a solvent and the T₁ decrease caused by light induction, a variable K (0 ≤ K < 100%) is introduced to erase the influence. K = 0 represents light induction having no influence on changes in T₁: a large K can be generally interpreted as a strong response under light induction. Figure 2c shows the relationship between K of GQDs in dispersion and the D₂O concentration in solvent. K values are 61.81%, 45.63%, 41.08%, and 36.12% when the D₂O concentrations in solvent are 0, 20, 40, and 60 wt.%, respectively, indicating that the influence of light induction becomes weaker when the amounts of exchangeable protons decrease. Therefore, light induction can enhance the proton exchange and the acidity of the microenvironment of GQDs and then shorten T₁. As a comparison, Fig. 2d lists the H₀ values of some superacids. The GQDs with light induction have an H₀ of –13.40 (H₂SO₄ as the reference), which is lower than that of H₂SO₄ and is comparable to those of superacids. It should be noted that the acidity in the microenvironment of GQDs is switchable. When the light induction is ON, the acidity is enhanced. Otherwise, the acidity is recovered to the level of the ground state.

The light-induced superacidity of GQDs in different conditions (including temperature, radiation intensity, and presence of ion/anion) was studied. As plotted in Fig. 2e, the difference between T₁ values of GQDs aqueous dispersion in the ground state and excited state is inclined to be large with the sample temperature increase, which is attributed to the increased degree of dissociation of solvent water. Simultaneously, the aqueous dispersion of GQDs possesses superacidity (ΔT₁ = 257.89 ms) with comparative low light intensity (50.3 mW cm^–2, Fig. 2f). Additionally, the ΔT₁ of the GQD aqueous dispersion tends to increase with increasing light intensity, meaning the superacidity of the microenvironment of GQDs has a positive correlation with light intensity. More importantly, –OH is a stable group, so no coordination will occur when the –OH functionalized GQDs are dispersed in IA group ions (Na⁺, K⁺) or simple anions (Cl^–, Br^–, I^–, SO\(\normalsize _4^{2-}\), NO\(\normalsize _3^-\)) containing solvent, which results in the considerable superacidity with a high ions/anions concentration (Fig. 2g, h). With the KCl concentration of 1 mmol L^–1, the GQDs still have a ΔT₁ of 247.12 ms. These properties enable the applications of GQDs in a sensitive reaction system (e.g., binding to protein) under mild conditions (room temperature, 298.15 K; low light intensity, 50.3 mW cm^–2; buffer system with different ions and anions).

Dynamics of GQDs’ interfaces in the excited state

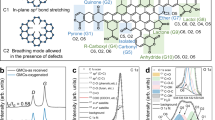
The –OH group has been experimentally proven to generate superacidity around the interfaces of GQDs in the excited state, as confirmed by classical thermodynamic calculations. To elucidate the interfacial thermodynamic mechanisms of –OH on GQDs in the ground and excited states, simulations with the ab initio level density functional theory (DFT) package CP2K/Quickstep^33,34 were performed. It is worth noting that the position and distribution density of –OH groups on GQDs also need to be considered. Additionally, the diversity of carbon nanostructures allows –OH groups to exist in different forms on GQDs, including phenolic and alcoholic –OH. Therefore, GQDs with different chemical structures (GQDs 1 to GQDs 7, Suppl. Fig. 14) were constructed initially to evaluate the proton exchange behavior of –OH groups on GQDs in the ground and excited states. The carbon core of all GQDs was set to contain 80 carbon atoms. To clarify the proton exchange behavior of GQDs with different quantities of –OH groups, the quantities of –OH groups (including different types of –OH) for GQDs 1 to GQDs 7 were set as 0, 5, 7, 5, 6, 8 and 10, respectively (Suppl. Fig. 14). To assess the effects of –OH positions (edge/lattice) on proton exchange behavior in the following simulations, GQDs 1 to GQDs 7 were set to have different edge –OH ratios of 0, 60.00%, 71.42%, 0, 33.33%, 50.00%, and 60.00%, respectively (Suppl. Fig. 14). To evaluate the functions of different forms of –OH (phenolic/alcoholic) on proton exchange behavior in the following simulations, GQDs 1 to GQDs 7 were set to possess different phenolic –OH ratios of 0, 60.00%, 71.42%, 60.00%, 50.00%, 62.50%, and 70.00%, respectively (Suppl. Fig. 14).

The superacidic microenvironment of GQDs induced by light induction was observed in the foregoing experiments by using T₁ to reflect the acidity of the microenvironment of GQDs. To simulate the proton exchange behaviors in the excited state, the bandgaps of GQDs 1 to GQDs 7 need to be determined. By using DFT calculations, the excited states of GQDs 1 to GQDs 7 are 1.83, 1.55, 1.51, 1.04, 1.13, 1.04, and 0.98 eV, respectively. The proton exchange processes were then simulated based on the optimized structures and the corresponding bandgaps.

The results of dynamic simulations show that all GQDs (except for GQDs 1) exhibit a high tendency to dissociate protons in the excited state (Suppl. Movies 1–7, Fig. 3a). Such a propensity is evident not only in the quantity of –OH groups dissociating protons but also in the time required to reach dissociation equilibrium. The equilibrium time is defined as when the maximum number of protons dissociation occurs, and no proton dissociation occurs within 0.5 ps. In the excited state, the ratios of proton-dissociating –OH groups are 100%, 85.71%, 40.00%, 16.67%, 62.50%, and 60.00% in GQDs 2 to GQDs 7, respectively (Fig. 3a). By contrast, only the –OH groups in GQDs 6 and GQDs 7 dissociate protons with the proportions of 12.50% and 10.00% in ground state, respectively. Due to the significant difference in electronegativity between the oxygen and hydrogen atoms, the O–H bond is a typical polar bond. Such a polarity results in an unequal charge distribution, with the oxygen atom being more electronegative (δ^–) and the hydrogen atom more electropositive (δ⁺). The degree of polarization of the O–H bond can be adjusted by altering the charge disparity, which in turn affects the bond’s energy. In general, an enhanced polarization decreases the O–H bond strength and thus reduces the activation energy barrier. By performing the atomic partial charge around the –OH of GQDs 1 to GQDs 7 via Bader’s definition, a significant alternation in the average partial charges of hydrogen and oxygen atoms in phenolic –OH (sp² –OH) is revealed once the light induction is applied. Specifically, the average partial charge on hydrogen in sp² –OH increases from 0.82 – 0.88 e, and that on oxygen in sp² –OH deepens from –1.16 to –1.48 e (Suppl. Fig. 15, Suppl. Table 5). In contrast, the average partial charges of oxygen and hydrogen in alcoholic –OH (sp³ –OH) of GQDs 1 to GQDs 7 remain unchanged. The average charge variation in sp² –OH leads to the enhancement of its polarization. Therefore, the activation energy barrier is largely reduced in the excited state, facilitating the formation of coordination bonds between protons and water molecules. Consequently, compared to the ground state, a substantial enhancement in the proton dissociation rate is observed when the GQDs are excited by light induction, highlighting the role of –OH groups in facilitating proton dissociation.

a A bar graph showing the quantities of different –OH groups in GQDs 2 to GQDs 7 in different states. b The proton dissociation of GQDs 7 at different simulation times in the ground and excited states. The gray frameworks, red atoms, and white atoms represent carbon frameworks, oxygens, and hydrogens in GQDs, respectively. The blue atoms represent the oxygen in proton-dissociated –OH. The dynamics of GQDs 7 in the ground and excited states can be found in Suppl. Movie 7. c The proton dissociation ratios of different –OH groups in GQDs 2 to GQDs 7 in excited states. The dissociation ratio was calculated as the (dissociated –OH groups) / (total –OH groups) at a specific simulation time. For each kind of –OH group, the dissociation ratio was dependently calculated. In the graphs of GQDs 2 and GQDs 3, the overlapped curves of edge –OH are the same as those of phenolic –OH, and the overlapped curves of lattice –OH are the same as those of alcoholic –OH. d The average proton dissociation rate of GQDs 2 to GQDs 7 in ground and excited states. e The average proton dissociation rate of edge –OH and lattice –OH of GQDs 2 to GQDs 7 in the excited state. f The average proton dissociation rate (\(\bar{r}\)) of phenolic –OH and alcoholic –OH of GQDs 2 to GQDs 7 in the excited state. Source data are provided as a Source Data file.

Full size image

The dissociation equilibrium time is faster in the excited state than in the ground state (Suppl. Movies 1–7). Typically, GQDs 7 reaches the dissociation equilibrium at 10 ps in the ground state, whereas it achieves dissociation equilibrium in the significantly shorter time of 5 ps in the excited state (Fig. 3b). The kinetic differences in the dissociation of protons in GQDs with different types of –OH (including edge –OH, lattice –OH, phenolic –OH, and alcoholic –OH) are further discussed in the excited state. Time-dependent proton dissociation ratios of different –OH dissociations are demonstrated for discussion. As shown in Fig. 3c, the proton dissociation ratios of lattice –OH and edge –OH reveal significant differences when GQDs are excited. The proton dissociation ratios of edge –OH in GQDs 2 to GQDs 3, and GQDs 5 to GQDs 7 are 100%, 100%, 50.00%, 75.00%, and 83.33% within 5 ps, respectively. In comparison, the proton dissociation ratios of lattice –OH in GQDs 2 to GQDs 3, and GQDs 5 to GQDs 7 are 100%, 100%, 0%, 50.00%, and 25.00%, respectively. This finding indicates that the edge –OH of GQDs is more prone to dissociate protons in the excited state, which suggests that the edge –OH may be the critical factor in generating the superacidity in the microenvironment of GQDs. Moreover, the proton dissociation ratios of phenolic –OH in GQDs 2 to GQDs 7 are 100%, 100%, 66.67%, 33.33%, 80.00%, and 85.71%, respectively. As a comparison, the proton dissociation ratios of alcoholic –OH in GQDs 2 to GQDs 7 are 100%, 100%, 0%, 0%, 33.33%, and 0%, respectively. Such results indicate that phenolic –OH is susceptible to generating protons and generating the superacidic microenvironment, which positively accelerates the proton exchange around these GQDs. Additionally, the dissociated protons keep exchanging with the surrounding water protons and binding with the oxygen in GQDs, thereby expressing the fluctuation in the proton dissociation ratio. The increased proton exchange between dissociated protons and the water around GQDs in the excited state also reduces the T₁ of the GQDs aqueous dispersion with light induction.

The defects are crucial for the proton dissociation of GQDs. Proton dissociation processes are generally associated with the phenolic –OH and occasionally occur at the alcoholic –OH (Suppl. Movies 2–7). However, proton dissociation is never observed at –CH₂ sites of GQDs (Suppl. Fig. 16). Such behavior can also be elucidated by analyzing the average partial charges of alcoholic –OH and –CH₂ in GQDs 2 to GQDs 7 via Bader’s definition in both ground and excited states. As shown in Suppl. Fig. 15, the average partial charges of the hydrogens remain constant for alcoholic –OH (0.76 – 0.74 e) and –CH₂ (0.10–0.09 e) upon excitation. By contrast, the average partial charges of the hydrogens in phenolic –OH of GQDs (0.82 – 0.88 e) increase. Therefore, the phenolic –OH of GQDs governs the proton dissociation upon excitation instead of the defects.

To intuitively assess the proton dissociation rate of –OH groups in GQDs, the average proton dissociation rate (\(\bar{r}\)) is defined below:

where N is the number of dissociated protons at the time of dissociation equilibrium, and t is the time the proton dissociation takes to the equilibrium. The equilibrium time is defined as when the maximum number of protons dissociation occurs, and no proton dissociation occurs within 0.5 ps. For a specific type of –OH, t is determined as the equilibrium time required to dissociate the specific –OH.

As shown in Fig. 3d, \(\bar{r}\) values of GQDs 6 and GQDs 7 are 0.17 and 0.21 ps^–1 in the ground state, respectively. Other GQDs do not dissociate protons in the ground state. However, the \(\bar{r}\) values of GQDs 2 to GQDs 7 in the excited state are 3.25, 3.75, 1, 0.87, 2.80, and 1.82 ps^–1, respectively. These data show the proton dissociation rate of GQDs is higher than that in the ground state, ensuring that the super-acidity of GQDs can be switched on under light induction and turned off by removing the light. Such behavior is significant in GQDs-related applications. The superacidity of GQDs brought by the dissociated protons of –OH groups can be temporarily excited via light induction and then bind to other molecules. Ulteriorly, the \(\bar{r}\) values of lattice –OH of GQDs 2, GQDs 3, GQDs 5, GQDs 6, and GQDs 7 decrease to 42.32%, 62.95%, 0%, 81.59%, and 99.48% of edge –OH, respectively (Fig. 3e), indicating that –OH at the edge of GQDs shows higher or equivalent proton dissociation rate compared to that of –OH at the lattice of GQDs. It is worth noticing that the reduction in \(\bar{r}\) of lattice –OH compared to that of edge –OH is attributed to the differences in the chemical environments of lattice –OH. As depicted in Suppl. Fig. 14, the lattice –OH of GQDs 4 to GQDs 7 includes phenolic –OH and alcoholic –OH. Therefore, the influences of phenolic –OH and alcoholic –OH are discussed as follows: the \(\bar{r}\) values of alcoholic –OH of GQDs 2 to GQDs 7 are decreased to 42.32%, 62.95%, 0%, 0%, 30.60%, and 99.48% of that of phenolic –OH (Fig. 3f), respectively, which conveys that the phenolic –OH of GQDs has a higher proton dissociation rate compared to that of alcoholic–OH of GQDs. The –OH at the edge and phenolic –OH of GQDs with high proton dissociation rate offer the binding sites of GQDs in the excited state when connecting to other molecules.

Applications of GQDs with light-induced superacidity

With the help of light-induced superacidity, GQDs possess feasible functionalization features and high catalytic performances. The functional groups (e.g., –OH, –COOH) of GQDs can be temporarily activated and then bind with other molecules via esterification or amidation with light induction. The functionalization of GQDs can be thus realized at room temperature without after-treatment or purification, and the time consumption of functionalization can be effectively reduced. The functionalization of GQDs can be molecules of different sizes, including small organic molecules, polymer chains, and bioactive macromolecules.

The pH decrease in cancer cells serves as one of the hallmarks of cancer^35,36, which can be used to develop fluorescence probes to detect cancer cells³⁷. GQDs with tunable fluorescence properties have been widely applied in pH-responsive cancer detection^38,39,40,41. As shown in Fig. 4a, structures 1 to 8 were used to synthesize a series of pH-sensitive probes using the light-induced superacidity of GQDs. Light induction (365 nm, 80 mW cm^–2, 20 min) was applied to connect GQDs and structures 1 to 8 at a ratio of 30 mg: 0.1 mmol, respectively. The resulting pH-sensitive probes are named GQDs-i (i = 1 to 8). As shown in Fig. 4b, the fluorescence of GQDs-i can be quenched in aqueous dispersion with different pH values (Suppl. Fig. 17). The fluorescence of GQDs-5 can be quenched in an environment with pH = 7 but shows high stability in various environments (Suppl. Fig. 18, including temperature; K⁺; Na⁺; Cl^–; H₂O₂; hydroxyl radical, ∙OH; superoxide dismutase, SOD; and nicotinamide adenine dinucleotide, NADH), which is suitable for differentiating cancer (pH = 6, B16F10) and non-cancerous (pH = 7, HaCaT) cells (Fig. 4c, d). After the incubation, most of GQDs-5 were taken up in the cytoplasm of cancer cells (Suppl. Figs. 19 and 20) and showed no obvious toxicity towards cancer and non-cancerous cells (Suppl. Fig. 20). Although the above results indicate the potential applications of GQDs-5 in differentiating cancer and non-cancerous cells in vitro, the optimizations of in vivo concentrations, metabolic kinetics, and emission wavelength of GQDs-5 should be conducted prior to further in vivo applications of GQDs-5.

a Structures of small organic molecules used for synthesizing pH-sensitive probes. b The photographs of pH-sensitive GQDs-i (i = 1 to 8) at different pH values. Scale bar: 3 cm. Confocal images of the coculture system of (c) B16F10 and (d) HaCaT incubated (200 μg mL^–1 for 48 h) with different pH-sensitive GQDs-i (i = 1 to 8). Scale bar: 50 μm. e Synthesis of the probe for MRS utilizing light induction to connect GQDs-PEG₈-Gd and Ab. Hexagons filled with aqua represent GQDs. Circles filled with lavender represent Ab. f The T₁ values of the probe synthesized with light induction for different times. The line connecting the dots represents the trend of the data. g Detection of S. aureus with different concentrations using the probe. h The linear relation between T₁ and the logarithm of S. aureus concentration. i Detection of S. aureus in urine samples. Error bars in (g), (h), and (i) denote the SD of three replicates of each test. The significance levels are shown as: n.s., no significance, P > 0.05; ^*P < 0.05; ^**P < 0.01; ^***P < 0.001; ^****P < 0.0001. j Statistics of T₁s measured from the negative and positive sample groups with the spike numbers of 10 and 20, respectively. The lines in the box and boxes represent the mean values and 25–75% distributions, respectively. Error bars indicate the SD of T₁ values in the two groups. Source data are provided as a Source Data file.

Full size image

GQDs with switchable acidity can also be used to construct magnetic resonance imaging (MRI) contrast agents by connecting GQDs with polymer chains under light induction (Suppl. Figs. 21, 22). The light induction time affects the longitudinal relaxivity of the contrast agents due to the binding amount of polymer chains (octaethylene glycol, PEG₈) per GQDs (Suppl. Figs. 23 to 29). The resulting contrast agents with high longitudinal relaxivity of 45.67 ± 0.63 L mmol^–1 s^–1 show low biotoxicity and high biocompatibility (Suppl. Figs. 30 to 32), which enables the contrast agents to be used in the in vivo MRI of nude mice (Suppl. Fig. 33).

The functionalization of GQDs with bioactive macromolecules usually requires tedious procedures, and the bioactivity of molecules should be retained throughout the procedure. As mentioned before, the GQDs exhibit superacidity in the microenvironment with a comparatively weak light intensity and in the anion/ion system. Therefore, the GQDs can bind antibodies as the probe of the magnetic relaxation switch (MRS) in a mild environment. As shown in Fig. 4e, the probe consists of GQDs-PEG₈-Gd, and antibodies (Ab) against Staphylococcus aureus (S. aureus) can be constructed with light induction. Compared to the EDC/NHS chemistry (Suppl. Fig. 34), the light-induced probe construction utilizes light to activate the groups of GQDs instead of the chemicals, which shows high maneuverability (laborious after-treatment is needless). More importantly, the time taken when using the light-induced method is reduced from 5 to 0.5 h compared to the EDC/NHS chemical method. As shown in Fig. 4f, the T₁ of the mixture of GQDs-PEG₈-Gd (0.02 mmol L^–1) and Ab (1 mg L^–1) decreases with the increase of the light-induction time and finally settles at around 345 ms (corresponding to a light-induction time of 25 min). The decreased T₁ indicates that GQDs-PEG₈-Gd is connected to Ab and leads to the reduced spacing between GQDs-PEG₈-Gd nanoparticles. Meanwhile, the combination ratio of Ab to GQDs-PEG₈-Gd intensively affects the average distance between GQDs-PEG₈-Gd nanoparticles and, thus, the T₁ of the probe. Suppl. Fig. 35 reveals the optimal combination ratio of Ab to GQDs-PEG₈-Gd, i.e., 1 mg of Ab per 0.2 mmol of GQDs-PEG₈-Gd.

With the prepared probe, the detection of S. aureus-containing samples can be conducted (Suppl. Figs. 36 to 38) using ULF NMR relaxometry. As depicted in Fig. 4g, when the S. aureus concentrations are 0 (blank), 1, 10, 10², 10³, 10⁴, 10⁵, and 10⁶ CFU mL^–1, the measured T₁ values of the sample are 341.33 ± 5.15, 352.58 ± 4.97, 360.85 ± 5.44, 427.25 ± 5.66, 474.04 ± 8.18, 524.14 ± 11.03, 575.21 ± 14.78, and 616.14 ± 9.39 ms, respectively. A linear relationship can be found in T₁ and the logarithm of S. aureus concentration (Fig. 4h) as y = 51.24 x + 316.78 (adjusted R² = 0.9918). The limit of detection (LOD) is estimated as 6 CFU mL^–1, which is sensitive compared to the reported MRS assays for pathogen detection^42,43,44,45. Additionally, the MRS assay shows guaranteed anti-interference performance (Suppl. Fig. 39), stability, and specificity (Suppl. Fig. 40).

Under these conditions, MRS was used to screen clinical samples collected from the hospital. Samples 1–10 and samples 11–30 are determined as negative and positive by the MRS, respectively (Fig. 4i). As an evaluation, the clinical method was also used to assay the samples. Samples 1–10 and 11–30 show the same result compared to that of MRS, indicating the recovery of MRS is 100%. Additionally, the positive group shows a significant difference in T₁ from the negative group (Fig. 4j), revealing that the MRS can differentiate positive samples from negative ones.

Finally, electrophilic aromatic substitution catalyzed by the light-induced superacidity of GQDs is realized. As a typical electrophilic aromatic substitution, Friedel-Crafts alkylation is used to verify the catalytic reactivity of GQDs. As shown in Fig. 5a, the carbenium ion is produced with the superacidity of GQDs under light induction. Then, the carbenium ion reacts with benzene via electrophilic aromatic substitution. To evaluate the performances of Friedel-Crafts alkylation, bromoethane and benzene were selected as the substrates. The benzene concentration decreases when the reaction time increases (Fig. 5b). Such a result indicates that GQDs can generate photo-induced acid²¹. With photo induction, an –OH group on the surface of GQDs dissolves in trace water to generate a free proton (H₃O⁺). Next, another proton is released from the reaction of the C = O group with H₃O⁺. An intermediate with an epoxy group is obtained after the O in C = O linked with HO⁻ by supramolecular interaction in a reversible way under light induction. Additionally, the reaction between bromoethane and benzene shows the character of a first-order reaction with a reaction rate constant k of 0.32 min^–1 (linear fit, adjusted R² = 0.99475). The product of the reaction in Fig. 5b is ethylbenzene (Suppl. Fig. 41).

a Scheme of Friedel-Crafts alkylation. R and X represent hydrocarbyl and halogen, respectively. b The logarithm of C_t/C₀ at different reaction times when benzene and chloroethane were reacted using light-induced GQDs as the catalysts. C₀ and C_t are benzene concentrations at the unreacted time and specific time t during the reaction, respectively. Error bars represent the SD of three repetitive tests. The negative slope k is obtained from the linear fit. c The k values of Friedel-Crafts alkylation of benzene and chloroethane using different catalysts. The contents of reactant (benzene), product (ethylbenzene), and by-products (diethyl benzene, triethyl benzene) during the Friedel-Crafts alkylation of benzene and chloroethane using (d) AlCl₃ and (e) light-induced GQDs as the catalysts. Et represents ethyl. The areas with different colors represent the contents of reactant, product, and by-products with the structures marked along the areas. f The k values and product yields of Friedel-Crafts alkylation adopting GQDs as the catalysts and different bromides (propyl bromide, 2-bromopropane, tert-butyl bromide, and benzyl bromide) as reactants. The structures are the products of Friedel-Crafts alkylation. Data in this figure were derived from experiments conducted at 298.15 K. Source data are provided as a Source Data file.

Full size image

Different catalysts were used to catalyze the Friedel-Crafts alkylation involving benzene and bromoethane for comparison. As listed in Fig. 5c, the k values of reactions using BF₃, light-induced GQDs, AlCl₃, FeCl₃, H₂SO₄, and H₃PO₄ as the catalysts are 0.33, 0.32, 0.20, 0.20, 0.10, and 0.07, respectively. The GQDs show higher catalytic reactivity than classical catalysts (AlCl₃, FeCl₃, H₂SO₄, and H₃PO₄). Although the GQDs show an equivalent k to that of BF₃ when catalyzing the Friedel-Crafts alkylation, the GQDs are safer than the toxic BF₃. Additionally, the GQDs have an enhanced k value with increasing temperature and exhibit a high k value at mild temperatures (Suppl. Fig. 42). The stability of light-induced GQDs is also high (Suppl. Fig. 43).

Compared to the classical catalysts of Friedel-Crafts alkylation, GQDs have a large steric hindrance, which suppresses the alkylation side reactions. Figure 5d,e compares the products of ethylbenzene alkylation using AlCl₃ and light-induced GQDs as catalysts. When AlCl₃ catalyzes the Friedel-Crafts alkylation, the content of the product (ethylbenzene) increases with increasing the reaction time, and the two by-products (diethyl benzene and triethyl benzene) are produced at 6 and 20 min separately after initiation of the reaction. At 60 min after the reaction began, the contents of benzene, ethylbenzene, diethyl benzene, and triethyl benzene are 13.55%, 44.69%, 31.32%, and 10.44%, respectively. The reaction is inefficient within 60 min and produces several by-products. When light-induced GQDs are used as the catalysts, the product (ethylbenzene) reaches 98.91% after 34 min the reaction begins. The undesired by-product is diethyl benzene with a content of 1.10% at the same moment (i.e., 34 min). Furthermore, the universality of GQDs in catalyzing the Friedel-Crafts alkylation was studied. As shown in Fig. 5f, the GQDs can catalyze the Friedel-Crafts alkylation between benzene and different bromides. The products are n-propylbenzene, isopropylbenzene, tert-butylbenzene, and diphenylmethane, respectively (Suppl. Figs. 44 to 47). The alkylation reactions show both a high reaction rate constant and product yield.

In summary, with the help of ULF NMR compatible with a light source, the increased proton dissociation and the resulting change in the acidity of the microenvironment of GQDs has been studied in-situ. Compared to the methods studying the macroscopic dynamics in bulk water, the NMR relaxometry can provide information on proton changes via the T₁. The ULF NMR system is free of superconducting magnets, which enables it to be compatible with other equipment, such as that used in magnetoencephalography⁴⁶. Especially, the ULF NMR system is compatible with a light source and thus provides the tool to observe the proton changes in an excited state, which benefits the in-situ, non-contact, and real-time studies of the interfacial dynamics and photocatalytic reactions during the experiments.

The –OH functionalized GQDs show the feature of a super-acid (H₀ = –13.40) in their microenvironment. The thermodynamic calculation reveals that the –OH groups of GQDs undergo the most considerable acidity enhancement in their microenvironment with light induction (\({\text{p}}{K}_{{\text{a}}}^{*}\) = –4.62, which is stronger than that of H₂SO₄). Dynamic simulations confirm the edge –OH, as well as the phenolic –OH of GQDs, mainly produce the protons around GQDs and enhance the acidity of the microenvironment of GQDs in the excited state. The super-acid state being limited in the microenvironment enables GQDs to bind small organic molecules as the pH-sensitive probes to differentiate tumor and non-cancerous cells, connect polymer chains as the MRI contrast agents, connect bioactive macro molecules as the MRS probes to sense S. aureus, and catalyze the Friedel-Crafts alkylation with the comparable performances of AlCl₃.

The observations of protons produced from the GQDs’ interfaces not only facilitate the study of interfacial properties of light-induced sp²–sp³ carbon nanostructure but also provide a tool to learn the interfaces of catalysts in photocatalysis. This finding will also promote the applications of GQDs.

The “top-down” approach used to synthesize GQDs in this study introduces significant impurities during the reactions, which makes the purification processes tedious. When simulating the proton exchange of GQDs, the structural models are complex to match perfectly against the structures of GQDs synthesized from experiments, which leads to a qualitative result with no mathematical correlation between the simulated proton dissociation time and T₁ of the sample.

Materials

Graphene powder, reduced graphene oxide powder, alumina inorganic membrane (220 nm), and dialysis bags (3500 g mol^–1) were procured from CASYUEDA Materials Technology Co., Ltd. (Shanghai, China) and used in their as-received state. Dimethyl carbonate (99.9%), sodium borohydride (98%), m-phenylenediamine (99.5%), diethylamine (99.5%), p-phenylenediamine (99%), 4-N-methylbenzene-1,4-diamine (97%), 4-N,4-N-dimethylbenzene-1,4-diamine (97%), 4-N,4-N-diethylbenzene-1,4-diamine (97%), 4-N,4-N-diphenylbenzene-1,4-diamine (97%), 4-N,4-N-di-tert-butylbenzene-1,4-diamin (97%), hydroquinone (99.5%), SOD (from bovine erythrocytes), NADH (98%), PEG₈ (98%), benzene (99.8%), bromoethane (99%), propyl bromide (98%), 2-bromopropane (99%), tert-butyl bromide (98%), and benzyl bromide (98%) were purchased from Aladdin Co., Ltd. (Shanghai, China) and used without further purification. D₂O (99.9%), H₂O₂ (30 wt.%), ethyl alcohol (99.5%), H₂SO₄ (98%), HNO₃ (68%), H₃PO₄ (85%), NaClO₃ (99%), NaOH (98%), KCl (99.5%), NaCl (99.5%), BF₃ (99.99%), AlCl₃ (99.5%), and FeCl₃ (99.9%) were also purchased from Aladdin Co., Ltd. (Shanghai, China) and used without further purification. The anti-Staphylococcus aureus (S. aureus) antibody (ab20920) was purchased from Abcam Plc. Deionized (DI) water (resistivity approximately 18.2 MΩ cm at 298 K) was obtained using a Milli-Q system and used throughout all the experiments.

Synthesis of GQDs

GQDs (also named GQDs-A) were synthesized using a modified Staudenmaier method²⁸. Briefly, graphene oxide powder (4 g) was added into concentrated H₂SO₄ (150 mL) and (80 mL) mix solution with stirring at 288.15 K for 2 h. NaClO₃ (40 g) aqueous solution was then added dropwise, and the temperature was kept at 276.15 K. Thereafter, the mixture was stirred at 288.15 K for 5 h (oxidation time). The reaction was terminated by adding deionized water (80 mL). Next, the pH of the solution was neutralized to 7 by adding NaOH before filtration by filter paper and alumina inorganic membrane with 220 nm pores. The obtained light-yellow filtrate was dialyzed in a 3500 g mol^–1 dialysis bag against deionized water to remove the remanent salt. The GQD solution was concentrated and then lyophilized into powder.

The –COOH functionalized GQDs (GQDs-B) were synthesized using GQDs-A and H₂O₂. Initially, 10 mg of GQDs-A powder and 0.01 mmol of H₂O₂ were dissolved in 10 mL of DI water for hydrothermal treatment (393.15 K, 3 h). Subsequently, the resulting product underwent sequential filtration using filter paper and an alumina inorganic membrane with 220 nm pores. The obtained filtrate was then dialyzed in a 3500 g mol^–1 dialysis bag against DI water for times to remove any unreacted molecules. Finally, the GQDs-B solution was concentrated and then lyophilized into powder.

The –C–O–C– functionalized GQDs (GQDs-C) were synthesized using GQDs-A and dimethyl carbonate. Initially, 10 mg of GQDs-A powder and 1 mL of dimethyl carbonate were dissolved in 10 mL of toluene for solvothermal treatment (393.15 K, 12 h). After that, the solvent of the obtained mixture was replaced by DI water. Subsequently, the resulting product underwent sequential filtration using filter paper and an alumina inorganic membrane with 220 nm pores. The obtained filtrate was then dialyzed in a 3500 g mol^–1 dialysis bag against DI water for times to remove any unreacted molecules. Finally, the GQDs-C solution was concentrated and then lyophilized into powder.

The –CHO functionalized GQDs (GQDs-D) were synthesized using GQDs-A and sodium borohydride. Initially, 10 mg of GQDs-A powder and 1 mg of sodium borohydride were dissolved in 10 mL of toluene for solvothermal treatment (393.15 K, 12 h). After that, the solvent of the obtained mixture was replaced by DI water. Subsequently, the resulting product underwent sequential filtration using filter paper and an alumina inorganic membrane with 220 nm pores. The obtained filtrate was then dialyzed in a 3500 g mol^–1 dialysis bag against DI water for times to remove any unreacted molecules. Finally, the GQDs-D solution was concentrated and then lyophilized into powder.

The –NH₂ functionalized GQDs (GQDs-E) were synthesized using m-phenylenediamine. Initially, 1.0 mmol of m-phenylenediamine was dissolved into 10 mL of ethyl alcohol for solvothermal treatment (433.15 K, 24 h). Following this, the solvent of the resulting mixture was replaced by DI water and then sequentially filtered by the filter paper and alumina inorganic membrane with 220 nm pores. Next, the obtained filtrate underwent dialysis in a 3500 g mol^–1 dialysis bag against DI water for times to eliminate any unreacted molecules. Finally, the GQDs-E solution was concentrated and then lyophilized into powder.

The method for synthesizing –N(C)₃ functionalized GQDs (GQDs-F) was similar to that of GQDs-E, the variations lay in the solvothermal conditions, which were adjusted to 513.15 K for 168 h.

The method for synthesizing –NH–C– functionalized GQDs (GQDs-G) was similar to that of GQDs-E, the variations lay in the solvothermal conditions, which were adjusted to 453.15 K for 72 h.

The method for synthesizing –OH functionalized GQDs with different –OH content (GQDs-H) was similar to that of GQDs-A, the only difference lay in the oxidation time, which was set as 4.5 h.

The –OH functionalized GQDs with different –OH content (GQDs-I) was similar to that of GQDs-A, the only difference lay in the oxidation time, which was set as 6 h.

Apparatus

The transmission electron microscopy (TEM), high-resolution TEM, and spherical aberration-corrected HAADF-STEM images were captured using JEM-ARM300F (JEOL Ltd.) operating at a voltage of 80 kV. The X-ray photoelectron spectroscopy (XPS) spectra were obtained with an Escalab 250Xi (Thermo Fisher Scientific, Inc.). The powder X-ray diffraction (PXRD) spectrum of GQDs was acquired using a D8 ADVANCE (Bruker) with an operating voltage of 40 kV. The excitation source was Cu Kα (8.04 keV) with a wavelength of 0.1541838 nm. The Raman spectra of GQDs were recorded using a Jobin Yvon HR800 (HORIBA). Ultraviolet-visible spectroscopy (UV-Vis, Cary 100 UV-Vis, Agilent Technologies, Inc.) was used to probe the UV-Vis absorbance of GQDs. An inductively coupled plasma-optical emission spectrometer (ICP-OES, ICPOES730, Agilent Technologies, Inc.) was utilized for quantifying the Gd³⁺ concentrations. The products of Friedel-Crafts alkylation were characterized using a 600 MHz nuclear magnetic resonance (NMR, DRX500, Bruker).

Calculation of optical band gap of GQDs using UV-Vis spectrum

According to the Tauc and Davis-Mott relation, the band gap of GQDs can be calculated from UV-Vis absorption spectroscopy using:

where α is the absorption coefficient, hν is the incident photon energy, n represents the nature of transition (n = 2 for direct band gap materials including GQDs, n = 1/2 for indirect band gap materials), K is the energy independent constant, E_g is the optical band gap of the GQDs, it can be calculated using the Fokker-Planck equation:

where h is the Planck constant with a value of 6.626 × 10^–34 J s, υ is the frequency of incident photon that can be expressed using the speed of light (c, 2.998 × 10^–8 m s^–1) and the wavelength of the incident photon (λ). Therefore, E_g can be written as:

The α in Eq. (3) can be calculated using the Beer-Lambert law:

where I is the intensity of transmitted light, I₀ is the intensity of incident light, and ℓ is the path length of light in which absorbance takes place (for the quartz cuvette used in the UV-Vis experiment, ℓ = 10 mm). Suppl. Equation 3 can be written as:

When calculating the E_g of GQDs, the energy and (αhν)² are plotted as the x-axis and y-axis, respectively. A linear fit is used to find the E_g of GQDs by using the condition of α = 0.

T ₁ measurement in ULF NMR relaxometry

The T₁, which describes the time the magnetization takes to return to its maximum value parallel to the static magnetic field (B₀), was measured using a homemade ULF NMR relaxometry. T₁ measured by ULF NMR relaxometry in the present work was performed using the following parameters (Suppl. Fig. 5):

B₀ = 118 μT, proton Larmor frequency (f_L) = 5030 Hz, B_p = 87 mT, B_p time (T_p) = 500 ms, interval time between π/2 and π pulses of B₁ (T_pe) = 32 ms, signal acquisition time (T_a) = 0.1 s, cooling time = 10 s. The total time consumption of a T₁ measurement is 1–2 min.

During the measurement, 10 mL of the sample was placed beneath the cryostat at room temperature. A water bath was used for preheating before the T₁ measurement for samples higher than room temperature. The sample temperatures were measured before and after the T₁ measurement to verify no significant change in sample temperature. As shown in Suppl. Fig. 5a, the sample was first pre-polarized by the B_p field for a B_p time T_p. After the B_p field was switched off adiabatically, the sample magnetization freely relaxed in the B₀ field for an evolution time \({\Delta T}_{1}^{{{\rm{delay}}}}\). Then, π/2 and π pulses were applied to excite the spin-echo signals. Ten \({\Delta T}_{1}^{{{\rm{delay}}}}\) values were chosen to derive the T₁ values based on single-exponential decay fit of signal amplitudes vs. \({\Delta T}_{1}^{{{\rm{delay}}}}\) values:

where y₀ is signal amplitude of the first data, t₀ represents the first \({\Delta T}_{1}^{{{\rm{delay}}}}\), A is the coefficient, and T₁ denotes the longitudinal relaxation time. Similarly, the relaxation rate (1/T₁) can be fitted to obtain from Eq. (8).

Additionally, the longitudinal relaxation rate (r₁) in the unit of L mmol^–1 s^–1 is the slope of the linear regression line by plotting 1/T₁ as the ordinate and the Gd³⁺ concentration as the abscissa.

T ₁ measurement with light induction

An additional light fiber that introduces light (always ON, Suppl. Fig. 5a) to the sample is used for measuring the T₁ with the light induction. The light introduced to the sample has a wavelength of 365 nm and turns on during the entire T₁ measurement. The light fiber passes through the waveguide into the shielded chamber.

T ₁ reduction of samples containing GQDs

As GQDs in aqueous dispersion show a similar T₁ to water, and no noticeable T₁ change can be observed when treated with light induction (Suppl. Fig. 6), 0.05 mmol L^–1 of Gd³⁺ is added throughout the experiments to shorten the T₁ of GQDs in aqueous dispersion (10 mg L^–1, Suppl. Fig. 7). The Gd³⁺ is a paramagnetic ion with seven unpaired electrons. Although the two neighboring ions (Dy³⁺ and Ho³⁺) have larger magnetic moments (due to the orbital contributions to electron angular momentum) than that of Gd³⁺, the asymmetry of these electronic states leads to very rapid electron spin relaxation. The symmetric S-state of Gd³⁺ is a more hospitable environment for electron spins, leading to a much slower electronic relaxation rate. In the intricate dance that gives rise to relaxivity, water protons hardly feel the effects of ions such as Dy³⁺, much like a leaf near the incredibly rapid wings of a hummingbird. Gd³⁺ electrons are more attuned to the frequency of oscillation of the proton²⁹.

General computational methods

The calculations utilized DZVP-MOLOPT-SR-GTH basic sets and plane wave functions expanded up to an 800 Ry absolute cutoff and a 40 Ry relative cutoff^47,48. Core electrons were treated with the Geodecker-Teter-Hutter (GTH) pseudopotential. In the ground state, the Perdew, Burke, and Ernzerhof (PBE) exchange-correlation functional, along with the DFT-D3 dispersion correction scheme, were adopted^49,50,51. Due to the high computation efficiency and popularity in the excited state⁵², the time-dependent density functional theory (TD-DFT) was often employed to estimate the singlet excitation energies and perform geometrical optimization of the excited state. In addition, the PBE0-ADMM-D3 hybrid function was used for the excited state⁵³.

Theoretical calculation of band gap of simulated GQDs

The structural stability of the seven GQD structures displayed in Fig. 3a was first checked in a vacuum by performing a series of structural optimizations. Geometry optimizations for the ground states of GQDs were first calculated by DFT. After the optimizations, TD-DFT calculations were performed to obtain the band gap of GQDs in the optimized ground state geometry.

Dynamic computational methods

After geometrical optimization, GQDs were embedded into 504 explicit water molecules. A periodic simulation box of dimensions 30 Å × 30 Å × 12 Å was constructed here. Then, a geometrical optimization was necessary to organize the H₂O molecules into a chemically relevant configuration. Subsequently, all the ab initio molecular dynamics (AIMD) simulations were conducted with a 0.5 fs timestep in the canonical ensemble (NVT), using canonical sampling through velocity rescaling (CSVR) thermostat⁵⁴ with a time constant of 1 ps at 298.15 K and all trajectories were generated after a 5 ps equilibration period: a time of 10 ps was used for the ground state while the calculation for structures in the excited state was terminated at 5 ps. The observations presented herein were acquired by analyzing the AIMD trajectories under different states.

T ₁-weighted image acquired in 7.0 T MRI

In-vivo magnetic resonance imaging (MRI) experiments were conducted using a 7.0 T animal MRI scanner (Bruker Biospec 70/20 USR). Isoflurane was used to anesthetize the mice which were then laid face down on the sample plane for scanning. T₁-weighted MRI was then performed in the coronal plane using a multi-slice spin-echo sequence with the following parameters: TE = 6.5 ms, TR = 1500 ms, averages = 2, repetitions = 1, echo spacing = 6.5 ms, rare factor = 4, image size = 256 × 256, field of view = 30 mm × 30 mm, slice thickness = 1 mm, slices = 20.

All animal experiments were conducted in accordance with protocols approved by the Institutional Animal Care and Use Committee of the Shanghai Ninth People’s Hospital.

Collection and pretreatment of clinical samples

Human urine samples from 30 participants were collected and stored at 277.15 K. The studies involving human participants were reviewed and approved by the Ethical Committee of Shanghai Ninth People’s Hospital. All participants provided their informed consent.

LOD estimation of MRS

Initially, a linear fit is used to quantify the relationship between the T₁ of the sample and the logarithm of the biomarker concentration. The LOD of MRS can then be determined from the linear curve when T₁ equals the T₁ of the control (blank) sample plus three times the SD.

Calculation of k in Friedel-Crafts reactions

The concentration of benzene (plotted on the y-axis) decreases with the increase of reaction time (plotted on the x-axis). A linear fit is adopted to fit the data, and the resulting slope’s absolute value is the k.

Statistical analysis

A two-tailed Student’s t-test is used to evaluate the significance of T₁ between the two groups. P value < 0.05 is deemed statistically significant.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.