Introduction

Dipole glass (DG) is characterized by a minimized polar order scale of individual dipoles, featuring chaotic dipole moments between neighboring dipoles, and exhibits hysteresis-free polarization versus electric field (P-E) loops, since the dipole reorientation is independent, preventing dipole entities from growing under an external electric field1,2,3. DG usually exists in either incipient ferroelectric (e.g., KTaO3:Nb) or paralelectric (e.g., BaZrO3:Ti), which contains dilute ferroelectric-active ions Nb and Ti, respectively1,4. This occurrence is observed beyond the local transition temperature T* that gives rise to the formation of static polar nanoclusters5,6 (Fig. 1a and Supplementary Fig. 1). In comparison with traditional relaxor ferroelectrics (RFEs) in ergodic relaxor (ER) state or superparaelectric (SPE) ER state7,8,9,10, a low dielectric constant (εr) and consequently a low maximum polarization (Pm) due to a rather low concentration of polar lattices with off-center cation displacement can be usually observed in DG even under high electric field range. Nevertheless, considering that a critical issue concerning the contradiction between recoverable energy storage density Wrec and energy efficiency η, represented by obviously enhanced polarization hysteresis and decreased η under a very high electric field, has still not effectively been solved in RFEs, because of growth of polar nanodomains7,8,9,10,11,12,13, DG seems to present a great potential for energy storage once the maximal polarization Pm can be significantly enhanced. However, it is an undeniable fact that achieving high Pm in canonical DG poses challenges. To this end, to break through the paradigm of canonical DG for designing a new DG system by synergistically minimizing the polar order scale and maintaining the high Pm will be of great significance for the simultaneous achievement of large Wrec and field-insensitive giant η, but so far remains elusive by simply either increasing or decreasing the off-center dipole concentration in DG state.

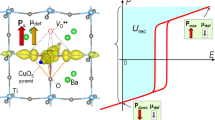
Fig. 1: Design strategy of HPCDG for high-performance dielectric capacitor.
figure 1

a The sketch of the temperature-dependent dielectric response for typical RFEs with different frequency f. The sketch of polar structure and the corresponding polarization response of nonergodic relaxor NR (or ferroelectric FE), ER, SPE ER, canonical DG, paraelectric PE states and HPCDG, and the schematic of the design strategies of HPCDG. The NR (or FE), ER, SPE ER, canonical DG and paraelectric PE states exist in the temperature range of T < Tf (or T<Tfr), Tf < T < Tm, Tm < T < T*, T* < T < TB, and T > TB, respectively, where Tf, Tfr, Tm, T*, TB denote the freezing temperature, FE-to-ER transition temperature, the temperature of dielectric maximum, the local transition temperature that gives rise to the formation of static polar nanoclusters and Burn temperature, respectively. The pink dashed box denotes the macrodomains in FE, whereas, the yellow dashed boxes denote the polar nanodomains in RFE. The dark cyan area in P-E loops denotes the stored recoverable energy Wrec, whereas the light purple area surrounded by the P-E loop denotes the energy loss Wloss. (The light purple area in ER, SPE ER, canonical DG and HPCDG is not shown). b Comparison of Wrec vs. E, η vs. E and Wrec /E vs. E for our prototype MLCC with state-of-the-art Pb-free and Pb-based MLCCs12,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35.

Full size image

In light of this challenge, we propose a promising alternative approach that has not yet been explored to design this new DG with highly polarizable and concentrated dipoles through introducing atomic-scaled chemical and polar heterogeneity, which is motivated by heterovalent ferroelectric-active cations and entropy-driven randomly mixed solution in multicationic equiatomic oxide systems14,15,16,17. This approach incorporates multiple heterovalent ferroelectric-active principal cation species on equivalent sites (Fig. 1a and Supplementary Fig. 1), defining the resulting structure as a highly polarizable concentrated dipole glass (abbreviated as HPCDG) to distinguish it from canonical DG. The key concept is to choose as many ferroelectric-active cations as possible, allowing for a great number of cations with spontaneous displacement. This would be beneficial for the formation of highly polarizable dipoles across numerous lattices, i.e., highly polarizable and concentrated dipoles. To counteract the formation of polar nanodomains due to neighboring dipole-dipole interaction, we further employed a dual strategy involving high configuration entropy (Sconfig) with multiple principal cations and multiple heterovalent cations. This approach may promote the atomic-scaled chemical heterogeneity without nanoscaled compositional aggregation, creating lattice charge imbalance and distortion in each lattice, respectively, leading to divergent random-electric field and random-strain field that differ in scale at the lattice level. This innovative strategy is designed to break the local periodicity and translational symmetry of the dipoles, and thus inducing the formation of the HPCDG.

Results and discussion

Composition strategy for achieving HPCDG

Following this strategy, we have designed a high-entropy perovskite oxide, denoted as (Bi1/3Ba1/3Na1/3)(Fe2/9Ti5/9Nb2/9)O3 (abbreviated as (BiBaNaFeTiNb)O) with six principal heterovalent cations to achieve the HPCDG. This composition is exclusively composed of the polar components of BiFeO3 (BF), BaTiO3 (BT), (Bi0.5Na0.5)TiO3 (BNT), and NaNbO3 (NN) (the ground state of NN is also a polar phase) with fixed molar ratio of 2/9BF-1/3BT-2/9BNT-2/9NN (Supplementary Table 1). Four types of polar BF, BT, BNT, and NN components were selected to introduce as many ferroelectric-active cations. To validate the HPCDG feature of (BiBaNaFeTiNb)O, we used BF as a matrix and introduced BT, BNT, and NN. Subsequently, we designed a series of (2/3-2x)BF-1/3BT-xBNT-xNN (denoted by BF-BT-xBNT-xNN) based on the phase field simulation. In this composition system, not only Sconfig but also the relative amount of heterovalent cations on equivalent sites can be regulated, concurrently, with varying x. The ideal Sconfig increases rapidly from medium-entropy of ~1.273 R (x = 0) to high-entropy of ~1.647 R (x = 0.04) and ~2.001 R (x = 0.12), and then increases slightly to ~2.094 R (x = 2/9, (BiBaNaFeTiNb)O) (Supplementary Fig. 2). Meanwhile, the molar fraction of heterovalent cations on equivalent sites tends to approach between each other. The similar molar fraction of cations on equivalent sites may promote the atomic-scaled chemical heterogeneity. On this basis, the atomic-scale random distribution of heterovalent cations with different valence states and ionic radii would facilitate the formation of atomic-scaled polar heterogeneity, as envisaged by our design. The x = 0 sample possesses a large amount of rhombohedral (R) domains. Although R ___domain size decreases obviously with increasing x, nanoscaled domains persist even in x = 0.12 despite its high Sconfig (Fig. 2a and Supplementary Fig. 3). By comparison, no obvious polar order regions corresponding to either macro-domains or polar nanodomains exist in (BiBaNaFeTiNb)O. Instead, highly polarizable dipoles with chaotic dipole moments between adjacent dipoles and without obvious non-polar region are dominated, coinciding with our design.

Fig. 2: Composition strategy and structural mechanism of the (BiBaNaFeTiNb)O HPCDG.
figure 2

a Phase-field-simulated two-dimensional ___domain structures of x = 0.12 (left) and x = 2/9 (middle) of BF-BT-xBNT-xNN and (BiBaNaFeZrNb)O (right), respectively. b HAADF image of atomic structure taken with the [010]c zone axis and the corresponding EDS maps for individual Bi, Ba, Na, Fe, Ti, Nb elements, and the A-site and B-site holistic EDS maps (the area corresponds to the purple dashed box) for the (BiBaNaFeTiNb)O. c Axial ratio c/a distribution mapping derived from the HAADF image. d Line profiles of displacement magnitude and direction of B-site cations for the (BiBaNaFeTiNb)O (lines 1–4 marked in Supplementary Fig. 7).

Full size image

For comparison, we also evaluated the ___domain structure of (Bi1/3Ba1/3Na1/3)(Fe2/9Zr5/9Nb2/9)O3 (abbreviated as (BiBaNaFeZrNb)O). It has the same Sconfig as (BiBaNaFeTiNb)O, but the ferroelectric-active Ti cations are completely replaced by the non-ferroelectric-active Zr cations. We found that (BiBaNaFeZrNb)O exhibits an obvious canonical DG feature, characterized by lowly concentrated electric dipoles with random orientation that embedded in a large amount of non-polar cubic (C) matrix (Fig. 2a), akin to the canonical DG state in Ba(Ti0.5Zr0.5)O36. This suggests that constructing the HPCDG in (BiBaNaFeTiNb)O depends not only on high Sconfig, but also on the concentration of heterovalent ferroelectric-active cations. Indeed, (BiBaNaFeTiNb)O allows for the highest possible molar fraction of each cation and ensures that heterovalent cations in equivalent sites have the same molar fraction as much as possible (Supplementary Fig. 2). By comparison, other BF-BT-xBNT-xNN compositions exhibit either relatively low Sconfig or relatively low concentration of heterovalent solute cations, whereas, the concentration of ferroelectric-active cations in (BiBaNaFeZrNb)O composition is too low to induce highly concentrated dipoles. This also explains why the currently-reported high-entropy dielectrics only exhibit typical RFE characteristics13,18.

We further fabricated a (BiBaNaFeTiNb)O prototype multilayer ceramic capacitor (MLCC) to evaluate its energy storage performance. The achieved values for Wrec and η reached unprecedented levels of ~26.3 J cm−3 and ~92.4% at 94 kV mm−1 concurrently (Fig. 1b). These values stand out significantly as compared with those of the state-of-the-art Pb-free and Pb-based MLCCs12,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35. To further estimate its merit, we introduced the concept of energy strength (Wrec /E)36, representing the electric field efficiency of the Wrec, and found that (BiBaNaFeTiNb)O MLCC surpasses the Wrec /E values of the state-of-the-art of Pb-free and Pb-based MLCCs12,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35. This indicates a more rapid increase in Wrec under the electric field. These findings underscore the tremendous potentials of the HPCDG as a promising candidate for future energy-storage dielectric capacitor.

Structural mechanism of the (BiBaNaFeTiNb)O HPCDG

We further analyze the multi-scaled characteristics of the (BiBaNaFeTiNb)O to understand the mechanism of HPCDG. The material exhibits a pure perovskite phase with an average cubic Pm-3m symmetry (Supplementary Fig. 4 and Table 2), possibly due to highly localized chemical disorder. To delve into the atomic-scaled chemical distribution, we employed the high-angle angular dark-field (HAADF) image and the corresponding atomic-resolution energy-dispersive X-ray spectroscopy (EDS) maps along with [010]c zone axis (Fig. 2b). The brightness of an individual spot depends on the abundance of the measured cations in the atomic subcolumn along the [010]c axis. All cations periodically occupy the corresponding sublattice with random fluctuation (Bi/Ba/Na cations in A-site and Fe/Ti/Nb cations in B-site, respectively). This is supported by line profiles of the atomic fraction derived from the EDS maps (Supplementary Fig. 5), wherein both A-site and B-site cations show irregular changes in atomic fraction between the neighboring columns. Moreover, we found that the fluctuation region of the A-site cations does not coincide with that of B-site cations (Supplementary Fig. 6). These observations suggest the atomic-scaled chemical heterogeneity in (BiBaNaFeTiNb)O, which can be further confirmed by the axial ratio c/a distribution derived from the HAADF image (Fig. 2c and Supplementary Fig. 7). This feature also suggests that, despite the lack of effectively quantitative calculation, (BiBaNaFeTiNb)O sample is more likely to reach its ideal Sconfig than those of previously reported RFEs and even the high-entropy RFEs, since the existence of the local chemical-order would reduce Sconfig value of the system.

Different from traditional RFEs9, no patches with a similar c/a value, corresponding to the nanoscale chemical order region, are present. The isolated lattice with large c/a value is interspersed with the isolated lattice with low c/a value, or vice versa, due to the atomic-scaled random-cation-distribution. Combined with the large variation span of axial ratio c/a of ~0.88–1.10 due to the large average-ionic-size difference (see Supplementary method), the (BiBaNaFeTiNb)O is expected to exhibit large and atomic-scaled divergent random strain fields. This is associated with the atomic-scaled divergent random electric fields arising from the charge-imbalance in each lattice induced by the atomic-scaled random distribution of heterovalent cations in the equivalent sites. These features, absent in traditional RFEs, strongly disturb the locally cooperative-alignment of dipoles, suppressing the formation of polar nanodomains. Indeed, no visual evidence of the local contrast corresponding to the polar nanodomains, or visible superstructure due to chemical aggregation can be observed, indicating not only the lack of aggregated nanoscale chemical clusters but also the absence of aggregated nanoscale polar clusters (Supplementary Fig. 8 and Table 3). We then calculated the off-centering displacement of A-site and B-site cations to better understand the local polar heterogeneity (Fig. 2d and Supplementary Fig. 7). Virtually almost all lattices exhibit non-negligible polarization magnitude, with average polarization magnitude reaching as large as ~0.129 ± 0. 002 Å and ~0.131 ± 0.002 Å for A-site and B-site cations, respectively (Supplementary Fig. 9). We attributed it to the large average displacement of ~0.42 ± 0.01 Å for Bi cations due to the lone-pair effect, and the large average displacement of ~0.16 ± 0.01 Å, ~0.12 ± 0.01 Å, ~0.14 ± 0.01 Å for ferroelectric-active Fe, Ti, and Nb cations, respectively, as determined from X-ray absorption fine structure (XAFS) spectra (Supplementary Figs. 10 and 11 and Table 4). These highly concentrated and polarizable off-center dipoles would be beneficial for high Pm.

Intriguingly, the distribution of the cation-displacement vectors is highly disordered in both magnitude and direction (Supplementary Fig. 9). The displacement magnitude, and more importantly, the displacement direction of each cation deviates from those of the adjacent cations at equivalent sites, as supported by line profiles of displacement magnitude and direction distribution of B-site cations (Fig. 2d and Supplementary Fig. 12) and A-site cations (Supplementary Fig. 13). This indicates that highly polarizable concentrated dipoles in (BiBaNaFeTiNb)O exhibit chaotic vectors with atomic-scaled polar heterogeneity. This phenomenon is closely related to the locally divergent random electric and strain fields that differ on the lattice scale, which strongly frustrate the dipole-dipole interaction. The polarization magnitude and direction of the off-center cations deviate from their ideal states to varying degrees due to the divergent electric and strain fields around the neighboring off-center cations, and thus contribute to the achievement of HPCDG. Although the electrostatic and strain energies ideally enhance with increasing the random electric and strain fields, the high Sconfig featuring multiple principal cations would prevent the compositional aggregation of solvent and solute cations. This compensates the increased electrostatic and strain energies, lowering the overall free energy of the system. More importantly, the delicately-designed composition and content of heterovalent ferroelectric-active cations, combined with high Sconfig, ensure that random electric and strain fields in (BiBaNaFeTiNb)O differ on smaller scales compared to traditional RFEs and even the recently-reported high-entropy RFEs, leading to the chaotic polar vectors between adjacent off-center dipoles, and thus inducing a minimized polar order scale.

Electrical properties of the (BiBaNaFeTiNb)O HPCDG bulk ceramic

We measured the temperature-dependent dielectric spectra of the (BiBaNaFeTiNb)O ceramic (Fig. 3a). Different from traditional RFEs (ref. 37) and other BF-BT-xBNT-xNN compositions (Supplementary Fig. 14), the εr value of the (BiBaNaFeTiNb)O reaches a plateau with minimal temperature dependence, rather than a steep decline as T > Tm, although all these samples exhibit a distinct dielectric relaxation behavior (Fig. 3a and Supplementary Figs. 14 and 15). The activation energy Ea of the (BiBaNaFeTiNb)O is notably large, measuring ~0.26 eV (Supplementary Fig. 15), significantly higher than that of the canonical relaxor Pb(Mg1/3Nb2/3)O3 (PMN)38. These features suggest that (BiBaNaFeTiNb)O exhibits slowly-frozen and weakly-coupled dipoles39. We further compare the P-E loops of (BiBaNaFeTiNb)O (HPCDG) with the x = 0.12 (canonical RFE) and (BiBaNaFeZrNb)O (canonical DG) samples in terms of their comparable Sconfig, and found that the highly polarizable and concentrated dipoles in HPCDG give significantly higher εr and Pm than those of the DG (~520% and ~550% enhancement of εr and Pm, respectively) (Fig. 3b, c and Supplementary Fig. 14). Pm is further slightly enhanced in x = 0.12 sample (~134% enhancement of Pm) at the expense of the significantly increased hysteresis and thus the decreased η. By comparison, HPCDG exhibits extremely-slim low-hysteresis and near-linear P-E loop, demonstrating comparable η but outstanding Wrec with respect to that of DG (Fig. 3b, c). This suggests that HPCDG has the advantages of high Pm of RFEs and high η with nearly-linear and low hysteresis P-E loop of DG concurrently. More intriguingly, extremely-slim low-hysteresis and near-linear P-E loop is maintained even near the breakdown strength Eb (Supplementary Fig. 16), leading to the nearly-linear increases in Pm and ΔP ((Fig. 3d and Supplementary Fig. 17).

Fig. 3: Electrical properties of the (BiBaNaFeTiNb)O bulk ceramic.
figure 3

a Temperature-dependent relative dielectric constant εr and loss tangent tan δ at different f. b P-E loops of x = 0.12, 2/9 ((BiBaNaFeZrNb)O) and (BiBaNaFeZrNb)O samples. c The comparison of the Wrec, η and Pm of (BiBaNaFeTiNb)O (HPCDG) with the x = 0.12 (canonical RFE) and (BiBaNaFeZrNb)O (DG) samples. Numbers 1, 2, 3 represent the x = 0.12, (BiBaNaFeTiNb)O, and (BiBaNaFeZrNb)O samples, respectively. d P-E loop of (BiBaNaFeTiNb)O measured at 67 kV mm−1. The inset is the evolution of Pm, Pr, and ΔP (Pm-Pr) as a function of electric field. e The comparison of the dynamic scaling behavior of our sample with that of representative RFEs9,13,40,41. f The evolution of total energy density Wtotal, Wrec, and η of the (BiBaNaFeTiNb)O bulk ceramic as a function of electric field.

Full size image

We further investigate the dynamic scaling behavior of HPCDG to understand its polarization response characteristic (Supplementary method). Note that a large Pm of ~53 μC cm−2 that can be comparable to that of traditional RFEs can be achieved in HPCDG (Fig. 3d), indicating that the highly polarizable concentrated dipoles in HPCDG can be reoriented under electric field. However, the HPCDG shows a single linear relation with a relatively small exponent α (~2.32) across the entire field range (Fig. 3e). On the contrary, traditional RFEs exhibit two linear stages with a relatively large α values in the first stage corresponding to the rapid growth and switching of polar nanodomains9,13,40,41. This suggests that the reorientation process of dipoles in HPCDG does not involve the growth of dipoles as a result of the difference in local symmetry between neighboring lattices, leading to a negligible polarization hysteresis even in a rather high electric field range. This is advantageous for achieving an electric-field-insensitive giant η value. Moreover, different driving fields are needed to rotate the dipoles with different polar vectors from their initial directions to the direction parallel to the external electric field42, meaning a relatively diffuse process of polarization reorientation, compared with traditional RFEs. The nearly linear increases of Pm and ΔP with low polarization hysteresis imply that the energy density of the HPCDG is nearly proportional to the square of the electric field (Fig. 3f), rather than a nearly linear increase of energy density observed in traditional RFEs12,13, i.e., a more rapid increase of energy density with increasing electric field, and more importantly, an electric-field-insensitive giant η. Combined with a high breakdown strength Eb (Supplementary Fig. 16), enhanced resistance (Supplementary Fig. 18), and the above-mentioned HPCDG feature, Wrec of ~15.9 J cm−3 can be obtained in (BiBaNaFeTiNb)O ceramic at 67 kV mm−1 (Fig. 3f). Of particular significance is that η maintains a value of ~93.3% with minimal electric field dependence, consistent with the dynamic scaling behavior analysis. The (BiBaNaFeTiNb)O ceramic also exhibits a power density PD of ~653 MW cm−3 and a discharge energy density WD of ~6.56 J cm−3 at 45 kV mm−1. All these values are superior to those of the state-of-the-art Pb-free RFE ceramics (Supplementary Figs. 19 and 20).

Energy storage performances of MLCC

Given that MLCC is one of the most extensively utilized dielectric capacitors, we further evaluated the energy-storage performance of the (BiBaNaFeTiNb)O MLCC. Employing a traditional tape casting technique, we fabricated the (BiBaNaFeTiNb)O prototype MLCC device, which included ten (BiBaNaFeTiNb)O layers with a single dielectric layer thickness of ~15 μm after sintering (Fig. 4a). The (BiBaNaFeTiNb)O prototype MLCC exhibits a similar polarization behavior to the bulk ceramic capacitor, showcasing a comparable trend in Pm and ΔP (Fig. 4 b, c). Moreover, it maintains a nearly linear increase of Pm and ΔP with extremely low hysteresis prior to the Eb (Fig. 4c). The achieved Pm value is competitive as compared with the state-of-the-art Pb-free RFE MLCCs12,19,20,21,22,23,24,25,26,27,28,29,30.

Fig. 4: Energy storage performances of the (BiBaNaFeTiNb)O HPCDG prototype MLCC.
figure 4

a The cross-section SEM image of the MLCC sample. b P-E loops as a function of electric field for the MLCC sample. c The evolution of Pm, Pr, and ΔP of the MLCC sample as a function of electric field. The fitting curve derived from the bulk ceramic data shows a good consistent with that of MLCC. d Comparison of the evolution of Wrec and η as a function of electric field for our MLCC sample with those of start-of-the-art Pb-free RFE MLCCs12,20,22. e Comparison of the temperature-dependent energy storage performances of our MLCC sample under 60 kV mm−1 with those of start-of-the-art Pb-free RFE MLCCs15,23,24. f Discharge reliability of the MLCC sample under an electric field of 60 kV mm−1.

Full size image

Benefiting from the enhanced Eb derived from the decreased ceramic thickness (Supplementary Fig. 16), and HPCDG feature, a record-breaking Wrec value of ~26.3 J cm−3 can be achieved at ~94 kV mm−1. More importantly, η value beyond ~92.4% can be maintained even at such high Wrec and electric field (Fig. 4d), surpassing the state-of-the-art Pb-free RFE MLCCs12,20,22. From a practical application viewpoint, we also evaluated the temperature stability and cycle reliability of the (BiBaNaFeTiNb)O prototype MLCC (Supplementary Fig. 21). Excellent temperature stability with a substantial Wrec of ~12.0 ± 0.7 J cm−3 and a superior η of 92.7 ± 0.4% over a wide temperature range from 25 °C to 150 °C can be observed at 60 kV mm−1 (Fig. 4e)15,23,24. The excellent temperature stability can be attributed to the minimal temperature dependence of the εr value, accompanied by robust A- and B-sites cation polarization across a wide temperature range (Supplementary Fig. 22). The prototype MLCC device also exhibits excellent cycle reliability, with only a slight decline in discharge energy density WD by ~8% after 106 cycles based on the charge-discharge measurement (Fig. 4f). Such a good cycle reliability can be attributed to the HPCDG with minimized polar scale, therefore suppressing the pinning of ___domain walls and the growth of polar order as much as possible. These features underscore the significant advantages of the HPCDG over traditional RFEs in energy-storage, making the (BiBaNaFeTiNb)O an excellent candidate for high-performance MLCC devices.

In summary, we have successfully engineered an HPCDG in (BiBaNaFeTiNb)O, which breaks a technique bottleneck of typical RFEs in energy storage that substantially increased energy density would generally sacrifice energy efficiency under superhigh fields. This achievement involved constructing a composition system with multiple heterovalent ferroelectric-active principal cation species in equivalent lattice sites, strategically minimizing the polar order scale with individual dipoles and inducing highly polarizable and concentrated dipoles. Both diffuse polar reorientation and negligible growth with electric fields would induce a nearly-linear polarization response and a rapid increase of Wrec, thus leading to a superhigh Wrec of ~15.9 J cm−3 and a field-insensitive η of ~93.3% concurrently, in a bulk ceramic capacitor, and a record-breaking Wrec of ~26.3 J cm−3 and a field-insensitive η of ~92.4% with excellent temperature and cycle stability, simultaneously, in a prototype MLCC. These results present substantial advantages as compared with those recently-reported state-of-the-art energy-storage RFE bulk ceramic capacitors and MLCCs. Our study introduces a groundbreaking solution to the longstanding challenge of collaborative improvement of Wrec and η in energy-storage capacitor dielectrics, paving the way for innovative advancement in this field.

Methods

Bulk ceramic preparation

A series of (2/3-2x)BF-1/3BT-xBNT-xNN (x = 0, 0.02, 0.04, 0.08, 0.12, 2/9) and (BiBaNaFeZrNb)O ceramics were fabricated by a solid-state reaction method. High purity Bi2O3 (99.5%), Na2CO3 (99.5%), BaCO3 (99.5%), Fe2O3 (99.5%), TiO2 (99.5%), Nb2O5 (99.5%), and ZrO2 (99.5%) (Sinopharm Chemical Reagent Co., Ltd) were selected as the raw materials and were weighed according to its stoichiometry and then mixed in ethanol by ball milling with Y2O3-stabilized zirconia balls for 6 h. The powder mixture was dried, and then calcined at 800 °C for 4 h. The calcined powders were further mixed with 0.2 wt% MnO2, 2 wt% BaCu(B2O5) powder and 0.5 wt% polyvinyl butyral via ball milling for 10 h. After drying and sieving, the powders were pressed into disk samples with a diameter of 10 mm under 200 MPa. The pellets were heated to 550 °C at 3 °C min−1 to burn out the binder and then sintered at 1000–1040 °C for 2 h in closed crucibles. The ceramics were polished into a thickness of ~0.05-0.12 mm for energy storage performance measurements and silver electrodes with a diameter of ~1–2 mm were pasted onto the two parallel surfaces of ceramic dicks.

MLCC fabrication

MLCC, including ten (BiBaNaFeTiNb)O layers with inner Pt electrodes, was prepared by a tape casting method, where the calcined (BiBaNaFeTiNb)O powder was used as raw material. The weighed calcined powders were ball-milled with Y2O3-stabilized zirconia balls for 48 h. The ceramic powder, together with dispersant, binder, and plasticizer, was re-milled for 48 h to make the pseudoplastic slurry. Various additives are added according to the weight percentage relative to the ceramic powders. The tape-casting slurry was prepared by dispersing the ceramic powders, ammonium polyacrylate dispersant (1 wt%), polyvinyl butyral binder (8.5 wt%), dioctyl pahthalate plasticizer (3.5 wt%), and the ethanol-ethyl acetate solvent with 1:1 weight ratio (130 wt%). After drying, green tapes were cut, and printed with Pt electrodes by using the Pt slurry. MLCCs with inner printed Pt electrodes were stacked layer by layer, then precisely aligned and finally isostatically laminated. The sample size of the MLCCs is 3.4 × 3.4 mm with the electrode area of 2.2 mm × 1 mm (before sintering), while the effective single layer electrode (overlap part) ~1 mm × 1 mm (overlap part). The single layer thickness is ~18 μm and ~15 μm before and after sintering, respectively. The stacked layers were sintered at 1020–1070 °C for 2 h. The thickness of Pt inner electrodes was ~0.5 μm after sintering. The shrinkage of MLCC was about ~16.7% after sintering, and thus the single-layered effective electrode area of the sintered sample was (1−0.167) × (1−0.167) = 0.689 mm2. Thus, the sample volume is 15 μm (thickness of single layer) × 10 (layers) × 0.83 mm × 0.83 mm (area of the overlapped electrodes) = ~0.11 mm3. After sintering, silver paste was used to terminate the opposite ends of the MLCC and form the outer electrode for electrical measurements.

Structure characterization

The average phase structure was determined by the synchrotron X-ray diffraction collecting at beamline 14B1 of Shanghai synchrotron radiation faculty (SSRF) (E = 18 keV). Structural refinement was carried out by using the Rietveld refinement program GSAS-II. Temperature-dependent Raman spectra were collected on well-polished pellets by 532-nm excitation using a Raman spectrometer (LabRam HR Evolution, HORIBA JOBIN YVON, Longjumeau Cedex, France). The microstructure was observed by using a field-emission scanning electron microscope (FE-SEM, SU8020, JEOL, Tokyo, Japan). Fe K-edge, Ti K-edge, Nb K-edge and Bi LIII-edge XAFS were performed with Si(111) crystal monochromators at the BL14W1 beamline at the SSRF. Before the data collection, samples were pressed into thin disks with 10 mm in diameter and sealed using Kapton tape film. The XAFS spectra were recorded at room temperature using a 4-channel Silicon Drift Detector (SDD) Bruker 5040. All elements were recorded in transmission mode. The handling of raw XAFS data contains normalization, E-k transformation, Fourier transformation and shell-fitting. k2-weighted χ(k) was Fourier transformed to R space. We used the Athena software and Artemis software of IFFEFIT package to achieve the former three steps and the last one, respectively. Initially, perfect TiO6, FeO6, NbO6 and BiO12 polyhedrons were assumed in the shell-fitting procedure since the average structure exhibits an obvious cubic Pm-3m symmetry. and then the off-center displacements of Bi, Ti, Fe and Nb relative to the first shell O atoms were incorporated to better fit the experimental data using the Artemis software.

The room temperature ___domain morphology and selected area electron diffraction (SAED) patterns were performed on a field-emission TEM (JEM-F200, JEOL, Japan) operated at 200 kV. The room-temperature HAADF imaging was performed on a Cs-corrected JEOL JEM-ARM300F microscope. Specimens for TEM and STEM measurements were prepared by a conventional approach combining mechanical thinning and finally Ar+ ion-milling in a Gatan PIPS II. Accurate atomic positions in the HAADF image were clarified by 2D Gaussian fitting. The polarization magnitude, polarization angle and axial ratio were calculated by customized MATLAB scripts.

The atomic-scale elemental analysis was performed using an EDS detector attached in the Cs-corrected TEM, and quantification was automatically carried out in ThermoFisher Velox software. The specimens were prepared by a dual-beam Focused Ion Beam (FIB, Helios 5 UC, ThermoFisher Scientific). The specimens were cut using Ga ions and lifted out by a Tungsten micromanipulator, and then bonded on commercial Cu grids. The accelerating voltage and current of Ga ions were 30 kV and 2.5 nA for initial lamella cutting, and both values were decreased gradually for further precisely thinning down, and finally 2 kV and 40 pA were used for the removal of surface amorphous layer. The final thicknesses of TEM lamellas were about 30-40 nm. The chemical compositions of TEM lamellas were investigated by a double spherical aberration corrected scanning transmission electron microscopy (STEM, Spectra 300, ThermoFisher Scientific) equipped with probe and image correctors and operated at 300 kV. The probe convergence angle and high-angle annular dark-field (HAADF) acceptance angles were 25 mrad and 48-200 mrad, respectively.

Electrical measurements

For the dielectric properties and impedance measurements, the ceramics were polished into a thickness of ~0.5 mm with a diameter of ~8.2 mm, and silver electrodes were pasted onto the two parallel surfaces of the ceramic dicks. For each composition, three samples were measured, and they showed a good consistency between each other. Dielectric properties using an LCR meter (Agilent E4980A, Santa Clara, CA) and a Wayne Kerr 6500B impedance analyzer (Wayne Kerr Electronic Instrument Co., Shenzhen, China) with the DMS-2000 dielectric measurement system (Partulab Technology Co., Wuhan, China) were measured over a wide temperature range of -140-550 °C and frequency range of 1-2000 kHz with a heating rate of 3 °C min−1. The P-E loops measured at 10 Hz were derived from the ferroelectric measurement system (Precision Multiferroelectric, Radiant Technologies Inc., Albuquerque, NM) connected with a high-temperature probing stage (HFS600E-PB2, Linkam Scientific Instruments, Tadworth, UK). The electrode size of ceramic samples used for P-E loop measurements is ~1.0–2.0 mm in diameter and ~0.06-0.10 mm in thickness. The electrode size is symmetrical between the upper and bottom ones. The Dielectric charge-discharge measurement system (DSC-1000, Balab Technologies, Wuhan, China) was used to measure the energy release properties. The storage energy was discharged under a load resistance RL of 100 Ω. Impedance spectroscopy measured at 400 °C was performed using an Agilent E4980A impedance AC analyzer (Agilent E4980A, Santa Clara, CA) on ceramics. The determination of Eb was derived from the voltage-withstand test device (BDJC-50KV, Beiguangjingyi Instrument Equipment Co. Ltd., Beijing, China) at room temperature. The sample size with the thickness of ~0.08 mm and the diameter of ~1.0 mm was used for the the pulsed charge-discharge test and the Eb measurement.

Phase-field simulations

The FE polarization vector \({{\boldsymbol{P}}}=\left({P}_{1},\, {P}_{2},\, {P}_{3}\right)\) is chosen as the only order parameter in the model. The free energy distribution and ___domain structure are obtained by solving the time-dependent Ginzburg–Landau equation

$$\frac{\partial {{\boldsymbol{P}}}}{\partial t}=-L\frac{\partial F}{\partial {{\boldsymbol{P}}}}+{{\boldsymbol{\xi }}}$$
(1)

where L is the kinetic coefficient, t is the time, and F is the free energy. \({{\boldsymbol{\xi }}}\) represents the impact of thermal noises, which is introduced owing to the increased local inhomogeneity in complex solid solutions11. The random noise satisfies a Gaussian function in the following form:

$$ < {{\boldsymbol{\xi }}} > =0, < {{\boldsymbol{\xi }}}({{\boldsymbol{r}}}),\, {{\boldsymbol{\xi }}}({{\boldsymbol{r}}}^{{{\prime} }}) > =m\sqrt{T}{{\boldsymbol{\delta }}}({{\boldsymbol{r}}}{{\boldsymbol{-}}}{{\boldsymbol{r}}}^{{{\prime} }})$$
(2)

where T is temperature (\(\sqrt{T}\) represents the square root of the thermal energy, which is then comparable to order parameter P), m is the magnitude of thermal noise, and δ is the Delta function. The bracket means to calculate an average of ξ over the entire space.

The free energy is expressed as the integral of the individual free energy densities:

$$F=\int \! \iint \left(f_{{{\rm{Landau}}}}+f_{{{\rm{gradient}}}}+f_{{{\rm{elastic}}}}+f_{{{\rm{electric}}}}\right){{\rm{d}}}V$$
(3)

The free energy terms are given by

$${f}_{{{\rm{Landau}}}}= {\alpha }_{1}\left({P}_{1}^{2}+{P}_{2}^{2}+{P}_{3}^{2}\right)+{\alpha }_{11}\left({P}_{1}^{4}+{P}_{2}^{4}+{P}_{3}^{4}\right)+{\alpha }_{12}\left({P}_{1}^{2}{P}_{2}^{2}+{P}_{2}^{2}{P}_{3}^{2}+{P}_{1}^{2}{P}_{3}^{2}\right) \\ +{\alpha }_{111}\left({P}_{1}^{6}+{P}_{2}^{6}+{P}_{3}^{6}\right)+{\alpha }_{112}\left[{P}_{1}^{4}\left({P}_{2}^{2}+{P}_{3}^{2}\right)+{P}_{2}^{4}\left({P}_{1}^{2}+{P}_{3}^{2}\right)+{P}_{3}^{4}\left({P}_{1}^{2}+{P}_{2}^{2}\right)\right] \\ +{\alpha }_{123}{P}_{1}^{2}{P}_{2}^{2}{P}_{3}^{2}+{\alpha }_{1111}\left({P}_{1}^{8}+{P}_{2}^{8}+{P}_{3}^{8}\right) \\ +{\alpha }_{1112}\left[{P}_{1}^{6}\left({P}_{2}^{2}+{P}_{3}^{2}\right)+{P}_{2}^{6}\left({P}_{1}^{2}+{P}_{3}^{2}\right)+{P}_{3}^{6}\left({P}_{1}^{2}+{P}_{2}^{2}\right)\right] \\ +{\alpha }_{1122}\left({P}_{1}^{4}{P}_{2}^{4}+{P}_{2}^{4}{P}_{3}^{4}+{P}_{1}^{4}{P}_{3}^{4}\right)+{\alpha }_{1123}({P}_{1}^{4}{P}_{2}^{2}{P}_{3}^{2}+{P}_{1}^{2}{P}_{2}^{4}{P}_{3}^{2}+{P}_{1}^{2}{P}_{2}^{2}{P}_{3}^{4})$$
$${f}_{{{\rm{gradient}}}}= {\frac{1}{2}G}_{11}\left({P}_{1,1}^{2}+{P}_{2,2}^{2}+{P}_{3,3}^{2}\right) \\ +\frac{1}{2}{G}_{44}\left[{\left({P}_{1,2}+{P}_{2,1}\right)}^{2}+{\left({P}_{2,3}+{P}_{2,3}\right)}^{2}+{\left({P}_{1,3}+{P}_{3,1}\right)}^{2}\right] \\ +\frac{1}{2}{G}_{44}^{{\prime} }\left[{\left({P}_{1,2}-{P}_{2,1}\right)}^{2}+{\left({P}_{2,3}-{P}_{2,3}\right)}^{2}+{\left({P}_{1,3}-{P}_{3,1}\right)}^{2}\right]$$
(4)
$$f_{{{\rm{elastic}}}}=\frac{1}{2}{C}_{{ijkl}}\big({\varepsilon }_{{ij}}-{\varepsilon }_{{ij}}^{0}\big)\left(\big({\varepsilon }_{{kl}}-{\varepsilon }_{{kl}}^{0}\big)\right.$$
(5)
$$f_{{{\rm{electric}}}}=-\frac{1}{2}{K}_{{ij}}{\varepsilon }_{0}{E}_{i}{E}_{j}-{E}_{i}{P}_{i}$$
(6)

where \(\alpha\), G, C, \({\varepsilon }_{{ij}}\), \({\varepsilon }_{{ij}}^{0}\), K, \({\varepsilon }_{0}\), and E are the Landau coefficients, gradient coefficients, elastic stiffness, total strain, spontaneous strain, background dielectric constant, dielectric permittivity of vacuum, and local electric field, respectively43,44.

In this work, we considered the (2/3-2x)BF-1/3BT-xBNT-xNN, and (BiBaNaFeZrNb)O as mixtures of every end member, and the Landau coefficients are listed in Supplementary Table 57,11,45. Considering that all end members are highly doped and the Curie temperature is changed, the Curie temperature in the second-order Landau term coefficient a1 is therefore adjusted46,47. The isotropic gradient energy coefficients are set as G11/G110 = 0.6, G12/G110 = 0 and G44/G110 = G'44/G110 = 0.3, where G110 = 6.8 × 10−11 C−2m4N (Ref. 41). The simulation grid has dimensions of \(64\Delta \times 64\Delta \times 1\Delta\) for 2D and \(32\Delta \times 32\Delta \times 32\Delta\) for 3D, where \(\Delta \,=0.4\,{{\rm{nm}}}\) is the grid spacing. The phase-field simulation was conducted using the commercial Mu-Pro package (http://mupro.co/).