Probing spin hydrodynamics on a superconducting quantum simulator

Transport properties of quantum many-body systems driven out of equilibrium are of significant interest in several active areas of modern physics, including the ergodicity of quantum systems^1,2,3,4 and quantum magnetism^5,6,7. Understanding these properties is crucial to unveil the non-equilibrium dynamics of isolated quantum systems^8,9. One essential property of transport is the emergence of classical hydrodynamics in microscopic quantum dynamics, which shows the power-law tail of autocorrelation functions⁸. The rate of the power-law decay, referred as to the transport exponent, characterizes the universal classes of hydrodynamics. In d-dimensional quantum systems, in addition to generally expected diffusive transport with the exponent d/2 in non-integrable systems^10,11,12, more attention has been attracted by the anomalous superdiffusive^{5,13,14,15,16} or subdiffusive transport^2,3,17,18,19, with the exponent larger or smaller than d/2, respectively.

Over the last few decades, considerable strides have been made in enhancing the scalability, controllability, and coherence of noisy intermediate-scale quantum (NISQ) devices based on superconducting qubits^20,21,22,23. With these advancements, several novel phenomena in non-equilibrium dynamics of quantum many-body systems have been observed, such as quantum thermalization^24,25, ergodicity breaking^26,27,28,29, time crystal^30,31,32, and information scrambling^33,34. More importantly, in this platform, the beyond-classical computation has been demonstrated by sampling the final Haar-random states of randomized sequences of gate operations^{35,36,37,38,39}. Recently, a method of measuring autocorrelation functions at infinite temperature based on the Haar-random states has been proposed, which opens up a practical application of pseudo-random quantum circuits for simulating hydrodynamics on NISQ devices^40,41.

In this work, using a ladder-type superconducting quantum simulator with up to 24 qubits, we first demonstrate that in addition to the digital pseudo-random circuits^{35,36,37,38,39,40,41}, a unitary evolution governed by a time-independent Hamiltonian, i.e., an analog quantum circuit, can also generate quantum states randomly chosen from the Haar measure, i.e., the Haar-random states, for measuring the infinite-temperature autocorrelation functions^42,43,44. Subsequently, we study the properties of spin transport on the superconducting quantum simulator via the measurement of autocorrelation functions by using the Haar-random states. Notably, we observe a clear signature of the diffusive transport on the qubit ladder, which is a non-integrable system^11,12,25.

Upon subjecting the qubit ladder to disorder, a transition from delocalized phases to many-body localization (MBL) occurs as the strength of the disorder increases⁴⁵. By measuring the autocorrelation functions, we experimentally probe an anomalous subdiffusive transport with intermediate values of the disorder strength. The observed signs of subdiffusion are consistent with recent numerical results and can be explained as a consequence of a Griffth-like region on the delocalized side of the MBL transition^{2,3,46,47,48,49}.

Finally, we explore spin transport on the qubit ladder with a linear potential, and it is expected that Stark MBL occurs when the potential gradients are sufficiently large^{28,50,51,52,53,54}. With a large gradient, the conservation of the dipole moment emerges^28,54, associated with the phenomena known as the Hilbert space fragmentation^55,56,57. Recent theoretical works reveal a subdiffusion in the dipole-moment conserving systems^17,19. In this experiment, we present evidence of a subdiffusive regime of spin transport in the tilted qubit ladder.

Experimental setup and protocol

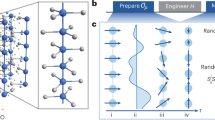
Our experiments are performed on a programmable superconducting quantum simulator consisting of 30 transmon qubits with the geometry of a two-legged ladder, see Fig. 1a, b. The nearest-neighbor qubits are coupled by a fixed capacitor, and the effective Hamiltonian of capacitive interactions can be written as^22,23 (also see Supplementary Note 1)

where ℏ = h/2π, with h being the Planck constant (in the following, we set ℏ = 1), L is the length of the ladder, \({\hat{\sigma }}_{j,m}^{+}\) (\({\hat{\sigma }}_{j,m}^{-}\)) is the raising (lowering) operator for the qubit Q_j,m, and \({J}_{j,m}^{\parallel }\) (\({J}_{j}^{\perp }\)) refers to the rung (intrachain) hopping strength. For this device, the averaged rung and intrachain hopping strength are \(\overline{{J}^{\parallel }}/2\pi \simeq 7.3\,{{{\rm{MHz}}}}\) and \(\overline{{J}^{\perp }}/2\pi \simeq 6.6\,{{{\rm{MHz}}}}\), respectively. The XY and Z control lines on the device enable us to realize the drive Hamiltonian \({\hat{H}}_{d}={\sum }_{m\in \{\uparrow,\downarrow \}}\mathop{\sum }_{j=1}^{L}{\Omega }_{j,m}({e}^{-i{\phi }_{j,m}}{\hat{\sigma }}_{j,m}^{+}+{e}^{i{\phi }_{j,m}}{\hat{\sigma }}_{j,m}^{-})/2\), and the on-site potential Hamiltonian \({\hat{H}}_{{{{\rm{Z}}}}}={\sum }_{m\in \{\uparrow,\downarrow \}}\mathop{\sum }_{j=1}^{L}{w}_{j,m}{\hat{\sigma }}_{j,m}^{+}{\hat{\sigma }}_{j,m}^{-}\), respectively. Here, Ω_j,m and ϕ_j,m denote the driving amplitude and the phase of the microwave pulse applied on the qubit Q_j,m, and w_j,m is the effective on-site potential.

a The schematic showing the ladder-type superconducting quantum simulator, consisting of 30 qubits (the blue region), labeled Q_1,↑ to Q_15,↑, and Q_1,↓ to Q_15,↓. Each qubit is coupled to a separate readout resonator (the green region), and has an individual control line (the red region) for both the XY and Z controls. b Schematic diagram of the simulated 24 spins coupled in a ladder. The blue and yellow double arrows represent the infinite-temperature spin hydrodynamics without preference for spin orientations. c Schematic diagram of the quantum circuit for measuring the autocorrelation functions at infinite temperature. All qubits are initialized at the state \(\left\vert 0\right\rangle\). Subsequently, an analog quantum circuit \({\hat{U}}_{R}({t}_{R})\) acts on the set of qubits Q_R to generate Haar-random states. This is followed by a time evolution of all qubits, i.e., \({\hat{U}}_{H}(t)=\exp (-i\hat{H}t)\) with \(\hat{H}\) being the Hamiltonian of the system, in which the properties of spin transport are of our interest. d Experimental pulse sequences corresponding to the quantum circuit in (c) displayed in the frequency (ω) versus time (T) ___domain. To realize \({\hat{U}}_{R}({t}_{R})\), qubits in the set Q_R are tuned to the working point (dashed horizontal line) via Z pulses, and simultaneously, the resonant microwave pulses represented as the sinusoidal line are applied to Q_R through the XY control lines. Meanwhile, the qubit Q_A is detuned from the working point with a large value of the frequency gap Δ. To realize the subsequent evolution \({\hat{U}}_{H}(t)\) with the Hamiltonian (1), all qubits are tuned to the working point.

Full size image

To study spin transport and hydrodynamics, we focus on the equal-site autocorrelation function at infinite temperature, which is defined as

where \({\hat{\rho }}_{{{{\bf{r}}}}}\) is a local observable at site \({{{\bf{r}}}},\, {\hat{\rho }}_{{{{\bf{r}}}}}(t)={e}^{i\hat{H}t}{\hat{\rho }}_{{{{\bf{r}}}}}{e}^{-i\hat{H}t}\), and D is the Hilbert dimension of the Hamiltonian \(\hat{H}\). Here, for the ladder-type superconducting simulator, we choose \({\hat{\rho }}_{{{{\bf{r}}}}}=({\hat{\sigma }}_{1,\uparrow }^{z}+{\hat{\sigma }}_{1,\downarrow }^{z})/2\) (r = 1)¹², and the autocorrelation function can be rewritten as

with \({c}_{\mu ;\nu }=\,{{\mbox{Tr}}}\,[{\hat{\sigma }}_{\mu }^{z}(t){\hat{\sigma }}_{\nu }^{z}] / {D}\) (subscripts μ and ν denote the qubit index 1 ↑ or 1, ↓).

The autocorrelation functions (2) at infinite temperature can be expanded as the average of \({C}_{{{{\bf{r}}}},{{{\bf{r}}}}}(\left\vert {\psi }_{0}\right\rangle )=\langle {\psi }_{0}| {\hat{\rho }}_{{{{\bf{r}}}}}(t){\hat{\rho }}_{{{{\bf{r}}}}}| {\psi }_{0}\rangle\) over different \(\left\vert {\psi }_{0}\right\rangle\) in z-basis. In fact, the dynamical behavior of an individual \({C}_{{{{\bf{r}}}},{{{\bf{r}}}}}(\left\vert {\psi }_{0}\right\rangle )\) is sensitive to the choice of \(\left\vert {\psi }_{0}\right\rangle\) under some circumstances (see Supplementary Note 7 for the dependence of \({C}_{{{{\bf{r}}}},{{{\bf{r}}}}}(\left\vert {\psi }_{0}\right\rangle )\) on \(\left\vert {\psi }_{0}\right\rangle\) in the qubit ladder with a linear potential as an example). To experimentally probe the generic properties of spin transport at infinite temperature, one can obtain (2) by measuring and averaging \({C}_{{{{\bf{r}}}},{{{\bf{r}}}}}(\left\vert {\psi }_{0}\right\rangle )\) with different \(\left\vert {\psi }_{0}\right\rangle\)¹⁵. Alternatively, we employ a more efficient method to measure (2) without the need of sampling different \(\left\vert {\psi }_{0}\right\rangle\). Based on the results in ref. ⁴⁰ (also see “Methods”), the autocorrelation function c_μ;ν can be indirectly measured by using the quantum circuit as shown in Fig. 1c, i.e.,

where \(\left\vert {\psi }_{\nu }^{R}(t)\right\rangle={\hat{U}}_{H}(t)[{\left\vert 0\right\rangle }_{\nu }\otimes \left\vert {\psi }^{R}\right\rangle ]\) with \(\left\vert {\psi }^{R}\right\rangle={\hat{U}{}_{R}\bigotimes }_{i\in {Q}_{R}}{\left\vert 0\right\rangle }_{i}\), and \({\hat{U}}_{R}\) being a unitary evolution generating Haar-random states. For example, to experimentally obtain c_1,↓;1,↑, we choose Q_1,↑ as Q_A, and the remainder qubits as the Q_R. After performing the pulse sequences as shown in Fig. 1d, we measure the qubit Q_1,↓ at z-basis to obtain the expectation value of the observable \({\hat{\sigma }}_{1,\downarrow }^{z}\).

Observation of diffusive transport

In this experiment, we first study spin transport on the 24-qubit ladder consisting of Q_1,↑, …, Q_12,↑ and Q_1,↓, …, Q_12,↓, described by the Hamiltonian (1). For a non-integrable model, one expects that diffusive transport C_1,1 ∝ t^−1/2 occurs¹². To measure the autocorrelation function C_1,1 defined in Eq. (3), we should first perform a quantum circuit generating the required Haar-random states \(\left\vert {\psi }^{R}\right\rangle\). Instead of using the digital pseudo-random circuits in refs. ^{35,36,37,38,39,40,41}, here we experimentally realize the time evolution under the Hamiltonian \({\hat{H}}_{R}={\hat{H}}_{I}+{\hat{H}}_{d}\), where the parameters Ω_j,m and ϕ_j,m in \({\hat{H}}_{d}\) have site-dependent values with the average \(\overline{\Omega }/2\pi \simeq 10.4\,{{{\rm{MHz}}}}\) (\(\overline{\Omega }/\overline{{J}^{\parallel }}\simeq 1.4\)) and \(\overline{\phi }=0\) (see “Methods” and Supplementary Note 3 for more details), i.e., \({\hat{U}}_{R}({t}_{R})=\exp (-i{\hat{H}}_{R}{t}_{R})\), which is more suitable for our analog quantum simulator. To benchmark that the final state \(\left\vert {\psi }^{R}\right\rangle={\hat{U}}_{R}({t}_{R})\left\vert 0\right\rangle\) can approximate the Haar-random states, we measure the participation entropy \({S}_{{{{\rm{PE}}}}}=-\mathop{\sum }_{k=1}^{D}{p}_{k}\ln {p}_{k}\), with D being the dimension of Hilbert space, p_k = ∣〈k∣ψ^R〉∣², and \(\{\left\vert k\right\rangle \}\) being a computational basis. Figure 2a shows the results of S_PE with different evolution times t_R. For the 23-qubit system, the probabilities p_k are estimated from the single-shot readout with a number of samples N_s = 3 × 10⁷. It is seen that the S_PE tends to the value for Haar-random states, i.e., \({S}_{{{{\rm{PE}}}}}^{{{{\rm{T}}}}}=N\ln 2-1+\gamma\) with N = 23 being the number of qubits and γ ≃ 0.577 as the Euler’s constant³⁶. Moreover, for the final state \(\left\vert {\psi }^{R}\right\rangle\) with t_R = 200 ns, the distribution of probabilities p_k satisfies the Porter-Thomas distribution (see Supplementary Note 4).

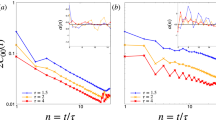
a Experimental verification of preparing the states via the time evolution of participation entropy. Here, we chose Q_R = {Q_1,↑, Q_2,↑, …, Q_12,↑, Q_2,↓, Q_3,↓, …, Q_12,↓} with total 23 qubits. The inset of (a) shows the corresponding quantum circuit. The dotted horizontal line represents the participation entropy for Haar-random states, i.e., \({S}_{{{{\rm{PE}}}}}^{{{{\rm{T}}}}}\simeq 15.519\). b Experimental results of the autocorrelation function C_1,1(t) for the qubit ladder with L = 12, which are measured by performing the quantum circuit shown in Fig. 1c, d. Here, we consider the state generated from \({\hat{U}}_{R}({t}_{R})\) with t_R = 200 ns, which is approximate to a Haar-random state. Markers are experimental data. The solid line is the numerical simulation of the correlation function C_1,1 at infinite temperature. The dashed line represents a power-law decay t^−1/2. Error bars represent the standard deviation.

Full size image

In Fig. 2b, we show the dynamics of the autocorrelation function C_1,1 measured via the quantum circuit in Fig. 1c with t_R = 200 ns. The experimental data satisfies C_1,1 ∝ t^−α, with a transport exponent α ≃ 0.5067, estimated by fitting the data in the time window t ∈ [50 ns, 200 ns]. Our experiments clearly show that spin diffusively transports on the qubit ladder \({\hat{H}}_{I}\)(1), and demonstrate that the analog quantum circuit \({\hat{U}}_{R}({t}_{R})\) with t_R = 200 ns can provide sufficient randomness to measure the autocorrelation function defined in Eq. (2) and probe infinite-temperature spin transport. We also discuss the influence of t_R in Supplementary Note 4, numerically showing that the results of C_1,1 do not substantially change for longer t_R > 200 ns. Moreover, in Supplementary Note 4, we show that for a shortly evolved time t_R ≃ 15 ns, the values of the observable defined in Eq. (4) are incompatible with the infinite-temperature autocorrelation functions. Given that the chosen initial state for generating the Haar-random state exhibits a high effective temperature associated with the Hamiltonian \({\hat{H}}_{R}\), the state would asymptotically converge to the Haar-random state with a sufficiently extended t_R. However, with t_R ≃ 15 ns, the time scale is too small to get rid of the coherence, and the value of S_PE for the state \(\left\vert {\psi }^{R}\right\rangle\) is much smaller than the \({S}_{{{{\rm{PE}}}}}^{{{{\rm{T}}}}}\) (see Fig. 2a), suggesting that \(\left\vert {\psi }^{R}\right\rangle\) with t_R ≃ 15 ns is far away from the Haar-random state, and cannot be employed to measure the infinite-temperature autocorrelation function (2). In the following, we fix t_R = 200 ns, and study spin transport in other systems with ergodicity breaking.

Subdiffusive transport with ergodicity breaking

After demonstrating that the quantum circuit shown in Fig. 1c can be employed to measure the infinite-temperature autocorrelation function C_1,1, we study spin transport on the superconducting qubit ladder with the disorder, whose effective Hamiltonian can be written as \({\hat{H}}_{D}={\hat{H}}_{I}+{\sum }_{m\in \{\uparrow,\downarrow \}}\mathop{\sum }_{j=1}^{L}{w}_{j,m}{\hat{\sigma }}_{j,m}^{+}{\hat{\sigma }}_{j,m}^{-}\), with w_j,m drawn from a uniform distribution [ − W, W], and W is the strength of disorder. For each disorder strength, we consider 10 disorder realizations and plot the dynamics of averaged C_1,1 with different W are plotted in Fig. 3a. With the increasing of W, and as the system approaches the MBL transition, C_1,1 decays more slowly. Moreover, the oscillation in the dynamics of C_1,1 becomes more obvious with larger W, which is related to the presence of local integrals of motion in the deep many-body localized phase⁵⁸.

a The time evolution of autocorrelation function C_1,1(t) for the qubit ladder with L = 12 and different values of disorder strength W, ranging from W/2π = 35 MHz (\(W/\overline{{J}^{\parallel }}\simeq 0.5\)) to W/2π = 70 MHz (\(W/\overline{{J}^{\parallel }}\simeq 9.6\)). Markers (lines) are experimental (numerical) data. b Transport exponent α as a function of W obtained from fitting the data of C_1,1(t). Error bars (experimental data) and shaded regions (numerical data) represent the standard deviation.

Full size image

We then fit both the experimental and numerical data with the time window t ∈ [50 ns, 200 ns] by adopting the power-law decay C_1,1 ∝ t^−α. As shown in Fig. 3b, we observe an anomalous subdiffusive region with the transport exponent α < 1/2. For the strength of disorder W/2π ≳ 50 MHz, the transport exponent α ~ 10⁻² indicates the freezing of spin transport and the onset of MBL on the 24-qubit system². Here, we emphasize that the estimated transition point between the subdiffusive regime and MBL is a lower bound since, with longer evolved time, the exponent α obtained from the power-law fitting becomes slightly larger (see Supplementary Note 6).

Next, we explore the transport properties on a tilted superconducting qubit ladder, which is subjected to the linear potential \({\hat{H}}_{L}=\mathop{\sum }_{j=1}^{L}\Delta j{\sum }_{m\in \{\uparrow,\downarrow \}}{\hat{\sigma }}_{j,m}^{+}{\hat{\sigma }}_{j,m}^{-}\), with Δ = 2W_S/(L − 1) being the slope of the linear potential (see the tilted ladder in the inset of Fig. 4a). Thus, the effective Hamiltonian of the tilted superconducting qubit ladder can be written as \({\hat{H}}_{T}={\hat{H}}_{I}+{\hat{H}}_{L}\). Different from the aforementioned breakdown of ergodicity induced by the disorder, the non-ergodic behaviors induced by the linear potential arise from strong Hilbert-space fragmentation^55,56,57. The ergodicity breaking in the disorder-free system \({\hat{H}}_{T}\) is known as the Stark MBL^{28,50,51,52,53,54}.

a Time evolution of autocorrelation function C_1,1(t) for the tilted qubit ladder with L = 12 and W_S/2π≤20 MHz. b is similar to (a) but for the data with W_S/2π≥24 MHz. Markers (lines) are experimental (numerical) data. c Transport exponent α as a function of W_S. For W_S/2π≤20 MHz and W_S/2π≥24 MHz, the exponent α is extracted from fitting the data of C_1,1(t) with the time window t ∈ [50 ns, 200 ns] and t ∈ [100 ns, 400 ns], respectively. Error bars (experimental data) and shaded regions (numerical data) represent the standard deviation.

Full size image

We employ the method based on the quantum circuit shown in Fig. 1c to measure the time evolution of the autocorrelation function C_1,1 with different slopes of the linear potential. The results are presented in Fig. 4a, b. Similar to the system with the disorder, the dynamics of C_1,1 still satisfies C_1,1 ∝ t^−α with α < 0.5, i.e., subdiffusive transport. Figure 4c displays the transport exponent α with different strengths of the linear potential, showing that α asymptotically drops as W_S increases.

Two remarks are in order. First, by employing the same standard for the onset of MBL induced by disorder, i.e., α ~ 10⁻², the results in Fig. 4c indicate that the Stark MBL on the tilted 24-qubit ladder occurs when W_S/2π ≳ 80 MHz (Δ/2π ≳ 14.6 MHz). Second, on the ergodic side (W_S/2π < 80 MHz and W/2π < 50 MHz for the tilted and disordered systems, respectively), the transport exponent α exhibits rapid decay with increasing W_S up to W_S/2π ≃ 20 MHz in the tilted system. Subsequently, as W_S continues to increase, the decay of z becomes slower. In contrast, for the disordered system, α consistently decreases with increasing disordered strength W. We note that the impact of the emergence of dipole-moment conservation with increasing the slope of linear potential on the spin transport, and its distinction from the transport in disordered systems remains unclear and deserve further theoretical studies.

Based on the novel protocol for simulating the infinite-temperature spin transport using the Haar-random state⁴⁰, we have experimentally probed diffusive transport on a 24-qubit ladder-type programmable superconducting processor. Moreover, when the qubit ladder is subject to sufficiently strong disorder, we observe the signatures of subdiffusive transport, accompanied by the breakdown of ergodicity due to MBL.

It is worthwhile to emphasize that previous experimental studies of the Stark MBL mainly focus on the dynamics of imbalance^50,59,60. Different from the disorder-induced MBL with a power-law decay of imbalance observed in the subdiffusive Griffith-like region⁶¹, for the Stark MBL, there is no experimental evidence for the power-law decay of imbalance^50,59,60. Here, by measuring the infinite-temperature autocorrelation function, we provide solid experimental evidence for the subdiffusion in tilted systems, which is induced by the emergence of strong Hilbert-space fragmentation^55,56,57. Theoretically, it has been suggested that for a thermodynamically large system, non-zero tilted potentials, i.e., Δ > 0, will lead to a subdiffusive transport with α ≃ 1/4^17,62. In finite-size systems, both results, as shown in Fig. 4 and the cold atom experiments on the tilted Fermi-Hubbard model⁶³ demonstrate a crossover from the diffusive regime to the subdiffusive one. Investigating how this crossover scales with increasing system size is a further experimental task, which requires quantum simulators with a larger number of qubits.

Ensembles of Haar-random pure quantum states have several promising applications, including benchmarking quantum devices^42,64 and demonstrating beyond-classical computation^{35,36,37,38,39}. Our work displays a practical application of the randomly distributed quantum state, i.e., probing the infinite-temperature spin transport. In contrast to employing digital random circuits, where the number of imperfect two-qubit gates is proportional to the qubit number^{36,37,38,39,40,41}, the scalable analog circuit adopted in our experiments can also generate multi-qubit Haar-random states useful for simulating hydrodynamics. The protocol employed in our work can be naturally extended to explore the non-trivial transport properties on other analog quantum simulators, including the Rydberg atoms^42,65,66,67, quantum gas microscopes^68,69, and the superconducting circuits with a central resonance bus, which enables long-range interactions^21,70,71.

Derivation of Eq. 4

Here, we present the details of the deviation of Eq. (4), which is based on the typicality^12,40,72. According to Eq. (2), \({c}_{\mu ;\nu }=\,{\mbox{Tr}}\,[{\hat{\sigma }}_{\mu }^{z}(t){\hat{\sigma }}_{\nu }^{z}]/D\), with D = 2^N. We define \({\hat{N}}_{\nu }=({\hat{\sigma }}_{\nu }^{z}+1)/2\), and then \({c}_{\mu ;\nu }=\frac{1}{D}\,{\mbox{Tr}}\,[{\hat{\sigma }}_{\mu }^{z}(t){\hat{N}}_{\nu }]\). By using \({\hat{N}}_{\nu }={({\hat{N}}_{\nu })}^{2}\), we have \({c}_{\mu ;\nu }=\frac{1}{D}\,{\mbox{Tr}}\,[{\hat{N}}_{\nu }{\hat{\sigma }}_{\mu }^{z}(t){\hat{N}}_{\nu }]\). We note that \({\hat{N}}_{\nu }\) is an operator which projects the state of the ν-th qubit to the state \(\left\vert 0\right\rangle\).

According to the typicality^12,40,72, the trace of an operator \(\hat{O}\) can be approximated as the expectation value averaged by the pure Haar-random state \(\left\vert r\right\rangle\), i.e.,

with N being the number of qubits. It indicates that the infinite-temperature expectation value \(\,{\mbox{Tr}}\,[\hat{O}]/D\) can be better estimated by the expectation value for the Haar-random state \(\langle r| \hat{O}| r\rangle\). Thus, \({c}_{\mu ;\nu }\simeq \langle r| {\hat{N}}_{\nu }{\hat{\sigma }}_{\mu }^{z}(t){\hat{N}}_{\nu }| r\rangle=\langle {\psi }_{\nu }^{R}(t)| {\hat{\sigma }}_{\mu }^{z}| {\psi }_{\nu }^{R}(t)\rangle\) for multi-qubit systems. Based on the definition of the projector \({\hat{N}}_{\nu },\, {\hat{N}}_{\nu }\left\vert r\right\rangle\) is a Haar-random state for the whole system except for the ν-th qubit, and in the experiment, only a (N − 1)-qubit Haar-random state is required.

Numerical simulations

Here, we present the details of the numerical simulations. We calculate the unitary time evolution \(\left\vert \psi (t+\Delta t)\right\rangle={e}^{-i\hat{H}\Delta t}\left\vert \psi (t)\right\rangle\) by employing the Krylov method⁴⁹. The Krylov subspace is panned by the vectors defined as \(\{\left\vert \psi (t)\right\rangle,\hat{H}\left\vert \psi (t)\right\rangle,{\hat{H}}^{2}\left\vert \psi (t)\right\rangle,\ldots,\, {\hat{H}}^{(m-1)}\left\vert \psi (t)\right\rangle \}\). Then, the Hamiltonian \(\hat{H}\) in the Krylov subspace becomes a m-dimensional matrix \({{\mbox{H}}}_{m}={{\mbox{K}}}_{m}^{{{\dagger}} }{\mbox{H}}{{\mbox{K}}}_{m}\), where H denotes the Hamiltonian \(\hat{H}\) in the matrix form, and K_m is the matrix whose columns contain the orthonormal basis vectors of the Krylov space. Finally, the unitary time evolution can be approximately simulated in the Krylov subspace as \(\left\vert \psi (t+\Delta t)\right\rangle \simeq {\,{\mbox{K}}\,}_{m}^{{{\dagger}} }{e}^{-i{{{{\rm{H}}}}}_{m}\Delta t}{{\mbox{K}}}_{m}\left\vert \psi (t)\right\rangle\). In our numerical simulations, the dimension of the Krylov subspace m is adaptively adjusted from m = 6 to 30, making sure the numerical errors are smaller than 10⁻¹⁴.

For the numerical simulation of the \({\hat{U}}_{R}({t}_{R})={e}^{-i{\hat{H}}_{d}{t}_{R}}\) in Fig. 1c, based on the experimental data of the XY drive, the parameters in \({\hat{H}}_{d}\) are Ω_j,m/2π = 10.4 ± 1.6 MHz, and ϕ_j,m ∈ [ − π/10, π/10].

Details of generating Haar-random states

In this section, we present more details about the generation of faithful Haar-random states. The analog quantum circuit employed to generate Haar-random states is \({\hat{U}}_{R}=\exp [-i({\hat{H}}_{I}+{\hat{H}}_{d})t]\), where \({\hat{H}}_{I}\) is given by Eq. (1) and \({\hat{H}}_{d}={\sum }_{m\in \{\uparrow,\downarrow \}}\mathop{\sum }_{j=1}^{L}{\Omega }_{j,m}({e}^{-i{\phi }_{j,m}}{\hat{\sigma }}_{j,m}^{+}+{e}^{i{\phi }_{j,m}}{\hat{\sigma }}_{j,m}^{-})/2\) is the drive Hamiltonian.

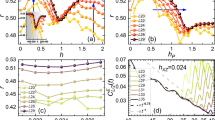
Here, we first numerically study the influence of the driving amplitude Ω_j,m. For convenience, we consider ϕ_j,m = 0, and isotropic driving amplitude, i.e., Ω = Ω_j,m for all (j, m). We chose Q_R = {Q_1,↑, Q_2,↑, …, Q_12,↑, Q_2,↓, Q_3,↓, …, Q_12,↓} with total 23 qubits. The dynamics of participation entropy S_PE for different values of Ω are plotted in Fig. 5a, and the values of S_PE with the evolved time t = 200 ns and 1000 ns are displayed in Fig. 5b. It is seen that for small Ω, the growth of S_PE is slow and with increasing Ω, it becomes more rapid. In this experiment, we chose \(\overline{\Omega }/\overline{{J}^{\parallel }}\simeq 1.4\) because the participation entropy can achieve \({S}_{{{{\rm{PE}}}}}^{{{{\rm{T}}}}}\) with a relatively short evolved time t ≃ 200 ns. As Ω further increases, the time when \({S}_{{{{\rm{PE}}}}}^{{{{\rm{T}}}}}\) is reached does not significantly become shorter. Based on the above discussions, \(\overline{\Omega }/\overline{{J}^{\parallel }}\simeq 1.4\) is an appropriate choice of the driving amplitude.

a The time evolution of the participation entropy S_PE for different driving amplitude Ω. b The value of S_PE at two evolved times t = 200 ns and 1000 ns, as a function of Ω. c The dynamics of S_PE with the phases of the microwave pulse drawn from [ − π, π]. Here, we present the numerical data of 5 different samples of the phases. The inset shows the dynamics in a shorter time interval. The horizontal dashed line represents the participation entropy for Haar-random states \({S}_{{{{\rm{PE}}}}}^{{{{\rm{T}}}}}\simeq 15.519\).

Full size image

Next, we numerically study the influence of the randomness for the phases of driving microwave pulse ϕ_j,m. In this experiment, by using the correction of crosstalk, the randomness of the phases is small, i.e., ϕ_j,m ∈ [ − π/10, π/10]. Here, we consider the phases with large randomness, i.e., ϕ_j,m ∈ [ − π, π]. The numerical results for the time evolution of S_PE with 5 samples of ϕ_j,m are plotted in Fig. 5c. With ϕ_j,m ∈ [ − π, π], the participation entropy can still tend to \({S}_{{{{\rm{PE}}}}}^{{{{\rm{T}}}}}\) around 200 ns. Only the short-time behaviors are slightly different from each other for the 5 samples (see the inset of Fig. 5c).