Introduction

Artificial intelligence is an important form of technology for human progress, which has a profound impact on the world’s economic recovery, social progress, and the life of all people1,2,3. However, the resulting problem is that traditional computers face serious challenges in terms of energy consumption4, computility5 and the limitations of Moore’s Law are forcing people to find a way to overcome this crisis6,7. Photonic integrated devices, on the other hand, have the inherent properties of high speed of photon transport, massive parallelism, and low power consumption, and have therefore received much attention as a promising candidate to realize fast and effective computation8,9.

Artificial neural networks have been introduced to photonics, i.e., optical neural networks (ONNs), which have been shown to be feasible in photonic integrated circuits and free-space optics10,11,12,13,14,15,16,17,18. These networks utilize both linear and nonlinear operations. Linear operations are implemented in a variety of ways, such as planar light conversion19, Mach-Zehnder interferometer (MZI) networks13, wavelength-division multiplexing20, and networks based on phase-change materials (PCM)12. The nonlinear operation involves the implementation of nonlinear activation functions (NAFs) on optical hardware platforms and is crucial for the training and decision-mapping process of the network. Existing solutions are categorized as optoelectronic or all-optical approaches. The response speed of optoelectronic devices limits the NAF based on optoelectronic methods and requires additional power consumption21,22,23. Therefore, an all-optical approach is required to realize large-scale scaling and high-speed applications of neuronal networks.

One of the challenges in achieving an all-optical approach is the insufficient nonlinear response of light in the medium for the photonic device to function as a neuron24,25,26. Although strong nonlinear materials have been discovered and structures that enhance nonlinearity have been designed through nonlinear activation using PCM, the slow recovery time of PCMs (approximately nanoseconds) and the need for additional energy stimulation hinder its suitability for high-speed optical computation27. Another form of all-optical NAF involves using two-dimensional (2D) material dispersions in combination with a rib waveguide relying on the evanescent field coupling (EFC)28. For example, the third-order nonlinearity of 2D MXene can be used on a silicon-based waveguide to realize the NAF26. However, the intrinsic EFC is generally weak along with large loss, which leads to a high activation threshold and high energy consumption, losing one of the most important advantages for optical computing. Furthermore, this approach is only applicable for 2D integration, and the working waveband is limited by the band gap of the waveguides (e.g., silicon). Therefore, there is an urgent requirement to establish a platform with a rapid response rate in a wide spectrum and 3D integration capability for efficient and low energy consumption all-optical NAFs. This will facilitate the development of miniaturized, intelligent, high-speed, and low-power all-optical neural networks.

We have proposed an integrated nonlinear optical activator that is based on butt-coupled 2D materials and OWGs obtained by femtosecond (fs) laser direct writing (FLDW) in glass. FLDW is an advanced rapid prototyping technology that enables the streamlined production of large-scale photonic circuits using a single control program29,30,31,32,33,34,35, which promotes intricate 3D internal machining and yields notable gains in spatial efficiency. The transparent characteristic of glass also enables the device to work in an ultra-broadband. For example, the typical transparent glass usually possesses a very wide bandgap (e.g., Eg > 3.5 eV for Eagle glass, Eg > 8.5 eV for silica glass) and the OWGs in the glass can work in a range from visible to near-infrared wavelength35,36,37. It is crucial that the waveguide optoelectronic field is tightly coupled to the medium. One possible solution is to utilize a near-surface waveguide or rib waveguide26,38, but this approach inherits the issues mentioned above. In contrast to the EFC, we realized that butt-coupling can enhance the light-matter interaction with the light directly transmitting through the integrated optical active components for the optical information modulation and decrease the optical loss. Furthermore, the glass matrix with embedded OWGs can act as an excellent substrate to support the 2D materials for integration on the edge side, which is difficult to achieve with other waveguides, such as silicon waveguides. 2D material is considered as a potential functional material for the NAF due to broadband nonlinear optical effect38,39. Consequently, an all-optical NAF based on 2D crystals/OWG devices could be realized by butt-integrating layered 2D materials to the end-face of OWGs via a dry transfer technique, which is very favorable for the on-chip integration of nonlinear computing devices.

In this study, we have developed nonlinear activators relying on the butt-coupling by integrating the 2D transition metal dichalcogenides (MoTe2) and OWGs. The activation function is achieved through the utilization of the saturable absorption (SA) and reverse saturable absorption (RSA) effect generated in the integrated system due to the interaction of light with a single-crystal 2D-MoTe2. To validate the principle, we carried out a benchmark machine-learning task. The MNIST handwritten digit recognition achieves remarkable accuracy using the optically measured activation function. Moreover, the same activation function is employed for a more intricate task, i.e., the classification of color images (CIFAR-10), and exhibits exceptional precision.

Results and discussion

Preparation of nonlinear activators

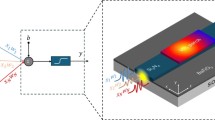
The on-chip device that achieves all-optical NAF consists of OWG and layered 2D material, in which the OWGs were prepared by FLDW. The experimental setup is shown in Fig. 1a, and the detailed preparation parameters are shown in the Methods section. After laser writing, the two ends of the samples are polished to obtain usable OWGs, whose top and side views are shown in Fig. 1b, c. The obvious discreteness of the OWG and the glass can be observed in the optical picture, which is mainly caused by the refractive index change due to the laser direct writing in the glass. The typical Raman spectra and mappings are shown in Supplementary Fig. 1, and the increase of the Raman intensity at around 487 cm−1 and 604 cm−1 confirms the densification of matter in the local region along with an increase of refractive index, which is related to the increase of the four-membered and three-membered rings inside the glass after the FLDW40, resulting in low-loss light guiding performance41.

Fig. 1: Preparation and characterization of optical waveguides (OWGs) in glass.
figure 1

a Schematic of femtosecond laser direct writing of OWGs in glass. b Top and (c) side view of OWGs. d The mode field images of OWGs in the range from visible to near-infrared range. Scale bar: 10 μm. The color bar represents the normalized intensity of light passing through the OWGs.

Full size image

To verify the usability of the OWGs, we investigated its transmission mode field and optical loss by a fiber-butt coupling method (Supplementary Fig. 2a). Initially, we employed an optical fiber to couple light into the OWG, and subsequently collected the light transmitted within the OWG using an objective lens to analyze the impact of light passing through the OWG. The insertion loss of the 1-cm OWG is 0.49 dB and 0.54 dB for 520 and 1550 nm, respectively. The propagation loss was determined to be 0.11 ± 0.02 dB/cm and 0.18 ± 0.02 dB/cm for 520 nm and 1550 nm, respectively (Supplementary Fig. 2b). Consequently, the potential coupling loss between the waveguide and fiber is 0.38 dB/facet. These results confirmed that the written waveguides show low loss performance in a broad range, which provides an excellent platform for photonic integrated devices.

Notably, in the visible to near-infrared region, the optical mode field that traversed through the OWG exhibited excellent symmetry, with a circular symmetry of Rx/Ry ~ 1, where Rx and Ry are the radii of the mode field in the X and the Y direction, as shown in Fig. 1d. According to the results, the OWGs with high symmetrical mode field in the visible to near-infrared range were obtained by FLDW technique, which satisfied the application of nonlinear activators in an ultra-broadband wavelength range (> 1000 nm).

For another component of the on-chip nonlinear activator, the 2D material, we selected layered 2H-MoTe2 due to its environmental and operation stability at room temperature42,43, which ensures stable and efficient use of the device, and potential applications in a broad wavelength range from visible to near-infrared44,45. 2D MoTe2 exhibits sub-picosecond carrier lifetimes46,47, predicting the material’s potential for ultrafast computing in the field of optical computing. 2D MoTe2 can significantly enhance the response range and device versatility by adjusting the bias48,49, which brings inspiration to extend the application range and increase the flexibility of the nonlinear activator. However, the traditional EFC activator can only use a small partial of the light in the waveguides and is not able to make full use of the optical modulation capability of 2D materials. We proposed a butt-coupling activator by integrating the 2D materials on the end surface of the OWGs in the glass. The preparation method of the nonlinear activator is depicted in Fig. 2a–c. Initially, we employed the mechanical exfoliation technique to acquire few-layered MoTe2 from bulk MoTe2, demonstrating its 2H structure through XRD results in Supplementary Fig. 3. Subsequently, employing a 2D material transfer system, we moved the few-layered MoTe2 to the end face of the OWG, creating the nonlinear activator with strong butt-coupling, as shown in Fig. 2c. Simultaneously, to explore the coupling between 2D MoTe2 and the OWG, we performed Raman characterization on the 3.7 nm thick MoTe2 activator, as depicted in Fig. 2d–f. The characteristic peaks of MoTe2, specifically A1g (172.3 cm−1) and E2g (232.9 cm−1), aligned with previous reports50. Figure 2e displays the mapping of E2g characteristic peak, distinctly illustrating the morphology of MoTe2 and the outline of the OWG. Worthy, the decrease in the Raman signal from A1g peak at the OWG ___domain results from the passing of signal through the OWG. Furthermore, in the feature peak mapping results at 487 cm−1, the outline of the OWG is discernible, suggesting effective contact between 2D MoTe2 and the OWG.

Fig. 2: Nonlinear activator preparation process.
figure 2

a The process of preparing a few layers of MoTe2, where PDMS stands for polydimethylsiloxane film. b Transferring 2D MoTe2 to OWG’s end face to form nonlinear activators. c Optical picture of a nonlinear activator and information on the thickness of few-layered MoTe2, where the thickness information was obtained by atomic force microscopy. Scale bar: 20 µm. d Raman spectra of a few layers of MoTe2. The scale bar in the inste is 20 µm. e 232.9 cm−1 mapping (MoTe2’s characteristic peak) and (f) 487 cm−1 mapping (OWG’s characteristic peak). The red dashed line is the outline of 2D MoTe2.

Full size image

Measurement of activation functions

To detect the NLO effect of 2D MoTe2 that was integrated to the end of the OWG, we used the double-balanced detection method as in Fig. 3a. Firstly, the power of the initial light (P0) is controlled by a tunable optical attenuator. Before being coupled into waveguides, the initial light was divided into two parts by a beam splitter with a splitting ratio of 9:1. The real power of the excitation light was calculated by 90%P0 - Ploss, which entered the optical power meter after passing through the nonlinear activator, and Ploss was the insertion loss including the propagation loss and coupling loss between the fiber and the OWG without MoTe2 that was determined above. The light with a power of 10%P0 was detected by another optical power meter as a reference. It is noteworthy that this method is able to eliminate the nonlinear effect of the OWG, ensuring that the resulting nonlinear signal is solely attributed to MoTe2 (see the discussion about Supplementary Fig. 4). Based on the NLO theory, the absorption coefficient of 2D MoTe2 is described as \(\alpha=\frac{{\alpha }_{0}}{1+I/{I}_{{sat}}}+\beta I\), where \(\alpha\) is the total absorption, α0 is a linear absorption coefficient, Isat is SA intensity, β is nonlinear absorption coefficient, the first term on the right-hand side denotes SA and the second term denotes RSA.

Fig. 3: Nonlinear optical (NLO) measurements of nonlinear activators.
figure 3

a Schematic diagram of the double-balanced detection setup for measuring the NLO properties of integrated devices. Optical response results of few-layer MoTe2 (b) under 1030 nm fs excitation and (c) under 515 nm fs excitation. The solid line is the fitted data. The nonlinear correlation between optical input and output of the activators (d) under 1030 nm fs excitation (e) under 515 nm fs excitation. The solid line represents the nonlinear activation function obtained from the result of Fig. 3b, c.

Full size image

For analyzing the SA response, the relationship between transmittance T and input light intensity I can be described as51,52:

$$T\left(I\right)=1-\Delta T\times \exp \left(-I/{I}_{{sat}}\right)-{T}_{{ns}}$$
(1)

where ∆T is the modulation depth, I is the input intensity, and Tns is the non-saturated loss. For the RSA response coexistence, we could get the following:

$$T\left(I\right)=1+\Delta T\times \exp \left(-\beta I\right)-{T}_{{ns}}$$
(2)

Figure 3b, c demonstrate the normalized transmittance for two samples (named as S1 and S2) as a function of the incident light intensity under 1030 nm and 515 nm fs laser excitation, respectively. The optical images and the thickness of the few-layered MoTe2 are shown in Supplementary Fig. 5. It is worth mentioning that, due to varying linear transmittance between S1 and S2, as displayed in Supplementary Fig. 6, we have opted for the normalized transmittance with respect to changes in incident light intensity to facilitate the presentation of the results.

The test results in Fig. 3b unequivocally show that, under 1030 nm fs light excitation, the transmittance of few-layered MoTe2 rises with an increase in the incident light intensity, which is attributed to the photobleaching (PB) effect induced by the Pauli exclusion principle, namely, the SA effect. The modulation depth ∆T for S1 and S2 is 0.11 and 0.12, respectively, and the SA intensity \({I}_{{sat}}\) is 37.17 μW and 15.17 μW, respectively. Furthermore, we confirm that the nonlinear photoresponse of the integrated devices remains unchanged after storage for one year at room temperature, as shown in Supplementary Fig. 7, which indicates the good stability of 2H-MoTe2. It is interesting that in contrast to the 1030 nm excitation, the optical response under 515 nm fs light excitation is RSA effect, and the transmittance of MoTe2 decreases with the increase of incident light intensity (Fig. 3c). The RSA effect has diverse causes, including the two-photon absorption effect and the excited state absorption effect53,54, which are elaborated in the Supplementary Fig. 8. The modulation depths ∆T for S1 and S2 are 0.02 and 0.39, respectively. To reveal how the nonlinear properties of the MoTe2/OWG integrated system are  affected by the thickness of MoTe2, we have carried out systematical investigations by integrating MoTe2 with varied thicknesses to OWGs and tested their nonlinear photoresponse. All the MoTe2 with a thickness from 10 to 80 nm in the integrated devices exhibited SA behavior under 1030 nm fs light excitation (Supplementary Fig. 9a–h). Isat first decreases and then increases with the increase of thickness, while ∆T changes oppositely, as shown in Supplementary Fig. 9i. The obtained smallest (largest) Isat (∆T) reaches 2.89 μW (0.177) with the thickness of MoTe2 at approximately 22.3 nm when excited by 1030 nm fs laser. The dependence of the third-order nonlinear susceptibility imaginary part (Imχ(3)) on the thickness may be responsible for the thickness dependence of Isat (see the discussion about Supplementary Fig. 9)55. In addition, MoTe2 exhibited SA effects under 800 nm and 1550 nm fs laser excitation, as shown in Supplementary Fig. 10. As a result, the nonlinear response of MoTe2 can operate in an ultra-broad wavelength range with the width larger than 1000 nm, thus supporting the ultra-broadband response of MoTe2/OWG devices.

Near all the 2D materials exhibit similar NLO response, SA, when the energy of the excitation light is bigger than that of the band gap56,57. However, the NLO response of MoTe2 is opposite at 1030 and 515 nm. In fact, under 515 nm optical excitation, the nonlinear response changes from RSA to SA as the power density increases, as shown in Supplementary Fig. 11. This is due to the competition between the many-body effect induced absorption enhancement and non-thermalized carriers induced bleaching53.

From the above nonlinear results, we can get four NAFs in the visible to near-infrared range. The nonlinear threshold was defined as the optical power required to generate a 50% change in the power transmission relative to the transmission with null input58,59. The nonlinear thresholds for the four activation functions are, therefore, 47.8 µW (S1 excited by 1030 nm laser), 14.2 µW (S2 excited by 1030 nm laser), 21.7 µW (S1 excited by 515 nm laser) and 5.5 µW (S2 excited by 515 nm laser), respectively. In addition, the activation threshold could be down to 4.9 μW by optimizing the thickness of MoTe2, as shown in Supplementary Fig. 12. Simultaneously, we illustrate the nonlinear correlation between optical input and output as the NAFs in the nonlinear activation unit, depicted in Fig. 3d, e. Therefore, the NAFs can be defined as \(f\left(I\right)=T\left(I\right)\times I\), which play a unique role in the nonlinear operation. In the following chapters, these NAFs are used to recognize and classify pictures in ONNs.

To study the response time of the all-optical device, we have investigated the kinetic process of carrier relaxation in the core material (MoTe2) of the nonlinear activator using transient absorption spectroscopy (TAS) and pump-probe techniques. The relaxation process of photogenerated carriers in the spectral range of 500–900 nm was investigated in detail using 400 nm as the pump light (Fig. 4a–c). The pump-probe results were obtained with 520 nm as the pump light and 1040 nm as the probe light (Fig. 4d). The positive photoinduced absorption (PIA) signal was observed in the range of 500–600 nm. The relaxation process of the photogenerated carrier initially exhibited a negative PB signal in the range of 700–900 nm caused by the state filling effect excited by the pump light (Fig. 4b).

Fig. 4: Transient photoresponse time of the MoTe2/OWG devices.
figure 4

a Transient absorption spectrum of MoTe2 excited by 400 nm at a pulse width of 200 fs. The change in optical absorption is in units of optical density (OD or mOD, where 1 OD = 1 × 103 mOD.) obtained from the probe intensities when the sample is pumped and unpumped. Black box range represents the positive photoinduced absorption (PIA) signal. Red box range is the negative photobleaching (PB) signal. b Transient absorption spectra with different pump-probe time delays. c Decay profiles of transient differential absorption monitored at different wavelengths. The solid lines represent the corresponding fitting results. d Transient reflection dynamics of MoTe2 at 520 nm with a pump intensity of 4.10 GW cm−2, while the solid lines represent the fitting. ∆R is the change in reflection.

Full size image

To further investigate the carrier relaxation processes, we fitted and analyzed the TAS (Fig. 4c for 500–900 nm) and pump-probe results (Fig. 4d for 1040 nm). The relaxation kinetic process of 2D MoTe2 can be expressed as:

$$g\left(t\right)={A}_{1}\exp \left(-\frac{t}{{\tau }_{1}}\right)+{A}_{2}\exp \left(-\frac{t}{{\tau }_{2}}\right)$$
(3)

where g(t) is the transient signal at the probe wavelength, A1, and A2 are the relative amplitudes, t is the delay time, and τ1 and τ2 are the lifetimes of the excited carriers for the fast and slow components of the relaxation process respectively. We attributed the first-lifetime process (τ1) to the thermal equilibrium of the hot carriers with the lattice. The second-lifetime process (τ2) is the electron-hole recombination process60,61. The time scale of the prompt relaxation process is in the picosecond range from 0.2 to 18.3 ps, which depends on the wavelength and is in agreement with the previously reported values46,47. Especially, the fast response time is 0.48 ps and 0.69 ps for 515 nm and 1040 nm, respectively. The fast carrier relaxation process determines the recovering rate of the nonlinear activator to its original state within τ1. Correspondingly, the response rate of this all-optical nonlinear activator is up to 2.08 THz at 515 nm and 1.45 THz at 1040 nm, which allows for ultrafast information processing.

Principle verification of on-chip NAFs

The schematic of the prepared ONN structure in the glass is shown in Fig. 5a, which includes an input layer, a linear operation, a nonlinear operation and an output layer. The optical interference unit performs the linear operation, and the nonlinear operation is performed by the nonlinear activation unit. The optical interference unit consists of MZIs array, and the nonlinear activation unit consists of 2D-MoTe2 and OWG. The calculation process of the constructed optical neuron is shown in Fig. 5b. The optical signal in the input layer passes (\({Z}_{i}^{l-1}\)) through the MZIs array to complete the linear matrix operation (\({\sum}_{i}{w}_{{ji}}^{(l)}{Z}_{i}^{(l-1)}\)), that is \({a}_{j}^{l}\), the input optical signal is weighted and combined. Then, the optical signal is operated through nonlinear operation (\(f({a}_{j}^{l})\)), and finally the output light is obtained (\({Z}_{j}^{l}\)). Therefore, we can take advantage of the NLO properties of 2D MoTe2 to perform nonlinear activation operations.

Fig. 5: Optical neuron computing process.
figure 5

a Optical interference and nonlinear activation units comprising optical neural networks (ONNs). b Schematic diagram of the computation of artificial neurons. \({Z}_{i}^{l-1}\) is the optical signal in the input layer. \({w}_{{ji}}^{(l)}\) stands for the linear matrix operation in the optical interference unit. \({a}_{j}^{l}\) is the result of the linear matrix operation. \(f({a}_{j}^{l})\) stands for the optical signal operated through nonlinear operation. \({Z}_{j}^{l}\) is the final output light.

Full size image

The Pytorch framework was utilized to perform picture recognition and classification using the experimentally measured SA and RSA NAFs. Specifically, the MNIST dataset and CIFAR-10 dataset were used for the feasibility verification of our all-optical NAFs, as shown in Figs. 6 and 7. The network’s performance is evaluated based on its accuracy in classifying images from the MNIST and CIFAR-10 datasets. The MNIST dataset is comprised of 70,000 grayscale images of handwritten digits, encompassing 60,000 images intended for training and 10,000 images designated for testing purposes. In parallel, the CIFAR-10 dataset is composed of 60,000 color images, with 50,000 images allocated for training purposes and 10,000 images reserved for testing. Images of the MNIST dataset are grayscale with a size of 28 × 28 pixels, and the CIFAR−10 dataset images are RGB-colored with 32 × 32 pixels in size.

Fig. 6: Classification performance on MNIST.
figure 6

MNIST is Modified National Institute of Standards and Technology database. a Fully connected layer network structure for the MNIST classification task. Construct the confusion matrix of the NAF test dataset from (b) the saturable absorption and (c) reverse saturable absorption activators.

Full size image
Fig. 7: Classification performance on CIFAR-10.
figure 7

The CIFAR-10 dataset (Canadian Institute For Advanced Research) is a collection of images that are commonly used to train machine learning and computer vision algorithms. a ONN architecture for the CIFAR-10 classification task. b, c Confusion matrices for the NAF test dataset constructed from the saturable absorption and reverse saturable absorption properties of MoTe2.

Full size image

For the MNIST dataset, the network consisted of a full connection layer that was three-layered, as shown in Fig. 6a. The initial layer was made up of 128 neurons with 784 × 128 connections. The second and third layers possess 64 and 10 neurons, respectively, equating to 128 × 64 and 64 × 10 connections, correspondingly. The third layer comprises merely ten neurons, representing ten digits ranging from 0 to 9 as its outputs. The initial two networks are activated by the SA or RSA activation function behind each layer, and the last layer utilizes a softmax function to convert input values to probability distributions. The corresponding loss function used is a cross-entropy loss function. For the following hyperparameter, a Stochastic gradient descent optimizer is employed with a learning rate of 0.001. The specific training process is presented in Supplementary Fig. 13. The greyscale values (0–255) of the pictures were normalized to be in the range from 0 to 1, and similarly, the input power of the experimentally measured NAF was normalized to be in the range from 0 to 126. The greyscale information of the pixels in the image was then mapped to the power in order to match with our experimentally measured NAF. Since it is possible for the weights and biases of each neuron to be negative during the simulation, we analogize to the ReLU function by defining f(x) = 0 for x < 0, i.e., only the part of the NAF that is positive is utilized, which is mainly due to the positive intensity of the optical signal captured by the photodetector.

The four NAFs obtained using the MoTe2 optical nonlinearities can be implemented for the MNIST classification task, as shown in Fig. 6b, c, and Supplementary Fig. 14. The dataset testing accuracy is 96.0% (S1–SA) and 97.4% (S2-RSA), respectively, which is better than or comparable with the previously reported values62,63. Moreover, the accuracy reaches 97.6% with a suitable thickness of MoTe2 (17.3 nm) (Supplementary Fig. 15). The results show excellent performance, and our four NAFs are comparable to commonly used electronic neural networks. Across 80 training epochs, we have showcased the accuracy and loss over varying cycle durations for four nonlinear activators, linear activation functions, and ReLU activation functions, as shown in Supplementary Fig. 16. Our findings unequivocally establish the superiority of the nonlinear activation function, which is constructed using the optical nonlinearity of MoTe2, in terms of image recognition capability, as it can effectively rival the ReLU function. Furthermore, supplementary materials (Supplementary Fig. 14) present the outcomes of the MNIST handwriting training employing both the linear activation function and the ReLU activation function.

To verify the broader applicability of these SA and RSA NAFs, we trained the activator on the CIFAR−10 dataset. This dataset is more complex in shape and has a richer color palette than the MNIST dataset. Figure 7a demonstrates a closer analysis of the trained network. The network is improved on ResNet-18, and the framework mainly consists of 17 convolutional layers and 2 fully connected layers. The RGB image is subjected to a 3 × 3 downsampling convolutional layer, followed by 4 layers of residual operations corresponding to 8 residual blocks. Each residual block consists of two 3 × 3 convolutional layers with two batch normalization (BN) operations. Each BN operation is followed by a nonlinear activation operation provided by our NAF. The data at the end of the residual operation is output through the fully connected layer. The detailed training procedure is described in the Supplementary Fig. 17. After 250 epochs of training, 10 types of RGB images can be easily identified and classified, as shown in Fig. 7b, c, and Supplementary Fig. 18. The dataset testing accuracies are 94.6% (S1–SA), and 94.3% (S1-RSA), respectively. Furthermore, more detailed testing results and details are shown in Supplementary Figs. 18 and 19. Despite exhibiting a slightly lower test accuracy on the CIFAR-10 dataset compared to the conventional ReLU function (95.5%), it demonstrates a remarkable enhancement in model recognition precision relative to scenarios devoid of any activation function (68.9%). This underscores its inherent advantages and potential applications within the ___domain of deep learning. Furthermore, the MoTe2 material exhibited a SA effect under 1550 nm excitation, as shown in Supplementary Fig. 20a. The NAF for optical signal input and output (Supplementary Fig. 20b), has an activation threshold of 0.94 μW, which is lower than previously reported threshold27,64,65. The activation function can also be used to identify handwritten digits (MNIST) and color photographs (CIFAR−10) (Supplementary Fig. 21). Based on the above results, the optical nonlinearity of MoTe2 on chip can effectively recognize and classify gray and RGB color images.

The high compatibility and integrability enable 2D materials transferred to various substrates, especially to the photonic circuits, such as silicon, silicon nitride, and lithium niobate waveguides, to construct the integrated devices and all-optical nonlinear activators for ONNs. However, most reported all-optical nonlinear activators based on the 2D materials/OWGs integrated systems rely on EFC, and the intrinsic low efficiency of EFC gives rise to large optical loss and a high activation threshold for ONNs, which prevents full use of the strong optical modulation capability and brings a high energy consumption62,63,66,67. In addition, the previous integration is generally limited in two-dimension and the working waveband is limited by the band gap of the waveguide materials. The current butt-coupling integrated system provides a distinctive platform to overcome these issues and enables advanced NAFs. Table 1 shows the different forms of activators. The activators in the form of MoTe2/OWG possess a lower nonlinearity threshold and a wider working waveband compared to the activators consisting of a silicon-based waveguide form. Our activators exhibit ultra-low power consumption down to 0.94 μW, and the single device size is about ~50 μm2, and both values are one order of magnitude smaller than most reported ones27,51,64,65,67,68. Furthermore, FLDW allows for 3D creation of OWGs in glass, which promises 3D integration for high-speed, ultra-broadband and dense integration ONNs, for large-scale photonic computation systems. First, 3D large-scale OWG arrays can be fabricated in glass by FLDW technique29,30,31,32,33,34,35 and integrated MoTe2/OWGs arrays have also been obtained (Supplementary Fig. 22). By using large-scale 2D material transfer techniques66,69,70, larger-scale and dense integrated devices can be created on one glass chip. Second, the activators formed by the butt-coupling mothed have excellent scalability, especially since it is possible to create multi-layer ONNs within a single substrate (Supplementary Fig. 23a) and multiple substrates (Supplementary Fig. 24). Within a single glass substrate, as shown in Supplementary Fig. 23a, multiple single-layer optical neurons could be prepared on a single glass substrate using FLDW. In each layer, the output of the linear transformation uses the butt-coupling strategy to form activators. Optical fibers can connect each layer of neurons to implement multi-layer ONNs within a single glass substrate. We have demonstrated the coupling of multiple layers of OWGs within a single substrate (Supplementary Fig. 23b). To this end, polymer OWG fabricated by fs laser two-photon polymerization may also be a possible alternative for interconnecting between ONN layers71,72,73. In addition, the NAF structure can be integrated with other layers using other substrates. A multi-layer neural network of optical neurons containing butt-coupled structures can be formed by aligning two MoTe2/OWG devices (Supplementary Fig. 24). Thus, our developed strategy and devices support large-scale, dense integration and multi-layer coupling networks, which implies that parallel and cascaded processing of large-scale data could be realized. Overall, our all-optical activator has the potential for lower optical thresholds and high-density integration and presents a substantial conceptual advance in ONN platforms.

Table 1 Comparison of optical thresholds and sizes of different NAFs
Full size table

In conclusion, we have successfully created an integrated all-optical nonlinear activator with a low activation threshold, an ultra-fast computational speed, and broadband response, utilizing a butt-coupling 2D MoTe2/OWG platform. The activator functions are derived from the optical nonlinearities of MoTe2, including the SA and RSA effects. The wideband optical nonlinearity significantly enhances the activator’s flexibility. The effectiveness of this activation function has received confirmation through the employment of MNIST handwriting dataset. An activation threshold is as low as 0.94 μW, which is one order of magnitude smaller than previously reported values and a high classification accuracy of 97.6% was achieved. The response rate of the all-optical nonlinear activator is up to 2.08 THz, which allows for ultrafast information processing. Additionally, the activator exhibited notable abilities regarding recognition and categorization when utilized on the more intricate and colorful CIFAR-10 dataset. Our approach presents an innovative solution for incorporating optical NAFs, exhibiting substantial potential and feasibility for the future development of 3D all-optical on-chip neural networks. The represented NAFs could also be used to process other data sets, such as video, audio, and text13,74,75. Combining the programmability of OWGs written by fs laser76,77,78 and the integrability of the light source in glass29,79,80, the applications of the present NAFs could be extended further.

Methods

Material synthesis

Optical waveguide: A diode-pumped Yb: KGW laser (PHAROS PH2, Light Conversion) provides 169 fs pulses at a central wavelength of 1030 nm with a repetition rate of 1 MHz. The laser beam is focused below the surface of borosilicate glass (Corning Eagle XG) samples. A high-precision XYZ translation stage (Aerotech, ABL1000WB-100) is used to control the 3D movement of the glass sample at the set routine and speed. The pulsed laser was focused through the objective (Nikon LU Plan, 50X, NA = 0.55).

MoTe2: 2H-MoTe2 crystal (product no. 100705) was purchased from Nanjing MKNANO Tech. Co., Ltd. (www.mukenano.com). Few-layered MoTe2 crystals are obtained by mechanical exfoliation method, and MoTe2 is transferred to the end surface of OWG using a self-constructed 2D material transfer system.

Material Characterization: Raman characterization of MoTe2 nanosheets and optical waveguide was carried out using a confocal microscopy system (RENISHAW, Invia) with a 532 nm continuous wave laser. The thickness of the MoTe2 nanosheets was measured using atomic force microscope (Bruker, Dimension ICON). XRD was performed using a Bruker D8 Advance.

Nonlinear optical measurements

The experimental sources of the Intensity-scan on chip were pulses of 169 fs from a diode-pumped Yb: KGW laser (PHAROS PH2, Light Conversion) operating at 1030 nm with a second harmonic at 515 nm and a pulse repetition rate of 1 MHz. The excitation light at other wavelengths (800 nm and 1550 nm) was obtained from a light parametric amplifier (Orpheus-NEO-UP, Light Conversion) with a pulse repetition frequency of 55 KHz.

Ultrafast carrier dynamic measurements

The carrier dynamic properties were measured using time-resolved degenerate pump-probe and transient absorption techniques. In the pump-probe system, the transient reflection was measured using a 380-fs pulse laser with a wavelength of 520 nm and a repetition rate of 10 kHz. The TAS was acquired using a fs transient absorption spectrometer (Light Conversion Harpia). The excitation source was a 200-fs pulsed laser at 400 nm wavelength with a repetition rate of 1 kHz, and the probe light was a continuous white light spectrum in the range 500–900 nm. The amount of change in optical absorption is in units of optical density (OD or mOD, where 1 OD = 1 × 103 mOD.), which is obtained from the probe intensities when the sample is pumped and unpumped (\(\Delta {OD}=-1000\times {\log }_{10}{I}_{{pumped}}/{I}_{{unpumped}}\)). When ∆OD > 0, it means that the pumped sample absorbs the probe light, i.e., the photoinduced absorption effect. When ∆OD < 0, it represents an increase in transmission of probe light by the pumped sample, i.e., the photobleaching effect.