Interfering Josephson diode effect in Ta₂Pd₃Te₅ asymmetric edge interferometer

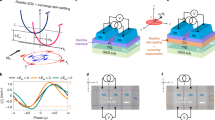
The semiconductor diode is a fundamental component in modern electronics due to the non-reciprocal responses¹. Analogous non-reciprocal charge transport in superconductors - namely superconducting diode effect (SDE) - has great potential for superconducting quantum electronics, since Josephson junctions (JJs) and superconducting quantum interference devices (SQUIDs) have been key components of superconducting quantum devices^2,3. SDE in the JJs - namely Josephson diode effect (JDE) - and in intrinsic superconductors has been theoretically proposed in various systems with broken time-reversal and inversion symmetries^{4,5,6,7,8,9,10,11,12}. Field-induced and field-free SDE/JDE has been experimentally observed in various superconductors^{13,14,15,16,17,18,19,20}, supercurrent interferometers^21,22,23,24, and other systems^{25,26,27,28,29}. Interestingly, asymmetric supercurrent interferometers or SQUIDs with a non-sinusoidal current-phase relation (CPR) provide a good platform to realize JDE (Fig. 1a) with ultra-small magnetic fields and ultra-low power consumption^21,22, both of which are crucial elements for applications at ultra-low temperatures. Moreover, it is quite feasible to promote their efficiency by varying the generic configuration⁹, which is compatible with state-of-the-art lithography technology, and integrate them into large-scale superconducting quantum circuits.

a JDE in the asymmetric SQUID formed by two asymmetric JJs. b An asymmetric SQUID formed by asymmetric edge states in Ta₂Pd₃Te₅ JJ and its device configuration. The upper and lower edges are the palladium and tantalum-tellurium atomic chain, respectively. The inset shows the photomicrograph of device S2, and the white scale bar corresponds to 1 μm. c–f Simulated CPR based on the minimal model. JDE only exists in (d) with different supercurrents, a nonzero magnetic field (ϕ/ϕ₀ ≠ 0), and higher harmonics in the CPR (α_n ≠ 0). The red and pink arrows represent the maximum(I_c+) and minimum(I_c−) current in the CPR, respectively. g Band structure of monolayer Ta₂Pd₃Te₅. Edge states (blue and red lines) exist near the Fermi level and are marked in the corresponding edges of (b). h \(\left\vert {I}_{b}\right\vert -\left\vert V\right\vert\) curves for positive and negative current sweep at B_z = 8.4 mT. i, j Alternating switching between the superconducting and normal states at B_z = 8.4 mT and 10 mK in device S2.

Full size image

Essentially, the appearance of JDE is related to the difference between maximum(I_c+) and minimum(I_c−) current in the CPR. The conventional CPR is an odd function of superconducting phase difference φ between superconducting leads, entailing a zero supercurrent at φ = 0, which shifts [meaning I(φ = 0) ≠ 0] when both time-reversal and chiral symmetries are broken^21,30,31. To achieve JDE, other mechanisms to cause the CPR deviating from standard sinusoidal I(φ) = I_c sin(φ) will also be introduced. The characteristics of CPR, which are usually inferred by the interference pattern of SQUIDs and the Shapiro steps due to AC Josephson effect, as well as the newly-discovered JDE with non-reciprocal critical current, have been widely harnessed to detect the anomalous superconductivity^32,33, such as proximitized helical/chiral topological edge states. In turn, in a SQUID constructed by two asymmetric edge states of the topological insulator, JDE with an unconventional CPR could be easily realized with highly-tunable efficiency⁵ and relatively easy fabrication (Fig. 1b). The relatively small number of edge supercurrent channels, in comparison to the case of bulk states transport, may contribute to the small critical current and power consumption^33,34.

More precisely, the interferometer formed by two asymmetric edge supercurrents (Fig. 1b) can be viewed as a SQUID with two different JJs and induces JDE with requirements similar to the asymmetric SQUID⁹ in Fig. 1a. According to Souto et al.⁹, a minimal model with n JJs concatenated in an interferometer array is applied to account for the origin of JDE, and the CPR only takes the first and second harmonic contribution into consideration. The current is written as \(I(\varphi,\phi /{\phi }_{0})=\mathop{\sum }_{1}^{n=2}{I}_{n}sin(\varphi+2\pi (n-1)\phi /{\phi }_{0})+{\alpha }_{n}{I}_{n}sin(2\varphi+ 4\pi (n- 1)\phi / {\phi }_{0})\) for two-JJs in parallel, where I_n (α_nI_n) is the amplitude of the first (second) harmonic content for the nth JJ, α_n is the current coefficient of the higher harmonic, ϕ is the magnetic flux and ϕ₀ = h/2e is the magnetic flux quantum. In Fig. 1c–f, the simulations of the CPR using the aforementioned formula serves the purpose of illustrating three key requirements that contribute to the difference between I_c+ (red arrow) and I_c− (pink arrow). First, an external magnetic field (ϕ/ϕ₀ ≠ 0) is necessary to break time-reversal symmetry and induce nonzero current at φ = 0 in the CPR (Fig. 1d–f). Second, the supercurrent of each edge, including all the harmonic contributions, should be different (see Fig. 1d, e and detailed simulations in Supplementary Fig. 2). This condition can be realized by two interfering edge states with different dispersion⁵. It can also be met, for example, by two superconducting quantum point contacts with different transmission coefficients⁹, which may be linked to various factors such as different edge states, disorder situations, among others. All of these can cause the different supercurrent of edges in our devices, which is actually quite unique in topological materials. Finally, at least one edge channel should be transmissive so that the CPR acquires a higher harmonic (α_n ≠ 0)^9,35 (see Fig. 1d, f).

Interfering JDE

In this work, highly efficient JDE, residing in the tilting supercurrent pattern, is reported in a Ta₂Pd₃Te₅ edge interferometer at very small B_z and is driven by low power consumption to achieve a highly stable rectification effect. It is also accompanied by fractional Shapiro steps, revealing the higher harmonic contributions of the non-negligible transmission channels. The choice of Ta₂Pd₃Te₅ is based on the following reasons: (1) Ta₂Pd₃Te₅ is a van der Waals material with quasi-one-dimensional (1D) chains³⁶ and can be easily mechanically exfoliated. (2) As a 2D topological insulator, where multiple layers could be viewed as simple stacking of monolayers due to very weak inter-layer coupling^37,38, it hosts excitonic insulator states^39,40,41 and edge states observed by scanning tunneling microscopy^40,42 and transport measurements^38,43. Notably, owing to the anisotropic bonding energy of 1D chains, the edges possess different atomic chains (Pd and Ta-Te atomic chains), resulting in asymmetric dispersion, as shown by the red and blue lines/arrows in Fig. 1b–g. (3) Superconductivity can be easily achieved in this system through doping or high-pressure techniques^44,45,46. Therefore, by proximity effect, the induced supercurrent (Supplementary Fig. 1) carried by edge states of Ta₂Pd₃Te₅ can be used to realize an asymmetric SQUID with the interfering JDE.

In Fig. 1h, JDE reaches up to 73% efficiency [\(\eta=2({I}_{c+}-\left\vert {I}_{c-}\right\vert )/({I}_{c+}+\left\vert {I}_{c-}\right\vert )\)] at an out-of-plane magnetic field B_z = 8.4 mT in \(\left\vert {I}_{b}\right\vert -\left\vert V\right\vert\) traces. The measurement is performed in the following sequence: (1) Zero-to-positive current sweep (0-p, red scatters); (2) Positive-to-zero current sweep (p-0, blue line); (3) Zero-to-negative current sweep (0-n, magenta scatters); (4) Negative-to-zero current sweep (n-0, cyan line). The retrapping current I_r+ (I_r−) and switching current I_c− (I_c+) are defined during the positive-to-negative (negative-to-positive) current sweep. I_r+ (\(\left\vert {I}_{r-}\right\vert\)) is nearly the same as I_c+ (\(\left\vert {I}_{c-}\right\vert\)), suggesting negligible capacitance in the JJ^6,11,25. Unlike reciprocal transport (\({I}_{c+}=\left\vert {I}_{c-}\right\vert\) and \({I}_{r+}=\left\vert {I}_{r-}\right\vert\)), the difference between I_c+ (I_r+) and \(\left\vert {I}_{c-}\right\vert\) (\(\left\vert {I}_{r-}\right\vert\)) indicates the presence of JDE in this JJ.

The superconducting half-wave rectification is observed at B_z = 8.4 mT and 10 mK in Fig. 1i, j. The ‘on’/‘off’ (superconducting/normal) states are switched by alternating current bias (I_b = ±400 nA). Many cycles of these alternating measurements are conducted over a measurement time exceeding 1.5 h, demonstrating the high stability of this rectification device, which is crucial for its potential applications. Intriguingly, the estimated switching power (\({I}_{b}^{2}{R}_{N}\)) reaches the picowatt level (6.4 pW for device S2 with R_N = 40 Ω, 0.56 pW for device S1 in Supplementary Fig. 1), which is four and eight orders of magnitude smaller than the field-free Josephson diode²⁵ and another bulk superconducting diode¹³, respectively. This power is also close to or even lower than the power of nanowire/nanoflake SDE systems^19,21,47,48 and thin film SDE systems^15,18,49. The ultra-low switching power in Ta₂Pd₃Te₅ Josephson diodes may be attributed to fewer edge supercurrent channels, making it a potential candidate for applications. Nonetheless, further technological advancements are required to optimize the efficiency, magnetic field conditions, and power consumption not only in this Josephson diode but also in other superconducting diodes.

To further study the origin of JDE, we measure the magnetic flux dependence of the JDE in the Ta₂Pd₃Te₅ JJ. In Fig. 2a, dV/dI as a function of B_z and I_b displays a SQUID pattern for device S1, suggesting the supercurrent interference of two channels in this JJ. The sawtooth-shaped I_c pattern shows up, usually indicating the involvement of higher harmonic components due to non-negligible transmission channels⁵⁰, consistent with findings from Supplementary Note 1. The position-dependent supercurrent density distribution (Fig. 2b) extracted from the SQUID pattern³³ and the estimated enclosed area formed by two interference supercurrents (see Supplementary Note 3 and 9) illustrate the supercurrent mainly originates from edge states of the JJ, confirming the reported edge state in Ta₂Pd₃Te₅^38,40,42. In Fig. 2c, the B_z-dependent I_c+ and \(\left\vert {I}_{c-}\right\vert\) extracted from Fig. 2a shows the asymmetric Josephson effect. Several features, such as the large deviation of I_c from zero at half flux quantum in Fig. 2c and JDE in Fig. 2d, indicate the asymmetric edge supercurrent channels in this JJ, as detailed in “Methods” section. Moreover, \(\Delta {I}_{c}={I}_{c+}-\left\vert {I}_{c-}\right\vert\) oscillates with B_z (orange curve in Fig. 2d), which can be called interfering JDE and is approximately described by the two-JJs model (black line in Fig. 2d, and see the detail in “Methods” section). This type of JDE has been theoretically predicted in Weyl semimetals with broken inversion symmetry and asymmetric helical edge states⁵. Furthermore, the oscillating Josephson diode efficiency (cyan line in Fig. 2d) shows a maximal efficiency η≈45% at 6.4 mT. It is intriguing that η can reach 10% at B_z = −0.5 mT. Also, the required field can be significantly reduced when the enclosed area of the SQUID loop is increased, which could be easily realized in the experimental setup^21,22.

a SQUID pattern of device S1 at 15 mK. b Position-dependent supercurrent density distribution. Inset: A sketch of edge supercurrents-formed JJ. c B_z-dependent I_c+ and \(\left\vert {I}_{c-}\right\vert\). The switching current I_c+ and I_c− are extracted by  ~15% of normal resistance. d Non-reciprocal critical current \(\Delta {I}_{c}={I}_{c+}-\left\vert {I}_{c-}\right\vert\), Josephson diode efficiency η and fitted ΔI_c (black line) as a function of B_z. e Temperature-dependent I_c+, I_c−, ΔI_c and η for device S1 at B_z = 6.4 mT. The error bars primarily stem from the definition of the switching current, which is determined by 15% ± 5% drop of the normal resistance. f SQUID pattern of device S2 at 10 mK. g Supercurrent density distribution. The inset is a draft of the JJ with three-edge supercurrents. h B_z dependence of I_c+ and \(\left\vert {I}_{c-}\right\vert\). i Oscillating ΔI_c, η and fitted ΔI_c (black line). j Temperature-dependent I_c+, I_c−, ΔI_c and η for device S2 at B_z = 8.4 mT. The error bars are obtained by the same method as in (e).

Full size image

Having demonstrated the JDE in Ta₂Pd₃Te₅ edge interferometer, we now show how to further enhance its efficiency. Interestingly, compared with device S1, the SQUID pattern of device S2 in Fig. 2f reveals two main periods, leading to a more pronounced asymmetry in the pattern (Fig. 2h, i) and an increased efficiency with η_max = 73% at 8.4 mT. The enhanced JDE can be explained by three-JJs in parallel. The formation of the middle edge state in the JJ may stem from the ladder-like structure induced by imperfect exfoliation (as indicated by the green arrow in the inset of Fig. 2g and supplementary Fig. 3d), which is a common occurrence during the exfoliation process of 2D flakes⁵¹. These three supercurrent channels form two sets of interference patterns (corresponding red and green dashed loops in the inset of Fig. 2g), leading to the asymmetric SQUID. The ΔI_c can also be approximately fitted by the three-JJs model (black line in Fig. 2i, and see the detail in “Methods” section). The optimization of η in device S2 (Fig. 2j), compared to device S1 in Fig. 2e, seems to be achieved by increasing the number of JJs in parallel, which is in line with the theoretically predicted method⁹.

Here, we examine the main mechanisms to determine which one best fits our data. (1) Magnetism mechanism²⁰ is initially excluded due to the absence of magnetism in the Ta₂Pd₃Te₅ JJ. (2) The Rashba-spin orbital coupling (SOC) mechanism is excluded as it typically requires in-plane magnetic fields, and Ising-SOC is also considered implausible because it is usually found in 2D superconductors⁵². (3) JDE/SDE caused by finite-momentum Cooper pairing generally also needs in-plane magnetic fields^8,14. The absence of obvious enhancement of the upper critical field under in-plane magnetic fields or the approximate butterfly interference pattern in our JJs¹⁴ (Supplementary Fig. 5) leads to the exclusion of finite-momentum Cooper pairing as a mechanism. (4) Nonlinear capacitance^6,28 is absent in this system due to the symmetric superconducting electrodes and the lack of obvious hysteresis between switching current and retrapping current (Fig. 1h). (5) Self-inductance is also found to be too small to be considered (see Supplementary Note 8). Therefore, the main origin of B_z-induced JDE in the Ta₂Pd₃Te₅ edge interferometer is attributed to asymmetric edge supercurrents, as detailed in the “Methods” section.

Fractional Shapiro steps

As discussed above, besides asymmetric edge supercurrents and time-reversal symmetry breaking, the remaining higher harmonic in the CPR is further studied to explain the JDE in our JJs. The Shapiro resonances have been widely used to reveal not only the exotic symmetry of Cooper pairing³² but also the higher harmonic or non-sinusoidal CPR^9,53. The Shapiro steps appear in the I–V curve at V = V_n ≡ nhf/2e (n is an integer) when the JJ is irradiated with the microwave. If the nth harmonic contributes to the CPR, m/nth Shapiro steps (m is an integer) will be present^9,53. In Fig. 3a, fractional Shapiro steps emerge at a microwave frequency of f = 5 GHz, indicating the significant transparency of the JJ (Supplementary Note 1). The  ±1/2th Shapiro steps at half flux quantum (n + 1/2)ϕ₀ are marked by black arrows, which is also observed in other works^24,54. The characteristic dV/dI valleys formed by half-integer steps can be clearly observed at marked positions in Fig. 3b at B_z = 5.5 mT (corresponding to 3/2 ϕ₀). In addition, half-integer Shapiro steps are also observed in device S2 with flux-dependent measurements (f = 4.64 GHz in Fig. 3c, d or 5.02 GHz in Supplementary Fig. 7) and power-dependent measurements at 3ϕ₀/2 (Fig. 3e). These experiments indicate the existence of the second harmonic in the CPR, which is also supported by the rapid suppression observed in temperature-dependent ΔI_c compared with I_c in device S1 (see Fig. 2e), because higher harmonics are quickly suppressed when temperature approaches T_c⁵⁵. The rapid suppression of ΔI_c in device S2 (Fig. 2j) seems less pronounced, possibly because its three-JJs model enhances the diode effect, therefore relatively weakening such suppression. In addition to their applications in Josephson diodes, the JJs with higher harmonics also have potential applications in 0 - π qubits, particularly if the first harmonic in the CPR can be effectively eliminated^56,57,58.

a Differential resistance (dV/dI) as a function of voltage characteristics and flux quantum at microwave power = −32 dBm, f = 5 GHz, and 30 mK for device S1. The  ±1/2th Shapiro steps are marked by black arrows. b dV/dI versus I_b at B_z = 5.5 mT (3/2 ϕ₀). Valleys characterized by half-integer steps are observed clearly. c Flux quantum and voltage dependence of dV/dI at microwave power = 10 dBm, f = 4.64 GHz, and 10 mK for device S2. d Valleys characterized by the  −1/2th Shapiro step at 6.7 mT (3/2 ϕ₀). e Microwave power dependence of dV/dI at 4.64 GHz and B_z = 6.7 mT in device S2. The  −1/2th Shapiro step is marked by black arrows. f Microwave power-dependent non-reciprocal critical current of the 0th Shapiro steps, which is extracted from (e). The switching currents here can be determined by peaks in the dV/dI - I_b curve, as shown in Supplementary Fig. 8c, and the error bars primarily originate from the broadening of these peaks.

Full size image

Furthermore, some features in Fig. 3 require further explanation. First, the disappearance of half-integer Shapiro steps at zero field (Fig. 3a, c) may be attributed to the relatively small contribution of the second harmonic in the CPR and the low microwave frequency⁵⁹. In device S1, a higher microwave frequency is utilized at zero field, and a small signal of half-integer steps appears in Supplementary Fig. 6d–f. No higher frequency is applied to detect half-integer steps at 0 T, considering the limitations of our microwave generator. Second, the integer Shapiro steps at 5.5 mT (3/2 ϕ₀) appear weaker in Fig. 3b (or Supplementary Fig. 6c) compared to those at 0 T in Supplementary Fig. 6b. This is due to the application of a magnetic field at half the flux quantum, causing a reduction in the sharpness of the integer steps because of a decrease in the first harmonic of the CPR. Subsequently, the second harmonic or fractional Shapiro steps become visible at half the flux quantum (Fig. 3a), in agreement with theoretical predictions^9,35 and experimental results^24,54. Third, in device S2 (Fig. 3c), half-integer steps vanish at  ±ϕ₀/2 due to the superposition of multiple SQUID patterns, which is slightly different from the single SQUID pattern observed in device S1. In the case of multiple SQUID patterns, the position of destructive interference for the first harmonic differs from that of a single SQUID pattern, leading to a notable contribution from the first harmonic and the absence of half-integer steps at  ±ϕ₀/2 (see Supplementary Note 6).

The JDE is also studied as a function of microwave power. In Fig. 3f, switching current \({I}_{c+}^{0th}\) and \({I}_{c-}^{0th}\) of the 0th Shapiro step are extracted from Fig. 3e. The quantity \(\Delta {I}_{c}^{0th}={I}_{c+}^{0th}-\left\vert {I}_{c-}^{0th}\right\vert\) (orange curve, see the detail in Supplementary Fig. 8) displays little variation and gradually decreases with increasing microwave power. This stable observation of the JDE under microwave irradiation represents one of the initial examples of such behavior and is a crucial feature in quantum information applications, where microwaves are commonly utilized².

Antisymmetric second harmonic transport

As another type of non-reciprocal behavior, the second harmonic resistance (R_2w) is usually measured to characterize magnetochiral anisotropy (MCA)^13,25,60, whose strength is often defined by the coefficient \(\gamma=\left\vert \frac{2{R}_{2w}}{{R}_{w}BI}\right\vert\). MCA typically exhibits antisymmetric behavior in R_2w with respect to magnetic fields and is generally used to characterize noncentrosymmetric or chiral features. In normal conductors, MCA is usually a minor effect, generally due to the weak SOC. However, a significant enhancement of MCA is observed in noncentrosymmetric superconductors, potentially offering additional insights into factors such as disparities between the Fermi energy and superconducting gap, the Rashba parameter, and spin-orbit splitting, among other factors^60,61. Moreover, the antisymmetric oscillations in B-dependent R_2w have been observed in an ionic liquid-gated chiral nanotube exhibiting the Little-Parks effect⁶², indicating its characteristic chiral symmetry.

Therefore, the second harmonic resistance in our supercurrent interferometer is measured to clarify its asymmetric features. In Fig. 4a, b, the first harmonic resistance (R_w) and R_2w of device S2 are measured using lock-in techniques. Below I_ac = 100 nA, a typical pair of antisymmetric peaks in R_2w is observed at critical fields (near the green dashed line in Fig. 4b). This is consistent with the previously reported antisymmetric peaks of R_2w with respect to B in noncentrosymmetric superconductors^13,60, suggesting the existence of asymmetry in our JJ. With increasing I_ac, the antisymmetric oscillations in R_2w become more pronounced due to the quantum interference of asymmetric edge supercurrents, similar to the behavior observed in chiral nanotubes⁶². At around 500 nA, the oscillating R_2w (black line in Fig. 4b) is analogous to the ΔI_c (orange line), and the similar behavior of device S1 can be seen in Fig. 4d (see the detail in Supplementary Note 7). This similarity suggests the antisymmetric oscillations in R_2w may be related to the polarity of JDE. At higher I_ac, the superconductivity is substantially suppressed and self-heating effects may begin to influence the second harmonic resistance, which is not further analyzed.

a R_w versus B_z at different currents. b B_z-dependent R_2w at various currents. Typical pairs of antisymmetric peaks (R_2w) are marked by dashed lines in matching colors. R_2w at 500 nA (black line) shows a similar behavior to ΔI_c (orange line). The green dashed line indicates the regions near the critical fields, while the other dashed line marks the areas near the oscillating peaks or valleys. c Typical \(\left\vert {R}_{2w}\right\vert\) as a function of current at 20 mK for different oscillating peaks. The average \(\left\vert {R}_{2w}\right\vert\) values are obtained using pairs of antisymmetric peaks near the dashed lines in (b). The error bars primarily originate from discrepancies between average \(\left\vert {R}_{2w}\right\vert\) and the observed values. d Antisymmetric R_2w and ΔI_c as a function of B_z in device S1. The R_2w is measured at I_ac = 70 nA.

Full size image

In addition, supercurrent interference-induced R_2w in our JJs appears more complex. In Fig. 4c, the current-dependent R_2w (red, magenta, and violet lines) extracted from the same oscillating peaks below critical fields does not intersect the origin, suggesting deviations from the R_2w = \(\frac{1}{2}\gamma {R}_{w}IB\) formula generally observed in other systems^63,64,65,66. Therefore, although the antisymmetric oscillations in R_2w at large I_ac display partial antisymmetric features of MCA, the 2R_2w/R_wIB calculated using the typical formula below the critical field may not accurately describe γ or MCA. The MCA in interference systems appears more complex and requires further investigation.

The Ta₂Pd₃Te₅ edge interferometer reveals a significant JDE under small out-of-plane magnetic fields. The JDE is accompanied by the enhanced antisymmetric second harmonic transport, which deserves further research. Moreover, the presence of asymmetric Josephson critical current alongside fractional Shapiro steps demonstrates the importance of the higher harmonic content in the JDE. It is noted that power consumption requires attention if SDE/JDE is to be applied at low temperatures in the future, and further optimization is necessary not only regarding mechanism but also in terms of device size. The Josephson diode efficiency can be further enhanced by concatenating interferometer loops. These findings offer a promising approach to exploring JDE with significant diode efficiency, ultra-low switching power at small magnetic fields, and stable JDE under microwave irradiation, rendering them potentially valuable for practical applications.

Device fabrication

Single crystals Ta₂Pd₃Te₅ were prepared by the self-flux method³⁶. Ta₂Pd₃Te₅ thin films were obtained through mechanical exfoliating bulk samples onto Si substrates with the 280-nm-thick SiO₂ on top, and then coated with PMMA in a glove box at 4000 rpm for 60 s, followed by annealing at 100 ^∘C for 120 s. Multi-terminal electrical contacts were patterned after electron-beam exposure and subsequent development. Ti/Al (5 nm/60 nm) electrodes were deposited after Ar etching in order to remove the oxidized layer. After the lift-off step, the device was coated with hexagonal boron nitride (hBN) to prevent oxidation. The entire fabrication process took place in a nitrogen atmosphere glove box. The rectangular film, with a long side along the b-axis of the crystal, was easily obtained due to its quasi-1D nature³⁸. The dimensions of device S2 (device S1) are as follows: thickness 37 nm (16 nm), width 1.9 μm (1.3 μm), and length 245 nm (400 nm), respectively.

Transport measurements

The electrical transport measurements were carried out in cryostats (Oxford instruments dilution refrigerator). The DC current bias measurements were applied using a Keithley 2612 current source. Both the first- (R_w) and second harmonic (R_2w) resistance were measured through a standard low-frequency (7–11 Hz) lock-in technique (LI5640, NF Corporation). The phase of the first- and second harmonic signal was set to be 0° and 90°, respectively. The current of the magnet was applied by a Keithley 2400 current source in order to control the magnetic field accurately. Before the measurement, the annealing process with 300 °C for  ~10 min was performed to obtain good contacts in the Ta₂Pd₃Te₅ JJs. I–V curves were obtained through the numerical integration process and the origin data were all dV/dI − I_b curves.

Transport measurements under microwave radiation

The electrical transport measurements under microwave radiation were carried out using PSG-A Series Signal generator (Agilent E8254A). The main microwave frequency between 4.64 and 5.02 GHz was applied due to the large absorption effect of microwave for devices S1 and S2. The dissipation of the microwave circuit existed during the measurement of device S2, while another microwave circuit for device S1 was good. So the applied power of the microwave was a little large but without inducing obvious thermal effect.

Band structure calculations

The first-principles calculations were carried out based on the density functional theory (DFT) with the projector augmented wave (PAW) method, as implemented in the Vienna ab initio simulation package (VASP)³⁷. The generalized gradient approximation (GGA) in the form of the Pardew-Burke-Ernzerhof (PBE) function was employed for the exchange-correlation potential. The kinetic energy cutoff for plane wave expansion was set to 400 eV, and a 1 × 9 × 1 k-mesh was adopted for the Brillouin zone sampling in the self-consistent process. The thicknesses of the vacuum layer along the x and z axis were set to  >20 Å.

Simulations of JDE

A minimal model with n JJs in parallel is used to explain the JDE⁹, where only the first and second harmonic contributions in the CPR are considered. The supercurrent is approximatively described as \(I(\varphi,\phi /{\phi }_{0})=\mathop{\sum }_{1}^{n}{I}_{n}sin(\varphi+2\pi {\zeta }_{n}\phi /{\phi }_{0})+ {\alpha }_{n}{I}_{n}sin(2\varphi+ 4\pi {\zeta }_{n}\phi / {\phi }_{0})\), where ζ_n is the modified ratio and ζ₁ = 0, ζ₂ = 1 (ζ₁ = 0, ζ₂ = 1, ζ₃ = 0.23) for the simulation of our two (three) JJs in parallel. ζ₃ represents the enclosed area ratio of two corresponding SQUID patterns in device S2. Preliminary switching currents for different channels are estimated in both devices without considering the second harmonic contribution, in order to simulate CPR and JDE. For device S1, the parameters used for simulating ΔI_c are: I₁ = 75 nA, I₂ = 15 nA, α₁ = 0.3 and α₂ = 0.5, while for device S2, the parameters are: I₁ = 330 nA, I₂ = 120 nA, I₃ = 158 nA, α₁ = 0.6, α₂ = 0.1 and α₃ = 0.2. The simulated ϕ/ϕ₀-dependent ΔI_c can approximatively explain the experimental data in both devices, as shown by black lines in Fig. 2d, i. The slight discrepancy between the simulation and experiment may arise from the omission of higher-order harmonics in the CPR, a reduction in critical current, and a potential variation of α with increasing magnetic field, or other contributing factors.

Asymmetric edge supercurrents

We will discuss edge supercurrents, their asymmetry, and the origin of such asymmetry in our cases, using device S1 as an example. Firstly, the SQUID-like pattern observed in Fig. 2a exhibits several interference features of two edge supercurrent channels, as supported by previous reports^38,40,42. In this pattern, both the width and amplitude of the center lobe are approximately equal to those of the other lobes. This is obviously contrast to a typical Fraunhofer pattern induced by the bulk transport^33,34, where the width of the center lobe is twice as large as that of the other lobes, while the amplitude of the center lobe is usually significantly larger than that of the other lobes.

Secondly, there are several features supporting asymmetric edge supercurrents in our devices: (1) Without considering the higher harmonics of CPR, we calculated two edge supercurrent channels (I₁ and I₂) from the SQUID pattern in Supplementary Note 3, and in device S1, the ratio between the supercurrents I₁:I₂ is approximately 3.5:1 (I₁:I₂:I₃~6:1:2 for device S2); (2) After considering the second harmonic, from a simple simulation using a two-JJs model in Supplementary Fig. 2e, the deviation of I_c from zero at half flux quantum alone cannot support asymmetric interference channels. However, the coexistence of this deviation and the JDE can support asymmetric supercurrents, as shown in Supplementary Fig. 2d, g, h, and device S1 satisfies this coexistence condition; (3) The position-dependent supercurrent density distribution shows a significantly asymmetric supercurrent distribution. However, it should be noted that such asymmetric supercurrent density distribution can also exist in a symmetric system^33,34 due to the relatively imperfect experimental data.

Finally, the origin of asymmetric edge supercurrents is further discussed: (1) The DFT calculations in Fig. 1g support the existence of asymmetric edge states, which contribute to asymmetric edge supercurrents and JDE⁵; (2) Different transmission coefficients⁹ of two edge JJs may also lead to asymmetric edge supercurrents, and can be caused by the different edge disorders, different coupling with the Al contacts, and other factors. Such conditions were not intentionally controlled in our devices.

Discussion of switching power

From a practical perspective, the power consumption of devices should be carefully considered at low temperatures. Although the current cooling power of commercial dilution refrigerators generally reaches the microwatt level at 10 mK⁶⁷, a Joule excitation power higher than a picowatt (or nanowatt) may raise the temperature of the device or sensor above 10 mK (or 100 mK) when the mixing chamber is kept at 10 mK^68,69. The self-heating effect is sometimes noticeable and can also be applied. For example, a microheater with a power output of a few picowatts can generate a temperature gradient as large as several millikelvins per micron and can be further used to conduct Seebeck or Nernst effect measurements in 2D devices at millikelvin base temperatures⁷⁰. Therefore, ultra-low power consumption is essential not only for basic measurements but also for applications in large-scale superconducting quantum circuits, which need ultra-low temperatures to enhance the precision of quantum state measurements.

The edge-induced JDE in Ta₂Pd₃Te₅ may offer distinct advantages in terms of power consumption. The edges of the topological system exhibit a low number of conducting channels compared to bulk states transport. This characteristic can result in a lower critical current and reduced power consumption^33,34.