Abstract
The Dzyaloshinskii-Moriya antisymmetric exchange interaction (DMI) stabilises topological spin textures with promising future spintronics applications. According to crystal symmetry, the DMI can be categorized as four different types that favour different chiral textures. Unlike the other three extensively-investigated types, out-of-plane DMI, as the last type that favours in-plane chirality, remained missing so far. Here we apply point-group-dependent DMI matrix analysis to show that out-of-plane DMI exists under reduced crystal symmetry. Through strain and structure engineering, we show how Cs symmetry is realized in ultrathin magnets and observe the out-of-plane DMI stabilised in-plane chirality using spin-polarized electron microscopy. Our results show that extremely low out-of-plane DMI strengths at µeV/atom are sufficient to stabilise topological spin textures, including merons and bimerons. We also demonstrate field-induced reversible control of the in-plane chirality and merons. Our findings open up untapped paths on topological magnetic textures and their potential applications.
Similar content being viewed by others
Introduction
Magnetic chirality, a preferred rotation sense in spin structures, enables a variety of fascinating chiral magnetic structures, including chiral spin-spirals1,2, skyrmions3,4,5, and chiral ___domain walls (DW)6,7, which have promising spintronics applications with potentially reduced energy consumption in data storage, logic and neuromorphic devices8,9,10. These spin textures give rise to intriguing topological effects such as the topological Hall effect11, skyrmion Hall effect12,13, and topological protection14,15, as a result of the topological charge associated with their spin textures11. More recently, the observation of new types of chiral spin textures, e.g., antiskyrmions16,17, merons18, fractional skyrmions19, and hopfions20, has led to fascinating physics21.
Typically, magnetic chirality is stabilised by an antisymmetric exchange interaction, the Dzyaloshinskii–Moriya interaction (DMI)22,23, which arises from the inversion symmetry breaking of the system. Its energy term \(-{{{{\bf{D}}}}}_{{ij}}\cdot ({{{{\bf{S}}}}}_{i}\times {{{{\bf{S}}}}}_{j})\), implies that the ___location and orientation of the DMI vector \({{{{\bf{D}}}}}_{{ij}}\) with respect to atomic spins \({{{{\bf{S}}}}}_{i}\) and \({{{{\bf{S}}}}}_{j}\) determines the chiral rotation mode. Earlier DMI studies often focused on two types of systems, one in which the \({{{{\bf{D}}}}}_{{ij}}\) vector in bulk materials that lacks centrosymmetry is parallel to the atomic distance vector \({{{{\bf{R}}}}}_{{ij}}\), thereby stabilising Bloch-type chirality1,4; or another where the \({{{{\bf{D}}}}}_{{ij}}\) at interfaces is perpendicular to \({{{{\bf{R}}}}}_{{ij}}\)24, prompting Néel-type chirality2,5,7. More recently, various new chiral modes have been observed that arise from novel DMI vectors. For instance, chiral bobbers can be stabilised in B20 systems by the \({{{{\bf{D}}}}}_{{ij}}\) being located between two vertically adjacent atoms25; the observation of antiskyrmions as a result of the anisotropic \({{{{\bf{D}}}}}_{{ij}}\) in bulk materials with specific symmetries17,26; and the in-plane/out-of-plane vertical chiral coupling in multilayers was attributed to an interlayer DMI27,28,29 where the \({{{{\bf{D}}}}}_{{ij}}\) is parallel to the interface but located at \({{{{\bf{R}}}}}_{{ij}}\) between two vertical layers.
These various types of DMI/chiral systems, described by the ___location and the orientation of \({{{{\bf{D}}}}}_{{ij}}\) that follow the Moriya rule23 and the Fert-Levy model24,30, can be linked to crystal symmetries with distinct point groups31,32, where a 3\(\times\)3 matrix is sufficient to describe all known DMI cases in non-centrosymmetric systems, using \({{{{\bf{D}}}}}_{{{{\rm{matrix}}}}}={({{{{\rm{D}}}}}_{{mn}})}_{1\le m\le {{\mathrm{3,1}}}\le n\le 3}\), where \(m\) corresponds to the orientations of the DMI vector, e.g., the DMI vector of \({{{{\rm{D}}}}}_{{mn}}\) in rows 1,2,3 (\(m={{\mathrm{1,2,3}}}\)) points to \(x,y,z\), respectively; \(n\) stands for the ___location of the DMI vector, e.g., the DMI vector of \({{{{\rm{D}}}}}_{{mn}}\) in column 1,2,3 (\(n={{\mathrm{1,2,3}}}\)) located at \({{{{\bf{R}}}}}_{{ij}}\) sites aligns along \(x,y,z\), respectively (Fig. 1a). In this matrix picture, interfacial-like DMI (conventional Néel-type) elements are located at \({{{{\rm{D}}}}}_{12}\) and \({{{{\rm{D}}}}}_{21}\), bulk-like DMI (Bloch-type) elements are located at \({{{{\rm{D}}}}}_{11}\), \({{{{\rm{D}}}}}_{22}\), and \({{{{\rm{D}}}}}_{33}\), anisotropic DMI (Anti-skyrmion type) elements are located at \({{{{\rm{D}}}}}_{11}\), \({{{{\rm{D}}}}}_{22}\), \({{{{\rm{D}}}}}_{12}\) and \({{{{\rm{D}}}}}_{21}\), and interlayer elements are located at \({{{{\rm{D}}}}}_{13}\) and \({{{{\rm{D}}}}}_{23}\), respectively (Fig. 1b). The last DMI type in this framework, with matrix elements located at \({{{{\rm{D}}}}}_{31}\) and \({{{{\rm{D}}}}}_{32}\), i.e. out-of-plane (OOP) \({{{{\bf{D}}}}}_{{ij}}\) located between planar \({{{{\bf{R}}}}}_{{ij}}\) sites, remains experimentally elusive. Despite theoretical discussions of the intriguing chiral structures favoured by such OOP-DMI, e.g., in-plane chiral rotation [(\(\uparrow\) \(\to\) \(\downarrow\)) or in-plane skyrmions (also called bimerons)33, in contrast to typical Bloch-type (⨀ ↑ ⊗)1 or Néel-type (⨀ → ⊗)2 rotations, the OOP-DMI is not experimentally discovered yet. This is partially due to the fact that the OOP-DMI isn’t expected in the commonly available systems with relatively high symmetry21,24, such as Cnv, O, T point groups, etc.
a Mathematical matrix and cartoon pattern representation of the DMI, with DMI vector configurations of all \({({{{{\rm{D}}}}}_{{mn}})}_{1\le m\le {{\mathrm{3,1}}}\le n\le 3}\) elements. b Major DMI types highlighted by various colourized DMI elements, and their favoured spin textures. The solid/striped areas represent the DMI vector with the same/different DMI strength. The area with the negative sign means that the sign of the DMI vector is opposite to the one with the same colour. c The DMI cartoon patterns corresponding to all non-centrosymmetric point groups (except C1) are shown. The definition of colours is the same as in panel b.
In this paper, we report the observation of in-plane magnetic chirality in Co/Pd ultrathin films grown on a W(110) substrate using spin-polarized low-energy electron microscopy (SPLEEM)34, where the OOP-DMI is attributed to the lowered crystal symmetry, from C3v of unstrained (111) oriented Pd layers, to Cs of strained-(111)-like Pd layers on the W(110) surface. The proposed DMI origin is supported by calculations based on the three-site Fert-Levy model30, micromagnetic simulations35, and DMI matrix analysis31,32. Remarkably, the DMI strength required to stabilise in-plane chirality is found to be several orders of magnitude lower than conventional DMI cases36, due to the fact that the dipole energy also favours the in-plane magnetic configuration. The OOP-DMI is found to stabilise merons/bimerons. The reversible control of in-plane chirality and magnetic meron writing/deleting are demonstrated experimentally. Micromagnetic simulations reveal a similar role of the OOP-DMI on antiferromagnetic materials.
Results
First we discuss DMI within the framework of crystal symmetry31. Here, the DMI energy for a given atom with six nearest cubic-neighbouring \({{{{\bf{R}}}}}_{{ij}}\) sites could be written as a 3\(\times\)3 matrix \({{{{\bf{D}}}}}_{{{{\rm{matrix}}}}}={({{{{\rm{D}}}}}_{{mn}})}_{1\le m\le {{\mathrm{3,1}}}\le n\le 3}\). Such a 3\(\times\)3 DMI matrix conveniently highlights various DMI types, where each DMI type is colourized differently, followed by the representative magnetic structures favoured by each type (Fig. 1b), including Néel-skyrmion (interfacial-like DMI)5, Bloch-skyrmion (bulk-like DMI)3,4, the vertical chirality in interlayer exchange coupling systems (interlayer-DMI)27,28 and meron/bimeron (OOP-DMI), respectively. Note that the recently observed antiskyrmion17 and chiral bobbers25 are stabilised as a result of opposite signs of \({{{{\rm{D}}}}}_{11}\), \({{{{\rm{D}}}}}_{22}\), and non-zero \({{{{\rm{D}}}}}_{33}\), respectively.
Further linking the DMI matrix to all types of non-centrosymmetric point groups reveals that the distribution of the DMI elements in the matrix is restricted by the type of point groups31,32 (Fig. 1c), e.g., the interfacial-like DMI (the matrix elements highlighted in purple) belongs to Cnv (n=2,3,4,6) point groups; the bulk-like DMI (highlighted in blue) belongs to T25, O37, or Dn (n=2,3,4,6) point groups; and the anisotropic DMI stabilising antiskyrmions belongs to D2d17 or S426 groups. Note that the C1 point group with all non-zero \({{{{\rm{D}}}}}_{{mn}}\) is not shown, and \({{{{\rm{D}}}}}_{{mn}}\) is commonly thought to be zero in centrosymmetric systems. The point group dependent DMI matrix suggests that the elusive OOP-DMI that we are searching for here is located at \({{{{\rm{D}}}}}_{31}\) or \({{{{\rm{D}}}}}_{32}\) (highlighted in orange in Fig. 1b) and its favoured in-plane chirality may exist in the C2 or Cs point groups (Fig. 1c), where the C2 point group contains axial symmetry under a 180° rotation, and the Cs point group exhibits planar symmetry across a mirror plane. Comparing to the typical DMI point groups such as Cnv, O, T point groups, both C2 and Cs point groups have less symmetry operations, which is consistent with the expectation that the OOP-DMI cannot exist in systems with relatively high symmetry21,24. For the Cs point group discussed in this paper, the \({{{{\rm{D}}}}}_{31}\) element appears when there is only one mirror plane \(\sigma\) along the \(y\)-direction, and \({{{{\rm{D}}}}}_{32}\) would appear with a mirror plane \(\sigma\) along the \(x\)-direction (see Methods).
Next, this DMI matrix picture is tested experimentally in in-plane magnetized ultrathin films. We first chose Co/W(110) system, where the Co/W interface is C2v-like24, therefore only \({{{{\rm{D}}}}}_{12}\) and \({{{{\rm{D}}}}}_{21}\) are expected without the OOP-DMI elements \({{{{\rm{D}}}}}_{31}\) or \({{{{\rm{D}}}}}_{32}\) (Fig. 1c), which also agrees with the Moriya rule that the \({{{{\bf{D}}}}}_{{ij}}\) at Co/W interface must lie in the plane23. A compound SPLEEM image of magnetic textures in a three monolayer (ML) Co film on W(110) shows two in-plane magnetized domains (highlighted by orange and blue) separated by 180° DWs (Fig. 2a), where the rotation sense of DWs appears as (\(\leftarrow \uparrow \to\)) in green DWs or (\(\leftarrow \downarrow \to\)) in magenta DWs. For clarity, a part of this data is represented as a magnetization vector array (Fig. 2b), which highlights the magnetization textures in the black box in Fig. 2a. The statistical representation of in-plane chirality is shown in the \(\chi\) histogram (Fig. 2c), where the two similar peaks at −90° and +90° indicate that the planar spin rotation is not chiral. Here the role of the OOP-DMI can be derived by measuring the planar spin rotations, i.e., planar spin rotation sense within ___domain walls, because the OOP-DMI lifts the DMI energy degeneracy for different in-plane chiralities (Supplementary Fig. S1), but the conventional interfacial DMI doesn’t. Therefore, the achiral nature of DWs in Co/W(110) indicates the absence of OOP-DMI.
a Compound SPLEEM image of 3 ML Co/W(110). The inset colour wheel indicates in-plane magnetization orientation, and white/black correspond to up/down magnetization. Scale bar, 2 µm. b Pixel-by-pixel vector array of the black box in panel a. c Histogram of χ derived from panel a. χ is the angle between the [1–10] direction and DW magnetization \({{{\bf{m}}}}\) (inset of Fig. 2f). d Compound SPLEEM image of 3 ML Co/ 3 ML Pd/ W(110). Scale bar, 2 µm. e Pixel-by-pixel vector map of the black box in panel d. f Histogram of χ derived from panel d.
By contrast, when a 3 ML Pd layer is inserted in between Co and W(110), in-plane chirality emerges in the compound SPLEEM image (Fig. 2d), e.g., from left to right spins always rotate as (\(\to \downarrow \leftarrow \uparrow \to\)), or orange-magenta-blue-green-orange (see an example of the arrow-based vector plot in Fig. 2e). Note that the magnetic chirality observed here remains in a 2D-plane parallel to the film, this 2D-nature is similar to the Néel-type chirality in thin films2,5,7, and differ from the 3D-chiral rotation in bulk-DMI systems1,3,4. The smaller average size of the magnetic ___domain observed in Fig. 2d than in Fig. 2a is possibly due to the smaller in-plane uniaxial magnetic anisotropy in Co/Pd/W(110). A statistical survey of \(\chi\) in Fig. 2f shows a single peak at -90°, which is defined as left-handed in-plane chirality (Supplementary Fig. S1). This robust in-plane magnetic homo-chirality can be reliably reproduced (Supplementary Fig. S2), serving as direct evidence for the existence of OOP-DMI in the Co/Pd/W(110) system.
To understand the physical origin of this OOP-DMI, the crystal structure of the layer adjacent to the Co film is monitored by low-energy electron diffraction (LEED) (Supplementary Fig. S3), showing that the 3 ML Pd film is fcc(111)-like, in contrast to the bcc(110) surface of W(110). This affects the stacking position of heavy atoms underneath the Co film when the \({{{{\bf{D}}}}}_{{ij}}\) lies entirely in-plane at the (110) interface (Supplementary Fig. S4). At the (111) interface the \({{{{\bf{D}}}}}_{{ij}}\) actually cants and contains out-of-plane components38 (Fig. 3a), according to the three-site Fert-Levy model30 (see Methods), although these OOP-DMI components are commonly neglected24. Interestingly, observations have shown that in-plane magnetized textures for a fcc(111)-type DMI system are achiral39, indicating that the OOP-DMI components at a fcc(111) interface do not stabilise chirality. This is because fcc(111)-type DMI for a given magnetic atom has six nearest-neighbour \({{{{\bf{D}}}}}_{{ij}}\), where the OOP components of three are pointing up and the other three pointing down (Fig. 3a), so the net OOP-DMI adds up to zero, just as the absence of OOP-DMI elements in the matrixized C3v case results from the vanishing sum of the OOP \({{{{\bf{D}}}}}_{{ij}}\) components. The planar achiral magnetic rotation is reproduced with the same fcc(111)-DMI using micromagnetic simulations (see Fig. 3b and Methods).
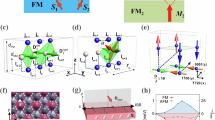
a Top-view and side-view of the DMI vectors (orange arrows) at C3v interface. White and black balls correspond to the FM and heavy metal atoms, respectively. The blue triangle highlights the three-sites relevant to the adjacent DMI vector. The length of the DMI vector indicates the strength of DMI. b Micromagnetic simulation with C3v-type DMI and the histogram of angle χ. The colour wheel shows in-plane magnetization direction, and white/black indicates up/down magnetization direction. c, e Shifted atom and DMI configurations in the presence of compressive strain (panel c, highlighted in red) or tensile strain (panel e, highlighted in green). The dashed circles outline the atom positions in panel a. d, f The micromagnetic simulation results of the strained system in panels c and e, respectively. The dashed black rectangle highlights the in-plane chiral structure. g Sketch of three OOP-DMI vector pairs under strain (marked by the blue arrows). h Dependence of OOP-DMI vector changes (\(\Delta {D}_{{{{\rm{z}}}}1}\), \(\Delta {D}_{{{{\rm{z}}}}2}\), \(\Delta {D}_{{{{\rm{z}}}}3}\)) and effective OOP-DMI on strain calculated using the Fert-Levy model.
In the case of Co/Pd/W(110), however, significant uniaxial strain appears in the Pd film grown on W(110)40 (Supplementary Fig. S3), which destroys the three-fold axial symmetry of the C3v interface, and lowers the symmetry of the Co/Pd interface from the C3v (a three-fold rotation axis and three mirror planes) to the Cs (only a mirror plane) point group. From the Fert-Levy model point of view, this also affects the orientation of the \({{{{\bf{D}}}}}_{{ij}}\) vectors, such that two \({{{{\bf{D}}}}}_{{ij}}\) along the strain direction vary more significantly compared to the other four \({{{{\bf{D}}}}}_{{ij}}\) (highlighted in Fig. 3c). The strain-induced non-zero effective OOP-DMI is further supported by \({{{{\bf{D}}}}}_{{ij}}\) calculations based on the Fert-Levy model (Fig. 3g, h), which is consistent with the DMI matrix picture. Micromagnetic simulations show that such non-zero OOP-DMI can indeed stabilise in-plane chiral structures (Fig. 3d), similar to the structures observed experimentally. In contrast to the conventional \({{{{\bf{D}}}}}_{{ij}}\) where the DMI sign is element-dependent, we found that the sign of the effective OOP-DMI, i.e., the sum of six OOP-DMI vectors (Fig. 3g), is additionally strain-type dependent (Deff in Fig. 3h), e.g., the sign of the effective OOP-DMI is opposite in case of compressive strain (Fig. 3c) versus tensile strain (Fig. 3e), because the strain-induced variation of two OOP-DMI vectors (\(\Delta {D}_{{{{\rm{z}}}}3}\) in Fig. 3h, appeared as blue vectors in Fig. 3g) along the strain direction is greater than the changes of the other four OOP-DMI vectors (\(\Delta {D}_{{{{\rm{z}}}}1}\) and \(\Delta {D}_{{{{\rm{z}}}}2}\) in Fig. 3h). The strain-dependent sign change of the effective OOP-DMI is further reproduced in micromagnetic simulations (Fig. 3c, dvs e, f). Note that this strain-dependent effective DMI sign dependence is different from the conventional strain-induced DMI41. The picture of the DMI matrix perfectly agrees with micromagnetic simulations, e.g., zero effective OOP-DMI in the C3v point group, but finite OOP-DMI in the Cs point group. In addition, we simulated the role of D33 (parallel to the vertically aligned atoms) in systems with relatively high symmetry, such as in the T point group25, which favours helical spirals with propagation direction along the \(z\)-direction, and we found that D33 doesn’t affect in-plane chirality (Supplementary Fig. S5).
Next, we discuss a few factors that determine the sign and strength of the OOP-DMI. Firstly, the OOP-DMI is the out-of-plane component of the canted interfacial DMI; therefore, the OOP-DMI scales with the sign and strength of the interfacial DMI. Secondly, the OOP-DMI is strain dependent, i.e., compressive and tensile strains induce opposite signs of the OOP-DMI, and the DMI strength is proportional to the strain (Fig. 3h). Thirdly, the nature of the in-plane chirality suggests that the chirality doesn’t remain the same upon a 180° rotation along the \(z\)-direction, meaning the C2 symmetry of the magnetic structure along the \(z\)-direction is broken. Compared to the case of the interfacial DMI, where the magnetic C2 symmetry along the in-plane direction is broken because of the interface, the case of the in-plane chirality also requires a morphological structure factor that breaks the C2 symmetry along the \(z\)-direction, which is attributed to the asymmetric fractional area of the structural stacking ___domain (Supplementary Fig. S7). The asymmetry of the stacking ___domain, in turn, affects the sign and the strength of the OOP-DMI (See Supplementary Note S1). Now, the strength of the effective OOP-DMI could be estimated by considering all three factors,
where \({{DM}}_{{{{\rm{Interfacial}}}}}\) is the conventional interfacial DMI strength36; \({\eta }_{{{{\rm{canting}}}}}\) stands for the C3v-like canting factor; \({\eta }_{{{{\rm{strain}}}}}\) represents the strain factor at the Pd/W(110) interface; and \(A\) is the asymmetry of the two types of stacking domains (Supplementary Fig. S8). The \({{DM}}_{{{{\rm{Interfacial}}}}}\) in the 3 ML Pd/ W(110) system is \(\sim\)0.41 meV/atom42, and \({\eta }_{{{{\rm{canting}}}}}\), \({\eta }_{{{{\rm{strain}}}}}\), \(A\) are \(\sim\)0.4, 1.25%, 16.8%, respectively, resulting in the estimate of \({{DM}}_{{{{\rm{OOP}}}}}^{{{{\rm{eff}}}}}\) in Co/Pd/W(110) as \(\sim\)0.35μeV/atom (see estimate details in Supplementary Note S2).
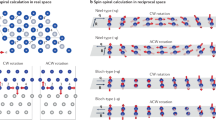
The estimated strength of the OOP-DMI is about three orders of magnitude lower than some typical cases of interfacial DMI36, yet it can stabilise in-plane chirality. This differs from out-of-plane magnetized systems, where an achiral Bloch wall has lower energy with insufficient interfacial DMI7. This substantial difference is attributed to how the various energy contributions balance in the out-of-plane and in-plane chirality cases. In the out-of-plane case7, the strength of the interfacial DMI (favouring chiral Néel type, Fig. 4a) must exceed the strength of the dipole interaction (favouring achiral Bloch type, Fig. 4b) for Néel-chirality to be stabilised. In contrast, in planar magnetism such as observed here in the Co/Pd/W(110) system, both the OOP-DMI and the dipole interaction favour planar rotation (Fig. 4c). Thus the dipole energy costs for two in-plane chiralities are degenerate, which explains how ultra-small OOP-DMI is sufficient to stabilise in-plane chirality. This picture is further corroborated by micromagnetic simulations (see Methods): in the out-of-plane magnetized case, the interfacial-DMI-dominated chiral Néel-type textures (Fig. 4d) gradually evolve to dipole-dominated achiral Bloch-type (Fig. 4e) as the ratio of interfacial DMI and dipole interaction decreases (Fig. 4d), which matches perfectly with experimental observations7; in the OOP-DMI case, the in-plane chirality remains stable for OOP-DMI-dominated (Fig. 4g) and dipole-dominated (Fig. 4h) cases, showing its greater chiral stability with ultra-small DMI (Fig. 4i). The stability of the in-plane chirality is also supported by our experiments. Previous results in out-of-plane magnetized [Ni/Co]n films on Pd/W(110) show a film thickness dependent chiral-to-achiral transition (Fig. 4l)42, which shares the same trend with the simulated chirality evolution in Fig. 4f. However, the in-plane chirality remains the same with increasing Co thickness (Fig. 4l), which is in good agreement with the micromagnetic simulations (Fig. 4i).
a–c Sketch of cycloid spin-spiral, helical spin-spiral and in-plane spin-spiral, respectively. Micromagnetic simulations of chirality dependence on the strength of (d–f) conventional Néel-type DMI in out-of-plane magnetized system and (g–i) OOP-DMI in in-plane magnetized system. j, k Co thickness dependent compound SPLEEM images in Co/3 ML Pd/W(110) system. Scale bars are 1 µm. The DW formed a zigzag structure to reduce the dipole energy on the head-to-head or tail-to-tail position (k). l Experimental dependence of in-plane and out-of-plane chirality on the FM film thickness. The out-of-plane chirality data is adapted from ref. 42.
The new chirality often opens up new functionalities21. For OOP-DMI, we demonstrate a reversible control of the in-plane chirality via a magnetic field. In-plane chirality can also be observed in a 3 ML Co/3 ML Au/W(110) structure (Fig. 5a). This chiral state can be overwritten to an achiral state (Fig. 5b) by applying an in-situ magnetic field of the order of a few Oe roughly along the +W[001] direction (green ___domain wall direction) (methods), which overcomes the DMI-like field on the ___domain wall43; and the chiral state is recovered upon the removal of the magnetic field (Fig. 5c), demonstrating the magnetic-field-dependent reversible control of the in-plane chirality (Fig. 5d). In-plane chirality also enables the writing/deleting of magnetic merons, which have spin structures corresponding to half-skyrmions18. In in-plane magnetized systems, merons could form at the joint locations of two neighbouring in-plane Néel walls33,44, i.e., where the magnetization along the ___domain wall boundary flips by 180° (see an example in Fig. 5e). We note that the detailed spin structure of a meron could be affected by variations in magnetic interactions, particularly magnetic anisotropies and the sign and strength of the DMI36,45. Here the SPLEEM spatial resolution is insufficient to resolve the out-of-plane component of the meron core, therefore only the in-plane curling magnetization is highlighted in Fig. 5. An in-situ magnetic field can be applied to delete the meron (Fig. 5f), similarly as Fig. 5b; and the DM-driven meron reappears at the same ___location once the field is removed (Fig. 5g), which highlights the reversible writing and deleting of magnetic merons (Fig. 5h). Note the mode of meron writing through OOP-DMI is fundamentally different from that utilizing changes of magnetic anisotropy18,44.
a–c Magnetic field dependent compound SPLEEM images of in-plane chiral Néel ___domain wall in the same locations on 3 ML Co/ 3 ML Au/ W(110). Scale bar is 1 µm. d Evolution of the chirality as a function of magnetic field. e–g Magnetic field dependent compound SPLEEM images of a meron in the same locations on 3 ML Co/ 3 ML Au/ W(110). Scale bar is 400 nm. h Evolution of the meron number as the function of a magnetic field. i Compound SPLEEM image of a meron bubble in 3 ML Co/3 ML Pd/ W(110). The colour wheel shows in-plane magnetization. “1” and “2” denote the merons. Scale bar is 500 nm. j Micromagnetic simulation of a meron bubble which is equivalent to a bimeron in the OOP-DMI system. The colour wheel shows in-plane magnetization, and white/black indicates up/down magnetization. k Sketch of spin blocks similar to panel j. l Dependence of topological number Q on various combinations of the two merons’ core polarities. m Micromagnetic simulation of the in-plane chiral antiferromagnetic spin-spiral considering OOP-DMI. n Pixel-by-pixel vector map of the black box region in m.
Because the in-plane chirality defines the merons’ ___location, two merons can be naturally locked between (\(\downarrow\)) spin and (\(\uparrow\)) spin along the wall boundary in an in-plane magnetized bubble-like ___domain (Fig. 5i, also see in Figs. 2g and 3d), which could potentially form a bimeron with topological charge \(\pm 1\)33. Determination of the total topological charge requires the detection of the out-of-plane component around the meron centre, for this the spatial resolution of the SPLEEM used in this work is insufficient. Therefore, micromagnetic simulations are carried out to understand the polarity of the meron (Fig. 5j), which is further visualized in a colourized vector plot (Fig. 5k). Here, the polarity of two merons in the black box results in variations of the total topological charge \(Q\) (Fig. 5l), and a bimeron can be realized when two merons’ polarity is opposite33.
Discussion
The observed in-plane chirality in the novel OOP-DMI system exists in DMI systems with Cs symmetry. One approach to realize OOP-DMI is the strain-induced symmetry change as shown in the Co/Pd/W(110) (Fig. 2g) or Co/Au/W(110) (Fig. 5a) systems. OOP-DMI may exist in other strained systems with fcc(111) or bcc(111) textures. Note that OOP-DMI can also exist in systems with C2 symmetry. Some molecules belong to the C2 point group, e.g., hydrogen peroxide molecules and hydrazine molecules. It is also possible to apply strain or other symmetry-breaking operations in materials to reduce the crystal symmetry to C2 or Cs point groups46. For example, by reducing the crystal symmetry, C4, C6, D2, D3, D4, D6, and S4 could be transformed into the C2 point group; C2v, C3v, C3h point groups could be converted to the Cs point group.
In addition, we expect that the OOP-DMI can stabilise in-plane chirality in antiferromagnetic systems, as shown in micromagnetic simulations (Fig. 5m, n); and the OOP-DMI could allow control of the position of antiferromagnetic merons, as well as to facilitate the formation of antiferromagnetic bimeron bubbles (Supplementary Fig. S9). The OOP-DMI could also induce some interesting chiral spin configurations in nano-structures (Details in Supplementary Note S3). The OOP-DMI elements located at D31 and D32 are the only ones that favour in-plane chirality propagating in the xy plane, promising to unravel intriguing aspects in three-dimensional nanomagnetics20,47,48, as the chirality stabilised by other DMI elements involves magnetization variation in the z-direction. Lastly, the DMI matrix for all the point groups with broken inversion symmetries interestingly shares the same mathematical representation as spin-orbit torque49, which may help the design of novel spin-orbitronic devices by jointly considering novel DMI and spin-orbit torques. The DMI in centrosymmetric materials has been commonly neglected in the past36. It’s worth noting a few exceptions: one is the theoretical prediction of the hidden DMI in the spin sublattice of systems BaCoS2 (D2h point group) or Ni2Sr4Br2O6 (D4h point group)50, while the other is the Mn3Sn compound (D6h point group) with Kagome lattice51, where Mn3Sn contains out-of-plane \({{{{\bf{D}}}}}_{{ij}}\) that helps to stabilise non-collinear magnetic order; however, this case is distinguished from the in-plane ferromagnetic chirality reported here.
In summary, we have observed the missing type of the DMI, the OOP-DMI that stabilises in-plane magnetic chirality in thin films. We revealed its Cs-symmetry-related physical origin through the combination of Fert-Levy model calculations, micromagnetic simulations, and DMI matrix analysis. The required OOP-DMI for stabilising chirality can be a few orders of magnitude lower than the conventional interfacial DMI due to the different energy landscapes where both OOP-DMI and dipole energy favour planar magnetic configuration with DMI lifting the chiral degeneracy. We also demonstrate the reversible control of in-plane chirality and writing/deleting magnetic merons via a magnetic field. We expect such OOP-DMI to exist in many strained systems with (111) textures, and that it will play a similar role in antiferromagnetic systems.
Methods
Sample preparation
The experiments were performed on Elmitec SPLEEM III at the National Laboratory of Solid State Microstructures and the Department of Physics at Nanjing University. The W(110) substrate was cleaned by cycles of flashing to 1850 °C in 3.0 × 10−8 Torr oxygen until the surface was free of carbon, confirmed in the low-energy electron microscopy (LEEM) and low-energy electron diffraction (LEED). Then, an additional flashing at a higher temperature removes the surface oxygen. Co, Pd, and Au layers were deposited by molecular beam epitaxy in the SPLEEM chamber under ultra-high vacuum, with a base pressure of \(\sim\) 4.0 × 10−11 Torr. The film thicknesses of the metal layers were detected via oscillations of the LEEM intensity. The spin-polarized source was obtained by photoemission from GaAs(001) activated by Cs and oxygen adsorption. The in-plane magnetic field applied to the sample surface is controlled by varying the distance between the sample and the objective lens with the field compensation coil turned off.
Magnetic imaging and chirality analysis
Real-space magnetic images were measured using the Elmitec SPLEEM III instrument. The contrast in SPLEEM images represents the asymmetry of the spin-dependent reflection between spin-polarized beams with opposite polarization (up and down), which is \(A=({I}_{\uparrow }-{I}_{\downarrow })/({I}_{\uparrow }+{I}_{\downarrow })\). \(A\) is proportional to \({{{\bf{P}}}}\cdot {{{\bf{M}}}}\) where \({{{\bf{P}}}}\) is the spin polarization of the incident electrons and \({{{\bf{M}}}}\) is the surface magnetization of the sample. The Cartesian components \({M}_{x}\), \({M}_{y}\), and \({M}_{z}\) of the magnetization \({{{\bf{M}}}}\) were imaged with the illumination beam spin polarization aligned along the W[1-10], W[001], and W[110] directions. All SPLEEM images were measured on the samples held at room temperature. The energy of the incident electron beam was set at 2\(\sim\)4 eV to optimize the magnetic contrast. The magnetization vector is represented in hue saturation lightness (HSL) colour space, where the in-plane magnetization direction is mapped on the hue and the out-of-plane component is mapped on the brightness. We defined the strength of Néel chirality \({\gamma }_{{{{\rm{IP}}}}}\) in the in-plane system as the asymmetry of the angle χ39: \({\gamma }_{{{{\rm{IP}}}}}=({N}_{{{{\rm{Left}}}}}-{N}_{{{{\rm{Right}}}}})/({N}_{{{{\rm{Left}}}}}+{N}_{{{{\rm{Right}}}}})\) (\({N}_{{{{\rm{Left}}}}}\) is the number of ___domain wall centre-line pixels with χ between −180° and 0° and \({N}_{{{{\rm{Right}}}}}\) is the number of ___domain wall centre-line pixels with χ between 0° and 180°). In the out-of-plane system, we defined \(\alpha\) as the angle between magnetization vector and ___domain wall normal vector measured in ___domain wall centre-line pixels, so that the strength of Néel chirality \({\gamma }_{{{{\rm{OOP}}}}}\) is defined as the asymmetry of the angle \(\alpha\): \({\gamma }_{{{{\rm{OOP}}}}}=\kappa \times ({N}_{{{{\rm{Left}}}}}-{N}_{{{{\rm{Right}}}}})/({N}_{{{{\rm{Left}}}}}+{N}_{{{{\rm{Right}}}}})\) (\({N}_{{{{\rm{Left}}}}}\) is the number of \(\alpha\) between −180° and 0° and \({N}_{{{{\rm{Right}}}}}\) is the number of \(\alpha\) between 0° and 180°). Here \(\kappa\) denotes the proportion of the Néel component. The out-of-plane chirality value in Fig. 4l has been normalized due to the difference of the noise levels in the experiments.
Calculating the DMI in the three-site Fert–Levy model
In the three-site Fert-Levy model30, \({V}_{1}\) is a parameter defined by the specific material. \({\lambda }_{{{{\rm{d}}}}}\) is the strength of the spin-orbit coupling and \(\Gamma\) is the interaction parameter between the localized spin and conduction electrons. \({E}_{{{{\rm{F}}}}}\) and \({k}_{{{{\rm{F}}}}}\) are the Fermi energy and Fermi wavevector, respectively. \({Z}_{{{{\rm{d}}}}}\) is the number of d electrons. \({{{{\bf{R}}}}}_{{in}}({{{{\bf{R}}}}}_{{jn}})\) is the vector joining the magnetic site \(i(j)\) to the NM site \(n\). According to the three-site Fert-Levy model, \({{{{\bf{D}}}}}_{{ijn}}\) is perpendicular to the plane of the triangle \({ijn}\) (Fig. 3a). Here we used \({\lambda }_{{{{\rm{F}}}}}=2{{{\rm{nm}}}}\) and \({Z}_{{{{\rm{d}}}}}=9.4\) for calculating the DMI under strain and only considered the nearest-neighbour (n. n.) atoms’ contributions (Fig. 3h). We set the n.n. atoms’ distance as \(a=0.25{{{\rm{nm}}}}\) and set the layer spacing as \(z=0.18{{{\rm{nm}}}}\). In the C3v interface, one atom has six n. n. atoms on the surface. The FM atoms’ positions are:
and the heavy metal atoms’ positions are:
The heavy metal atoms’ positions in another twinned C3v interface are:
Micromagnetic realization (continuum model) of DMI
We will discuss in the framework of micromagnetism (continuum model), where an atom has only six nearest-neighbour atoms for cubic symmetry. The DMI energy density can then be written as
Utilizing the Liftshitz invariants \({{{{\mathcal{L}}}}}_{{ij}}^{(k)}={m}_{i}{\partial }_{k}{m}_{j}-{m}_{j}{\partial }_{k}{m}_{i}\), the DMI can be simplified as
Furthermore, we can use a matrix to present the DMI:
Here, we discuss the reduction of the DMI matrix under the Cs point group as an example. For the axial tensor \(D\), \(D=\det \left(R\right){RD}{R}^{-1}\) is satisfied for all symmetry operations \(R\). We chose the symmetric operator element in the Cs point group to be the mirror operation along the y-z plane, which is the same situation as Fig. 3c, e.
Substituting \(R\) into \(D=\det \left(R\right){RD}{R}^{-1}\) we find that \({D}_{11}={D}_{22}={D}_{23}={D}_{32}={D}_{33}=0\). The DMI matrix in the Cs point group can be written as:
Thus, the OOP-DMI is oriented along the \(x\)-direction (direction along the strain), which is consistent with the micromagnetic simulation results.
Micromagnetic simulation
The micromagnetic simulations were carried out based on a two-dimensional model35, where exchange interaction, dipolar interaction, in-plane uniaxial magnetic anisotropy, as well as OOP-DMI are considered. The Hamiltonian is written as:
where \({{{{\bf{S}}}}}_{i}\) and \({{{{\bf{S}}}}}_{j}\) are spin moments located on atomic sites \(i\) and \(j\) in a two-dimensional plane, \({{{{\bf{r}}}}}_{i}\) and \({{{{\bf{r}}}}}_{j}\) are the position vectors of the spin blocks in sites \(i\) and \(j\). \(J\), \({D}_{{{{\rm{dip}}}}}\) and \({K}_{{{{\rm{u}}}}}\) correspond to exchange interaction, dipole interaction and uniaxial anisotropy, respectively. In a C3v interface, each spin is surrounded by six neighbouring spins. The Hamiltonian of the OOP-DMI can be written as:
The dimensionless parameters \(J\), \({D}_{{{{\rm{dip}}}}}\), \({K}_{{{{\rm{u}}}}}\), \({D}_{z1}\), \({D}_{z2}\) and \({D}_{z3}\) are used for simulating ___domain wall spin structures. For the simulation results summarized in Fig. 3 and Supplementary Fig. S6f, g, the values \(J=1\), \({D}_{{{{\rm{dip}}}}}=0.1\), \({K}_{{{{\rm{u}}}}}={K}_{x}=0.075\) were assumed. Domain configurations shown in Fig. 4 are simulated using 500 × 300 spin block arrays with periodic boundary conditions applied for both directions. The initial state is set to a random state, followed by annealing to an energetically stabilised state. The system temperature is represented by allowing spins to fluctuate according to Boltzmann statistics35. The OOP-DMI \({D}_{z1}={D}_{z2}={D}_{z3}=0.2\) was used for simulating the un-strained situation (Fig. 3b). \({D}_{z1}={D}_{z2}=0.2,{D}_{z3}=0.3\) was used in the compressive strain situation (Figs. 3d, 5j and Supplementary Fig. S6f). \({D}_{z1}={D}_{z2}=0.2,{D}_{z3}=-0.3\) was used in another twinned situation (Supplementary Fig. S6g). \({D}_{z1}={D}_{z2}=0.2,{D}_{z3}=0.1\) was used in the tensile strain situation (Fig. 3f). In Fig. 4d, e, f, the perpendicular magnetic anisotropy was obtained by setting \({K}_{{{{\rm{u}}}}}={K}_{z}=0.8\). In the antiferromagnetic conditions, we utilized a square lattice. The values of \(J=-1\), \({D}_{{{{\rm{dip}}}}}=0\), \({D}_{z3}=0.3\) were applied in Fig. 4m and the values of \(J=-1\), \({D}_{{{{\rm{dip}}}}}=0\), \({K}_{{{{\rm{u}}}}}={K}_{y}=0.1\), \({D}_{z3}=0.1\) were used in Supplementary Fig. S9. Micromagnetic simulations of OOP-DMI in nano-structures in Supplementary Fig. S10 were performed using Mumax3 software52.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Uchida, M., Onose, Y., Matsui, Y. & Tokura, Y. Real-space observation of helical spin order. Science 311, 359–361 (2006).
Bode, M. et al. Chiral magnetic order at surfaces driven by inversion asymmetry. Nature 447, 190–193 (2007).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Heinze, S. et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 7, 713–718 (2011).
Thiaville, A., Rohart, S., Jué, É., Cros, V. & Fert, A. Dynamics of Dzyaloshinskii ___domain walls in ultrathin magnetic films. Europhys. Lett. 100, 57002 (2012).
Chen, G. et al. Novel chiral magnetic ___domain wall structure in Fe/Ni/Cu(001) films. Phys. Rev. Lett. 110, 177204 (2013).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mat. 2, 17031 (2017).
Luo, Z. et al. Current-driven magnetic ___domain-wall logic. Nature 579, 214–218 (2020).
Song, K. M. et al. Skyrmion-based artificial synapses for neuromorphic computing. Nat. Electron. 3, 148–155 (2020).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Jiang, W. et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 13, 162–169 (2016).
Litzius, K. et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat. Phys. 13, 170–175 (2016).
Je, S.-G. et al. Direct Demonstration of Topological Stability of Magnetic Skyrmions via Topology Manipulation. ACS Nano 14, 3251–3258 (2020).
Chen, G. et al. Ultrasensitive Sub-monolayer Palladium Induced Chirality Switching and Topological Evolution of Skyrmions. Nano Lett. 22, 6678–6684 (2022).
Hoffmann, M. et al. Antiskyrmions stabilized at interfaces by anisotropic Dzyaloshinskii-Moriya interactions. Nat. Commun. 8, 308 (2017).
Nayak, A. K. et al. Magnetic antiskyrmions above room temperature in tetragonal Heusler materials. Nature 548, 561–566 (2017).
Yu, X. Z. et al. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 564, 95–98 (2018).
Gao, S. et al. Fractional antiferromagnetic skyrmion lattice induced by anisotropic couplings. Nature 586, 37–41 (2020).
Zheng, F. et al. Hopfion rings in a cubic chiral magnet. Nature 623, 718–723 (2023).
Göbel, B., Mertig, I. & Tretiakov, O. A. Beyond skyrmions: Review and perspectives of alternative magnetic quasiparticles. Phys. Rep. 895, 1–28 (2021).
Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958).
Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 120, 91–98 (1960).
Crépieux, A. & Lacroix, C. Dzyaloshinsky–Moriya interactions induced by symmetry breaking at a surface. J. Magn. Magn. Mater. 182, 341–349 (1998).
Zheng, F. et al. Experimental observation of chiral magnetic bobbers in B20-type FeGe. Nat. Nanotechnol. 13, 451–455 (2018).
Karube, K. et al. Room-temperature antiskyrmions and sawtooth surface textures in a non-centrosymmetric magnet with S4 symmetry. Nat. Mat. 20, 335–340 (2021).
Fernández-Pacheco, A. et al. Symmetry-breaking interlayer Dzyaloshinskii–Moriya interactions in synthetic antiferromagnets. Nat. Mat. 18, 679–684 (2019).
Han, D.-S. et al. Long-range chiral exchange interaction in synthetic antiferromagnets. Nat. Mat. 18, 703–708 (2019).
Vedmedenko, E. Y., Riego, P., Arregi, J. A. & Berger, A. Interlayer Dzyaloshinskii-Moriya Interactions. Phys. Rev. Lett. 122, 257202 (2019).
Fert, A. & Levy, P. M. Role of Anisotropic Exchange Interactions in Determining the Properties of Spin-Glasses. Phys. Rev. Lett. 44, 1538–1541 (1980).
Ma, T. Magnetic antiskyrmions in tetragonal Heusler materials with D2d structure. Dissertation, Halle (Saale), (Martin-Luther-Universität Halle-Wittenberg, 2021).
Di Pietro, A., Ansalone, P., Basso, V., Magni, A. & Durin, G. Gauge theory applied to magnetic lattices. Europhys. Lett. 140, 46003 (2022).
Göbel, B., Mook, A., Henk, J., Mertig, I. & Tretiakov, O. A. Magnetic bimerons as skyrmion analogues in in-plane magnets. Phys. Rev. B 99, 060407 (2019).
Chen, G. & Schmid, A. K. Imaging and tailoring the chirality of ___domain walls in magnetic films. Adv. Mat. 27, 5738–5743 (2015).
Kwon, H. Y. & Won, C. Effects of Dzyaloshinskii–Moriya interaction on magnetic stripe domains. J. Magn. Magn. Mater. 351, 8–15 (2014).
Kuepferling, M. et al. Measuring interfacial Dzyaloshinskii-Moriya interaction in ultrathin magnetic films. Rev. Mod. Phys. 95, 015003 (2023).
Li, W. et al. Emergence of skyrmions from rich parent phases in the molybdenum nitrides. Phys. Rev. B 93, 060409 (2016).
von Bergmann, K., Menzel, M., Kubetzka, A. & Wiesendanger, R. Influence of the local atom configuration on a hexagonal skyrmion lattice. Nano Lett. 15, 3280–3285 (2015).
Robertson, M. et al. In-plane Néel wall chirality and orientation of interfacial Dzyaloshinskii-Moriya vector in magnetic films. Phys. Rev. B 102, 024417 (2020).
Kemmer, J. & Bode, M. Structural analysis of ultra-thin Pd films on W(110). Surf. Sci. 657, 44–50 (2017).
Gusev, N. S., Sadovnikov, A. V., Nikitov, S. A., Sapozhnikov, M. V. & Udalov, O. G. Manipulation of the Dzyaloshinskii–Moriya interaction in Co/Pt multilayers with strain. Phys. Rev. Lett. 124, 157202 (2020).
Chen, G. et al. Large Dzyaloshinskii-Moriya interaction induced by chemisorbed oxygen on a ferromagnet surface. Sci. Adv. 6, eaba4924 (2020).
Je, S.-G. et al. Asymmetric magnetic ___domain-wall motion by the Dzyaloshinskii-Moriya interaction. Phys. Rev. B 88, 214401 (2013).
Jani, H. et al. Antiferromagnetic half-skyrmions and bimerons at room temperature. Nature 590, 74–79 (2021).
Yang, H., Liang, J. & Cui, Q. First-principles calculations for Dzyaloshinskii–Moriya interaction. Nat. Rev. Phys. 5, 43–61 (2023).
Kitchaev, D. A., Beyerlein, I. J. & Van der Ven, A. Phenomenology of chiral Dzyaloshinskii-Moriya interactions in strained materials. Phys. Rev. B 98, 214414 (2018).
Fernández-Pacheco, A. et al. Three-dimensional nanomagnetism. Nat. Commun. 8, 15756 (2017).
Bhattacharya, D. et al. 3D Interconnected Magnetic Nanowire Networks as Potential Integrated Multistate Memristors. Nano Lett. 22, 10010–10017 (2022).
Ciccarelli, C. et al. Room-temperature spin–orbit torque in NiMnSb. Nat. Phys. 12, 855–860 (2016).
Cui, Q. et al. Anatomy of Hidden Dzyaloshinskii-Moriya Interactions and Topological Spin Textures in Centrosymmetric Crystals. Nano Lett. 24, 7358–7365 (2024).
Nagamiya, T., Tomiyoshi, S. & Yamaguchi, Y. Triangular spin configuration and weak ferromagnetism of Mn3Sn and Mn3Ge. Solid State Commun. 42, 385–388 (1982).
Vansteenkiste, A. et al. The design and verification of MuMax3. AIP Adv. 4, 107133 (2014).
Acknowledgements
This work has been supported by the National Key R&D Program of China (Grant No. Grant No. 2022YFA1403601) and the National Natural Science Foundation of China (Grants No. 12374113, No. 92165103, No. 12274204, and No. 12274203). H.Y.K acknowledges support by the National Research Foundation of Korea (NRF) funded by the Korean Government (NRF-2021R1C1C2093113). T.M. acknowledges support by the National Natural Science Foundation of China (Grant No. 12304133). C.O. acknowledges support from the U.S. Department of Energy Early Career Research Program. Y.Z.W. acknowledges support by the National Natural Science Foundation of China (Grant No. 11974079) and the Shanghai Municipal Science and Technology Major Project (Grant No. 2019SHZDZX01). K.L. acknowledges support from the US-NSF (DMR-2005108). S.S.P.P. acknowledges support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – project no. 328545488, Collaborative Research Centre / Transregio (SFB/TRR) 227, project B10 and project no. 471731263. C.W acknowledges support by the National Research Foundation of Korea (NRF) funded by the Korean Government (NRF-2023R1A2C1006050). Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the US Department of Energy under contract no. DE-AC02-05CH11231 (A.K.S.).
Author information
Authors and Affiliations
Contributions
G.C. conceived the study. G.C. and H.D. supervised the project and SPLEEM facility. H.N. carried out the experiments and analysed the data. H.N. and C.O. contributed to the imaging analysis algorithm. H.K. and C.W. performed micromagnetic simulations. T.M. and S.S.P.P. contributed to the DMI matrix analysis. H.N., Z.C., B.M., L.S., Y.W., K.L., A.K.S., H.D. and G.C discussed and interpreted the results. H.N., H.D. and G.C. prepared the manuscript. All authors commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Niu, H., Kwon, H.Y., Ma, T. et al. Reducing crystal symmetry to generate out-of-plane Dzyaloshinskii–Moriya interaction. Nat Commun 15, 10199 (2024). https://doi.org/10.1038/s41467-024-54521-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-54521-6
This article is cited by
-
Nonvolatile current-induced topological charge imbalance of magnetic textures
Communications Physics (2025)