Time-___domain signatures of distinct correlated insulators in a moiré superlattice

Moiré materials offer unprecedented and highly tunable platforms for understanding the emergence of quantum phases of matter and for exploring future device applications. Among the quantum phases realized in these systems, the correlated insulators stand out as the most commonly observed^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}. Other quantum phases, including mixed bosonic-fermionic states^16,17,18, superconductors^19,20, and various quantum Hall states^{21,22,23,24,25,26,27,28}, are often directly related to or appear in the vicinity of correlated insulators. Despite the obvious importance of correlated insulators in moiré systems, an understanding of the hierarchy of stabilizing/destabilizing interactions remains largely limited to a reliance on simple models, such as the Hubbard Hamiltonian^29,30. Establishing how correlated insulators differ mechanistically is essential to understanding their properties, such as varying critical temperatures (T_c), and connections to other quantum phases. We focus on the most robust quantum states discovered to date at moiré interfaces—correlated insulators at integer filling factors of moiré superlattices in transition metal dichalcogenide heterobilayers^{2,3,4,5,6,7,8,9,10,11,12,13,14,15}. We choose the angle-aligned WSe₂/WS₂ moiré system, where the ν = −1 and ν = −2 correlated insulator states exhibit high T_c of ~150 K and ~80 K, respectively^2,3,6,8,11. Recently, we suggested that the observed high T_c is, in addition to many-body e–e interactions, related to polaronic stabilization due to e–ph interactions³¹.

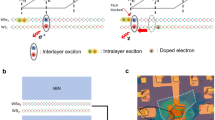
In the angle-aligned WSe₂/WS₂ moiré system studied here, there are two potential wells at high symmetry points in each moiré unit cell, leading to the formation of two narrow moiré bands^32,33. Recently, this was experimentally confirmed by Park et al. via reflective magnetic circular dichroism measurements¹⁶. At half filling (ν = −1) of the first moiré band (lower energy), many-body correlation results in gap opening near the top of the valence band and the formation of an upper and a lower Hubbard band (UHB and LHB, respectively). The second moiré band is believed to be located within the Hubbard gap of the first moiré band and the ν = −1 correlated insulator is properly called a charge-transfer (CT) insulator³² instead of a Mott insulator³⁴. At ν = −2, the inter-band Coulomb energy (U’, rather than the intra-band Coulomb energy, U) favors the half filling of both bands and the result is a two-band Mott insulator¹⁶ rather than a trivial band insulator⁶. To understand these correlated insulators, we take a time-___domain approach³¹ in which a pump pulse creates holons and doublons across the correlated gap and a probe pulse detects the disordering dynamics³⁵ via exciton sensing of the dielectric environment^2,3,6,8. Such an approach directly accesses the timescales relevant to electronic or atomic motions that are not accessible in steady-state spectroscopy or transport measurements. In particular, disordering of a correlated state occurs on a timescale of the characteristic system response, linked to either electron hopping or the oscillation period of a relevant phonon mode, depending on whether e–e or e–ph interactions play the dominate role in stabilizing the state³⁶. Here, we apply such an approach coupled with fluence-dependent measurements. Through this lens, we map the mechanistic regimes governing correlated insulator stability/instability in moiré systems as a function of photoexcitation density, n_ex.

Steady-state and transient correlated state sensing

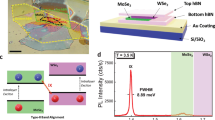
Figure 1a illustrates the WSe₂/WS₂ heterostructure (AB stacked, θ = 60 ± 1°) featuring top and bottom gates, each consisting of a hexagonal boron nitride (h-BN) dielectric spacer and a few-layer graphene (Gr) electrode. The dual-gate structure allows either hole (ν < 0) or electron (ν > 0) doping from an applied gate voltage (V_g), while the electric field at the moiré interface can be maintained at zero. Figure 1b illustrates the static reflectance spectrum of the device as a function of V_g and moiré filling factor ν (defined here as charge filling per moiré unit cell). In the reflectance measurement, the excitonic oscillator strength, sensitive to changes in the dielectric environment, is an effective probe of correlated state formation. We choose the lowest energy moiré exciton of WSe₂ as our dielectric sensor for its high oscillator strength and therefore high sensitivity. At ν = ±1, ±2, we observe an increased exciton signal as the effective dielectric constant decreases upon the formation of correlated insulator states^2,3,6,8. Further device characterization can be found in Supplementary Fig. 1.

a Schematic of device architecture where the WSe₂/WS₂ heterobilayer is symmetrically encapsulated by top and bottom gates (V_t and V_b, respectively) consisting of hexagonal boron nitride (h-BN) and few-layer graphene (Gr). b Gated (V_g = V_t = V_b) steady-state reflectance spectrum of the lowest energy moiré exciton of WSe₂. Here, Δ R = R – R₀ where R is the reflected signal from the bilayer and dual gate region while R₀ is the reflected signal from a region with gates and no bilayer. c–e Gated (V_g = V_t = V_b) transient reflectance response as a function of pump fluence at Δt = 2, 8, 50 ps, respectively. Shown is the integrated response centralized around the lowest energy WSe₂ moiré exciton sensor. The different fluence-dependent responses have been offset and multiplied by −1 for clarity. Associated fluence labels are shown on the side of panel e and are consistently colored throughout the other panels. Here, ΔR = R_on – R_off where the subscript indicates either pump-on or -off spectra. See Methods for further details. All data were collected at 11 K.

Full size image

By introducing pulsed laser excitation (and detection), we can further perform transient reflectance measurements on the same device architecture³¹. This allows us to obtain both time-resolved and gate-dependent reflectance spectra (see Supplementary Figs. 2–3). For excitation, we employ a pump with photon energy (1.55 eV) below the optical gaps of WSe₂ and WS₂ to uniquely target the correlated states. This avoids pump-induced interlayer exciton formation which would result in long-lived responses on the nanosecond time scale³³. The absorption of a pump photon excites a hole from the LHB of the correlated insulator deep into the valence band(s). The excited holes relax within this continuous manifold on ultrafast time scales, typically of the order of 10s–100s femtoseconds due to scattering with other carriers and optical phonons³⁷, towards the upper unoccupied band(s) (the UHB or the CT band)³². The result is the formation of holon-doublon pairs across the correlation gap (see Supplementary Fig. 4 for schematic). The presence of holons and doublons leads to disordering of the correlated insulator on characteristic timescales determined by e–e or e–ph interactions³⁶. Recovery of the charge order reaches the so-called “bottleneck” on a timescale determined by recombination of holons and doublons across the gap³⁵. The timescale of disordering is captured by the transient increase in the effective dielectric constant, monitored through the exciton sensor covered by a probe pulse centered at 1.65 eV (spanning the lowest energy moiré exciton of WSe₂). We note that in the current measurements, we focus on the hole doping side because our transient measurements are most sensitive to the correlated states which reside exclusively in the same layer as the WSe₂ excitonic sensor due to the type-II band alignment at the WSe₂/WS₂ interface^2,3. Correlated state recovery is tracked through the subsequent reduction in the effective dielectric constant as the original insulator behavior reemerges.

Figure 1c–e show transient reflectance spectra integrated around the lowest energy moiré transition of WSe₂ as functions of both applied gate voltage, V_g, and pump-probe time delay, Δt, at varying pump fluences. The pump fluence is increased until saturating behavior is reached in the transient response (Supplementary Fig. 5). In agreement with the static reflectance spectra, correlated state responses at ν = −1, −2 are observed in the time-resolved spectra, with the maximum response (disordering) in a few ps and recovery (reordering) in tens of ps. With increasing fluence, the magnitude of the correlated state response also increases. Intriguingly, the response of the ν = −2 state to pump-induced disordering occurs in a broader V_g range than the ν = −1 state does (Fig. 1c–e), in contrast to the steady-state measurement (Fig. 1b). This may suggest that the transient measurements are particularly sensitive to an expanse of otherwise hidden states with varying charge ordering around ν = −2, as predicted for lower filling factors^38,39. In the present case, the magnitude of the transient response around ν = −2 indicates a significant change in the dielectric environment and therefore a substantial non-equilibrium photoinduced response. The states in this region also appear to have varying recovery timescales (Fig. 1e) which can be seen as a narrowing in the transient response along the V_g axis at later Δt, particularly at lower pump fluence. In the following, we focus on the disordering and reordering dynamics at ν = −1, −2.

Distinct temporal responses of correlated insulator states

Figure 2a, b show the transient reflectance responses of the ν = −1, −2 states for the indicated pump fluences (f = 3–85 µJ/cm²). Following the coherent artifact arising from pump-probe overlap at Δt = 0 ps, the non-equilibrium response of the correlated states is initially related to disordering of the equilibrium charge configuration, as evidenced by an increase in the effective dielectric constant detected through bleaching of the exciton transition. In each case, the disordering reaches a maximum magnitude after a few ps and subsequently recovers. The black solid curve in each case is a fit consisting of a single exponential decay (disordering) and either a single exponential first order (ν = −1) or a second order (ν = −2) recovery (reordering); further fit details can be found in the Methods section (fit residuals shown in Supplementary Fig. 6 and unnormalized data and fits in Supplementary Fig. 7). The chosen functional form for the recovery dynamics will be explicitly discussed further below. Finally, an additional offset is also included to account for the much longer timescale (»100 ps) recovery dynamics. This offset is negligible at low excitation fluence but becomes significant at f > 14 µJ/cm². As detailed in control experiments on the undoped charge neutral state (ν = 0, Supplementary Fig. 8) the long-lived offset can be attributed to hole injection into the WSe₂/WS₂ moiré structure from thermionic emission of hot electrons in the unavoidably photo-excited Gr electrodes at sufficiently high excitation densities (Supplementary Fig. 9)^40,41. Concomitant with the dynamic responses from disordering and recovery are temporal oscillations of interlayer phonon modes which have been discussed elsewhere⁴². These modes are coherent phonon wavepackets launched from strain fields induced by the pump at the Gr electrodes. These wavepackets propagate through the h-BN prior to impinging on the heterobilayer with an apparent delay as determined by the phonon group velocity.

a, b Fluence-dependent temporal response of the ν = −1, −2 states, respectively. The time traces were averaged in a narrow window about the maximum of the lowest energy WSe₂ moiré exciton sensor. Each fluence-dependent transient has been normalized for clear comparison of the dynamical response (see Supplementary Fig. 7 for unnormalized data where the overall signal trend is preserved). Data are shown in shaded colors while the fits used for time constant extraction are shown in black. See the Methods section for further details. Throughout the panels, increasing pump fluence is shown from light to dark shades. All fluence-dependent data are colored consistently for each of the filling factors throughout the figure. All data were collected at 11 K. c, d To more easily and directly visualize the trends in the fluence-dependent dynamics (without the substantial interlayer phonon response), the normalized fits from (a, b) are shown in (c, d), respectively. Arrows indicating the time constants associated with the disordering dynamics (τ_d) and recovery dynamics (τ_r) are labeled in (d).

Full size image

To more clearly view the disordering and recovery dynamics without interference from the coherent phonon oscillations, we replot the normalized fits independently from the data in Fig. 2c, d for ν = −1, −2, respectively. The disordering and recover dynamics of the ν = −1 state are found to be independent of fluence in the entire investigated range (f = 3–85 µJ/cm²). In contrast, the ν = −2 state exhibits distinct behavior—both the disordering and the recovery accelerate with increasing fluence. To quantitatively compare the two correlated insulator states, we plot in Fig. 3a, b the disordering time (τ_d) for the at ν = −1 and −2 states, respectively, as functions of fluence.

a Disordering time constant (τ_d) for ν = −1 as a function of fluence. The linear fit trend line is shown in black. b Disordering time constant (τ_d) for ν = −2 as a function of fluence. Shown in black is the fit of the form \(\propto 1/\sqrt{{{n}}_{{\mbox{ex}}}}\) + τ_const. Throughout the figure, all error bars indicate 99% confidence intervals. Large circle outlines have been added to aid with data visualization. The fluence-dependent shaded colors for the ν = −1, −2 states are consistent with the data shown elsewhere in the text. See the Methods section for further details.

Full size image

For the ν = −1 state, disordering occurs with a time constant τ_d = 3.3 ± 0.2 ps, independent of the photoexcited carrier density, n_ex, of the correlated insulator (up to saturation of the observed transient response in the investigated pump fluence range). This result precludes a pure electronically-driven disordering mechanism, the rate (=1/τ_d) of which should increase with n_ex due to carrier screening of the many-body electronic interactions. Instead, the constant τ_d suggests a time scale characteristic of e–ph interactions and rate-limited by the oscillation period of the relevant phonon mode(s), often described as the amplitude mode in charge density wave (CDW) systems^36,43. Our initial pump-probe measurements on the ν = −1 correlated insulator state in the WSe₂/WS₂ moiré superlattice revealed thermal activation behavior in the disordering process, suggesting the polaronic nature of the correlated insulator, in agreement with an ab initio calculation³¹. The independence of disordering rate on n_ex observed here not only confirms the polaronic interpretation, but also reveals the dominance of e–ph interactions in stabilizing the charge order in the ν = −1 correlated insulator. Such a polaronic and ordered correlated state is similar to a CDW state⁴⁴; however, unambiguous delineation between Mott insulators versus CDW ordering remains a subject of discussion⁴⁵.

The observed τ_d can be understood as relating to the oscillation period (typically taken as either a half or quarter period) of phonon mode(s) involved, as shown in the related CDW systems^36,43. The corresponding mode frequency is consistent with the fact that the moiré deformation potential likely involves acoustic phonons accessible via the momentum range defined by the mini-Brillouin zone of the moiré superlattice³¹. Interestingly, in the fit residuals, a low frequency oscillation attributable to this phonon mode is potentially present at Δt < 10 ps; however, this remains speculative as this feature is obscured by the interlayer modes after only a single period (Supplementary Fig. 6). Further suggestive, this behavior is noticeably absent in the control ν = 0 data (Supplementary Fig. 8).

In stark contrast to the behavior of the ν = −1 state, the disordering time, τ_d, for the ν = −2 state displays a strong dependence on fluence (Fig. 3b). This is unexplainable by only consiring e–ph interactions and instead suggests the importance of many-body electronic interactions. In particular, we find that the disordering time can be well-described by the functional form \({{{{\rm{\tau }}}}}_{{{{\rm{d}}}}}\propto 1/\sqrt{{{{n}}}_{{{{\rm{ex}}}}}}\) + \({{{{\rm{\tau }}}}}_{{{{\rm{const}}}}}\) (solid black curve in Fig. 3b). The square root dependence on doping density is well-known for the 2D plasmon frequency^36,43. In other words, disordering as a result of photoexcited carrier screening occurs on a characteristic timescale inversely proportional to the plasmon frequency, ω_p³⁶, as reported for the ultrafast collapse of order in the excitonic insulator 1T-TiSe₂⁴³. We conclude that disordering of the ν = −2 correlated insulator at the WSe₂/WS₂ moiré interface observed here is determined by the electronic response, namely screening by photodoped holons and doublons. Our previous measurement on temperature-dependent disordering of the ν = −2 state shows a thermal activation energy lower than that of the ν = −1 state³¹. The current result, in combination with our previous finding, reveals that plasmonic screening overwhelms polaronic stabilization in the disordering of the ν = −2 correlated insulator. We note that, while the observed τ_d is dominated by screening as shown by the \(1/\sqrt{{n}_{{\mbox{ex}}}}\) dependence, there seems to be a fundamental limit to τ_d as captured by the offset, τ_const = 2.2 ± 0.1 ps. The exact origin of this offset is not known, but we speculate it may be associated with either additional e–ph interactions³¹ or a deviation from the pure 2D plasmon response in the moiré superlattice⁴⁶. Papaj and Lewandowski recently theoretically proposed that the coupling of charge order to the collective plasmon response can result in plasmon band folding and gap opening, leading to an upper bound in the plasmon frequency⁴⁶. These issues deserve further investigations.

The fundamental distinction between the ν = −2 and ν = −1 insulator states can be understood from the difference in charge occupation of each moiré unit cell. In the ν = −2 state, there are two holes (on two different sites) within each moiré unit, giving rise to the Coulomb repulsion energy U’. For comparison, U’ is absent for the ν = −1 state where the second site remains unoccupied. The magnitude of U’ (on the order of 50–100 meV)^16,32 dominates over the polaron stabilization energy (~13 meV estimated from thermal activation)³¹. As a result, photodoping of the two-band correlated insulator, ν = −2, leads to a free carrier-like plasmonic response. In contrast, the stronger polaronic localization for the ν = −1 state diminishes the collective plasmon character for holons and doublons.

The fundamental distinction between ν = −1 and ν = −2 is also reflected in the recovery dynamics, which are determined by holon-doublon recombination across the correlation gap³⁵. Figure 4a shows the reordering time constants obtained from single exponential fits to the recovery component of the data in Fig. 2. For the ν = −1 state, the reordering is captured as a first order process implied in the mono-exponential fit and verified by the approximate independence of recovery time constants τ_r on n_ex. Such a first-order kinetic process reveals that recombination of the perturbed ν = −1 state derives from a “single body”, i.e., a local holon-doublon pair called a Hubbard exciton⁴⁷. This local holon-doublon pair is fortified by polaronic stabilization, which inhibits their separation into a free holon and a free doublon.

a Reordering time constant (τ_r) for ν = −1 and ν = −2 as a function of fluence. Here, τ_r was extracted based on considering the recovery as a first order process (mono-exponential functional form, inset in a). The black line for ν = −1 shows the linear fit trend line for τ_r as a function of fluence. The dotted black line for ν = −2 shows the linear interpolation between data points to highlight the data trend. b Effective reordering time constant (τ_{r, eff}) for ν = −2 as a function of fluence. Here, τ_{r, eff} was extracted based on considering the recovery for ν = −2 as a second order process (inset in b). The black line shows the linear fit for τ_{r, eff} as a function of fluence. Throughout the figure, all error bars indicate 99% confidence intervals. Large circle outlines have been added to aid with data visualization. The fluence-dependent shaded colors for the ν = −1, −2 states are consistent with the data shown elsewhere in the text. See the Methods section for further details and Supplementary Fig. 10 for plots of k_r (= 1/τ_r).

Full size image

However, for ν = −2, the single-exponential recovery time constant τ_r decreases with n_ex, indicating the failure of the first order kinetic model and that the recovery process is of higher order in n_ex (see Supplementary Fig. 10a). We find that the recovery for ν = −2 is second order, i.e., the recovery rate is proportional to n_ex². To fit the recovery to a second order kinetic scheme, we use the functional form A_r/(1+A_r∙t/τ_{r, eff}), where A_r is a constant proportional to n_ex⁽⁰⁾, the initial concentration of photo-excitation as controlled via the pump fluence. Figure 4b shows the resulting effective second order recovery time constant, τ_{r, eff}, which is correctly n_ex-independent (see Supplementary Fig. 10b). The apparent second order process supports the two-body recombination kinetics of a holon and a doublon, in excellent agreement with the free-carrier nature of photo-doping of the ν = −2 correlated insulator state.

In summary, we find distinct disordering and reordering mechanisms for the ν = −1 and −2 states in the WSe₂/WS₂ moiré superlattice. The non-equilibrium response of the ν = −1 state reveals its dominant polaronic nature, leading to disordering determined by a characteristic phonon time and re-ordering by the first-order recombination of a localized holon-doublon pair. In contrast, in the ν = −2 state, e–e interactions dominate over e–ph interactions. As a result, photodoping of the ν = −2 state results in free carrier-like holons and doublons, leading to disordering dominated by carrier screening and re-ordering dominated by second-order recombination of free holons and free doublons. The distinct non-equilibrium responses of the two correlated states define the richness of behavior accessible by a time-___domain view. While we do possess sufficient sensitivity in the experiments presented here to resolve the correlated insulators at fractional filling of the moiré superlattice^6,8, further improvement in signal-to-noise ratio may allow us to resolve these states at fractional fillings and reveal their distinct dynamics. This remains a key objective of our research program on time-___domain views of moiré quantum matter. Overall, the delicate balance or competition between e–e and e–ph interactions may provide an additional angle in understanding and ultimately controlling quantum phases on the moiré landscape or even in realizing otherwise hidden metastable phases.

60° device fabrication and gating

The WSe₂ and WS₂ monolayers are mechanically exfoliated from flux-grown bulk WSe₂ crystals and commercially purchased bulk WS₂ crystals (HQ Graphene), respectively. Prior to transfer, the crystal orientation of WSe₂ and WS₂ monolayers are first determined via polarization-resolved second harmonic generation (P-SHG). The monolayers are then stacked together by a dry-transfer technique with a polycarbonate stamp. To distinguish between R- and H-stacked configurations, P-SHG is again applied to the heterobilayer region after the device is fabricated, with results compared to individual monolayers. The error bars for the angle determination are well within ±1°. The sample is grounded via Gr contacts connected to the heterobilayer and single crystal h-BN dielectrics and Gr gates are used to encapsulate the device and provide control of the carrier density and displacement field (if desired) via external source meters (Keithly 2400). SF6 radiofrequency plasma is applied to the stack to etch the encapsulating h-BN and create connection to the Gr gates contacts. All electrodes are defined with electron beam lithography and made of a three-layer metal film of Cr/Pd/Au (3 nm/17 nm/60 nm).

Spectroscopic measurements

For the spectroscopic measurements, the sample is cooled down to T = 11 K under vacuum (<10⁻⁶ torr) with a closed-cycle liquid helium cryostat (Fusion X-Plane, Montana Instruments). We note that no laser-induced continuous heating was observed at any of the employed pump fluences. Steady-state reflectance measurements are carried out with a 3200 K halogen lamp (KLS EKE/AL). A 715 nm low pass filter is employed to avoid potential photodoping effects. Following collimation, the lamp light is focused onto the sample/substrate with a 100X, 0.75 NA objective. The reflected light is collected by the same objective and then dispersed with a spectrometer onto an InGaAs array (PyLoN-IR, Princeton Instruments). The steady-state reflectance spectrum is obtained by contrasting the reflected signal from the sample (R), which includes the bilayer and dual gate region, and the effective substrate (R₀), which includes a region with gates and no bilayer as follows: (R-R₀)/R₀. For the spatially-resolved reflectance experiments used for mapping of the bilayer, a dual-axis galvo mirror scanning system is employed⁴⁸. Following spatial scanning of the sample as controlled via the angles of the galvo mirrors, the reflected light is spatially filtered through a pinhole and collected by the detector.

The steady-state photoluminescence (PL) experiments are performed with a HeNe laser (Model 31-2140-000, Coherent). The excitation power is set to the range 50–100 nW and focused onto the sample. The PL signal was spectrally filtered from the laser using a long-pass filter prior to dispersal with a spectrometer and detection (the same detection system described above is employed here).

The pump-probe experiments are seeded by femtosecond pulses (250 kHz, 1.55 eV, 100 fs) generated by a Ti:sapphire oscillator (Mira 900, Coherent) and regenerative amplifier (RegA 9050, Coherent). The output is then split to form the pump and probe arms. For the probe, a fraction of the fundamental is focused into a sapphire crystal to generate a white light continuum which is then spectrally filtered (750 ± 40 nm band pass filter) to cover the lowest energy WSe₂ moiré exciton. The pump beam (800 nm, fundamental) is then directed towards a motorized delay stage to control the time delay, Δt, and passed through an optical chopper to generate pump-on and -off signals. Following this, the pump and probe arms are directed collinearly to the sample through an objective (100X, 0.75 NA). The pump and probe spot diameters are ~2.36 μm and ~0.9 μm, respectively. Due temporal broadening from the objective, our instrument response function is ~200 fs. The same objective is used to collect the reflected light which is spectrally filtered to remove the pump and dispersed onto an InGaAs detector array (PyLoN-IR, Princeton Instruments). The pump-on and -off spectra at varying Δt are then used to calculate the transient reflectance signal (ΔR/R) where ΔR = R_on – R_off with the subscript indicates either pump-on or -off spectra.

Assignment of filling factors

The charge density, n, in the WSe₂/WS₂ heterostructure, controlled by the applied gate voltages (V_t and V_b for the top and bottom gates, respectively), is determined using the parallel-plate capacitor model: \(n=\frac{\varepsilon {\varepsilon }_{0}{\Delta {{{\rm{V}}}}}_{{{{\rm{t}}}}}}{{d}_{{{{\rm{t}}}}}}+\frac{\varepsilon {\varepsilon }_{0}{\Delta {{{\rm{V}}}}}_{{{{\rm{b}}}}}}{{d}_{{{{\rm{b}}}}}}\), where \(\varepsilon \approx 3\) is the out-of-plane dielectric constant of hBN, \({\varepsilon }_{0}\) is the permittivity of free space, ΔV_i is the applied gate voltage relative to the valence/conduction band edge, and \({d}_{{\mbox{i}}}\) is the thickness of the hBN spacer. The moiré density, n₀, is determined based on the moiré lattice constant, a_M\(,\) and is given by \({n}_{0}=\frac{2}{\sqrt{3}{a}_{M}^{2}}\). The filling factor, v, estimated as the ratio between the charge doping and moiré densities, is fit based on the experimental gate-dependent steady-state reflectance and photoluminescence measurements (Fig. 1b and Supplementary Fig. 1b). For the 60° device, the thickness of the top and bottom hBN spacers is determined to be \({d}_{{\mbox{t}}}\,\approx \,36.4\) and \({d}_{{\mbox{b}}}\,\approx \,39.6\) nm, respectively. The twist angle is determined to be ~0.8°.

Data analysis

In the following we describe the data processing involved in analyzing both the overall transient signal and the disordering/recovery dynamics. The data is first collected as a function of probe energy and pump-probe delay, Δt, at varying V_g and pump fluence. To generate Supplementary Fig. 2–3, pump-probe spectra are collected at a series of Δt at varying V_g and pump fluence. At each Δt and for each fluence, the V_g-dependent spectra are then combined as a function of probe energy versus V_g to generate two-dimensional pseudo-color plots. We take V_g = V_t = V_b unless otherwise specified. The data from these plots are then integrated in the range 1.67–1.69 eV about the maximum of the lowest energy WSe₂ moiré sensor, normalized, offset, and multiplied by -1 to generate Fig. 1c–e.

To analyze the time traces, the signal in a ~0.01 eV window about the maximum of the lowest energy moiré band of WSe₂ is averaged (e.g., Fig. 2a, b, Supplementary Figs. 7 and 8a). For Fig. 2a, b, these traces are then normalized for better comparison of the dynamics specifically. The overall |ΔR/R| trend (Supplementary Fig. 5) is analyzed by averaging the rectangular region about the maximum signal along both the probe energy axis (in a ~0.01 eV window about the maximum of the lowest energy moiré band of WSe₂) and temporal dimensions (in the Δt window from 7.5 to 8.5 ps).

To isolate the dynamics from the abovementioned time traces, fits are performed. For ν = −1 and −2, the normalized fits compared directly to the data are shown in Fig. 2a, b (black lines) as well as separately in Fig. 2c, d. The corresponding normalized residuals are shown in Supplementary Fig. 6. A comparison between the unnormalized fits and data for both states is shown in Supplementary Fig. 7. For ν = 0, Supplementary Fig. 8a shows the fits (where applicable) in red where the corresponding residuals are shown in Supplementary Fig. 8b, c. For all fits, the coherent artifact region arising from pump-probe overlap is omitted. All errors are given by 99% confidence intervals.

The ν = −1 data for pump fluence f = 3, 7, 10, and 14 µJ/cm² are fit by a biexponential function with disordering captured by the functional form A_d exp[t/τ_d] and recovery by A_r exp[t/τ_r]. The ν = −1 data for pump fluence f = 28, 56, and 85 µJ/cm² are fit using the aforementioned form with the inclusion of an additional term, A_∞ exp[t/τ_∞], to account for the additional component relating to thermionic emission (discussed further below). Here, τ_∞= 500 ps is fixed as the timescale for this process is beyond the duration of the present experiment and is therefore unresolvable. Figures 3–4 show the obtained time constants for disordering, τ_d, and recovery, τ_r, as a function of fluence. Supplementary Fig. 10 shows the corresponding rate of recovery, k_r = 1/τ_r, as a function of fluence.

The ν = −2 data for pump fluence f = 3, 7, 10, 14, 28, and 56 µJ/cm² are fit using a function with disordering captured by the functional form A_d exp [t/τ_d] and recovery by A_r /(1+A_r∙t/τ_{r, eff}). As explained in the text and supported by Fig. 4 (τ_r/τ_{r, eff} as a function of fluence) and Supplementary Fig. 10 (k_r/k_{r, eff} as a function of fluence), the recovery for ν = −2 is best represented by a second order process as captured by the employed functional form for recovery. Figure 3 shows the corresponding τ_d as a function of fluence. The ν = −2 data for pump fluence f = 85 µJ/cm² is fit using the above form with the inclusion of an additional term, A_∞ exp[t/τ_∞], to account for the additional component relating to thermionic emission (discussed further below). Here, τ_∞= 500 ps is fixed as the timescale for this process is beyond the duration of the present experiment. We note that unlike ν = −1, this term was not necessary for fitting the f = 28 and 56 µJ/cm² data. This is likely because the overall increased signal strength for ν = −2 versus ν = −1 obscures contributions from this component at f = 28 and 56 µJ/cm² in the former.

The ν = 0 data for pump fluence f = 28, 56, and 85 µJ/cm² is fit using a function with rise captured by the functional form A_rise exp[t/τ_rise] and an additional long-lived component by A_∞ exp[t/τ_∞]. Here, τ_∞= 500 ps is again fixed as the timescale for this process is beyond the duration of the present experiment. The average τ_rise = 1.4 ± 0.4 ps (see Supplementary Fig. 8d). Meaningful fits were unable to be attained for f < 28 µJ/cm².

We attribute the observed dynamics for ν = 0 with f > 14 µJ/cm² (as well as the presence of the additional long-lived component, τ_∞, for ν = −1, −2) to hot hole injection (into the WSe₂/WS₂ bilayer) via thermionic emission following unavoidable photo-excitation of the Gr electrodes at sufficiently high excitation densities (schematically depicted in Supplementary Fig. 9)^40,41. We note that in Supplementary Fig. 9, the shown Gr and h-BN band alignment is based on ref. ⁴¹, while the WSe₂ and WS₂ band alignment is based on ref. ⁴⁹. As described in refs. ^40,41, photoexcited carriers in the Gr can rapidly thermalize via scattering (e.g., Auger-like process). Following this, ‘hot’ carriers (specifically holes) in the tail of the resulting thermal distribution have sufficient energy to overcome the Gr/h-BN/WSe₂ (or Gr/h-BN/WS₂) energetic barrier (i.e., valence band offset) and to undergo interlayer transfer. Further, this process is highly pump fluence-dependent, as also captured clearly in the time traces of the ν = 0 where dynamics are only observed for f > 14 µJ/cm². This is consistent with the additional long-lived component only being necessary in this same high fluence regime for proper fitting of the correlated state dynamics. Interlayer charge transfer ultimately driven via thermionic emission is linked to a multi-component timescale with a faster (<90 fs) and a slower (~1 ps) contribution⁴¹. While the former is unresolvable within our instrument response function (and is mainly related to the thermalization rather than the transfer process), the latter agrees well with the fit τ_rise for ν = 0 as expected (and is mainly related to interlayer transfer). The long-lived component (τ_∞) in our measurement (for ν = 0, −1, −2) may result from, in addition to this thermionic hole transfer and charging, transient lattice heating. This process does not interfere with the observed disordering/reordering of the ν = −1, −2 states.