Introduction

Non-Hermitian systems host a range of intriguing phenomena in physics, such as reconfigurable light routing1, potential for enhanced sensitivity2,3 and unidirectional invisibility4, that are deeply rooted in symmetry and topology. One such phenomenon is the non-Hermitian skin effect (NHSE) where a macroscopic fraction of the eigenmodes of a finite system become exponentially localized at its boundary5,6. This localization is a direct consequence of the nontrivial (topological) winding of the system’s eigenvalues in the complex energy plane7,8,9. Disorder and small variations in the system do not change the winding number which is a topological invariant9.

Over the last few years, the NHSE has been demonstrated on a variety of platforms5,10,11. Exemplary platforms include acoustics and phononics12, topo-electric circuits13, and photonics14. These developments are in part motivated by the profound impact of NHSE on band topology7,15,16, spectral symmetry17, and dynamics18,19. Particularly in photonics, recently the NHSE has enabled intriguing demonstrations of the tuneable directional flow of light20, near-field beam steering21, engineering arbitrary band topology22 and topological funneling of light14. Nevertheless, these demonstrations have been limited to systems that can be effectively described by time-independent Hamiltonians23. The introduction of time-dependent non-Hermitian Hamiltonians can lead to a dynamic control over the skin effect and also lead to fundamental advances in novel non-Hermitian topological phases that are not accessible using time-independent systems. Here we demonstrate dynamical control of the two-dimensional non-Hermitian photonic skin effect, that is, corner skin modes, using purely synthetic temporal dimensions. Specifically, using time-multiplexed light pulses in fiber loops, we show manipulation of the gain/loss in the system at a scale that is faster than the dynamics of light pulses in the lattice. Using this dynamical manipulation, we demonstrate gradual control over the degree of localization of the corner skin modes, gradual tweezing of light where we move the corner skin modes along a predefined trajectory in the lattice, and 2D funneling of light where photons always funnel to the corner skin modes irrespective of their initial position in the 2D lattice. Finally, by introducing controlled disorder in the system in the form of random variations in gain and loss, we quantitatively investigate the robustness of the corner skin modes against such disorders. Our work opens up an avenue to explore the rich physics of time-dependent non-Hermitian models such as non-Hermitian Floquet systems.

2d quantum walk with non-Hermitian topology

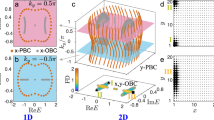
Our system simulates a discrete-time quantum walk of photons on a two-dimensional non-Hermitian square lattice, as illustrated schematically in Fig. 1a. Specifically, we implement a split-step walk where the walker first randomly steps to either left or right (corresponding to the X direction) with equal probability, then up or down (corresponding to the Y direction). To introduce non-Hermiticity, we introduce an additional gain e+δx when the walker steps to the left, and an additional loss e−δx when the walker steps to the right. Similarly, the walker experiences a gain e+δy when moving down and a loss of e−δy when moving up. The parameters δx and δy then indicate the degree of non-Hermiticity of the walk.

Fig. 1: Two-dimensional quantum walk in non-Hermitian synthetic lattice.
figure 1

a Example of photonic quantum walk in a 2D synthetic lattice. The blue and red curved arrows show the direction-dependent loss and gain. b Winding of effective eigenenergies ϵup/down(kx, ky) in the complex energy plane for a single bulk non-Hermitian lattice with periodic boundary condition, showing line-gapped topology (indicated by the green line). Here we choose five different values ky ≡ 0, ± π/4, ± 3π/8. c Four bulk lattices with different gain-loss patterns are glued along their edges to form a corner. Note that δx > 0 implies gain for a step towards −X and loss for a step toward +X. For δx < 0 the gain-loss is inverted. A similar rule applies for δy. d Averaged spatial profile of corner skin modes formed in the system shown in c, by taking non-Hermitian parameters δx = δy = 0.175. The lattice size is 30 × 30. e The time-multiplexed experimental scheme, with which the lattice parameters can be (dynamically) controlled by the intensity modulators. EDFA: Erbium-doped fiber amplifier. PD: Photodiode.

Full size image

For this quantum walk, a concept of complex energy can analogously be defined, by solving for the eigenmodes of the non-unitary quantum walk evolution operator Û and taking the logarithm of the corresponding eigenvalue uj. Namely, this can be formulated as ϵj = ilog(uj), where Û |uj〉 = uj |uj〉. If we further impose periodic boundary conditions (PBCs) in both x and y for the bulk in Fig. 1a, we can apply the Bloch theorem for the walk and obtain the complex energy bands ϵup/down(kx, ky). (The two bands seen in Fig. 1b arise due to the up/down channel configuration of our experiment, see Supplementary Information (SI) for derivation details). The non-unitary time evolution of the walk leads to a nontrivial winding of ϵ(kx, ky) for each band in the complex energy plane as one continuously varies Bloch vector (kx, ky) along a certain curve in the Brillouin zone. To illustrate this, in Fig. 1b, we plot the complex energies ϵup/down(kx, ky) of the bulk lattice shown in Fig. 1a as we vary kx from −π to π while keeping ky fixed to different values 0, ± π/4, ± 3π/8. As (kx, ky) varies along each of these directed horizontal curves in the Brillouin zone, both ϵup(kx, ky) and ϵdown(kx, ky) winds one loop in the counterclockwise direction, thus exhibiting an integer-valued winding number −1. This is a topological invariant for our non-Hermitian quantum walk. Also, the two winding loops contributed from the two bands ϵup/down exhibit a line-gapped topology24, such that the two winding loops never cross the line Re(ϵ) = 0 in the complex plane. Windings of complex energy along other curves in the Brillouin zone are shown in the supplementary information (SI) section 3.

In a finite system, the nontrivial winding of the complex energies and the associated 2D non-Hermitian skin effect24 is manifested as corner skin modes, that is, localization of the walker can happen at an interface between regions with opposite windings (or bulk band topologies). Figure 1c shows one exemplary case which consists of four distinct regions, represented by the four different color patches. The gray patch is identical to the system described in Fig. 1a. The other three regions exhibit an inverted gain-loss relation (indicated by a change in the sign of the gain parameter) either along the x or y-axis, or both. This inversion of gain-loss leads to different windings for each region. Non-Hermitian skin effect occurs in such a system, and we numerically verify in Fig. 1d that the averaged eigenmodes of the quantum walk exhibit clustering at the junction between the four regions - as indicated by the red dot in Fig. 1c.

To simulate the quantum walk described above, we use classical light pulses in a time-multiplexed setup shown in Fig. 1e. We note that for this linear system, the evolution of classical light pulses in the lattice exactly follows that of the quantum walk of single photons in the lattice. We map the state space of the 2D square lattice of size 30 × 30 into different time-delays in two fiber feedback loops, as introduced in previous works25,26. To introduce non-Hermiticity, we use four intensity modulators that introduce individually controllable loss when the walker moves along any direction. We also use two erbium-doped fiber amplifiers (EDFAs) that provide gain in the system, and together with the intensity modulators, introduce a gain-loss mechanism that can be controlled at each step of the walker. We specifically choose electro-optic modulators with a high bandwidth to allow reconfigurability of the system’s topology at each step of the quantum walk. A full discussion of the experimental setup is provided in the SI sections 1 and 2.

Results

Skin effect under static control

To show the presence of non-Hermitian corner skin modes, we first construct the model as shown in Fig. 1c, with the corner located at the lattice origin (x = 0, y = 0). We inject a single light pulse into the time bin corresponding to the lattice origin and choose non-Hermitian parameters |δx| and |δy| to be 0.175 as in Fig. 1c. In Fig. 2a, we plot the snapshots of the light distribution in the lattice for different time steps 1, 9, and 21, which are obtained by measuring the pulse power at each time bin. The evolution of distribution shows that the walker stays localized at the origin, confirming the presence of a corner skin mode. In sharp contrast, when we set δx and δy to 0, we observe a significant spreading of the intensity distribution, indicating the absence of any corner skin modes (see Supplementary Sections 4 and 5 in the SI for the experimental data).

Fig. 2: Light localization and light funneling for static control.
figure 2

a Light localization at the corner skin modes located at (x, y) = (0, 0) for non-Hermitian parameter |δx | = |δy | = 0.175. Here a single pulse is initialized at (x, y) = (0, 0) in the up channel. b Light funneling for the same lattice parameter and pulse initialization, but the corner skin mode is located at (x, y) = (−10, 10). Here the skin effect allows light to flow to the corner skin mode and localize there. In both a and b, from left to right the snapshots are shown for time steps 1, 9, 21, respectively.

Full size image

Having shown the localization of light at the corner skin mode, we next demonstrate the skin-effect-induced funneling of light. Namely, the system dynamics bring any initial state towards the corner skin modes. We set the corner skin mode to be at the lattice site (x = −10, y = 10) while light pulses are still injected at x = 0, y = 0, which is now in the bulk of the lattice (Fig. 2b). As the system evolves, initially light spreads in bulk, but finally converges to the corner site. As shown in the SI for several different lattice configurations, light pulses always converge to the corner regardless of the initialization ___location. This funneling of light to the corner skin mode is a manifestation of the skin effect where all the eigenmodes of the system are localized at the corner. Schematic illustration of this funneling effect can be seen in Supplementary Movie 1. Our experimental results are in good agreement with our theoretical prediction shown in Fig. 2b.

Dynamically controlling the non-Hermitian lattice and skin effect

The use of time as a synthetic dimension allows us to dynamically reconfigure our non-Hermitian lattice as a function of time. Specifically, by controlling the intensity modulators at each time step of the quantum walk, we achieve temporal modulation of the gain/loss parameters δx(t) and δy(t) such that they are time-dependent. Using this time dependence, first, we demonstrate dynamical control over the degree of localization of the corner skin modes. At the start of the evolution, we adopt the configuration as in Fig. 1c and set |δx(0)| = |δy(0)| = 0.175, and inject a single light pulse at the corner skin mode situated at the origin. As the system evolves, we reduce both |δx|,|δy| by 50% for every four time-steps and continue doing so until step 16 (Fig. 3a). Because of this reduction, we observe that the corner skin modes become less confined to the origin. This is because the smaller non-Hermitian parameter exhibits eigenmodes distributed over a larger area, as predicted theoretically (see Supplementary Fig. S4 in the SI). Thereafter, starting from step 17, we reverse the process, that is, we increase the gain /loss parameters |δx|,|δy| back to its original value at the same rate. We now observe a relocalization of light at the origin.

Fig. 3: Dynamical control of the corner skin mode.
figure 3

a Dynamical control of corner skin mode spatial profile. As the non-Hermitian parameter is gradually reduced from |δx,max | = |δy,max | = 0.175 to |δx,max | = |δy,max | = 0.02 and back to |δx,max | = |δy,max | = 0.175, the corner skin mode becomes delocalized and then localized. From left to right the snapshots are shown for time steps 1, 9, 17, 25, 37, respectively. b Dynamically tweezing localized light along a designed “L”-shaped trajectory using the skin effect. Localized light is first moved in the +Y direction for 8 steps and then to the −X direction for 10 steps.

Full size image

Next, we demonstrate gradual repositioning of the corner skin modes in the lattice. We use the same lattice geometry shown in Fig. 1c and fix the non-Hermitian parameter to δx = δy = 0.175. As the system evolves, we gradually move the interface between the four distinct topological regions, repositioning the corner skin mode as a function of time. We first move the position of the corner skin mode upwards for 8 unit cells, and then leftward for 10 unit cells. As before, we inject light pulses at the corner skin mode. As the system evolves, we observe that the center of the intensity distribution follows the position of the corner skin mode as it gradually moves along the given L-shaped trajectory from its initial ___location (x = 0, y = 0) to its final ___location at (x = −10, y = 8). Furthermore, during this process, the intensity distribution remains tightly localized close to the corner skin mode. Evidently, the corner serves as a non-Hermitian tweezer of light, which allows us to gradually move trapped photons along a given trajectory in the synthetic lattice. Note that non-Hermitian light steering has been demonstrated in real-space lattices1, and our demonstration in synthetic time dimensions portends the potential for such photonic control using the temporal degree of freedom of light.

Schematic illustrations of the tapering and relocation effects can be seen in Supplementary Movies 2 and 3, respectively.

Robustness of the skin effect

The topological nature of the non-Hermitian skin effect ensures its robustness against disorder in gain/loss parameters δx, δy. To quantitatively investigate this robustness, we introduce a disorder on the gain/loss. At each lattice site, we randomly pick both δx, δy from a uniform distribution on the interval [δmax(1 − η), δmax], where max is the maximum gain parameter and is the disorder parameter which quantifies the variance of the gain parameter. In our experiment, we vary the disorder parameter between 0 (no disorder) and 2 (max disorder).

We find that the skin effect is robust when the disorder parameter η < 1. In Fig. 4a, b, we plot the evolution of light pulses in the lattice for two different values η = 0.5 and η = 1. For both cases, we inject light pulses at the corner skin mode located at the origin. We observe that, even though the localization of the intensity distribution reduces as the disorder increases, the distribution still stays confined around the origin, indicating the existence of corner skin modes even in the presence of disorder. Nevertheless, once we increase the disorder parameter to 1.5 and 2 (Fig. 4c, d), the intensity distribution diffusively spreads away from the origin, indicating the breakdown of corner skin mode. Our experimental observation agrees with the intuitively expected behavior that, for η < 1, even though there is a disorder in the modulation amplitudes, the gain for the step towards the corner is always larger than that of the outwards direction. Thus the four regions maintain their distinct non-Hermiticity and the corner skin mode exists. But, when η > 1, a direction-dependent gain for the time steps is no longer always valid and therefore the four regions are no longer distinct and the corner skin mode ceases to exist.

Fig. 4: Robustness of the skin effect at the presence of different degrees of lattice disorder.
figure 4

The randomness is introduced to the intensity modulation of the lattice and the pulse is injected at (x, y) = (0, 0). a, b Experimental observation of robustness of the corner skin mode and skin effect in a lattice with moderate disorder (ηy = ηx = 0.5, 1). Here the disorder leads to a relaxed spatial confinement of light without breaking the localization of light. c, d Breakdown of the localization in the presence of strong disorder (ηy = ηx = 1.5, 2). Light can diffuse arbitrarily far away until they are limited by the size of the experiment. In a–d, from left to right the snapshots are shown for time steps 1, 5, 13, respectively.

Full size image

To better characterize the robustness and breakdown of the skin effect, we compute the evolution of the mean-square displacement of the intensity distribution in the lattice as a function of time. The mean-square displacement is quantified as <r2> (n) = ∑x,y Px,y(n)(x2 + y2), where Px,y(n) is the time-varying intensity distribution of light. Figure 5 shows the calculated <r2> (n) for several values of the disorder parameter for both theoretical calculations and experimentally measured values. Each experimental curve corresponds to an average of eight independent experimental realizations of disorder, while the theory corresponds to eight averages. Due to the limited size of the lattice (30 × 30), we only collect data from step 1 to step 15, and plot <r2> (n) for the odd steps. The violet, red, and green curves correspond to the weak disorder, with disorder parameters being 0, 0.5, and 1, respectively. All three curves saturate to a fixed value which is well below a certain threshold. This behavior thus implies the robustness of the skin effect. However, for larger disorders of 1.5 and 2, corresponding to the yellow and blue curve, the mean squared distance does not converge. Instead, it spreads out until it becomes limited by the finite size of the lattice, indicating a complete breakdown of the skin effect.

Fig. 5: Breakdown threshold of the robustness.
figure 5

a Theory and b Experimental evolution of space-averaged displacement <r2> = <x2 + y2> as a function of step number under different lattice disorders. For disorder strength lower than the threshold η = 1, the disorder increases the effective spatial diameter of the corner skin mode, as shown in the evolution of average displacement with time. For disorders higher than the threshold, light diffusively spreads to large distances on the lattice. Standard deviations are also shown at each step.

Full size image

Discussion

In conclusion, we demonstrated robust dynamical control over the photonic non-Hermitian skin effect in a 2D synthetic lattice. We created a corner skin mode that localizes light and dynamically tuned the degree of light localization. Moreover, we dynamically steered trapped light along any given trajectory in the 2D lattice. We also demonstrate the robustness of the skin effect under lattice disorder below a certain threshold. Our results demonstrate that useful control mechanisms in spatial landscapes such as reconfigurable light steering1 can be extended to synthetic dimensions.

Looking forward, the dynamic techniques developed in this work can be further applied to investigate Floquet non-Hermitian models27,28,29, in particular in synthetic dimensions30. Further, one can create an analogue of on-site interaction by imposing a nonlinear phase shifter after the linear optical transformations, and investigate non-Hermitian models of interacting particles31. Such nonlinearities could also have implications in the recently discovered regime of topological frequency combs32,33,34 as well as temporal mode-locked lasers35 due to the periodic temporal pulses that define our platform. Moreover, the two-fold spin characteristics in our system can potentially be extended to non-Hermitian models for lattice gauge theories with higher spins and non-Abelian statistics, by increasing the number of loops36. Another intriguing direction can be exploring NHSE-enabled morphing of photonic topological modes which was recently demonstrated in mechanical lattices37. Finally, our non-hermitian lattice can be enriched with engineered synthetic gauge fields38 as demonstrated recently for both Hermitian39 and non-Hermitian models20, to explore intriguing proposals such as the quantum Skin Hall effect40.

Methods

Experimental setup

To encode the 2D lattice in time we consider two fiber loops shown in Fig. 1, labeled up channel and down channel. The length of each fiber loop is ∼3 (km), and one circulation of light in the loop is equivalent to one step of the walk. Hence, we can encode the entire 2D lattice within a time-duration (or time-delay) of ∼15,000 (ns) without mixing time-bins in step n and step (n + 1). We first encode 30 Y-time bins in both the up and down channels, each of time duration 250 (ns) in a total time duration of 7500 (ns). Each Y-time bin is then occupied by 30 X-time bins, each of time duration 7.5 (ns). At any time, the state of the system is thus represented by a complex vector (Ux,y, Dx,y), encoded in the phase and amplitude of the light pulse circulating in the two fiber loops.

Measurement

To initialize the system, we inject a single pulse into the down channel of the fiber loop. We use a continuous wave CW laser with 1550 (nm) wavelength (Optilab DFB-1551-SM-10) and by modulation of this laser using a Thorlabs SOA (SOA1013SXS), we have generated pulses of width ∼6 (ns) at a repetition rate of 1 (pulse/ms). We then control the polarization of the laser with an inline fiber polarization control (PC) before injecting the light into the down channel with a 90/10 beam splitter. Note that we use two identical 90/10 beam splitters, one for each channel. The 90/10 beam splitter in the down channel is used to inject light into the quantum walk, whereas the 90/10 beam splitter in the up channel is used to weakly couple light pulses out of the quantum walk so that we can measure the pulse power after n steps of evolution using the up channel’s PD. Note that the EDFA placed immediately prior to the up channel’s PD is merely used to amplify the light pulses coming out of the quantum walk experiment, making it easier for the PD to detect it.

As a pulse enters the system, by default we recognize it as entering the (x = 0, y = 0) time bin, and thus the initial state is D0,0 = 1. The pulse then sequentially passes through a 50/50 beam splitter denoted as ±X-beam splitter, a pair of time-varying intensity modulators (Optilab IMP-1550−20-PM) is used to impose the correct gain/loss as each time bin (x, y) passes through it, controlled by RF signal generated from Teledyne Lecroy arbitrary waveform generator (T3AWG3252). We then impose a delay of 3 (m) in the up channel and no delay in the down channel. The same procedure then repeats for Y.

To combat photon loss in the walk, we use two Thorlabs erbium-doped fiber amplifiers (EDFA) (EDFA100S), one for each channel. Before amplifying the pulse, we use wavelength division multiplexers (WDM) (DWDM-SM-1-34-L-1−2) to couple a 1543 (nm) CW laser (DFB-1543-SM-30) to the pulses so that the spontaneous emission noise during the amplification is reduced. We decouple the 1550 (nm) pulses from the 1543 (nm) CW laser with the same WDM after the amplification is done. Finally, we use PC to ensure the correct linear polarization for the 1550 (nm) signal pulses. After this, a complete quantum walk step is finished.