Separating nanobubble nucleation for transfer-resistance-free electrocatalysis

Guo, Shasha; Yu, Maolin; Lee, Jinn-Kye; Qiu, Mengyi; Yuan, Dundong; Hu, Zhili; Zhu, Chao; Wu, Yao; Shi, Zude; Ma, Wei; Wang, Shuangyin; He, Yongmin; Zhang, Zhengyang; Zhang, Zhuhua; Liu, Zheng

doi:10.1038/s41467-024-55750-5

Download PDF

Article
Open access
Published: 22 January 2025

Separating nanobubble nucleation for transfer-resistance-free electrocatalysis

Nature Communications volume 16, Article number: 919 (2025) Cite this article

5673 Accesses
3 Citations
4 Altmetric
Metrics details

Subjects

Abstract

Electrocatalytic gas-evolving reactions often result in bubble-covered surfaces, impeding the mass transfer to active sites. Such an issue will be worsened in practical high-current-density conditions and can cause sudden cell failure. Herein, we develop an on-chip microcell-based total-internal-reflection-fluorescence-microscopy to enable operando imaging of bubbles at sub-50 nm and dynamic probing of their nucleation during hydrogen evolution reaction. Using platinum-interfacial metal layer-graphene as model systems, we demonstrate that the strong binding energy between interfacial metal layer and graphene—evidenced by a reduced metal-support distance and enhanced charge transfer—facilitates hydrogen spillover from platinum to the graphene support due to lower energy barriers compared to the platinum-graphene system. This results in the spatial separation of bubble nucleation from the platinum surface, notably enhancing catalytic activity, as demonstrated in both microcell and polymer electrolyte membrane cell experiments. Our findings offer insights into bubble nucleation control and the design of electrocatalytic interfaces with minimized transfer resistance.

Operando visualization of the hydrogen evolution reaction with atomic-scale precision at different metal–graphene interfaces

Article 14 October 2021

Numerical computation of electrical potential on a gas evolving electrode

Article Open access 31 January 2023

Electrochemical on-surface synthesis of a strong electron-donating graphene nanoribbon catalyst

Article Open access 29 July 2024

Introduction

The worldwide deployment of sustainable technologies, e.g., green hydrogen, urgently requires the development of efficient and cost-effective catalysts capable of operating under industrially relevant conditions, especially at high current densities (HCD, > 200 mA cm⁻²)¹. For example, the proton exchange membrane (PEM) electrolysis is expected to reach a current density of 4–6 A cm⁻² at a cell voltage of < 1.7 V, with a voltage efficiency of > 80% by 2050². It is worth highlighting that gas-evolving reaction is a complex gas-liquid-solid phase process. While considerable advancements have been made in the structural engineering of solid catalysts to enhance intrinsic activity and in the modulation of liquid electrolytes to optimize microenvironments^3,4, little attention has been directed toward controlling the gas phase—a key factor for efficient mass transfer.

In fact, at HCD conditions, the electrode is fully covered by vigorously-generated bubbles, which would reduce the effective electrocatalytic area, obstruct ion conduction and transport, as well as change ion concentration gradients. Consequently, those negative factors will together cause deactivation, increased ohmic and concentration overpotentials, and even the sudden death of the working cells⁵. To mitigate those challenges, electrode-wettability strategies have been developed to promote the detachment of bubbles^6,7. For example, micro/nanostructures with superaerophobic or superhydrophilic properties⁸ have been developed to reduce bubble size and prevent bubble adhesion. However, despite these progress, the regulation of bubble nucleation behaviors remains underexplored, largely due to the lack of in-situ techniques with sufficient spatiotemporal resolution and well-defined material systems.

In this work, we developed an on-chip microcell-based single-molecule total internal reflection fluorescence microscopy (TIRF) platform, termed on-chip-TIRF, to operando probe how nanobubbles nucleate at the surface of graphene-supported Pt film (denoted as Pt-graphene) with a high spatial resolution of 26 nm and a temporal resolution of 16.7 ms. Next, we observed that introducing interfacial metal layers (IMLs) between the Pt and graphene layers can effectively regulate the nanobubble nucleation. Specifically, a notable amount of nanobubbles were observed to form on the graphene support in addition to Pt active sites, termed delocalized nanobubble evolution (DNE). Later, our first-principles calculations on the Pt-Ti-graphene system indicated that introducing the Ti IML induces substantial electron transfer at the interface, reducing the kinetic barrier for hydrogen spillover^{9,10,11,12,13,14,15,16,17}. Consequently, adsorbed hydrogen atoms (H_a) can efficiently migrate to the carbon support and form H₂ gas thereon. Furthermore, a linear relationship has been established between the DNE strength and the IML-graphene binding energy. Finally, as a proof-of-concept application, micro-cell measurements and the assembled electrolyzers confirm the notable contribution of such delocalized bubble evolution to practical water splitting.

Results and Discussion

Operando imaging of nanobubbles at sub-50 nm

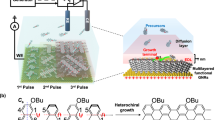
To in-situ monitor the behaviors of nanobubbles generated on the electrochemical interface, we developed an on-chip-TIRF platform by assembling single-molecule TIRF^18,19,20 with an on-chip electrocatalytic micro-cell system (see scheme in Fig. 1a and Supplementary Figs. 1–3). In the on-chip-TIRF, the micro-cell plays two roles: i) making model catalytic interfaces like Pt-graphene or Pt-IML-graphene by micro-/nano-processing technologies and ii) opening the reaction window at the region of interest to improve the imaging resolutions (see Supplementary Figs. 3, 4, as well as Methods for details). Monolayer graphene was used as the supporting substrate due to its catalytic inertness, transparency, and high conductivity (Supplementary Fig. 5). Metal films were then precisely patterned and deposited onto the graphene as the catalytic surface (Supplementary Fig. 4). Taking the Pt-Ti-graphene as an example, our experiment successfully demonstrated a clear sandwich interface structure consisting of a top Pt layer (4 nm), an interfacial Ti layer (2 nm), and a bottom graphene layer (Fig. 1a and Supplementary Figs. 6–8 and Supplementary Note 1).

Our super-resolution imaging of nanobubbles is based on the adsorption of a fluorescence dye under TIRF illumination^21,22. In detail, upon the application of voltage, a Rhodamine 6 G (R6G) molecule could adsorb onto the emerging gas-liquid interface, resulting in a fluorescent spot within the evanescent field (~55 nm) (inset of Fig. 1a and Supplementary Note 2). As shown in Fig. 1a and Supplementary Movie 1, generated nanobubbles would result in stochastic fluorescence bursts at many localized spots on the atomically flat surface.

In a typical HER process, we observed that the nanobubble sizes are usually varied with the applied overpotential, as shown in Fig. 1b. The percentage is determined by percentage$={N}_{i}/\sum {N}_{i}$, where ${N}_{i}$ is the number of nanobubbles with a height of $i$ nm. It turns out that higher overpotential results in larger nanobubble sizes; for example, the average height of nanobubbles increases from 32.6 nm at −50 mV versus a reversible hydrogen electrode (denoted as mV_vsRHE) to 35.3 nm at −100 mV_vsRHE, 38 nm at −150 mV_vsRHE, and 41.3 nm at −200 mV_vsRHE (Supplementary Note 3). Furthermore, Fig. 1c presents the fluorescence intensity (FL) trace of a randomly selected spot in Fig. 1a under −200 mV_vsRHE. It is evident that stochastic off-on signals could be recorded for the entire movie, capturing the dynamic behavior of nanobubbles (frequently nucleate and burst) on the Pt-Ti-graphene surface. The estimated lifetime of nanobubbles was ~7.5 ms (Fig. 1d, Supplementary Note 4 and Figs. 9–11), which matches well with the results predicted by Epstein and Plesset²³, and Ljunggren²⁴. Taking together, using such a system with high-speed camera recording (60 Hz), sufficient high R6G concentration¹⁸, as well as the spatially-confined reaction window, we are capable of visualizing nanobubble dynamic behaviors with a spatial resolution of 26 nm and temporal resolution of 16.7 ms (Supplementary Fig. 12 and Supplementary Note 5).

Demonstration of delocalized bubble evolution

We first investigated the Pt-graphene interface due to the widespread use of Pt-C catalysts in industries (Fig. 2a). The on-chip-TIRF platform recorded the response of such a device at −150 mV_vsRHE for 180 s in 0.5 M H₂SO₄ with 10 nM R6G. As expected, most nanobubbles in the Pt-graphene device were observed exclusively on the active Pt surface but not on the graphene support (Fig. 2b), which is consistent with the previous study²⁵. Contact angle experiments were performed to examine the surface wettability of graphene and Pt surfaces, respectively. As shown in Supplementary Fig. 13, the contact angle of the gas-Pt surface (104.2°) is ~18.3° larger than that of the gas-graphene surface (85.9°), suggesting that bubbles nucleate on the graphene more easily than on the Pt surface, which is opposed to our observations. A similar contradictory phenomenon was also observed in the MoS₂-graphene device, where nanobubbles nucleate on the MoS₂ active sites but not on the lower-surface-energy graphene (Supplementary Fig. 14). In addition, we investigated the pure graphene device, showing negligible nanobubbles (Supplementary Fig. 15 and Supplementary Movie 3). These results indicate that surface wettability should not be the prominent factor in the nanobubble nucleation process, although it has been intensively studied in promoting micro-/millimeter-sized bubble nucleation⁶.

**Fig. 2: Demonstration of delocalized nanobubble evolution.**

Next, we introduced a 2 nm Ti IML between the Pt and graphene layers and investigated its possible impact on the nanobubble nucleation. Interestingly, for the Pt-Ti-graphene device, a significant amount of nanobubbles were detected on the graphene support, in addition to the active surface (Pt) (Fig. 2c). The average nanobubble density on the graphene support is approximately equal to that on Pt. Noteworthy, it is also ~700 times higher than that on the graphene support in the Pt-graphene device. These findings suggest that in the Pt-Ti-graphene system, some chemisorbed H_a migrate from Pt active sites to the graphene support, followed by H₂ desorption and bubble nucleation on graphene. We term this phenomenon DNE in the following discussions. Such DNE would trigger graphene hydrogenation due to its surface’s chemisorbed H_a, which is verified by Raman characterizations. Supplementary Fig. 16 shows the emergence of a sharp D peak after the application of electrochemical potentials, which is attributed to the breaking of the translational symmetry in C-C sp² bonds following the formation of C-H sp³ bonds²⁶.

To give a better visualization of this DNE phenomenon, we fabricated a Pt-Ti-graphene device with a large reaction window (260 µm by 80 µm), showing a distribution gradient of the bubble density from the metal pattern towards the graphene periphery (Supplementary Fig. 18). Additionally, real-time hydrogen migration was observed by monitoring the nanobubble distribution on a graphene-supported 1D Pt-Ti nanowire diffusion device. Supplementary Fig. 17 show that H_a diffuse rapidly after applying a fixed potential of −50 mV_vsRHE, eventually reaching the right edge in 1.17 s (70 frames). It is worth mentioning that, owing to the absence of this DNE phenomenon in some gas-evolving catalysts (e.g., widely-used Pt/C for HER), the violently generated bubbles will cover the catalytic surface, severely obstructing ion transport at the gas-liquid-solid three-phase interface^6,7 and thus leading to efficiency deterioration.

The above observations imply that introducing IML (e.g., Ti layer) would play a crucial role in the DNE phenomenon. To clarify this, we conducted a systematic study involving Pt-Co-graphene, Pt-Au-graphene, Pt-Al-graphene, Pt-Pd-graphene, and Pt-Ni-graphene (Fig. 3). Note that the Pt and IML thicknesses are kept the same for all devices—~4 and 2 nm, respectively—in our experiment, in consideration of the transparency of films and the dependency of DNE on the IML thickness (Supplementary Fig. 19). The fabricated devices were subjected to the same conditions as the ones in Fig. 2. Our studies present several interesting phenomena. First, as for Al and Au IMLs, most nanobubbles nucleate on the Pt surface while few on the graphene surface (Figs. 3b, d), mirroring the behavior observed in the Pt-graphene device. Second, with respect to Pd, Ni, and Co, nanobubbles are observed to nucleate on both the Pt and graphene surfaces (Fig. 3c and e, f), akin to that observed on Pt-Ti-graphene. Third, after a detailed statistical analysis on tens of devices, we plot the nanobubble densities on the graphene surface versus the type of IMLs, indicating an order of Au< Al< Pd< Co< Ni< Ti in strengthening the DNE behavior.

**Fig. 3: Impact of IMLs on delocalized nanobubble evolution.**

Mechanism insights

To gain an insight into the IML-modulated DNE mechanism, we performed systematic first-principles calculations, in which different computational parameters, the potential impact of titanium oxides, and the influence of strain and hydrogen coverage have been examined (Supplementary Note 7 and Supplementary Figs. 20–37). Furthermore, we conducted detailed analyzes of minimum energy paths (MEPs) and electronic properties (i.e., Bader charge, charge density difference and density of state (DOS)), as shown in Fig. 4. A summary of the computational details is provided in the “Methods” section.

**Fig. 4: Mechanism of H_a-migration in delocalized nanobubble evolution.**

We first examined hydrogen migration across the Pt-graphene and Pt-Ti-graphene interfaces. Figure 4a shows that the calculated plane-averaged charge density difference, Δρ(z), across the Pt-Ti-graphene interface is larger than that across the Pt-graphene interface, suggesting enhanced charge transfer between Pt-Ti heterolayer and graphene. This behavior can be ascribed to the reduced catalyst-support distance of 2.1 Å and the subsequently stronger binding energy (0.14 eV/ Å²) in the Pt-Ti-graphene, compared to the Pt-graphene interface (3.1 Å and 0.04 eV/Å²). Note that the metal-support distances were estimated by DFT calculations. As a result, the H_a migration barrier (0.49 eV) across the Pt-Ti-graphene interface is much lower than that of the Pt-graphene (1.89 eV, see Supplementary Fig. 26). This finding is consistent with the experimental observations in Fig. 2, which shows a higher density of nanobubbles on graphene in the Pt-Ti-graphene system compared to the Pt-graphene system.

Furthermore, the enhanced charge-transfer behavior leads to a lowered d band center and a reduced DOS peak for Pt atoms in proximity to the interface with Ti (Figs. 4b and Supplementary Fig. 27), in contrast to the case in the Pt-graphene system (Supplementary Fig. 28). As such, the active Pt sites around the Pt-Ti interface exhibit decreased reaction energies and reduced barriers for H_a migration, transforming the high-energy migration reaction (Supplementary Fig. 26) into a sequence of hydrogen migration steps with much lower reaction energies and energy barriers, as depicted by the light blue lines in Fig. 4c. Notably, the calculated maximum change in free energy is only 0.39 eV and the highest migration barrier encountered within these pathways is only 0.49 eV, comparable to that for direct H_a desorption on Pt (Supplementary Note 8 and Supplementary Fig. 29).

Under HCD conditions, external factors such as hydrostatic pressure (Supplementary Fig. 30) and electrode potential^27,28 tend to increase the H_a coverage (θ) on the Pt surface. This, in turn, raises the chemical potential of H_a, manifesting as decreased adsorption energy or a shift of the adsorbed hydrogen towards a free atom. Herein, we further calculated the free energy evolutions for H_a migration across the Pt-Ti-graphene interface at three θ (Figs. 4c and Supplementary Fig. 31). At θ = 1.04, the H_a migration from Pt(111) to graphene is overall endothermic by 1.12 eV. As θ increases, the migration behavior gradually becomes thermodynamically favorable. At θ = 1.22, the final state (G site) is even lower than the initial state (A site), showing a spontaneous process. On the support side, the graphene layer can be readily hydrogenated under the electric double-layer^29,30, which benefits the H_a migration process. Consequently, the free energy change between the final and initial states is reduced from 0.40 to −0.35 eV along the F-G paths, and the kinetic barrier is reduced to only 0.1 eV (red lines in Fig. 4c). Together, these results indicate that H_a migration-enabled DNE on graphene is preferable under HCD conditions.

On the graphene support, the water-assisted H_a migration³¹ barrier was estimated to be as low as 0.29 eV (Supplementary Fig. 32), which corresponds to a ${D}_{{{\mbox{H}}}_{{\mbox{a}}}}$ of ~3.98 × 10⁻⁶ cm² s⁻¹ at 298 K (Methods). In addition, we examined the hydrogen desorption from graphene, showing a low barrier of 0.47 eV via the Heyrovsky pathway (Supplementary Fig. 33). These results collectively suggest that H_a migration (from the active Pt to the inert graphene support) can be modulated by the Ti IML, and the involved kinetic processes present lower barriers compared to the conventional HER pathway on Pt.

We further studied the effect of metal-graphene interaction on facilitating H_a-migration behaviors in other Pt-IML-graphene systems, including Ni, Co, Pd, Al, and Au. In our work, we adopted metal-graphene binding energy (ΔE_b) calculated by local density approximation (LDA) functional due to its close agreement with experimental data²³. Figure 4d illustrates various ΔE_b as a function of ρ measured in our experiments. Interestingly, a nearly linear relationship with a Pearson correlation coefficient (r) of 0.96 was extracted, suggesting that a stronger IML-graphene interaction leads to more efficient H_a migration. Furthermore, we examined the relationship between IML-graphene interaction and the previously reported H_a spillover descriptor, i.e., work function difference (W-W_G, where W and W_G represent the work function of the metal and graphene, respectively)¹⁰. As shown in Supplementary Fig. 34, r for ΔE_b-(W-W_G) and (W-W_G)-ρ are only −0.35 and −0.37, respectively, indicating poor correlations of ΔE_b-(W-W_G) and (W-W_G)-ρ. In addition, IML-graphene interaction or H_a-migration behavior cannot be accurately accessed by the adsorption energy of a single metal atom on graphene (ΔE_m), as demonstrated by the weak correlation coefficients: an r value of only −0.24 between ΔE_b and ΔE_m, and an r of only −0.42 between ΔE_m and ρ (Supplementary Fig. 35). These results suggest that ΔE_b, rather than (W-W_G) or ΔE_m, serves as an adequate descriptor for H_a migration and associated DNE strength in our systems. This principle may potentially be used to explain previously reported heterostructure catalysts, such as Pt₂Ir/CoP (HER)¹⁰, Ir/Ni(OH)₂ (OER)³², Cu/NiFe double layer hydroxide (HER/OER)³³, and Ag/ordered-ligand interlayer (CO₂RR)³⁴.

Additionally, Supplementary Fig. 36 plotted ρ against the calculated free energy of hydrogen adsorption on various metals (ΔG_H). It was found that when the hydrogen adsorption strength on the IML (ΔG_H-IML) is larger than that on the Pt (ΔG_H-Pt), the presence of the IML enhances nanobubble evolution, as indicated by a higher ρ value compared to pure Pt-graphene. In contrast, when ΔG_H-IML < ΔG_H-Pt, the ρ value of Pt-IML-graphene is similar to that of Pt-graphene. Therefore, ΔG_H-IML > ΔG_H-Pt might serve as a prerequisite in finding IML materials.

Performance evaluation in microcell and full-cell

It is well-known that gas-evolving catalysts (e.g., widely used Pt/C for HER) suffer from efficiency deterioration due to the violently generated bubbles. As discussed above, DNE would facilitate the separation of nanobubbles from the active Pt surface, potentially eliminating mass transport limitations for hydrogen production. We next employed micro-cell measurements to evaluate the contribution of the DNE to the HER performance of the Pt-Ti-graphene system (Fig. 5a). In our experiment, the Pt area percentage (P_Pt = A_Pt/A_RW, where A_Pt and A_RW represent the areas of the exposed Pt and the reaction window, respectively) was used as the descriptor. Figure 5b shows the optical images of the devices, where the reaction windows with P_Pt varying from 100% to 5% were precisely defined. Their corresponding LSV curves are presented in Fig. 5c. Importantly, a nearly linear increase of j_Pt (current density based on the area of Pt) can be identified at −50 and −100 mV_vsRHE as P_Pt decreases from 100% to 5% (Fig. 5d). Devices with delocalized bubble evolution effect exhibited notably improved performance compared to pure Pt surfaces (P_Pt = 100%). For example, a 16-fold improvement in j_Pt at −100 mV_vsRHE was observed for the device with P_Pt = 5%. In addition, this specific device (P_Pt = 5%) exhibited a ~ 10-fold increase in activities relative to previously reported Pt/C catalysts (Supplementary Table 1). This effect can be further magnified by increasing the ratio of graphene support. A current density as high as 1.35 × 10⁴ mA cm⁻² at −100 mV_vsRHE was realized for the device with P_Pt = 0.03%, representing a nearly 50-fold enhancement compared to a pure Pt film (Supplementary Figs. 38, 39). Moreover, the slope of j_Pt versus P_Pt at −100 mV_vsRHE is larger than that at −50 mV_vsRHE, indicating efficient ion transport under HCD. It is worth mentioning that both carbon and Pt in the DNE system contributed to the overall catalytic efficiency, making the Pt-to-C area ratio another critical factor in this catalyst design. For example, by normalizing the activity over the entire electrode area (j_RW), we identified an optimized P_Pt in the range of 50%–70% (Supplementary Fig. 40).

**Fig. 5: Performance contribution and practical application.**

As a proof of concept in practical application, we assembled a PEM electrolyzer to demonstrate the real-world implications of the elucidated DNE in water splitting (Fig. 5e). Utilizing conventional carbon papers (2.5 cm by 2.5 cm) as supporting substrates, we selectively deposited Pt-Ti metal pattern arrays onto the support using a shadow mask, which served as the cathode in PEM. The deposited regions exhibit a distinctly darker contrast in the optical images (Supplementary Fig. 42). Carbon paper-supported pure Pt metal pattern arrays were also fabricated for comparison. A Nafion 115 membrane was adopted to isolate gas diffusion electrodes and exchange protons. As shown in Fig. 5g, the Pt-Ti-carbon paper-based cell exhibits a lower voltage compared to its Pt-carbon paper counterpart under the same condition. The EIS spectra in Fig. 5f indicate that the Pt-Ti-carbon paper cathode gives a ~ 2-fold reduction in charge transfer resistance and a lower value of ohmic resistance, compared to the Pt-carbon paper cathode (Supplementary Tables 2, 3). Finally, the durability of the cell at the actual working conditions in a PEM electrolyzer was examined (Fig. 5h). The Pt-Ti-carbon paper-based cell exhibits negligible degradation over ~250 hrs at 2.0 V under a high current density of 500 mA cm⁻².

In summary, we have conducted model studies using Pt-IML (Ti, Ni, Co, Pd, Al and Au)-graphene catalytic interfaces on the on-chip-TIRF platform, showing that the bubble nucleation behavior can be well-controlled by the IML. It is worth mentioning that spatial separation of nanobubble nucleation from active sites was realized, potentially mitigating the negative effects of gas-induced mass transport resistance. Our calculations verified this DNE phenomenon and revealed IML-support binding energy as a key descriptor for the DNE strength. Moreover, the micro-cell measurements show that at P_Pt = 0.03%, the device’s current density is nearly 50-fold higher than that of a pure Pt surface, highlighting a notable contribution of the observed DNE to HER efficiency. In practical applications, the assembled PEM cell with the Pt-Ti-carbon paper as a cathode outperformed the one with the Pt-carbon paper. Our findings offer a promising solution to gas-induced mass transport blockage on the gas-evolving catalytic surface, advancing scalable gas production in various electrochemical reactors.

Methods

Chemicals

Ti (99.999%), Pt (99.999%), Au (99.999%), Al (99.999%), Pd (99.999%), Co (99.999%), Ni (99.999%) metal targets were purchased from Premier Solutions Pte Ltd. 0.5 M Sulfuric acid (H₂SO₄, ≥99.9%, pH = 0) was obtained from Honeywell Research chemicals, which was properly sealed and stored in a cool, dark chemical storage area at 20 °C. The hydrogen reference electrode and leakless Ag/AgCl reference electrode were bought from Bronjo Medi. Double-pointed carbon rods, which were used as counter electrodes in on-chip micro-cell and on-chip-TIRF measurements, are purchased from Ellipsiz DSS Pte Ltd. A Nafion 115 membrane with a thickness of 0.127 mm (Grade RT membrane), carbon papers, Ti substrate, and Iridium oxide (IrO₂) was purchased at Suzhou Sinero Technology Co., LTD. Hydrogen peroxide (H₂O₂, 30 wt.%) was obtained from Sinopharm Chemical Reagent.

The setup of the in-situ single molecule on-chip-TIRF measurement

The in-situ single-molecule on-chip-TIRF experiments were conducted on an inverted fluorescence microscope (Nikon Eclipse Ti-U) (Supplementary Fig. 1). An adjustable 100 mW, 532 nm laser beam (L6CC Oxxius) with circular polarization was focused onto the material-solution interface via a dichroic mirror ((Di02-R635-25 × 36, Semrock) by a 100× infinity-corrected microscope objective lens (Nikon Plan Apo λ, NA 1.45). Further, to achieve an evanescent field of illumination—tens of nanometers into the solution—the illumination configuration was adjusted to wide-field total internal reflection (TIR). This was achieved by employing a transition stage to shift the laser beam towards the edge of the objective lens, enabling an incidence angle close to the critical angle of the glass-water interface. The emission passed through a quad-edge laser dichroic mirror (Di03-R405/488/532/635-t1-25 × 36, Semrock), followed by being filtered by a band-pass filter (ET605/70 m, Chroma), and then collected through the oil-immersion objective lens with f = 75 mm. The fluorescence images were captured by an EMCCD camera (Andor iXon3) cooled to −70 °C at 60 frames per second for a frame size of 256 × 256 pixels.

The super-resolved image analysis method

As described before, the imaging was recorded by the TIRF microscope at an exposure time of 16.7 ms per frame. The super-resolution analysis method—Point Accumulation for Imaging in Nanoscale Topography (PAINT)^35,36—is based on the photo-switchable nature of the used fluorescence probe, R6G. Typically, hundreds or thousands of photons can be emitted from one molecule during one frame (16.7 ms). The raw image data were analyzed using previously described methods^37,38,39. Then, the super-resolution images can be reconstructed from the positions of all single R6G molecules in all recorded frames (around 8000). Raw data of several super-resolved images in this work have been provided as Supplementary Movies. The R6G molecules labeled nanobubbles can be well-identified due to the high contrast compared to the dark background.

The fabrication method of on-chip devices

Three types of microcell on-chip devices are fabricated in this work (Supplementary Figs. 3, 4). Type 1 microcell on the transparent glass substrate (150 μm thickness) is capable of in-situ monitoring the dynamic behavior of hydrogen nanobubbles during the gas-evolving reaction; Type 2 microcell is used to explore the possibility of using nanobubbles as activity indicators; Type 3 microcell is used to optimize the hydrogen migration induced hydrogen evolution on SiO₂/Si substrates, and the exposed platinum and graphene area accessible to the electrolyte can be well-controlled during fabrication. The optimal area ratio of Pt/C can be determined by comparing the area-based HER activity of the devices with the varied area ratio of exposed Pt and graphene. As shown in Supplementary Fig. 4, the typical fabrication process of types 1 and 3 consists of 5 major steps. First, conventional photolithography was adopted to pattern the 32 Au contact pads on 20 × 20 mm glass chips (160 μm) or 20 × 20 mm² SiO₂ (275 nm)/Si or glass chips. Second, the chemical vapor deposition prepared monolayer graphene was transferred onto the chips via the standard PMMA assist method. Third, conventional EBL and reactive ion etching (RIE) using O₂ gas (20 W, 40 s) were employed to cut the whole graphene into several electrically separated pieces. Fourth, the Pt patterns were defined by EBL, followed by the deposition of transparent Ti (2 nm)/Pt (5 nm) film with a rate of 0.1 Å/s. The 2 nm Ti layer was used as an adhesive layer to enhance the Pt-graphene contact; Otherwise, the interaction between Pt film and graphene is not substantial. For example, the Pt film was easily peeled off from the graphene film during the reaction. Fifth, the reaction window was exposed by EBL in a 1-μm-thick PMMA film, allowing the single-entity measurements. For the fabrication of type 2 devices, all the steps are the same as those of types 1 and 2 except step 4, where exfoliated/CVD-grown MoS₂ was transferred onto the substrates.

On-chip electrochemical microcell measurements

Figure 5a–d presents data obtained from three-electrode on-chip electrochemical microcell measurements⁴⁰. In this setup, the counter electrode was connected to a double-pointed carbon rod, while the reference electrode was connected to a leakless Ag/AgCl electrode, respectively. The Pt-Ti-graphene micro-cell device with various P_Pt was connected to the working electrode to collect its electrocatalytic signals during HER. During all experiments, only materials within the reaction window (Fig. 5b) can participate in the electrochemical reaction, while area outside this reaction window were protected by a PMMA film. Electrochemical potential scans were conducted at a rate of 5 mV per step. The current density in Fig. 5c, d was calculated by normalizing the observed current to the exposed Pt area. To ensure accuracy, the electrochemical potential of the leakless Ag/AgCl electrode was calibrated by a standard hydrogen electrode (Supplementary Fig. 45).

The PEM device fabrication and measurement

First, the Nafion 115 membrane was washed using 5 wt.% H₂O₂ and deionized water at 80 °C for one hour each to remove any organic contaminants, followed by immersing in 0.5 M H₂SO₄ and deionized water at 80 °C for one hour each to achieve H⁺ ion exchange. Second, the anode catalyst-coated membrane (CCM) was prepared by applying IrO₂ ink onto the Nafion 115 membrane (2.5 cm by 2.5 cm) using an ultrasonic spray method to ensure even distribution, achieving an area density of 2.5 mg cm⁻². Third, to prepare the cathode, Ti (2 nm)/Pt (10 nm) pattern arrays or Pt (10 nm) pattern arrays were deposited onto a carbon paper (2.5 cm by 2.5 cm) through a template mask at a rate of 0.1 Å s⁻¹. Finally, the PEM device was assembled by hot pressing cathode layer, CCM, Ti substrate (as anode current collector) at 130 °C for 2 minutes under a pressure of 2 MPa, and insulated by polytetrafluoroethylene gaskets.

The mass loading of metal on the cathode can be approximately determined from the area percentage of metal pattern arrays on the carbon paper—which is 17.43% (Supplementary Fig. 42), and the pattern thickness (2 nm for Ti and 10 nm for Pt). Using the density of Ti (4.54 g cm⁻³) and Pt (21.42 g cm⁻³), the Ti and Pt mass loading can be calculated using the formula: M = thickness ${{\rm{\times }}}$ density ${{\rm{\times }}}$ unit area ${{\rm{\times }}}$ area percentage. As a result, the Ti and Pt loading on the cathode is 1.58 × 10⁻⁶ g cm⁻³ and 3.73 × 10⁻⁵ g cm⁻³, respectively.

The PEM water electrolyzer was tested using an Ivium Stat workstation. The deionized water flow rate through the serpentine channel in the bipolar plate is 4 mL min⁻¹. The temperature of the deionized water was maintained at 80 °C using two temperature sensors located near the flow field in the bipolar plates. The EIS measurements were conducted at 1.6 V versus the counter electrode. Stability tests were performed at a constant current density of 500 mA cm⁻² without iR correction.

First-principles calculations

First-principles calculations were performed using the Vienna Ab initio Simulation Package (VASP) code⁴¹, with the revised Perdew-Burke-Ernzerh (RPBE) parametrization of the generalized gradient approximation (GGA) as the exchange-correlation potential and projector-augmented wave (PAW) method for the core region, respectively. To adopt the most appropriate exchange-functional, we examined the effects of different exchange-correlation functionals on the free energy (ΔG) for H adsorption on Pt(111). Supplementary Fig. 22a shows that rPBE functional produced an ΔG value closest to zero and was selected for our calculations. According to the examination in Supplementary Fig. 22b, the kinetic energy cutoff of 400 eV was chosen for the plane-wave expansion. A vacuum region of 20 Å was set to avoid spurious interaction between adjacent slabs. In Supplementary Fig. 22c, we also investigated the effects of various van der Waals correction methods on the distance (d) between Pt and graphene. The zero-damping DFT-D3 method by Grimme yielded a d value most close to the experimental result and, thus, was selected for our systems⁴². The optimized structures can be found in the Supplementary Data 1.

The Pt-graphene and Pt-Ti-graphene structures were modeled in nanoribbon configurations, as shown in Supplementary Fig. 26. For the Pt-Ti-graphene system, three-layer fcc(111) Pt and two-layer hcp(0001) Ti slabs with a width of ~19 Å were placed on graphene along the zigzag direction with a lattice mismatch of ~2%. The stacking sequences of Pt and Ti slabs have been adjusted to achieve the most stable configuration (Supplementary Fig. 23). During our device fabrication process (Supplementary Fig. 4), the graphene device was loaded into e-beam evaporation chamber under ultra-high vacuum (< 1e⁻⁹ torr), where ~2 nm Ti layer and ~4 nm Pt layer was deposited sequentially, resulting in a Pt-Ti-graphene sandwiched structure in the bulk region and trapezoid-like morphology at the edge of the deposited metal pattern (Supplementary Figs. 6, 7). Therefore, to mimic the experimental structure, we proceeded to employ Pt layers to cover the first Ti layer. The bottom Ti layer remained pure Ti due to the tenfold stronger binding energy between Ti and graphene compared to Pt and graphene, emphasizing the significant role of the robust Ti-graphene interaction in binding metal catalysts to graphene. Then, the Pt-Ti-graphene model was fully relaxed by ab initio molecular dynamics (AIMD) simulations for 6 ps at 300 K, with the metal atoms in the interior fixed to simulate bulk conditions. As illustrated in Supplementary Fig. 25, the structure remained stable with converged energy, suggesting the stability of the Pt-Ti-graphene system. The Pt-Ti-graphene model contains 302–310 atoms, comprising 144 carbon, 48 titanium, 62 platinum, and 48–56 hydrogen atoms for different hydrogen coverages. It has been shown that the lattice mismatch has only a limited impact on the calculation of energy barriers and free energy, as indicated in Supplementary Fig. 24. The Brillouin zone integration was sampled by a 3 × 1 × 1 k-grid mesh for the large supercell of interfacial structures. Structures were fully relaxed until the force on each atom was less than 0.01 eV/Å. Implicit solvent through Poisson-Boltzmann continuum approximation was used to take solvent effect into account, which was implemented in the VASPsol code⁴³. The energy barriers of hydrogen migration were computed with the climbing image nudged elastic band (NEB) method⁴⁴. The hydrogen coverage is defined as θ = N_H/N_M (where N_H and N_M denote the numbers of H_a and surface metal atoms, respectively).

Theoretical calculation of hydrogen diffusion coefficient

According to the random walk model for diffusion⁴⁵, the diffusion coefficient, ${D}_{{H}_{a}}$, of activated hydrogen atoms on graphene can be computed as

$${D}_{{H}_{a}}=\frac{{v}{{a}}^{2}}{{z}},$$

(1)

where a is the traveling distance of H_a in a single hop, v denotes the microscopic jump frequency, and z is the number of neighboring sites to which the hydrogen atoms can hop. According to the transition state theory⁴⁶, the microscopic jump frequency v is related to the activation energy E_act for surface diffusion and can be determined by the equation

$${v}=\frac{{kT}}{{h}}\frac{{{Z}}^{{\mbox{TS}}}}{{{Z}}^{{\mbox{IS}}}}\exp \left(\frac{{-{E}}_{{\mbox{act}}}}{{kT}}\right),$$

(2)

where T is temperature, k is the Boltzmann constant, and h is the Planck constant. The Z^TS and Z^IS are partition functions of the transition state and the initial state, respectively. The Z^TS/Z^IS can be calculated as

$$\frac{{{Z}}^{{\mbox{TS}}}}{{{Z}}^{{\mbox{IS}}}}=\frac{{\prod }_{{i}=1}^{3{N}-1}\frac{\exp (\frac{-{h}{{v}}_{{i}}^{*}}{2{kT}})}{1-\exp (\frac{-{h}{{v}}_{{i}}^{*}}{{kT}})}}{{\prod }_{{i}=1}^{3{N}}\frac{\exp (\frac{-{h}{{v}}_{{i}}}{2{kT}})}{1-\exp (\frac{-{h}{{v}}_{{i}}}{{kT}})}},$$

(3)

where ${v}_{i}^{*}$ and v_i are the real normal modes of vibration on the transition state and the initial state, respectively, and N is the number of vibrating atoms. It should be noted that there is one real normal mode less at the transition state than at the initial state.

Theoretical calculation of hydrogen thermodynamic phase diagram

The thermodynamic phase diagram of H on the Pt-Ti-graphene surface is obtained by comparing the difference of the surface free energy ΔG between the pristine and the hydrogenated models as follows⁴⁷,

$$\Delta G={E}_{{\mbox{hyd}}}-{E}_{{\mbox{pri}}}-{n}_{{\mbox{H}}}\cdot {\mu }_{{\mbox{H}}}+\Delta {F}_{{\mbox{vib}}},$$

(4)

where E_hyd and E_pri are the energies of pristine and hydrogenated models, respectively. ΔF_vib is the vibrational contribution differences of H on the Pt-Ti-graphene surface. n_H is the number of H atoms, and μ_H is the chemical potential of H. ΔF_vib is calculated as

$${\Delta {F}}_{{\mbox{vib}}}={hv}\left(\frac{1}{2}+\frac{1}{\exp \left(\frac{{hv}}{{kT}}\right)-1}\right)+{kT}\left\{\frac{\frac{{hv}}{{kT}}}{\exp \left(\frac{{hv}}{{kT}}\right)-1}-{\mathrm{ln}}\left[1-\exp \left(-\frac{{hv}}{{kT}}\right)\right]\right\},$$

(5)

where v is the real normal mode of H vibration. The chemical potential of H is a function of T and P, which can be written as

$${2\mu }_{{\mbox{H}}}={E}_{{{\mbox{H}}}_{2}}-{kT} \, \, {\mathrm{ln}}(g\cdot {Z}_{{\mbox{trans}}}\cdot {Z}_{{\mbox{rot}}}\cdot {Z}_{{\mbox{vib}}}),$$

(6)

where ${E}_{{{\mbox{H}}}_{2}}$ is the energy of H₂ at 0 K, and g = 2 is the degree of degeneracy of the electron energy level. Z_trans, Z_rot and Z_vib are translational, rotational and vibration motions, respectively, which are computed by

$${{Z}}_{{\mbox{trans}}}=\frac{{kT}}{{P}}\cdot {\left(\frac{2{\pi}{mkT}}{{{h}}^{2}}\right)}^{\frac{3}{2}},$$

(7)

$${{Z}}_{{\mbox{rot}}}=\frac{8{\pi }^{2}{IkT}}{{\sigma}{{h}}^{2}},$$

(8)

$${Z}_{{\mbox{vib}}}=\frac{\exp \left(-\frac{{hv}}{2{kT}}\right)}{1-\exp \left(\frac{-{hv}}{{kT}}\right)},$$

(9)

where m is the mass of an H₂ molecule, σ = 2 is the symmetry number for H₂, and I is the moment of inertia I.

Data availability

The authors declare that the data supporting the conclusions of this study are available within the paper and its supplementary information. Source data are provided with this paper.

References

Luo, Y., Zhang, Z., Chhowalla, M. & Liu, B. Recent advances in design of electrocatalysts for high-current-density water splitting. Adv. Mater. 34, 2108133 (2022).
Article CAS Google Scholar
Dhabi, A. Making The Breakthrough: Green Hydrogen Policies And Technology Costs. (International Renewable Energy Agency, United States, 2021).
Goyal, A. & Koper, M. T. M. The interrelated effect of cations and electrolyte pH on the hydrogen evolution reaction on gold electrodes in alkaline media. Angew. Chem. Int. Ed. 60, 13452–13462 (2021).
Article CAS Google Scholar
Li, X., et al. Microenvironment modulation of single-atom catalysts and their roles in electrochemical energy conversion. Science Advances 6, eabb6833 (2020).
Angulo, A. E., Frey, D. & Modestino, M. A. Understanding bubble-induced overpotential losses in multiphase flow electrochemical reactors. Energy Fuels 36, 7908–7914 (2022).
Article CAS MATH Google Scholar
Iwata, R. et al. Bubble growth and departure modes on wettable/non-wettable porous foams in alkaline water splitting. Joule 5, 887–900 (2021).
Article CAS MATH Google Scholar
Lu, Z. et al. Ultrahigh hydrogen evolution performance of under-water “superaerophobic” MoS₂ nanostructured electrodes. Adv. Mater. 26, 2683–2687 (2014).
Article ADS CAS PubMed MATH Google Scholar
Li, M., Xie, P., Yu, L., Luo, L. & Sun, X. Bubble engineering on micro-/nanostructured electrodes for water splitting. ACS Nano 17, 23299–23316 (2023).
Article CAS PubMed Google Scholar
Karim, W. et al. Catalyst support effects on hydrogen spillover. Nature 541, 68–71 (2017).
Article ADS CAS PubMed MATH Google Scholar
Li, J. et al. A fundamental viewpoint on the hydrogen spillover phenomenon of electrocatalytic hydrogen evolution. Nat. Commun. 12, 3502 (2021).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Prins, R. Hydrogen spillover. facts and fiction. Chem. Rev. 112, 2714–2738 (2012).
Article CAS PubMed MATH Google Scholar
Zhao, Z.-J. & Gong, J. Golden touch of the nanoparticles. Nat. Nanotechnol. 15, 1–2 (2020).
Article ADS CAS PubMed MATH Google Scholar
Li, C. et al. Efficient hydrogen evolution promoted by short pathway-hydrogen spillover over P-doped Pt₃Co. ACS Energy Lett. 8, 5161–5169 (2023).
Article ADS CAS MATH Google Scholar
Zhou, Y.-N. et al. Boosting hydrogen evolution through hydrogen spillover promoted by Co-based support effect. J. Mater. Chem. A 11, 6945–6951 (2023).
Article CAS MATH Google Scholar
Dai, J. et al. Hydrogen spillover in complex oxide multifunctional sites improves acidic hydrogen evolution electrocatalysis. Nat. Commun. 13, 1189 (2022).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Li, J. et al. Boosting electrocatalytic activity of Ru for acidic hydrogen evolution through hydrogen spillover strategy. ACS Energy Lett. 7, 1330–1337 (2022).
Article CAS MATH Google Scholar
Li, M. et al. Hydrogen spillover as a promising strategy for boosting heterogeneous catalysis and hydrogen storage. Chem. Eng. J. 471, 144691 (2023).
Article ADS CAS Google Scholar
Hao, R., Fan, Y., Howard, M. D., Vaughan, J. C. & Zhang, B. Imaging nanobubble nucleation and hydrogen spillover during electrocatalytic water splitting. Proc. Natl Acad. Sci. 115, 5878–5883 (2018).
Article ADS CAS PubMed PubMed Central Google Scholar
Huang, T.-X., et al. Single-molecule photocatalytic dynamics at individual defects in two-dimensional layered materials. Science Advances 7, eabj4452 (2021).
Dong, J. et al. Direct imaging of single-molecule electrochemical reactions in solution. Nature 596, 244–249 (2021).
Article ADS CAS PubMed MATH Google Scholar
Chan, C. U. & Ohl, C.-D. Total-internal-reflection-fluorescence microscopy for the study of nanobubble dynamics. Phys. Rev. Lett. 109, 174501 (2012).
Article ADS PubMed MATH Google Scholar
Zheng, X.-Y., Harata, A. & Ogawa, T. Study of the adsorptive behavior of water-soluble dye molecules (rhodamine 6G) at the air–water interface using confocal fluorescence microscope. Spectrochimica Acta Part. A: Mol. Biomolecular Spectrosc. 57, 315–322 (2001).
Article ADS CAS Google Scholar
Epstein, P. S. & Plesset, M. S. On the stability of gas bubbles in liquid‐gas solutions. J. Chem. Phys. 18, 1505–1509 (1950).
Article ADS CAS MATH Google Scholar
Ljunggren, S. & Eriksson, J. C. The lifetime of a colloid-sized gas bubble in water and the cause of the hydrophobic attraction. Colloids Surf. A: Physicochemical Eng. Asp. 129-130, 151–155 (1997).
Article MATH Google Scholar
Sihag, A. et al. DFT insights into comparative hydrogen adsorption and hydrogen spillover mechanisms of Pt₄/graphene and Pt₄/anatase (101) surfaces. J. Phys. Chem. C. 123, 25618–25627 (2019).
Article CAS Google Scholar
Elias, D. C. et al. Control of graphene’s properties by reversible hydrogenation: evidence for graphane. Science 323, 610–613 (2009).
Article ADS CAS PubMed MATH Google Scholar
Tan, T. L., Wang, L.-L., Johnson, D. D. & Bai, K. Hydrogen deposition on Pt(111) during electrochemical hydrogen evolution from a first-principles multiadsorption-site study. J. Phys. Chem. C. 117, 22696–22704 (2013).
Article CAS Google Scholar
Kunimatsu, K., Senzaki, T., Samjeské, G., Tsushima, M. & Osawa, M. Hydrogen adsorption and hydrogen evolution reaction on a polycrystalline Pt electrode studied by surface-enhanced infrared absorption spectroscopy. Electrochim. Acta 52, 5715–5724 (2007).
Article CAS Google Scholar
Singh, A. K., Ribas, M. A. & Yakobson, B. I. H-Spillover through the catalyst saturation: an ab initio thermodynamics study. ACS Nano 3, 1657–1662 (2009).
Article CAS PubMed Google Scholar
Alfarano, S. R. et al. Stripping away ion hydration shells in electrical double-layer formation: Water networks matter. Proc. Natl Acad. Sci. 118, e2108568118 (2021).
Article CAS PubMed PubMed Central MATH Google Scholar
Zhao, Y. & Gennett, T. Water-mediated cooperative migration of chemisorbed hydrogen on graphene. Phys. Rev. Lett. 112, 076101 (2014).
Article ADS PubMed MATH Google Scholar
Zhao, G., Li, P., Cheng, N., Dou, S. X. & Sun, W. An Ir/Ni(OH)₂ Heterostructured electrocatalyst for the oxygen evolution reaction: breaking the scaling relation, stabilizing iridium(V), and beyond. Adv. Mater. 32, 2000872 (2020).
Article CAS Google Scholar
Yu, L. et al. Cu nanowires shelled with NiFe layered double hydroxide nanosheets as bifunctional electrocatalysts for overall water splitting. Energy Environ. Sci. 10, 1820–1827 (2017).
Article CAS MATH Google Scholar
Kim, D. et al. Selective CO₂ electrocatalysis at the pseudocapacitive nanoparticle/ordered-ligand interlayer. Nat. Energy 5, 1032–1042 (2020).
Article ADS CAS MATH Google Scholar
Zhuang, X. Nano-imaging with STORM. Nat. Photonics 3, 365–367 (2009).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Jungmann, R. et al. Multiplexed 3D cellular super-resolution imaging with DNA-PAINT and Exchange-PAINT. Nat. Methods 11, 313–318 (2014).
Article CAS PubMed PubMed Central MATH Google Scholar
Rust, M. J., Bates, M. & Zhuang, X. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methods 3, 793–796 (2006).
Article CAS PubMed PubMed Central Google Scholar
Bates, M., Huang, B., Dempsey, G. T. & Zhuang, X. Multicolor super-resolution imaging with photo-switchable fluorescent probes. Science 317, 1749–1753 (2007).
Article ADS CAS PubMed PubMed Central Google Scholar
Dempsey, G. T., Vaughan, J. C., Chen, K. H., Bates, M. & Zhuang, X. Evaluation of fluorophores for optimal performance in localization-based super-resolution imaging. Nat. Methods 8, 1027–1036 (2011).
Article CAS PubMed PubMed Central Google Scholar
He, Y. et al. Self-gating in semiconductor electrocatalysis. Nat. Mater. 18, 1098–1104 (2019).
Article ADS CAS PubMed MATH Google Scholar
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Mater. Sci. 6, 15–50 (1996).
Article CAS MATH Google Scholar
Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).
Article ADS PubMed Google Scholar
Mathew, K., Sundararaman, R., Letchworth-Weaver, K., Arias, T. A. & Hennig, R. G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 140, 084106 (2014).
Article ADS PubMed Google Scholar
Henkelman, G., Uberuaga, B. P. & Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Article ADS CAS MATH Google Scholar
Seebauer, E. G. & Allen, C. E. Estimating surface diffusion coefficients. Prog. Surf. Sci. 49, 265–330 (1995).
Article ADS CAS MATH Google Scholar
Kong, X.-S. et al. First-principles calculations of hydrogen solution and diffusion in tungsten: temperature and defect-trapping effects. Acta Materialia 84, 426–435 (2015).
Article CAS MATH Google Scholar
Reuter, K. & Scheffler, M. Composition, structure, and stability of RuO₂ (110) as a function of oxygen pressure. Phys. Rev. B 65, 035406 (2001).
Article ADS MATH Google Scholar
Khomyakov, P. A. et al. First-principles study of the interaction and charge transfer between graphene and metals. Phys. Rev. B 79, 195425 (2009).
Article ADS MATH Google Scholar

Download references

Acknowledgements

Z.L. acknowledges funding from the Singapore Ministry of Education (AcRF MOE2019-T2-2-105 and AcRF Tier 1 RG7/21). Z.L. also acknowledges funding from the Ministry of Education, Singapore, under its Research Center of Excellence award to the Institute for Functional Intelligent Materials (Project No. EDUNC-33-18-279-V12). Z.Z. acknowledges the support from the National Natural Science Foundation of China (1221101035, 12225205, 22073048, T2293691), the National Key Research and Development Program of China (2019YFA0705400), and the Priority Academic Program Development of Jiangsu Higher Education Institutions. Z.Y.Z. thanks the Singapore Ministry of Education (AcRF Tier1 RG10/20 and RG60/21) and the Singapore Agency for Science, Technology and Research (A*STAR) (AME YIRG grant No. A2084c0065 and MTC IRG No. M21K2c0110). M.Y. acknowledges funding from the National Natural Science Foundation of China (12202194), the Natural Science Foundation of Jiangsu Province (BK20220875), the Jiangsu Funding Program for Excellent Postdoctoral Talent (2022ZB208) and China Postdoctoral Science Foundation (2023M731669). Y.H. acknowledges the support from Hunan Provincial Natural Science Foundation of China (2023JJ10004).

Author information

These authors contributed equally: Shasha Guo, Maolin Yu, Jinn-Kye Lee, Mengyi Qiu.

Authors and Affiliations

Department of Chemistry and Chemical Biology, Cornell University, Ithaca, NY, USA
Shasha Guo
State Key Laboratory of Mechanics and Control for Aerospace Structures, Key Laboratory for Intelligent Nano Materials and Devices of Ministry of Education, and Institute for Frontier Science, Nanjing University of Aeronautics and Astronautics, Nanjing, China
Maolin Yu, Zhili Hu & Zhuhua Zhang
School of Chemistry, Chemical Engineering and Biotechnology, Nanyang Technological University, Singapore, Singapore
Jinn-Kye Lee & Zhengyang Zhang
College of Chemistry and Chemical Engineering, Hunan University, Changsha, China
Mengyi Qiu, Zude Shi, Shuangyin Wang & Yongmin He
SEU-FEI Nano-Pico Center, Key Lab of MEMS of Ministry of Education, School of Electronic Science and Engineering, Southeast University, Nanjing, China
Dundong Yuan & Chao Zhu
School of Materials Science and Engineering, Nanyang Technological University, Singapore, Singapore
Yao Wu, Wei Ma & Zheng Liu
CINTRA CNRS/NTU/THALES, UMI 3288, Research Techno Plaza, Singapore, Singapore
Zheng Liu
Institute for Functional Intelligent Materials, National University of Singapore, Singapore, Singapore
Zheng Liu

Authors

Shasha Guo
View author publications
Search author on:PubMed Google Scholar
Maolin Yu
View author publications
Search author on:PubMed Google Scholar
Jinn-Kye Lee
View author publications
Search author on:PubMed Google Scholar
Mengyi Qiu
View author publications
Search author on:PubMed Google Scholar
Dundong Yuan
View author publications
Search author on:PubMed Google Scholar
Zhili Hu
View author publications
Search author on:PubMed Google Scholar
Chao Zhu
View author publications
Search author on:PubMed Google Scholar
Yao Wu
View author publications
Search author on:PubMed Google Scholar
Zude Shi
View author publications
Search author on:PubMed Google Scholar
Wei Ma
View author publications
Search author on:PubMed Google Scholar
Shuangyin Wang
View author publications
Search author on:PubMed Google Scholar
Yongmin He
View author publications
Search author on:PubMed Google Scholar
Zhengyang Zhang
View author publications
Search author on:PubMed Google Scholar
Zhuhua Zhang
View author publications
Search author on:PubMed Google Scholar
Zheng Liu
View author publications
Search author on:PubMed Google Scholar

Contributions

Z.L. and S.G. designed the study. S.G. conducted the device fabrication and micro-cell test. S.G. and J.L. performed the in-situ on-chip-TIRF test. W.M. synthesized monolayer graphene. M.Q., S.W., and Y.H. conducted PEM electrolyzer measurements. Z.Z., Z.H., and M.Y. performed the theoretical calculation and model analysis. D.Y., Y.W., and C.Z. performed STEM experiments and analysis. S.G., Z.S., Z.Y.Z., and Y.H. conducted the result interpretation. Z.L., Z.Z., and Z.Y.Z. conceived the experiments. S.G. and M.Y. wrote the manuscript. Z.L., Z.Z., Y.H., Z.Y.Z. commented on and amended the manuscript and Supplementary Materials. All authors discussed and contributed to the work.

Corresponding authors

Correspondence to Yongmin He, Zhengyang Zhang, Zhuhua Zhang or Zheng Liu.

Ethics declarations

Competing interests

The Authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Yongquan Qu and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Files

Supplementary Movie 1

Supplementary Movie 2

Supplementary Movie 3

Supplementary Movie 4

Supplementary Data 1

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Guo, S., Yu, M., Lee, JK. et al. Separating nanobubble nucleation for transfer-resistance-free electrocatalysis. Nat Commun 16, 919 (2025). https://doi.org/10.1038/s41467-024-55750-5

Download citation

Received: 14 April 2024
Accepted: 24 December 2024
Published: 22 January 2025
DOI: https://doi.org/10.1038/s41467-024-55750-5