Introduction

The bulk–boundary correspondence of topological phases dictates protected metallic states at the boundary of a bulk topological order1,2,3,4. For example, the surface of a three-dimensional topological insulator hosts surface Dirac cone states5. The existence of such surface Dirac bands serves as direct evidence for the bulk topology6,7 even if the chemical potential does not lie in the bulk band gap so that the bulk carriers play a part in the charge transport and relaxation of surface carriers8. For a 2-dimensional (2D) insulator, the nature of the edge state is a direct manifestation of the topological invariant of the bulk. A quantum spin Hall insulator9,10,11,12 conserves time-reversal symmetry (TRS) and hosts helical edge states13,14,15. When TRS is broken in the bulk and proximitized with an s-wave superconductor, the edge is predicted to host exotic excitations useful for topological quantum computation16,17,18.

A quantum anomalous Hall (QAH) insulator is an interesting topological phase that breaks TRS19,20. Its edge hosts the chiral edge state (CES), which represents the Chern number characterizing the TRS-broken topological invariant. In principle, along the edge of a macroscopic sample, such CES must propagate either clockwise (Fig. 1a) or counter-clockwise (Fig. 1b), depending on the direction of magnetization. Due to the chirality as a consequence of broken TRS, CES cannot be localized by weak disorder21, thus suppressing backscattering22. Such a one-dimensional fermionic state carries a current along the perimeter of the sample. In spite of the crucial role of CES in not only QAH but also the closely related quantum Hall effect, unlike its TRS counterpart, it has not been directly observed so far. Magnetic imaging experiments to detect chiral edge current have revealed complicated physics in the quantum Hall23 and even a conflicting ‘bulk-dominant’ current distribution picture for QAH insulators24, which cast doubts on the validity of the CES picture.

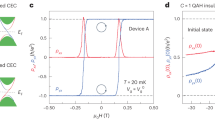
Fig. 1: Chiral edge current detection scheme under an alternating current bias.
figure 1

a and b Illustration of the direction of chiral edge current in a quantum anomalous Hall (QAH) insulator. The chirality of the edge current is clockwise and counter-clockwise under opposite out-of-plane magnetization M, respectively. c Optical image of a MnBi2Te4 device consisting of a 7-septuple layer (SL) which potentially hosts QAH. There is also a 10-SL flake that has no net M and zero Chern number. d Waveform of a pure alternating current (AC) bias applied to QAH with period T. It has positive (negative) chemical potential \({\mu }_{{{\rm{AC}}}}\) relative to ground during the first (second) half-cycle. e and f Current flow in the first and second half of the cycle, respectively, under the AC current bias in (d). Since the instantaneous current \({I}_{1,2}=\left|{\mu }_{{{\rm{L}}}}-{\mu }_{{{\rm{R}}}}\right|\frac{e}{h}\) always flows from the higher potential to the lower, the chirality of the edge state forces the current \({I}_{2}\) during the second half-cycle (when \({\mu }_{{{\rm{L}}}} > {\mu }_{{{\rm{R}}}}\)) to flow on the top edge. \({\mu }_{{{\rm{L}}}}\) (\({\mu }_{{{\rm{R}}}}\)) is the chemical potential on the left (right) electrode; \(e\) and \(h\) are the electron charge and Planck’s constant, respectively. g A lock-in amplifier adds a \(\pi\) phase shift to the current flux signal from the second half-cycle, which makes the currents from the top and bottom edges appear to be propagating in the same direction with demodulated current \({I}_{{{\rm{AC}}}}=\frac{{\mu }_{{{\rm{AC}}}}}{2}\frac{e}{h}\) on both. In the presence of edge–bulk scattering, the ‘co-propagating’ edge currents due to the chiral edge state appear similar to non-chiral bulk flow. h–k Illustration of the situation when a direct-current (DC) offset is added to the AC bias. If the DC offset is larger than the AC amplitude, the chemical potential is higher on the right electrode during the entire period. The current flows unidirectionally on the bottom edge with \({I}_{{{\rm{AC}}}}={\mu }_{{{\rm{AC}}}}\frac{e}{h}\), because the demodulated flux signal is proportional to the amplitude of the AC amplitude and independent of the DC offset (twice the area of the pink region and thus twice the edge current in g).

Full size image

A key consequence of CES in the QAH order is the quantized Hall conductance at zero field25,26,27. For a small enough bias on the leads, CES carries a chiral edge current, which ideally leads to quantized Hall conductance equal to \({e}^{2}/h\), where e is the electron charge and h is the Planck constant, even at zero magnetic fields. Quantized anomalous Hall conductance was first observed in a magnetically doped topological insulator25. As this material required a delicate balance between a large magnetization and a low initial carrier doping, the quantization temperature was limited by magnetic disordering due to the randomly distributed magnetic dopants28,29,30. The edge current was absent, and instead, current transport was bulk-dominant within the QAH regime of the doped system24. Furthermore, recent work nullified the earlier observation of edge Majorana fermions when proximitized by a superconductor31. Magnetic disorder is considered detrimental to the robustness of QAH and, therefore, possibly CES.

The recent discovery of a van der Waals antiferromagnet, MnBi2Te4, with a topological band structure brings hope of a clean material host for quantized Hall conductance and CES32,33. MnBi2Te4 consists of stacked Te-Bi-Te-Mn-Te-Bi-Te septuple layers (SL) and displays an A-type antiferromagnetic order in which the magnetic moments of Mn order ferromagnetically within each SL and antiferromagnetic between neighboring SL. Under a large magnetic field, odd-SL MnBi2Te4 thin flakes showed quantization temperatures up to a few tens of kelvin34,35,36. However, at zero magnetic fields, the reported quantization was either not exact37 or, in most cases, far from it34,35,36,38,39,40. Compared to the exfoliated MnBi2Te4 thin flakes, it is even harder for molecular beam epitaxy-grown MnBi2Te4 thin films to get close to the quantized regime, not to mention QAH at zero field41,42,43,44. Serious concerns were raised about the nature of the electronic state and magnetic order of MnBi2Te4 thin flakes at zero field, especially the fate of QAH. It is thus essential to elucidate the relationship between the current flow, CES, and the quantum transport in an intrinsic QAH.

Results

Detecting chiral edge current under an alternating current bias

In this work, we study odd-SL MnBi2Te4 thin flakes with a finite net magnetization at zero field (Fig. 1c). The 7-SL sample is gate-tuned to its charge neutral regime by applying a back-gate voltage of \({V}_{{{\rm{g}}}}=\) 50 V. Consistent with many previous reports34,35,36,38,39,40, our transport measurement of the sample at the base temperature of 1.7 K yields a small anomalous Hall resistivity \({\rho }_{{yx}}\, \sim \,820\,\Omega\) after magnetizing the sample under a 9 T field, seemingly suggesting a failed QAH under zero field (Supplementary Fig. 10c). In order to image the current distribution under weak perturbation, we employ the high flux sensitivity of scanning superconducting quantum interference device (sSQUID) microscopy. As a local magnetometer, sSQUID images flux through its pickup loop of 2 μm in diameter in our experiment45. The nano-SQUID employed for this work has a spatial resolution of about 2.5 μm derived from the magnetometry of a superconducting vortex and a 5 μm Nb checkerboard (Supplementary Fig. 1). Such magnetic flux has two sources: one from the non-zero net magnetization of 7-SL MnBi2Te4, and the other from the applied bias current through the device. We apply an alternating current (AC) with a small amplitude for lock-in detection of current flux to distinguish the magnetic field generated by the applied current from that of the magnetization.

The lock-in detection of chiral edge current under an AC bias is quite different from that of non-chiral current. First, suppose we apply a pure AC drive \({\mu }_{{{\rm{AC}}}}\) without any direct-current (DC) offset and bias the device from the right side into a QAH with clockwise CES (Fig. 1d). Since the current always flows from a higher potential to a lower one, the current flows along the bottom edge from right to left in the first half-cycle (Fig. 1e). During the second half, the chemical potential on the right electrode becomes lower than the one on the left (Fig. 1d). The left-to-right current flow and the chirality of the edge state dictate that the current flows on the top edge (Fig. 1f), in consistent with the Landauer–Büttiker picture46. The lock-in amplifier adds a \(\pi\) phase shift to the flux signal in the second half-cycle, reversing the sign of the current flux on the top edge. Consequently, the edge currents will appear to propagate along the same direction (Fig. 1g), and the overall current flow is consistent with the direction of the applied current. As we shall see later, under the influence of edge–bulk scattering, it is challenging to distinguish chiral edge current with such a detection scheme. By adding a DC offset to the AC bias, we overcome the limitation of the lock-in detection of CES. For a non-chiral current transport, a DC offset has no effect on the current signal demodulated by the lock-in amplifier. The situation is quite different for CES. When the DC offset is larger than the AC amplitude (Fig. 1h–k), the current flows on the bottom edge for the whole period since the chemical potential on the right electrode is constantly higher than on the left. The \(\pi\) phase shift to the flux signal subtracts the contribution from the second half-cycle (Fig. 1h, green shaded area), and we obtain demodulated current on the bottom edge \({I}_{{{\rm{AC}}}}={\mu }_{{{\rm{AC}}}}\frac{e}{h}\) (Fig. 1k), which will be twice as big as the \({I}_{{{\rm{AC}}}}\) on each edge obtained with a pure AC bias (Fig. 1g). Performing a time-reversal transformation (reversing the magnetization as shown in Fig. 1b) reverses the chirality. Using a negative DC offset maintains a higher potential on the left electrode during the entire cycle and leads to a current on the top edge instead, essentially reversing the parity of the current configuration.

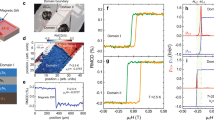
We perform sSQUID microscopy of the chiral edge current of the MnBi2Te4 sample following the detection scheme we have discussed (Fig. 1h–k). We magnetize the sample under 9 T or −9 T out-of-plane magnetic fields at the base temperature and then remove the field for the measurements so that the nano-SQUID operates in the most sensitive state. The magnetizations are opposite using opposite fields on the 7-SL part but show little contrast on the 10-SL flake because of the antiferromagnetic interlayer coupling (Fig. 2a, b). At the charge neutral point (CNP) for the 7-SL of \({V}_{{{\rm{g}}}}=50\,\)V, we apply an \({I}_{{{\rm{DC}}}}=\) 1 \({{\rm{\mu }}}\)A offset to \({I}_{{{\rm{AC}}}}=\) 500 nA current bias on the right or left electrodes for both magnetizations to obtain four different current flux images (Fig. 2c–f). Current flux images obtained at an even lower current bias (Supplementary Fig. 20) are consistent with these images though they have lower signal-to-noise. According to Biot–Savart’s law, the out-of-plane magnetic field generated by a current stripe has opposite signs on the two sides of the stripe, and the field is zero at the center. Due to the difference in the CNP, the 10-SL is bulk-conductive at \({V}_{{{\rm{g}}}}=50\,\)V and the current flows through it evenly, with its center part appearing white. The current flux does not change there as magnetization is reversed (Fig. 2c, d, or e, f). The sign of the flux exactly reverses when the direction of the current bias is reversed (Fig. 2c, e, or d, f). The DC offset in the bias also does not change the current flux of 10-SL (Supplementary Fig. 15), which is consistent with non-chiral transport.

Fig. 2: Chirality of the 7-SL edge states under opposite magnetization.
figure 2

a and b Static magnetic flux images after the sample are magnetized under 9 T (a) and −9 T (b), respectively. The 7-SL region shows net M. c and d Current flux images corresponding to the magnetization in (a and b), respectively. A 500 nA AC current plus a 1 μA DC offset is applied to the right electrode. e and f Current flux images with the same current bias as in (c and d) but applied to the left electrode. All the current flux images are taken at \({V}_{{{\rm{g}}}}=50\,\)V. The streamlines are current flows around the 7-SL edge reconstructed from the current flux images. They show the edge current (\({I}_{{{\rm{l}}}}\) for the lower edge and \({I}_{{{\rm{u}}}}\) for the upper edge) and its chirality (magenta/+ for clockwise and blue/− for counter-clockwise), which predominantly carry the current under each configuration.

Full size image

The current flow in the 7-SL flake is distinctively different from that in the 10-SL flake. For positive magnetization and biasing on the right electrode (Fig. 2c), the current flows predominantly along the lower edge and the boundary between the 7-SL and 10-SL. Meanwhile, there is little current flux contrast on the upper edge, even though it has a shorter path than the one the current takes. On the other hand, biasing from the left electrode with the same magnetization leads to the current flowing on the upper edge clockwise (Fig. 2e). This is an indication of edge current breaking TRS in an odd-SL-layer sample at a charge neutral point. Using a negative DC offset in the AC current bias also changes the edge the current flows on and gives a reversed chirality from the real one (Supplementary Fig. 15). This is consistent with our earlier analysis on the lock-in detection of chiral edge current (Fig. 1) and rules out any heating artifact. The real chirality of the edge current switches upon changing the magnetization. Biasing from the right (left) electrode with negative magnetization, the current flows from the upper (lower) edge anti-clockwise (Fig. 2d, f). Overall, the chirality of the edge current is determined by the magnetization, whereas the edge that the current passes through depends on both the chirality and the source of the current bias. The current flux patterns under the four configurations are antisymmetric about a time-reversal transformation and a parity transformation. Therefore, they are in complete agreement with our model for lock-in detection of chiral edge current (Fig. 1). These pieces of evidence unequivocally show the existence of CES at zero field despite the poor Hall quantization.

The heating effect of the bias current24 and the electric coupling between the SQUID and the sample47 may induce current flux artifacts, which need to be carefully addressed. First of all, applying a negative DC offset significantly alters the current path in the current flux image (Supplementary Fig. 15), which is inconsistent with these artifacts. Secondly, the second harmonic response of the applied AC current (Supplementary Fig. 19c–f), which may be a result of demagnetization from current heating, shows a null signal. Thirdly, direct measurements of the magnetic flux (Supplementary Fig. 22b, d–f) and the electrostatic force on the SQUID (Supplementary Fig. 22c) in response to a modulation gate voltage exhibit no observable signal beyond the noise. Lastly, CEC current flux images at different current frequencies (Supplementary Fig. 23) do not show typical sign reversal caused by electric coupling. These results indicate that the heating effect of the current bias and electric coupling have negligible impact on the CEC of MnBi2Te4 above the noise level of our sSQUID. The incompressible dissipationless current picture of QAH proposed in previous sSQUID measurements on magnetically doped TI24 is also inconsistent with the flux response to back-gate voltage in our sample (Supplementary Figs. 21a and 22b).

Edge–bulk scattering of chiral edge current

In the following, we investigate the influence of the bulk on the CES by varying the gate voltage. We fix the magnetization of 7-SL to be negative (Fig. 2b). At \({V}_{{{\rm{g}}}}=0\,\)V, the Fermi level is within the bulk valence band, and the current is predominantly carried by the bulk (Fig. 3a). Reversing the bias direction reverses the current flux signal (Fig. 3b), which is consistent with the bulk current flow being non-chiral. Taking a line-cut across the 7-SL sample (Fig. 3a, b, magenta and blue dashed lines, respectively), we map out the continuous evolution of the current distribution as a function of \({V}_{{{\rm{g}}}}\) (Fig. 3c, d). For the right electrode bias, the current distribution is mostly bulk-centered below \({V}_{{{\rm{g}}}}=30\,\)V, at which point the center of the current starts to shift towards the top edge (Fig. 3c). The center reaches the top edge at \({V}_{{{\rm{g}}}}=50\,\)V and then turns back towards the middle upon further increasing \({V}_{{{\rm{g}}}}\). The overall trend is similar for biasing from the left electrode (Fig. 3d). The center of the current shifts towards the bottom edge instead. The \({V}_{{{\rm{g}}}}\) dependence of the current distribution rules out the bulk anomalous Hall effect as a cause for the chiral current flow at CNP. Instead, it shows that the observed chiral edge current originates from the in-gap CES in 7-SL MnBi2Te4, while outside the band gap the current is non-chiral and carried by the bulk states.

Fig. 3: Evolution of the chiral edge current with gate tuning under opposite current bias direction.
figure 3

a and b Current flux images at \({V}_{{{\rm{g}}}}=\) 0 V with bias current on the right and left electrodes, respectively. The sample is magnetized with a −9 T field. c and d Line scans of current flux as a function of \({V}_{{{\rm{g}}}}\) along the dashed line in (a) for the two bias directions. The yellow dashed lines delineate the two edges of the device. The evolution of the current flux distribution with \({V}_{{{\rm{g}}}}\) suggests that the chiral edge current appears only within the bulk magnetic exchange gap.

Full size image

Aware of any possible non-chiral current in the CNP regime, we quantitatively analyze the current distribution between the edge and the bulk in order to compare it with the resistance measurements. We assume the current in the four configurations (Fig. 2c–f) as the sum of two components \({I}_{{{\rm{u}}}({{\rm{l}}})}^{+(-)}+{I}_{{{\rm{n}}}}\), where the first term is the chiral edge current (chirality +/−) either on the upper edge (\({I}_{{{\rm{u}}}}\)) or the lower edge (\({I}_{{{\rm{l}}}}\)) and the second term is the non-chiral bulk current. We obtain the edge-only chiral current flux (Fig. 4a) by taking the difference of the current flux images with opposite chirality but the same bias direction (Fig. 2c, d). This difference image cancels the \({I}_{{{\rm{n}}}}\) component and leaves the flux contribution only from a clockwise chiral edge current: \({I}_{{{\rm{l}}}}^{+}-{I}_{{{\rm{u}}}}^{-}={I}_{{{\rm{l}}}}^{+}+{I}_{{{\rm{u}}}}^{+}={I}^{+}\). By implementing the current reconstruction (Supplementary Note 2) from the difference image (Fig. 4a), we obtain the current density distribution, which circles around the boundary of the 7-SL flake (Fig. 4b). Alternatively, we can take the difference between current flux images from the left bias (Fig. 2e, f), and the result is similar. The sum (Fig. 4c) of the current flux images with the same bias but opposite chirality (Fig. 2c, d) has three components: \({I}_{{{\rm{l}}}}^{+}+{I}_{{{\rm{u}}}}^{-}+2{I}_{{{\rm{n}}}}\). This sum image is very similar to the one obtained under zero DC offset (Supplementary Fig. 16a), which is expected to be half the current amplitude of the sum under the same \({I}_{{{\rm{AC}}}}\) according to our earlier analysis (Fig. 1). The reconstructed current density from the sum image exhibits all three components (Fig. 4d). All these observations support the coexistence of chiral edge and non-chiral bulk currents at CNP.

Fig. 4: Analysis of the current distribution in the CNP regime.
figure 4

a Difference image of the two current flux images with opposite magnetization and the same bias direction (Fig. 2c, d). b Current density image reconstructed from the difference current flux image in (e). The subtraction removes the flux contribution from the non-chiral bulk current (\({I}_{{{\rm{n}}}}\)) while keeping one of the chiral edge currents (\({I}_{{{\rm{l}}}}^{+}\)) and reversing the \({I}_{{{\rm{u}}}}^{-}\) to \({I}_{{{\rm{u}}}}^{+}\) so that the difference image shows a circulation around the 7-SL clockwise. c and d The sum current flux of Fig. 2c, d and its current density reconstruction, respectively. The sum image doubles the non-chiral contribution while adding the chiral edge currents with opposite chirality: 2\({I}_{{{\rm{n}}}}+{I}_{{{\rm{l}}}}^{+}+{I}_{{{\rm{u}}}}^{-}\). Thus, the direction of flow in the sum image is the same for both bulk and two edge currents. e Line cuts from the difference (orange) and sum (green) current flux images across the upper and lower edges shown by the dashed lines in (a and c), in comparison with that from the current flux obtained with a pure AC current (red) at the same ___location. The purple curve is a cut from the current flux image at \({V}_{{{\rm{g}}}}=\) 0 V (Fig. 3a), representing the current carried mostly by the bulk. Note that the sum current flux (green) is two times larger than the pure AC current flux (red) with a similar profile, in quantitative agreement with our analysis of the two measurement schemes (Fig. 1g, k). f Line cuts from the current density J images in (b and d) at the same position, representing the chiral (orange) and the sum (green), respectively. A cut from J obtained with pure AC drive (red) is shown in comparison with the sum (green). The non-chiral current density (black) is obtained by subtracting the chiral current density from the sum and then dividing by 2. The bulk current (purple) is obtained from the line cut of J reconstructed from the current flux image at 0 V (Fig. 3a).

Full size image

In order to separate the non-chiral current from the chiral current at CNP, we take line profiles from the difference and sum images. The line profile from the difference flux image is unipolar (Fig. 4e, orange), which could only be a result of circulating current. The current flux line profile from the sum (Fig. 4e, green) has a similar line shape and is twice as large as that under the pure AC drive (Fig. 4e, red). In contrast, both line shapes are different from the current flux of bulk conduction at \({V}_{{{\rm{g}}}}=0\,\)V (Fig. 4e, purple). And the line profile from the difference current density image shows peaks corresponding to the upper and lower edges (Fig. 4f, orange). Meanwhile, the sum current density exhibits a broad spread (Fig. 4f, green) in agreement with its flux pattern (Fig. 4e, green) and the magnitude is larger than that of the chiral edge current density (Fig. 4f, orange) everywhere on the sample (Fig. 4f, gray region). However, there are still two (though less distinctive) peaks in the sum current density (Fig. 4f, green), which distinguishes it from a uniform current ribbon. After subtracting the difference current density line profile from the sum and then dividing by two, we obtain a pure contribution from the non-chiral current \({I}_{{{\rm{n}}}}\) (Fig. 4f, black). The line shape of \({I}_{{{\rm{n}}}}\) is nonuniform across the bulk. It is heavily centered in the middle, with little distribution on either edge. (The finite density outside the sample may be attributed to the limited spatial resolution of our sSQUID and the finite scanning range.) Furthermore, it has a different shape from the current density from the bulk carriers (Fig. 4f, purple), which is reconstructed from the current flux image at 0 V (Fig. 3a). This suggests that the non-chiral current at CNP is different from the conventional uniform bulk current without edge states. After integrating the respective current density over the width of the line profile, we find that about 70% of current flows along the upper and lower edges as chiral current, while the remaining 30% is non-chiral and non-edge.

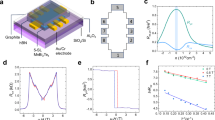
The coherence length of ballistic chiral edge transport is much smaller than the size of a realistic open conductor. Historically, a confining potential for the edge current was proposed, which limits both elastic and inelastic scattering of edge carriers to be within the edge channel so that the quantization of Hall conductance could still be possible22. Nevertheless, longitudinal scattering within the edge channel is not enough to explain significant bulk conduction in the bulk exchange gap, and edge–bulk scattering is necessary. Indeed, the coexistence of chiral edge channels and conducting bulk/surface channels has been studied by transport measurements48,49,50. On the other hand, recent experiments suggest MnBi2Te4 suffers from strong chemical and magnetic disorders due to its metastable phase character42,44,51,52,53. One consequence of such disordering is the spatial fluctuation of the density of state (DOS) at the Fermi level, as reported in several scanning tunneling microscopy studies. Because the DOS at the Fermi level are mainly from the Bi-Te p orbitals, such fluctuation implies local variations of the Bi and Te orbitals, which would affect the magnetic exchange interaction, leading to spatial variation of the magnetic exchange gap \(\Delta \left(r\right)\). Such inhomogeneity assists the electron hopping from the edge to the bulk, especially in the regions where \(\Delta \left(r\right)\) diminishes. The transport configuration of shunting all the edge electrodes to the ground15 supports this scenario (Fig. 5a). When \({V}_{{{\rm{g}}}}\) is tuned to CNP (Fig. 5b), we find that the voltage drop over the 7-SL peaks at around 4 mV while the bulk current reaches minimum of 2 nA. The finite conductance at CNP suggests that when the bulk carriers are depleted (see SOM for more quantitative analysis), the current still has a limited flow which cannot be shunted into grounded electrodes as a consequence of bulk–edge scattering (Fig. 5c). When the external magnetic field increases, \(\Delta \left(r\right)\) increases with it, which effectively suppresses the edge–bulk scattering. At 9 T, the system reaches a Chern insulator state with pure dissipationless chiral edge transport (Supplementary Fig. 10e). Note that it differs from the magnetic field-driven quantum phase transition in even layer MnBi2Te415,36. Considering the edge–bulk scattering scenario, we develop a realistic model to compare with the transport experiment.

Fig. 5: Landauer–Büttiker multi-terminal simulation of chiral edge transport with edge–bulk scattering.
figure 5

a Setup for measuring \({V}_{{{\rm{BH}}}}/{I}_{{{\rm{BH}}}}\) using electrodes B and H on the 7-SL with all the other electrodes grounded. b The voltage drop and the current between electrodes B and H as a function of \({V}_{{{\rm{g}}}}\) under the configuration shown in (a). At the CNP, \({I}_{{{\rm{BH}}}}\) is suppressed but \({V}_{{{\rm{BH}}}}\) peaks, suggesting enhanced edge–bulk scattering. c Illustration of the edge–bulk scattering at the CNP. Puddles of chemical potential inhomogeneity (dashed circles) act as bulk scattering centers for chiral edge current carriers (orange balls). CES: chiral edge state. d Schematics to simulate chiral edge transport between two electrodes with finite bulk–edge scattering. The bulk–edge scattering is taken into account by inserting various numbers of virtual electrodes (N = 2, 4, 8, and 12). e Simulated gate dependence \({\rho }_{{xx}}\) as a function of \({V}_{{{\rm{g}}}}\) under different N. \({\rho }_{{xx}}\) increases with increasing N at CNP, which suggests enhanced dissipation of chiral edge transport due to scattering with the bulk. N = 12 (orange circles) overlaps with experimental \({\rho }_{{xx}}\) data at zero field (orange line). f Gate dependence of simulated \({\rho }_{{yx}}\) for N = 12 (black squares) and experimental \({\rho }_{{yx}}\) data at zero field (blue line), which suggests that the edge–bulk scattering suppresses the quantization of Hall resistance of QAH.

Full size image

We construct a modified Landauer–Büttiker (LB) multi-terminal model46 to quantitatively understand the chiral transport under finite edge–bulk scattering (see supplementary S3 for details of the simulation). In the LB approach, one uses the transmission matrix elements \({T}_{j,i}\) to quantify the transmission probability between two electrodes i and j and, therefore, \({I}_{i}=\frac{{e}^{2}}{h}{\sum}_{j}({T}_{j,i}{V}_{i}-{T}_{i,j}{V}_{j})\) is the total current passing through the electrode i. To account for the chirality of a ballistic edge channel, one usually assigns 1 and 0 to \({T}_{j,i}\) and \({T}_{i,j}\), respectively, where electrodes i and j are the two nearest neighbors, and sets others to 0. Here we modify this method by assuming a uniform bulk conductivity (\({\sigma }_{{{\rm{bulk}}}}\)) and evenly adding virtual contacts (number denoted as N) along the edge to mimic the finite edge–bulk scattering (Fig. 5d). Specifically, we allow non-zero transmission matrix elements between any two terminals of the device because electrons can hop between them through either edge or bulk. Moreover, the edge transmissions, either 0 or 1, are straightforward from LB theory, while the bulk transmission matrix is simulated by inputting \({\sigma }_{{{\rm{bulk}}}}\) as the single parameter using Laplace’s equation based on the device shape. Thus, the dimension of the conductance matrix increases with N. Adding such virtual probes effectively increases the probability of edge–bulk scatterings because electrons will experience multiple scatterings among these virtual probes as they transmit from one real electrode to the other. Each scattering event has contributions from the bulk, i.e., electrons are scattered from the edge to the bulk and then back to the edge. The fitting procedure for obtaining the optimal N and \({\sigma }_{{{\rm{bulk}}}}\) is detailed in the supplementary information.

At N = 12, the simulated \({\rho }_{{{\rm{xx}}}}({V}_{{{\rm{g}}}})\) (Fig. 5e, orange circles) matches the experimental data exactly (Fig. 5e, orange line), showing a peak at CNP and small resistance outside the gap. If \({\sigma }_{{{\rm{bulk}}}}\) is fixed, when the number of scattering events is small, the effective mean free path of the edge channel is large. Even when N = 0, the bulk conductivity is larger than ideal because the fixed finite \({\sigma }_{{{\rm{bulk}}}}\) is obtained from the actual \({\rho }_{{{\rm{xx}}}}\) in Fig. 5e without refitting for smaller N. But as expected for adding bulk conduction to ballistic chiral edge transport, the bulk current is finite. The effect of having a small edge–bulk scattering on the corresponding longitudinal resistivity is significant, which deviates from zero at CNP (Fig. 5e, blue circles). The simulated gate-dependent longitudinal resistance \({\rho }_{{xx}}({V}_{{{\rm{g}}}})\) for different N from 0 to 8 (Fig. 5e) shows that in the CNP regime, the system undergoes a transition from dissipationless to dissipative transport as N increases.

For \({\rho }_{{yx}}({V}_{{{\rm{g}}}})\), the simulation also quantitatively agrees well with the experimental data in CNP and \({V}_{{{\rm{g}}}}=\) 0 (Fig. 5f). Some discrepancies appearing right outside the Zeeman exchange gap are possibly due to the global coexistence of QAH and the metallic domains when Fermi level EF is in the intermediate mixed region between gap and valence/conduction band with spatial fluctuation, which is likely illustrated by a percolation picture rather than our simple model of only considering edge–bulk scattering at the edges. Our model simulation demonstrates that significant edge–bulk scatterings play a major role in the quantization breakdown of the odd-SL sample. A reduced edge–bulk scattering, achievable through a more homogenous ferromagnetic exchange gap, may lead to better \({\rho }_{{yx}}\) quantization and suppress the dissipation.

Discussion

We have observed chiral edge current in odd-layer MnBi2Te4 at zero field, confirming the topological nature of its bulk electronic state, i.e., such CES comes from the topological nontrivial band structure. However, the finite bulk conduction and edge–bulk scattering affect the transport quantization of such a QAH state. Our work establishes the chiral edge current as a more robust feature than the quantized transport to identify a QAH phase.

Methods

Crystal growth

The high-quality MnBi2Te4 bulk single crystals were grown by direct reaction of a 1:1 mixture of Bi2Te3 and MnTe in a sealed silica ampoule under a dynamic vacuum. The mixture was first heated to 973 K, then slowly cooled down to 864 K. The crystallization occurred during the prolonged annealing at this temperature.

Device fabrication

Thin MnBi2Te4 flakes were exfoliated by using the Scotch tape method onto 285 nm-thick SiO2/Si substrates, which were pre-cleaned in air plasma for 5 min at 125 Pa. Before spinning-coating Polymethyl methacrylate (PMMA), the surrounding thick flakes were removed by a sharp needle. A marker array was first prepared on the substrates for precise alignment between the selected flake and the patterned electrodes. All the device fabrication processes were carried out in an argon-filled glove box with O2 and H2O levels below 0.1 PPM. By using electron-beam lithography, metal electrodes (Cr/Au, 5/50 nm) were deposited in a thermal evaporator connected to the glove box. When transferred between the glove box, electron-beam lithography, and the cryostat, the devices were covered by a layer of PMMA to mitigate air contamination and sample degradation.

Transport measurement

Electrical transport measurements were carried out in a commercial cryostat Attodry 2100 with a base temperature of 1.7 K and a magnetic field of up to 9 T. The longitudinal and Hall voltages were detected simultaneously by using a lock-in amplifier (Stanford Research System 830). The bottom-gate voltages were applied by a Keithley 2400 multimeter.

Scanning SQUID measurement

Scanning SQUID measurements were carried out in the same cryostat as transport measurements. The nano-SQUID sensors used for this study were scanning 2-junction SQUID susceptometers with two balanced pickup loops of 2 μm diameter in a gradiometric configuration, each surrounded by a one-turn field coils of 10 μm diameter. These devices were planarized throughout, which minimized the spacing between the pickup loop-field coil pair and the sample surface. The SQUID is ~1 μm above the sample during the scan. The spatial resolution was limited by both the size of the pickup loop and the height of it from the sample.

For the scanning SQUID measurements throughout this paper, we employed two different modes to probe magnetic properties. Magnetometry (\(\Phi\)) is a DC measurement of flux through the pickup loop as a function of position and shows the intrinsic magnetization of the sample. Because the pickup loop is parallel to the sample surface, it is only sensitive to the local out-of-plane magnetic field. The magnetometry was performed simultaneously with current flux imaging. The DC static flux signal was measured using a voltage meter (Zurich Instrument HF2LI), while the current flux signal generated by the AC + DC current flowing through the device was demodulated using a lock-in amplifier (Stanford Research System 830), and the frequency of the AC current bias is 155.55 Hz for the current flux images shown in the main text unless otherwise stated.