Introduction

Inspired by the environmental compatibility of natural organisms, actively morphing materials and structures1,2,3 have been studied extensively and developed in many engineering domains, such as microstructure assembly4, biomedical devices5,6 and soft robotics7,8,9,10. In pursuit of high versatility, soft robotics alter their shapes and deployment in response to specific activation when performing diverse tasks. The active shape morphing of soft robotics has been attained by adopting various actuation strategies, including pneumatic, magnetic, and thermal stimulation. Pneumatic active shape morphing is the most used in soft robotics. Generally, by compressing air into the channels inside the soft bodies, the strains of soft bodies, including the expansion of elastomers11,12 and the structural reconfiguration of non-stretchable materials13,14,15, are generated to balance the internal pressure increase. Incorporating with the local stiffness modulation engineering technologies16, such as inhomogeneous wall thickness distribution17 and stiffening by adhesives18, strain mismatch occurs across the thickness of soft bodies under inflation, inducing the shape morphing of soft robotics. Bubble casting pneumatic actuators have a variety of deformable shapes when inflated, because their wall thickness distribution can be tuned by adjusting the position of the bubbles within the uncured elastomer melts19. Inspired by bulliform cells in leaves of monocotyledon plants, a pneumatic active morphing unit is proposed and employed as the internal structure of a flat panel to achieve programable bending and in-plane distortions simultaneously20. Besides, for soft robotics with bodies composed of discrete architectural elements, their body shapes are capable of assembling and reconstructing through vacuum pressure21. Compared to pneumatically driven methods, magnetic field actuation provides feasible remote control in enclosed and confined space. Ferromagnetic soft materials are developed by embedding ferromagnetic microparticles into a soft substrate. Controlling the orientation of particles by external magnetic fields enables their precise shape transformation22,23,24. Furthermore, soft robotics employing thermal responsive materials require no complex energy field for active shape morphing25,26,27,28. Liquid crystal elastomers (LCE) generate large and repeatable contractile strains upon heating above their nematic-to-isotropic transition temperature29. The strain direction is tunable by aligning rigid mesogens during fabrication. By composing two layers with different strain directions (usually in the form of 0°/90°), the LCE bilayers bend under thermal stimuli due to strain mismatch and are utilized in soft robotics30,31.

In general, the out-of-plane bending (manipulation of surface curvature) is the fundamental morphing form for soft substrates. Specific geometry configurations and movements of a soft body can be achieved by the combination of local bending of its each joint. Responsive materials exhibit superior performances when used for morphing of soft robotics, involving large local bending angle range and remote controllability. Nevertheless, their design space is severely limited, usually at the millimeter scale, due to high cost and instability during the manufacturing procedures. For pneumatic morphing soft robotics, the classic design of elastomers with internal air chambers is taken as a reference. They are scalable, yet their achievable shapes are generally restricted owing to their insufficient local surface curvature (bending angle) ranges32. They mostly rely on the uneven strains (strain mismatch) across the thickness of soft bodies to transform shapes. However, during the inflating process, their body bending stiffness increases with increasing input pressure and strains generally33,34. Therefore, optimized parameters are adopted in structure design to achieve larger bending amplitudes35. Nevertheless, some extreme geometric configurations are still a challenge, such as large curvature curling of bodies. Besides, soft robotic morphing originated from strain mismatch always incorporates stiffness modulation methods. Commonly used stiffness modulation methods, such as inhomogeneous wall thickness distribution and passive layer stiffening, are not tunable, so the bending direction (outward or inward) of soft bodies is non-adjustable in general. Some soft robotic designs focusing on the local bending of body joints, such as pouch motors36 and origami-based bellows37,38, have also been proposed. By mounting accordion or biased Yoshimura bellows on soft substrates, a maximum local bending angle of 360° can theoretically be fulfilled as then.

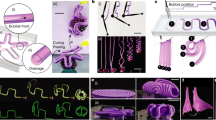
A Möbius strip39 is produced by twisting a ribbon of material through 180° and joining its two ends, creating a unique single-sided topology. It has inspired artistic and engineering innovations and is a clear icon of mathematics that has been absorbed into wider culture40,41. The elastic energy contained in a Möbius strip changes with its topological geometry and material properties42,43. In this work, inspired by the characteristics of the Möbius strip, we proposed the pneumatic torsion strip (PTS), a new approach towards the tunable local curvature manipulation of soft bodies. Like a Möbius strip, a pneumatic torquing strip is formed by bending and twisting an inextensible ribbon of a flat tube (bladder) as shown in Fig. 1a. Interestingly, its shape recovery elastic energy as well as restoring torque increase with internal pressure. When making a pneumatic torsion strip fixed at a segment of a soft body, its controllable elastic energy tends to locally bend the soft body, as demonstrated in Fig. 1b. This bending motion is not due to the strain mismatch of the soft body but from the rotational torque originating from the elastic energy of pneumatic torsion strips. Compared with conventional morphing methods based on strain mismatch, pneumatic torsion strips show obvious advantages in local bending manipulation and scalability. To clarify, the induced curvature of a soft body can be discretized as \(\kappa=\frac{\gamma }{\lambda }\), where \(\lambda\) is the spatial periodicity of the body joints distribution, \(\gamma\) is the slope of the tangent to the ribbon. In addition, since the pneumatic torsion strips directly generate torque to bend the soft body, they can not only easily drive the final shape transformed (bending angle of each body joint) but also the morphing speed (angular velocity of each body joint) of a soft body. For transforming a soft body to a specific shape in a certain time, we just need to adjust the torque output through controlling the inflation rate. The tunability of torque output through changing geometry and input pressure will be demonstrated. Also, there is no need to pre-design the soft body structure and stiffness commonly when using pneumatic torsion strips. In some applications, such as microstructure assembly, only restricted modifications to the soft bodies are allowed. Distinguished by surface orientations, pneumatic torsion strips can be divided into positive pneumatic torsion strips (PPTS) and negative pneumatic torsion strip (NPTS). By assembling pneumatic torsion strips in specific arrangements (sequential or alternating distribution), not only the out-of-plane bending but also the in-plane contraction of soft bodies can be achieved, as in Fig. 1c, e. To demonstrate the unique local curvature operation to soft bodies, the pneumatic torsion strips are employed to some soft robotic applications. In Fig. 1d, the artificial muscle based on the contraction mechanism “planar to wavy shape transformation” is exhibited. Meanwhile, a 2 kg meter-scale transformable carpet enables curl like plant tendrils as shown in Fig. 1f.

Fig. 1: Pneumatic torsion strips inspired by the shape of a Möbius band.
figure 1

a A ribbon bladder (flat tube) is bent and twisted to form a pneumatic torsion strip. b The soft body shape is locally bent by the pneumatic torsion strip. Pneumatic torsion strips are arranged to achieve in-plane shrinkage (c) and out-of-plane bending (d) of the braided soft body. e The artificial muscle contracts obeying the “planar to wavy shape transformation” mechanism. f A meter-scale transformable carpet can curl like plant tendrils. Source data are provided as a Source Data file.

Full size image

Results

Locally bend soft bodies by pneumatic torsion strips

A pneumatic torsion strip is formed by bending and twisting an inextensible ribbon of bladder. The position of the strip end needs to be fixed to define a specific PTS initial geometry, and the strip length needs to be large enough, which will be carefully introduced in the supplementary information. When locating a pneumatic torsion strip on a soft body, its intrinsic elastic energy always tends to bend the soft body. The elastic energy of a pneumatic torsion strip is adjustable and correlated with its geometric configuration and internal-pressure-dependent material properties. As demonstrated in Fig. 1b, the inflated pneumatic torsion strip overcomes the resistance from the soft body and nearly folds it in half. Then, a soft substrate can achieve local bending over a large curvature range (maximum local bending angle approximates 360°) at almost any position through a pneumatic torsion strip, as in Fig. 2a(ii, iii). For real engineering use, a complete pneumatic torsion strip can be divided into a driving section, where the curvature and torsion of the strip surface is changing continuously, and a connecting section, where joins itself with a soft body. In fact, the driving section basically determines the properties of a pneumatic torsion strip and is mainly studied and analyzed in this paper. Additionally, for a pneumatic torsion strip with fixed ends, it can be stabilized in two symmetric geometry shapes (positive and negative) with opposite surface orientations. These two shapes correspond to the same elastic energy and adverse soft body bending directions (outward and inward) and are mutually convertible as in Fig. 2a(i). The supplementary video 1 demonstrates the transformation process from PPTS to NPTS and corresponding soft body deformation.

Fig. 2: The mechanism and geometry of a pneumatic torsion strip.
figure 2

a Paper shape morphing (i) The transformation from PPMS to NPMS and responding paper deformation. (ii) The paper morphs from an inverted U shape to a U shape. (iii) Locally bend a paper. (b) The pneumatic torsion strip geometry established by mathematical model. c The torque output of pneumatic torsion strips is linearly proportional to their input pressure. d The elastic energy of pneumatic morphing strips is decreasing linearly during the bending process. e Pneumatic torsion strips made of different materials show distinct performance. Source data are provided as a Source Data file. All error bars are defined as standard deviations.

Full size image

Geometrical model

The geometry of a pneumatic torsion strip can be described by a bent and twisted inextensible strip. A strip is defined as a surface that is bounded by two parallel directrices. Firstly, the strip surface centerline is denoted by \(r\left(s\right)\in {{\mbox{R}}}^{3}\), where \(s\in [0,L]\) is the arc length along the centerline and L is its length, as expressed in Eq. (S5). Then, If the two directrices is known, denoted by \(a\left(s\right)\) and \(b\left(s\right)\in {{\mbox{R}}}^{3}\), the shape of this pneumatic torsion strip can be expressed as:

$$\begin{array}{c}S\left(s,v\right)=a\left(s\right)+{vu}(s),\\ u\left(s\right)=b\left(s\right)-a(s),\,s=\left[0,L\right],\,v=\left[0,\,1\right].\end{array}$$
(1)

Here, \(S\left(s,v\right)\) can be regarded as the pneumatic torsion strip surface or geometry model. In this paper, we consider the centerline and directrices of a pneumatic torsion strip as the splicing of two symmetric elliptical helixes. Then the first directrices \(a\) as well as the second directrices \(b\) is presented respectively as:

$$a=\left\{\begin{array}{c}{X}_{1}=\left(g-w\right)\cos (t) \\ {Y}_{1}=\left(h+q\right)\sin (t) \hfill \\ {Z}_{1}={d}_{1}{\sin (t)}^{2} \hfill \end{array}\right. \\ \,b=\left\{\begin{array}{c}{X}_{2}=\left(g+w\right)\cos (t)\\ {Y}_{2}=\left(h-q\right)\sin (t) . \hfill \\ {Z}_{2}={{d}_{2}\sin (t)}^{2} \hfill \end{array}\right.$$
(2)

Here, as illustrated in Fig. 2b, 2g is the gap between two centerline ends, \(h\) is the height of the centerline, 2\(w\) represents the width of strip, \(q\) indicates the height difference between centerline and directrices, and \({d}_{1}\) and \({d}_{2}\) represent the depth of directrices a and directrices b, respectively. According to Eqs. (1) and (2), we enable establish the geometry model of a pneumatic torsion strip as shown in Fig. 2b. For real engineering use, once the ends gap \(2G=2g-2w\), strip length \(L\), and strip width 2\(w\) are known, the geometry shape of a pneumatic torsion strip is completely determined. Other parameters can be solved according to some geometric relationships, which will be detailed in the supplementary information. In addition, the ends twist angle of geometry model built above is 90°.

Elastic energy of a pneumatic torsion strip

In this study, we propose that a pneumatic torsion strip can locally bend a soft body by increasing its internal elastic energy. The relationship between elastic energy and geometry as well as the material properties of a pneumatic torsion strip will be analyzed in this section. First, we assume that the membrane thickness of the pneumatic torsion strip is small enough to satisfy \(P\gg Y{\lambda }^{3}/{(2w)}^{3}\). This means that the energy required to bend the pneumatic torsion strip membrane or expand the pneumatic torsion strip is negligible15. Then, assuming the material obeys the Hooke’s linear law for bending, its elastic energy is proportional to the integral of the mean curvature squared over the surface:

$$\begin{array}{c}V=\frac{1}{2}D\int {H}^{2}{dA}\\ H=\frac{{eM}+{mE}-2{fF}}{2({EM}-{F}^{2})},\end{array}$$
(3)

where \(H\) is the mean curvature of two principal curvatures, \(D\) is the flexural rigidity or bending stiffness, and \({dA}=\sqrt{{EM}-{F}^{2}}{dsdv}\) is the area element of the surface. [E M F] and [e m f] are the coefficients of first fundamental form and second fundamental form of the strip surface respectively. Here, an inflated pneumatic torsion strip can be considered as an air beam to depict its bending stiffness. Referring to an inflated beam, the flexural rigidity is expressed as:

$$D=\left(Y+\frac{P{A}_{P}}{{A}_{{cs}}}\right)I,$$
(4)

where \(Y\) is the young’s modulus of strip material, \(P\) is the internal pressure, \({A}_{P}\) is the cross-sectional area that pressure acts (spindle area), \({A}_{{cs}}\) is the membrane cross-sectional area, and \(I\) is the moment of inertial of the cross-sectional shape44,45,46. The detailed characterization and derivation of bending stiffness \(D\) as well as the mean curvature calculation will be clarified in supplementary information. \(V\) in Eq. (4) presents the elastic energy of a strip that it is planar when relaxed, while the pneumatic torsion strip remains U-shaped when relaxed after its ends are fixed. Therefore, \(V\) needs to subtract the energy required to maintain the U shape \({V}_{U}=\frac{1}{2}D\int {{H}_{U}}^{2}d{A}_{U}\) to get the elastic energy for bending the soft body \({V}_{b}\):

$${V}_{b}=\frac{{YI}}{2}\left(\int {H}^{2}{dA}-\int {{H}_{U}}^{2}d{A}_{U}\right)+\frac{P{A}_{P}I}{2{A}_{{cs}}}\left(\int {H}^{2}{dA}-\int {{H}_{U}}^{2}d{A}_{U}\right),$$
(5)

where \({H}_{U}\) is the mean curvature of U-shaped strip. The shape and elastic energy of a U-shaped strip is explained in detail in supplementary information. According to Eq. (5), the elastic energy of a pneumatic torsion strip used to bend a soft body is affected by both its geometric design \(\int {H}^{2}{dA}-\int {{H}_{U}}^{2}d{A}_{U}\) and material properties \(\left(Y+\frac{P{A}_{P}}{{A}_{{cs}}}\right)I\). We will demonstrate and analyze the effects from these two aspects respectively through experiment results.

Input air pressure dependent behavior of pneumatic torsion strips

With the driving mechanism of pneumatic torsion strips analyzed, the effect that they contribute to soft substrates can be estimated (characterized as torque outputs in practical use). When the geometrical parameters of a pneumatic torsion strip are defined after being connected with a soft body, we enable compressed air into the bladder to increase its elastic energy and further torque output. Once the torque exerted by the pneumatic torsion strip on a specific soft substrate joint is determined, the resulting bending angle of that joint can also be known by analyzing its material properties (bending resistance). Here, we have conducted several tests to present the response of pneumatic torsion strips when inflating. To be mentioned, a multiple-layer pneumatic torsion strip is the stacking of several single-layer pneumatic torsion strips with the same geometric structure, as exhibited in Fig. S7. The relationship between input pressure and corresponding torque output of pneumatic torsion strips with different stacking times (layer number) is demonstrated in Fig. 2c. It shows that the torque output of pneumatic torsion strips is linearly proportional to their input air pressure, which conforms to the mathematical model established. The torque output generated by a multiple-layer pneumatic torsion strip can be simplified as the collective effect by the corresponding layer number of single-layer pneumatic torsion strips. Besides, the torque output changes of a pneumatic torsion strip in response to the increasing soft body bending angle from −180° to 180° (from an inverted U shape to an U shape) under different pressure input are described in Fig. 2d. The torque yielded will decrease linearly as the bending angle increases.

Performance of pneumatic torsion strips made of different materials

To investigate how the material used affects the performance of pneumatic torsion strips, we have adopted five materials to make the strips, including Nylon, flexible Polyvinyl Chloride (PVC), low density polyethylene (PE), Spandex fabric, and Thermoplastic polyurethane (TPU), as exhibited in Fig. S8. The elasticity of these five materials increases in sequence \(({Y}_{{nylon}} \, > \, {Y}_{{pvc}} \, > \, {Y}_{{ldpe}} \, > \, {Y}_{{span}} \, > \, {Y}_{{tpu}})\), among which the elasticity difference between PE and polyester fabrics is not significant. With the same geometric parameters (length, width, ends gap, ends twist angle), the relations between torque output and input pressure of these strips are illustrated in Fig. 2e. According to Eqs. (5), (S8), and (S9), when the geometric shape is determined, the material inherent properties only affect the initial elastic energy or initial torque output of the PTS (input pressure \(P\)=0). And the initial torque output of the strip is proportional to the Young’s modulus of the material. After the strip is pressurized, its torque output increment is only related to the input pressure. As can be seen from Fig. 2e, the experimental results are basically consistent with our analysis. The initial torque output (the intersection with the y-axis) increases as the Young’s modulus of the material increases. The five strips have almost the same torque output growth trend (slope of the line). To be mentioned, because the thin-walled TPU strip has the smallest Young’s modulus, it may not be considered inextensible anymore. Then its strip width will enlarge when inflated, so its torque output increments are larger than the other four strips.

Tuning the pneumatic torsion strip performance by changing geometrical parameters

In this section, we present several tests to exhibit the actual influence of geometrical parameters on pneumatic torsion strip behavior and correlate this with the mechanism analysis mentioned. Here, four factors are involved, including the gap between strip ends \(2G=2g-2w\), the strip length \(L\), the strip width \(2w\), and the strip ends twist angle \(\theta\). Taking a landscape of elastic energy of a pneumatic torsion strip as exhibited in Fig. 3a, the associations between torque output and each of these four factors are demonstrated in Fig. 3b–e respectively. As the strip end gap G increases, the torque generated decreases initially and rebounds at a critical point. For the strip length \(L\), the torque output decreases monotonically as it increases. The energy used by the pneumatic torsion strips to bend a soft body is approximately equal to their torsional energy. In the precondition of constant surface twisting (\(\pi\) for pneumatic torsion strips), the longer the strip length, the smaller the surface twisting rate as well as the torsion energy will be. In contrast, when the strip width \(2w\) increases, the elastic energy (the integral of mean curvature along the strip surface) of pneumatic torsion strips will enlarge substantially. The torque output grows exponentially as the strip width increases. For the strip end twist angle \(\theta\), the strip torsion energy intuitively increases as it increases. As expected, it can be observed that the torque output as well as the angular velocity when actuating a body joint increases monotonically with the strip end twist angle \(\theta\), as shown in Figs. 3e and S9. The effect of end twist angle on performance of pneumatic torsion strips is further discussed in supplementary information. Then, based on obtained properties, we enable purposefully modify the performance of pneumatic torsion strips. In Fig. 3f, the two pneumatic torsion strips with different geometry shapes share almost the same input pressure versus torque output correlation. While in Fig. 3g, the torque growth rates (slope of the curve) of the two pneumatic torsion strips shows a two-fold relationship approximately. In addition, we induce a scaled end twist angle \(\theta \frac{2w}{L}\) to present the ends twist angle per length for the strip of a certain width. As in Fig. 3h, with the same scaled ends twist angle, varying \(L\) is more effective than varying \(\theta\) for moderating PTS performance (larger torque output range). Finally, as demonstrated in Fig. 3i, when the condition PTS thickness \(\lambda \, \ll \, \root 3 \of {8P{w}^{3}/Y}\) (here calculated as 3.53 mm) is not satisfied, no obvious pressure-dependent behavior can be found.

Fig. 3: Geometric effect on pneumatic torsion strip performance.
figure 3

a Theoretical contour map of the elastic energy of a pneumatic torsion strip (width 2w = 12 mm, pressure P = 100 kPa) as a function of strip end gap 2 G and strip length L. Under a certain pressure input, the torque output of pneumatic torsion strips is determined by (b) strip end gap 2 G, (c) Strip Length L, (d) strip width 2w. and (e) ends twist angle \(\theta\). f Two pneumatic torsion strips with different geometry shapes share almost the same performance. g The torque growth rates of these two pneumatic torsion strips are tuned to a two-fold relationship. h In the case of the same scaled ends twist angle \(\theta \frac{2W}{L}\), varying L has a larger torque output range than varying \(\theta\). i The PTS membrane thickness \(\lambda\) needs to be small enough to have significant pressure dependence. Source data are provided as a Source Data file. All error bars are defined as standard deviations.

Full size image

The manipulation of a body joint by pneumatic torsion strips

The overall shape deformation of a soft body is a combination of the bending or rotation of its each body joint. Therefore, the manipulation of body joints, including control of bending angle and rotation speed (angular velocity), is the basis for active shape Morphing. Here we utilize pneumatic torsion strips to actuate and control a single body joint as shown in Fig. 4a. Some load is added to increase joint stiffness. Figure 4c indicates the rotation angle of the body joint is controlled by the torque output generated by pneumatic torsion strips, which is linearly dependent on the input pressure. The peak torque output reaches 1.44 Nm under 100 kPa. The joint with 200 g end load rotates across 110 deg in 0.4 s under 100 kPa pressure input as demonstrated in Fig. 4d. In addition, the rotational speed or angular velocity of the body joint is also determined by the input pressure, as in Fig. 4e. Rotating the same range, the peak angular velocities of the body joint at 100 kPa and 40 kPa are 13.63 rad/s and 8.56 rad/s respectively. Combining PPMS with NPMS, which are mutually antagonistic, the dual directional actuation and rapid positioning of the body joint can be then achieved as illustrated in Fig. 4f. The body joint can be positioned to rotation angles of 80° and 40°, respectively, at almost the same rotation speed. Based on the superior manipulation ability to body joints of pneumatic torsion strips, including the control of both rotation angle and speed as mentioned, the shape deformation of an entire soft body can be further realized.

Fig. 4: A body joint manipulation by pneumatic torsion strips.
figure 4

a A body joint with end load (b) can be manipulated by pneumatic torsion strips. Based on the torque output control (c) by pneumatic torsion strips, both the rotation angle (d) and angular speed (e) of the body joint are determined. The dual directional actuation and rapid positioning of a body joint (f) are achieved by the cooperation of PPTS and NPTS. Source data are provided as a Source Data file.

Full size image

Pneumatic torsion strips for soft robotic applications

After understanding how pneumatic torsion strips work, we may design a pneumatic torsion strip array (PTSA) on a soft body to achieve a specific morphing shape. The disposition of a PTSA can basically be divided into alternating distribution for the in-plane contraction of soft body and sequential distribution for the out-of-plane curl of soft body. In addition to distribution, the PTSA is also determined by each pneumatic torsion strip setting within it. Then, each PTSA has a corresponding deformed shape. A soft body may be manipulated by multiple PTSAs simultaneously to obtain diverse deformed shapes. In this study, we explore the possibility of PTSAs in several soft robotics applications including the shape-morphing-based artificial muscle, the meter-scale transformable carpet, the dual modes mobile robots, and the bionic frog tongue, to demonstrate the large potential of pneumatic torsion strips in actual engineering use. Each soft robotics application will be displayed in supplementary video 1. To mention, taking the PTSAs of the dual-mode mobile robot as an example, we illustrate the dimension and composition of a specific PTSA in Fig. S13.

Shape-morphing-based artificial muscle

Pneumatic artificial muscles (PAMs) commonly share the same actuation principle of “converting radial expansion into axial contraction”47,48,49. However, when a planar structure deforms into a wave shape, its axial length also decreases. This contraction mechanism is simple but is not easily applied to artificial muscles due to difficulties in structure morphing. Supporting by the outstanding local curvature manipulation capability of pneumatic torsion strips and their alternating distribution, we realize the type of artificial muscle based on its own shape morphing. The maximum contraction ratio of A shape-morphing-based artificial muscle (SAM) is corelated with its deformed shape. Wave with less periods indicates a larger maximum contraction ratio as shown in Fig. 5a. The basic force-contraction relationship of a SAM is exhibited in Fig. 5b. This SAM prototype has an original length of 150 mm, width of 110 mm, weight of 55.2 g and its deformed shape is a wave with period number 2. In addition, two double-layer pneumatic torsion strips are symmetrically arranged at each bending joint of this SAM. At 150 kPa pressure input, it contracts over 40% and generates a 74.2 N force output, more than 135 times its weight. Besides, using a SAM prototype with the length of 340 mm, width of 120 mm and periodicity of 5, the contraction as a function of the applied load (up to 10 kg) is demonstrated in Fig. S12. Compared with other PAMs, the main advantages of SAMs are high adjustability and space saving (small radial expansion between uninflated and inflated state). Their significant performance, including maximum contraction ratios and force outputs, are both tunable by modifying their pneumatic torsion strip arrays.

Fig. 5: Morphing soft robotic applications based on pneumatic morphing strips.
figure 5

a The artificial muscles contracts based on the “planar to wavy shape transformation” mechanism. b The SAM performance under isotonic actuation. c The dual mode morphing mobile robot enable accomplish (i) crawling motion, and (ii) rolling motion based on shifting process between different shapes. d A meter-scale transformable carpet can morph to divergent shape and achieve rolling motion by shape shifting. e The bionic frog tongue sticks out and roll back for predation. Source data are provided as a Source Data file. All error bars are defined as standard deviations.

Full size image

Dual mode morphing mobile robot

In nature, many animals achieve locomotion through body shape morphing, such as inchworm. Here, we mount four PTSAs into a soft body, making it a dual mode morphing mobile robot. The robot body is a spliced fabric sheet, with each half of the body controlled by two mirrored sequential- distributed PTSAs (surface orientation of each pneumatic torsion strip is opposite). Therefore, each half of the body enables bend inward and outward. The robot has a body length of 285 mm, width of 150 mm, height of 5 mm, and enables two locomotion modes involve crawling and rolling. The crawling mode can be described as the back-and-forth change of body from a planar shape to a mountain shape with specific curvature. Meanwhile, though the final shapes are always the same, to possibly eliminate the hinder from friction force, the morphing speeds of each half robot body are programed during the transformation process, as exhibited in Fig. 5c. The robot can move with a speed of 0.4 body lengths per second in crawling mode. To accomplish the rolling movement, the robot transforms its body from a planar shape to a full scroll cylinder shape and adjusts the exertion position (which part of the body is in contact with the ground) at the same time, as illustrated in Fig. 5c. Relying on the rolling mode, the robot capable of overcoming obstacles more than 10 times its height. The concrete gait instructions of this robot in two modes are introduced in Fig. S14.

Meter-scale transformable carpet and bionic frog tongue

It is always challenging to increase the size of soft robotics due to the difficulties in manufacturing and actuation. In this work, we demonstrate how to actively morph a carpet with a length of 1 m, a width of 0.7 m, and a weight of 2 kg. Under the manipulation of two mirrored sequential-distributed PTSAs, each half of the carpet can bend inward and outward, with its bending curvature adjustable through input pressure. In Fig. 5d, several appearances that the carpet can be transformed, including a single-side cylinder, a full-stroll cylinder, a double-side cylinder, a wavy shape, and a mountain shape. A rolling motion of the carpet is also realized during the continued shape shifting process. In addition, thanks to the superior local curvature control capabilities of the pneumatic torsion strips, the carpet body can curl like plant tendrils (Large curvature) after adjusting its PMSAs settings. Generally, structures with a large aspect ratio approximating to 1 are harder to curl in that way than slender structures. Possessing a similar curling transformation, a bionic frog tongue is created by arranging a sequential-distributed PTSA to a slender sheet made of ribbon bladders and fabric slices. As in Fig. 5e, the bionic frog tongue completes the sticking out and rolling back process in 0.5 s and 0.7 s respectively and mimics the predation procedure when adhesive substances are attached.

Reliability and scalability of pneumatic torsion strips

To pursue the practical engineering use of pneumatic torsion strips, their reliability and scalability need to be studied. Here, we use a single-layer LDPE PTS to actuate a body joint with load over 15000 times. The body joint is actively bent by PTS drive and then recovers due to its own weight. After 15000 strokes, the performance of PTS has no obvious degradation, as shown in Fig. S16. In addition, the possibility of micro- (< 1 mm) and large-scale (>1 m) PTS is also considered. Firstly, we give the torque output predictions for PTSs on different scales, as shown in Fig. S17a. For micro-scale PTSs, their thickness must be less than the threshold thickness \({\lambda }_{{threshold}}=\root 3 \of {8P{w}^{3}/Y}\) (\(P\ge Y{\lambda }^{3}/{(2w)}^{3}\)), otherwise the PTS cannot expand. However, \({\sigma }_{{threshold}}\) is always 1 to 2 orders of magnitude smaller than the strip width. Then the fabrication of micro-PTS may encounter difficulties. As for large-scale PTSs, their large membrane tension \(T={PR}\) under inflation may cause material rupture. Therefore, the material tensile strength must be larger than membrane stress\(\,T/\lambda\). We give references for threshold thickness \({\lambda }_{{threshold}}\) and membrane tension \(T\) of micro- and large-scale LDPE PTSs, as demonstrated in Fig. S17b.

Discussion

In this work, we propose the pneumatic torsion strips characterized with input pressure dependent elastic energy, enable the tunable local curvature manipulation of soft bodies. Without a complicated manufacturing process, a pneumatic torsion strip is formed by just bending and twisting an inextensible ribbon of bladder. Unlike conventional strain-mismatch based morphing methods, pneumatic torsion strips directly apply torque to the soft body without generating in-plane strain and affecting the body inherent rigidity. Both the geometric and material factors of pneumatic torsion strips can be modified to achieve control of their torque output. Then, the local body joint curvatures of a soft substrate can be manipulated through pneumatic torsion strips to achieve precise shape control. Therefore, because of the tunability, discretizability and unique driving mechanism, pneumatic torsion strips are a good choice for deforming soft robots, especially large-scale robots. We demonstrate the active shape shifting and movement of a meter-scale transformable carpet through pneumatic torsion strips.

Although the presented pneumatic torsion strips exhibit promising performance and application prospects, some challenges still exist, pointing to several areas for future investigation. Here, we mainly use LDPE tubes as the fundamental material of pneumatic torsion strips. However, twisted and bent LDPE pipes can easily form creases under high input pressures and large payload. This issue can only be partially alleviated by increasing the membrane thickness or using some other materials, such as TPU tubes, which will be detailed in supplementary information. In addition to large-scale soft robots, we will also explore the potential application of pneumatic torsion strips in micro-soft robots. But as mentioned above, the limitations of the manufacturing process (the membrane of micro-PTS is very thin) and material properties (high tensile strength of very large PTS) need to be overcome. Furthermore, we assemble the pneumatic torsion strips into soft structures only manually in this study, such as braiding and attaching. Our future research will consider other programmable and automated methods for the fabrication and assembly of pneumatic torsion strips, such as 3D printing. We have also made some 3D-printed TPU strips of different membrane thicknesses. Theoretically, based on 3D-printing technology, we can program the material properties by changing printing parameters (such as infill density). However, the thickness of PTS needs to be small enough to satisfy \(P\gg Y{\lambda }^{3}/{(2w)}^{3}\). Otherwise, a non-negligible amount of energy must be used to inflate the strip. In addition, the printed strips need to be airtight. Therefore, using FDM 3D printers, we can only make viable TPU PTS with a minimum thickness of 0.4 mm. In our future research, we will try other 3D printing methods, such as SLA and DIW, to pursue the programmability of the material properties of PTS. Finally, the application of pneumatic torsion strips in soft robots is still in a very preliminary stage. We expect our study can stimulate more research interests in them and explore their applications in various fields.

Methods

Materials

In this paper, we bend and twist ribbon of bladders to form pneumatic torsion strips and apply them to several soft robotic applications. The ribbon bladders used in robot prototypes are mainly low-density polyethylene (LDPE) tubes with a membrane thickness of 0.2 mm and a Young’s modulus of 0.28 GPa. Besides, several other materials are used to make PTSs, including Nylon fabric (1.5 GPa), flexible PVC (0.64 GPa), Spandex fabric (0.23 GPa), TPU (0.05 GPa). These tubes are readily commercially available and are at a low cost. Four types of LDPE tubes with different pressed widths, including 12 mm, 23 mm, 30 mm, and 40 mm are employed in experiments. In addition, we utilize polyester fabric splice sheets as the soft bodies of prototypes. To simplify the manufacturing process of prototypes, we directly braid long LDPE tubes into the fabric sheets through a typical warp-and-weft weaving method to form pneumatic torsion strip arrays (PTSA) and fixate their positions. The SAM prototype for testing contains an alternating distributed PTSA with 8 pneumatic torsion strips in 4 rows and 2 columns. Each pneumatic torsion strip stabilizes in the geometry of 10 mm strip end gap \(2G\), 60 mm strip length \(L\), and 12 mm strip width \(2w\). For the dual mode morphing mobile robot, two mirrored sequential distributed PTSAs with 12 pneumatic torsion strips in 6 rows and 2 columns are mounted in it. The geometrical factors 2 G, \(L\), and \(2w\) are 5 mm, 50 mm, and 12 mm respectively. For the transformable carpet, two mirrored sequential distributed PTSAs with 77 pneumatic torsion strips in 11 rows and 7 columns are deployed on each half of the body. Finally, a sequential distributed PTSAs with 8 pneumatic torsion strips in 4 rows and 2 columns is fixed in the bionic frog tongue.

Experiment setup

To characterize the actuation behavior of pneumatic torsion strips and their manipulation of a body joint as well as the performance of SAM prototypes, several tests have been accomplished in this study. The pneumatic torsion strip behavior tests were conducted through the experimental platform as shown in Fig. S1. A pneumatic torsion strip with specific geometric configuration is fixed in a 3D printed hinge structure, which connects with a static torque sensor (DYJN-104, Dayang, China) or a dynamic torque sensor (SBT8121, SIMBATOUCH, China). When the pneumatic torsion strip inflates, the torque generated can be measured by the torque sensor. The sampling frequency, resolution, and measuring range of the static torque sensor are 1000 Hz, 0.001 Nm, and 2 Nm respectively. And the sampling frequency, resolution, and measuring range of the dynamic torque sensor are 1000 Hz, 0.002 Nm, and 2 Nm respectively. An IMU (IM948, Zhenyi, China) is used for the body joint manipulation test. For the SAM prototype isotonic test, the experiment setup is demonstrated in Fig. S2. One side of the SAM is fixed, and the other side connects with a force sensor (DS2-200 N, Zhiqu, China) through wire ropes. The force sensor is installed on a stabilized linear guide with an encoder, whose displacement is detected by a laser displacement sensor (GC05-200PW, HEPU, China) and recorded by a data terminal (USB-3211, Smacq, China). The sampling frequency and resolution of the force sensor are 1000 Hz and 0.1 N respectively. The input pressure’s amplitude and frequency are controlled by a pressure regulator. To develop a contraction force versus contraction ratio relationship, applying an input pressure to the SAM prototype first. Then, the SAM is loosened continually with the linear guide movement until a zero display of the force sensor emerges, and the displacement as well as contraction force change during the process are recorded.