Introduction

GRS 1915+105, a well-known Galactic fast-spinning black hole (BH)1 X-ray binary (also named as microquasar) at a distance of 8.6 kpc2, possesses a relativistic magnetized jet that exhibits superluminal motion through its radio emission3,4. The source has shown the strong and complex variability in different time scales and energy bands since its discovery, which is quite different from other BH X-ray binaries. The X-ray variability can be classified into approximately 14 separate classes, depending on its light curves and color-color diagrams5,6. Each variability patterns have transitions between three basic states6: a hard state and two soft states with different luminosities7. In the hard state generally associated with radio jets8, quasi-periodic oscillations of X-ray flux with frequencies ranging from 0.1–10 Hz are observed9,10. Previous works suggested that the radio emission in GRS 1915 + 105 is produced in jets which is fed by instabilities in the accretion disk11,12 by which the inner part of the accretion flow is ejected13,14,15.

Quasi-periodic oscillations (QPOs) as prominent timing characteristic features in black hole systems are reported in multi-wavelength observations, e.g., radio, optical, X-ray and gamma-ray bands9,16,17,18,19,20. These QPOs show the modulations in the emission flux light curves, however, the production mechanism is still unknown. Radio emissions produced by relativistic jets and the variations have been observed in different mass-scale black holes21,22. Magnetic fields anchored to a rotating BH23 or accretion disc24 could accelerate and collimate jets of the BH systems. At present magnetic field configuration near the black hole, as well as particle acceleration in jets is not well understood.

In this work, we use the Five-hundred-meter Aperture Spherical radio Telescope (FAST) to perform a high-sensitivity, subsecond-resolution radio study of GRS 1915 + 105, aiming to study fast variations in GHz bands and instability of relativistic jets from the BH25. Here, we show the discovery of the QPOs of the GHz-band polarization and flux at the period around 17 and 33 s. These observed polarized radio QPOs will connect to special features of magnetized jets with possible jet-disk couplings.

Results

GRS 1915+105 was observed by FAST from 01:25:00–03:15:00 (UTC) on 25 January 2021 with a 99 microsecond sampling time using the tracking-mode observation pattern on the source in the 1.05–1.45 GHz band with the central beam of the 19-beam receiver26. At the beginning and end of the observations, two off-source mode observations were performed for calibration. The four full Stokes polarization parameters were recorded. After data reduction and calibration (see methods, subsection observations and data reduction), we derived the variations of the total flux intensity and polarization parameters over the observing time intervals with a time resolution of 0.5 s (Fig. 1). The radio flux density was relatively stable at early times but started to increase after 1500 s. After a continuous rise of the flux at 2700 s, multiple mini flares appeared for a duration of 400 s. The linear polarization degree also increases from 27% to 31%. The bottom panel of Fig. 1 also shows the dynamical power spectrum of the linear polarization light curve, and polarization oscillations with the periods of 17 and 33 s appear as prominent features during the mini flares in the dynamical power spectrum.

Fig. 1: Light curves of flux and linear polarization in the whole observation.
figure 1

Top panel: The light curve of total intensity flux density observed by FAST in the 1.05–1.45 GHz band from 2021-01-25:01:45:00 to 2021-01-25:03:04:57 (UT). The flux density began to increase from the time  ~1500 s and reached a peak around 3200 s. Middle panel: the light curve of the linear polarization (LP) degree. Bottom panel: The dynamical power spectrum of the LP curve for the observed time ___domain. During the increasing phase of the radio flare, there exist transient quasi-periodic signals at  ~17 and 33 s for LP during the interval 2700–3100 s. The orange contour in the bottom panel represents the line of 95% confidence levels. Source data are provided as a Source Data file.

Full size image

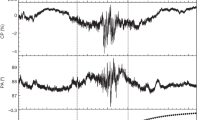
Significant evolution with time for other polarization parameters was also detected during the quasi-periodic flares (see Fig. 2). We present the detailed variation structure of the flux from 2400 to 3200 s, and the corresponding light curves of linear polarization (LP) degree, circular polarization (CP) degree, and position angle (PA). Then the power density spectral analysis of these light curves shows the significant QPO peaks at 17 and 33 s both in the linear polarization and flux density (Fig. 3). In addition, transient periodic signals with similar periods are confirmed through wavelet analysis (see Fig. 4). The flux density increased from 480 to 620 mJy during this epoch and became dramatically variable between 2700 and 3100 s, during which the average power spectrum of the flux density reveals peaks with apparent periods of 17 and 33 s. The light curve of the LP degree, which ranges from (27−32)%, exhibits a quasi-periodic modulation behavior similar to the flux, although the peaks in LP always correspond to valleys in flux: the two are strongly anti-correlated (Pearson correlation coefficient r = −0.79 ± 0.05) during the quasi-periodic flares (Fig. 5). But there exist no correlations between LP and flux when the QPO signals are not detected. The CP degree varied from  −(0.5 − 2.5)%, and the linear PA, distributed at 87°−89°, also fluctuated during the quasi-periodic epoch. While the CP and PA curves show the weak transient periodic oscillations at 40−50 s, they are also different from those of flux and LP. There are no correlations between the flux and CP or PA (see Fig. 6 and methods, subsection correlation analysis).

Fig. 2: The light curves during the radio polarized QPOs.
figure 2

Flux density (FD), degree of LP, degree of circular polarization (CP), and polarization position angle (PA) show the modulations from  ~2400−3200 s when the rapid flux density variations were observed. From  ~2700−3100 s, the variation pattern of flux density is anti-correlated with that of LP (the peaks of flux density always correspond to the valleys of LP). Source data are provided as a Source Data file.

Full size image
Fig. 3: Power density spectrum analysis of the light curves from 2400-3200 s.
figure 3

We show the PDSs for four parameters: (a) radio flux density (FD), (b) linear polarization (LP), (c) circular polarization (CP) and (d) position angle (PA), and the corresponding residuals of the fittings. The black crosses are normalized with the rms normalization with error bars (1σ), the black dashed lines indicate the Lorentzfian components for the fitting, and the red solid line is the result of the fitting. The pink dashed lines indicate the mean background PDSs of the simulated light curves for the four parameters66, blue and orange dashed lines indicate the confidence levels of the PDS peaks at 3σ and 5σ (see methods, subsection periodicity studies). In (a) the centroid frequencies of the Lorentzian peaks for the FD are around 31, 58 mHz respectively, and there exists a weak peak around 75 mHz which is below 3σ. For LP in (b) the peak centroid frequencies appear around 30 and 55 mHz above 5σ, which are similar to the QPO frequencies of the flux. In (c) the CP light curve shows the different variation patterns, the power has three weak Lorentzian peaks with the centroid frequencies around 20 mHz, 35 mHz and 45 mHz; while in (d) the PA curve show weak peaks with the frequencies around 25 mHz, 45 mHz and 66 mHz. Both peaks in CP and PA are not significant with around or below 3σ. Source data are provided as a Source Data file.

Full size image
Fig. 4: Wavelet analysis results of flux density and polarization parameters.
figure 4

Transient QPO signals are shown for all parameters (from top to bottom): FD, LP, CP, and PA. The solid red lines indicate the 95% confidence contours for a red-noise process. Light yellow regions and the black dashed lines indicate the “cone of influence” where edge effects become nonnegligible. The two blue dash-dotted horizontal lines in each panel flag the locations of the two QPO signals at 17 and 33 s detected in the linear polarization and flux density light curves. All light curves exhibit oscillations in some time intervals. However, only the LP oscillation signal correlates with the flux density. No significant relationship exists between the other polarization parameters (CP and PA) and flux density. The gray, black solid lines and red dashed lines in the right panels indicate the Fast Fourier transform (FFT) spectra, wavelet spectra, and the 95% confidence levels, respectively. Source data are provided as a Source Data file.

Full size image
Fig. 5: The linear fitting of the data points for flux density and linear polarization during the polarized QPOs.
figure 5

Top panel: the linear regression result between flux density and linear polarization for the observed time interval from 2400 s to 3200 s. The purple circles with error bars mean the original scatter points based on flux density and linear polarization. The orange dashed line indicates the best fitting result. The Pearson correlation coefficient (PCC) between flux density and linear polarization during the QPO intervals is −0.795, suggesting a strong anti-correlation. Bottom panel: the corner plot of the parameters of slope and intercept of the linear fitting shown in the top panel. The fitting was implemented with Markov Chain Monte Carlo (MCMC) sampling. Source data are provided as a Source Data file.

Full size image
Fig. 6: Variation patterns between radio flux and linear polarization of GRS 1915+105 based on the FAST observations.
figure 6

During the time interval from 2400 s–3200 s with the QPO signals, flux and LP show the distribution of the evident negative correlation with the PCC = −0.795 between flux density and linear polarization during the QPO intervals. However, for other time intervals without QPO features, the flux and LP distribute randomly and do not correlate with each other. The blue solid lines in the top and right panels are the normal fitting of the histogram. Source data are provided as a Source Data file.

Full size image

Discussion

Previous radio observations of GRS 1915 + 105 have revealed flux quasi-periodic oscillations on timescales of 20–50 minutes5,27,28. While their physical origin is uncertain, the hour timescale of the radio oscillations appears to be connected to X-ray variations on similar timescales5,29. Recently FAST has reported the radio flux oscillations of the period at 0.2 s16, and this timescale is similar to the low-frequency QPOs with periods from 0.1 − 1 s detected in the X-rays9,10. Here the new findings report rapid QPOs for the light curves of both polarization parameters and flux density in this microquasar with a modulation period down to 17 s. In addition, the polarization periodic oscillations only last about twenty periods, in contrast to the relatively persistent low-frequency QPOs in BH X-ray binaries30.

Quasi-periodic modulations in radio light curves, as detected in GRS 1915 + 105, are also frequently observed in different BH systems. Long-period radio oscillations with periods ranging from about one hundred days to several years have been reported in some radio-loud active galactic nuclei (AGNs), specially blazars31,32,33,34. These radio oscillations generally last for tens of cycles, which can reflect the dynamics of relativistic jets. Quasi-periodic oscillations with a period of 15 h in radio band were found in a gamma-ray X-ray binary LS I  +  61°30335, however, only two or three cycles were observed. A five-Hz radio quasi-periodic oscillations in GRS 1915 + 105 is reported based on FAST observations16. In the previous observations for both stellar mass BHs and SMBHs, however, only the flux modulations are reported, without polarization detection or discovering the periodic oscillations in polarization curves. In this work, we show the detection and properties of polarization quasi-periodic oscillations in BH systems.

Many models are proposed to explain quasi-periodic oscillations in radio bands. In stellar mass BH systems, for example, GRS 1915 + 105, the radio periodic oscillations with a period of about half-hour may be related to the X-ray oscillations with similar periods5. In LS I  +  61°303, the radio modulations is probably due to the multiple shocks in a jet35. However, there isn’t any suitable model to explain the physical origin of five Hz radio quasi-periodic oscillations in GRS 1915 + 105 yet, which could be due to the possible jet precession, jet wobbling, or the helical motion of the relativistic jet knots25. In the framework of AGNs, various different models have been proposed to explain the radio oscillation. The year-long oscillations are generally considered due to the orbital motion of binary SMBH systems. The magnetic fields and plasma trajectory are expected to have a helical structures if the jet is magnetically dominated36. Quasi-periodic oscillations with periods around hundreds of days in radio, optical, or gamma-ray bands in blazars can be interpreted by helical motion of blobs or shocks in relativistic jets18,37.

It has been suggested that in a rapidly spinning, accreting BH system, a helical magnetic field configuration is naturally produced in the relativistic jets predicted in theoretical magnetohydrodynamical (MHD) models36,38,39. Jets are prone to many instabilities such as pressure-driven (PD), current-driven (CD), and Kelvin-Helmholtz (KH) instabilities (plus any combination of them)40,41. The final nonlinear outcome of these instabilities can reach from a simple internal redistribution of jet quantities to the production of internal shocks and/or MHD turbulence42. There are some models that may be able to explain the polarized QPOs in GRS 1915 + 105. In the followings, some of these models are summarized, which would be directly connected to jet dynamics and emission, or arise from disk-jet couplings near the BH.

  1. 1.

    The linear polarization mainly comes from synchrotron emission of electrons in relativistic jets, the polarization degree may be quasi-periodic if the modulation of the magnetic field is quasi-periodic. A group of recurrent jets with similar periods can probably excite the observed quasi-periodic oscillations. If the jets are recurrent, the magnetic field may be modulated by some periodic processes43, which would lead to modulations of linear polarization as well as the radio flux light curve. However, the origin of recurrent jets remains uncertain, and it is unclear whether a group of jets can be generated with a similar interval.

  2. 2.

    MHD simulation shows that magneto-rotational instability (MRI) can lead to a quasi-periodical shock in accretion disk and results in a quasi-periodical flux variation44. The MRI can generate jets and modulate the magnetic field which may lead to the QPO phenomenon. Therefore, the MRI model may explain both X-ray QPOs and radio QPOs observed in hard states of GRS 1915 + 105. Unfortunately, the present MHD simulations didn’t consider polarization properties.

  3. 3.

    The radio modulation can also originate from the helical motion of emitting blobs in the relativistic jet45. A model based on helical trajectories of emitting blobs may explain the QPO phenomenon45 and possible anti-correlations between the electric polarization angle, the degree of polarization and flux46. The radio and γ-ray quasi-periodic variability seen on a timescale of tens to hundreds of days in some blazars have been attributed to the helical structure of jet blobs moving18,31. If the QPO originated from helical motion, we should observe the QPO during the whole period of the jet, while the polarized QPO only appears during 2700 ~3200 s and disappears later. This geometric origin would be difficult to explain the transient behaviors of QPOs.

  4. 4.

    Recent 3D general relativistic magnetohydrodynamic simulations show that a tilted geometrically thin accretion disk can be torn due to the Lense-Thirring torque47,48,49. QPOs can be observed due to the precession of infalling accretion matter. In addition, a pair of relativistic jets can be produced in such a system. In some situations, the disk-jet interaction can be very strong that the jets run into the outer sub-disk48. This can possibly lead to instability in jets and generate QPOs in the radio band. However, the simulations assume a high tilt angle, 45°–65°, and there is no observation result indicating that GRS 1915 + 105 has such a high tilt angle.

  5. 5.

    Kink instability is a kind of current-driven plasma instability, which causes transverse displacements of plasma and twists the magnetic field structure. Global MHD simulations show that jets will expand and loose transverse causal contact after being launched, making them stable for current-driven instabilities. As the jet moves away from the center black hole, the pressure of the interstellar medium becomes important, and the flow will recollimate and regain its causal contact50,51. Consequentially, the jet becomes narrower and the cross-section is reduced, such area is natural for kink instabilities to develop52,53. The kink instability can distort the magnetic field and generate an induced electric field. The combination of an induced electric field and a distorted magnetic field is an effective nonthermal particle accelerator. Depending on the set up of simulation, (10−50)% magnetic energy can be dissipated, which will be transferred to accelerated particles with a power-law spectrum50,54. Particles accelerated via kink instability can give rise to synchrotron emission which accounts for observed polarization signatures55. Besides, relativistic magnetohydrodynamic simulations show that kinked structure appears with periodic signature along the jet direction, which will lead to QPO signatures of polarization52,55. However, the simulation shows the QPO signatures are still weak and only last for several periods and it’s not clear whether the instability can last long enough to generate the observed QPOs that last for tens of periods.

As a summary, some simulations of kink instability show the quasi-periodic energy release that would produce radio flux modulations, and the LP degree shows a similar weak QPO signature and is anti-correlated with the flux. However, there is no evidence supporting this mechanism as capable of sustaining a QPO over multiple cycles. In addition, present simulations on helical motions, MRI or disk tearing have not precisely predicted the polarization behaviors. Therefore, there is no clear evidence that any model is preferred according to the present observations. In any case, the polarized radio QPOs provide the new clues for understanding magnetic field configuration near black holes and particle acceleration in jets.

Methods

Observations and data reduction

Our astronomical monitoring targeting the microquasar GRS 1915 + 105 was conducted using the FAST. The primary observation employed tracking mode through the central beam of the 19-beam receiver, operating within the nominal 1–1.5 GHz frequency range, while the 50 MHz bands at both spectral boundaries need to be excluded. This observation started at 01:35:00 UTC on January 25, 2021, sustaining data collection for 90 minutes with a 98 microseconds temporal resolution. The field of view of the central beam is ~2.9 arcminutes. For calibration purposes, periodic noise injections (0.210326592 seconds) were conducted in five-minute intervals both preceding and following the source tracking observation. High power noise diode mode was used in our observations for calibration, in which the noise and noise temperature are 100% linear polarized and 12.5 K, respectively.

The observational data of FAST are stored in the standard PSRFITS format56. Our data reduction pipeline starts with the preprocessing of FITS file using astropy package57. The preprocessing involves two operations: (1) systematic re-sampling of the original data across full 4096 frequency channels and 128 subints, (2) concatenating the re-sampled preprocessed data files. The PRESTO software suite performs subsequent analysis on the merged data file, generating an uncalibrated lightcurve time series and radio frequency interference (RFI) mitigation mask through automated detection. The common detected interference patterns include the strong noisy signal in the periodogram (such as 50 Hz alternating current noise and its harmonics persisting throughout observations), non-negligible short-time spikes caused by noise in channels 650–820 (1080–1100 MHz), and broadband RFI peaks around channels 1500–2200. Following standard RFI mitigation protocols, we excluded these affected spectral regions from our analysis. The processed time series, now cleansed of these interference components, contains relative flux intensity measurements ready for subsequent calibration.

Flux density calibration

The temperature of the observed source in the on-off mode is

$${T}_{src}(t)={T}_{cal}\cdot \frac{ON}{ONCAL-ON}-{T}_{sys}(t),$$
(1)

where Tcal is the temperature of the injected reference signal from the noise diode, ON and ONCAL are the intensity values in the turning-off and turning-on states of the noise diode, respectively, when the telescope is directed at the celestial source in the on-off mode for the calibration scans before and after the tracking observations, and Tsys(t) is the time-dependent system temperature of the telescope when the telescope is pointing at the background sky, which is given by

$${T}_{sys}={T}_{cal}\cdot \frac{OFF}{OFFCAL-OFF},$$
(2)

OFFCAL and OFF are the intensity values in the turning-on and turning-off states of the noise diode, respectively, when the telescope is directed at the background sky.

Then the flux density can be calculated by the following formula,

$$Flux(t)=\frac{I(t)-OFF}{ON-OFF}\cdot {T}_{src}(t)\cdot \frac{1}{G},$$
(3)

where I(t) is the observed intensity value from the telescope with time in the tracking mode observations, G = ηG0 differs from the measured gain G0 = 25.6 K/Jy by a factory η, is the full gain of FAST in the sky coverage, η is the aperture efficiency58.

Polarization calibration

The original data files are processed using DSPSR59 and PSRCHIVE56, with each file folded over its own duration to extract four time series corresponding to the recorded Stokes parameters. These are denoted as \({I}_{1}^{2}\), \({I}_{2}^{2}\), CR, and CI60, where CR and CI represent the real and imaginary components of the complex product I1*I2. In practical observations, the feed systems are seldom ideal, and two main instrumental effects relative gain imbalance (often referred to as leakage) and channel phase offset must be accounted for through calibration. The observed and calibrated Stokes vectors are indicated by the subscript o and c respectively, are typically related via the system s Mueller matrix61,62. Thus we have,

$$\begin{array}{r}{S}_{o}={{{\mathcal{M}}}}\times {S}_{c}=\left[\begin{array}{cccc}1&f&0&0\\ f&0&0&0\\ 0&0&cos2\delta &-sin2\delta \\ 0&0&sin2\delta &cos2\delta \end{array}\right]\times {S}_{c}\end{array}$$
(4)

where \({\prime}\) means the injected reference signal, and the leakage \(f=\frac{{Q}_{o}^{{\prime} }}{{I}_{o}^{{\prime} }}\). We calibrated the phase error as \({\delta }^{{\prime} }=\frac{1}{2}\arctan \frac{{V}_{o}^{{\prime} }}{{U}_{o}^{{\prime} }}\), then removing the error from orientation, we can get the calibrated values of the four Stokes parameters:

$$\begin{array}{rcl}{I}_{c}&=&\frac{{I}_{o}\, -\, f \,*\, {Q}_{o}}{1\, -\, {f}^{2}}\hfill \\ {Q}_{c}&=&\frac{{Q}_{o}\, -\, f \,*\, {I}_{o}}{1\, -\, {f}^{2}}\hfill \\ {U}_{c}&=&P\cos 2\delta \cos 2{\delta }^{{\prime} }+P\sin 2\delta \sin 2{\delta }^{{\prime} }\hfill \\ {V}_{c}&=&P\sin 2\delta \cos 2{\delta }^{{\prime} }+P\cos 2\delta \sin 2{\delta }^{{\prime} },\end{array}$$
(5)

where \(P=\sqrt{{U}_{o}^{2}+{V}_{o}^{2}}\). Finally, the degrees of linear and circular polarization, and polarization position angle are calculated as

$$LP=\frac{\sqrt{{Q}^{2}+{U}^{2}}}{I},\quad CP=\frac{V}{I},\quad PA=\frac{1}{2}\arctan \frac{U}{Q}$$
(6)

Periodicity studies

The main aim of the timing analysis here is to search for the quasi-periodic oscillations (QPOs) ranging from  ~1−100  s in the light curves of both radio flux density and polarization parameters. QPOs are generally studied in the Fourier ___domain and show up in the power density spectrum as narrow peaks. We used Numpy.fft.fft and Stingray in Python packages to perform the power density spectrum (PDS) analysis, including the production and fitting of the PDS.

The PDS calculated with the packages mentioned above is the Fourier transform of the light curve and is unnormalized. In X-ray observations, such PDS need to be normalized so that the evolution of the QPO can be studied by computing some physical quantities such as the QPO factor for observations of the same QPO but in different equipments. However, unlike the photon number distribution in X-ray observations, the flux density observed in the radio band is highly related to instrument response, system noise, and so on. In order to facilitate the adjustment of fitting parameters and the generation of dynamic PDS, the following procedures are performed: when computing the PDS, we treat the flux density in the radio band as the number of photons in X-ray observations, and then normalize the PDS with the Leahy and rms normalizations. When computing the dynamic PDS, we divide the light curve into segments of 200 s duration and calculate the PDS independently for each segment. To minimize the inaccuracy caused by such crude segmentation and the distortion to the light curve structures, each segment is shifted in 80 s steps.

Wavelet analysis is a valuable approach for analyzing time series having a wide range of timescales or variations which would decompose the time series into time-frequency space, so that we can check both the dominant modes of variability and how those modes vary in time63. In reality, wavelet analysis would also perform the FFT of time series. Unlike traditional FFT for PDS, wavelet analysis would use wavelet functions with different time and amplitude scales for further analysis; however, the most important feature of wavelet analysis is that it would assume a background noise at different scales, which would be useful for calculating the 95% confidence contour. Meanwhile, the shortcomings of dynamic PDS which are inevitable would not appear in wavelet analysis. But the mother wavelet utilized in analyzing processing might have a considerable impact on the end outcome, such as how ‘Morlet’ provides better temporal localization, whereas ‘Paul’ provides better frequency localization. Wavelet analysis, however, has been applied to the timing analysis of X-ray light curves in some X-ray binaries64,65.

For wavelet analysis in our data, we have used the ‘Morlet’ wavelet function for analysis and taken red noise into account in wavelet analysis by calculating the correlation functions of the time series. A simple model to compute red noise is the univariate lag-1 autoregressive process, so that we estimate the red noise from \(({\alpha }_{1}+\sqrt{{\alpha }_{2}})/2\), where α1 and α2 are the lag-1 and lag-2 autocorrelations of the time series. On the other hand, the wavelet analysis would also give the significance levels of the power spectrum based on the red noise model63. In our results (see Fig. 4), the regions enclosed by black solid curves and colored with blue denote the promising signals whose confidence levels are higher than 95%. The result of wavelet analysis would clearly show the evolution of periodic signals both in the time and frequency domains.

At first, we calculated the power density spectrum for every two hundred seconds data set of the calibrated flux time series, checking the possible periodic signals in the PDS, then we arranged them in chronological order to get a set of spectra which is called the dynamical power spectrum (see Fig. 1 for the whole observational time series on January 25 2021). For the most observational time regimes, there are no periodic signals detected in the dynamical PDS, while only for the time interval from 2700−3100 s when the flux density was still increasing near to the peak, there existed the multiple periodic signals at 17 and 33 s. We also presented the average power density spectrum of the calibrated flux density light curve (see the PDSs in Fig. 3) from the observed time interval from 2400 s to 3200 s. The periodic peaks around 17 and 33 s have significance levels higher than 5σ based on the light curve simulation algorithm66, in which we have simulated 20000 light curves with power-law distributed noises appropriate for our data and re-sampled these light curves to ensure the resolution that matched our observation data.

In Fig. 3, we also present the PDSs for the light curves of three polarization parameters (LP, CP and PA). The LP light curve shows similar variation patterns of the flux density and has significant QPO signals at the periods of 17 and 33 s  (> 5σ). The CP and PA light curves exhibit very weak QPO signals, with periods of ~50 s, 30 s, and 20 s for CP, and 40 s, 30 s, and 15 s for PA. All possible PDS peaks detected in both CP and PA have low significance levels (below or around 3σ). Therefore, the light curve of LP shows similar variation patterns with that of flux density. The CP and PA curves would have similar variation patterns, but are quite different from the curves of both flux density and LP.

Then, wavelet analysis for flux and polarization parameters has also been conducted. The results are shown in Fig. 4, in which the light-yellow regions and the red dashed curves mark the ’cone of influence’ due to edges effects, the blue regions enclosed by red solid curves suggest the existence of promising signals with their confidence levels are higher than 95 %. Meanwhile, the blue dash-dotted horizontal lines in Fig. 4 represent the positions of the two periodic signals for flux and LP light curves (17 and 33 s) in the wavelet analysis results. For a more profound comprehension of the wavelet results as shown in Fig. 4, one may regard Fig. 4 as results of dynamic PDS calculated by FFT, with abscissa and ordinate indicating the time and period (frequency) domains. The reason of selecting wavelet for timing analysis stems from its ability to dynamically adapt the scale of the mother wavelet according to the local features of the signal. In contrast to traditional FFT, the wavelet analysis method can effectively avoid the negative impact of signal discontinuity caused by truncation, enabling a more accurate and flexible reflection depiction of the signal’s instantaneous features and abrupt changes. In our wavelet results, the high time-resolution power density with time shows more details of the variations for these periodic oscillation signals. The strongest period modulation of 33 s appeared near 2760 s in both total flux density and LP light curves, but could not be seen at 3050 s. The signal at 17 s is relatively weak and has similar time intervals to the 33 s signal. The light curve of CP shows the strong periodic signal at  ~50 s from 2600 s–2800 s, while has a possible 25 s period from 2800 s to 2900 s. And PA also shows the periodic signal around 40–50 s from 2800 s to 2900 s.

Correlation analysis

The light curves in the Figure 2 clearly illustrate an anti-correlated relationship between flux density and linear polarization during the oscillation stage: the peaks of the flux always correspond to the valleys of the LP. We use linear regression analysis on flux density and linear polarization to confirm this anti-correlation.

Pearson correlation coefficient (PCC) is the best method for measuring the magnitude of the linear association between variables since it is based on the utilization of covariance and is defined as:

$$\begin{array}{l}{\rho }_{X,Y}=\frac{cov(X,Y)}{{\sigma }_{X}{\sigma }_{Y}},\end{array}$$
(7)

where ρX,Y is the PCC and on or between  −1 and  +  1, and σX and σY are the standard deviations of X and Y, respectively. Since cov(X, Y) is the covariance of variable X and Y, so the formula of PCC can be written as:

$$\begin{array}{l}{\rho }_{X,Y}=\frac{{\mathbb{E}}[(X\, -\, {\mu }_{X})(Y\, -\, {\mu }_{Y})]}{{\sigma }_{X}{\sigma }_{Y}}\end{array}$$
(8)

We used the Seaborn and SciPy.stats in Python package to do the linear regression analysis and the PCC calculation. In addition, we performed the linear fitting for the relationship between the flux and LP from the duration of  ~2700–3100 s, as shown in Fig. 5. An apparent anti-correlated relationship is observed between flux density and LP, with the Pearson correlation coefficient of −0.795 and a slope of −0.04, when the flux and LP have similar QPO periods. Meanwhile, the PCCs between the flux density and other polarization parameters were also determined, which are smaller than ∣ −0.25∣ or even smaller, denoting a weak or no relation between these parameters. In addition, before 2700 s or after 3100 s, the variations of the flux and LP have no significant correlation with each other (e.g., PCC <  ∣ −0.2∣) when they show no periodic oscillations (see Fig. 6).