Introduction

Realizing universal, fault-tolerant quantum computation is a long sought-after objective. Measurement-based quantum computation offers a possible path toward more rapid scaling of computational resources to achieve this aim1,2,3. This paradigm relies on a class of entangled states known as graph states, of which linear cluster states and GHZ states (locally equivalent to star graph states) are prominent examples4,5. In this regard, photonic graph states are ideal candidates due to their limited sensitivity to decoherence6.

Photonic graph states were first generated using linear optics gates7,8 and parametric down-conversion sources9, but these approaches have severe scaling limitations inherent to the probabilistic nature of the gates and sources. Recently, better scaling was obtained using efficient deterministic single-photon sources based on semiconductor quantum dots (QDs)10,11,12. However, the most efficient way to generate such graph states relies on deterministic entanglement mediated by the spin of a quantum emitter13,14. Such schemes have recently been demonstrated in the optical ___domain with trapped atoms and QDs15,16,17,18,19,20,21, and in the microwave ___domain with superconducting qubits22,23. In this regard, QD deterministic sources of graph states are highly promising because they offer emission in the optical ___domain for long-distance propagation, solid-state integration, and record single photon generation rates24,25,26. However, to date, only limited topology of entanglement has been generated18,19,20,21, without at-will reconfigurability.

In this work, we demonstrate the generation of 4-partite entanglement with arbitrary topology by producing a class of entangled graph states called caterpillar graph states27. These states are the most general type of graph state that can be generated with a single emitter and include linear cluster, GHZ, and redundantly encoded linear cluster states. Moreover, these caterpillar states can be used for efficient fusion operations, which are crucial for generating multi-dimensional graph states and implementing quantum error correction protocols3,28. We achieve this result using an optical method that provides full control of the spin state of a single electron trapped in a QD while retaining compatibility with the entanglement generation scheme14. In addition, we demonstrate that our protocol allows for on-demand reconfigurability of the entanglement generation.

Results

Controllable platform for spin-photon entanglement

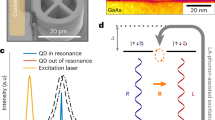
Our platform for generating graph states is based on spin-photon entanglement using an InGaAs semiconductor QD in an optical cavity, as shown in Fig. 1a. The QD is deterministically embedded in the center of a micropillar cavity using the in-situ lithography technique29. The QD-cavity coupling provides a significant and unpolarized Purcell enhancement of the single photon emission, with a corresponding photon radiative lifetime of 200 ps, as well as a high collection efficiency. The cavity is electrically contacted, allowing us to apply an electrical bias to tune the QD energy24.

Fig. 1: Complete spin control for versatile spin-photon entanglement.
figure 1

a Scanning electron micrograph of an electrically contacted QD-micropillar cavity device and a schematic representation of entanglement between QD spin and emitted photons. b Optical selection rules of a negatively charged QD under a small (< 100 mT) transverse magnetic field \({\overrightarrow{B}}_{y}\). LA-phonon assisted excitation is used to excite the QD with a blue detuning of 0.8 nm. The fast (4ps), red-detuned and circularly polarized optical spin rotation pulse (OSRP) induces an AC Stark shift that imprints a phase shift between the \(\left\vert {\uparrow }_{z}\right\rangle\) and \(\left\vert {\downarrow }_{z}\right\rangle\) states, which is equivalent to a coherent rotation about the z-axis. c Spin projection along the z-axis (Sz) as a function of time (and equivalent rotation angle θ), illustrating the coherent Larmor precession undergone by the electron spin for B = 60 mT. d (Left) Spin projection Sz as a function of OSRP power (and equivalent rotation angle φ), demonstrating rotation of the electron spin about the z-axis. The 3-pulse sequence (inset) used to measure Sz is composed of two excitation pulses (labeled LA) and one OSRP with variable power. Error bars are derived from Poissonian statistics. (Right) Equivalent quantum circuit diagram, which features the unitary gate U(θ, φ), we can perform by combining Larmor precession and OSRP. e Representation of spin control in the Bloch sphere. Starting from a measurement of a photon in the R polarization basis, which heralds the spin state in up \({\left\vert \! \uparrow \right\rangle }_{z}\) (marked 0), a 60 mT transverse magnetic field induces a Larmor precession in the xz-plane. After an arbitrary rotation by angle θ, an OSRP rotates the spin about the z-axis with an angle φ.

Full size image

A single electron is trapped in the QD, serving as a host spin that can be optically addressed. For such a charged QD, the two excited states are trion transitions consisting of two electrons and one hole (\(\left\vert \! \uparrow \downarrow \Uparrow \right\rangle\) or \(\left\vert \! \uparrow \downarrow \Downarrow \right\rangle\)). The optical selection rules for this system (depicted in Fig. 1b) couple the spin of the electron in the ground state, either \(\left\vert \! \uparrow \right\rangle\) or \(\left\vert \! \downarrow \right\rangle\), to the polarization of the emitted photon, circular right (R) or circular left (L), respectively. In this work, we make use of these optical selection rules to successively entangle the polarization degree of freedom of emitted photons with the state of the single spin.

To take advantage of the mapping between the spin state and photon polarization, we use longitudinal-acoustic (LA) phonon-assisted excitation. Laser pulses that are blue-detuned from the QD transition by approximately 0.8 nm populate the trion state. This gives us high occupation probability, high photon indistinguishability30, and access to the polarization degree of freedom of the emitted photons31, as opposed to the resonant excitation scheme24.

In order to fully harness the spin-photon interface for versatile entangled state generation, we require multi-axis control over the electron spin state in the Bloch sphere. We use a 60 mT external magnetic field, along the y-direction, perpendicular to the growth direction z. This enables the coherent Larmor precession of the electron spin about the y-axis, effectively implementing the rotation gate Ry(θ), where θ represents the rotation angle. We measure the Larmor precession using polarization-resolved time-correlations by exciting the QD with a linearly-polarized continuous wave laser and monitoring the evolution over time of the spin projection along the z-axis Sz. This is accomplished with a two-photon correlation measurement. The detection of the first photon in the R polarization basis heralds the spin in the \(\left\vert \! \uparrow \right\rangle\) state, due to the optical selection rules. We then measure the polarization of the second emitted photon as a function of time (or equivalently, as a function of the rotation angle θ) to quantify the spin projection along the z-axis, defined as \({S}_{z}=\frac{{I}_{R} \, - \, {I}_{L}}{{I}_{R}+{I}_{L}}\), where IR (IL) are the conditional detection counts in R (L) polarization. The observed oscillations evidence a Larmor period of  ≈ 1.85 ns and are damped by the electron coherence time of approximately 2 ns, as shown in Fig. 1c.

For additional control over the spin, we use a fast (4 ps) optical spin rotation pulse (OSRP) to deterministically rotate the electron spin about the optical z-axis32,33,34,35. It consists of a circularly-left polarized, red-detuned (Δ = 1.2 nm) laser pulse that couples to one of the two trion transitions. This induces an AC Stark shift (represented in Fig. 1b) and leads to a rotation in the xy-plane of the Bloch sphere for the duration of the pulse. This rotation is described by the gate Rz(φ), where φ depends on the OSRP power. We measure this rotation using a three-pulse sequence, sketched in the inset of Fig. 1d. The first linearly-polarized pulse is used to excite the QD, with photon detection in R again, heralding the spin in the \(\left\vert \! \uparrow \right\rangle\) state. We then let the spin precess about the magnetic field axis for a time corresponding to the precession θ = π/4. Following this, we apply an OSRP with variable power. After another θ = π/4 precession, we then finally measure the spin projection Sz through a polarization measurement of the second emitted photon, which is obtained using an additional linearly-polarized excitation pulse. The entire sequence is summarized as a quantum circuit in Fig. 1d (right), where we define a unitary gate U(θ, φ) = Ry(θ/2)Rz(φ)Ry(θ/2). We find Sz to oscillate as a function of the OSRP power (see Fig. 1d, left), indicating control over the spin about the z-axis.

By combining the Ry(θ) and Rz(φ) rotation gates, controlled by the external magnetic field and the OSRP, respectively, we demonstrate full control over the spin within the Bloch sphere, as depicted in Fig. 1e. This allows the implementation of arbitrary quantum gates, which we use to generate various spin-photon graph states in the following section.

Versatile graph state generation

To generate 4-partite spin-photon entanglement we use four linearly-polarized excitation pulses with equal delays t = 600 ps between them, leading to the emission of four successive photons, as sketched in Fig. 2a. The time t between pulses is set to match a quarter of the spin precession period for a 60 mT magnetic field, while accounting for spontaneous emission time that effectively delays the spin precession. This ensures the spin undergoes an effective Ry(π/2) rotation during that time. The 60 mT magnetic field amplitude is chosen so that the spin undergoes multiple π/2 precession periods within its coherence time, while still mostly preserving circular optical selection rules. In addition, this field amplitude sets the π/2 precession time to exceed the spontaneous emission time, thereby preventing significant degradation of the state fidelity. Because the ≈ 2 ns spin coherence time of the spin is significantly smaller than the 12 ns repetition period of our scheme, we assume the spin begins the sequence in a mixed state with equal probability of \(\left\vert \! \uparrow \right\rangle\) and \(\left\vert \! \downarrow \right\rangle\). The first emitted photon is measured in the R (L) polarization basis, heralding the spin state in \(\left\vert \! \uparrow \right\rangle\) (\(\left\vert \! \downarrow \right\rangle\)). After a time t, in the absence of decoherence, the spin is in the superposition state \(\frac{1}{\sqrt{2}}\left(\! \pm \left\vert \! \uparrow \right\rangle+\left\vert \! \downarrow \right\rangle \right)\), where the sign depends on the spin heralding. The photon emission triggered by laser pulse #2 then leaves the system in the spin-photon entangled state \(\left\vert {{{\Psi }}}_{2}\right\rangle=\frac{1}{\sqrt{2}}\left(\pm \left\vert {R}_{2},\uparrow \right\rangle+\left\vert {L}_{2},\downarrow \right\rangle \right)\), assuming an instantaneous photon emission lifetime. The indices refer to the order of photon emission (i.e., R2 refers to photon #2). We now apply two unitary gates, U(θ1, φ1) and U(θ2, φ2), acting on the spin, and each followed by an excitation pulse that leads to photon emission #3 and #4. By controlling θ1,2 and φ1,2 through adjustments in the time delay between the excitation pulses and the OSRP power, we generate various 4-partite spin-photon entangled graph states. Fig. 2a illustrates the experimental sequence and the corresponding quantum circuit diagram.

Fig. 2: Reconfigurable generation of caterpillar graph states.
figure 2

a Optical excitation sequence and corresponding quantum circuit diagram used to generate an arbitrary 4-partite caterpillar graph state. The labeled numbers in the circuit denote the order of photon emission. The first and last emitted photons allow for initialization and readout of the spin state, respectively. The Larmor precession of the spin acts as a Ry(θ) gate, while the OSRP serves as an Rz(φ) gate, together forming an unitary gate U(θ, φ). b 4-partite spin-photon linear cluster state generated with θ1,2 = 0 and φ1,2 = 0, along with the measured real part (see imaginary part in Supplementary Fig. 1) of the density matrix of photon pair #2 and #3, conditioned on photons #1 and #4 being measured in R/R (top left), R/L (top right), L/R (bottom right) or L/L (bottom left). c–e Graph representation, unitary gate parameters (θ1,2 and φ1,2), and corresponding real part (see imaginary part in Supplementary Fig. 1) of the two-photon density matrix, conditioned on photons #1 and #4 being measured in R/R (top) or R/L (bottom), for multiple 4-partite states generated by this protocol: GHZ state (c), linear cluster states with redundant encoding between photons #2 and #3 (d) and linear cluster states with redundant encoding between photons #3 and #4 (e). f Measured (symbols) and simulated (solid line) visibility \({{{{\mathcal{V}}}}}\) of four-photon correlations as a function of the angle φ2 of the second unitary gate in the sequence, demonstrating continuous variation in the generated state. Error bars are derived from Poissonian statistics. The states corresponding to points (A), (B), and (C) are defined in the main text. The simulated sinusoidal fit is obtained using model parameters extracted from fitting the two-photon density matrices of (b–e).

Full size image

For θ1,2 = π/2 and φ1,2 = 0, i.e., with no OSRP as in refs. 18,19,20, we generate a state locally equivalent to a four-qubit linear cluster (4LC) state (see Supplementary Note 1 for detailed calculations),

$$\left\vert {{{\Psi }}}_{4-{\mbox{LC}}}\right\rangle=\frac{1}{2}(\left\vert {\mp }_{2},{R}_{3}\right\rangle -\left\vert {\pm }_{2},{L}_{3}\right\rangle )\left\vert {R}_{4}\right\rangle \left\vert \uparrow \right\rangle \\+(\left\vert {\mp }_{2},{R}_{3}\right\rangle+\left\vert {\pm }_{2},{L}_{3}\right\rangle )\left\vert {L}_{4}\right\rangle \left\vert \downarrow \right\rangle$$
(1)

where \(\left\vert \!+\! \right\rangle\) and \(\left\vert -\right\rangle\) are respectively defined as \(\left\vert \!+\! \right\rangle=\frac{1}{\sqrt{2}}\left(\left\vert R\right\rangle+\left\vert L\right\rangle \right)\) and \(\left\vert -\right\rangle=\frac{1}{\sqrt{2}}\left(\left\vert R\right\rangle -\left\vert L\right\rangle \right)\).

We then disentangle the spin from the photonic chain to minimize additional decoherence. This is done by measuring the last emitted photon in the R/L polarization basis, as its polarization state is directly mapped to the spin state. This ideally leaves the system in one of the four fully photonic entangled Bell states, depending on the polarization state measured for the first and last photon:

$${\left\vert {\tilde{\phi }}_{\pm }\right\rangle }_{R}=\frac{1}{\sqrt{2}}\left(\left\vert \! -,{R}_{3}\right\rangle \pm \left\vert \! {+}_{\!2},{L}_{3}\right\rangle \right)\\ {\left\vert {\tilde{\psi }}_{\pm }\right\rangle }_{L}=\frac{1}{\sqrt{2}}\left(\left\vert \! {+}_{2},{R}_{3}\right\rangle \pm \left\vert {-}_{2},{L}_{3}\right\rangle \right)$$

where the indices indicate the first photon polarization measurement outcome. Fig. 2b presents the measured polarization density matrices of the photon pair conditioned on the measure of the first and last photon in the R/L basis. We find fidelities \({F}_{{\tilde{\phi }}_{+}}=0.78\pm 0.04\), \({F}_{{\tilde{\phi }}_{-}}=0.69\pm 0.02\), \({F}_{{\tilde{\psi }}_{+}}=0.80\pm 0.04\) and \({F}_{{\tilde{\psi }}_{-}}=0.73\pm 0.01\) to the ideal corresponding Bell states, and concurrences \({C}_{{\tilde{\phi }}_{+}}=0.69\pm 0.09\), \({C}_{{\tilde{\phi }}_{-}}=0.44\pm 0.05\), \({C}_{{\tilde{\psi }}_{-}}=0.65\pm 0.08\) and \({C}_{{\tilde{\psi }}_{+}}=0.49\pm 0.03\). The variations in concurrence and fidelity are likely due to a small polarized Purcell effect, which leads to a residual (≈ 4%) polarized single photon emission. Uncertainties are obtained assuming a shot noise limited error on the total number of 4-photon coincidences. Both the fidelity and concurrence are fundamentally limited by the spin coherence time of  ≈ 2 ns, as well as the 200 ps trion radiative lifetime. The latter limitation is caused by the spontaneous emission time jitter interrupting the spin evolution, resulting in an effective emission-induced spin dephasing. This jitter is minimized when the trion g-factor is much smaller than the electron g-factor36. We thus chose a 60 mT magnetic field, corresponding to a 600 ps π/2 precession period, to compromise between emission-induced and nuclear-induced spin dephasing. A shorter trion radiative lifetime can further mitigate this issue by reducing the emission jitter on the spin gate. Nonetheless, to the best of our knowledge, this is the highest reported fidelity for an entangled pair within a multipartite QD spin-photon cluster state20. Additionally, by using a numerical model to simulate these measurements, we can evaluate all the relevant parameters of our experiment (summed up in Supplementary Table 1) and then estimate a fidelity for the 4-partite linear cluster state. Our model exploits the zero-photon-generator method37, allowing direct access to the conditional polarization photon coincidences of the 4-partite state without requiring the computation of multi-time integrated correlation functions. Due to spin decoherence, the state fidelity degrades over time, and we thus chose to evaluate it at 600 ps after the final excitation pulse, as it corresponds to one more π/2-rotation of the spin. We find \({F}_{4}^{sim}=0.66\pm 0.05\). We note that for our experimental parameters, we estimate an upper bound on the 4-partite fidelity of 0.79, due only to the emission-induced spin dephasing. This upper bound increases to 0.95 for a trion lifetime of 50 ps, which can be achieved using a micropillar cavity with a Purcell factor of around 24. From our simulations, we predict that this improvement would bring the 4-partite fidelity to 0.73, then primarily limited by electron-nuclear interactions. More details about the simulation model can be found in Supplementary Note 4.

Another class of entangled states that are fundamental resources for photonic quantum computing are the so-called GHZ states4, locally equivalent to star graph states. With our protocol, GHZ states are generated by setting θ1,2 = π/2 and φ1,2 = π. In this configuration, the unitary gate U(θ, φ) becomes a Z gate, which fully flips the spin about the z-axis by the time the following photon is emitted. This leads to the generation of a 4-partite GHZ state (in the following, we only consider the heralded \(\left\vert \! \uparrow \right\rangle\) case) :

$$\left\vert {{{\Psi }}}_{4-{\mbox{GHZ}}}\right\rangle=\frac{1}{\sqrt{2}}\left(\left\vert {R}_{2},{R}_{3},{R}_{4}\right\rangle \left\vert \! \uparrow \right\rangle+\left\vert {L}_{2},{L}_{3},{L}_{4}\right\rangle \left\vert \\ \! \downarrow \right\rangle \right)$$
(2)

Now, when measuring the last photon in the R/L basis to disentangle the spin, the remaining photon pair is projected onto a fully separable state, \(\left\vert {R}_{2},{R}_{3}\right\rangle\) or \(\left\vert {L}_{2},{L}_{3}\right\rangle\). The measured density matrices for these two states, obtained through 4-photon correlations, are shown in Fig. 2c. We find a fidelity to the ideal state of 0.71 ± 0.02 and 0.68 ± 0.02, respectively. The 4-partite GHZ state fidelity is estimated to be \({F}_{4}^{sim}=0.45\pm 0.05\). This reduced fidelity compared to the linear cluster state is primarily attributed to optically induced dephasing from the OSRP.

It is worth noting that these GHZ states can be generated without using OSRP (φ = 0) by letting the spin undergo a θ = 2π (or π for a locally equivalent state) precession between excitation pulses. However, this approach increases the spin precession time, which leads to a reduced state fidelity due to the limited spin coherence time. Optical spin control circumvents this problem as we can use arbitrary time delays between successive excitation pulses, limited only by the photon radiative lifetime. In the following, we continue to use a 600 ps delay as it provides an optimal working point with an overlap between successive photons of only 5%.

When now setting θ1,2 = π/2, φ1 = π, and φ2 = 0, we generate a redundantly encoded linear cluster state (RLC). Redundantly encoded qubits are crucial resources for quantum computation, as they can be used to perform efficient fusion operations with a higher success rate than ancilla-assisted fusions28,38,39. We represent these redundantly encoded states as a horizontal chain of qubits while the redundancy is introduced by attaching additional qubits vertically, thus creating a state locally equivalent to a caterpillar graph state (see Supplementary Note 2), as represented in Fig. 2d. More specifically, the generated state is a 4-partite linear cluster state with photon #2 and #3 being redundantly encoded:

$$\vert {\psi }_{4-{\mbox{RLC}}1}\rangle=\frac{1}{2}\left(\right.(\vert {R}_{2},{R}_{3}\rangle+\vert {L}_{2},{L}_{3}\rangle )\vert {R}_{4}\rangle \vert \! \uparrow \rangle \\+(\vert {R}_{2},{R}_{3}\rangle -\vert {L}_{2},{L}_{3}\rangle )\vert {L}_{4}\rangle \vert \! \downarrow \rangle \left)\right.$$
(3)

One can see that for this state, when disentangling the spin by measuring the last photon in the R/L basis, we are left with a photonic Bell state of the form:

$$\left\vert {\phi }_{\pm }\right\rangle=\frac{1}{\sqrt{2}}\left(\left\vert {R}_{2},{R}_{3}\right\rangle \pm \left\vert {L}_{2},{L}_{3}\right\rangle \right)$$

The measured density matrix corresponding to \(\left\vert {\phi }_{+}\right\rangle\) and \(\left\vert {\phi }_{-}\right\rangle\) are shown in Fig. 2d. We find a fidelity to the target Bell state of 0.58 ± 0.03 and 0.61 ± 0.02 and a concurrence of 0.41 ± 0.06 and 0.45 ± 0.04, respectively, while the 4-partite entanglement is estimated to be \({F}_{4}^{sim}=0.53\pm 0.05\).

We finally generate yet another redundantly encoded 4-partite linear cluster by setting θ1,2 = π/2, φ1 = 0, and φ1 = π. This yields the state:

$$\left\vert {\psi }_{4-{\mbox{RLC}}2}\right\rangle=\frac{1}{\sqrt{2}}\left(-\left\vert {-}_{2},{R}_{3}\right\rangle \left\vert {R}_{4}\right\rangle \left\vert \! \uparrow \! \right\rangle+\left\vert {+}_{2},{L}_{3}\right\rangle \left\vert {L}_{4}\right\rangle \left\vert \! \downarrow \right\rangle \right)$$
(4)

for which now photon #3 and #4 are redundantly encoded. When disentangling the spin by measuring the last photon in R or L, we are now left with a separable state \(\left\vert {-}_{2},{R}_{3}\right\rangle\) or \(\left\vert \! {+}_{2},{L}_{3}\right\rangle\). The measured density matrices for these two states are shown in Fig. 2e, for which we extract a fidelity to the ideal two-photon state of 0.67 ± 0.02 and 0.66 ± 0.02 and a simulated 4-partite fidelity of \({F}_{4}^{sim}=0.53\pm 0.05\). All the experimental data are reproduced using our simulation model, and are shown in Supplementary Note 4 along with a summary table that details all measured and simulated fidelities (Supplementary Table 2). We find that our simulations show excellent agreement with the experimental results, with an average absolute difference of only 3 ± 2%.

As a final illustration of the versatility of our approach, we now fix θ1 = π/2, θ2 = π, φ1 = π, and we scan φ2 between 0 and 3π. By doing so, we continuously change the output 4-partite spin-photon entangled state. In order to quantify this effect, we measure oscillations in the visibility \({{{{\mathcal{V}}}}}\) defined as :

$${{{{\mathcal{V}}}}}=\frac{{C}_{{R}_{1}{R}_{2}{R}_{3}{R}_{4}}+{C}_{{R}_{1}{L}_{2}{L}_{3}{L}_{4}}-{C}_{{R}_{1}{R}_{2}{R}_{3}{L}_{4}}-{C}_{{R}_{1}{L}_{2}{L}_{3}{R}_{4}}}{{C}_{{R}_{1}{R}_{2}{R}_{3}{R}_{4}}+{C}_{{R}_{1}{L}_{2}{L}_{3}{L}_{4}}+{C}_{{R}_{1}{R}_{2}{R}_{3}{L}_{4}}+{C}_{{R}_{1}{L}_{2}{L}_{3}{R}_{4}}}$$

where \({C}_{{R}_{1}{R}_{2}{R}_{3}{R}_{4}}\), \({C}_{{R}_{1}{L}_{2}{L}_{3}{L}_{4}}\), \({C}_{{R}_{1}{R}_{2}{R}_{3}{L}_{4}}\), and \({C}_{{R}_{1}{L}_{2}{L}_{3}{R}_{4}}\) are four-photon coincidences measured in the R or L polarization basis. When φ2 is set to zero, we ideally generate the state (A) = \(\frac{1}{\sqrt{2}}\left(-\left\vert {R}_{2},{R}_{3},{L}_{4}\right\rangle \left\vert \! \uparrow \right\rangle+\left\vert {L}_{2},{L}_{3},{R}_{4}\right\rangle \left\vert \! \downarrow \right\rangle \right)\), which corresponds to \({{{{\mathcal{V}}}}}\) = − 1. The polarization of the last photon is inverted relative to the GHZ state defined in Eq (2), as the spin undergoes a π precession between the last two excitation pulses. At a rotation angle φ2 = π/2, we obtain the state (B) = \(-i(\left\vert {R}_{2},{R}_{3}\right\rangle+\left\vert {L}_{2},{L}_{3}\right\rangle )\left\vert {R}_{4}\right\rangle \left\vert \! \uparrow \right\rangle -(\left\vert {R}_{2},{R}_{3}\right\rangle -\left\vert {L}_{2},{L}_{3}\right\rangle )\left\vert {L}_{4}\right\rangle \left\vert \! \downarrow \right\rangle\), for which \({{{{\mathcal{V}}}}}=0\). Finally, when φ2 reaches π, it fully flips the spin about the z-axis, and we recover the GHZ state (C) defined in Eq (2) (\({{{{\mathcal{V}}}}}\) = + 1). Fig. 2f presents both the measured and simulated visibility \({{{{\mathcal{V}}}}}\) as a function of OSRP angle φ2. We find \({{{{\mathcal{V}}}}}\) to oscillate as described above, demonstrating continuous control over the state. The simulation, performed using parameters obtained from fitting the two-photon density matrices of Fig. 2b–e, shows good agreement with the experimental data, further validating our model. We attribute the reduced amplitude visibility from −0.6 to 0.6 to spin decoherence and the imperfect spin rotation gate fidelity of 0.87 ± 0.05, which we extract from our simulation model.

The protocol described in this work can be extended to generate fully photonic caterpillar graph states of arbitrary topology. Figure 3 shows an example of a 10-photon caterpillar graph state, along with the pulse sequence that combines excitation pulses and OSRPs. The time interval between excitation pulses corresponds to a Ry(π/2) rotation of the spin, ensuring that each photon emitted following only a Ry(π/2) gate is encoded as a new node of the caterpillar graph state. However, applying an OSRP with φ = π between consecutive excitation pulses effectively performs a Z gate, causing the newly emitted photon to be redundantly encoded with the previous one. This creates highly redundant nodes that locally resemble GHZ or star graphs, within the caterpillar graph state.

Fig. 3: Near-future example of all-photonic arbitrary caterpillar graph state generation.
figure 3

Pulse sequence combining excitation pulses (LA) and OSRP (φ = π, equivalent to a Z spin gate) for the generation of an all-photonic arbitrary caterpillar graph state that can be generated with our protocol. Each photon emitted following a Ry(π/2) gate will be encoded in a new node of the caterpillar graph state, whereas photons emitted after a Z gate will be redundantly encoded with the previous one, within the same node. The simulated fidelity of this state is estimated to be 0.80 ± 0.01 using a realistic near-term positive trion source whose parameters are described in Supplementary Fig. 5b.

Full size image

Discussion

In this work, we demonstrated a versatile approach to the on-demand generation of multipartite entangled states consisting of a solid-state spin and single photons. We have shown that with an optical pulse, we can rotate the spin to continuously vary the type of entangled state that we produce. With this approach, we report for the first time with a solid-state spin the versatile generation of 4-partite linear cluster states, GHZ states, and redundantly-encoded cluster states with two-photon entanglement fidelities of up to 0.80. Notably, the emitted photons maintain high indistinguishability (M > 82%, see Supplementary Fig. 2) across all protocols described in this work. This is a crucial requirement for generating higher-dimensional graph states using fusion operations38. Indeed, photon distinguishability induces a fusion measurement error with probability (1 − M)/2, which remains below 10% for our system. Owing to the inherent qubit redundancy of the caterpillar graph generation scheme, we can combine these fusion operations with a repetition code to further mitigate logical fusion measurement errors (below 3% and 1% with respectively 3 and 5 successful fusion operations)40. In addition, using a semiconductor source of indistinguishable single photons in a weak magnetic field makes this approach compatible with commercial integration to obtain a plug-and-play source of multiphoton entanglement41,42 with, for instance, a permanent magnet in a compact cryostat43.

We do acknowledge several areas for improvement. In particular, the device used does not show the state-of-the-art brightness that has been achieved by an InGaAs QD-cavity platform26. Improved Purcell enhancement will allow for more photon emission during the spin coherence time and improve fidelity owing to the reduced trion excited state lifetime. We could also extend the coherence time of the spin through the use of a hole spin31, or well-documented nuclear spin cooling44,45,46,47 and dynamical decoupling techniques48,49.

With realistic near-term improvements to the source - specifically a positive trion with a 100 ps radiative lifetime - and improved spin rotation gate fidelity (0.995), our simulation model predicts the generation of entangled states with up to 30 photons (see Supplementary Fig. 5). Notably, the entanglement fidelity remains above 80% for the 10-photon caterpillar graph state shown in Fig. 3, which represents a realistic aim for the near future.

The building blocks of the caterpillar state generation demonstrated in this work have direct implications for scalable quantum architectures. For instance, in the fusion-based quantum computation framework, a 14-photon caterpillar state source could enable the efficient production of 24-photon Shor-encoded (2,2) 6-ring resource states50. This approach significantly reduces the number of required sources while relaxing loss tolerance constraints in fusion and switch networks. Furthermore, the techniques developed here are essential for remote spin-spin entanglement protocols within the spin-optical quantum computing (SPOQC) architecture40,51,52. As a result, the versatility of our method paves the way for generating more complex entanglement resources, offering a promising path towards practical fault-tolerant quantum computation.

Methods

Device and experimental procedure

The device used here consists of a self-assembled InGaAs QD grown by molecular beam epitaxy in a GaAs matrix. The QDs are positioned in the center of a λ GaAs cavity between two sets of distributed Bragg reflectors (DBRs). Each set consists of alternating pairs of GaAs and Al0.9Ga0.1As, with 14 pairs on top and 28 on the bottom. The cavity is etched into a micropillar structure with radial support arms to allow connecting to a planar mesa with an electrical contact. The QD and cavity are inside of a p-i-n diode with a 20 nm AlxGa1−xAs tunneling barrier to aid in trapping charge carriers.

The QD-cavity device is operated at 4K in a closed-cycle Montana cryostat. Superconducting magnetic coils allow application of up to 500 mT magnetic field in the in-plane y-direction. Both the LA phonon-assisted excitation (Δ = − 0.8 nm) and OSRP (Δ = + 1.2 nm) pulses come from a femtosecond (110 fs) Ti:Sapphire laser with a repetition rate of 81 MHz. The pulses are spectrally filtered using a 4-f pulse-shaping line with a spatial light modulator to obtain 15 ps and 4 ps pulses, respectively. The beams are then spatially separated with a band-pass filter, with their power and polarization independently controlled using variable neutral density filters and waveplates, before being recombined on a second band-pass filter. A combination of fiber and free-space delays are used to produce a sequence, consisting of up to four excitation pulses separated by 600 ps and up to two OSRPs, which repeats every 12.2 ns. A second laser set to 860 nm is used in continuous wave at very low power to stabilize the charge environment of the QD and reduce blinking. The emitted photons are collected through a lens with a numerical aperture of 0.7 in a confocal microscope configuration. The laser is separated from the single photons with narrow band-pass filters (0.8 nm bandwidth).

To quantify entanglement, we measure four-photon polarization correlation measurements. Due to detector dead-time (≈ 30 ns), the polarization measurements are performed in a time-to-spatial demultiplexed tomography setup composed of three 50:50 beamsplitters that split the emitted photons into four paths with equal probability. Each path consists of a quarter and half waveplate with a polarizing beamsplitter and a pair of superconducting nanowire single photon detectors (SNSPDs). Two of the paths are set to measure the first and last photons in the R/L polarization basis for spin initialization and readout. The other two are set to perform full quantum state tomography of the pair of photons #2 and #3 in order to reconstruct their polarization states. The overall photon detection efficiency before the tomography setup is approximately 4%, resulting in a 4-photon event rate of around 200 Hz with an 81 MHz laser repetition rate. With photon demultiplexing in the tomography setup and accounting for additional optical losses, the measured useful 4-photon event rate is reduced to about 0.5 Hz. A full schematic of the experimental setup is shown in Supplementary Fig. 6.

Simulation

Estimation of experimental parameters and state fidelity are based on a four-level trion system evolving following a Markovian master equation to describe the impact of spontaneous emission. The hyperfine interaction between the electron spin and the nuclei is captured by an additional Zeeman Hamiltonian to model the fluctuating Overhauser (OH) field with an isotropic Gaussian distribution. The excitation pulses and OSRPs are modeled as instantaneous unitary rotations of the trion system, each followed by a possible pure dephasing channel to capture optically-induced decoherence. To obtain entangled light-matter states, the master equation model is used to compute the light-matter process matrix that maps a single-qubit electron spin state to a two-qubit spin-polarization state at a later point in time. This map is used repeatedly in conjunction with single-qubit rotations to construct the desired multipartite density matrices corresponding to each studied pulse configuration. Additional details about the simulation model can be found in the Supplementary Note 4.