Abstract
Predicting organic reaction feasibility and robustness against environmental factors is challenging. We address this issue by integrating high throughput experimentation (HTE) and Bayesian deep learning. Diverging from existing HTE studies focused on niche chemical spaces, in this work, our in-house HTE platform conducted 11,669 distinct acid amine coupling reactions in 156 working hours, yielding the most extensive single HTE dataset at a volumetric scale for industrial delivery. Our Bayesian neural network model achieved a benchmark for prediction accuracy of 89.48% for reaction feasibility. Furthermore, our fine-grained uncertainty disentanglement enables efficient active learning, reducing 80% of data requirements. Additionally, our uncertainty analysis effectively identifies out-of-___domain reactions and evaluates reaction robustness or reproducibility against environmental factors for scaling up, offering a practical framework for navigating chemical spaces and designing highly robust industrial processes.
Similar content being viewed by others
Introduction
Predicting the feasibility of any given reaction has been a fundamental yet long perplexing problem for organic chemists. Addressing this issue would enable organic chemists to swiftly rule out non-viable reactions during the synthesis design process, thereby saving enormous time while navigating complex pathways to synthesize highly valuable compounds1. This is particularly critical in the field of medicinal chemistry, where time and cost constraints are crucial during stages such as early drug discovery and preclinical process development2,3. However, to date, no universal “oracle” exists to definitively predict the feasibility of a reaction before experimental validation4. Although theoretical advances in the reactivity of organic compounds have progressed rapidly, a complete understanding of the causal relationships between molecular structures and reaction outcomes based solely on first principles remains elusive. Emerging statistical learning methods that leverage existing literature data show promise but are still in their early stage, mainly due to the lack of negative results in published data5,6. In practice, identifying feasible reactions is still a task that highly relies on the expertise and intuition of seasoned experts in organic chemistry7. Training such experts requires both smart learning strategies and rigorous efforts. Similarly, developing an artificial intelligence (AI) system that matches the performance of such experts requires smart strategies to navigate global chemical space using minimal data amount and systematically acquiring extensive, unbiased wetlab data automatically. Despite many promising pioneering works2,5,8,9,10,11, researchers are still in the early exploring stage to build an AI system that can steadily serve as an “oracle” to predict the feasibility of any given organic reaction.
Beneath the surface of predicting reaction feasibility lies a more complex challenge: assessing the robustness of reactions. The results of organic reactions can be influenced by many factors, e.g., minor changes in environments (moisture, oxygen level, light, etc.), nuanced differences in analytical and separation methods, and subtle variations in manual operations. This intrinsic stochasticity often makes certain sensitive reactions difficult to replicate across different laboratories. Scaling up such sensitive reactions to an industrial level requires enormous efforts in process and operational control. Consequently, process engineers frequently seek alternative reactions that are less sensitive and more reliable whenever possible. Therefore, there is a strong demand for an AI system capable of pre-emptively assessing reaction robustness. However, this task is also extremely challenging. The main reasons lie in two aspects: firstly, to build such an AI system, a high-throughput and autonomous method to navigate the enormous chemical space is needed, but not attainable. Secondly, to understand the underlying uncertainty for organic reactions, fine-grained uncertainty analysis and disentanglement based on the results of chemical space exploration is necessary, however, there has been no such demonstration to dig the intrinsic stochasticity of chemical reactions systematically. To date, the problem of estimating the robustness of chemical reactions is still unsolved.
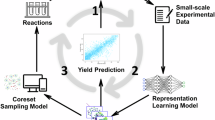
In this work, we demonstrate a synergistic and systematic solution based on high-throughput experimentation (HTE) and Bayesian deep learning to effectively tackle the challenges of feasibility and robustness estimation in organic reactions. We present (1) an extensive wetlab dataset based on an automated HTE platform developed by our team; (2) a model uncertainty-driven learning strategy to navigate a broad chemical space with minimal data requirements to predict reaction feasibility; and (3) a data uncertainty analysis procedure to grasp intrinsic stochasticity for the estimation of reaction robustness. The overall workflow described in this work is shown in Fig. 1. Specifically, we focus on acid amine coupling reactions, which are most widely reported and used in organic synthesis, yet remain challenging to assess for feasibility and robustness, even for experienced bench chemists12. We conduct 11,669 reactions for 8095 target products at 200–300 μL scale, covering 272 acids, 231 amines, 6 condensation reagents, 2 bases, and 1 solvent, on an in-house HTE platform within 156 instrument working hours to explore both the substrate and condition space of general acid amine condensation reactions rationally and globally. The overall chemical space explored is shown in Fig. 2a. To the best of our knowledge, this is the most extensive single reaction-type HTE dataset covering a broad chemical space at a volume scale practical for industrial delivery13. It is also the HTE dataset that covers the most target products to date. Based on the HTE data, our Bayesian neural network (BNN) model achieves a feasibility prediction accuracy of 89.48% and an F1 score of 0.86, outperforming existing feasibility prediction approaches on broad chemical spaces. With fine-grained uncertainty disentanglement, we identify the modeling and chemical origins of prediction uncertainty and demonstrate that an active learning strategy saves ~ 80% data for feasibility prediction. At the same time, we discover that extensive experimental exploration contributes to high-quality uncertainty estimation. We correlate the intrinsic data uncertainty with the robustness of chemical reactions. This is validated by the analysis of reactions reported on the mg scale and in the kg/ton scale in the literature. We note here that our work focuses on the reaction process without considering the feasibility or robustness during the separation process. Diverging from nearly all existing HTE works in organic synthesis, our approach demonstrated a potential way to combine HTE and Bayesian deep learning to systematically answer the questions about reaction feasibility and robustness, thus enabling highly efficient organic synthesis and scaling up.
Wetlab data is collected using automated HTE, followed by probabilistic modeling using Bayesian neural networks. The uncertainty is disentangled into epistemic uncertainty and aleatoric uncertainty. Epistemic uncertainty originates from insufficient data and is used for further design of experiments (DoE). Aleatoric uncertainty is linked to the intrinsic noise of experimentation and is demonstrated to be an indicator of reaction robustness. We also found extensive HTE exploration enhances the quality of uncertainty estimation.
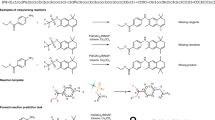
a Overview of acid-amine condensation reactions executed in this work. 1-Hydroxybenzotriazole (HOBt); Dimethylformamide (DMF); N,N-Diisopropylethylamine (DIEA); 1-Methylimidazole (NMI); O-(7-azabenzotriazol-1-yl)-N,N,N',N'-tetramethyluronium hexafluorophosphate (HATU); Chloro-N,N,N',N'-tetramethylformamidinium hexafluorophosphate (TCFH); benzotriazol-1-yloxytris(dimethylamino)phosphonium hexafluorophosphate (BOP); Bromotripyrrolidinophosphonium hexafluorophosphate (PyBrOP); benzotriazol-1-yloxytripyrrolidinophosphonium hexafluorophosphate (PyBOP); 1-(3-Dimethylaminopropyl)-3-ethylcarbodiimide hydrochloride (EDCI). b Categorical distributions in patent and commercially available datasets for carboxylic acids and amines. The carbon attached to the reaction center (carboxyl or primary amine group) is in a carbocyclic aromatic ring (SingleHomoAromatic), or a carbocyclic aromatic ring system (PolyHomoAromatic), or a single hetero aromatic ring (SingleHeteroAromatic), or a hetero aromatic ring system (PolyHeteroAromatic), or a single aliphatic ring (SingleAliphaticRing), or an aliphatic ring system (PolyAliphaticRing), or an aliphatic chain (AliphaticChain). The additional 2 categories for amines represent whether a secondary amine is cyclic. c, d Analysis after down-sampling includes t-SNE visualizations and Kernel density estimation (KDE) plots of Bottcher complexity for acids and amines. In the t-SNE plots, selected acids (red) or amines (blue) are displayed alongside a random subset of 2000 compounds extracted from patent data (gray). The KDE plots illustrate the probability density functions of the Bottcher molecular complexity for three groups: selected compounds (red), patent compounds (yellow), and purchasable compounds (blue).
Results
Diversity-guided substrates down-sampling
The overall workflow is shown in Fig. 1. We first formulate a finite and industrially relevant exploration space as the representation of the acid-amine condensation reaction. In history, chemists have reported millions of structures of carboxylic acid and amine14. Given that our target final users are mainly industrial medicinal chemists, we choose acid-amine condensation reactions reported in the patent dataset Pistachio15 as the reference chemical space. Exploring every possible substrate combination for acid-amine condensation reported in Pistachio is intractable16. Down-sampling the desired chemical space into a representative and structured sub-space is necessary. Furthermore, many reported structures are not commercially available, making unrealistic synthesis and time costs for the exploration task. Therefore, in this work, we use commercially available compounds that resemble the structure of the substrates used in Pistachio to curate a sub-chemical space of acid-amine condensation reactions (Fig. 2a). To minimize ambiguity from competing functional groups, we specifically choose substrates that contain only one carboxyl or amine group. All the reactions in our HTE dataset are novel compared to the Pistachio dataset, ensuring the uniqueness of our work.
We analyze the distribution of structures of all substrates in Pistachio and commercially available compounds from local vendors in Shanghai (Supplementary Section 2.2.2). As Fig. 2b shows, the commercially available structures deviate significantly from the patent dataset Pistachio in terms of molecular structures. Considering the reactivity16, we categorize carboxylic acids and amines into seven and nine distinct categories (Supplementary Table 2) based on the type of carbon atom attached to the reaction center (carboxyl or amine group). To fill the gap in structural distribution and ensure representative sampling, we match the categorical proportions in Pistachio in our sampled substrates and use the MaxMin sampling method17 within each category to ensure structural diversity (Supplementary Section 2.2.2).
A challenge in using purchasable compounds to represent those compounds used in actual patents is maintaining the structural complexity of the latter. To evaluate the structural complexity of the sampled substrate sets, we calculate the Bottcher structural complexity18 (Supplementary Section 2.2.3). The commercially available compound library is significantly simpler in structure than the actual compounds used in patent data, which is in line with our expectation (Fig. 2b for carboxylic acids and amines, respectively). Selected by our down-sampling strategy, the sampled carboxylic acids and amines demonstrate a much closer alignment with patent distribution, underscoring the efficacy of our approach. Figure 2b also shows T-distributed stochastic neighbor embedding (t-SNE) visualizations using Jaccard distance5, further validating that our sampled substrate set robustly represents the substrates in the patent dataset.
In addition to ensuring the representativeness of the sub-sampled commercially available substrates, in the experimental design phase, we also address the issue of inadequate negative data in existing reaction datasets11 by incorporating expert rules. In this work, we introduce potentially negative reaction examples by leveraging known chemical concepts such as nucleophilicity and steric hindrance effects (Supplementary Section 1.1). With an additional 5600 reactions introduced by chemist-designed rules, our final dataset size stands at 11,669 reactions for 8095 target products, making it the largest HTE dataset collected at regular early-stage drug discovery scale (200–300 μL) for a single type of organic reaction reported to date. Compared with recent HTE datasets10,19,20, our dataset covers a broader substrate space with extensive data coverage dedicated on the certain reaction type of acid-amine condensation.
Automated high throughput experimentation and reaction dataset analysis
Figure 3a shows the design of the HTE platform used in this work (ChemLex’s Automated Synthesis Lab-Version 1.1, CASL-V1.1), detailed in Supplementary Section 2.1.1. The HTE experimentation procedure is described in Supplementary Section 2.1.2 to 2.1.7. To determine the yields, we follow the protocol widely used in academia and industry and use the uncalibrated ratio of ultraviolet (UV) absorbance in liquid chromatography-mass spectrometry (LC-MS) as reported in Smith et al.19 (Supplementary Section 2.1.8).
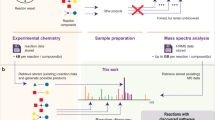
a The HTE equipment used for our wetlab experiments (Left: side view; Right: top view). b Proportion of accessible chemical space for HTE and literature data. NiCOlit5; AZ ELN: AstraZeneca’s Electronic Lab Notebooks9; Suzuki HTE10; BH HTE: Buchwald-Hartwig HTE20. The yield distribution are shown for the HTE dataset in this work and other widely used literature/HTE datasets, along with SciFinder query44 and Pistachio15. c t-SNE visualization of products in our HTE data (in purple) and patent data(in gray). d Surprising reactions with known factors (upper: steric hindrance, lower: partial charge on the nitrogen atom in the amine group) that impede the reaction result in fairly good reaction yields. (Yield: 62.12% (Upper), 73.97% (Lower)).
We demonstrate the broadness of our HTE dataset by comparing it with other reaction datasets generated from literature or HTE platforms, including literature-derived NiCOlit5, AstraZeneca’s Electronic Lab Notebooks (AZ ELN)9, Suzuki-Miyaura HTE10, and Buchwald-Hartwig HTE20. We quantify the accessible chemical space as the total number of possible combinations of discrete variables, such as reactants, catalysts, etc. (Fig. 3b), following the definition of Schleinitz et al.5. Existing HTE datasets, like the Buchwald-Hartwig20 and Suzuki-Miyaura10, typically achieve thorough exploration within narrowly defined substrate combinations, making them particularly suitable for yield optimization tasks21,22,23. Consequently, models trained on such datasets may lack generalizability5. Unlike Bayesian optimization frameworks that focus on condition refinement within fixed chemical spaces16,24, our dataset’s emphasis on substrate diversity under standardized conditions enables feasibility prediction across broader reaction landscapes. Other datasets obtained from ELNs or literature can cover a broader chemical space, but the proportion of explored data may be insufficient for training a generalizable model for the entire target chemical space9. In addition, universal control of data quality and reproducibility for these datasets are hard to achieve, potentially introducing unknown noise that could impede model learning. Focusing on the broad reaction space of acid-amine condensation reactions, our HTE dataset covers a broad sub-space with a significant explored proportion. In addition, the t-SNE plot of the products from the HTE dataset in this work and those in the patent dataset is shown in Fig. 3c, demonstrating a good representation of the reference patent reaction dataset.
Our HTE dataset also alleviates the long-standing challenge of literature-derived datasets: bias towards positive results5,11,16,25. Figure 3d highlights the differences in yield distributions of patent/literature data and HTE data. Patent/literature data skews towards higher yield, whereas the HTE dataset contains richer low-yield reactions. By designing potentially negative examples based on known ___domain knowledge, the distribution of our HTE dataset is better steered towards non-reactive regions, leading to more comprehensive exploration. At the same time, existing chemical knowledge from seasoned chemists cannot replace real wetlab experimentation in terms of feasibility prediction. Similar to the results reported by Haas et al.12, we also encounter “surprising” results. Figure 3d presents such reactions where reactants with known factors—steric hindrance (upper) and partial charge on the nitrogen atom in the amine group (lower)—impede the reaction. Despite these factors, the reactions yield fairly good results, with yields of 62.12% for the upper example and 73.97% for the lower example.
Probabilistic models for reliable uncertainty estimation
To thoroughly explore the chemical space of acid amine condensation, our objectives extend beyond merely devising a model to predict the feasibility of a given reaction, but also to assess the confidence of the model26. In this work, we introduce a probabilistic Bayesian Neural Network (BNN)27 that outputs the parameter of a Bernoulli distribution, representing the probability of a reaction being feasible. The network architecture is shown in Supplementary Fig. 6. Rather than conventional point estimation, the parameters of each layer in BNN are modeled as learnable probability distributions with a given prior distribution. Details regarding prior identification can be found in Supplementary Section 2.2.8. We compare various methods, including Bayesian approaches like Monte Carlo dropout (MCdropout)28 and Deep Kernel Learning Gaussian Process (DKLGP)29, as well as model ensemble (Ensemble)30 (Supplementary Section 2.2.5). For BNN, we use Stochastic Variational Inference (SVI)27 and No-U-Turn Sampler (NUTS)31 to approximate the predictive posterior distribution for BNN. Details of model training and convergence analysis can be found in Supplementary Section 2.2.7 and 2.2.9.
We evaluate the model performance on public Pfizer Suzuki-Miyaura HTE datasets (10-fold validation)10 and our own HTE data. For our HTE data, in addition to the conventional random split, we introduce other two strategies for dataset partitioning following2, i.e., the stratified splits. These strategies are designed to cover scenarios of “one reactant unseen” and “both reactants unseen” in the test set, as illustrated in Supplementary Section 2.2.4. Such partitioning tends to use minimal overlap of reactants between the test and training sets, resulting in significant ___domain shifts between different data splits, as shown in Fig. 4a. The comparison results on these different datasets and splits are presented in Fig. 4b, Supplementary Tables 3, 7, 11, and Fig. 5a–c, covering accuracy, F1-score and the Receiver Operating Characteristic (ROC). The results show that BNN + NUTS stands out in terms of classification performance regardless of the splits and metrics. On our HTE dataset, BNN+NUTS achieves the highest accuracy, F1-macro scores and Area Under the Curve (AUC)-ROC in random splits (89.48%, 0.86, 0.94), stratified splits (one unseen: 80.84%, 0.74, 0.87; both unseen: 72.47%, 0.65, 0.79), and overall average (80.93%, 0.75, 0.87). Similar performance is observed on the public dataset (Supplementary Tables 4–6, Tables 8–10, Tables 12–14, Fig. 5d), where BNN + NUTS leads in all metrics with the highest average accuracy (88.61%), F1-macro (0.87) and AUC-ROC (0.95). Other methods like MCdropout, Ensemble, BNN + SVI, and DKLGP show good performance but are generally outperformed by BNN + NUTS, particularly in the challenging stratified splits and standard K-fold validations. We also demonstrate that our model can generalize to other binary classification tasks without the need for additional hyperparameter tuning (Supplementary Section 2.2.6). Our model’s consistent performance across different datasets and splits highlights its robustness and effectiveness in capturing underlying data distributions and providing reliable uncertainty estimates, making it a strong choice for predictive modeling in diverse scenarios.
a t-SNE visualization with KDE contours of different data split strategies. In the random split, the training and test sets are closely fused, indicating minimal ___domain shift and similar structures in both sets. Domain shift increases with substrate novelty in stratified splits ("one substrate unseen” and “both substrates unseen''), presenting more challenging learning tasks for modeling methods. b The receiver operating characteristic (ROC) curve for the random split in our HTE dataset. A larger area under the ROC curve (AUC) indicates better model performance. c The calibration curve for the random split in our HTE dataset. The closer the calibration curve is to the diagonal line, the better the model’s predicted probabilities reflect the actual outcomes. d The wrong-prediction curve for the random split in our HTE dataset. A larger area under this curve indicates a better linkage between uncertainty and identifying challenge samples. e–g The active learning performance with different sampling methods under different data split strategies. We start with 100 data entries and incrementally add 100 until reaching 2000, selecting samples based on predictive (predictive_unc_based), aleatoric (aleatoric_unc_based), or epistemic uncertainty (epistemic_unc_based), or randomly (random_selection). e Model performance under random split. f Model performance under stratified split (one substrate unseen). g Model performance under stratified split (both substrates unseen).
a The box plot of the yields among the three repetition experiment subsets. Dashed lines denote the 20% yield threshold between positive and negative reactions. b The ICC of three subsets grouped by aleatoric uncertainty. c Cases with high aleatoric uncertainty from the HTE dataset. d KDE of the PDF differences between reactions from the discovery phase and the process phase. e KDE-estimated PDF after down-sampling the data to the same volume as in (d). Blue bars and line: discovery phase; red bars and line: process phase. f Similar reactions from a practical pharmaceutical case with aleatoric uncertainty difference, (Bortezomib (Johnson & Johnson): Approved for Waldenström’s macroglobulinemia; Acute lymphoblastic leukemia; Mantle cell lymphoma; Multiple myeloma).
To assess the model’s confidence in its predictions, we compare calibration curves32 in Fig. 4c (random split of our HTE data) and Supplementary Fig. 9a, b (stratified split of our HTE data and the public data). A perfectly calibrated model aligns with the 45-degree diagonal line, indicating that the probabilities predicted by the model vary in line with the actual probabilities of occurrence33. BNN + NUTS outperforms the other methods in calibration, revealing that BNN + NUTS captures the inner connection between confidence and actual probabilities34. The quantitative Expected Calibration Error (ECE)35 in Supplementary Table 15 demonstrates similar results, indicating that BNN + NUTS produces well-calibrated probabilities in these binary classification tasks.
We further evaluate uncertainty estimation (Supplementary Section 2.2.11) using the wrong-prediction curve36, which links uncertainty to predictive accuracy (Fig. 4d for random split of our HTE dataset, Supplementary Figs. 10a, b for stratified split of our HTE data and the public data). A larger area under the wrong-prediction curve indicates better performance in uncertainty estimation, as areas with higher uncertainty cover more erroneous examples. This correlation demonstrates that by analyzing the uncertainty of the model, we can identify which samples are difficult for the model. Notably, the best-performing BNN + NUTS (denoted in red) covers more than 70% of the total prediction errors within 30% of the samples with the highest uncertainty levels. In all the aforementioned analyses, our BNN + NUTS model gives consistently outstanding performance among different Bayesian inference methods and posterior distribution estimation methods.
Fine-grained Uncertainty Disentanglement
Having estimated predictive uncertainty, we dive into a comprehensive analysis of their origins. In general, predictive uncertainty can be grouped into epistemic and aleatoric uncertainty37. Aleatoric uncertainty arises from inherent noise in the data, while epistemic uncertainty stems from the model’s limited understanding of certain data areas (Fig. 1). We follow Depeweg et al.38 to separate these uncertainties in BNNs, detailed in Supplementary Section 2.2.11. We demonstrate that epistemic uncertainty helps guide data-efficient chemical space exploration (active learning39) and detect out-of-distribution (OOD) samples (Supplementary Section 2.2.14), while aleatoric uncertainty reflects intrinsic stochasticity in reactions, which can be useful for scaling up processes in the industry.
To evaluate the efficacy of uncertainty disentanglement, we conduct a pool-based Active Learning (AL) experiment40. We start with a pool of unlabeled samples and aim to sequentially select some for labeling. The goal is to train a model on these labeled samples so that it can provide the most accurate predictions for the remaining unlabeled samples. For this experiment, based on the three data split strategies previously mentioned Fig. 4a, we use all unlabeled samples from the training set as our pool set, forming three distinct AL tasks for random splits, one unseen and both unseen stratified splits, respectively with F1-marco score shown in Fig. 4e–g. Notably, the curve representing random sampling (gray) consistently shows the poorest performance, regardless of the dataset’s split strategy. This outcome suggests that while random sampling provides data to the model, it barely contributes to information gain. In contrast, the approaches of sampling by predictive uncertainty (or overall uncertainty, blue) and by epistemic uncertainty (orange) display similar patterns and significantly outperform the method based on aleatoric uncertainty. Importantly, our analysis (see Supplementary Section 2.2.13) indicates that uncertainty estimates become more reliable as the dataset grows. In early AL phases (with < 500 samples), uncertainty decomposition is limited by unstable epistemic estimates and the risk of overfitting—thus, the benefits of decomposing uncertainty are minimal, and the epistemic-only strategy (orange) initially underperforms predictive uncertainty strategy (blue). However, in the mature AL phase (> 1000 samples), as the uncertainty estimation stabilizes, decomposition of uncertainty source becomes operationally valuable: the epistemic component guides sampling efficiently by targeting at model-knowledge gaps, while the aleatoric component prevents wasting resources on chemically noisy reactions which are less useful for the improvement of model performance. This similarity in performance trajectories highlights a strong link between the model’s effectiveness and epistemic uncertainty. For aleatoric uncertainty, once a certain level of precision is reached, its contribution to enhancing model performance plateaus, regardless of the addition of more data. This indicates that incorporating samples with high aleatoric uncertainty offers limited information gain for the model in terms of exploring the entire data space. The study also reveals that, focusing on classification performance, similar results can be achieved with just ~ 1/5 of the samples (Fig. 4e–g), saving time and effort in building reaction datasets.
Aleatoric uncertainty reveals the inherent stochasticity in the reaction procedure. In organic chemistry reactions, we argue that the experiments with high aleatoric uncertainty may be relatively more sensitive to experimental conditions or analytical methods, and thus are difficult to reproduce without advanced condition control technology. To demonstrate this, we design replicated experiments (Supplementary Section 2.2.15) and form three distinct subsets from the test set (in descending order of aleatoric uncertainty): 25 reactions with the highest aleatoric uncertainty (Top-25), 25 with the lowest (Lowest-25), and 25 chosen at random from between the two extremes (Random-25). We repeat the experiments three times for each subset. As depicted in Fig. 5a, the box plots illustrate the variations in yields among the three replicated experiments. These plots reveal that Top-25 indeed exhibits poor reproducibility. Another common metric for evaluating consistency, the Intraclass Correlation Coefficient (ICC)41, shows similar results in Fig. 5b. Lowest-25 demonstrates exemplary reproducibility, with an ICC of 0.97, nearly perfect 1, signifying the consistency across multiple trials. Conversely, Top-25 exhibits poor reproducibility, with their ICC significantly lower than that of Lowest-25. The reproducibility of Random-25 falls between these two extremes. The high aleatoric uncertainty may be related to side reactions that poses challenges in kinetics control, as well as stability issues of the starting materials or products. Further mechanistic analysis can be found in Supplementary Section 2.2.15.
Figure 5c shows two representative reactions from the top 25 cases exhibiting the highest aleatoric uncertainty. We analyze the chemical factors that affect the reproducibility of the cases here. In Case 1, the resulting yields for 3 repetitive reactions are 0.0%, 20.8%, and 35.3%. Possible reasons of the poor reproducibility are the competitive side reactions due to environmental moisture, such as the reaction of phenolic hydroxyl groups with HATU42,43. Details of the potential byproducts and corresponding LC-MS results are provided in Supplementary Figs. 13–15. In Case 2, the yields are 0.0%, 10.2%, and 23.2% in 3 repetitive experiments. The amide hydrogen of the product is highly acidic due to the electron-withdrawing acyl and aryl groups, making it easily deprotonated by the base. This deprotonation can lead to further reaction with the coupling reagent (HATU), which is sensitive to environmental conditions, potentially resulting in poor reproducibility42,43. Details of the potential byproducts and LC-MS results for this case can be found in Supplementary Figs. 16–18.
Aleatoric uncertainty analysis for reaction robustness
In process development, reactions sensitive to environmental factors usually take more process and operational control, thus, more robust reactions are preferred. We find that aleatoric uncertainty separated in this work is a good indicator of robustness against these factors. To validate this, we analyze industrial data from the literature to validate the potential application. We curate an extensive collection of single-step acid-amine condensation reaction data from SciFinder searches (Supplementary Section 3.2)44. The data for the discovery phase, derived from milligram-level (mg-level) reactions, were collected from three journals: Bioorganic & Medicinal Chemistry Letters (BMCL), Journal of Medicinal Chemistry (JMC), and European Journal of Medicinal Chemistry (EJMC). In contrast, the process phase data, which includes kilogram-level (kg-level) reactions, were sourced from Organic Process Research & Development (OPRD). In total, we have 17,332 reactions in the discovery phase and 84 reactions in the process phase. Figure 5d and Supplementary Table 16 show that aleatoric uncertainty is significantly lower in process phase reactions. Considering that the trade secrets involved in the process phase may lead to fewer available data, we employed random down-sampling from the discovery phase data to match the quantity of data analyzed in the process phase to ensure the data amount does not bias our analysis. The results, as depicted in Fig. 5e, reaffirm that the aleatoric uncertainty of process phase reactions remains notably lower than that of discovery phase reactions, reinforcing the validity of our findings.
Our conclusion is supported by real cases in the pharmaceutical industry. An example of the production of the FDA-approved Bortezomib by Johnson & Johnson is shown in Fig. 5f. Our model’s analysis reveals that the aleatoric uncertainty of the discovery phase reaction (lower reaction in Fig. 5f) is 0.264, while the same uncertainty of the process phase reaction (upper reaction in Fig. 5f) is 0.209, demonstrating the ability of our model to identify more robust reactions. The lower aleatoric uncertainty could be attributed to the boronic ester in the amine being more resistant to hydrolysis due to increased steric hindrance around the boron atom created by the diol moiety45. This contrasts with the boronic ester in the amine used in the discovery phase reaction and may account for better reproducibility against humidity during both the reaction procedure and the analysis/separation processes.
Discussion
The workflow presented in this paper integrates Bayesian machine learning with HTE, establishing a standardized framework for efficient exploration of the chemical space. Focusing on the common acid-amine condensation reactions, we have constructed the largest publicly available HTE dataset for a single reaction type, encompassing the widest range of substrates and the most extensive collection of negative examples. Moreover, our model demonstrates efficient feasibility prediction and robustness estimation. By incorporating uncertainty estimation and disentanglement of probabilistic models, we have successfully identified samples that offer the greatest learning gain for the model and reactions with low reproducibility. This is beneficial for guiding subsequent experimental designs and process production. We have also demonstrated that extensive chemical space exploration leads to improved uncertainty estimation. Future work will focus on exploring additional tasks within the reaction type of acid-amine condensation and using this workflow to explore broader chemical reactions, aiming to develop a universal feasibility and robustness prediction model that enhances the efficiency of chemical synthesis both in the synthesis planning phase and reaction execution phase.
Methods
Automated Platforms
CASL-V1.1 system currently consists of four automation platforms, capable of performing independent laboratory processes: Laboratory Information Management Systems (LIMS), operation UI, experiment execution (automated synthesis device - version 1.1, provided by MegaRobo), and reaction analysis (Agilent 1290 Infinity II + G6125C MSD).
The automated synthesis device for version 1.1 consists of three parts: the feeding bin, transfer bin, and reaction bin. The feeding bin can be set according to the experimental environment requirements to determine whether N2 protection is required. And it is equipped with a whole set of set-up module, including a solid dispensing station, a liquid dispensing station, the Capper (responsible for opening and closing the caps of the chem vials), oscillating station, and a scanning station. The transfer bin is mainly responsible for the transfer of material trays in and out of the device, as well as the transfer of material trays between the feeding bin and the reaction bin. The reaction bin is equipped with a plate moving station, a bottle moving station, and 9 shakers with 12 wells, which can support 144 reactions simultaneously and can execute 240–288 reactions one day. The device supports 24–h operation. A general CASL-V1.1 experiment workflow is detailed in Supplementary Section 2.1.
Wetlab dataset split
We establish three distinct dataset split strategies following2,46, leading to different levels of difficulty in learning tasks. These are Random Split, Stratified Split (One Reactant Unseen), and Stratified Split (Both Reactants Unseen).
Random Split: This is the most common setup in machine learning. We randomly selected 70% of the experimental data as the training set and the remaining 30% as the test set.
Stratified Split (One Reactant Unseen): Considering our acid-amine condensation data, each reaction involves an acid and an amine. To test the model’s capability in exploring the entire chemical space (generalization ability towards unseen reactants), we divide the dataset following this strategy, the test set includes either an acid or an amine that was not present in the training set, shown in Supplementary Fig. 4a.
Stratified Split (Both Reactants Unseen): Taking a step further, we select a subset from the entire wetlab dataset such that all acids and amines in the test set are unseen in the training set, while still maintaining the 70% training and 30% test set distribution, denoted in Supplementary Fig. 4b. This setup presents the most challenging and demanding task among all, as it tests the model’s ability to generalize to completely unseen reactants.
BNN Prior and sampling strategy
Our BNN consists of two fully connected layers, where both the weights and biases are modeled as random variables, as illustrated in Supplementary Fig. 6. In this framework, selecting appropriate priors is essential for robust learning because priors encode our beliefs about the parameters before observing any data. Although the isotropic Gaussian prior is commonly used, it may not always be optimal for BNNs. To address this, we follow an empirical approach47: we first perform maximum a posterior (MAP) training to derive an empirical distribution of the fitted weights. When this empirical distribution deviates from a standard Gaussian—for example, by exhibiting higher peaks and lighter tails (see Supplementary Fig. 7)—a single Gaussian prior may not sufficiently capture the weight characteristics. Instead, we propose a composite prior that combines a Laplace distribution with a smaller scale parameter (to better model the central region) with a Gaussian distribution having a larger scale parameter (to better capture the tails).
For posterior sampling, we employ the NUTS within a Monte Carlo Markov Chain (MCMC) framework. We run 4 independent chains and use the Gelman-Rubin convergence diagnostic48 to ensure that the within-chain variance is comparable to the between-chain variance, thereby confirming convergence of the posterior distribution. For more details, please refer to Supplementary Section 2.2.9.
BNN Uncertainty quantification and disentanglement
Let D represent the training data and w denote the model parameters. Our objective is to estimate the posterior distribution p(w∣D) of the model parameters given the training data. Using the NUTS, we obtain multiple samples from the posterior, each denoted as w(i) ~ p(w∣D). Given an input x*, we compute a Bernoulli distribution parameter
And for each Bernoulli distribution, a binary outcome is drawn as
The final classification result is determined by comparing the mean of these binary outcomes with a threshold:
where N represents the total number of sampled Bernoulli distributions. In practice, if more than half of the samples classify the input as 1, the final classification is set to 1; otherwise, it is 0.
Since the model is verified to be well-calibrated—that is, its outputs accurately reflect the true probabilities—we further quantify the predictive uncertainty by leveraging the entropy of the induced Bernoulli distribution (detailed in Supplementary Section 2.2.10). In information theory, entropy measures the inherent disorder or unpredictability of a probability distribution, making it an appropriate metric for uncertainty. The predictive distribution is given by:
and its associated entropy H(y*∣x*, D), provides a quantitative estimation of the prediction uncertainty for the specific input x*.
To gain a deeper understanding of both aleatoric and epistemic uncertainty, and to offer insight for experimental procedures and model development, we follow38 and disentangle the predictive uncertainty. Specifically, the term
defines the aleatoric uncertainty. Given that this term represents the average entropy with static weights, it stands as a model-agnostic uncertainty. The epistemic uncertainty is then obtained as the difference
which quantifies the uncertainty not arising from the inputs, but from the model’s weight. For inputs with high epistemic uncertainty, different weight samples yield diverse predictions.
Data availability
The HTE dataset generated in this study has been deposited in Zenodo at https://doi.org/10.5281/zenodo.12920294. Data supporting the findings of this manuscript are also available from the corresponding author upon request.
Code availability
Codes are publicly available in the GitHub repository (https://github.com/Chemlex-AI/bayesian-reactivity-prediction)49.
References
Wender, P. A. & Miller, B. L. Synthesis at the molecular frontier. Nature 460, 197–201 (2009).
Raghavan, P. et al. Incorporating synthetic accessibility in drug design: Predicting reaction yields of suzuki cross-couplings by leveraging abbvie’s 15-year parallel library data set. J. Am. Chem. Soc. 146, 15070–15084 (2024).
Sen, M., Arguelles, A. J., Stamatis, S. D., García-Muñoz, S. & Kolis, S. An optimization-based model discrimination framework for selecting an appropriate reaction kinetic model structure during early phase pharmaceutical process development. React. Chem. Eng. 6, 2092–2103 (2021).
Schwaller, P., Vaucher, A. C., Laino, T. & Reymond, J.-L. Prediction of chemical reaction yields using deep learning. Mach. Learn. Sci. Technol. 2, 015016 (2021).
Schleinitz, J. et al. Machine learning yield prediction from nicolit, a small-size literature data set of nickel catalyzed c–o couplings. J. Am. Chem. Soc. 144, 14722–14730 (2022).
Raccuglia, P. et al. Machine-learning-assisted materials discovery using failed experiments. Nature 533, 73–76 (2016).
Sandfort, F., Strieth-Kalthoff, F., Kühnemund, M., Beecks, C. & Glorius, F. A structure-based platform for predicting chemical reactivity. Chem 6, 1379–1390 (2020).
Probst, D., Schwaller, P. & Reymond, J.-L. Reaction classification and yield prediction using the differential reaction fingerprint drfp. Digit. Discov. 1, 91–97 (2022).
Saebi, M. et al. On the use of real-world datasets for reaction yield prediction. Chem. Sci. 14, 4997–5005 (2023).
Perera, D. et al. A platform for automated nanomole-scale reaction screening and micromole-scale synthesis in flow. Science 359, 429–434 (2018).
Voinarovska, V., Kabeshov, M., Dudenko, D., Genheden, S. & Tetko, I. When yield prediction does not yield prediction: an overview of the current challenges. J. Chem. Inf. Model. 64, 42–56 (2023).
Haas, B. C., Goetz, A. E., Bahamonde, A., McWilliams, J. C. & Sigman, M. S. Predicting relative efficiency of amide bond formation using multivariate linear regression. Proc. Natl. Acad. Sci. USA 119, e2118451119 (2022).
Baranczak, A. et al. Integrated platform for expedited synthesis–purification–testing of small molecule libraries. ACS Med. Chem. Lett. 8, 461–465 (2017).
Dunetz, J. R., Magano, J. & Weisenburger, G. A. Large-scale applications of amide coupling reagents for the synthesis of pharmaceuticals. Org. Process Res. Dev. 20, 140–177 (2016).
Sayle, R. A., Mayfield, J. W., Lagerstedt, I. & Pirie, R. Nextmove software pistachio. http://www.nextmovesoftware.com/pistachio.html (2022).
Angello, N. H. et al. Closed-loop optimization of general reaction conditions for heteroaryl suzuki-miyaura coupling. Science 378, 399–405 (2022).
Ashton, M. et al. Identification of diverse database subsets using property-based and fragment-based molecular descriptions. QSAR 21, 598–604 (2002).
Bottcher, T. An additive definition of molecular complexity. J. Chem. Inf. Model. 56, 462–470 (2016).
King-Smith, E. et al. Probing the chemical ‘reactome’with high-throughput experimentation data. Nat. Chem. 16, 633–643 (2024).
Ahneman, D. T., Estrada, J. G., Lin, S., Dreher, S. D. & Doyle, A. G. Predicting reaction performance in c–n cross-coupling using machine learning. Science 360, 186–190 (2018).
Shields, B. J. et al. Bayesian reaction optimization as a tool for chemical synthesis. Nature 590, 89–96 (2021).
Ranković, B., Griffiths, R.-R., Moss, H. B. & Schwaller, P. Bayesian optimisation for additive screening and yield improvements in chemical reactions–beyond one-hot encoding. Digit. Dicov. 3, 654–666 (2023).
Chen, L.-Y. & Li, Y.-P. Machine learning-guided strategies for reaction conditions design and optimization. Beilstein J. Org. Chem. 20, 2476–2492 (2024).
Taylor, C. J. et al. Accelerated chemical reaction optimization using multi-task learning. ACS Cent. Sci. 9, 957–968 (2023).
Neves, P. et al. Global reactivity models are impactful in industrial synthesis applications. J. Cheminformat. 15, 20 (2023).
Scalia, G., Grambow, C. A., Pernici, B., Li, Y.-P. & Green, W. H. Evaluating scalable uncertainty estimation methods for deep learning-based molecular property prediction. J. Chem. Inform. Model. 60, 2697–2717 (2020).
Blundell, C., Cornebise, J., Kavukcuoglu, K. & Wierstra, D. Weight uncertainty in neural network. In Proceedings of the 32nd International Conference on Machine Learning 1613–1622 (2015).
Gal, Y. & Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of The 33rd International Conference on Machine Learning 1050–1059 (PMLR, 2016).
Wilson, A. G., Hu, Z., Salakhutdinov, R. R. & Xing, E. P. Stochastic variational deep kernel learning. In Advances in Neural Information Processing Systems,29 (2016).
Lakshminarayanan, B., Pritzel, A. & Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. In Advances in Neural Information Processing Systems,30 (2017).
Hoffman, M. D. & Gelman, A. et al. The no-u-turn sampler: adaptively setting path lengths in hamiltonian monte carlo. J. Mach. Learn. Res. 15, 1593–1623 (2014).
Wilks, D. S. On the combination of forecast probabilities for consecutive precipitation periods. Weather Forecast. 5, 640–650 (1990).
Guo, C., Pleiss, G., Sun, Y. & Weinberger, K. Q. On calibration of modern neural networks. In Proceedings of the 34 th International Conference on Machine Learning 1321–1330 (2017).
Lichtenstein, S., Fischhoff, B. & Phillips, L. D. Calibration of Probabilities: The State of the Art, 275–324 (Springer, 1977).
Naeini, M. P., Cooper, G. & Hauskrecht, M. Obtaining well Calibrated Probabilities Using Bayesian Binning. In Proceedings of the AAAI Conference on Artificial Intelligence. (2015).
Kopetzki, A.-K., Charpentier, B., Zügner, D., Giri, S. & Günnemann, S. Evaluating robustness of predictive uncertainty estimation: Are dirichlet-based models reliable. In Proceedings of the 38 th International Conference on Machine Learning. 5707–5718 (PMLR, 2021).
Kendall, A. & Gal, Y. What uncertainties do we need in bayesian deep learning for computer vision. In Advances in Neural Information Processing Systems, 30 (2017)
Depeweg, S., Hernandez-Lobato, J.-M., Doshi-Velez, F. & Udluft, S. Decomposition of uncertainty in bayesian deep learning for efficient and risk-sensitive learning. In Proceedings of the 35 th International Conference on Machine Learning. 1184–1193 (PMLR, 2018).
Zhang, Y. et al. Bayesian semi-supervised learning for uncertainty-calibrated prediction of molecular properties and active learning. Chem. Sci. 10, 8154–8163 (2019).
Sugiyama, M. & Nakajima, S. Pool-based active learning in approximate linear regression. Mach. Learn. 75, 249–274 (2009).
Koo, T. K. & Li, M. Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 15, 155–163 (2016).
Vrettos, E. I. et al. Unveiling and tackling guanidinium peptide coupling reagent side reactions towards the development of peptide-drug conjugates. Rsc Adv.7, 50519–50526 (2017).
Zhang, S., Amso, Z., De Leon Rodriguez, L. M., Kaur, H. & Brimble, M. A. Synthesis of natural cyclopentapeptides isolated from dianthus chinensis. J. Nat. Prod. 79, 1769–1774 (2016).
Scifinder. https://scifinder-n.cas.org/?referrer=scifinder.cas.org.
Bernardini, R. et al. Stability of boronic esters to hydrolysis: a comparative study. Chem. Lett. 38, 750–751 (2009).
Xu, J. et al. Roadmap to pharmaceutically relevant reactivity models leveraging high-throughput experimentation. Preprint at https://doi.org/10.26434/chemrxiv-2022-x694w (2022).
Fortuin, V. et al. Bayesian neural network priors revisited. In International Conference on Learning Representations (2022).
Gelman, A. & Rubin, D. B. Inference from iterative simulation using multiple sequences. Stat. Sci. 7, 457–472 (1992).
Zhong, H. Towards global organic feasibility and robustness prediction with high throughput data and bayesian deep learning. Zenodo. https://doi.org/10.5281/zenodo.15165244 (2024).
Acknowledgements
H.Z., Y.L.L., H.S., Y.R.L., R.Z., B.L., Y.Y., S.L., P.W., and X.W. received funding from ChemLex Technology Co., Ltd.
Author information
Authors and Affiliations
Contributions
H.Z. and X.W. conceived the project. H.Z. carried out the computational experiments. Y.L.L. and R.Z. carried out the wet lab experiments. H.S., B.L., and Y.R.L. processed the HTE data and performed the DFT calculations. Y.L.L. and R.Z. organized the case study under the supervision of P.W. and S.L. Y.H. provided the prototype of the HTE equipment and took part in the design of the HTE equipment used in this work. K.F. and F.M. proposed the model application and reviewed the medicinal chemistry part. Y.Y., F.Y., and T.Y. discussed and guided the machine learning studies with H.Z. and X.W. X.W. supervised the project. H.Z., X.W., Y.L.L., and T.Y. prepared the manuscript. All authors discussed the results and contributed to the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
H.Z., Y.L.L., H.S., Y.R.L., R.Z., B.L., Y.Y., S.L., P.W., and X.W. are employed by ChemLex, a company specializing in high-throughput synthesis. Y.H. serves as the Chief Executive Officer of MegaRobo, which provides high-throughput experimentation (HTE) equipment. The remaining authors (K.F., F.M., F.Y., and T.Y.) declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Ana Bellomo, Yizhe Chen, and Xiaonan Wang for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhong, H., Liu, Y., Sun, H. et al. Towards global reaction feasibility and robustness prediction with high throughput data and bayesian deep learning. Nat Commun 16, 4522 (2025). https://doi.org/10.1038/s41467-025-59812-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-59812-0