Trait macroevolution in the presence of covariates

Phylogenetic comparative methods allow researchers to characterise the macroevolution of species’ traits over the historical timeframe of a phylogenetic tree, where we take macroevolution here to mean the origin and evolution of the major differences among species¹. Macroevolutionary statistical models have been designed to identify trends^2,3 and episodic bursts of trait evolution^4,5 or posit the existence of global (tree-wide) or local optima towards which traits are drawn^6,7,8,9. Most rely on one or a small number of homogeneous processes assumed to describe trait evolution throughout the tree^{2,3,4,6,7,8,9} or in other cases, a heterogenous distribution of effects is explored⁵. The Fabric model¹, introduced in 2022, identifies historical instances of two distinct evolutionary phenomena that affect the phenotype as it evolves along the branches of the phylogenetic tree: directional shifts such as phenotypes getting larger/smaller or becoming faster/slower, and changes in evolvability or the capacity of a trait to explore its trait-space or niche. Both effects can occur anywhere in the tree, and the model identifies their occurrence, polarity and strength throughout the phylogeny.

The Fabric model, along with many other macroevolutionary models, was designed to study a single trait in isolation. Frequently, it will be the case that traits co-vary across taxa with other traits, such as observed in, but not limited to, the allometric relationships that many morphological, physiological, demographic and life history traits have with body size. These relationships likely identify multivariate phenotypes¹⁰ of adaptive interest in their own right. But the presence of covariation can make it difficult to separate macroevolutionary changes in some focal trait of interest that may be attributable to changes in its covariates, from independent changes to the trait that might occur in response to some other unknown or unmeasured influence—variance shared with covariates can obscure or even mask evolutionary changes that occur independently. The Fabric-regression model estimates the same two evolutionary processes as described for the Fabric model while simultaneously accounting for the variance an evolving trait shares with other traits, leaving the trait’s unique variation for macroevolutionary characterisation. Its use brings perspectives on trait evolution not available to the Fabric model and other single-trait models, or not always studied in multivariate approaches, and it can return descriptions of trait evolution that are not visible when the trait is studied on its own.

The Fabric-regression model’s null expectation (like that of the Fabric model) is that trait evolution can be described statistically as a random walk that follows a neutral Brownian process. The fundamental parameter of a Brownian process is its variance, denoted by the parameter \({\sigma }^{2}\). It is a measure of the size of the infinitesimally small random steps that comprise the random walk, and these steps are used statistically as a metaphor for gradual evolution. A small Brownian variance means that the random steps of evolution are small and vice versa. After some period of time t, a neutral Brownian process that is re-run many times will yield a range of outcomes that is symmetrical about its starting point and has variance \({\sigma }^{2}t\). This is another way of saying that neutral Brownian processes are not directional—their expected change is zero, but do provide a measure of a trait’s exploratory ability.

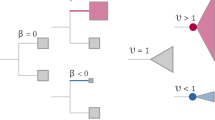
The Fabric and Fabric-regression models identify departures from this null model of trait evolution in the form of directional and evolvability changes. We summarise these two processes here, having described them previously¹. Directional shifts, denoted by the parameter \(\beta\), record instances of traits either increasing (β > 0) or decreasing (β < 0) over some period of time t along the interior or tip branches of the phylogeny. They correspond to changes that exceed what would be expected from the random (directionless) walk of Brownian motion; the null value is \(\beta=0\). Directional changes can occur anywhere in the tree and do not imply or entail any alteration in evolvability, that is, in the variance of evolutionary change. This is true even when the directional changes occur rapidly in evolutionary time and appear as bursts or pulsed episodes of change^1,4,11. Instead, along with others^12,13 we have previously shown¹ how even these apparent bursts of change do not require any special evolutionary mechanism: they are small enough when measured over macroevolutionary time to be compatible with selection acting on the variance that is available within populations, or even with neutral drift. This process can go on indefinitely without exhausting the supply of variants if selection is not too strong^14,15, and studies show that genetic variation in fitness is plentiful in wild populations¹⁶.

We take the Brownian variance to be an estimate of the realised evolvability of the trait. It is a measure of a trait’s observed or historical exploratory capacity as an outcome of the macroevolutionary process (this is in contrast to its use in quantitative genetics^17,18 where evolvability is understood as the capacity of a trait residing within a population to respond to selection, typically as reflected by its genetic or mutational variance). Changes to the realised evolvability are denoted in the Fabric-regression model by the parameter \(\upsilon\) (upsilon), which alters the evolutionary (Brownian) variance locally in parts of the tree according to \(\upsilon {\sigma }^{2}\). Changes to evolvability do not alter the mean value of a trait. The default or null value for \(\upsilon\) = 1; a value of \(\upsilon\, > \,1\) signals an increase in the variance such as might be expected if, for example, some key innovation, change to a developmental mechanism or perhaps an environmental change permits or even encourages a greater variety of some trait among a monophyletic group of species, or possibly because the underlying genetic mutation rate has increased, thereby producing more variants per unit time; a value of υ < 1 indicates the reverse.

As with directional effects, the magnitude of the evolvability changes can vary throughout the tree, and they can follow any pattern over the long term. By comparison, early burst models² posit a parametric trend of rapidly increasing evolutionary variance early in a clade, with the pace of increase slowing over time but never reaching an equilibrium; a more general version of this model allows the evolutionary variance to accelerate or decelerate throughout the tree¹⁹. Models of pulsed change⁴ rely on a specific pulse process with its own variance and macroevolutionary models of the Ornstein–Uhlenbeck (OU) process propose that a trait’s evolutionary variance is small when it is sitting far from its optimum, reflecting strong selection towards the optimum, but then increases to a value roughly in line with that of a Brownian process as it approaches equilibrium at the evolutionary optimum where it is held in place by stabilising selection⁷.

The Fabric-regression model can be written as

where the \({Y}_{i}\) are the observed data for the trait of interest on the ith species (i = 1…n), the \({X}_{{ij}}\) are the values of the j covariates, and the \({\beta }_{j}\) are their associated regression coefficients. As we have described previously in ref. ¹, the summation on the right-hand side of Eq. 1 is over one or more local directional shifts in the trait value that occur along the k branches leading from the root of the phylogeny to the observed value of the trait at the tip of the phylogeny for the ith species. We denote these as \({\beta }_{{ik}}\) to distinguish them from the regression coefficients. They measure the inferred amount of change in the magnitude of the trait from the ancestral to the descendant state in the kth branch along the path leading to species i (and to any other of the species that descend from that branch, e.g. \({\beta }_{1k}\) and \({\beta }_{2k}\) would be identical if species 1 and 2 are both descendants of branch k). The \({e}_{i}\) are \(\sim N\left(0,{\upsilon \sigma }^{2}\right)\) and constitute the variance of the Brownian process.

The log-likelihood of this model (for simplicity, written with a single covariate) is

where \({{\boldsymbol{Y}}}\) and \({{\boldsymbol{X}}}\) are vectors of length i corresponding, respectively, to the trait data and a covariate in the i species, \(\alpha\) is the estimated value of the trait at the root, the summations are over the i species and then separately for each species over the k directional effects that occur in the branches along the path length leading from the root to the tips of the tree. In principle, any number of covariates (\({{\boldsymbol{X}}}\)) can be included, and each would receive its own \({\beta }_{j}\) parameter.

Equations 1 and 2 can be interpreted as defining species-specific optima given by the combination of the values of the covariates and independently by the \({\sum}_{k}{\beta }_{{ik}}{\Delta t}_{{ik}}\), and to which the model assumes species adapt instantaneously in macroevolutionary time. The covariates describe, via their regression coefficients, how species’ optima differ as a function of differences in these measured variables. Unlike some OU models^20,21 we do not characterise the evolution of the variables \({{\boldsymbol{X}}}\) but treat them as fixed. The \({\beta }_{{ik}}\) defined optima that deviate from those defined by the covariates and are presumed to arise in response to unknown, independent and to-be-discovered influences on the \({Y}_{i}\). For example, one might wish to test for an association between the \({\beta }_{{ik}}\) and some environmental or behavioural variable.

The relationships between the covariates and \({{\boldsymbol{Y}}}\) defined by the \({\beta }_{j}\) parameters can be allowed to vary among taxa or clades via the addition of appropriate categorical codes to \({{\boldsymbol{X}}}\) along with their interactions with the covariates. The remaining residual error comprising the e_i of Eq. 1 measures variation in species \({Y}_{i}\) values around the optima defined in Eq. 2 and, as mentioned, is used to estimate the Brownian variance of the model. This variance will include unknown components reflecting the historical strength of stabilising selection, but also variation arising from other unmeasured influences on the species’ values.

The matrix \({{{\boldsymbol{V}}}}_{{{\boldsymbol{\upsilon }}}}\) in Eq. 2 is the expected variance-covariance matrix of the residual errors (the \({e}_{i}\) from Eq. 1), given Brownian motion and any changes to evolvability. Conventionally, this matrix is given by the phylogeny, and the expected variance under Brownian motion after time t is \({\sigma }^{2}\upsilon t\). The model of Eq. 2 fits the covariates and the directional and evolvability changes simultaneously and is not equivalent to conducting a phylogenetically corrected regression of a trait onto its covariate or covariates, extracting residuals and then studying them in the original Fabric model or by some other means. Instead, the directional and evolvability effects can modify the relationship of the covariates to the Y variable to the extent that they compete to explain its variance.

The number, placement and magnitudes of both the directional and evolvability parameters are not fixed in advance but discovered statistically from patterns in the species’ data and the structure of the tree. Let Φ be the unknown vector of the parameters of the model of trait evolution comprising the nominal root \(\alpha\), the regression coefficient(s) \({\beta }_{j}\), the vector of directional change parameters \({{\boldsymbol{\beta }}}\), and the vector of variance-scaling parameters \({{\boldsymbol{\upsilon }}}\). We estimate the posterior density of Φ in a Bayesian Reversible-Jump Markov chain Monte Carlo (RJ-MCMC)²² setting that allows the number of directional and evolvability parameters that depart from their default values \(\left(\beta=0,\upsilon=1\right)\) to vary around a stationary set from one iteration to the next (stationarity is defined in the usual way as no average change in the likelihood or average values of parameters over a large number of independent iterations of the Markov chain). The posterior density is written as

where \(L\left({D|}\Phi \right)\) is given by Eq. 2, the \(p\left(\varPhi \right)\) are the prior distributions of the parameters of the model of trait evolution, and the Monte Carlo integration is over \(d\left({{\boldsymbol{\Phi }}}\right)\). We choose the \(p\left({{\boldsymbol{\Phi }}}\right)\) to be compatible biologically with the processes they represent (“Methods”, see ref. ¹).

Our particular interest in developing the Fabric-regression approach is to identify the \({\beta }_{{ik}}\) and evolvability changes and to study how they differ from the univariate characterisation of the same trait, but the method can also be used to study the multivariate space defined by \({{\boldsymbol{Y}}}\) and \({{\boldsymbol{X}}}\). In this latter regard, the model joins a variety of other multivariate phylogenetic comparative methods that have been proposed including the investigation of differences in slopes of the regression line among clades²³, the contribution of punctuational evolution²⁴, a multivariate OU model²¹ and multivariate characterisation of the phenotypic space¹⁰.

In this work, we apply the Fabric and Fabric-regression models to study brain-size evolution in 1504 mammalian species using a dataset compiled in a previous study²⁵, and arrayed on a phylogeny from the Time Tree of Life²⁶. The strong association between brain and body size raises the possibility that much of the variation in brain size arises from pressures imposed by having a larger body, including but not limited to physiological, life history and behavioural differences among species of different size. We use these data as a familiar example with which to illustrate features of the model, rather than to test any new hypotheses about brain evolution. Our intent is to show how studying traits alone vs after having accounted for their covariation with other variables can yield qualitatively different outcomes and insights about, in this case, the macroevolutionary history of brain-size evolution. Accordingly, we focus on the number and polarity \((\beta\, < \,0\,{or}\, > \,0;\upsilon\, < \,1\,{or}\, > \,1)\) of the directional and evolvability parameters the method discovers throughout the tree, contrasting results for whole-brain and brain-size having accounted for its allometric association with body-size. We find that inferences about brain size, having accounted for body size, differ qualitatively from those derived when brain size is studied alone, including many new effects that are not visible in the whole trait.

We estimated the Fabric and Fabric-regression models using a RJ-MCMC approach (“Methods”). Simulation studies (ref. ¹, Supplementary Note 1, and Supplementary Tables 1 and 2) confirm that the method estimates parameters well, discriminates between the directional and evolvability changes and the models are identifiable. We also estimated simple phylogenetic generalised least-squares (PGLS) regression models for predicting brain size from body size using an MCMC framework to estimate their parameters. Drawing on previous work on brain-size evolution in the mammals²⁵ we included linear and quadratic effects of body-size in the Fabric-regression and PGLS regression models.

Marginal likelihoods of the models calculated using stepping-stones²⁷ favoured the Fabric-regression model with linear and quadratic effects of body size over the same model but including only the linear component of body size (Table 1, BayesFactors averaged over 18 independent Markov chains = 25), and over the PGLS model including the linear and quadratic effects of size (BayesFactors > 230).

The PGLS model with linear and quadratic effects returns an R² of \(\sim\)0.86 (Table 1, phylogenetically corrected and average of the posterior distributions from 18 Markov chains) for the relationship between log₁₀(brain size) and log₁₀(body size). The linear regression coefficient was 0.69 ± 0.0004, but the quadratic coefficient was −0.023 ± 0.00006, indicating that increases in brain size slow as body size increases, as has been reported previously²⁵. Including the directional and evolvability effects of the Fabric-regression model R² increases to \(\sim\)0.91 (Fig. 1a, b and Supplementary Data 1), meaning the directional and evolvability effects account for roughly 5% of the variance in whole brain size and 36% of the variance that remains in brain-size after accounting for variance associated with body-size.

a Observed brain size vs predicted brain size as derived from two models: magenta dots are predictions from a phylogenetic least squares regression model with linear and quadratic components (phylogenetically corrected R² ~ 0.86); yellow dots are predictions derived from the Fabric-regression model including directional and variance scaling effects and mostly fall closer to the regression line (phylogenetically corrected R² ~ 0.91); b residuals from the two models in (a) showing the narrower range of the residuals from the Fabric-regression model.

Full size image

The linear and quadratic effects of the Fabric-regression model are both smaller than their corresponding values in the PGLS regression (Table 1, t-tests > 100, \({p} \, < \, {1\times 10}^{-8}\), two-tailed), suggesting that some of the parametric form of the linear and quadratic effects may be brought about by clade or even species-specific directional effects, and illustrates why fitting all of the parameters simultaneously is important. Together, these two coefficients yield an instantaneous rate of change (slope) of brain size against body size evaluated at the average body size of \(\frac{d({{{\rm{brain}}}\; {{\rm{size}}}})}{d({{{\rm{body}}}\; {{\rm{size}}}})}{|}_{\bar{x}}=0.56\) where the average log₁₀(body size) in this dataset is 2.79. This is very close to the 0.55 value reported for the average of n = 116 brain-body regressions fitted within-genera²⁸ where any quadratic effect would be expected to be small, and to the linear PGLS model reported here and to one previously fitted to a smaller sample of brain and body-size data³ (see also supporting information to ref. ²⁵).

Numbers of directional and evolvability shifts differ in whole-brain vs independent-brain and are distinct processes

In what follows, we shall refer to independent brain size to denote that the variation being studied in the Fabric-regression model is independent of variation in its covariates. This independent variation is not equivalent to studying the variation in residuals from a PGLS regression line because the parameters of the Fabric-regression model (body size, body size², the directional shifts and the changes to evolvability) are estimated simultaneously, not in a two-step process, and as seen above they change the values of the regression coefficients (\({\beta }_{j}\)).

Directional changes

The Fabric model applied to whole brain data found 244 instances of directional phenotypic shifts in brain size widely scattered throughout the phylogeny (Fig. 2a; “Methods”: model fitting and posterior data and Selection of Model Parameters; Supplementary Data 2). This corresponds to a directional shift occurring in approximately 8.4% of branches, slightly higher than the 7.7% we reported previously¹ for body size, and corresponds to one directional shift appearing somewhere in the tree approximately every 750,000 years throughout the 176 million-year history of the Mammalian clade on the Time-tree-of-life.

a The position of directional effects in whole brain (red dots) and independent-brain (blue dots); b the position of changes to evolvability in whole (red squares) and independent brain size (blue squares). Black symbols in both panels indicate branches in which an effect occurred in the whole-brain and in the independent-brain.

Full size image

The Fabric-regression model, now studying the evolution of brain-size simultaneously accounting for linear and quadratic components of changes to body-size, yields just 68 instances of directional shifts, a 71% reduction in the frequency of changes observed in whole brains (Fig. 2a), and corresponding to a change in independent brain size roughly every 2.6 million years: evidently there have been far fewer directional selective forces acting specifically on independent brain size than on whole brain or its covariates. The majority of the 68 directional changes in independent-brain size (n = 44, 64%) were not apparent in whole brain—they occur in branches in which there was no significant overall change in whole brain size (Table 2, left panel), and only 24 are common to both analyses. Had brain size been studied on its own, these independent directional changes would have been missed. Equally, many apparent changes to brain size when studied on its own would have arisen from its relationship with body size. This illustrates the potential for methods that do not account for covariation to mischaracterise the rate of adaptation, timings and inferred optima of evolving traits.

Independent brain size can move in the opposite direction to whole brain (Table 2, right panel): 13 or roughly 20% of the directional changes in independent brain size differ in sign from those observed empirically in the same 68 cases for whole brain. For example, whole brain size increases significantly in the Black-footed tree-rat (Mesembriomys gouldii, β_ik = 0.55), but its independent brain size significantly decreases (β_ik = −0.22). When the data are in logarithmic form a directional change translates in the unlogged data to the ratio of the descendant to the ancestral state, which here implies a 10^0.55 or 3.55-fold increase in whole brain size during the 8.25 million years in the branch leading to this species, but a 40% reduction in independent brain size: Black-footed tree-rats appear to have got bigger but simultaneously less ‘brainy’ at some point in the past.

Evolvability changes

Unlike the frequency of directional changes, which declines for independent brain size, the frequency of changes in evolvability increases. We observe 180 evolvability changes in whole-brain but 228 in independent brain size (Fig. 2b), and just 47 of these occur in the same branch of the tree (Table 3, left panel, \({\chi }_{1}^{2}=88.4,\;p\, < \,0.0001\)). This leaves 181 of the changes in independent-brain size evolvability that are not present in the whole-brain measure: accounting for covariation of brain size with body size has unmasked an increased realised evolvability of independent-brain size that is not apparent in whole-brain data. As with directional changes, changes to evolvability can differ in polarity between whole-brain and independent brain (Table 3, right panel). Among the 228 instances of changes in evolvability of independent brain size, around a quarter show the opposite empirical pattern in whole-brain.

Directional and evolvability changes are distinct processes

We have emphasised that directional shifts do not necessarily require any change to the Brownian variance of evolution. They can arise from selection acting on the variance available within populations. In this important sense, they are distinct from shifts in evolvability which, by definition, involve either an increase or a decrease in the evolutionary exploratory behaviour of the null Brownian process while saying nothing about the direction of change: the neutral Brownian process has a mean expected change of zero, whatever the value of \({\sigma }^{2}\).

Still, it is an open and fundamental question of macroevolution whether changes in macroevolutionary exploratory behaviour are often linked to directional change. Across all species, there are slightly more pairs of branches than expected by chance in which a directional shift in whole brain size occurs in parallel with a change in evolvability (Table 4, left panel, \(\left.{\chi}_{1}^{2}=27.59,p \, < \, 0.0001\right)\). But even in this instance, there are 210 instances of a directional change occurring on its own and a further 146 in which evolvabilities change without a directional change in brain size.

The two processes do not even show this weak linkage in the case of changes in independent brain size (Table 4, right panel, \({\chi }_{1}^{2}=1.52,n.s.\)): directional shifts in independent brain size, both getting larger and smaller, occur independently of any change to the Brownian variance. Independent brain size in the bats (Order Chiroptera) decreases around 3.1-fold (~70% reduction) along the long branch leading to the common ancestor of this Order. This is followed by an approximately 4-fold decrease in the Brownian variance within the Order compared to other Mammals (υ = 0.26). But in a subset of 51 species of the fruit bats (Sub-Order Macro-Chiroptera), independent brain size nearly doubles (~1.8-fold increase) with no concomitant change to evolvability.

The making of a relatively big (or small) brain: two case studies

Residuals calculated from a phylogenetically corrected regression identify species with relatively large or small values of some trait, having accounted for variance shared with covariates. But the residual does not reveal when during the history of the species the change or changes occurred that led to that outcome, and can mask other effects; the same is true of measures such as the encephalisation quotient²⁹ that rely on the ratio of brain to some function of body size. The Fabric-regression makes it possible to pinpoint those events or events and to ask whether the pattern of changes differs among species. We give two examples.

Homo sapiens’ residual brain size as measured from the PGLS regression line including the linear and quadratic components of body size is 0.80, the largest in this dataset, in line with conventional thinking that humans have the largest relative brain size of any mammal. The Fabric-regression model identifies two large directional increases in independent brain size in H. sapiens’ history, one in the branch leading to the New and Old World monkeys (Catarrhini and Platyrrhini, directional \({\beta }_{{ik}}\) = 0.47, 2.95-fold increase) and then the second in the branch leading to H. sapiens from our common ancestor with the chimpanzees (directional \({\beta }_{{ik}}\) = 0.52, 3.3-fold increase; the two \(\beta\) values do not need to sum to the value of the residual).

The Asian Elephant (Elephas maximus) also has a relatively large brain with a residual from the same PGLS regression line of 0.49. But unlike H. sapiens, there is just a single large directional change reconstructed in independent brain size in its history—at least as reflected by the extant species—and it occurred along the branch leading to the African and Asian elephants from their common ancestor with the small Hyrax (Procavia) species. This is the largest directional change in independent brain size along a single branch (β_ik = 0.90, a 7.94-fold increase in independent-brain size) in the data set, even larger than the final event of encephalisation in humans.

The difference between these two cases suggests that humans share some features (and possibly causes) of our relatively large brains with other monkey species (excluding Prosimians), and a component that is unique to the Hominins. Elephants’ relatively large brains might be linked to a single event, unique to them; alternatively, fossil taxa could reveal that the extant elephants share this increased encephalisation with one or more directional changes that occurred in a larger, now mostly extinct, group. This example points to the important contribution that fossils can make and more generally calls attention to how differences in the timings and patterns of change between different groups of species could guide research that attempts to link different brain structures to life history, development, other aspects of morphology or the environment.

We find qualitatively different patterns of macroevolutionary behaviour in independent-brain size compared to whole brain, including differences in the direction of change and the polarity of evolvability. Directional shifts in independent brain size are far less common than in whole brain, but changes to evolvability—the majority towards increased evolvability—are more common. These results seem to suggest that while specific directional forces acting on independent brain size are few, the variation in brain size that is independent of body size reflects adaptations to an ever-expanding range of forms over macroevolutionary time. Where the whole brain might include many sources of variation, the variation in the independent component may implicate any of the numerous functionally-specific regions of the brain and may reflect the influence of specific ecological factors, although how best to characterise brain size given its relationship to body size remains contentious^30,31.

Many of the traits studied in phylogenetic-comparative analyses have allometric relationships to body size raising the prospect that traits other than brain size will show similar qualitative differences when studied alone vs in concert with body size. More generally, the \({{\boldsymbol{X}}}\) matrix of Eqs. 1 and 2 can include variables such life history traits, or latitudinal and climatic effects that might need to be accounted for in studies of productivity. Categorical factors that identify differences among species in diet or mating system, or used to test for interactions between categorical variables and covariates can also be included in \({{\boldsymbol{X}}}\) either alone or alongside morphological traits. Fossil taxa can be incorporated into the tree either as branches that go extinct before the present, or to specify ancestral states. Their use can enhance confidence in relationships inferred from extant taxa alone³².

The ability to accommodate one or more covarying traits in statistical comparative analyses means that researchers can use the formal methods of causal inference to gauge support for hypothesised causal pathways, while accounting for conditioning, confounding and colliding variables³³. In trying to understand whether selected ecological variables, such as sociality and diet³⁴, might affect brain size, body size is a conditioning variable. In this setting a rooted phylogeny—a form of directed acyclic graph—acts as powerful inferential aide by bringing a real or hypothesised arrow of time to the setting. The approach would be to identify on the branches of the phylogeny changes in diet or sociality and then link them to directional changes in brain size conditioning upon body size.

If accounting for the influence of covariates unveils new components of variation that conventionally go unseen, a class of macroevolutionary questions beckons to be tested on independent trait variation. We showed that directional and evolvability shifts are weakly linked in the case of whole brains but not linked for independent brain size. This result is an example of a far more general macroevolutionary question regarding the factors that may lead to phylogenetic radiations of species. One definition³⁵ proposes that radiations comprise “the evolution of ecological and phenotypic diversity within a rapidly multiplying lineage” that descends from a common ancestor. A study of mantellid frogs (Mantellidae) does something close to this by including speciation rates alongside estimates of phenotypic diversity in comparisons among chosen clades³⁶. The evolvability parameter, \(\upsilon \, > \, 1\), provides a statistical definition of increased phenotypic diversity, and using the \(\upsilon \, > \, 1\) test either alone or in conjunction with tests of speciation rates could put this widely used macroevolutionary concept on a testable empirical footing, and without having to specify in advance which clades might be ‘radiating’.

Quantitfying what we mean by radiation is important^36,37: a test of phenotypic diversity would not class the 298 species of the Chiroptera clade in this dataset as a radiation because their phenotypic diversity has declined \((\upsilon \sim 0.24)\), and this includes reduced diversity in body size^1,5. Reduced diversity in brain and body size might not be representative of other measures of this clade’s evolution, but we emphasise the value of attempting to operationalise changes to phenotypic diversity statistically. Using an empirically-derived measure such as \(\upsilon\), it is straightforward to ask whether directional shifts in traits are linked to changes in evolvability and whether this holds for variation in independent trait values (that is, variation having removed the effects of covariates). More generally, do directional shifts tend to precede, follow or bear no relationship to evolvability? Studies document how Brownian variances can vary with, for example, developmental³⁸ or trophic behaviours³⁹, but this central question of macroevolution regarding the causal direction linking directional and evolvability changes has not, to our knowledge, been investigated systematically. Applying statistical criteria to either whole or independent traits, and in a setting that allows both kinds of effect to evolve anywhere in the tree, could test this notion rigorously.

Many other macroevolutionary hypotheses await empirical testing with independent trait values. Elsewhere we¹ have shown how Mammalian body size seems to evolve punctuationally or in bursts along branches of the Mammal phylogeny, and we have shown that the rate of accumulation of these punctuational episodes is close to constant throughout the many millions of years of Mammalian evolution. Others report that perhaps half of all Primate speciation events yield evidence of accelerated changes in brain and body size²⁴. Is this punctuational pattern widespread taxonomically and does it hold once the effects of covariates such as body size are accounted for? Is it linked to the number of directional changes that occur along a path leading to a species such as we investigated for H. sapiens and the elephants? Equally, evolvability changes seem to have a strong bias towards greater than towards lesser evolvability within clades, and this holds true here for both brain size and independent brain size (Table 2). Perhaps this is what we expect from a constantly shifting environment in which species must compete for their existence^1,40 ? More traits need to be tested to establish this pattern’s generality.

The existence of large numbers of instances of increased evolvability throughout the tree and right up to the present for both whole and independent trait size (Fig. 1b) suggests that neither species’ brain sizes nor their independent brain sizes are settling down around stable global or even local optima. Instead, clades seem to be expanding their exploratory capacities in response to an ever-expanding range of opportunities such as might be represented in the ‘blunderbuss’ pattern⁴¹. Rapid temporal fluctuations in the selective environment are common⁴², rendering optima highly ephemeral, so much so that one study of cetacean body size likened the surface of the adaptive landscape to that of a “turbulent ocean”⁴³. This is a point with independent empirical^44,45 and theoretical⁴⁵ support, even when fossil taxa are available to augment the historical signal⁴³, and it is this turbulence that the directional effects (\({\beta }_{{ik}}\)) can potentially discover⁴³. Arnold⁴⁶ (p435), summarising over twenty years of modelling macroevolutionary phenomena, adopts the view that models of “trait means chasing a perpetually moving adaptive peak provides a strong basis for understanding adaptive evolution”, and that Brownian motion provides a good characterisation of an expanding range of adaptive peaks^45,46.

Darwin feared that one day someone might find a complex trait that had not evolved according to his notions of gradualism, saying, “If it could be demonstrated that any complex organ existed, which could not possibly have been formed by numerous, successive, slight modifications, my theory would absolutely break down. But I can find no such case.” Macroevolution sits in the privileged position of observing traits evolving over time periods long enough to witness events relevant to Darwin’s daring hostage to fortune. And it is statistical models of macroevolution such as developed in recent years (e.g. refs. ^{6,20,21,24,46,47}) that allow us to ask if what we observe on a macroevolutionary timescale is compatible with Darwin’s microevolutionary mechanism^1,48. Without this goal the study of macroevolution risks being little more than a phenomenological undertaking.

Data

The brain- and body-size data are available from Venditti et al. ²⁵.

Model estimation

Let Φ be a vector of the parameters of the model of trait evolution including the nominal root, \(\mu\), the vector of directional change parameters, β, the vector of evolvability parameters, υ. We estimate the posterior density of Φ in a Bayesian RJ-MCMC²² setting that allows the number of directional and evolvability parameters that depart from their default values to vary around a stationary set from one iteration of the chain to the next. The posterior density is written as in Eq. 3 in the main text, repeated here:

where \(L\left({D|}\Phi \right)\) is given by Eq. 2 (main text), the \(p\left(\varPhi \right)\) are the prior distributions of the parameters of the model of trait evolution, and the Monte Carlo integration is over \(d(\varPhi )\).

Priors

We choose the \(p\left(\varPhi \right)\) to be compatible biologically with the processes they represent (see ref. ⁹). In practice choice of a prior arises from a series of preliminary analyses in which a range of prior distributions is tried, looking for evidence that a prior does not constrain the posterior set of parameters while simultaneously not being overly lenient and allowing biologically unrealistic values (Supplementary Note 2, Supplementary Fig. 1, and Supplementary Tables 3 and 4). We apply a Gamma prior to the evolvability parameters \(\upsilon\) ~ Gamma (\(\alpha,\beta\)), where \(\alpha\) = 1.2 and \(\beta\) = 5. This produces a right-skewed distribution with a lower limit of zero and a mode of 1, the default value. Values of the variance scalars become less probable the further they are from 1. As a prior on the directional effects, we assume |β| ~ Gamma (\(\alpha,\beta\)), where \(\alpha\) = 3.2 and \(\beta=0.2\), giving a right-skewed distribution with a lower limit of zero, a mean of ≈0.64 and a standard deviation of 0.36. Priors on the linear and quadratic regression coefficients were ~N(0, 2) and ~N(0,1). The prior on \({\sigma }^{2}\) was U(0,1).

Model fitting and posterior data

We find the set of parameters in Φ using an RJ-MCMC procedure that we have employed elsewhere to search high-dimensional spaces^49,50. The stationary Markov chain yields posterior distributions of directional and variance-scaling parameters at each node or branch of the tree (some or even many of the nodes and branches will never receive a parameter and thereby be centred at their null values).

We ran the Markov chain of Eq. 3 (main text) until it reached a stationary state, then drew 1000 posterior samples from the stationary chain at widely spaced intervals to ensure a low (r ~ 0.1) autocorrelation among successive sampled iterations. The parameter values we report for the directional and evolvability effects are means averaged over these 1000 samples, having adjusted the sample size for autocorrelation.

Selection of model parameters

For inferences about the numbers and locations of directional and evolvability parameters throughout the tree, we drew on six independent RJ-Markov chains and selected as significant only those parameters that appeared in all six chains at frequencies greater than expected by chance¹. This procedure ensures that parameters are chosen based on their consistency in appearing in the model and not on their magnitudes. Among the 15 pairs of runs from the six independent chains, directional parameter values intercorrelated on average >0.99 and evolvability parameters >0.95. Where we report the occurrence and polarity of directional and evolvability effects, these will be identical across all six runs used for inference. In a small number of examples where we report the magnitude of an effect, we have taken the value from one of the runs chosen at random rather than averaging across the six runs. This maintains a direct link between the data and results, but any of the runs would have led to the same conclusions.

Measurement error

Trait data may contain errors of measurement, and their effect, if present, will tend to be most prominent in the terminal branches of the phylogeny, where they may be indistinguishable from real directional and evolvability changes. The Fabric and Fabric-regression models do not estimate errors of measurement, but instead, we advocate checking directional and evolvability effects that occur in terminal branches or clades for evidence of unusual or unexpected trait values.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.