Introduction

Nano-kirigami, inspired by the ancient art of paper cutting and folding, has recently emerged as a promising method for three-dimensional (3D) nanomanufacturing1,2,3,4,5,6. Unlike traditional layer-by-layer stacking, nano-kirigami enables the direct transformation of 2D precursors into 3D architectures through out-of-plane folding, bending, and/or twisting. Such in-situ shape transformation significantly simplifies the fabrication of 3D nanostructures and has obtained attention across diverse fields, including microelectromechanical systems (MEMS)7, extraordinary mechanics8,9,10,11,12,13, biomedical devices14,15,16,17, acoustic materials18,19,20,21, energy storage systems22,23,24,25, microwave metamaterials26,27, and terahertz spectroscopy28.

Another key advantage of nano-kirigami is its ability to create smooth, continuous curvature changes compared to the abrupt boundary transitions seen in layer-stacked structures29. This characteristic is particularly beneficial for the motion of free electrons. In micro-nanophotonics, for example, nano-kirigami structures can excite collective surface plasmons, enabling the exploration of chiroptical properties in metallic metasurfaces and allowing for dynamic regulation of electromagnetic waves30,31. However, the performance of these metastructures is often limited by Ohmic losses inherent in metals32,33. This issue can be alleviated by utilizing dielectric materials, among which silicon-on-insulator (SOI) platforms emerge as an ideal solution. SOI, being highly commercialized and CMOS-compatible, is widely used in integrated optics and on-chip photonic devices34,35,36. Therefore, the integration of precise nano-kirigami techniques with silicon-based materials could hold great potential to unlock versatile deformation paradigms and expand the performance boundaries of various technologies.

In this study, we present a profound study on three deformation behaviors in silicon-based nano-kirigami structures, including plastic deformation with bidirectional three-stage reversal, elastic deformation with 10 nano-Newton (nN) level mechanical response, and hysteretic deformation with bistability. Exotic observations reveal that nano-kirigami designs are capable of enabling rich deformation states with the same material platform under specific conditions, showcasing remarkable adaptability and delicate responses to external modulations. The underlying mechanisms, including ion-induced progressive stress competition and residual charge accumulation in the SiO2 layer, are thoroughly investigated. The designable elastic and hysteretic deformation modes are further employed to demonstrate the applications in dynamic optical information encryption. Our research provides a comprehensive understanding of the versatile deformation processes, paving the way for future technological innovations and underscoring the vast potential for a wide range of applications from responsive and adaptive materials to functional nanoscale devices.

Results

Nano-kirigami on SOI

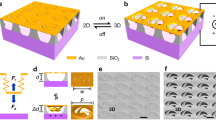
Here a commercial SOI wafer is used as the silicon-based platform, which consists of three layers: a Si device layer (with thickness t), a buried SiO2 layer, and a Si substrate layer (750 µm in thickness). As illustrated in Fig. 1a, the 2D precursor structures can be directly patterned into the top silicon layer by using standard focused ion beam (FIB) milling or electron beam lithography (EBL)1,5,29,30,31,37. Following this process, a precisely controlled wet etching process is employed to free the structures from the integrated substrate. These suspended 2D structures are then deformed into 3D configurations—either upwards or downwards—depending on the applied stress, as shown in step III or IV of Fig. 1a. For ease of understanding, here three representative types of deformations are defined in Fig. 1b–d, which will be investigated in the following sessions.

Fig. 1: Illustrations of SOI-based nano-kirigami.
figure 1

a Flowchart of the nano-kirigami process on an SOI chip. 2D precursors are patterned by FIB or EBL followed by a wet etching process, which can be deformed upward or downward upon request. b Plastic deformation exhibiting permanent bidirectional deformations under FIB irradiation. c Elastic deformation exhibiting instantaneous recovery under mechanical or electrostatic forces. The vertical axis in the inset is displayed in arbitrary units (a.u.). d Hysteretic deformation exhibiting time-dependent recovery under variable electrostatic forces due to charge accumulation and relaxation. Scale bars: 1 µm.

Full size image

Plastic deformation (Fig. 1b). This type of deformation is permanent, meaning the structure does not return to its original shape after ion irradiation.

Elastic deformation (Fig. 1c). The structure deforms due to mechanical pressure or electrostatic attraction, which quickly returns to its original shape once the stimulus is removed.

Hysteretic deformation (Fig. 1d). Unlike the rapid recovery seen in elastic deformation, hysteretic deformation recovers much more slowly. Additionally, after the external field is removed, the structure can still be deformed due to residual effects.

Bidirectional plastic deformation

Figures 2a–e show silicon nano-kirigami structures with versatile geometries, which are directly fabricated with FIB (see Methods). Compared with nano-kirigami structures made of gold1,31,37,38, silicon-based nano-kirigami has three features. First, silicon39 has a higher Young’s modulus than gold40, making it more resistant to capillary forces after wet etching. This enables the fabrication of widely spanned silicon structures without adhering to the substrate, which is highly desirable for the large-range deformation process, such as the mushroom-like structures and Fibonacci triple windmills in Fig. 2c–d. Figure 2e further shows the successful suspending and deformation of a 15-μm-wide spring-like structure with a length-to-thickness ratio of more than 200 (see Supplementary Movie 1). Second, the beneath SiO2 supporters can be clearly identified since the top device layer is less than 100 nm, such as the region enclosed by the dashed lines in Fig. 2a and the central dark parts in Fig. 2b, which are very helpful for the accurate control of the wet etching process and the stable support of large structural arrays (Fig. 2f–h). Third, the silicon-based nano-kirigami technique is fully compatible with CMOS processes, which are desirable for massive production (see Supplementary Movie 2 for the simultaneous deformations of an array). As shown in Fig. 2f, by leveraging the efficiency and uniformity of EBL, a large array of 19,044 windmill structures is readily fabricated on the SOI substrate. It should be mentioned that such a large number of 2D structures were transformed into 3D states within just 120 sec under a rapid low-dose FIB irradiation, as shown in Fig. 2f–h. Such high-speed and high-uniformity 3D deformations emphasize the vast potential of SOI-based nano-kirigami in a wide range of applications, such as microelectromechanical systems (MEMS), pressure sensors, and integrated circuits. For example, the high-order photonic bands are observed in the 3D deformed windmill array of Fig. 2g, which are not visible in the 2D structure of Fig. 2f (see Fig. S1b) and demonstrate an application potential of 3D plastic deformation.

Fig. 2: SEM images of silicon nano-kirigami structures before and after FIB irradiation.
figure 2

a, b Windmill structures with (a) upward and (b) downward deformations after FIB irradiation. c A mushroom-like and (d) a twisted triple Fibonacci spiral structure, showing downward deformation after FIB irradiation. e A widely spanned plate with nano-spring in the center shows successful suspending and upward buckling after FIB irradiation. f, g Windmill structures in a square lattice before and after FIB irradiation. h Top-view SEM image of a large windmill array. The overall size of the array is 200 μm × 200 μm, with a period of 1.45 μm in (f–h), showing high uniformity, large-scale, and rapid 3D deformable manufacturing of the method. Scale bars: 1 µm. Structural parameters: t = 55 nm in (a, f–h); t = 70 nm in (b–e).

Full size image

An interesting observation in Fig. 2a–e is that the plastic deformations are bidirectional and dependent on different geometries. More specifically, it is found in the same platform (t = 70 nm) that the deformation direction of the cantilever beam structure reverses from downward to upward (see Fig. S2 and Supplementary Movie 3), of which the windmill structure reverses from upward to downward, while the Archimedean-like spiral structure (Archi-270, the types of which are defined in Fig. S3a) exhibits a three-stage bidirectional plastic deformation with double reversals (see Fig. S3 and Supplementary Movie 4), as shown in Fig. 3a. Although the first reversal (from downward to upward) of the cantilever can be readily explained by the change from compressive to tensile forces with the increase of irradiation dose1,41, the second reversal of the windmill (from upward to downward) is abnormal. To find out the behind rule, the same windmill structure is continuously irradiated by gallium ions (Ga+) beams with increased doses to quantify the observations, the center height of which is extracted as a function of the irradiation dose in Fig. 3b. It is observed that the windmill begins to reverse its deformation direction at a dose of 4.08 × 1015 atoms/cm².

Fig. 3: Bidirectional deformation mechanism of windmill structures.
figure 3

a SEM images of cantilever (deformed firstly downward and then upward), windmill (reversed from up to down) and Archi-270 spiral structure (reversed from downward to upward, and then back to downward) under FIB irradiation with increased dose. Scale bars: 1 µm. b Deformation height of the windmill in (a) (measured at point C) versus irradiated Ga+ dose. The Ga+ irradiations are with (I) zero dose, (II) low dose of 4.08 × 1015 atoms/cm² and (III) high dose of 6.8 × 1015 atoms/cm². c Schematic diagram of silicon thin film under Ga+ irradiation. d Distributions of the induced vacancies and the probability distribution of Ga+ implantation versus the depth of silicon film. e Calculated distribution of resultant forces within a silicon film and the schematic illustration of moments. (\(\left|{k}_{1}/{k}_{2}\right|\,=\,2.15\)). f Calculated deformation heights and corresponding moments of windmill structures versus \(\left|{k}_{1}/{k}_{2}\right|\). Inset, numerically simulated images of the deformed windmill at each case.

Full size image

The fundamental reason for such bidirectional plastic deformation is the distinct residual stress distribution in the silicon layer under gallium ion irradiation. Specifically, the collisions of high-energy Ga+ simultaneously create vacancies and implantations within the irradiated materials, introducing tensile and compressive stresses, respectively, as illustrated in Fig. 3c. According to the simulations, the distributions of vacancies and implantations in silicon extend more than 50 nm from the top surface, comparable with the silicon film’s thickness (70 nm). As a result, the stresses in the upper half layer and lower half layer of silicon film play an opposite role in determining the deformation direction. For example, the same tensile stress in the upper layer exerts an upward force on the silicon film (as illustrated by the schematic III-state in Fig. 1b). In contrast, in the lower layer, the tensile stress exerts a downward force (as illustrated by the schematic IV-state in Fig. 1b). Another important point is the spatial misalignment between the concentration peaks (located around 18 and 28 nm, respectively, in Fig. 3d) which delineate the regions of the tensile and compressive stress, making the deformation behaviors highly sensitive to the structural stiffness and the Ga+ irradiation dose. The resultant stress competition induces bidirectional deformation that evolves in three stages, which entirely or partially appear in different nano-kirigami designs with distinct topological geometry and mechanical stiffness (see the discussion in Supplementary Discussion). Compared to the observation of single deformation reversal in previous studies41,42, such a finding of two reversals offers a more comprehensive understanding of the evolution of induced stress within silicon thin film under ion irradiation.

Quantifying such a reversal phenomenon is challenging due to the complicated and dynamic change in atomic-level collisions. To address this issue, the results are analyzed by using a linear cascade sputtering theory and atomic peening model43. Specifically, the compressive stress induced by gallium ions implantation is proportional to the number of ions, and the tensile stress caused by vacancies is proportional to the number of vacancies. The irradiation of each gallium ion creates multiple vacancies along the way and finally stops at a certain depth. The probability distribution of the ions and the distribution of vacancies are defined as \({D}_{G{a}^{+}}(z)\) and \({D}_{{Vac}}(z)\), respectively, as calculated and plotted in Fig. 3d. Therefore, the two forces along the Z direction under dose \(j\) can be expressed as \({F}_{G{a}^{+}}={k}_{1}{{jD}}_{G{a}^{+}}\) and \({F}_{{Vac}}={{k}_{2}{jD}}_{{Vac}}\), where both \({k}_{1}\) and \({k}_{2}\) are the proportionality parameters that are related to the dose. Due to the opposite directions of tensile and compressive forces, we define \({k}_{1}\) has a negative sign and \({k}_{2}\) has a positive sign. The resultant stress at each depth can then be obtained through the combination of these two forces:

$${F}_{N}={k}_{1}\;j{D}_{G{a}^{+}}+{k}_{2}\;j{D}_{{Vac}}$$
(1)

as shown in Fig. 3e (see Fig. S4 and Supplementary Note). The influence of the resultant stress on the deformation can be estimated by using the torque model: the resultant moment can be calculated by integrating the moment at each depth as:

$${{\bf{M}}}=\int {{\bf{r}}}\times {{{\bf{F}}}}_{{{\bf{N}}}}{dr}$$
(2)

Setting the center of the silicon film thickness at \(Z=0\), the structure deforms upward when \(M > 0\) and deforms downward when \(M < 0\). Meanwhile, with the increase of ion dose \(j\), the generation of vacancies tends to be saturated44 (\({k}_{1}\) is nearly constant while \({k}_{2}\) decreases), which causes the increase of \(\left|{k}_{1}{/k}_{2}\right|\). In such a case, the deformation height at the equilibrium state (\(\varDelta Z\)) and the resultant moment (\(M\)) are plotted as a function of \(\left|{k}_{1}{/k}_{2}\right|\), as shown in Fig. 3f. It can be seen that the evaluation of \(\varDelta Z\) and \(M\) are highly correlated: the windmill initially deforms upward when \(M > 0\), and gradually tends to deform downward when \(M < 0\). The greater the absolute value of positive or negative \(M\), the larger the upward or downward deformation, agreeing well with the trend in experiments. Therefore, with the above torque model, the observed reversal of the deformation changes from upward to downward in windmill structures is successfully explained by the stress competition induced by the spatial misalignment of vacancies and implanted ions.

It should be mentioned that such bidirectional plastic deformation properties are found to be dependent on the silicon thickness. Our experimental results (Fig. S5a–c) show that the 80-nm-thick windmills exhibit bidirectional deformation behaviors similar to the 70-nm-thick samples, but with dramatically reduced upward displacement height. In comparison, the 55-nm-thick windmills show unidirectional upward deformation only. Such observations are well consistent with theoretical results (Fig. S5d), indicating that there is an optimal thickness where both notable downward and upward deformation can be observed. For silicon films much thinner than this optimal, the windmills simply deform upward. While for silicon films much thicker than this optimal, only downward deformation is evident.

Meanwhile, the bidirectional plastic deformation properties are also found to be material-dependent. Compared with previous studies with gold, the usage of Si is not merely a material replacement but a substantial leap forward. First, besides the CMOS compatibility, the nano-kirigami designs are found helpful to increase the failure strain of bulky silicon and robust to high voltage (see the next sections). Second, the proposed stress competition mechanism exhibits material-dependent applicability governed by fundamental material characteristics. As demonstrated by SRIM simulations (Fig. S6), for thin films made of light elements such as silicon and aluminum, the distribution peaks of Ga+ implantation and vacancies exhibit large separation, enabling strong stress competition. In comparison, for heavy elements like silver and gold, the distributions exhibit compressed profiles with smaller separation between the peaks of implantation and vacancies, which are compromised and result in weak competition. Such numerical predictions are verified by the dramatically different bidirectional deformation phenomena between gold and aluminum (Fig. S7). Therefore, the bidirectional deformation mechanism is justified and provides transformative insights into nanoscale plasticity across material systems.

Elastic deformation and dynamic modulation

As silicon has been widely employed in MEMS structures, here the silicon-based nano-kirigami structures are also very desirable for elastic deformation and dynamic modulation. In this aspect, a web-like kirigami structure is proposed in Fig. 4a, which consists of a central disk and surrounding concentric arcs (here treated as a reticular nano-spring). The diameter of the disk and the width of the surrounding nano-spring can be flexibly designed with variable mechanical properties, such as the Web-6 and Web-8 structures shown in Fig. 4b. One feature of such a design is that the external forces can be exerted on the suspended central disk while the elasticity of the surrounding nano-spring structures supports the reversible displacement, as the probe-landing scheme illustrated in Fig. 4a and the simulation results shown in Fig. 4c. For experimental demonstration, a multifunctional in-situ SEM nanoindenter (FT-NMT04, FemtoTools) is employed to repeatedly press and release the nano-spring structures at a constant speed of 10 nm/s, as illustrated in Fig. 4b and Supplementary Movie 5. The recorded data in Fig. 4d show that the maximum deformation height is ~1.25 µm since the landing time is ~125 seconds. The maximum restoring forces of the Web-6 and Web-8 are measured at 55 and 20 µN, respectively, and both structures show elastic behaviors without damage. It should be mentioned that benefiting from the nanoscale kirigami designs, the maximum strain values of silicon during deformations in this study can be as high as 9.04% (Fig. S8), which is much larger than the failure strain of bulky silicon while comparable with that of silicon nanowires45. This ensures the test repeatability without structural damage.

Fig. 4: Elastic deformation of reticular nano-spring structures.
figure 4

a Schematic of the nano-spring structure with a central disk and surrounding concentric arcs (reticular nano-spring), and the reversible probe landing scheme. b SEM images of two structures under the deformation process. The width of Web-6 and Web-8 structures are 6 and 8 µm, respectively, while the diameters of central disks are both at 3 µm. c Stress distribution diagrams of Web-6 and Web-8 structures with deformation height of 1.25 μm, corresponding to maximum strain values of 9.04% and 3.78%, respectively. d Recorded force applied onto the central disk versus time when the probe pushes the structure first, touches the substrate, and retracts backward at a constant speed of 10 nm/s. e Measured (dotted lines, with minimum response force of 10 nN) and calculated (thick gray lines) force versus the vertical displacement of the central disk, showing high consistency. The inset illustrates a simplified nano-spring model of the web structures, which is valid in the small-deformation region (solid lines). f SEM image of a reticular structure with a central disk diameter of 10 µm and overall width of 18 µm. g Schematic of the electromechanical reconfiguration of the reticular structure in (f). h Measured reflected intensity versus time at wavelength 732 nm when an alternative voltage of 200 Hz is applied on the reticular structure in (f). Scale bars: 1 µm.

Full size image

To test the response of the reticular nano-spring structure to tiny force, the probe-landing experiment is further conducted by utilizing an AFM probe (RTESPA-300, Bruker), with which a force of 10 nN is able to induce a visible displacement of larger than 2.5 nm for the reticular structure. The relationship between the exerting forces and the displacement of the central disk is plotted in Fig. 4e (dotted lines), which agrees well with the numerical calculations (thick gray lines) and is highly repeatable (see Fig. S9a). Furthermore, such a nano-spring structure can be simplified as a spring-mass system in the inset of Fig. 4e, where the concentric kirigami arms surrounding the central disk function as a spring (with mass m, spring constant k, and length l). One end of the spring connects to the central disk (with mass M), while the other end is attached to the fixed-top silicon membrane. With displacement (\(d\)) as the disk movement in Z-direction, the vibration frequency of this system can then be expressed as46 \(f=\frac{1}{2\pi }\sqrt{\frac{k}{{m}_{{eff}}}}\), where the effective mass \({m}_{{eff}}\) is given by \({m}_{{eff}}=M+\frac{1}{3}m\). Here, \(M\) and \({m}\) can be calculated from the volume and density of silicon, and \(f\) can be obtained based on numerical calculations. As such, one can then obtain the spring constant by

$$k=4{\pi }^{2}\left(M+\frac{1}{3}m\right){f}^{2}$$
(3)

It can be seen in Fig. 4e that the calculated curves by \(F={kd}\) agree well with the experimental data when d < 200 nm, indicating such a nano-spring model is valid in the small-deformation region.

One important feature of such a design is that both sides of the central disk and the surrounding nano-spring can be readily customized (Fig. 4f), forming a platform for potential applications. For example, by applying electrostatic force between the top and bottom layers, reversible elastic deformation in the vertical direction is induced, as schematically illustrated in Fig. 4g. In this process, the central plate of the web and the surface of the bottom substrate form a Fabry-Pérot (F-P) cavity. When a voltage of less than 25 voltage (V) is applied, the web structure is deformed and the F-P cavity length changes thus the spectral response is varied. To quantify such an effect, the web structure is characterized by measuring the reflection signals under different voltages, and significant modulations of multiple F-P resonant peaks are observed (see Figs. S9c and S9d). The measured modulation frequency reaches 200 Hz, demonstrating good sensitivity and reversibility of dynamic modulations, as shown in Fig. 4h. These findings unambiguously emphasize the rich versatility of silicon-based nano-kirigami in both mechanical and electrostatic force-driven reconfigurations.

Hysteretic deformation

In addition to the above plastic and elastic behaviors, another interesting phenomenon observed in this work is the hysteretic deformation in silicon-based nano-kirigami. An illustrative example is the planar spring structure shown in Fig. 5a, which consists of a suspended main plate and two side-connected springs. The wet etching process is carefully controlled to keep 200-nm-thick silicon dioxide unetched. When a high voltage (>100 V) is applied between the structural layer and the bottom silicon substrate, the main plate is rapidly pulled toward the substrate due to the strong electrostatic force of induced charges as schematically shown in Fig. 5b. After turning off the voltage, the plate tends to swiftly return to its initial flat state due to the mechanically restoring force. Surprisingly, it is observed that when the applied voltage exceeds a certain threshold (>140 V), the structure that instantly returned to its flat state when the voltage was off will be pulled down to the substrate again, as shown by the microscopy image in the IV state of Fig. 5c and corresponding schematic illustration in Fig. 5d (also see Supplementary Movie 6).

Fig. 5: Hysteretic deformation of silicon nano-kirigami.
figure 5

a Side-view SEM image of a planar spring structure with size of 9.0 × 9.0 µm2 after wet etching. Scale bar: 1 µm. b Schematic illustration of the charge distribution within the structure during electrical tuning. c Top-view microscope images of the four distinctive states of the planar spring during the charge and discharge process. The four states are I: Initial state; II: Voltage-on state; III: Instant rebound state (swiftly returning to the flat state after cutting off the supplied voltage); and IV: Re-collapsed state following the instant rebound state. d Side-view schematic images of corresponding four states in (c). e Relative light intensity (defined as I/I0) versus time when the voltage is turned on and off at 140 V and λ = 950 nm. f Modulation contrast versus time [corresponding to the enlarged time period of the dashed rectangle in (e)] when different DC voltages are applied as noted. The light blue and blue regions denote the period when the voltage is turned off at 0 s, showing clear hysteretic effects.

Full size image

These observations unambiguously demonstrate that electrostatic forces persist even after the electric power is off, i.e., a prominent hysteresis effect occurs. A plausible explanation is that a capacitor forms between the planar spring structure and the bottom silicon substrate, with silicon dioxide serving as the dielectric medium. When voltage is applied, positive and negative charges accumulate on the two sides of the silicon dioxide layer, creating a strong electric field. This electric field induces charge migration within the silicon dioxide, leading to the excitation of electrons and the formation of high-energy electrons. Under the influence of the strong electric field, these high-energy electrons can overcome the band gap, resulting in ionization processes. During this process, electrons are trapped in electron traps within the silicon dioxide or captured around the localized defects47. This mechanism causes negative charges to accumulate near the anode, while positive charges accumulate near the cathode, ultimately leading to the accumulation of opposite charges at the interfaces, as illustrated by the distribution of residual charges in the SiO2 layer shown in Fig. 5b. After power-off, these charges within the SiO2 layer persist for an extended period, attracting charges in the silicon layers and thereby generating electrostatic forces. When the voltage exceeds the threshold (>140 V, 7 MV/cm), the reformed electrostatic force is sufficient to cause the structure to recontact with the substrate. Over time, the charges gradually dissipate, and the structure returns to its flat state.

To better characterize the entire deformation process, we measured the reflected light signal at wavelength 950 nm over time under a voltage of 140 V. The time-series responses in Fig. 5e further confirm the four observed states in Fig. 5c. Specifically, in the initial state (state I), the relative light intensity is 100%. When 140 V is applied, the relative light intensity drops to about 45% due to the deformation, indicating that the plate is in contact with the bottom layer (state II). After turning off the voltage, the relative light intensity quickly rebounds to nearly 100%, indicating that the structure is in state III of Figs. 5c–d. After 12 sec, the relative light intensity drops again to about 45%, indicating that the structure has contacted the bottom layer again, reaching state IV. ~40 sec later, the modulation contrast suddenly changes back to 75%, indicating that the structure detaches from the substrate. Finally, after a prolonged recovery period, the relative light intensity returns to 100%, representing the back to the initial state (state I). Such a hysteretic deformation process of the nano-kirigami structure is repeatable, as shown by the complete cycles in Fig. 5e.

Figure 5f further plots the time-series signals of relative light intensity under different voltages. It can be seen that for voltages below the threshold (110 and 130 V), the light signal rebounds to 75% instead of 45%, demonstrating that the reformed electrostatic force is insufficient to cause the structure to re-contact the bottom substrate. For voltages at or above the threshold (140, 150, and 160 V), the relative light intensity returns to 45%. Notably, the time required for the structure to re-contact decreases as the voltage increases, indicating a larger amount of accumulated charges within the silicon dioxide, which makes electrostatic force easier to be dominant in competition with mechanical recovery force. This also suggests that states IV and V of the structure represent two relatively stable states during the deformation process, which may provide an interesting methodology for potential studies on bistability. It should be mentioned that such a hysteretic deformation is not limited to this special planar spring structure but also exists in other structures, such as the linked windmill structures in Fig. S10 (also see Supplementary Movie 7).

Silicon-based nano-kirigami for optical information encryption

Both elastic and hysteretic deformations are of great significance for realizing functional 3D architectures with controllable mechanical responses, as they provide desirable versatility, stability, and tunability for a wide range of applications. Here, as a proof of concept, the silicon-based nano-kirigami is employed to demonstrate the potential in dynamic optical information encryption based on the precisely controllable deformation modes. As shown by the SEM image in Fig. 6a, two types of Archimedean-like spirals that possess different arm length and graded stiffness (i.e., \({k}_{{Archi}-240} > {k}_{{Archi}-270}\), see Fig. S3a) can be arranged to form a pattern with encoded information (capital letters “SOI”). When no voltage is applied (0 V), the microscope image in Fig. 6b shows no information due to the indistinguishable structural difference. When the voltage is increased from 90 to 130 V, the “SOI” letters emerge gradually because \({k}_{{Archi}-240} > {k}_{{Archi}-270}\), and only Archi-270 spirals in the letter areas deform when the electrostatic forces reach a certain level. However, when the voltage reaches 200 V and the electrostatic forces are large enough, both Archi-240 and Archi-270 spirals undergo significant deformation simultaneously, making the letters invisible again.

Fig. 6: Proof-of-concept demonstration of silicon-based nano-kirigami structures for optical information encryption.
figure 6

a SEM images of a SOI pattern encoded with the capital letters “SOI”. The spiral patterns in the letter area are composed of (i) Archi-270 spirals, while the other area is composed of (ii) Archi-240 spirals. b In-situ microscope images of the same SOI pattern when turning on the voltages of 0, 90, 130, and 200 V, respectively, showing the voltage-dependent deformation properties. c In-situ microscope images of the four distinctive states of the “SOI” pattern during the charge and discharge process at 210 V. The four states are consistent with those in Fig. 5c, d. Under this high voltage, the encoded information can only be displayed after turning off the voltage for toff = 1 s due to the hysteretic deformation. d In-situ microscope images of the “SOI” pattern at the hysteretic deformation state after prolonged exposure to a high voltage of 170 V with durations of ton = 5, 15, 30, and 1800 s, respectively, with no damage observed. e SEM images of a pattern encoded with capital letters “SONIC”. The letter “SOI” area is composed of (i) Archi-270 spirals, and the “NC” area consists of (ii) Archi-240, while the other area is formed by (iii) Archi-210 spirals. f Microscope images of the encoded “SONIC” pattern displayed under a voltage of 150 V for 600 s. Under this voltage, elastic deformation occurs, and the structure returns to its initial state after turning off the voltage. g In-situ microscope images of the encoded “SONIC” pattern with an applied voltage of 210 V. At the on state, the full letters “SONIC” are displayed due to the elastic deformation, while at the off state, only letters “SOI” are displayed due to the hysteretic deformation and the different stiffness of nano-kirigami designs. Scale bars:10 µm.

Full size image

Interestingly, under a high voltage of 210 V, the hysteretic deformations induce a completely different information encryption effect. As shown in Fig. 6c, when the high voltage is “on”, both Archi-240 and Archi-270 spirals undergo significant deformation simultaneously due to the strong electrostatic forces, making the letters invisible at state II. After the voltage is “off” for a while (state IV), only Archi-270 spirals undergo significant deformations due to the hysteretic effect, while the electrostatic force is not strong enough to deform Archi-240 spirals, making the letters “SOI” clearly displayed (see Supplementary Movie 8). Such hysteretic deformation is further found to be dependent on the duration of the applied voltage. As shown in Fig. 6d, when a voltage of 170 V is continuously applied from 15 to 30 s and then turned off, the letters “SOI” emerge gradually due to the deformation of Archi-270 spirals induced by the residual charge accumulation. When the duration increases from 30 to 1800 s, the accumulated charges increase to a high level, and consequently, the Archi-240 spirals also start to deform due to the increased electrostatic forces. As a result, the letters “SOI” are hidden again since all the spiral structures are deformed significantly. Such interesting observations clearly demonstrate the versatility of elastic and hysteretic deformations, as well as the non-volatile memory functionality through charge accumulation effects.

Such a scheme can be further expanded by multiplexing the versatile nano-kirigami designs. In Fig. 6e, for example, a “SONIC” pattern is formed by combining Archi-210, Archi-240, and Archi-270 spirals in different areas. Under an applied voltage of 150 V in Fig. 6f, the letters “SONIC” are fully displayed through selective elastic deformation of Archi-240 and Archi-270 spirals, while the Archi-210 spirals are not deformed. When a high voltage of 210 V is applied, the Archi-210 spirals start to deform, reducing the visibility of the letters (top of Fig. 6g). After the applied voltage is removed for a few seconds, and due to the hysteretic deformation, the letters transit from “SONIC” to “SOI” because only Archi-270 spirals are deformed due to their smallest stiffness (see more details in Fig. S11). This dual-mode operation combines both volatile and non-volatile responses within a single platform, where the elastic deformation provides immediate pattern control and the hysteretic effects enable delayed information display.

The comprehensive observations in Fig. 6 (together with Figs. S11–S12) demonstrate the reliable operation across different deformation modes without structural degradation, while the amplitude, duration, and sequence of the applied voltage can be precisely programmed to create complex encryption behaviors. These capabilities position silicon nano-kirigami as a versatile platform for developing encoded optical devices that benefit from both the material’s semiconductor compatibility and the design’s mechanical programmability, opening possibilities for anti-counterfeiting technologies and dynamic information displays.

Discussion

In summary, we have demonstrated well-controllable plastic, elastic, and hysteretic deformations in silicon-based nano-kirigami, enabling a wide variety of nano-geometries. Three-stage plastic deformations with double reversals were achieved based on the misalignment between the distributions of gallium ion implantation and induced vacancy in silicon, as well as the saturation in vacancy generation, overwhelming the observations of conventional two-stage deformation paradigm41,42. A torque model was developed to uncover the dose-dependent resultant moment that determines the deformation direction of the structure, providing a deep understanding of the plastic deformation process in silicon. Furthermore, an elastic deformation was readily achieved in the same platform by employing the mechanical or electrostatic forces in the silicon-based nano-kirigami structure, resulting in a reticular nano-spring capable of detecting forces down to 10 nN and with high repeatability of optical modulation.

Importantly, extraordinary hysteretic deformation was firstly observed in a planar spring structure under the actuation of electrostatic forces. It was found that under operation with high voltages (>100 V), the nearly recovered 2D nano-kirigami structures can still be deformed downward into the 3D state even after the voltage is turned off. Detailed time-dependent analysis reveals that the device behaves like a capacitor and the charges stored in the SiO2 layer under high voltage take responsibility for the hysteretic deformations after the turn-off of the voltage. Meanwhile, during the dissipation of the stored charges, the structure does not straightforwardly return to its initial flat state but jumps to an intermediate deformation level, which implies that the silicon-based nano-kirigami structure possesses a bistable state, i.e., there exists a discontinuity during the deformation process.

The precisely controllable elastic and hysteretic deformation modes of silicon-based nano-kirigami have been further employed to demonstrate the potential applications in dynamic optical information encryption. By designing multiple nano-kirigami spirals with graded stiffness and applying voltages with variable amplitude, duration, and sequence, versatile optical information encryption was achieved. Moreover, it is found that the silicon nano-kirigami structures exhibit robust long-term stability (Fig. S12), and both the repeated cycling (Fig. 5e) and prolonged exposure to high voltage (Fig. 6d) will not eventually alter the mechanical properties of the structure once the accumulated charges are dissipated (see details in Figs. S12–13). In such a case, the combination of hysteresis-mediated states and stiffness-graded designs of silicon nano-kirigami was demonstrated as a strategy for dynamic optical information encryption and displays.

Considering the wide applications and high sophistication of silicon technologies, these coexisting deformation modes in the same material platform, each with distinct triggering thresholds and temporal responses, not only expand the fundamental understanding of silicon’s mechanical behaviors under external stimuli, but also establish a promising design framework for creating multifunctional nanodevices where programmable mechanical responses can be encoded into a single material system. Thus, this work could provide insightful methodologies for the development of micro-electromechanical systems (MEMS), nano-opto-electromechanical systems (NOEMS), micro-/nano-actuators, micro-/nano-sensors, micro-/nano-machinery, memristors, etc., paving the way for future innovations in nanotechnology and materials science on SOI platforms.

Methods

Numerical simulations

The mechanical deformation was simulated by using the solid mechanics module in finite element analysis software (COMSOL). The initial stress distribution along the z-direction in the silicon film was set as the torque model presented to trigger the deformation. The thickness of the silicon film is set to 70 nm, with a Young’s modulus of 100 GPa and a Poisson’s ratio of 0.22 for silicon. The line width of the windmill structure is 70 nm. Geometric nonlinearity analysis in COMSOL is used to achieve a more accurate simulation and prediction of the real behavior of materials and structures under complex loading conditions. The steady-state equations are typically based on the following fundamental equations: the equilibrium equation

$$\nabla \cdot \sigma+F=0$$
(4)

where \(\sigma\) is the stress tensor within the material, \(F\) denotes the volume force acting on the structure; the stress-strain relationship (Hooke’ Law) \(\sigma=C:\epsilon\), where \(C\) is the elastic modulus tensor, \(\epsilon\) is the strain tensor; the boundary condition of fixed constraint \(u=0\), and the displacement formula

$$\epsilon=\frac{1}{2}(\nabla u+\nabla u{\left(\nabla u\right)}^{T}+{\left(\nabla u\right)}^{T})$$
(5)

For the force-displacement curve simulation, a uniformly distributed force was applied vertically at the center of the web structure, and a circular boundary was set outside the structure (corresponding to the actual wet etching situation) as fixed constraint. Regarding the frequency simulation, eigenfrequency analysis was performed on the initial process of small deformation applied to the web structure. More details about the parameters can be found in Supplementary Table 1.

Sample fabrications

The silicon-based structures were fabricated by using a nano-kirigami process on two kinds of SOI platforms that consist of three layers: a Si device layer (t = 70 or 55 nm in thickness), a buried SiO2 layer (2 or 0.145 µm in thickness), and a Si substrate layer (750/750 µm in thickness). The windmills in Fig. 2a and Figs. 2f–h were fabricated with t = 55 nm, while other structures were fabricated with t = 70 nm. Upon different sample sizes, the samples were prepared by using two methods, i.e., FIB process and EBL process. For the FIB process, a 2D pattern was first milled on the SOI at a high dose of 1.02 × 1018 atoms/cm² (30 kV, 40 pA, Helios G4 UC FIB-EBL dual-beam system). Then, the SiO2 substrate under the 2D structure was etched with hydrofluoric acid (HF) solution (40% hydrofluoric acid, 1:4). The etching time was controlled at 9 minutes to ensure the structure was fully suspended. After the wet etching process, global ion beam was irradiated on the sample area by scanning with a relatively low dose of 3.4 × 1015 atoms/cm². It should be mentioned that the Ga+ irradiation induces controlled modifications to silicon’s transport properties and plasmonic behaviors, resulting in the decrease in the electrical resistance and the increase in optical reflectance after the FIB irradiation (results not shown). For the EBL process, the sample surface was first spin-coated with 350-nm-thick electron resist PMMA (AR-P-672.05) and baked at 180 °C for 60 s. Then, exposure was completed at 20 kV, 50 pA with a dose of 400 µC/cm². After developing in MIBK/IPA = 1:3 for 40 s and fixation, the sample was etched by ICP for 25 sec and then underwent a 4-minute RIE process for resist removal. The subsequent etching and deformation processes were the same as in the FIB process.

Optical characterizations

Optical measurements were conducted by using a homemade spectroscopy system. For reflection measurements, a light source (HL-2000, Ocean Optics) was delivered into the detection system via an optical fiber (100 µm in diameter). After passing through a beamsplitter, the light was perpendicularly incident to the sample under the optical microscope, forming a focal spot of around 10 µm in diameter. The reflected light from the sample was collected by the same objective and coupled into another optical fiber. The collected signal was then delivered to and measured by a spectrometer (400–1000 nm in wavelength band, PG2000-PRO, IDEAOPTICS).