Introduction

Charge-4e superconductivity (4e-SC) is an exotic order in which four fermions are bound together and condense1,2,3,4,5,6, with a nonvanishing order parameter ~〈ψiψjψkψl〉 (where ψj is some fermion field with a proper quantum number j). Compared with the more common charge-2e superconductivity (2e-SC) whose order parameter is ~〈ψiψj〉, it breaks the global U(1) symmetry to a discrete \({{\mathbb{Z}}}_{4}\) symmetry, in a sense that the discrete global gauge transformation ψj → ψj einπ/2 (n = 1, 2, 3, 4) leaves the order parameter invariant. The fact that a 4e-SC state is from binding four fermions can be reflected by the Little-Parks experiment, which was used as a direct proof of Cooper pairing phenomenon in 2e-SC state. A recent such study was carried out on the Kagome metal CsV3Sb57, where a charge-4e signal was observed in the normal state. However, whether one can observe the charge-4e bounding in the superconducting state remains an active ongoing research topic. On the theory side, recent progress has been made in understanding the properties of a 4e-SC8,9, which is in general an nontrivial interacting system even at the mean-field level (unlike the Bogoliubov-de Gennes Hamiltonian of a 2e-SC in which fermionic excitations are free). It was found8 that 4e-SC has a superfluid density perturbative in the order parameter, and is in general a gapless system.

However, the mechanism for 4e-SC from interacting fermions remains a theoretical challenge. Unlike 2e-SC which follows from an arbitrarily weak attractive interaction, there lacks a logarithmic divergence for the “quadrupling" susceptibility for 4e-SC. Some early speculations of inducing 4e-SC by disorder10 or condensing skyrmions in a quadratic band touching system11 exist. In recent years, a promising framework for understanding 4e-SC has emerged from the perspective of intertwined orders12, in which a plethora of orders breaking distinct symmetries can naturally emerge from the partial melting of certain primary electronic orders13,14,15,16,17,18,19,20. The starting point of such analyses is typically a Ginzburg-Landau (GL) theory for the primary orders, and when the underlying fermionic models are taken into full account, the intrinsic leading instability toward 4e-SC are in general subleading to those toward non-superconducting states, either nematic or ferromagnetic18,21,22,23. It remains a major theoretical challenge to search for microscopic mechanisms for 4e-SC as a leading instability. Furthermore, in fermionic systems with repulsive interaction, 2e-SC orders can emerge with unconventional pairing symmetries; while the pairing symmetry of 4e-SC order has been largely unexplored20,22 (see also ref. 24 for an example in cold atom systems).

In this work, we directly demonstrate that in a range of two-dimensional (2d) fermionic models with pair density wave (PDW) instabilities25,26,27,28,29,30,31,32, a 4e-SC order naturally emerges as the leading instability once fluctuation effects are taken into account. Extending the PDW flavor number to large-M which justifies the mean-field treatment of the 4e-SC order, we establish the GL theory for the 4e-SC state by incorporating a higher order of interactions for the primary fluctuating PDW fields. (Of course, for M = 1, the phase transition in 2d is of Kosterlitz-Thouless nature, and the mean-field transition represents a crossover above the actual transition, but the transition is still driven by precisely the same attractive interaction we identify in this work.) From this effective GL free energy we can determine the nature of 4e-SC transition. We find the resulting 4e-SC order has a d-wave symmetry, and the phase transition from high temperature normal state to 4e-SC state is first-order. The transition occurs at Tc > TPDW, where TPDW is the mean-field onset temperature of the primary PDW order. An important quantity that determines Tc is the stiffness κ of the PDW fluctuations, and we find that smaller stiffness yields a higher Tc as well as a larger gap amplitude ∣Δ4e∣, as a larger κ tends to suppress fluctuation effects and is hence detrimental for the development of composite orders. This may shed some new light on finding suitable platform materials for realizing the exotic 4e-SC state.

Model and methods

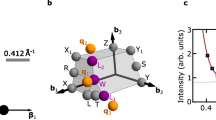
The starting point of our theory, the PDW state, is by itself an exotic type of superconductivity with Cooper pairs carrying non-zero momenta. We emphasize that a microscopic mechanism for a PDW ground state in connection with realistic materials is not a settled issue. However, in recent years it has been intensely studied and shown to emerge via various microscopic mechanisms33,34,35,36,37,38,39,40,41,42,42,43,44,45,46,47,48,49,50,51,52,53 to emerge. Regardless of the mechanism for PDW, the instability toward 4e-SC can be understood as the pairing instability due to interactions among PDW bosons. While in unconventional 2e-SC the effective interaction among fermions stems from exchanging bosons, here the effective interactions among bosons result from exchanging fermions, e.g., as illustrated in Fig. 1(a). To make this effective interactions significant, the four fermions in Fig. 1a need to be as close to the Fermi surface as possible, and this can be realized by invoking a simple geometric relation in a C4 symmetric system.

Fig. 1: 4e-SC from fluctuating PDW.
figure 1

a The effective pairing interaction for PDW bosons via exchanging fermions. Here ± Q and ± P are related by consecutive π/2 rotations. When Eq. (1) is satisfied, the internal fermions are on the Fermi surface. b Continuum model for PDW with O(2) symmetry from ref. 49. The orange area is the filled Fermi sea, and the PDW momentum Q takes values on the Bose surface represented by the red circle. The model can be continuously tuned such that \(| {\boldsymbol{Q}}| =\sqrt{2}{k}_{F}\). c The PDW model realized on a square lattice when the fermions relevant for pairing are close to the Van Hove points (0, π) and (π, 0) and the PDW momentum is close to (π, π). d PDW flucutations in the spin-fermion model42,44. The four hot spots (black dots) near (π, 0) form a square, and the momenta for the potential PDW orders also form a square. The models in c and d satisfy the condition in Eq. (1).

Full size image

In general, these PDW fluctuations can lead to different vestigial orders including CDW, nematic, and 4e-SC that are of comparable strength (see, e.g., refs. 18,22). However, we will show below that in a C4 symmetric system, as long as the PDW momentum Q satisfies

$$\frac{| {\boldsymbol{Q}}| }{\sqrt{2}}=\left\vert {{\boldsymbol{k}}}_{F}\,\mathrm{mod}\,\,(\pi,0)\right\vert ,$$
(1)

4e-SC order is naturally favored energetically over nematic and CDW orders. Here kF corresponds to one of the Fermi surface (FS) portions that are connected by the PDW order parameters, i.e., the PDW hotspots.

Notably, there are several microscopic theoretical models for PDW in which Eq. (1) is satisfied. For example, in ref. 49, PDW order was shown to emerge from finite-range pair-hopping interactions, either in the continuum (illustrated in Fig. 1b) or on a square lattice (Fig. 1c). In refs. 42,44, PDW orders develop due to antiferromagnetic exchange interactions in the spin-fermion model proposed for the underdoped cuprates. While the applicability of these microscopic models to real materials remains an open issue, the ubiquity of the relation (1) implies a generic formalism for 4e-SC.

Further, we stress that no fine-tuning is needed — we will see that even if Eq. (1) is approximately satisfied, our results will hold. In the continuum, all possible values of Q form a ring49, and the ratio Q/kF can be continuously varied. Moreover, we show in the Supplementary Note I that in several lattice models, this condition is automatically satisfied for various values of kF and Q that changes with doping. Below we show that when Eq. (1) is satisfied, the particular interaction in Fig. 1a among PDW bosons with momenta ± Q and ± P (wavevectors related by π/2 rotations) is parametrically enhanced.

The pairing interaction for PDW bosons are repulsive. We find that the repulsive interaction can lead to bosonic pairing (4e-SC) with uncoventional d-wave symmetry. We note that this is reminiscent of the situation in fermionic pairing in unconventional superconductors. We develop a mean-field theory to capture the phase transition into the 4e-SC phase. To that end, we introduced additional fields corresponding to bosonic bilinears, including the 4e-SC order parameter, along with several Lagrange multiplier fields. After integrating out the auxilary fields, we obtain a free energy for 4e-SC, and find that the phase transition is of first order.

Attractive interaction from fluctuating PDW

As a starting point, we consider a model for fluctuating PDW order with a C4 symmetry. The analysis for the case with continuous rotation symmetry will be qualitatively similar. Denoting the bosonic PDW field by Ψi(q), where q is measured from the ordering momentum Qi ∈ { ± P, ± Q}, the generic free energy up to quadratic order for PDW fluctuations of those examples depicted in Fig. 1 can be written as

$$F=\mathop{\sum }\limits_{i=1}^{4}\int\frac{{d}^{2}{\boldsymbol{q}}}{4{\pi }^{2}}\left[\alpha (T)+\kappa {{\boldsymbol{q}}}^{2}\right]{\left\vert {\Psi }_{i}({\boldsymbol{q}})\right\vert }^{2}+{\mathcal{O}}({\Psi }^{4})$$
(2)

where κ is the amplitude stiffness for the PDW orders obtained by expanding the particle-particle susceptibility to \({\mathcal{O}}({{\boldsymbol{q}}}^{2})\), and below the mean-field (4) below, this hierarchy allows the 4e interaction to be dominant over other channels. In general, the dispersion of the PDW bosons is anisotropic in q, but as can be directly checked, for 4e-SC instabilities the anisotropy factor can be absorbed into a redefinition of qx and qy around each PDW ordering momenta see the Supplementary Note III. For PDW fluctuations intrinsically driven by finite-range electronic interactions, κ comes from both the particle-particle bubble and from the q dependence of the interaction, and for weak interactions we assume that 1/κ ≪ EF. Further, as will be explained later, for analytical control of the theory, we are interested in the regime 1/κ ≪ TPDW ≪ EF. This corresponds to a regime in which PDW and 4e-SC develop at low energies, and the phase fluctuations of PDW are not “too strong"; see discussions around Eq. (4) and Eq. (10) below. Indeed, in the microscopic theory of ref. 49, κTPDW can be freely tuned by the interaction strength. Hereafter we measure all lengths against n−1/2, where n is electron density, and all energies against the Fermi energy, which, is defined as \({E}_{F}\equiv {v}_{F}\sqrt{n}\).

The effective interaction between the PDW bosons starts at the order of ∣Ψ∣4. It can be viewed as arising from exchanging fermionic degrees of freedom (see Fig. 1a). As is usually done for itinerant fermions, the processes involved are described by square diagrams. The key insight here is that, for dominant four-boson interactions, the internal fermions need to come from the vicinity of the FSs. For systems satisfying Eq. (1), this consideration alone singles out three types of interactions

$${\beta }_{1}| {\Psi }_{0}{| }^{4}+{\beta }_{2}| {\Psi }_{\pm {\boldsymbol{P}}}{| }^{2}| {\Psi }_{\pm {\boldsymbol{Q}}}{| }^{2}+\beta({\Psi }_{{\boldsymbol{P}}}{\Psi }_{-{\boldsymbol{P}}}{\Psi }_{{\boldsymbol{Q}}}^{* }{\Psi }_{-{\boldsymbol{Q}}}^{* }+h.c.),$$
(3)

where we have used the shorthands, e.g., \(| {\Psi }_{0}{| }^{4}\equiv {\sum }_{i}{\int}_{{{\boldsymbol{q}}}_{1},{{\boldsymbol{q}}}_{2},{{\boldsymbol{q}}}_{3}}{\Psi }_{i}({{\boldsymbol{q}}}_{1}){\Psi }_{i}^{* }({{\boldsymbol{q}}}_{2}){\Psi }_{i}({{\boldsymbol{q}}}_{3}){\Psi }_{i}^{* }({{\boldsymbol{q}}}_{1}-{{\boldsymbol{q}}}_{2}+{{\boldsymbol{q}}}_{3})\), and \({\int}_{{\boldsymbol{q}}}\equiv \int\frac{{d}^{2}{\boldsymbol{q}}}{4{\pi }^{2}}\). Importantly, the last interaction with coefficient β, depicted diagrammatically in Fig. 1a, is of appreciable strength only when the condition Eq. (1) is satisfied; otherwise at least two fermion propagators would come from regions far away from the FS. The coefficients β1,2 and β can be readily obtained by integrating out low-energy fermions, and by linearizing the fermionic dispersion we obtain (see ref. 54 and also the Supplementary Note II for details

$${\beta }_{1} \sim 1,{\beta }_{2} \sim \ln \frac{1}{T},\,\text{and}\,\,\beta =\frac{1}{16T}.$$
(4)

Observe that parametrically, β ≫ β1,2 as long as T ≪ 1 (in original units, T ≪ EF). Due to the large separation between β and β1,2, we expect that even if Eq. (1) hold approximately, one can safely neglect β1,2.

The last term in Eq. (3) represents a repulsion for the bosons corresponding to PDW fluctuations. As is familiar from 2e-SC, repulsive interactions may have attractive components in pairing channels with higher-angular momenta. To this end, we introduce bilinear operators Φs and Φd for 4e-SC with s-wave and d-wave components

$${\Phi }_{s/d}({\boldsymbol{q}})\equiv {\int}_{{\boldsymbol{p}}\!}{\Psi }_{{\boldsymbol{Q}}}({\boldsymbol{p}}+{\boldsymbol{q}}){\Psi }_{-{\boldsymbol{Q}}}(-{\boldsymbol{p}})\pm {\Psi }_{{\boldsymbol{P}}}({\boldsymbol{p}}+{\boldsymbol{q}}){\Psi }_{-{\boldsymbol{P}}}(-{\boldsymbol{p}})$$
(5)

such that the β interaction can be rewritten as

$$\frac{\beta }{2}\int\frac{{d}^{2}{\boldsymbol{q}}}{4{\pi }^{2}}| {\Phi }_{s}({\boldsymbol{q}}){| }^{2}-\frac{\beta }{2}\int\frac{{d}^{2}{\boldsymbol{q}}}{4{\pi }^{2}}| {\Phi }_{d}({\boldsymbol{q}}){| }^{2}.$$
(6)

Just like their 2e-SC counterparts, Φs,d are distinguished by their transformation properties under the C4 rotation: Φs is even and Φd is odd. From this decomposition it is evident that in d-wave channel the charge-4e pairing interaction is attractive.

Let us comment on other couplings and fluctuations in other channels. The β1 term corresponds to a local repulsive interaction between the PDW bosons. The β2 term is repulsive, but it can be written as \({\beta }_{2}{(| {\Psi }_{{\boldsymbol{P}}}{| }^{2}+| {\Psi }_{{\boldsymbol{Q}}}{| }^{2})}^{2}/4-{\beta }_{2}{(| {\Psi }_{{\boldsymbol{P}}}{| }^{2}-| {\Psi }_{{\boldsymbol{Q}}}{| }^{2})}^{2}/4\), revealing its tendency toward a nematic instability with the order parameter \({\mathcal{N}} \sim | {\Psi }_{{\boldsymbol{P}}}{| }^{2}-| {\Psi }_{{\boldsymbol{Q}}}{| }^{2}\). In several recent works18,22 based on two uniform superconducting orders, it was generally found that the vestigial nematic order is more favorable. However, our microscopic calculation has shown that in our PDW-based model, thanks to the C4 symmetry and the condition in Eq. (1), 4e-SC is favored energetically, as β ≫ β2.

We also note that the decomposition of the β-term interaction is not unique. Notably, it can also be decomposed such that there is an equally attractive interaction for a charge-density-wave (CDW) composite order, with e.g., \({\rho }_{{\boldsymbol{P}}-{\boldsymbol{Q}}}={\Psi }_{{\boldsymbol{P}}}{\Psi }_{{\boldsymbol{Q}}}^{* }-{\Psi }_{-{\boldsymbol{Q}}}{\Psi }_{-{\boldsymbol{P}}}^{* }\). The interplay between CDW and 4e-SC has been systematically studied in a phenomenological model15. However, in our microscopic model the CDW instabilities are secondary to that of 4e-SC. Qualitatively, the reason is similar to the situation in a fermionic theory — in 2d and higher dimensions with weakly-coupled fermions, the CDW instability requires nesting of the FS, that is, fermionic dispersions at different momenta with a fixed difference need to be the same, while the 2e-SC instability does not.54 Here the same reasoning holds for interacting bosons, where the bosonic dispersion for ΨP and ΨQ is clearly not nested, which can be directly seen from Fig. 1. Therefore, the CDW is suppressed compared with the d-wave 4e-SC, even if attractive interactions for these channels are equal (see the Supplementary Note V for a quantitative analysis).

Just like the quartic interactions, higher-order interactions come microscopically from higher-order processes of exchanging low-energy fermions. Making use of the condition in Eq. (1), again only a subset of diagrams need to be included. We present all the dominant interactions at sixth and eighth order in Supplementary Note II (See the supplementary material for information about (i) why the models that we use are free from fine tuning, (ii) how to obtain the complete expansion of the pdw fields to eighth order, iii) how the vestigial cdw order is suppressed (iv) how to obtain the gl free energy for the d-wave charge-4e superconductivity and find that the sixth-order coupling constant γ and eighth-order coupling constant are given by γ = 1/(768T 3), and ζ = 1/(7680T 5).

Formation of d-wave 4e-SC

We obtain a phase transition into a d-wave 4e-SC, conspired by fluctuations of the PDW bosons described by Eq. (2), and the attractive interaction in Eq. (6). Formally, the mean-field theory can be justified by extending Φi(q) to an M-component field \({\Phi }_{i}^{J}({\boldsymbol{q}})\) where J ∈ [1, M]54,55.

We first take the mean-field ansatze \({\mathcal{N}}={\Phi }_{s}=0\). We then have up to eighth order in Ψ (see details in Supplementary Notes III and IV).

$$\begin{array}{l}F\,=\,\sum _{i}{\int}_{{\boldsymbol{q}}}[\alpha (T)+\kappa {{\boldsymbol{q}}}^{2}]{\left\vert {\Psi }_{i}({\boldsymbol{q}})\right\vert }^{2}-\frac{\beta }{2}{\int}_{{\boldsymbol{q}}}| {\Phi }_{d}({\boldsymbol{q}}){| }^{2}\\ \qquad-\frac{\gamma }{4}{\int}_{{\boldsymbol{q}},{\boldsymbol{p}}}{\Phi }_{d}({\boldsymbol{q}}){\Phi }_{d}^{* }({\boldsymbol{q}}+{\boldsymbol{p}})\phi ({\boldsymbol{p}})\\ \qquad+\frac{\zeta }{16}{\int}_{{\boldsymbol{q}},{\boldsymbol{k}},{\boldsymbol{p}}}{\Phi }_{d}({\boldsymbol{q}}){\Phi }_{d}^{* }({\boldsymbol{q}}+{\boldsymbol{p}}){\Phi }_{d}({\boldsymbol{k}}){\Phi }_{d}^{* }({\boldsymbol{k}}-{\boldsymbol{p}})\\ \qquad-\frac{\zeta }{16}{\int}_{{\boldsymbol{q}},{\boldsymbol{k}},{\boldsymbol{p}}}{\Phi }_{d}({\boldsymbol{q}}){\Phi }_{d}^{* }({\boldsymbol{q}}+{\boldsymbol{p}})\phi ({\boldsymbol{k}}){\phi }^{* }({\boldsymbol{k}}-{\boldsymbol{p}})+{\mathcal{O}}({\Psi }^{10}),\end{array}$$
(7)

where ϕ ≡ ∣ΨP∣2 + ∣Ψ−P∣2 + ∣ΨQ∣2 + ∣Ψ−Q∣2 is the Gaussian fluctuation.

The decoupling of the interaction terms of Ψ at any order can be achieved by introducing two sets of ancillary fields λd, μ and Δd, φ, where λd and μ are Lagrange multiplier fields ensuring Δd = Φd and φ = ϕ. We can then replace the bilinear operators ϕ and Φd with local fields. For quartic interactions we show in the Supplementary Note VI that the result is the same as that from the HS transformation. As a mean-field ansatz, we consider spatially uniform saddle-point solutions, with Δd(q) = Δdδ(q), and φ(q) = φδ(q). Using the regularization δ(q = 0) = V where V is the volume (area) of the system and defining the free energy density \({\mathcal{F}}\equiv F/V\), we have

$$\begin{array}{rcl}{\mathcal{F}}[\Psi ,{\Delta }_{d},\varphi ,{\lambda }_{d},\mu ]&=&\sum _{i,{\boldsymbol{q}}}[r+\kappa {{\boldsymbol{q}}}^{2}]{\left\vert {\Psi }_{i}({\boldsymbol{q}})\right\vert }^{2}-\frac{\beta }{2}| {\Delta }_{d}{| }^{2}+\frac{\zeta }{16}| {\Delta }_{d}{| }^{4}-\frac{\zeta }{16}| {\Delta }_{d}{| }^{2}{\varphi }^{2}\\ &&\,\,+{\lambda }_{d}({\Delta }_{d}^{* }-{\Phi }_{d}^{* })+{\lambda }_{d}^{* }({\Delta }_{d}-{\Phi }_{d})+\mu \varphi +{\mathcal{O}}({\Psi }^{10}),\end{array}$$
(8)

where \(r=\alpha (T)-\frac{\gamma }{4}| {\Delta }_{d}{| }^{2}-\mu ,{\lambda }_{d}\equiv {\lambda }_{d}({\boldsymbol{q}}=0)/V,\mu \equiv \mu ({\boldsymbol{q}}=0)/V\), and we have used the fact that V∫q ≡ ∑q in the continuum limit. We note that \({\mathcal{F}}\left[\Psi ,{\Delta }_{d},\varphi ,{\lambda }_{d},\mu \right)\) is at most quadratic in the field Ψ(q).

Assuming r > 0, we can integrate out the PDW fields and get a free energy density \({\mathcal{F}}({\Delta }_{d},\varphi ,{\lambda }_{d},\mu )\). Generalizing to large-M and taking the saddle points for φ, λd, μ, we get up to constant terms

$${\mathcal{F}}({\Delta }_{d})/M=A(T)| {\Delta }_{d}{| }^{2}+B(T)| {\Delta }_{d}{| }^{4}+C(T)| {\Delta }_{d}{| }^{6}+\cdots \,,$$
(9)

where the GL coefficients A(T), B(T), and C(T) are determined by the microscopic parameters κ, α, β, γ and ζ and their full expressions are listed in Supplementary Note IV. One important feature of these coefficients is each of them contains terms that are organized in increasing powers of 1/κT ≪ 1 or 1/κα. Assuming κα ≳ 1 as we will justify below, the coefficients can be greatly simplified by keeping the leading contributions,

$$\begin{array}{ll}A(T)\,\approx \,\frac{2\pi \alpha \kappa }{T}-\frac{\beta }{2},B(T)\,\approx\, -\frac{4{\pi }^{3}\alpha {\kappa }^{3}}{3{T}^{3}},\\ C(T)\,\approx \,\frac{64{\pi }^{5}\alpha {\kappa }^{5}}{45{T}^{5}}\end{array}$$
(10)

Driven by the temperature dependence of α(T), the quadratic coefficient A(T) becomes negative upon lowering temperature when ακ = βT/4π ≈ 0.005. At this point, we see that B(T) < 0, i.e., Δd = 0 is no longer a local minimum of the free energy. Instead, the global minimum of free energy is given by Δd ≠ 0. Therefore, a first-order phase transition must have already occurred at a higher temperature. The transition temperature is thus set by

$${\alpha }_{c} \sim 1/\kappa ,\quad {T}_{c} > {T}_{{\rm{PDW}}},\,$$
(11)

which can be directly confirmed by minimizing (9) up to sixth order. We see that a smaller stiffness term κ leads to a higher Tc.

Complementary to the analytical approach when κT ≫ 1, we also solved numerically for saddle points using the full expressions for A(T), B(T), and C(T) in the Supplementary Note IV, as is shown in Fig. 2. We see that ∣Δd∣ increases monotonically as T decreases below Tc. Once ∣Δd∣ becomes large enough, r in Eq. (8) will eventually become negative, invalidating our perturbative analysis. In practice, in the region of r < 0 one needs to keep expanding to higher orders of the PDW order parameters. We also show the free energy profile for T > Tc, T = Tc and T < Tc, from which the nature of first-order phase transition is seen directly. In order to show the impact of the stiffness κ on various quantities for the 4e-SC order, we show in Fig. 2b and c the plot of Tc and ∣Δd(Tc)∣ as a function of κ. It is clear that a larger κ yields a smaller Tc and ∣Δd(Tc)∣. This is consistent with Eq. (11) obtained in the limit that κT ≫ 1.

Fig. 2: Phase transition of the leading d-wave 4e-SC.
figure 2

a 4e-SC gap amplitude as a function of T obtained for TPDW = 0.1 and κ = 10. Insets: GL free energy as a function of Δd. b, c The impact of κ on Tc and Δd.

Full size image

It is possible that deep inside the 4e-SC state, the translation symmetry is further broken, so that 〈ρp−q〉 ≠ 0. By symmetry, this is when the primary PDW order develops, but the actual transition temperature for the PDW state does not coincide with the mean-field TPDW, and it can only set in via a Kosterlitz-Thouless transition (since a U(1) translation symmetry is broken) at a much lower temperature, which is beyond the scope of our GL analysis and calls for other approaches, e.g., numerics or the nonlinear sigma model in ref. 15.

Outlook

The d-wave symmetry for the 4e-SC order can be directly measured by phase-sensitive experiments, just like its 2e-SC counterpart56. Our theory has interesting implications for unconventional superconductors. There exists strong evidence for PDW in underdoped cuprates such as in LBCO near 1/8 doping, where in-plane superconducting fluctuations, together with intertwined density-wave orders, develop at a higher temperature than the bulk superconducting temperature.25 The PDW wave vector was proposed to be unidirectional within each Cu-O plane and alters between x and y ordering direction between neighboring planes43, which is consistent with recent measurements in c-axis transport57. Our work points to a possibility of 4e-SC with a relative sign change between neighboring Cu-O planes with perpendicular PDW wavevectors, although microscopic details, such as whether Eq. (1) is approximately satisfied, call for a separate analysis. In addition, both PDW and 4e-SC (and 6e-SC) have been proposed to exist in the Kagome metal CsV3Sb558,59,60,61,62. It would be interesting to generalize our theory to hexagonal systems, which may be applied to CsV3Sb5.

Finally, we note that our theoretical treatment of the 4e-SC transition, like many previous analyses of vestigial orders18,21,22,54,55, is ultimately a mean-field theory, which focuses on certain channels of fluctuation while neglecting others. In our work, based on analytical calculations, we specifically neglected fluctuations in the nematic, CDW, and s-wave 4e-SC channels. Nevertheless, it would be interesting to test our results via unbiased numerical simulations, such as quantum Monte Carlo. We leave this to future work.