Abstract
The Himalayas, which host glaciers, modulate the Indian Monsoon and create an arid Tibetan Plateau, play a vital role in distributing freshwater resources to the world’s most populous regions. The Himalayas formed under prolonged crustal thickening and erosion by glaciers and rivers. Chomolungma (8,849 m)—also known as Mount Everest or Sagarmāthā—is higher than surrounding peaks, and GPS measurements suggest a higher uplift rate in recent years than the long-term trend. Here we analyse the potential contribution of a river capture event in the Kosi River drainage basin on the renewed surface uplift of Chomolungma. We numerically reconstruct the capture process using a simple stream power model combined with nonlinear inverse methods constrained by modern river profiles. Our best-fit model suggests the capture event occurred approximately 89 thousand years ago and caused acceleration of downstream incision rates. Flexural models estimate this non-steady erosion triggers isostatic response and surface uplift over a broad geographical area. We suggest that part of Chomolungma’s anomalous elevation (~15–50 m) can be explained as the isostatic response to capture-triggered river incision, highlighting the complex interplay between geological dynamics and the formation of topographic features.
Similar content being viewed by others
Main
Chomolungma, also known as Mount Everest or Sagarmāthā (Fig. 1a), is the highest mountain on Earth, towering over other peaks in the Himalayas (Fig. 1b). At 8,849 m above sea level, Chomolungma is ~250 m higher than the other tallest peaks in the Himalaya. This is surprising given the relative along-strike uniformity of tectonics in the Himalayas, which provides mountain peak buoyancy with local, small-scale variability1,2, and relatively uniform climatic conditions and erosional processes3,4. Despite this, Chomolungma deviates from the linear trend of the elevation of Himalayan peaks plotted against their elevation rank (Fig. 1b). A simplistic analysis hints that this anomalous elevation (on the order of one to two hundred metres) could be the result of a scenario where peak elevations were relatively uniformly distributed, but an additional component of elevation has been added to only some of the peaks (including the highest peak). Only the highest of these affected peaks would disrupt the linear trend, whereas lower peaks affected by the additional elevation simply move up the ranking (Fig. 1b). Further evidence suggests a disconnect between the short-term rock uplift rate of Chomolungma measured from GPS data (~2 mm yr−1)5 and its long-term rock uplift rate recorded by thermochronology (~1 mm yr−1)6 (Supplementary Text 1), which raises the question, is there an underlying mechanism raising Chomolungma’s anomalous elevation ever higher?
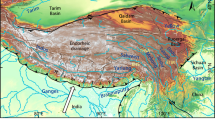
a, A photograph of Chomolungma taken from its northern side. At this ___location, the Arun River flows towards the north away from Chomolungma before turning south through the Arun Gorge. b, Mountain peaks above 7,500 m in the Himalaya ranked by elevation. Chomolungma is off the almost linear relationship between rank and elevation. This relationship can be approximated with peaks drawn from a uniform distribution of elevations between 7,500 m and 8,400 m (blue curve) with an additional 300 m of uplift affecting 30% of these peaks, including the highest point (red curve). c, The enigmatic drainage network of the Kosi River. Local relief is highest where the gorge cuts through the Himalaya and elevation varies from 8,481 m to 1,140 m over a distance of only 35 km. The main faults of the Himalaya are the Main Frontal Thrust (MFT), the Main Boundary Thrust (MBT), the Main Central Thrust (MCT) and the South Tibetan Detachment System (STDS). The zone of high rock uplift rates is associated with the development of a mid-crustal duplex and is resolved with thermochronometry6. The rock uplift rate in this zone is set to 4 mm yr−1 and is 0.5 mm yr−1 to the south and 1 mm yr−1 to the north. d, The χ map for the Kosi River catchment. e, Most of the divides between the catchments of tributaries and across the Himalayan divide are relatively stable. f, In contrast, in the Arun River and the tributaries to the east and west, χ varies considerably.
One potential mechanism to explain Chomolungma’s anomalous elevation and recent increased rock uplift rates becomes apparent when inspecting its surrounding rivers. The Arun River, a major tributary of the Kosi River, drains a large area to the north of Chomolungma before turning south, passing by the world’s tallest peak and cutting a deep gorge through the core of the Himalayas. Ever since the earliest expeditions to Chomolungma, there has been debate as to whether this unusual drainage pattern represents antecedent drainage patterns that the Himalayas have pushed through7 or if the Arun River has captured Tibetan rivers8. This capture event could be related to localized tectonics triggered by fluvial erosion9,10, though the timing of this event is unconstrained.
This scenario of recent drainage piracy has implications for Chomolungma’s elevation. Drainage piracy, facilitated by headward erosion, alters water flow and sediment transport routes by reshaping the drainage divide and network11,12,13,14. If recent drainage piracy is responsible for the drainage pattern of the Kosi River and Arun River, an increase in river discharge due to capture would drive gorge incision. This incision would trigger isostatic compensation, causing Earth’s crust to rebound, resulting in surface uplift of the unincised parts of the surrounding area, including the mountain peaks15,16. The size of the surrounding area that rebounds due to incision is controlled by the strength of the lithosphere. Flexural isostatic rebound, and resulting surface uplift, in response to capture-driven incision of the Arun River could therefore explain part of the observed elevation anomaly of Chomolungma.
The identification of drainage piracy mainly relies on morphological and geological clues. Drainage piracy can be inferred from large variations in χ values (a parameter that characterizes river network topology and geometry) on either side of the divide17, or the presence of wind gaps within divides18,19, but neither indicator provides absolute time constraints. In contrast, provenance changes of sedimentary basins provide indirect insights on drainage reorganization and potential timing constraints20,21. Direct time constraints can be inferred by assessing the rapid incision of rivers22, but isolating the signal of capture from changes in tectonics or climate is challenging.
To understand the drainage evolution of the Kosi River, and the implications of this evolution for Chomolungma, we combine a simple stream power model (SPM) with the Neighbourhood Algorithm23. This approach allows us to reconstruct the capture process of a river, estimate fluvial erosion parameters and quantify uncertainties. Our study sheds light on recent rock uplift rates and the anomalous elevation of Chomolungma, unveiling the interplay between river capture and mountain uplift.
Characteristics of the Kosi River drainage
Located in the heart of the central Himalayas (Fig. 1c), the Kosi River, and its major tributary the Arun River, traverse the highest regions of the Himalayas. The Arun River drains the southern expanse of Tibet and the northern slopes of Chomolungma before flowing through a narrow gorge that drops 7 km in elevation over 35 km (Fig. 1c and Extended Data Fig. 1).
The Kosi River has a distinctive river profile and planform characteristics (Fig. 2a and Extended Data Fig. 2). Whereas there are other rivers in the Himalayan region that have east–west headwaters, such as the Sutlej and Ghagra (Extended Data Fig. 2a), their longitudinal profiles are typically concave. In contrast, the longitudinal profile of the Kosi River shows a pronounced convexity (Extended Data Fig. 2h). The modern topography provides compelling evidence that the Kosi River system is in an unsteady state in which erosion rates are not balanced by rock uplift rate (Fig. 1d–f).
a,b, Distance to base level versus elevation (a) and χ versus elevation (b) for the Arun River and rivers to the east (Tamor River) and west (Dudh Kosi River and Likhu Khola River). The overall form of the rivers is similar in a but the Arun River has the additional area from the Tibetan Plateau. The transformation from distance to χ should collapse rivers that have experienced a common rock uplift rate on to the same curve. This is the case for the Tamor River, Dudh Kosi River and Likhu Khola River, and we argue these are in steady state with the regional rock uplift rate pattern. However, the central trunk channel does not collapse on the same overall curve.
Examining a χ–elevation plot24,25 of the region (Fig. 2b), it is clear that the eastern and western tributaries of the Kosi River have a similar rock uplift history. They converge on a common form and their tributaries exhibit similar behaviour. In contrast, the Arun River, the major tributary in the middle, deviates from this form, despite the similar lithology and tectonic setting. Whereas there is some evidence for differential tectonics, with thrust faults on either side of the Arun River, these tectonic processes are minor. We therefore suggest that the χ–elevation relationships of the Arun River are different due to an ongoing adjustment of river elevation in response to a recent increase in stream power (Extended Data Fig. 3).
Modelling erosion from a river capture event
Our approach focuses on modelling the capture process through changes in the upstream reaches. Before the capture event, we assume that all rivers are at topographic steady state (Supplementary Text 1) with the long-term rock uplift rate inferred previously with thermochronometry6, and the Arun River does not extend upstream of the capture point (Extended Data Fig. 4a–c). After capture, the upstream area of the modern Arun River is included, assuming it has its current morphology (Extended Data Fig. 4d). The tributaries to the east and west of Arun River do not experience this same increase in upstream drainage area and are assumed to remain in a state of equilibrium. In contrast, the Arun River responds to the addition of new upstream drainage area by capture, the timing of which is unknown and is referred to as tc.
We simulate this capture event using the detachment-limited SPM26:
where h is elevation, t is time and thermochronological data and thermokinematic modelling6 are used to constrain the rock uplift rate (U) (Extended Data Fig. 5). The upstream drainage area (A) evolves from a pre-capture network to a post-capture network at tc, and S is the channel slope. The unknown model parameters are the area exponent (m), the slope exponent (n), the erodibility (K) and the time of capture (tc). We model the Kosi River network, including rivers that are impacted by the capture event and stable rivers not impacted by the capture event. In our forward model, we use an implicit method27,28 to predict river nodes through time. The initial condition assumes a topographic steady state landscape that is predicted using defined values of m, n and K. Using common values of n = 1, m = 0.45 and K = 8 × 10−6 yr−1, about 76 thousand years is required to erode the Arun Gorge from the initial topographic steady state landscape.
However, SPM parameters are uncertain, with some studies based on cosmogenic nuclide datasets suggesting that the slope exponent n > 2 (refs. 29,30). Therefore, to propagate uncertainties from these parameters to uncertainties in the capture time, we use an inverse model. The Neighbourhood Algorithm23 is applied to infer values of m, n, K and tc. At each iteration of this algorithm, the selected values of m, n and K are used to build an initial, pre-capture landscape, that is, considered as an initial condition. The capture event is then simulated with these parameters and the capture time. Misfit is calculated for both the topographic steady state landscape not impacted by the capture event and the Arun River that is adjusting to the capture event. The ability of the model and data to resolve these model parameters is discussed in the Methods. A similar inversion scheme has been introduced by ref. 31 that focused only on fitting a single knickpoint, however, our approach includes simulation of the entire drainage network, providing improved resolution.
Modelling results highlight excellent agreement between model predictions and topography. Residuals are centred around zero (Extended Data Fig. 6), although some areas show notable differences between observed and predicted elevations. In general, the trunk streams are accurately predicted, whereas certain headwaters of tributaries may be susceptible to over- or under-prediction (Fig. 3a). We observe that rivers tend to be over- and under-predicted across drainage divides32 where active migration is evident, a factor not accounted for in our model. Furthermore, the highest parts of our river network are also poorly reproduced, which may be due to glacial erosion. Nonetheless, our model and its associated parameters show a good fit to the data, providing confidence in our results.
a, The model residuals show relatively low misfits across all aspects of the model ___domain. In some upper tributaries, residuals are large, and we attribute this to glacial erosion and ongoing drainage divide migration. b, The recovered profile matches the trunk stream well, and the overall form of the tributaries are reproduced. Furthermore, concavities on the tributaries are reproduced, highlighting the transient wave of incision associated with increased upstream drainage area. The zone of high rock uplift rate for the main stem of the Kosi River is shown in grey shading. c, The four model parameters are well resolved as shown by the tight clustering of low misfit values. The parameters m and n covary with one another, as would be expected; however, a clear minimum corresponding to m = 0.43 and n = 0.97 is observed. The star shows the ___location of the optimal solution. d, The parameters K and tc also covary, but a best fitting value of K = 1.16 × 10−5 m1–2m yr−1 and tc = 89 ka can be identified. The star shows the ___location of the optimal solution. We note that the units of K are variable because m varies. For the best fitting model parameter combinations of n = 1 and m = 0.42, the units correspond to m0.16 yr−1.
Our best-fit values of m, n and K are 0.43 and 0.97 and 1.16 × 10−5 m1–2m yr−1, respectively (Fig. 3b,c), and the posterior probabilities are 0.45 ± 0.083, 1.07 ± 0.17 and −5.07 ± 0.58 for m, n and log10 K, respectively. The posterior probability distributions for these parameters are shown in Extended Data Fig. 7. Although the ratio between m and n is almost identical to the value constrained for the Himalayas in previous studies33,34,35,36, our value for n supports evidence from studies of fluvial erosion that river incision rate scales linearly with slope (n = 1)37,38,39. This contradicts a number of studies suggesting that n may be greater than 1 in tectonically active regions29,40 and in the Arun River41. However, these studies are based on catchment-wide erosion rates from cosmogenic nuclide concentration measurements that are sensitive to both fluvial and hillslope erosion and are based on a steady state assumption. In the Himalayas, for example, the transient wave of incision we identify would invalidate this key assumption. Our results also help explain some of the very high rates of erosion recorded in the catchment-wide cosmogenic nuclide data41. In particular, erosion rates up to 10 km per million years were attributed to local landsliding and deemed unreliable; however, such high transient rates are actually predicted by our model.
Influence of precipitation and extreme events
Our best-fit model estimates that capture of the Arun River occurred 89 thousand years ago (ka), whereas other well-fitting models suggest capture events between 50 ka and 100 ka (Fig. 3d). The posterior probability of the capture time is asymmetric with a maximum value of ~70 ka (Extended Data Fig. 7). This closely matches the age of pluvial sediments upstream of the capture point, dating back to about 30–90 ka (refs. 42,43). It also supports the validity of our inferred capture timing, indicating that the pluvial sediments represent the final stages of a High Himalaya drainage divide rather than a recent blockage event caused by phenomena such as landslides.
In other Himalayan rivers, it has been suggested that catastrophic erosion events are essential to maintain high erosion rates44,45 and cut deep gorges that are in topographic steady state with rock uplift rates. However, the similarity in our capture time to pluvial lake sediments and the landscape’s adjustment to increased drainage area suggests additional catastrophic events (failure of small blockages of the narrow gorge due to landslides or glaciers) might not be necessary for the Arun Gorge formation. Furthermore, the Arun River’s morphology supports ongoing landscape adaptation to the larger upstream drainage area (Figs. 1d and 2).
It is important to recognize that we do not account for the spatial variability of precipitation. Modern precipitation patterns across the Himalayas show an increase from south to north before decreasing within the southern Tibetan Plateau. Taking this into account would imply that capturing the Tibetan portion of the Kosi catchment, where precipitation rates are lower, would result in a smaller change in discharge along the Kosi River than simulated in our model. As a result, the time required to produce the observed changes in headwater stream elevations and the retreat of knickpoints along its tributaries may be even longer than our estimate. It is worth noting, however, that there is limited understanding of how precipitation evolved during the Pleistocene, how the landscape changes we have identified would affect precipitation patterns, and the precise impact of precipitation on erosion rates. Therefore, we prefer our simple model, in which the capture time corresponds to the age of pluvial sediments, coupled with qualitative analysis of extreme events and the influence of precipitation.
River incision and recent surface uplift of Chomolungma
Following the capture event resolved by our model, downstream incision rates increase due to the increased upstream drainage area. Here we define incision rate as the difference between the rock uplift rate and the river erosion rate. In this way, incision is a non-steady process that generates topographic relief. According to our model results, downstream of the capture point, incision rates vary between 5 and 10 mm yr−1 in the upper reaches, 1–5 mm yr−1 in the middle reaches and less than 1 mm yr−1 in the lower reaches (Fig. 4a). This result is consistent with previous incision rate estimates based on terrace dating near Tumlingtar46.
a, The difference between rock uplift rate and erosion rate is greatest in the High Himalaya. Due to the recent change in fluvial incision, it is expected that the highest parts of the landscape have not responded to this increased erosion. Therefore, these areas will experience isostatic surface uplift. b, The flexural response to enhanced erosion of the Kosi River leads to enhanced surface uplift across the highest Himalaya for Te = 20 km.
The incision of the Arun Gorge (Extended Data Fig. 8), driven by the capture of the upstream drainage area, represents a dynamic and non-steady component of erosion. In the main rivers flanking the Arun River to the east and west, the high rates of erosion balance the rock uplift and peaks remain at a constant elevation (Fig. 4a). Conversely, the transient component of incision in the Arun River drainage triggers an isostatic response. Due to flexure of the lithosphere, an area extending over tens of kilometres experiences renewed surface uplift, contributing to the elevation of the world’s highest mountains. Montgomery16 suggested that 20–30% of Himalayan peak elevation can be attributed to isostatic rebound induced by river incision. This conclusion extends the earlier findings of Wager15. However, these results were unusually high because they assumed that an extensive flat topography existed before all the material between the peaks was eroded. On the basis of normal response times of landscapes47, and given that the mean elevation has been consistent in the Chomolungma area since the Miocene48, we expect this area has achieved topographic steady state before Quaternary fluvial capture. Following capture, enhanced incision produced an isostatic component of rock uplift (Extended Data Figs. 9 and 10). On the basis of our inferred SPM parameters, the wave of fluvial incision associated with the river capture has not propagated significantly along the tributaries. Under topographic steady state assumptions, the surrounding peaks are therefore expected to be eroding at the previous rock uplift rate and so experience flexural isostatic surface uplift. With an effective elastic thickness of 10–30 km, this phenomenon would lead to an increased surface uplift rate for Chomolungma of 0.16–0.53 mm yr−1. This isostatic response contributes an additional rock uplift component equivalent to approximately 10–50% of the current GPS-derived rock uplift rate5. GPS stations in proximity to the area of rapid non-steady incision will be more strongly affected, with important implications for the analysis of interseismic strain accumulation and earthquake hazard49.
We suggest that Chomolungma partly owes its anomalous elevation to drainage capture and river incision (Fig. 4b), though tectonic processes governing crustal thickness and rock uplift are clearly the fundamental cause of Chomolungma’s elevation4. Our study uncovers a previously unrecognized, additional mechanism of rock uplift active since river capture. River incision lowers the elevation along the river channel, but the regional area is subject to rock uplift by isostatic rebound. Because tributary rivers take time to respond to this incision, erosion rates lag behind the isostatic rock uplift rate leading to surface uplift. To estimate the magnitude of additional elevation, we calculate the total amount of river incision between the capture time and the present. This provides an estimate of the eroded volume, which can be converted to flexural isostatic surface uplift. In particular, the integrated isostatic surface uplift of ~15–50 m may help explain part of the anomalous height of Chomolungma (8,849 m) with respect to K2 (8,611 m) and the next three highest peaks in the Himalaya (8,586 m; 8,516 m; 8,485 m), which differ in elevation by no more than 100 m between one peak and the next. However, Chomolungma and the neighbouring highest peaks (Lhotse and Makalu) experienced similar amounts of surface uplift, moving up the rankings, but not disrupting the linear relationship between peak elevation and ranking (Fig. 1b). In contrast, Chomolungma has been raised to an even higher elevation. We therefore attribute part of Chomolungma’s anomalous elevation to the enhanced surface uplift it experiences due to Arun River gorge incision.
Methods
Forward and inverse models
We applied a series of forward models to simulate river evolution, using the stream power model to predict river network elevations based on model parameters and rock uplift rates. We assumed a temporally homogeneous but spatially variable uplift rate. The rock uplift rate is based on the extensive thermochronometric studies carried out in this area, which has constrained a narrow band of enhanced rock uplift rate associated with movement over a deeper ramp structure6 (Extended Data Fig. 5). In the initial condition of the model, the Arun River contains only the portion downstream the capture point, whereas the river morphology of other tributaries (Tamor River, Dudh Kosi River and Likhu Khola River) is consistent with the current state (Extended Data Fig. 4c). The capture point is determined by inspection of the digital elevation model (DEM), but our results are robust with respect to the exact capture point. Considering that these tributaries do not have obvious knickpoints and the channel profiles are essentially in equilibrium, we have assumed that the rivers are in topographic steady state at the start of the model (Extended Data Fig. 4a,b). After capture, the morphology of the western and eastern tributaries remains unchanged and therefore at topographic steady state. The Arun River adds an upstream portion that is consistent with the present morphology (Extended Data Fig. 4d) and begins to incise due to the increase in upstream area.
We used TopoToolbox 250 to extract the drainage network from NASADEM elevation data51 at a resolution of ~ 30 m and resampled to 100 m to improve computational speed. We defined the river network as all areas draining more than 1 km2. The residuals in Fig. 3a and Extended Data Fig. 6 are calculated based on the difference between the model and real elevations at the river nodes.
Considering that these parameters have been reported to be highly variable in the natural environment, we need to propagate the uncertainties on m, n and K to capture time. The nonlinear inverse model uses the neighbourhood algorithm (NA)23 to propagate uncertainties and search optimal model parameters. We solve for four free parameters—the area exponent (m), the slope exponent (n), the erodibility (K) and the time of capture (tc). The m value is between 0.2 and 0.7, n from 0.5 to 2, K from 1 × 10−7 to 1 × 10−4 m1–2m yr−1 and tc from 0 to 500 ka.
It is important to consider the potential of the model and data to resolve the model parameters. The model and data are able to resolve the area exponent (m) from the elevation and fluvial response times of river nodes along stable river profiles and the requirement that these nodes converge along a consistent elevation–response time curve52. The value of slope exponent (n) is resolved using a similar principle, taking into account the shapes of tributaries to the Kosi River, which respond to the same wave of incision but may have different local gradients. Erodibility (K) is determined by ensuring that the stable rivers match the thermochronologically constrained rock uplift rate. It is important to note that m, n and K are interrelated53. However, by incorporating transient river profiles, knowledge of spatially variable rock uplift rates and a relatively simple geomorphic model, we can resolve these parameters independently. The relative timing of capture is determined by assessing the differences between the stable pre-capture Kosi River and its tributaries compared with the modern transient profile. The ability to resolve K impacts our ability to determine the absolute value of tc; however, we find that these parameters are independently resolved.
The algorithm works by running a series of forward models that predict observed data. We use an L1 norm to calculate a misfit (M) between the model predicted elevations and the observed elevations.
where N is the number of river nodes, pi is the predicted river node elevation and oi is the observed river node elevation. This ensures that our parameter estimation is robust with respect to outliers. Only river nodes of Tamor River, Dudh Kosi River, Likhu Khola River and downstream of the capture point for Arun catchment are used to assess the performance of the forward model and model parameters. River nodes with elevations higher than 4,000 m were excluded to avoid the expected impact of glacial erosion; river nodes with upstream drainage areas smaller than 5 × 106 m2 were excluded to ensure that we do not include hillslopes. A total of 51,000 forward models were run split into 51 iterations with 1,000 models per iteration. At each iteration, the NA resamples promising areas of parameter space but maintains flexibility to explore and discover new promising areas.
To provide robust parameter estimation, we integrate information across parameter space using the second stage of the NA. The posterior probability density functions are based on the likelihood function L, which is defined as:
where σ is the data uncertainty (10 m) and M is misfit. The 1D marginal of the posterior probability distributions for the four parameters are shown in the Extended Data Fig. 7.
Flexural model
After the river capture, the isostatic rebound induced by non-steady incision would produce an additional surface uplift. Here we used a two-dimensional flexure model54 to calculate the vertical deflection of an elastic by a Fourier transform approach. In this model, the crust is considered as an elastic sheet with a flexural rigidity (D).
where E is Young’s modulus (1 × 1011 N m−2), v is Poisson’s ratio (0.25) and Te is effective elastic thickness.
On the basis of the best-fit model, we calculated present-day isostatic uplift rates (Fig. 4b and Extended Data Fig. 9) according to the present-day incision rate (Fig. 4a). We also estimated the total amount of isostatic uplift since the timing of capture (Extended Data Fig. 10) based on the total non-steady incision amount (Extended Data Fig. 8). On the basis of seismological data and gravity data, the effective elastic thickness of Himalaya is 10–30 km (refs. 55,56) (Supplementary Text 2). Our analysis explored a reasonable range of the effective elastic thickness (Te) at 10, 20 and 30 km. The maximum rate of current surface isostatic uplift induced by river incision ranged from 0.2 to 1.1 mm yr−1 (Extended Data Fig. 9). Specifically, Chomolungma experiences uplift rates of 0.16 to 0.53 mm yr−1, whereas Makalu exhibits uplift rates of 0.18 to 0.77 mm yr−1. Since the capture, the maximum total uplift due to non-steady incision ranges from 16 to 84 m (Extended Data Fig. 10). This includes 13 to 41 m uplift for Chomolungma and 14 to 60 m for Makalu. We note that we do not model hillslope erosion. We expect that hillslopes immediately adjacent to the incising channel will also experience enhanced erosion. This would increase the area of enhanced erosion and increase the isostatic response. In this way, our isostatic calculations are minimum estimates of surface uplift rates and total surface uplift.
Data availability
The DEM data used for topographic analysis and river model can be downloaded via https://search.earthdata.nasa.gov/search?q=NASADEM. All model results data associated with the paper are available via Zenodo at https://doi.org/10.5281/zenodo.13208960 (ref. 57).
Code availability
The code for simulating river capture process is available at https://github.com/hanxu95/River_Capture_Model.
Change history
16 January 2025
A Correction to this paper has been published: https://doi.org/10.1038/s41561-025-01643-1
References
Whipp, D. M., Beaumont, C. & Braun, J. Feeding the ‘aneurysm’: orogen-parallel mass transport into Nanga Parbat and the western Himalayan syntaxis. J. Geophys. Res. Solid Earth 119, 5077–5096 (2014).
Searle, M. P., Simpon, R. L., Law, R. D., Parrish, R. R. & Waters, D. J. The structural geometry, metamorphic and magmatic evolution of the Everest massif, high Himalaya of Nepal–South Tibet. J. Geol. Soc. 160, 345–366 (2003).
Thiede, R. C. & Ehlers, T. A. Large spatial and temporal variations in Himalayan denudation. Earth Planet. Sci. Lett. 371–372, 278–293 (2013).
Wolf, S. G., Huismans, R. S., Braun, J. & Yuan, X. Topography of mountain belts controlled by rheology and surface processes. Nature 606, 516–521 (2022).
Wang, L. & Barbot, S. Three-dimensional kinematics of the India–Eurasia collision. Commun. Earth Environ. 4, 164 (2023).
Herman, F. et al. Exhumation, crustal deformation, and thermal structure of the Nepal Himalaya derived from the inversion of thermochronological and thermobarometric data and modeling of the topography. J. Geophys. Res. Solid Earth 115, B06407 (2010).
Wager, L. R. The Arun River drainage pattern and the rise of the Himalaya. Geogr. J. 89, 239–250 (1937).
Heron, A. M. Geological results of the Mount Everest expedition, 1921. Geogr. J. 59, 418–431 (1922).
Robl, J., Stuewe, K. & Hergarten, S. Channel profiles around Himalayan river anticlines: constraints on their formation from digital elevation model analysis. Tectonics 27, TC3010 (2008).
Montgomery, D. R. & Stolar, D. B. Reconsidering Himalayan river anticlines. Geomorphology 82, 4–15 (2006).
Bishop, P. Drainage rearrangement by river capture, beheading and diversion. Prog. Phys. Geogr. Earth Environ. 19, 449–473 (1995).
Shugar, D. H. et al. River piracy and drainage basin reorganization led by climate-driven glacier retreat. Nat. Geosci. 10, 370–375 (2017).
Bender, A. M. et al. Late Cenozoic climate change paces landscape adjustments to Yukon River capture. Nat. Geosci. 13, 571–575 (2020).
Maher, E., Harvey, A. M. & France, D. The impact of a major Quaternary river capture on the alluvial sediments of a beheaded river system, the Rio Alias SE Spain. Geomorphology 84, 344–356 (2007).
Wager, L. R. The rise of Himalaya. Nature 132, 28 (1933).
Montgomery, D. R. Valley incision and the uplift of mountain peaks. J. Geophys. Res. Solid Earth 99, 13913–13921 (1994).
Willett, S. D., McCoy, S. W., Perron, J. T., Goren, L. & Chen, C.-Y. Dynamic reorganization of river basins. Science 343, 1248765 (2014).
Shelef, E. & Goren, L. The rate and extent of wind-gap migration regulated by tributary confluences and avulsions. Earth Surf. Dyn. 9, 687–700 (2021).
Buceta, R. E., Schoenbohm, L. M. & DeCelles, P. G. Glacial and fluvial erosion in the Dolpo Basin, Western Nepal. Geomorphology 354, 107033 (2020).
Jaiswara, N. K., Pandey, P. & Pandey, A. K. Mio-Pliocene piracy, relict landscape and drainage reorganization in the Namcha Barwa syntaxis zone of eastern Himalaya. Sci. Rep. 9, 17585 (2019).
Cina, S. E. et al. Gangdese arc detritus within the eastern Himalayan Neogene foreland basin: implications for the Neogene evolution of the Yalu-Brahmaputra River system. Earth Planet. Sci. Lett. 285, 150–162 (2009).
Lanari, R. et al. Exhumation and surface evolution of the western high atlas and surrounding regions as constrained by low‐temperature thermochronology. Tectonics 39, e2019TC005562 (2020).
Sambridge, M. Geophysical inversion with a neighbourhood algorithm—I. Searching a parameter space. Geophys. J. Int. 138, 479–494 (1999).
Royden, L. & Perron, J. T. Solutions of the stream power equation and application to the evolution of river longitudinal profiles. J. Geophys. Res. Earth Surf. 118, 497–518 (2013).
Goren, L., Fox, M. & Willett, S. D. Tectonics from fluvial topography using formal linear inversion: theory and applications to the Inyo Mountains, California. J. Geophys. Res. Earth Surf. 119, 1651–1681 (2014).
Howard, A. D., Dietrich, W. E. & Seidl, M. A. Modeling fluvial erosion on regional to continental scales. J. Geophys. Res. Solid Earth 99, 13971–13986 (1994).
Hergarten, S. Self-Organized Criticality in Earth Systems (Springer Berlin Heidelberg, 2002); https://doi.org/10.1007/978-3-662-04390-5
Braun, J. & Willett, S. D. A very efficient O(n), implicit and parallel method to solve the stream power equation governing fluvial incision and landscape evolution. Geomorphology 180–181, 170–179 (2013).
Harel, M.-A., Mudd, S. M. & Attal, M. Global analysis of the stream power law parameters based on worldwide 10Be denudation rates. Geomorphology 268, 184–196 (2016).
Leonard, J. S., Whipple, K. X. & Heimsath, A. M. Isolating climatic, tectonic, and lithologic controls on mountain landscape evolution. Sci. Adv. 9, eadd8915 (2023).
Scherler, D. & Schwanghart, W. Drainage divide networks—part 1: identification and ordering in digital elevation models. Earth Surf. Dyn. 8, 245–259 (2020).
Fox, M., Goren, L., May, D. A. & Willett, S. D. Inversion of fluvial channels for paleorock uplift rates in Taiwan. J. Geophys. Res. Earth Surf. 119, 1853–1875 (2014).
Kirby, E. & Whipple, K. Quantifying differential rock-uplift rates via stream profile analysis. Geology 29, 415–418 (2001).
Kirby, E. & Whipple, K. X. Expression of active tectonics in erosional landscapes. J. Struct. Geol. 44, 54–75 (2012).
Hodges, K. V., Wobus, C., Ruhl, K., Schildgen, T. & Whipple, K. Quaternary deformation, river steepening, and heavy precipitation at the front of the Higher Himalayan ranges. Earth Planet. Sci. Lett. 220, 379–389 (2004).
Wobus, C. W., Hodges, K. V. & Whipple, K. X. Has focused denudation sustained active thrusting at the Himalayan topographic front? Geology 31, 861–864 (2003).
Wobus, C. W., Whipple, K. X. & Hodges, K. V. Neotectonics of the central Nepalese Himalaya: constraints from geomorphology, detrital 40Ar/39Ar thermochronology, and thermal modeling. Tectonics 25, 2005TC001935 (2006).
Glotzbach, C. Deriving rock uplift histories from data-driven inversion of river profiles. Geology 43, 467–470 (2015).
Smith, A. G. G. et al. One million years of climate-driven rock uplift rate variation on the Wasatch fault revealed by fluvial topography. Am. J. Sci. 324, 1 (2024).
Adams, B. A., Whipple, K. X., Forte, A. M., Heimsath, A. M. & Hodges, K. V. Climate controls on erosion in tectonically active landscapes. Sci. Adv. 6, eaaz3166 (2020).
Olen, S. M. et al. Understanding erosion rates in the Himalayan orogen: a case study from the Arun Valley. J. Geophys. Res. Earth Surf. 120, 2080–2102 (2015).
Chen, Y., Aitchison, J. C., Zong, Y. & Li, S.-H. OSL dating of past lake levels for a large dammed lake in southern Tibet and determination of possible controls on lake evolution: evolution of a large dammed lake in Tibet. Earth Surf. Process. Landforms 41, 1467–1476 (2016).
Chiu, H. Sedimentology and Geomorphology of Modern and Relict Lake Systems in Tibet (The Univ. of Hong Kong, 2011).
Dahlquist, M. P. & West, A. J. The imprint of erosion by glacial lake outburst floods in the topography of central Himalayan rivers. Earth Surf. Dyn. 10, 705–722 (2022).
Turzewski, M. D., Huntington, K. W., Licht, A. & Lang, K. A. Provenance and erosional impact of Quaternary megafloods through the Yarlung-Tsangpo Gorge from zircon U-Pb geochronology of flood deposits, eastern Himalaya. Earth Planet. Sci. Lett. 535, 116113 (2020).
Lave, J. & Avouac, J. P. Fluvial incision and tectonic uplift across the Himalayas of central Nepal. J. Geophys. Res. Solid Earth 106, 26561–26591 (2001).
Whipple, K. X. Fluvial landscape response time: how plausible is steady-state Denudation? Am. J. Sci. 301, 313–325 (2001).
Gébelin, A. et al. The Miocene elevation of Mount Everest. Geology 41, 799–802 (2013).
Bettinelli, P. et al. Plate motion of India and interseismic strain in the Nepal Himalaya from GPS and DORIS Measurements. J. Geod. 80, 567–589 (2006).
Schwanghart, W. & Scherler, D. Short communication: TopoToolbox 2—MATLAB-based software for topographic analysis and modeling in earth surface sciences. Earth Surf. Dyn. 2, 1–7 (2014).
NASA SRTM Subswath Global 1 Arc Second V001 (NASA JPL, 2021); https://doi.org/10.5067/MEaSUREs/NASADEM/NASADEM_SSP.001
Goren, L. A theoretical model for fluvial channel response time during time-dependent climatic and tectonic forcing and its inverse applications. Geophys. Res. Lett. 43, 10753–10763 (2016).
Croissant, T. & Braun, J. Constraining the stream power law: a novel approach combining a landscape evolution model and an inversion method. Earth Surf. Dyn. 2, 155–166 (2014).
Watts, A. B. Isostasy and Flexure of the Lithosphere (Cambridge Univ. Press, 2001).
Hammer, P. et al. Flexure of the India plate underneath the Bhutan Himalaya. Geophys. Res. Lett. 40, 4225–4230 (2013).
Hetényi, G., Cattin, R., Vergne, J. & Nábělek, J. L. The effective elastic thickness of the India Plate from receiver function imaging, gravity anomalies and thermomechanical modelling. Geophys. J. Int. 167, 1106–1118 (2006).
Dai, J.-G., Han, X. & Fox, M. Recent uplift of Chomolungma enhanced by river drainage piracy. Zenodo https://doi.org/10.5281/zenodo.13208960 (2024).
Acknowledgements
This research was supported by the National Natural Science Foundation of China (number 42488201), Second Tibetan Plateau Scientific Expedition and Research Program (number 2019QZKK0204), and Fundamental Research Funds for the Central Universities (number 2652023001) grants to C.-S.W. and J.-G.D., the Jiangsu Innovation Support Plan for International Science and Technology Cooperation Program (number BZ2022057) grant to C.-S.W. and NERC (NE/X009408/1) grant to M.F. We also thank A. Carter for insightful, constructive comments on this paper.
Author information
Authors and Affiliations
Contributions
X.H., J.-G.D. and M.F. conceived the idea. J.-G.D., C.-S.W. and M.F. directed the project. X.H., A.G.G.S. and M.F. constructed the numerical models. X.H., S.-Y.X. and B.-R.L. made the figures. All authors discussed the results and implications. M.F., X.H. and J.-G.D. wrote the original paper, and all authors participated in paper revisions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Geoscience thanks Kurt Stuewe and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Alireza Bahadori and Tamara Goldin, in collaboration with the Nature Geoscience team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Topographic profile along Himalaya.
a, Topographic map of Tibetan Plateau showing profile ___location. b and c, The 30-km-wide swath profiles show average (yellow line) and maximum and minimum (blue lines) elevations. The average elevation has been smoothed over a length scale of 30 km to reflect long wavelength topographic variations. These profiles highlight that Chomolungma is the highest point along the arc of the Himalaya and is within a broad extensive area of high peaks. This extensive area is likely controlled by long-term tectonics. The deep Kosi River is also clear on these profiles, highlighting that this is also an iconic feature of the central Himalaya.
Extended Data Fig. 2 Distribution of rivers on the southern slopes of the Himalaya and channel profiles of their trunk rivers.
Distribution of rivers on the southern slopes of the Himalaya (a) and channel profiles of their trunk rivers (b-o). The channel profiles correspond to the trunk in red in panel a. The Kosi River displays a unique convex shape (h), but smaller convexities can be identified in other catchments, hinting that multiple catchments have experienced capture events at different times.
Extended Data Fig. 3 Map of normalized channel steepness (ksn) as a reference for stream power.
The normalized channel steepness is calculated by Topotoolbox 2 with m/n = 0.45. The north-south trending reach of the Arun River shows a higher channel steepness than other tributaries.
Extended Data Fig. 4 Initial steady profile of east and west tributaries and Arun River.
Initial steady profile of east and west tributaries (a) and Arun River (b). The total amount of incision predicted by the model is the difference between the two profiles in panel b and in Fig. 3b. However, this is only the amount of incision for one combination of model parameters and different incision magnitudes are expected as model parameters change during the iterative process. Comparison of the pre-capture (c) and post-capture (d) Kosi drainage networks. Colours of the trunk (Arun River) and east and west tributaries correspond to Fig. 2. No change is simulated in the planform geometry of the tributaries before or after the capture event. In contrast, the Arun River experiences a sudden increase in upstream drainage area due to capture.
Extended Data Fig. 5 Distribution of rock uplift rate in the model.
The rock uplift rate is constrained by previous thermochronological research6.
Extended Data Fig. 6 The histogram of the model-residuals shows that the residuals are centred on zero.
In some places the residuals are large and negative. These large residuals may be the result of drainage divide migration not simulated in our model, glacial erosion, or landslides blocking rivers and preventing incision. Additionally, inconsistencies between the rock uplift rate used in the model and the actual rock uplift rate could result in either higher or lower modelled channel elevations in specific areas. Furthermore, large residuals are permitted due to our use of the L1 norm, that is less sensitive to outliers.
Extended Data Fig. 7 1D marginals of the posterior probability distribution of the model parameters.
a-d, 1D marginals of the posterior probability distribution of area exponent (a), slope exponent (b), capture time (c), and erodibility (d). All parameters have clear peaks in probability, but the capture time and erodibility are both quite asymmetric.
Extended Data Fig. 8 The total non-steady river incision since river capture.
This model prediction is from the best fitting selection of model parameter. Almost 800 m of river incision is predicted through the highest Himalaya.
Extended Data Fig. 9 Distribution characteristics of current isostatic uplift rates.
a-c, Current isostatic uplift rate due to non-steady incision for different elastic thicknesses (Te). d, Isostatic uplift rate profile along section x-x′ in panel a, showing the position of Chomolungma and Makalu.
Extended Data Fig. 10 Distribution characteristics of total isostatic uplift amount.
a-c, Total isostatic uplift amount since river capture due to non-steady incision for different elastic thicknesses (Te). d, Isostatic uplift amount profile along section x-x′ in panel a, showing the position of Chomolungma and Makalu.
Supplementary information
Supplementary Information
Supplementary Texts 1 and 2.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Han, X., Dai, JG., Smith, A.G.G. et al. Recent uplift of Chomolungma enhanced by river drainage piracy. Nat. Geosci. 17, 1031–1037 (2024). https://doi.org/10.1038/s41561-024-01535-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41561-024-01535-w
This article is cited by
-
How do mountains grow?
Nature Reviews Earth & Environment (2025)
-
Why Mount Everest is the world’s tallest mountain
Nature (2024)