Abstract
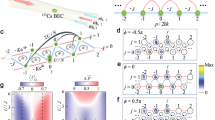
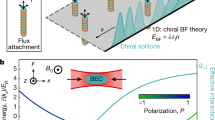
Surface currents arise in superconductors under magnetic fields and are a key signature of the Meissner effect. Similarly, chiral dynamics have been observed in quantum simulators under synthetic Abelian gauge fields. These simulators offer flexible control, enabling the engineering of non-Abelian gauge fields, although their influence on chiral dynamics remains unclear. Here, we implement a synthetic SU(2) gauge field in a spinful one-dimensional ladder and investigate the resulting chiral dynamics by developing a Raman momentum-lattice technique. We confirm the non-Abelian nature of the synthetic potential by observing the non-Abelian Aharonov–Bohm effect on a single plaquette. Furthermore, we find that the chiral current along the two legs of the ladder is spin dependent and highly tunable through the gauge potential parameters. We experimentally map out different dynamic regimes of the chiral current, revealing the competition between overlaying flux ladders with different spin compositions. Our experiment demonstrates the impact of non-Abelian gauge fields on chiral dynamics and offers a viable approach to implementing exotic synthetic gauge fields using Raman momentum lattices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
27,99 € / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
269,00 € per year
only 22,42 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Experimental data, any related experimental background information not mentioned in the text, and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
References
Higgs, P. W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 13, 508–509 (1964).
Kibble, T. W. B. Symmetry breaking in non-Abelian gauge theories. Phys. Rev. 155, 1554–1561 (1967).
Senthil, T. & Fisher, M. P. A. Z2 gauge theory of electron fractionalization in strongly correlated systems. Phys. Rev. B 62, 7850–7881 (2000).
Stormer, H. L., Tsui, D. C. & Gossard, A. C. The fractional quantum Hall effect. Rev. Mod. Phys. 71, S298–S305 (1999).
Lee, P. A. From high temperature superconductivity to quantum spin liquid: progress in strong correlation physics. Rep. Prog. Phys. 71, 012501 (2007).
Lin, Y.-J., Compton, R. L., Jiménez-García, K., Porto, J. V. & Spielman, I. B. Synthetic magnetic fields for ultracold neutral atoms. Nature 462, 628–632 (2009).
Aidelsburger, M. et al. Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013).
Miyake, H., Siviloglou, G. A., Kennedy, C. J., Burton, W. C. & Ketterle, W. Realizing the Harper Hamiltonian with laser-assisted tunneling in optical lattices. Phys. Rev. Lett. 111, 185302 (2013).
An, F. A., Meier, E. J. & Gadway, B. Direct observation of chiral currents and magnetic reflection in atomic flux lattices. Sci. Adv. 3, e1602685 (2017).
Li, H. et al. Aharonov–Bohm caging and inverse Anderson transition in ultracold atoms. Phys. Rev. Lett. 129, 220403 (2022).
Atala, M. et al. Observation of chiral currents with ultracold atoms in bosonic ladders. Nat. Phys. 10, 588–593 (2014).
Roushan, P. et al. Chiral ground-state currents of interacting photons in a synthetic magnetic field. Nat. Phys. 13, 146–151 (2017).
Fang, K., Yu, Z. & Fan, S. Photonic Aharonov–Bohm effect based on dynamic modulation. Phys. Rev. Lett. 108, 153901 (2012).
Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 6, 782–787 (2012).
Umucalılar, R. O. & Carusotto, I. Artificial gauge field for photons in coupled cavity arrays. Phys. Rev. A 84, 043804 (2011).
Mittal, S. et al. Topologically robust transport of photons in a synthetic gauge field. Phys. Rev. Lett. 113, 087403 (2014).
Schine, N., Ryou, A., Gromov, A., Sommer, A. & Simon, J. Synthetic Landau levels for photons. Nature 534, 671–675 (2016).
Yang, Z., Gao, F., Yang, Y. & Zhang, B. Strain-induced gauge field and Landau levels in acoustic structures. Phys. Rev. Lett. 118, 194301 (2017).
Mathew, J. P., Pino, J. D. & Verhagen, E. Synthetic gauge fields for phonon transport in a nano-optomechanical system. Nat. Nanotechnol. 15, 198–202 (2020).
Chen, Y. et al. Synthetic gauge fields in a single optomechanical resonator. Phys. Rev. Lett. 126, 123603 (2021).
Xiao, M., Chen, W.-J., He, W.-Y. & Chan, C. T. Synthetic gauge flux and Weyl points in acoustic systems. Nat. Phys. 11, 920–924 (2015).
Bardeen, J. Theory of the Meissner effect in superconductors. Phys. Rev. 97, 1724–1725 (1955).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957).
Dalibard, J., Gerbier, F., Juzeliūnas, G. & Öhberg, P. Colloquium: artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523–1543 (2011).
Goldman, N., Juzeliūnas, G., Öhberg, P. & Spielman, I. B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 77, 126401 (2014).
Zhai, H. Degenerate quantum gases with spin-orbit coupling: a review. Rep. Prog. Phys. 78, 026001 (2015).
Lin, Y.-J., Jiménez-García, K. & Spielman, I. B. Spin–orbit-coupled Bose–Einstein condensates. Nature 471, 83–86 (2011).
Wang, P. et al. Spin-orbit coupled degenerate Fermi gases. Phys. Rev. Lett. 109, 095301 (2012).
Huang, L. et al. Experimental realization of two-dimensional synthetic spin–orbit coupling in ultracold Fermi gases. Nat. Phys. 12, 540–544 (2016).
Wu, Z. et al. Realization of two-dimensional spin-orbit coupling for Bose–Einstein condensates. Science 354, 83–88 (2016).
Liu, X.-J., Law, K. T. & Ng, T. K. Realization of 2D spin-orbit interaction and exotic topological orders in cold atoms. Phys. Rev. Lett. 112, 086401 (2014).
Di Liberto, M., Goldman, N. & Palumbo, G. Non-Abelian Bloch oscillations in higher-order topological insulators. Nat. Commun. 11, 5942 (2020).
Wang, Z.-Y. et al. Realization of an ideal Weyl semimetal band in a quantum gas with 3D spin-orbit coupling. Science 372, 271–276 (2021).
Sun, W. et al. Highly controllable and robust 2D spin-orbit coupling for quantum gases. Phys. Rev. Lett. 121, 150401 (2018).
Zhang, S.-L. & Zhou, Q. Two-leg Su–Schrieffer–Heeger chain with glide reflection symmetry. Phys. Rev. A 95, 061601 (2017).
Lang, L.-J., Zhang, S.-L. & Zhou, Q. Nodal Brillouin-zone boundary from folding a Chern insulator. Phys. Rev. A 95, 053615 (2017).
Li, C.-H. et al. Bose–Einstein condensate on a synthetic topological Hall cylinder. PRX Quantum 3, 010316 (2022).
Khan, N., Wang, P., Fu, Q., Shang, C. & Ye, F. Observation of period-doubling Bloch oscillations. Phys. Rev. Lett. 132, 053801 (2024).
Wunderlich, J., Kaestner, B., Sinova, J. & Jungwirth, T. Experimental observation of the spin-Hall effect in a two-dimensional spin-orbit coupled semiconductor system. Phys. Rev. Lett. 94, 047204 (2005).
Liang, M.-C. et al. Realization of Qi–Wu–Zhang model in spin-orbit-coupled ultracold fermions. Phys. Rev. Res. 5, L012006 (2023).
Sugawa, S., Salces-Carcoba, F., Perry, A. R., Yue, Y. & Spielman, I. B. Second Chern number of a quantum-simulated non-Abelian Yang monopole. Science 360, 1429–1434 (2018).
Sugawa, S., Salces-Carcoba, F., Yue, Y., Putra, A. & Spielman, I. Wilson loop and Wilczek–Zee phase from a non-Abelian gauge field. npj Quan. Inf. 7, 144 (2021).
Horváthy, P. A. Non-Abelian Aharonov–Bohm effect. Phys. Rev. D. 33, 407–414 (1986).
Yang, Y. et al. Synthesis and observation of non-Abelian gauge fields in real space. Science 365, 1021–1025 (2019).
Chen, Y. et al. Non-Abelian gauge field optics. Nat. Commun. 10, 3125 (2019).
Huo, M.-X., Nie, W., Hutchinson, D. A. & Kwek, L. C. A solenoidal synthetic field and the non-Abelian Aharonov–Bohm effects in neutral atoms. Sci. Rep. 4, 5992 (2014).
Dhar, A. et al. Chiral mott insulator with staggered loop currents in the fully frustrated Bose–Hubbard model. Phys. Rev. B 87, 174501 (2013).
Sachdeva, R., Metz, F., Singh, M., Mishra, T. & Busch, T. Two-leg-ladder Bose–Hubbard models with staggered fluxes. Phys. Rev. A 98, 063612 (2018).
Osterloh, K., Baig, M., Santos, L., Zoller, P. & Lewenstein, M. Cold atoms in non-Abelian gauge potentials: from the Hofstadter “moth" to lattice gauge theory. Phys. Rev. Lett. 95, 010403 (2005).
Goldman, N., Kubasiak, A., Gaspard, P. & Lewenstein, M. Ultracold atomic gases in non-Abelian gauge potentials: the case of constant Wilson loop. Phys. Rev. A 79, 023624 (2009).
Yang, Y., Zhen, B., Joannopoulos, J. D. & Soljačić, M. Non-Abelian generalizations of the Hofstadter model: spin–orbit-coupled butterfly pairs. Light Sci. Appl. 9, 177 (2020).
Zamora, A., Szirmai, G. & Lewenstein, M. Layered quantum Hall insulators with ultracold atoms. Phys. Rev. A 84, 053620 (2011).
Goldman, N. et al. Realistic time-reversal invariant topological insulators with neutral atoms. Phys. Rev. Lett. 105, 255302 (2010).
Xiao, T. et al. Periodic driving induced helical floquet channels with ultracold atoms in momentum space. Eur. Phys. J. D. 74, 152 (2020).
Acknowledgements
We acknowledge the support from the National Key Research and Development Programme of China under Grant Nos. 2023YFA1406703 and 2022YFA1404203, The National Natural Science Foundation of China under Grant Nos. U21A20437, 12074337, 11974331, 12374479 and 12174339, Natural Science Foundation of Zhejiang Province under Grant No. LR21A040002 and LR23A040003, Zhejiang Province Plan for Science and Technology Grant No. 2020C01019, the Fundamental Research Funds for the Central Universities under Grant Nos. 2021FZZX001-02 and 226-2023-00131, the China Postdoctoral Science Foundation under Grant No. 2023M733122 and the Science Specialty Programme of Sichuan University under Grant No. 2020SCUNL210.
Author information
Authors and Affiliations
Contributions
Q.L., Z.D., H.W. and H.L. performed the experiments and data analysis. J.P. and Q.L. performed the theoretical modelling and calculations. Z.Y., W.Y. and B.Y. initiated and supervised this project. All authors discussed the results and contributed to the preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Eric Meier and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–6, Table 1 and Discussion.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liang, Q., Dong, Z., Pan, JS. et al. Chiral dynamics of ultracold atoms under a tunable SU(2) synthetic gauge field. Nat. Phys. 20, 1738–1743 (2024). https://doi.org/10.1038/s41567-024-02644-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-024-02644-4
This article is cited by
-
Strongly interacting Meissner phases in large bosonic flux ladders
Nature Physics (2025)
-
Non-Abelian lattice gauge fields in photonic synthetic frequency dimensions
Nature (2025)