Strongly interacting Meissner phases in large bosonic flux ladders

Floquet engineering via periodic modulation has emerged as a powerful tool for Hamiltonian engineering¹. It enables the exploration of novel quantum matter across various platforms including photonics², neutral atoms in optical lattices^1,3,4, superconducting qubits^5,6, Rydberg atom arrays^7,8 and, increasingly, even solid-state systems^9,10. A central goal of current research with synthetic quantum systems is to combine Floquet-engineered gauge fields^11,12 with strong interparticle interactions. Their interplay can give rise to topologically ordered phases of matter, both of fundamental interest and with practical applications, for example, in fault-tolerant quantum computing^13,14. Despite this potential, large-scale quantum simulations of such systems have been hindered by the susceptibility of interacting Floquet systems to heating^{15,16,17,18,19,20,21}, restricting experimental studies to few-particle systems^22,23,24,25.

In this work, we experimentally realize the interacting Mott–Meissner phase in large bosonic ladder systems with a synthetic gauge field on a neutral atom quantum simulator. The gauge field breaks time-reversal symmetry, realizing the Hofstadter–Bose–Hubbard (HBH) model that is known to host topologically ordered phases such as fractional Chern insulators^26,27,28. A quasi-one-dimensional ladder geometry is the minimal system to observe orbital physics and, hence, ideally suited to benchmark experimental implementations. Furthermore, interacting flux ladders were predicted theoretically to exhibit an extraordinarily rich phase diagram, featuring, for example, vortex and Meissner states, chiral superfluids and chiral Mott insulators, or charge density wave states^{29,30,31,32,33,34,35,36}. However, so far, optical flux ladders have only been realized with periodic driving either in the non-interacting or weakly interacting limit^37,38 or via synthetic dimensions^{39,40,41,42,43}.

A crucial challenge for realizing large many-body phases consists of identifying a suitable adiabatic preparation sequence. In this work, we present two different pathways and identify stable parameter regimes with minimal Floquet heating during the entire ramp to realize strongly interacting flux ladders with 48 sites at half-filling. To study the properties of our many-body system, we combine quantum gas microscopy with local basis rotations⁴⁴ to measure particle currents with local resolution across large systems. To this end, we extend our previously developed technique to many-body systems and measurements of currents on bonds with complex tunnel coupling. We experimentally probe the local current distribution with full spatial resolution, revealing the emergence of equilibrium chiral currents that are directly connected to the topologically protected chiral edge modes in a two-dimensional (2D) quantum Hall system⁴⁵. We further use Feshbach resonance to tune the interaction strength over a wide range and study its effect on chiral currents. This reveals a characteristic interaction scaling, which is a direct experimental signature and hallmark feature of the interacting Mott–Meissner phase. Finally, we benchmark our experimental results against numerical simulations for small systems to estimate the effective temperature, which is on the order of the tunnel coupling. This establishes an important reference for future studies of topological quantum matter in periodically driven many-body systems.

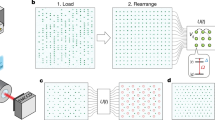
The experiment is carried out in a caesium quantum gas microscope, which allows us to create strongly interacting quantum gases and probe occupations with single-site resolution and currents with single-bond resolution^44,46,47. We start with a ¹³³Cs Bose–Einstein condensate in a single 2D plane of a vertical optical lattice, which is then loaded into a 2D horizontal lattice geometry. The horizontal lattice comprises a bichromatic superlattice along x (short spacing, a_s = 383.5 nm; long spacing, a_l = 767 nm) as well as a monochromatic lattice (with short spacing a_s) in the y direction, realizing a chain of double wells along x that are coupled in the perpendicular direction. In plane, the system is confined in a box potential projected via a digital micromirror device, with a size of 40 × 40 lattice sites. Using a deep long x lattice and shallow short lattices, the dynamics is constrained to 20 independent copies of isolated ladders with a length of up to 40 sites (Fig. 1a). To engineer an effective magnetic flux, we use a laser-assisted tunnelling scheme based on an additional, superimposed optical running wave. In an effective Floquet description, this time-periodic modulation results in a complex-valued tunnel coupling along the rung direction of the form Ke^iφ(l,r) (refs. ^37,48). Here φ(l, r) is a complex phase factor, which varies in space and creates an artificial magnetic field (Supplementary Section I-B). Its spatial dependence is determined by the lattice geometry and, in our case, is fixed to increase by π/2 per bond, resulting in a synthetic magnetic flux of π/2 per plaquette (a quarter flux quantum). In the presence of the complex tunnel coupling, the system can be described by the HBH model^49,50

where \({\hat{a}}_{l,r}^{\dagger }\) and \({\hat{n}}_{l,r}\) are the bosonic creation and particle number operators for site l = 1, 2 of the rth rung, respectively; J and K are the tunnel couplings in the leg and rung directions, respectively; U is the on-site interaction strength; and φ = π/2 denotes the Peierls phase. This Hamiltonian hosts a multitude of different ground-state phases depending on filling, flux and K/J (refs. ^30,31,32). The characteristics for each phase are different configurations of persistent particle currents that emerge due to the synthetic magnetic field. In our work, we mainly focus on the strongly interacting Meissner phase, which appears for large rung couplings K/J > (K/J)_cr (refs. ^30,51,52). It is characterized by homogeneous, chiral leg currents and vanishing rung currents (Fig. 1a). At half-filling and beyond a critical interaction strength that depends on the specific value of K/J, there is a phase transition from a superfluid to a fractional Mott insulator, known as the Mott–Meissner phase, with a chiral current magnitude that characteristically depends on the interaction strength³⁰.

a, HBH model on two leg ladders, parameterized by a real-valued tunnel coupling J along the leg direction, complex-valued tunnel coupling Ke^irφ along the rung direction and a repulsive on-site interaction U. Here r is the rung index, and l = 1 and 2 indexes the leg. Persistent particle currents emerge due to the synthetic magnetic field (middle ladder, blue arrows). b, Measurement of currents in a many-body system with complex tunnelling. After quenching the interactions to zero via a Feshbach resonance, the leg current operator is measured via a DW basis rotation with real coupling (right), whereas for the rung current operator, it has to be performed in a driven DW with complex coupling (left). \({\hat{\sigma }}_{x}\) is the Pauli X operator and T is the tunnelling time in the DW (as defined in the main text).

Full size image

The operators describing such currents along the leg (\({\hat{j}}_{{{l}},{{r}}}^{\,\parallel }\)) and rung (\({\hat{j}}_{{\rm{r}}}^{\,\perp }\)) directions (Fig. 1a) are given by^30,53

Experimentally, we can measure the leg current (equation (2)) with single-bond resolution by locally rotating the measurement basis using an optical superlattice^44,53. As illustrated in Fig. 1b (right), we project bonds locally into symmetrically coupled, isolated double wells (DW), by suddenly turning on an additional long-period lattice along the leg direction. The periodic time evolution in each bond under the DW Hamiltonian can then be interpreted as a local rotation of the measurement basis. After holding for a quarter rotation period (T/4 = h/(8J_DW), where J_DW is the DW coupling and h is Planck’s constant), the local bond current is encoded in the density difference \({\hat{n}}_{{\rm{L}}}-{\hat{n}}_{{\rm{R}}}\) and can be directly read out using optical imaging. For a generic many-body state, interactions need to be switched off during the rotation, which otherwise modify the applied transformation. We implement this by switching the scattering length to approximately zero via a magnetic Feshbach resonance. To measure the rung currents (equation (3)), we have to adapt the protocol to account for the synthetic gauge field. Otherwise, the previous DW rotation would measure only the trivial, laser-induced phase φ(l, r) rather than the emerging ground-state currents. To measure the actual rung current operator, we perform the basis rotation in the presence of the periodic drive, that is, in DWs that have the same spatially varying complex coupling phase as the rung bonds (Fig. 1b (left) and Supplementary Section I-D). In summary, this technique provides access to snapshots of local particle currents on all bonds with microscopic resolution, which we will demonstrate in the following.

We start by investigating the ground states of isolated plaquettes with two interacting particles each. This is an ideal system to benchmark the current detection in a many-body phase for both real and complex couplings, as it hosts stable currents that circulate around all four bonds of each plaquette (Fig. 2a, zoomed-in view). To prepare the plaquette ground states, we begin with a product state in which every ‘rung’ is occupied by one particle. Both long lattices in the x and y directions are kept deep throughout the sequence to define the plaquette geometry and suppress tunnelling between the plaquettes (residual coupling in the leg direction is J′/h < 5 Hz and that in the rung direction is K′/h = 1.5 Hz). In the presence of a strong tilt in the rung direction, the particle is initially localized in the energetically lower site. Next, we adiabatically turn on the running-wave modulation in 30 ms and simultaneously remove a weak additional tilt. This couples the two sites to a final strength K/h = 140(1) Hz and delocalizes each particle symmetrically across a rung bond. In the final step, the short lattice in the leg direction is lowered in 15 ms to couple the two rungs and transfer the system to the plaquette ground state at a final K/J value. Throughout the sequence, a strong repulsive on-site interaction is maintained. After finishing the state preparation, we measure the particle currents on all bonds by rotating the measurement basis as described above (Fig. 1b). Figure 2a shows the distribution of currents across 140 isolated plaquettes, evaluated in a central sub-region of the whole system. We observe a homogeneous distribution of chiral currents originating from the homogeneous flux threading each plaquette. Analysing the leg currents in more detail (Fig. 2b), we find that the width of the current distribution is approximately consistent with the projection noise at the experimental sampling of 200 snapshots for each bond, with a slight broadening probably originating from on-site potential disorder (potential disorder amplitude, ~h × 30 Hz; Supplementary Section II-F).

a, Spatially resolved map of the currents across a large array of 140 isolated plaquettes for K/J ≃ 1.4 and U/K ≃ 10. The direction of current is indicated by the arrow, and the current magnitude is encoded in the colour, where the leg currents are shaded in blue and the rung currents, in red. Zoomed-in view: an example plaquette, indicating the orientation of the real (complex) tunnel couplings on the leg (rung) bonds as defined in equation (1). b, Distribution of leg currents across the entire system shown in a. The left bonds have a mean current (1σ deviation) of 0.18(8)J and the right bonds, –0.19(8)J, as illustrated by the normal distributions (dashed line). c,d, Scaling of the leg (c) and rung (d) currents as a function of K/J (averaged over 140 plaquettes and 200 snapshots per point). The solid line is a fit of an ED simulation of the ideal currents, with the amplitude as a single free parameter, yielding 0.78(4) for the legs and 0.71(4) for the rungs; the shaded area denotes the 1σ confidence interval of the fit. The dashed lines indicate the currents in a non-interacting plaquette with the same fit amplitude. The error bars denote the standard error of the mean (s.e.m.), and if not visible, are smaller than the marker size. All the numerical simulations take into account the reduced flux in isolated plaquettes of 0.71(2) × π/2 (Supplementary Section II-E).

Full size image

To further study the ground-state phase diagram, we tune K/J, and track the behaviour of the bond currents. The interaction energy is, on average, U/K ≃ 9.8, varying between U/K = 8.5(3) and U/K = 11.0(3) as we tune K/J via the short y-lattice depth. The measured dependence of the leg currents is shown in Fig. 2c. After an initial rise, it exhibits a maximum at around K/J ≈ 1.5 as well as a suppression of the currents towards higher K/J. The suppression is a characteristic for the interacting state and is markedly different from the case of non-interacting plaquettes (dashed lines). This behaviour is in excellent agreement with numerical simulations based on the exact diagonalization (ED) of the two-particle plaquette ground state apart from an overall reduction in the ideal current to 78(4)%. This is repeated for the currents on the rungs (Fig. 2d), where we find similarly good agreement. The measured current amplitudes are probably limited by the finite switching speed of our offset coils, causing a residual non-zero U during the basis rotation, as well as a not fully adiabatic state preparation. The above measurements demonstrate our capability to resolve both types of bond current for interacting states with local resolution. We note that the single-shot sampling of the current operators also allows to measure current–current correlation functions, which further reveal strong features due to the micromotion (Supplementary Section III).

Next, we study extended ladder systems at half-filling with tunable interactions. Realizing such a system with a Floquet scheme is highly non-trivial, since in addition to the challenges of an adiabatic preparation, drive-induced heating needs to be minimized. In particular, heating resonances have to be avoided during preparation, limiting the accessible parameter space⁵⁴. To address this, we conduct extensive loss spectroscopy, identifying a narrow window around modulation frequencies of 5 kHz with negligible losses (atom loss of ~2% compared with the initial state), bounded from below by interaction-mediated heating and bounded from above by interband resonances.

To prepare strongly interacting Meissner states, we use a rung coupling sequence. We start with a product state of one particle per rung, which is delocalized across both sites in the presence of the complex tunnel coupling. For strong interactions, this state corresponds already to a Meissner-like state in the (K/J→∞) limit and is, thus, readily connected to the full Meissner regime by increasing the leg coupling. After the state preparation, we probe the current and density distributions with local resolution. Figure 3a shows a current and density map for a strongly interacting Meissner state. We restrict the evaluation to the central region of the whole 40 × 40 site system to avoid edge effects due to the finite wall sharpness of the box potential, and average over all the ladder copies (residual coupling between ladders K′/h = 1.5 Hz). Note that we only access every other bond in the leg direction due to the DW array created with a superlattice. We find strong, chiral currents along the leg bonds, uniformly distributed across the ladder, accompanied by strongly suppressed currents on the rungs (Fig. 3b), as it is a characteristic of the Meissner regime. In addition, we find a homogeneous filling at an average of 0.45(2) across the ladder without any imbalance between the legs, where the slight deviation from ideal half-filling originates mostly from an imperfect initial state (Fig. 3c).

a, Spatially resolved density and leg and rung current distributions on ladders with 48 sites in the Meissner regime for K/J = 1.98(5) and U/J = 11.02(5). The width and colour of each arrow is given by the average magnitude of the respective bond current averaged over 140 repetitions and 14 ladders. Note the inverted axes orientations. b, Locally resolved bond currents for the state in a. The average currents are 0.24(4)J on the upper leg, –0.23(3)J on the lower leg and 0.01(4)K on the rungs, as indicated by the horizontal lines. c, On-site densities for the state in a, yielding a homogeneous density profile with an average density of 0.45(2). For b and c, each data point was averaged over 140 repetitions and 14 ladders. d, Suppression of the chiral current with increasing interaction energy U and K/J. The solid lines are fits of a DMRG simulation of the ideal chiral current with the amplitude as a single free parameter, the shaded areas denote the 1σ confidence interval of the fits and the dashed lines are perturbative approximations using the effective spin-1/2 model, scaled to the same fit amplitude. The grey dot–dashed trace indicates the non-interacting current from an ED simulation at the same amplitude as the lowest U/K measurement. The inset shows the fit amplitude as a function of U/K. The legend indicates the average U/K for each curve, with the uncertainty denoting the 1σ variation throughout the K/J range. Each data point is averaged over 60 repetitions and 14 ladders with 48 sites. In all plots, the error bars denote the s.e.m., and if not visible, are smaller than the marker size.

Full size image

A second key feature arising from the strongly correlated nature of the state is a characteristic suppression of the chiral current with increasing interaction strength U as well as coupling ratio K/J (ref. ³⁰). This can also be understood by noticing that the Meissner ladder in the limit of K ≫ J and U ≫ J can be mapped onto a pseudo-spin-1/2 chain, where the ground state in the U→∞ limit is a product state of rung triplets, that is, each rung r is in the state \({\left\vert \downarrow \right\rangle }_{r}=({\left\vert 1,0\right\rangle }_{r}+{{\rm{e}}}^{{\rm{i}}r\uppi /2}{\left\vert 0,1\right\rangle }_{r})/\sqrt{2}\). At half-filling, a perturbative relation for the chiral current, defined as the average difference between the two leg currents, \({j}_{{\rm{c}}}=\frac{1}{2L}\vert {\sum }_{r}\langle\;{{\hat{j}}_{1,r}^{\,\parallel }}\rangle -\langle\;{\hat{j}}_{2,r}^{\,\parallel}\rangle \vert\), can be derived as j_c = (J²(4K + U)²)/(2KU(2K + U)) (ref. ³⁰). We can experimentally verify this behaviour by tuning the interaction strength independent from the tunnel couplings via a magnetic Feshbach resonance. Again, using the rung coupling sequence, we set a fixed K/h = 155(1) Hz, and vary the final J to tune K/J for different interaction strengths. Figure 3d shows the dependence of the chiral current j_c on K/J for four different average interaction energies. Note that U varies slightly around the average value as a function of K/J (the calibration is shown in Supplementary Section II-B). Qualitatively, we find that the current is suppressed for a higher coupling ratio as well as with increasing interaction energy. This is in stark contrast to a non-interacting ladder for which the chiral current remains constant with K/J (Fig. 3d, grey dot–dashed trace). Comparing this more closely with theory, we observe good agreement of the scaling with a zero-temperature density matrix renormalization group (DMRG) simulation (Fig. 3d, solid lines), as well as the perturbative approximation for K/J ≳ 5. For low U/K, we observe up to 88(5)% of the ideally predicted current strength, which then drops towards higher U values. In agreement with the plaquette benchmark, the current amplitude is probably limited by a residual non-zero U during the basis rotation, with an increasing effect for larger initial U.

Although the previously used sequence allows for an efficient realization of Meissner states, it cannot be used to access the entire ground-state phase diagram of the ladder HBH model. In particular, decreasing K/J below a critical value (K/J)_cr ≈ 1 that depends on the interaction strength, the system undergoes a phase transition into a vortex phase. Here the chiral Meissner current breaks up into several smaller current loops that are separated by current vortices. This results in a spatial modulation of the leg current alongside a decrease in the chiral current as well as non-zero rung currents. At the phase transition, a many-body gap closing separates the two phases, preventing a use of the rung coupling sequence for an adiabatic preparation (Fig. 4a). To reach the vortex regime, we introduce a second tuning parameter J′, corresponding to a staggered tunnel coupling along the leg direction (Fig. 4a, vertical axis). Making use of this additional parameter, the plaquette coupling sequence starts from isolated plaquette ground states (J′ ≪ J), where we can prepare any K/J adiabatically (Fig. 4a, horizontal path (i)). In the second step, the plaquettes are connected together by increasing J′/J→1 at constant K/J (Fig. 4a, vertical path (ii)). To compare the two sequences, we track the evolution of the currents during the final ramps when preparing an interacting Meissner state. In the rung coupling sequence, we start with no currents on leg or rung bonds, and only the leg currents gradually build up with an opposing sign (Fig. 4b). By contrast, the plaquette sequence starts with initial opposing currents on the leg and rung bonds (Fig. 4c). On connecting the plaquettes to a Meissner ladder, the leg currents remain finite, whereas the rung currents vanish. Both sequences can be used to prepare Meissner states, but the plaquette coupling sequence results in slightly smaller currents due to the longer preparation path.

a, Many-body gap as a function of K/J and interplaquette coupling J′/J for U/J = 10, as simulated using DMRG. The solid purple arrows indicate the paths taken by the rung and plaquette coupling sequences to prepare the example Meissner state in b and c, denoted by the black star. The green arrows show the path for the preparation of a vortex state with the plaquette sequence, circumventing the gap closing (white triangle). b,c, Evolution of the currents during the adiabatic ramp with duration T_ramp in the rung (b) and plaquette (c) coupling sequences for a final Meissner state with K/J = 1.98(5) and U/J = 11.02(5). The dashed lines are guides to the eye. u (l) denotes the upper (lower) leg, and e (o) indexes the even (odd) rungs in an alternating fashion. The error bars denote the s.e.m., and if not visible, are smaller than the marker size. Each data point is averaged over 30 repetitions and 14 ladders with 48 sites.

Full size image

We use the plaquette coupling sequence to explore the ground-state phase diagram between the vortex and Meissner regimes. One striking signature of the phase transition to the vortex phase is the sudden drop in the chiral current on crossing the critical point at (K/J)_cr ≈ 1. With strong interactions, the transition point is predicted to be substantially lower than in the non-interacting case, where it was previously shown that \({(K/J\,)}_{{\rm{cr}}}^{U = 0}=\sqrt{2}\) (refs. ^37,51). We experimentally probe this behaviour by varying K/J for strong interactions. Figure 5a shows the experimentally measured chiral current around the phase transition between the vortex and Meissner regimes. Indeed, we see a sudden drop in the chiral current around (K/J)_cr ≈ 1, signalling a transition to the vortex regime. The observed behaviour agrees well with a zero-temperature DMRG simulation (Fig. 5a, solid line), with our measurements finding around 57(3)% of the ideally predicted current. Compared with the rung coupling sequence, the current amplitude is reduced due to the longer preparation path (Supplementary Section III-A shows the current lifetimes), as well as smaller tunnel couplings. Note that below the phase transition, we observe enhanced fluctuations in the measured currents as reflected by the large error bars. We attribute this to a small many-body gap, which makes the system highly susceptible to technical heating.

a, Average chiral current as a function of K/J for U/J = 11.02(5) Hz and J/h = 71(1) Hz, prepared using the plaquette coupling sequence. The solid line is a fit of the expected chiral current from a DMRG simulation with scaling factor A as a free parameter, yielding A = 0.57(3). The blue-shaded area denotes the 1σ confidence interval of the fit. The dashed trace shows the non-interacting current, scaled down to the same amplitude, and the vertical line denotes the critical point without interactions. The top panel indicates the many-body gap across the phase diagram. Each data point is averaged over 80 repetitions and 14 ladders with 48 sites. b, Effective description of the flux ladder system in terms of two coupled Luttinger liquids (K ≪ J) and a one-dimensional spin chain (K ≫ J, U ≫ J). c, Enhancement of the average rung-wise density anti-correlations with increasing U and K/J. The orange-shaded areas indicate finite-temperature ED simulations (2 × 6 sites) of the density correlations from k_BT = 0.5J (bottom line) to k_BT = 1J (top line) for both interaction energies. Each data point was averaged over 30 repetitions and 14 ladders with 48 sites. The error bars denote the s.e.m., and if not visible, are smaller than the marker size.

Full size image

Last, we probe the fractional Mott-insulating nature of the Mott–Meissner phase. In the strong rung coupling limit (that is, deep in the Meissner regime), the effective pseudo-spin-1/2 model predicts the ground state to be a product state of rung triplets (Fig. 5b). Adding a second particle to one rung costs an energy of ~K, similar to having a one-dimensional Mott-insulating chain of these triplets with a fractional charge of 1/2 (also called a rung Mott insulator)^30,55. The presence of exactly one particle on each rung results in a strong density anti-correlation across the rungs, which is experimentally accessible. Figure 5c shows the measured rung density correlator \({C}_{r}=\langle {\hat{n}}_{1,r}{\hat{n}}_{2,r}\rangle\)\(-\langle {\hat{n}}_{1,r}\rangle \langle {\hat{n}}_{2,r}\rangle\), averaged over all the rungs, as a function of K/J for two different interaction energies. We find significantly negative density correlations, which are enhanced for increasing U as well as increasing K/J, in accordance with the prediction of the effective spin model. In the U→∞ and K ≫ J limit, one would expect a correlation of –1/4, with the mass gap persisting as long as K > J. In comparison, the measured correlations are weakened due to the deviation from half-filling (where one strictly does not expect a perfect Mott state), finite U and, most importantly, a finite temperature that softens the Mott transition and decreases the anti-correlation.

In fact, the density correlations are very temperature sensitive, which allows us to provide a rough estimate of the effective temperature of our many-body state. To this end, we perform small-scale ED simulations on 2 × 6 sites, revealing that rung-wise density correlations decay smoothly as the temperature increases from zero to the scale of the leg tunnel coupling. The simulation also accounts for initial-state imperfections as well as parity projection. As shown by the orange-shaded areas in Fig. 5c, a comparison of the correlator strength with the simulation indicates a temperature on the order of k_BT ≈ J in the Meissner regime, consistent also with the observed chiral current magnitudes. A temperature on this order is also compatible with the predicted elementary excitations with energy K of the spin model, since at this scale, doubly occupied or empty rungs can be formed, both bringing the correlator closer to zero. In the vortex regime (K < J), the effective temperature is probably higher due to the smaller gap and overall lower energy scales. To predict finite-T effects deep in the vortex phase, an effective description in terms of two weakly coupled Luttinger liquids can be applied (Fig. 5b)^30,51,55. This shows that the Mott gap is exponentially small in K; furthermore, the gapless excitations along the leg direction quickly wash out any current modulation or rung current patterns, rendering a direct observation of vortices challenging at a finite temperature (the simulated currents are shown in Supplementary Section V-C).

In our work, we demonstrated an experimental realization of the interacting Mott–Meissner phase on large bosonic flux ladders with 48 sites at half-filling. By combining quantum gas microscopy with local basis rotations, we uncovered the key microscopic features of this phase: persistent chiral currents along the legs of the ladder accompanied by strongly suppressed rung currents, a characteristic interaction-induced suppression of the chiral current and a density anti-correlation across the rung bonds, which is a direct signature of the fractional Mott insulator behaviour at half-filling. Comparing our measurements with small-system numerics allowed us to estimate the effective temperature, setting a new benchmark for interacting, periodically driven quantum systems, which provides an important reference point for future theoretical and experimental efforts.

The control and microscopic detection over a large, interacting ladder system, as shown here, opens an exciting avenue towards the realization of topological quantum matter. In particular, the platform can be directly used to study transport phenomena in time-reversal-symmetry-broken many-body phases^{34,36,56,57,58,59,60}. Moreover, the current measurement scheme is immediately applicable to time-resolved experiments, offering a novel probe of non-equilibrium dynamics. By further mapping out the rich phase diagram of two interacting leg ladders, we can uncover various additional many-body phases, including vortex, chiral Mott/superfluid and charge density wave states^29,30,32. Key future steps to this end involve developing advanced preparation techniques^61,62 and mitigating Floquet heating⁶³. Finally, extending this system via multileg ladders to a full 2D geometry provides a controlled pathway towards large-scale, analogue quantum simulation of fractional Chern insulators with hundreds of atoms^64,65,66.