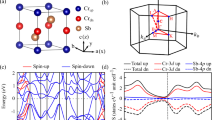
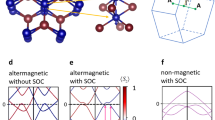
Abstract
Crystal symmetry guides the development of condensed matter. The unique crystal symmetry connecting magnetic sublattices not only distinguishes altermagnetism1,2,3,4,5,6 from ferromagnetism and conventional antiferromagnetism but also enables it to combine the advantages of ferromagnetism and antiferromagnetism4,5. Altermagnetic order is essentially a magnetic crystal order7, determined by the magnetic-order (Néel) vector and crystal symmetry. Previous experimental studies have concentrated on manipulating the altermagnetic symmetry by tuning the Néel vector orientations8,9,10,11,12. However, manipulation of the crystal symmetry, which holds great promise for manipulating the altermagnetic order, remains challenging. Here we realize the manipulation of altermagnetic order in chromium antimonide (CrSb) films via crystal symmetry. The locking between the Dzyaloshinskii–Moriya vector and the magnetic space symmetry helps to reconstruct the altermagnetic order, from a collinear Néel vector to a canted one. It generates a room-temperature spontaneous anomalous Hall effect in an altermagnet. The relative direction between the current-induced spin polarization and the Dzyaloshinskii–Moriya vector determines the switching modes of altermagnetic order, that is, parallel for the field-assisted mode in CrSb\((1\bar{1}00)\)/Pt and non-parallel for the field-free mode in W/CrSb\((11\bar{2}0)\). The Dzyaloshinskii–Moriya vector induces an asymmetric energy barrier in the field-assisted mode and generates an asymmetric driving force in the field-free mode. In particular, the latter is guaranteed by the emerging Dzyaloshinskii–Moriya torque in altermagnets. Reconstructing crystal symmetry adds a new twist to the manipulation of altermagnetic order. It not only underpins the magnetic-memory and nano-oscillator technology4,5 but also inspires crossover studies between altermagnetism and other research topics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
27,99 € / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
199,00 € per year
only 3,90 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data are available in the main text or Supplementary Information. Source data are provided with this paper.
References
Yuan, L.-D., Wang, Z., Luo, J.-W., Rashba, E. I. & Zunger, A. Giant momentum-dependent spin splitting in centrosymmetric low-Z antiferromagnets. Phys. Rev. B 102, 014422 (2020).
Hayami, S., Yanagi, Y. & Kusunose, H. Bottom-up design of spin-split and reshaped electronic band structures in antiferromagnets without spin–orbit coupling: procedure on the basis of augmented multipoles. Phys. Rev. B 102, 144441 (2020).
Ma, H. Y. et al. Multifunctional antiferromagnetic materials with giant piezomagnetism and noncollinear spin current. Nat. Commun. 12, 2846 (2021).
Šmejkal, L., Sinova, J. & Jungwirth, T. Beyond conventional ferromagnetism and antiferromagnetism: a phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 12, 031042 (2022).
Šmejkal, L., Sinova, J. & Jungwirth, T. Emerging research landscape of altermagnetism. Phys. Rev. X 12, 040501 (2022).
Krempaský, J. et al. Altermagnetic lifting of Kramers spin degeneracy. Nature 626, 517–522 (2024).
Šmejkal, L., MacDonald, A. H., Sinova, J., Nakatsuji, S. & Jungwirth, T. Anomalous Hall antiferromagnets. Nat. Rev. Mater. 7, 482–496 (2022).
Feng, Z. et al. An anomalous Hall effect in altermagnetic ruthenium dioxide. Nat. Electron. 5, 735–743 (2022).
Gonzalez Betancourt, R. D. et al. Spontaneous anomalous Hall effect arising from an unconventional compensated magnetic phase in a semiconductor. Phys. Rev. Lett. 130, 036702 (2023).
Wang, M. et al. Emergent zero-field anomalous Hall effect in a reconstructed rutile antiferromagnetic metal. Nat. Commun. 14, 8240 (2023).
Han, L. et al. Electrical 180° switching of Néel vector in spin-splitting antiferromagnet. Sci. Adv. 10, eadn0479 (2024).
Reichlova, H. et al. Observation of a spontaneous anomalous Hall response in the Mn5Si3 d-wave altermagnet candidate. Nat. Commun. 15, 4961 (2024).
Zhu, Y. P. et al. Observation of plaid-like spin splitting in a noncoplanar antiferromagnet. Nature 626, 523–528 (2024).
Fedchenko, O. et al. Observation of time-reversal symmetry breaking in the band structure of altermagnetic RuO2. Sci. Adv. 10, eadj4883 (2024).
Reimers, S. et al. Direct observation of altermagnetic band splitting in CrSb thin films. Nat. Commun. 15, 2116 (2024).
González-Hernández, R. et al. Efficient electrical spin splitter based on nonrelativistic collinear antiferromagnetism. Phys. Rev. Lett. 126, 127701 (2021).
Bose, A. et al. Tilted spin current generated by the collinear antiferromagnet RuO2. Nat. Electron. 5, 267–274 (2022).
Bai, H. et al. Observation of spin splitting torque in a collinear antiferromagnet RuO2. Phys. Rev. Lett. 128, 197202 (2022).
Karube, S. et al. Observation of spin-splitter torque in collinear antiferromagnetic RuO2. Phys. Rev. Lett. 129, 137201 (2022).
Shao, D.-F., Zhang, S.-H., Li, M., Eom, C.-B. & Tsymbal, E. Y. Spin-neutral currents for spintronics. Nat. Commun. 12, 7061 (2021).
Šmejkal, L., Hellenes, A. B., González-Hernández, R., Sinova, J. & Jungwirth, T. Giant and tunneling magnetoresistance in unconventional collinear antiferromagnets with nonrelativistic spin–momentum coupling. Phys. Rev. X 12, 011028 (2022).
Šmejkal, L., González-Hernández, R., Jungwirth, T. & Sinova, J. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 6, eaaz8809 (2020).
Zhang, Z. et al. Terahertz-field-driven magnon upconversion in an antiferromagnet. Nat. Phys. 20, 788–793 (2024).
Zhang, Z. et al. Terahertz field-induced nonlinear coupling of two magnon modes in an antiferromagnet. Nat. Phys. 20, 801–806 (2024).
Leenders, R. A. et al. Canted spin order as a platform for ultrafast conversion of magnons. Nature 630, 335–339 (2024).
Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958).
Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91–98 (1960).
Soumyanarayanan, A. et al. Emergent phenomena induced by spin–orbit coupling at surfaces and interfaces. Nature 539, 509–517 (2016).
Bogdanov, A. N. & Panagopoulos, C. Physical foundations and basic properties of magnetic skyrmions. Nat. Rev. Phys. 2, 492–498 (2020).
El Kanj, A. et al. Antiferromagnetic magnon spintronic based on nonreciprocal and nondegenerated ultra-fast spin-waves in the canted antiferromagnet α-Fe2O3. Sci. Adv. 9, eadh1601 (2023).
Yang, S. H., Ryu, K. S. & Parkin, S. Domain-wall velocities of up to 750 m s−1 driven by exchange-coupling torque in synthetic antiferromagnets. Nat. Nanotechnol. 10, 221–226 (2015).
Bläsing, R. et al. Exchange coupling torque in ferrimagnetic Co/Gd bilayer maximized near angular momentum compensation temperature. Nat. Commun. 9, 4984 (2018).
Mishra, R. et al. Anomalous current-induced spin torques in ferrimagnets near compensation. Phys. Rev. Lett. 118, 167201 (2017).
Yu, J. et al. Long spin coherence length and bulk-like spin–orbit torque in ferrimagnetic multilayers. Nat. Mater. 18, 29–34 (2019).
Chernyshov, A. et al. Evidence for reversible control of magnetization in a ferromagnetic material by means of spin–orbit magnetic field. Nat. Phys. 5, 656–659 (2009).
Železný, J. et al. Relativistic Néel-order fields induced by electrical current in antiferromagnets. Phys. Rev. Lett. 113, 157201 (2014).
Wadley, P. et al. Electrical switching of an antiferromagnet. Science 351, 587–590 (2016).
Železný, J. et al. Spin–orbit torques in locally and globally noncentrosymmetric crystals: antiferromagnets and ferromagnets. Phys. Rev. B 95, 014403 (2017).
Chakraborty, A. et al. Strain-induced phase transition from antiferromagnet to altermagnet. Phys. Rev. B 109, 144421 (2024).
Zhao, J. H. et al. Room-temperature ferromagnetism in zincblende CrSb grown by molecular-beam epitaxy. Appl. Phys. Lett. 79, 2776–2778 (2001).
Gilbert, T. L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 40, 3443–3449 (2004).
Tsai, H. et al. Electrical manipulation of a topological antiferromagnetic state. Nature 580, 608–613 (2020).
Takeuchi, Y. et al. Chiral-spin rotation of non-collinear antiferromagnet by spin–orbit torque. Nat. Mater. 20, 1364–1370 (2021).
Higo, T. et al. Perpendicular full switching of chiral antiferromagnetic order by current. Nature 607, 474–479 (2022).
Liu, P., Li, J., Han, J., Wan, X. & Liu, Q. Spin-group symmetry in magnetic materials with negligible spin–orbit coupling. Phys. Rev. X 12, 021016 (2022).
Acknowledgements
We thank J. Han for discussion. This experimental part is supported by the National Natural Science Foundation of China (grant numbers 52225106, 12241404, T2394471 and 12022416), the National Key Research and Development Program of China (grant numbers 2022YFA1402603 and 2021YFB3601301), the Open Fund of the State Key Laboratory of Spintronics Devices and Technologies (grant number SPL-2401), the Open Fund of Key Laboratory of Advanced Materials (Advmat-2410) and the Hong Kong Research Grants Council (16303821, 16306722 and 16304523).
Author information
Authors and Affiliations
Contributions
C.S. and Z.Z. designed the experiments and proposed the theoretical mechanisms for the two spin–orbit torque switching modes. Z.Z. prepared the samples, carried out transport measurements, made the theoretical analysis about the exchange-coupling torques, performed the simulations and made a list of material candidates. Z.Z., X.C. and M.H. carried out the symmetry analysis. X.C. and M.H. performed the first-principles calculations. R.C. prepared the devices. J.L., F.P., H.B., L.H. and R.C. analysed the data of microstructural characterizations and provided valuable suggestions. This work was conceived, led, coordinated and guided by C.S. and F.P. All the authors contributed to the writing of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Rafael González-Hernández and the other, anonymous, reviewer(s) for their contribution to the peer review of this work
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Switching configurations for the electrical 180° reversal of altermagnetic order.
a, Measurement set-up for the electrical switching experiments. b, Dependence of ΔEDM on the direction of n and on the relative direction between p and D. Note that p has a component that is orthogonal to n here.
Extended Data Fig. 2 Altermagnetic anomalous Hall effect of CrSb films.
a, Anomalous Hall resistance (RAH) of CrSb\((1\bar{1}00)\) film (configuration II) at different temperatures. b, Dependence of RAH on temperature for CrSb\((11\bar{2}0)\) film (configuration III). c, Temperature dependence of the coercive field of RAH in CrSb\((1\bar{1}00)\) film (configuration II). d, Temperature dependent coercive field of RAH for CrSb\((11\bar{2}0)\) (configuration III).
Extended Data Fig. 3 Schematic of the rotation of the Néel vector under the current-induced spin polarization and the exchange-coupling torques in different configurations.
TexA(B) represents the exchange-coupling torque exerted onto the magnetic sublattice mA(B). TexA(B) = TJA(B) + TDMA(B), where TJA(B) and TDMA(B) represent the antiferromagnetic exchange-coupling torque and DM torque, respectively. Noted that a type of exchange-coupling torque can be viewed as the driving force, only when it has a component that is orthogonal to both n and p and meanwhile the driving torques exerted on the two magnetic sublattices are orientated along the opposite direction. a, Configuration where D = 0. b, Configuration where p is parallel to D. c, Configuration where p is orthogonal to D.
Extended Data Fig. 4 Normalized RAH-J curve under zero external magnetic field in CrSb\(({\bf{1}}\bar{{\bf{1}}}{\bf{00}})\)/Pt.
RAH is normalized by the zero-field anomalous Hall resistance and J represents the current density in the heavy metal layer. a, Electric current is applied parallel to CrSb[0001], thus it is denoted as J[0001]. b, Electric current is applied parallel to CrSb\([11\bar{2}0]\).
Supplementary information
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhou, Z., Cheng, X., Hu, M. et al. Manipulation of the altermagnetic order in CrSb via crystal symmetry. Nature 638, 645–650 (2025). https://doi.org/10.1038/s41586-024-08436-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-024-08436-3
This article is cited by
-
Néel vector-dependent anomalous transport in altermagnetic metal CrSb
npj Quantum Materials (2025)
-
Symmetry and minimal Hamiltonian of nonsymmorphic collinear antiferromagnet MnTe
npj Quantum Materials (2025)
-
Altermagnets as a new class of functional materials
Nature Reviews Materials (2025)