Background & Summary

Wheat (Triticum aestivum L.) is one of the world’s primary staple crops, being a crucial source of dietary calories and protein1. In the global context, China holds a significant position as both the largest producer and consumer of wheat, thereby exerting substantial influence over worldwide wheat dynamics2. Notably, within China, winter wheat takes on a pivotal role, contributing to approximately 85% of the nation’s total grain output during the summer harvest3. This prominence is attributed to its exceptional yield, elevated protein content, and adaptability to local environmental conditions and dietary preferences4. Therefore, under the conditions of frequent climate change and escalating geopolitical conflicts, the timely acquisition of comprehensive production performance information at a broad regional scale for winter wheat is instrumental for an improved understanding of food supply, which is pivotal for achieving food security and sustainable development goals. Although previous research5,6,7 has primarily focused on wheat yield estimation, recent studies8,9,10 have increasingly emphasized the importance of grain quality estimation. Grain quality is as vital as grain yield because it directly influences the demand strength of the consumer markets, international market competitiveness, and the profitability of production systems11. The grain protein content (GPC) of wheat is a crucial trait that characterizes grain quality, significantly affecting the viscoelastic properties and milling characteristics of flour10. Furthermore, it direct determines the nutritional and economic value of wheat12. Thus, an accurate understanding of wheat GPC holds paramount economic and practical significance.

Spatial monitoring of GPC has evolved over time. It initially began with labor-intensive methods like manual sampling. These samples were georeferenced and interpolated using geostatistics to create spatial GPC layers13. With advancements in remote sensing (RS) and earth observation technologies, RS-based GPC monitoring has provided more potential. Beyond conventional GPC mapping, it offers the capability for early estimation. Sensors, spanning from handheld devices14 to proximal ground-based systems15,16, aerial platforms17,18,19, and satellite platforms20,21,22, have progressively emerged as increasingly favored data acquisition tools due to their economic efficiency and non-destructive advantages. These sensors are integrated with ground-based GPC observations, enabling the establishment of a predictive system for generating spatial GPC layers with predetermined levels of accuracy23. RS sensors utilize received spectral reflectance signals, particularly in the red and near-infrared wavelengths, to rapidly capture crop growth characteristics and health information24,25,26. Nonetheless, there is a common need to enhance the information of interest while disregarding responses that are less relevant and considered as noise. For instance, GPC is closely related to crop nitrogen, chlorophyll, and water content27,28, making information sensitive to these variables worthy of additional consideration. This highlights the significance of vegetation indices (VIs). The widely applied Normalized Difference VI (NDVI) in agriculture provides comprehensive and actionable vegetation information29,30. However, it can encounter saturation effects in areas with high vegetation cover31. Three-band VIs, especially the Enhanced VI (EVI), have been highlighted due to their ability to mitigate saturation31. This is crucial for GPC monitoring as the critical phase for grain protein synthesis often occurs in the later stages of crop growth32, coinciding with high biomass. Previous efforts33,34,35 have shown that EVI has the strongest correlation with GPC among numerous VIs. Relying exclusively on RS-based GPC monitoring may yield favorable results in small-scale experimental fields or individual growing seasons9,10. However, these methods often fall short when extended to large-scale and multi-year applications36,37. Different environments exert different influences on the response of RS factors to GPC. These environmental factors usually include variables directly related to GPC8,35,38,39, such as evapotranspiration (ET), temperature (Tem), precipitation (Pre), and solar radiation (SR). They influence the protein nutritional value of wheat grains by exerting effects on photosynthesis, growth rates, nutrient utilization efficiency, and the translocation of carbon and nitrogen from source to sink40,41. In light of this prior knowledge, researchers have chosen to employ multisource data fusion for GPC estimation, which has led to the development of various methods.

There are three primary categories of methods used for predicting GPC. The first category is empirical methods, including empirical regression based on simple mathematical models and complex machine learning algorithms. Empirical regression methods typically requiring fewer data points, offering transparent models that are easy to comprehend42. However, these methods often lack precision and exhibit relatively weak generalization capabilities18. Research on machine learning algorithms for GPC estimation has been increasing9,10,43, and such methods typically demand a substantial amount of data for accurate model training. By adjusting factors such as algorithm complexity and regularization, model generalization can be enhanced44. Nevertheless, most machine learning algorithms are commonly perceived as “black boxes” due to their limited interpretability12. The second category is physically-based process models. These models aim to simulate and predict crop growth and development by considering various factors, such as soil properties, meteorological conditions, and agricultural management practices45. Data assimilation provides a method for integrating RS observations into process models. Leaf area index or leaf nitrogen content are often used as state variables in data assimilation systems to correct crop growth model behavior, thereby improving model accuracy46. The application of GPC simulation using these methods has yielded favorable results at field and small-scale levels34,47,48. However, the high demand for dense data input and substantial localized parameter calibration makes employing these models for large-scale yield estimations more challenging. The third category involves semi-mechanistic models. These models combine fundamental mechanistic equations or rules, explaining the core mechanism of an observed phenomena, with empirical parameters to account for complexities or uncertainties that the model may not fully describe49,50. Given these advantages, semi-mechanistic models have garnered increased attention, particularly in estimating agricultural surface parameters51,52,53. Among them, Li, et al.54 has elucidated the effectiveness of the hierarchical linear model (HLM) for GPC estimation that integrates climate-RS spatial nesting theories in interannual application scenarios, and Xu, et al.35 has reiterated it within cross-regional application scenarios. However, most research still focuses on limited regions and years, and the scalability of the results requires further validation. Additionally, there are only a limited number of studies regarding the monitoring of national wheat GPC in China and its correlation with climate8,38. Due to data limitations, the minimum geographic units analyzed in current studies are at the county-level, rather than undergoing more detailed pixel-level assessments.

The synergy of advancements in RS technology, the application of sensor technology, agricultural information management systems, agricultural digitization, and open data policies has propelled the generation of vast agricultural resource products55,56. These products encompass datasets related to crop planting distribution57,58,59, crop phenology60,61,62, and yield63,64,65, among others. The creation of these datasets holds significant value, as it contributes to the realization of sustainable agricultural development, food security, grain production, and rural economic growth. Nevertheless, so far, no large-scale and long-term datasets related to wheat GPC have been made publicly available. This data gap in the field signifies a need for further research and data acquisition to fill it.

In view of this situation, this study leveraged multi-source climate and RS data spanning from 2008 to 2019 to develop a nationwide GPC estimation model based on HLM for China. This model was employed to generate a high-resolution, long-term GPC dataset with a spatial resolution of 500 m (CNWheatGPC-500). Specifically, first, a multi-source meteorological dataset was integrated, encompassing evapotranspiration, temperature, precipitation, and solar radiation, based on pixel-by-pixel phenological attributes. This integration effectively alleviated the phenological variations across different regions. Secondly, taking into account different levels of spatial data structures and integrating meteorological datasets with maximum EVI, an HLM-based GPC estimation model was constructed. Finally, the performance of the GPC estimation model was rigorously assessed through extensive multi-model comparisons and cross-validation. The model validated for its performance was applied to the entire wheat cultivation areas of China to generate the CNWheatGPC-500.

Methods

Study area

China’s winter wheat cultivation is a result of its conducive natural environment, rich cultivation history, and alignment with dietary preferences. With its vast territory covering approximately 9.6 million km², China displays a wide range of climate and soil conditions, which, in turn, leads to the varying adaptability of winter wheat across different regions. Each region boasts suitable planting areas. The focus of this study includes 13 provinces and municipalities directly under the Central Government (Fig. 1(a)), encompassing nearly all major winter wheat cultivation regions in China. These regions have been further categorized into five primary agricultural subregions based on climate characteristics, soil conditions, and topography. The vector data utilized for these delineations is derived from the Agricultural Zoning Map of China, depicted in Fig. 1(b). Subregion A covers the northwestern region of Gansu and Xinjiang, while Subregion B includes the Loess Plateau, notably the Guanzhong Plain. Subregion C corresponds to the North China Plain, and Subregion D is the southwestern regions that includes the Sichuan Basin. Subregion E includes the plain areas in the middle and lower reaches of the Yangtze Valley.

Fig. 1
figure 1

(a) Provinces involved in the study and the spatial distribution of ground-measured grain protein content (GPC) observations (green points) and (b) the five distinct agricultural subregions identified within the study area.

Full size image

Data acquisition and preprocessing

In this study, a comprehensive dataset was employed, encompassing geospatial data for winter wheat, satellite imagery, historical meteorological data, and field-based GPC data. These diverse data sources were selected to facilitate analysis of winter wheat characteristics and enhance the precision of GPC estimation models. The geospatial data of winter wheat provides key information about wheat planting patterns and phenology, serving as the base layer for this study and establishing the temporal framework for meteorological data synthesis. Satellite imagery data refines the spatial scale by offering high-resolution imagery of the research area. This is particularly valuable for closely monitoring the growth and nutritional status of winter wheat. The utilization of historical meteorological data plays a pivotal role in driving grain protein synthesis and nutrient transfer within the wheat. The pronounced variability in meteorological conditions among different regions exerts a direct influence on the diversity in GPC. Consequently, the inclusion of meteorological data can facilitate the development of more robust GPC estimation models, particularly in the presence of spatial heterogeneity. Finally, field-based GPC data serves to calibrate and validate GPC estimation models based on RS and meteorological data. Together, these datasets form a robust foundation for creating the CNWheatGPC-500 dataset, as elaborated in the subsequent sections and Table 1.

Table 1 Input dataset details for CNWheatGPC-500 generation.
Full size table

Geospatial data for winter wheat

The winter wheat phenological data and spatial distribution data in this study were obtained from the winter wheat phenological dataset in China from 2000 to 2019 produced by Luo, et al.60. In this dataset, the wheat layer was extracted from a 1 km national land cover dataset (NLCD) Detailed information about the NLCD dataset can be found at http://www.resdc.cn/Default.aspx. Notably, the dataset comprises essential winter wheat phenological periods, namely, green-up and emergence (GE), heading (HE), and maturity (MA). Of particular significance is that it provides spatiotemporal coverage that aligns with the specific needs of this study.

Satellite imagery data

The Moderate Resolution Imaging Spectroradiometer (MODIS) MCD43A4 dataset was accessed through the Google Earth Engine (GEE) platform. This dataset includes data from 2000 onward and features a spatial resolution of 500 m along with a retrieval period of 16 days. The utilization of RS features from this dataset is widespread in the study of surface crop parameter inversion66,67. Among these features, EVI stands out as an improvement of NDVI, specifically designed to minimize the impact of atmospheric scattering effects68. This refinement significantly bolsters the detectable vegetation signals, providing a more precise estimation of vegetation growth and health status, even in the face of varying conditions across different temporal and spatial contexts69. Hence, considering the accessibility of high-resolution, long-term time series data, this study proceeded to compute the EVI using MODIS data for estimating wheat GPC. The calculation equation is as follows:

$${\rm{EVI}}=2.5{\rm{\times }}\frac{\left({\rm{NIR}}-{\rm{R}}\right)}{\left({\rm{NIR}}+6{\rm{\times }}{\rm{R}}-7.5{\rm{\times }}{\rm{B}}+1\right)},$$
(1)

where NIR, R, and B represent the reflectance values of MODIS products in the near-infrared, red, and blue bands, respectively. It is worth noting that the EVI employed in this study corresponds to the maximum synthesis achieved during the winter wheat growth season. This specific choice is grounded in the fact that the maximum EVI value typically conveys vital information about the physiological characteristics and growth status of wheat during the heading stage51,60. This period is crucial as it directly influences the processes of wheat photosynthesis and nutrient transfer, which are closely tied to protein synthesis70,71.

Historical meteorological data

The ET, Tem, Pre, and SR data were chosen to reconstruct the required historical meteorological input dataset for this study. ET represents the combined processes of soil water evaporation and plant transpiration, comprehensively reflecting water demand, water stress, and the management of agricultural water72. ET plays a pivotal role in influencing crop growth and protein synthesis and has been widely employed in crop yield estimation73. However, its incorporation into the estimation of GPC at the national scale represents an unexplored approach. Furthermore, there is a well-established recognition that Tem, Pre, and SR are critical in facilitating nutrient absorption, translocation, and protein synthesis within wheat plants39,74,75. Previous studies35,76 harnessed these factors to estimate wheat GPC, yielding favorable results. The ET data for this study was obtained through the MODIS MOD16A2 product via the GEE platform. Tem, Pre, and SR data were sourced from European Centre for Medium-Range Weather Forecasts (ECMWF), ensuring consistent data sources across these data. Detailed data specifications can be found in Table 1.

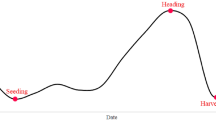
Considering the challenges of regional and interannual phenological variations across extensive spatial and temporal scales, this study integrated phenological grid data with their inherent temporal structures to reconstruct meteorological datasets on a pixel-by-pixel basis, as depicted in Fig. 2. First, wheat phenological data was paired with meteorological grids. This started by determining the day of year (DOY) corresponding to MA for each pixel within the meteorological grid. Subsequently, cumulative values for the respective meteorological variables were computed at 30-day intervals, over a total period of 90 days before MA, resulting in the generation of three effective cumulative values for each meteorological variable. These 30-day time intervals were denoted as T1, T2, and T3, substituting the conventional empirical selection of specific months. The 90-day timeframe generally encompasses the critical phenological stages of wheat growth (e.g. HE and MA). This observation period should capture the influence of the most critical phenological stages on wheat grain protein synthesis, which is essential for accurate monitoring and analysis of GPC35,41.

Fig. 2
figure 2

Illustration of the methodology used for combining phenology and meteorological variables. In response to distinct maturity (MA) observed among individual pixels, specific time durations were selected for synthesizing relevant features on a pixel-by-pixel basis. Note: T1 represents the first 30-day interval to the MA, T2 is the second 30-day interval, and T3 is the third 30-day interval. SE: sowing and emergence period, GE: green-up and emergence period, HE: heading period.

Full size image

Field-based GPC data

Ground survey points were densely distributed in the study area, as illustrated in Fig. 1(a). A total of 2648 GPC data points for winter wheat were collected in the field from 2008 to 2019, which followed a normal distribution (Fig. 3(a)). The data size across different provinces is illustrated in Fig. 3(b), with Anhui, Hebei, Henan, Jiangsu and Henan exhibiting the most extensive datasets. These provinces are situated in the primary cultivation regions for winter wheat in China, accounting for 60% of the nation’s total wheat acreage77. It should be noted that data for the year 2015 were not available, while the data for the subsequent years exhibited consistent and comprehensive coverage, as illustrated in Fig. 3(c). The on-site measurement of GPC strictly adheres to standard measurement methods. Specifically, first, during the annual maturity period, sample points were randomly selected and precisely located within each sample area using GPS. Second, winter wheat was manually harvested from each 1 m² sample area employing the five-point sampling method. Each sample area was positioned at a minimum distance of 2 m from the field’s edge to mitigate edge effects. Thirdly, the samples were transported to the laboratory, where the plants were separated, impurities were removed, and the grains were dried to attain a standardized moisture content of 14%. Finally, the wheat grains were weighed. The protein content was then measured using an Infratec TM 1241 near-infrared grain analyzer (FOSS A/S, Hillerød, Denmark).

Fig. 3
figure 3

Statistics of all study samples (a), by province (b), and by year (c). The data for Tianjin and Hebei Province have been integrated and are collectively represented as “Hebei”.

Full size image

Workflow

Figure 4 illustrates the workflow of this study. The first step is data acquisition and preprocessing, which involves the fusion of multisource meteorological data with phenological information at the pixel level, the extraction of RS data, and on-site GPC measurements. These data are used to create the calibration and validation dataset. The subsequent step encompasses model development and accuracy evaluation indicator, in which the GPC estimation model is constructed using this dataset and the HLM approach. Multiple evaluations, including model comparisons and cross-validation, are employed to assess the GPC estimation models. The final step, labeled dataset and validation, leverages the GPC estimation model to create the CNWheatGPC-500 dataset, which covers the study area from 2008 to 2019.

Fig. 4
figure 4

The workflow framework for generating CNWheatGPC-500.

Full size image

Development of hierarchical linear model (HLM)

The generation of large-scale and long-term GPC datasets typically faces challenges of spatial heterogeneity and interannual phenological differences. The conventional strategy is to comprehensively utilize multi-source environmental data such as RS and meteorology to address this challenge. However, RS data is typically acquired at relatively high resolutions, offering detailed information about wheat growth for each small-scale geographic unit (pixel). Meteorological data, on the other hand, is usually collected at larger geographic units, covering extensive geographic regions. These geographic regions with distinct climates influence the relationship between GPC and RS data. Consequently, the complex interactions among these diverse data sources result in significant data nesting. HLM is a powerful tool employed for the explanation and modeling of nested data78, and it has found widespread application in studies related to vegetation growth, crop yield and GPC estimation35,51,52,53,54,79,80. HLM enables the partitioning of variability in nested data into two components: one arising from the individual level (i.e., how RS data responds to GPC), and the other stemming from the group level (i.e., how meteorological data influences the relationship between RS data and GPC). The general forms of the two-level relationships are presented as:

$$\,\mathrm{Layer}\,1:GP{C}_{{\rm{ij}}}={\beta }_{{\rm{oj}}}+{\beta }_{1{\rm{j}}}\times {\rm{EVI}}+{{\rm{r}}}_{{\rm{ij}}}$$
(2)

where the GPCij is the grain protein content of an individual i within the population j, β0j and β1j represents intercept and slope, respectively. rij represents the random error. In this layer, the first linear structure of EVI response to wheat GPC is formed. The selected meteorological data has an impact on the relationship between wheat GPC and EVI, resulting in variations in slope and intercept:

$${\rm{Layer}}\,2:{\beta }_{{\rm{mj}}}={\gamma }_{{\rm{m0}}}+{\sum }_{1}^{n}({\gamma }_{{\rm{mn1}}}\times {{\rm{ET}}}_{{\rm{n}}})+{\sum }_{1}^{n}({\gamma }_{{\rm{mn2}}}\times {{\rm{Tem}}}_{{\rm{n}}})+{\sum }_{1}^{n}({\gamma }_{{\rm{mn3}}}\times {{\rm{Pre}}}_{{\rm{n}}})+{\sum }_{1}^{n}({\gamma }_{{\rm{mn4}}}\times {{\rm{SR}}}_{{\rm{n}}})+{{\rm{\mu }}}_{{\rm{mj}}},$$
(3)

where βmj represents the β0 and β1 from the Level 1 model respectively, γm0 is the intercept. γmn1 to γmn4 represent coefficient of each factor. The n values are 1, 2, and 3, representing the meteorological data synthesized for the n-th time interval (T1, T2 and T3). And μmj is the random effect of the Level-2, used to consider the correlation and variability between individuals within group. The fixed and random effects parameters in HLM are estimated using maximum likelihood estimation81. The construction of the model and the estimation of parameters in this study were carried out utilizing the Jamovi statistical software (The jamovi project)82, adhering to rigorous scientific methodology. Furthermore, it should be noted that this study employs centralization to set the mean of the independent variables to zero. This approach can reduce parameter collinearity and uniform scaling, thereby enhancing the quality and interpretability of the model.

To further characterize the level of data nesting in the GPC estimation model, this study uses the Intraclass Correlation Coefficient (ICC). ICC serves as a crucial statistical metric for assessing the correlation among individual-level data within group-level data, the variability between different groups, and the effectiveness of hierarchical data53. Its value ranges from 0 to 1, and a higher ICC value indicates a better fit to the characteristics of nested data, making it more suitable for HLM. The calculation is as follows:

$${\rm{ICC}}={{\rm{\sigma }}}_{{\rm{\mu }}0}^{2}/\left({{\rm{\sigma }}}_{{\rm{\mu }}0}^{2}+{{\rm{\sigma }}}^{2}\right),$$
(4)

where σ2 is the within-group variance, σμ02 is the between-group variance.

Comparative regression algorithms

In addition to HLM, several other machine learning and statistical algorithms have been considered for estimating GPC in wheat. The algorithms tested in the present work include Random Forest (RF), Support Vector Machine (SVM), and Multiple Linear Regression (MLR). Each of these methods possesses its unique characteristics, offering valuable insights into agricultural parameter estimation in previous study73,83,84.

RF is an ensemble learning algorithm widely used in agricultural modeling and RS applications. And it is particularly attractive for GPC estimation due to its capability to handle high-dimensional datasets and nonlinear relationships. The RF algorithm employs multiple decision trees created from bootstrapped samples85. Each tree splits nodes using random feature subsets. The outcomes from each tree are aggregated using either majority voting or averaging of the predicted values. Moreover, RF provides opportunities for performance optimization through hyperparameter tuning. In this study, grid search and cross-validation techniques are utilized to identify the optimal hyperparameter combination, resulting in a precisely calibrated RF model for GPC estimation.

SVM is another powerful algorithm employed in the ___domain of agricultural modeling and RS, making it an appealing choice for these data. SVM operates by determining the ideal hyperplane for effectively distinguishing between various data point categories86. This hyperplane is identified by maximizing the margin between the nearest data points of different categories. The effectiveness of SVM lies in its ability to capture complex relationships in the data, which is especially valuable for the GPC estimation. Similarly, grid search and cross-validation techniques are used to fine-tune the SVM model.

MLR is a statistical method used to model the relationship between a dependent variable and multiple independent variables by fitting a linear equation87. Its primary purpose is to predict the dependent variable’s values based on the values of the predictor variables. MLR provides quantifiable coefficients for each predictor variable, representing the strength and direction of their relationships with GPC. Simplicity and transparency of MLR offer a useful reference against more complex algorithms, contributing to a comprehensive evaluation of their respective performance.

Experimental setup

  1. a)

    Evaluating the hierarchy and variability in multi-source environmental data employed for GPC estimations across different interannual and regional groupings, using ICC computations. This approach aims to enhance our comprehension of the advantages associated with the HLM.

  2. b)

    Model comparison: The experimental setup for this study entailed the random selection of model calibration and validation datasets, maintaining a 60% to 40% ratio respectively. The calibration dataset served as the basis for constructing the HLM model, which was subsequently validated using the separate validation dataset. In parallel, the exact same subsets of data were used to calibrate and validate the comparison modelling approaches (RF, SVM and MLR).

  3. c)

    Model robustness: Cross-validation was executed using two distinct methods: leave-one-year-out and leave-one-region-out. These methods ensured that model validation occurred independently of the data used for model training.

The CNWheatGPC-500 dataset was generated by retraining the model with the best performing model using the entire available dataset, and individual models were crafted for each province to accommodate the substantial data available from each region. Exploration of the spatiotemporal patterns was carried out using the generated CNWheatGPC-500 dataset. This experimental design allowed for rigorous model assessment, validation, and the investigation of GPC variations at both regional and temporal scales, ensuring the reliability of the results.

Statistical analysis methods

The R-squared (R2), Root Mean Square Error (RMSE), and normalized RMSE (nRMSE) serve as essential metrics for the comparison and assessment of the GPC estimation models. These metrics are widely used in quantifying the models’ accuracy and effectiveness35,88. The calculation formula is as follows:

$${{\rm{R}}}^{2}=1-\frac{{\rm{SSE}}}{{\rm{SST}}},$$
(5)
$${\rm{RMSE}}=\sqrt{\frac{\mathop{\sum }\limits_{i=1}^{n}{({y}_{i}-{\hat{y}}_{i})}^{2}}{n}},$$
(6)
$$nRMSE=\frac{RMSE}{{\bar{y}}_{i}},$$
(7)

Where SSE is the Sum of Squared Errors, representing the fitting error of the regression model. SST is the Total Sum of Squares, representing the overall variability of the data. n is the number of sample points. \({y}_{i}\) is the actual observation value of the i-th sample point. \(\hat{{y}_{i}}\) is the predicted value of the model for the i-th sample point. \(\bar{{y}_{i}}\) is the average of the actual observation value.

Data Records

The first 500-meter spatial resolution, long-term winter wheat dataset covering major planting regions in China (CNWheatGPC-500) was created by integrating multi-source data from ERA5 and MODIS. Distributed under the Creative Commons Attribution 4.0 International license, the CNWheatGPC-500 dataset not only advances our understanding of winter wheat GPC in China but also facilitates research and analysis in an open and collaborative manner. The dataset is designated as YearCNWheatGPC-500, where “Year” represents the years spanning from 2008 to 2019. It encompasses a comprehensive 12-year dataset presented in TIF format. The CNWheatGPC-500 product generated in this study is aavailable at https://doi.org/10.5281/zenodo.1006654489. Kindly contact the authors for further inquiries and more detailed information.

Technical Validation

Inter-group variability in multisource data

Significant variations across years were observed by calculating Intraclass Correlation Coefficient (ICC) for various provinces (Fig. 5(a)). Gansu Province displayed relatively lower interannual differences (ICC = 0.20), while Shanxi Province exhibited higher interannual variations (ICC = 0.79). This suggests that a significant proportion of the total variability, ranging from 20% to 79%, can be attributed to inter-group variance. Furthermore, the analysis extended to provincial differences for various years (Fig. 5(b)). For instance, a relatively low ICC value was found in 2018, indicating minimal differences among provinces and a higher degree of consistency within that year. Conversely, 2010 exhibited a notably high ICC value, implying substantial differences among provinces during that particular year. Despite these discrepancies, the overall ICC values remained notably high, highlighting the multi-layered nature of spatial data, where a level of consistency exists within groups, but disparities between groups are pronounced. Incorporating diverse agricultural subregions into the analysis has generated additional insights (Fig. 5(c–g)). While scatter plots suggest that the relationship between GPC and the EVI may not be overt, it does exhibit a notable degree of correlation within different groups.

Fig. 5
figure 5

Regional variations in HLM: relationships between dependent and first-level independent variables with group effects. Panel (a) displays intraclass correlation coefficient (ICC) calculations grouped by years within various provinces, while (b) displays ICC calculations grouped by provinces within different years. Panels (c–g) depict intergroup mixed effects and ICC for the five agricultural subregions. R: Grouped by region. Y: Grouped by year.

Full size image

Assessment and selection of GPC estimation models

Evaluating the performance of GPC estimation models is essential for validating the reliability of CNWheatGPC-500. Figure 6 presents the performance and accuracy of various models on the calibration dataset. The RF model (Fig. 6(a)) exhibits a favorable performance with an R2 of 0.59, RMSE of 0.89%, and nRMSE of 6.39%. However, a slight bias is visible as it tends to underestimate high GPC values and overestimate low GPC values. In Fig. 6(b), the performance of the SVM model is shown, presenting acceptable results (R2 = 0.43, RMSE = 1.04%, nRMSE = 7.5%), though worse than RF in terms of accuracy. The MLR model results, shown in Fig. 6(c), exhibited the lowest accuracy with an R2 of 0.11, RMSE of 1.29%, and nRMSE of 9.32%. Lastly, an R2 value of 0.57, an RMSE of 0.89%, and an nRMSE of 6.43% are observed for the HLM in Fig. 6(d). While HLM slightly underperformed compared to RF in terms of R2, the HLM displayed a more balanced estimation performance, particularly aligning with actual values in the lower and higher GPC ranges.

Fig. 6
figure 6

Performance comparison of winter wheat GPC estimation models based on RF (a), SVM (b), MLR (c), and HLM (d) in the calibration dataset. The data for Tianjin and Hebei Province have been integrated and are collectively represented as “Hebei”.

Full size image

The performance of the GPC estimation models on the validation dataset can be observed in Fig. 7. The R2, RMSE, and nRMSE (Fig. 7(a)) for the GPC estimated by RF compared to the measured GPC were 0.39, 0.99%, and 7.12%, respectively. Although it still delivered reasonable estimations, the performance of RF was comparatively diminished in the validation dataset. Figure 7(b) shows the SVM model results (R2 = 0.29, RMSE = 1.09%, nRMSE = 7.86%) indicating a drop in performance as well. In Fig. 7(c), the MLR model maintained its R2 at 0.11, but experienced an increase in both RMSE (1.19%) and nRMSE (8.61%), and continued to be the worst performing model. Notably, Fig. 7(d) reveals the robust performance of the HLM in the validation dataset with an R2 of 0.45, RMSE of 0.96%, and nRMSE of 6.90%. Among all models, HLM stands out with the highest validation accuracy.

Fig. 7
figure 7

Performance comparison of winter wheat GPC estimation models based on RF (a), SVM (b), MLR (c), and HLM (d) in the validation dataset. The data for Tianjin and Hebei Province have been integrated and are collectively represented as “Hebei”.

Full size image

Cross-validation of HLM across multiple years and regions

Further cross-validation was performed to evaluate the performance of HLM. Figure 8(a) illustrates the results of a leave-one-region-out cross-validation conducted across provinces in China, where each province’s results represent its independent validation, having not participated in the model training. While R2 values varied across provinces, ranging from 0.07 in Hebei to 0.41 in Xinjiang, the overall precision remained acceptable, illustrating the influence of regional differences. The RMSE plays a more crucial role than R² in assessing the validation accuracy of HLM. The RMSE values, ranging from 0.90% in Gansu to 1.32% in Anhui, displayed a relatively consistent pattern across provinces. Figure 8(b) displays the accuracy of leave-one-year-out cross-validation. The R2 values exhibit variance across years due to sample size discrepancies, ranging from 0.19 to 0.62. Conversely, the RMSE values exhibit a relatively balanced distribution, ranging from 0.77% to 1.11%. Each year’s results consistently demonstrated a satisfactory performance. In summary, the cross-validation results demonstrated the resilience of HLM. Even when faced with data gaps for a specific year, the HLM models constructed by individual provinces consistently generated satisfactory GPC estimations for that particular year, emphasizing the reliability of the GPC dataset.

Fig. 8
figure 8

Cross-validation of the GPC estimation model based on HLM using leave-one-region-out (a) and leave-one-year-out (b) approaches, where the number on each bar represents the size of the validation set. ** indicates extremely significant level (p < 0.01).

Full size image