Background & Summary

Leaf Area Index (LAI) is an important indicator of vegetation defined as one half of the total green leaf area per unit horizontal ground surface area1,2. It is a critical parameter for depicting vegetation situation and has been used in assessing vegetation dynamics3, building land surface models4, assisting crop yield estimation5 and supporting forest management6,7. Projecting future vegetation changes under different climate scenarios requires using model simulations. The Coupled Model Intercomparison Project (CMIP) has tried to use climate models to make such projections, and the sixth phase – usually known as CMIP 6 – started years before8. These models which predict global variables including precipitation, air temperature, humidity, and LAI are called Global Climate Models (GCMs). GCMs contribute significantly to future climate research on a global scale and are an important basis for analyzing global change9. LAI data from GCMs has different resolutions, usually 100 or 250 km, such as 100 km data from BCC-CSM2-MR10 and 250 km data from UKESM1-0-LL11. Some higher resolution GCMs like HighResMIP12 can provide LAI at 25 km resolution, but it only simulates future vegetation under one scenario (highres-future). This limitation in resolution or scenario coverage restricts the potential usage of GCMs. Therefore, downscaling is necessary to be applied to GCMs to improve the applicability of GCM data for local studies.

There are mainly two kinds of downscaling methods: dynamic downscaling and statistical downscaling13. A good example of dynamic downscaling is Regional Climate Models (RCMs). However, generating an RCM is computationally expensive, and its accuracy is restricted by the original GCM14. On the contrary, statistical downscaling is easily applicable, and it can further remove bias in GCMs13, allowing the simulation to be close to the truth. Perfect Prognosis (PP) is one of the structures to fulfill the statistical downscaling. It links the large-scale observed predictors to local-scale observed predictands by a statistical model, and then applies the model to predictors from GCMs to generate downscaled results13. Various statistical models are used in the PP downscaling procedure such as the General Linear Model (GLM)13, Convolution Neural Network (CNN)15, and Quantile Mapping16. Recent research has explored the integration of super-resolution techniques, like applying Skip connections and Upsampling in Super Resolution Deep Residual Network (SRDRN)17,18 to enhance downscaling performance. Other architectures may also be suitable for downscaling, such as stacking residual blocks in Super Resolution Residual Network (SR-ResNet)19 and the usage of PixelShuffle in Enhanced Deep Super-resolution Network (EDSR)20.

Existing downscaling methods designed for precipitation and temperature are not fully applicable for downscaling LAI because of the different target resolutions. Much existing research downscaled precipitation or temperature by a factor of 4, which means from 100 km to 25 km or 200 km to 50 km15,21. Nevertheless, LAI needs a higher resolution to be useful. A review7 of LAI indicated that the dataset with the lowest spatial resolution among major global long-term LAI products is GIMMS LAI (1/12°) which is used widely in global and regional vegetation research2,22, while other moderate-resolution data like GLOBMAP23 have even higher resolution. Focusing on application, research aiming at grasslands24, droughts25 and streamflow26 in provinces, countries and continents used LAI data with a resolution of about 0.1°. Some other applications like urban green space planning need even higher resolution27.

The purpose of this study is to provide Future 0.05° LAI (F0.05D-LAI) data across historical and future scenarios in a high resolution in China, allowing researchers to understand possible vegetation patterns in the future, expanding the application of GCMs from the global scale to the regional scale. China is a large country with an intricate climate and vegetation structure. The climate in China influenced by the monsoon and the Qinghai-Tibet Plateau, exhibits significant variation from one region to another, resulting in a diverse range of vegetation. Nowadays, the Chinese government is making an effort to environmental protection and vegetation restoration, launching multiple ecological programs like the ‘Three-North Shelter Forest Program’, and LAI is used in detecting fragile regions28. Our research declared and applied a deep learning network to downscale the LAI under a scaling ratio of 20 (from 1° to 0.05°) and did a comparison with other benchmarks. We also used our data to do a simple analysis of future vegetation and its degradation risk, showing an example of the data usage. Although the data represents potential LAI only under four scenarios and may be influenced by future human activities, it remains a valuable support dataset for analyzing future vegetation, assessing degradation risks and growth potential.

Methods

Data source

The data used in this study can be summarized as low-resolution data (climate data) and high-resolution data (topography and LAI reference data).

The main low-resolution data in this work include climate data (air temperature, relative humidity and precipitation) from CMIP 610 and European Centre of Medium-Range Weather Forecasts Reanalysis v5 (ERA-5)29.

The CMIP 6 climate simulation data are derived from the BCC-CSM2-MR experiment10. BCC-CSM2-MR is a medium-resolution climate system model developed by the National (Beijing) Climate Center with a time range of 1850–2100, with a temporal resolution of 1 month and a spatial resolution of 1°. BCC provides a detailed validation of climate factors especially in East Asia, making it a widely used model in China or East Asia climate projection. In the future period covered by CMIP6 (2015–2100), we selected four Shared Socio-economic Pathways (SSPs): SSP-126, SSP-245, SSP-370, and SSP-585 scenarios to represent the future possibilities since they are the high-priority scenarios among SSPs, and most climate models usually simulate these four scenarios30,31. We used air temperature and relative humidity at different pressure levels (1000hpa, 850hpa, 700hpa, and 500hpa) along with ground precipitation data as model input, while the LAI was utilized for result comparison purposes.

ERA-5 reanalysis dataset was selected as the source of climate data, with a 0.25° horizontal resolution for the period from 1940 onwards29. The used variables are the same as CMIP 6 climate data except for LAI. ERA-5 reanalysis data is widely used in downscaling research18,32, and it is also a recommended data source in the VALUE framework21.

Two main high-resolution data in this work include Global Land Surface Satellite (GLASS) LAI33 and ALOS World 3D – 30 m Digital Elevation Model (AW3D30 DEM)34.

GLASS LAI was selected as a high-resolution product in this work to represent the reference LAI. GLASS LAI product is a widely used LAI dataset with 0.05° horizontal resolution and 8 days temporal resolution from 1981 to 201833. Compared with MODIS LAI, which only ranges from 2000 to 2023, GLASS LAI can provide better data coverage on the time range, increasing the sample size that can be used in training. The monthly LAI data was calculated from the average LAI in the month.

AW3D30 DEM34 data derived from the Japan Aerospace Exploration Agency was also used in this study since topography has a clear impact on vegetation. It can provide more accurate topography data across latitudes with a 30-meter horizontal resolution35. It is also regarded as a constant across years since humanity has not been able to drastically change the terrain.

Downscaling procedure

The downscaling process includes three primary parts: Data Acquisition, LAI Downscaling Network (LAIDN) Model Training, and Downscaling LAI. “Data Acquisition” comprises downloading data and data preprocessing. “LAIDN Model Training” contains model fitting and model validation. Finally, “Downscaling LAI” includes bias-adjustment, producing downscaled data, data post-processing, and its practical application.

Data acquisition

This part is shown in the top frame of Fig. 1. We first preprocessed our data, which included clipping them to the range of China and resampling. To avoid potential biases caused by convolution or window-based algorithms, data were all clipped to a rectangular region spanning from 5.50°N, 55.50°E to 71.75°N, 155.75°E, ensuring a buffer zone along China’s borders.

Fig. 1
figure 1

Downscaling procedure.

Full size image

Then we did some resampling to bridge the resolution gap between different data. Low-resolution data, including air temperature, relative humidity, and precipitation derived from ERA-5, were resampled to a horizontal resolution of 1°. High-resolution data including GLASS LAI and DEM, were resampled to a horizontal resolution of 0.0625° (1/16°).

LAIDN model training

The model claimed and used in our study is the LAIDN, utilizing residual blocks36, PixelShuffle37, and the Parametric ReLU (PReLU)38. It is a deep learning network receiving climate data and topography constant data as input, GLASS LAI as a reference and yields the downscaled high-resolution LAI data as output.

Figure 2 shows the Downscaling Block which is the core structure of LAIDN. It utilized the PixelShuffle block to effectively extend the resolution of low-resolution climate data by compressing their channels. By applying the Downscaling Block twice to the low-resolution climate data, it enhanced their resolution to match that of high-resolution DEM data and GLASS LAI. Subsequently, the concatenated climate and DEM data were processed through additional convolutions and residual blocks to reach the model output with a resolution of 0.0625°. To ensure ease of use, the data was finally interpolated to 0.05° using cubic interpolation.

Fig. 2
figure 2

The structure of the downscaling block.

Full size image

Mean Square Error (MSE) and the optimizer Adam39 are selected as the loss function and optimizer in model training. We ended the training when the loss function converged. The initial learning rate was 0.02 and was halved when training reached the 5, 25, 50 and 100 epochs. The hardware platform was RTX 3060, the software platform was CUDA12.1, and the training was performed on Windows Subsystem Linux 2 Ubuntu operating system through Pytorch deep learning framework.

After training the model, we validated our model to prove that our model is stable and robust in different situations. To quantitatively assess the downscaling performance of each method, we employed three validation techniques: (1) calculation and comparison of R2 and Root Mean Square Error (RMSE) between GLASS LAI and the downscaled results, (2) analysis of LAI value distribution charts and Structural Similarity Index Measure (SSIM) distribution charts, and (3) time series validation in different regions of China.

RMSE and R2 are both generously used metrics in evaluating the correctness. In historical periods, we calculated these metrics between GLASS LAI and downscaled results among training, validation, and test sets. In plotting the LAI distribution charts, the Kernel Density Estimate (KDE) curve of downscaled LAI data from different methods and the GLASS LAI data were painted into the same figure. The result performance will be better if there is less discrepancy between downscaled LAI’s and GLASS LAI’s KDE curves. Besides, to compare the reservation of spatial textures in results, we used SSIM as the metric to compare the similarity of textures between GLASS LAI and downscaled LAI. SSIM is a widely used metric to compare structural similarity, and it also provides additional information for distinguishing model performance40. It calculates the brightness, contrasts, and structures in patches of the image clipped by a sliding window, ranging from −1 to 1. The larger the value, the more effective the downscaling method is. To show the distribution of spatial similarity, we showed the KDE plot of SSIM calculated in each sliding window rather than an average value of SSIM. The result performance will be better if the peak is near 1. In the time series validation, we chose six points in different regions of China and painted the LAI time series in each point based on GLASS LAI, GCM LAI, F0.05D-LAI, and benchmarks downscaled LAI. The performance will be better if there is less divergence between the downscaled LAI and the GLASS LAI time series curves.

The two selected benchmarks are GLM and SRDSN. GLM is a simple regression method to do downscaling and is a widely used benchmark method in the VALUE framework41 and other downscaling research21. Recently, many models have shown a better performance than GLM, including deep-learning-based models like SRDSN17. SRDSN is a novel super-resolution network that can migrate from different variables and shows better downscaling results. Therefore, we selected GLM and SRDSN as benchmarks.

Downscaling LAI

This part is shown in the bottom frame of Fig. 1. Before we produce the final downscaled result, we should first do bias-adjustment on CMIP 6 climate data. The adjustment is for matching the PP assumption. The “PP assumption” assumes that the predictors used in our model can be correctly simulated by GCM and convincingly projected to the future13,15,42. However, because of the systematic bias in GCMs, there are always significant differences between GCM and observation predictors43. Thus, the bias-adjustment methods should be used to reduce or eliminate the differences to fulfill the PP assumption32. As the PP assumption should be satisfied in the whole-time range, the adjustment is both applied in the historical period and future scenarios.

Baño-Medina32 provided a simple strategy to do the adjustment in both historical periods and future scenarios.

$${{x}^{j,t}}_{{\rm{BA}}}={{x}^{j,t}}_{{GCM}}-{{\bar{x}}^{j}}_{{GCM},i}+{{\bar{x}}^{j}}_{{ERA},i}$$
(1)

Equation 1 shows the algorithm of the bias-adjustment process. j refers to a particular variable of climate data, t refers to time, and \(i=\mathrm{1,2},\ldots ,12\) refers to the month of the year. \({{x}^{j,t}}_{{BA}}\) refers to the variable j in time t after the bias-adjustment procedure; \({{x}^{j,t}}_{{GCM}}\) refers to the variable j of climate data in time t simulated by GCM; \({{\bar{x}}^{j}}_{{GCM},i}\) refers to the average value of variable j in i th month in historical period simulated by GCM; \({{\bar{x}}^{j}}_{{ERA},i}\) refers to the average value of variable j in i th month from ERA-5.

After the process, the PP assumption can be fulfilled, and we can transfer the model to future scenarios and do the projection. The transferred model receives GCM data after bias-adjustment and DEM data then yields the downscaled LAI data. Data were all interpolated from 0.0625° to 0.05° to ensure ease of use. We also provided some examples of data applications such as detecting future vegetation degradation risk in local areas.

Data Records

This F0.05D-LAI dataset is available under the Open Science Framework (https://doi.org/10.17605/OSF.IO/9QZ4K), containing 5 data records in historical (1983–2014), SSP-126, SSP-245, SSP-370 and SSP-585 (2015–2100)44. The data is multiplied by 100 and is stored in int32 data type and GeoTiff file format with the WGS 1984 coordinate system. The temporal resolution is 1 month, and the spatial resolution is 0.05°.

All data were named ‘lai_<experiment>_<year>_<month>.tif’. The ‘experiment’ field can be one of ‘historical’, ‘ssp126’, ‘ssp245’, ‘ssp370’ and ‘ssp585’, representing the scenario of the data. The ‘year’ field and ‘month’ field represent the time of the data.

Please note that the LAI data presented here is potential LAI data only. Due to the complexity and unpredictability of human activities in the future, the actual LAI in the future may differ significantly from predictions.

Technical Validation

Validation in historical period

In the “LAIDN Model Training” step, we calibrated our model after data collection and preprocessing. The metrics during the training process can be seen in Supplementary Figure 1. Since the input of the model was bias-adjusted GCM (BA-GCM) data, we downscaled in historical period using BA-GCM data and calculated their R2 and RMSE to show that the model would keep convincing after changing its input. The metrics of downscaled LAI by different methods are shown in Table 1.

Table 1 Downscaled result metrics. The result is calculated using the BA-GCM data as input.
Full size table

Table 1 shows that the LAI downscaled by LAIDN has the highest R2 and lowest RMSE in general. Besides, despite changing the input of the LAIDN model from ERA-5 to BA-GCM, it kept a rather accurate downscaling performance. Therefore, we believe that our model has good downscaling ability.

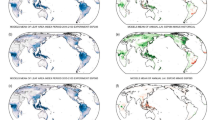
The spatial distribution of downscaled LAI is illustrated in Fig. 3.

Fig. 3
figure 3

Sample results of downscaling. All data are selected from the test set. The first row is the F0.05D-LAI data, while the second row is the GLASS LAI. The third row is the scatter plots which show the accuracy of downscaling. Each column is a representation of a season.

Full size image

In general, our model has good downscaling performance. Regarding the value, the scatter plots in the bottom line also show that our model has convincing results in different seasons. Points are distributed around the 1:1 line, and metrics show the results are accurate. Regarding the spatial structure, the downscaled result closely resembles the GLASS LAI. The texture of the mountains in southwest China, the edge of the Sichuan basin in central China, and the high vegetation coverage in the northeast mountains are shown clearly in our result. Regarding the seasonal changes, the downscaled LAI shows the same seasonal vegetation changes, with the highest LAI in summer and the lowest LAI in winter.

To show the advantage of our model in expressing spatial details, we compared our model with benchmarks in a higher resolution. The comparison is in Fig. 4.

Fig. 4
figure 4

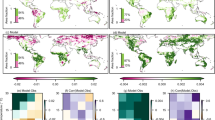
Comparison between different downscaling methods. All data are selected from July 2014. The first row is the LAI in China. The second row (Sample Area 1) is the LAI in southwest China, and the third row (Sample Area 2) is in north China. The columns are GLASS LAI, F0.05D-LAI, GLM downscaled LAI and SRDSN downscaled LAI. The bottom row is the quantitative comparison between each downscaling method. The light green solid lines are the KDE curve of the downscaled LAI, and the dark green dashed lines are the KDE curve of the GLASS LAI. The axes of those two green lines are at the left and top. The orange lines are the KDE curve of the SSIM values whose axes are at the right and bottom.

Full size image

Figure 4 picks two sample areas in different regions of China. Among the three downscaled LAI, F0.05D-LAI shows higher accuracy, with clearer mountain and basin edges. Although some tiny vegetation texture still disappears, vegetation texture on medium-size mountains is still preserved correctly. GLM only produces a normal result, without intricate texture and edges. Another benchmark, SRDSN LAI is better than GLM LAI, but since SRDSN is not designed for downscaling LAI, its spatial pattern is not as clear as that of F0.05D-LAI. The KDE curves in the bottom row also indicate the advantages of our model. There is less discrepancy between F0.05D-LAI, SRDSN LAI and GLASS LAI while the difference is more significant in GLM LAI results, which means deep learning methods are good at projecting the LAI value. However, considering the SSIM curve, the peak of F0.05D-LAI reaches about 18, while SRDSN’s reaches about 12, implying that F0.05D-LAI has more regions with high spatial similarity. Therefore, we can further conclude that our LAIDN model shows a better performance in downscaling LAI, and F0.05D-LAI is a rather accurate LAI dataset.

Since time series analysis is an important usage of LAI45, we depicted the time series curve of five kinds of LAI datasets in six locations in Fig. 5.

Fig. 5
figure 5

Time series curve of GCM LAI, GLASS LAI and different downscaled LAI in different regions of China. The blue, bold line is the GLASS LAI, the orange bold lines are F0.05D-LAI, and the other dotted light lines are the SRDSN LAI, GLM LAI and GCM LAI.

Full size image

To clearly show the accuracy of the time series, we calculated two metrics to evaluate the similarity between F0.05D-LAI, SRDSN LAI, GCM LAI and GLASS LAI in Table 2. Here we use two widely-used time-series similarity measurements: Dynamic Time Warping (DTW)46 and Euclidean Distance47.

Table 2 Time series similarity between F0.05D-LAI/SRDSN LAI/GCM LAI and GLASS LAI.
Full size table

According to Fig. 5, in most regions, F0.05D-LAI has a rather high similarity to the GLASS LAI, especially in the Tibet Plateau, Northeast China, North China Plain, and the Loess Plateau. In South China and Mt. Hengduan which are filled with mountains and hills with complex vegetation patterns, there is a larger discrepancy between downscaled LAI and GLASS LAI, but our model can still produce a better result. Metrics in Table 2 show a similar conclusion: regardless of what metric has been used, F0.05D-LAI shows a higher similarity in time series comparison. Therefore, LAIDN can be concluded as a rather appropriate method for LAI downscaling, and F0.05D-LAI can be considered as a relatively accurate dataset for future LAI.

Comparison in future scenarios

After the downscaling method has been validated in the historical period, we can transfer the model and produce downscaled LAI data in future scenarios. The general trends of vegetation in future scenarios are shown in Fig. 6. To show the dispersion of LAI each year, we painted the shaded area within the range of mean value ± standard error48 of monthly averaged LAI.

Fig. 6
figure 6

The trend of average GCM LAI and F0.05D-LAI in China. The scenario and increasing rate of each chart is marked in the upper left of it. The shaded area depicts the mean value ± standard error of the monthly averaged LAI in each year.

Full size image

From Fig. 6, the vegetation in China shows an increasing trend in all scenarios, and the greening phenomenon is more significant in higher emission scenarios. In SSP-126 which is the lowest emission scenario, the LAI in China shows a slightly increasing trend of about 3.7 × 10−4 per year. In a higher emission scenario, SSP-245, the slope of average LAI is about 8.1 × 10−4 per year, much higher than SSP-126. High emission scenarios, SSP-370 and SSP-585 show the most significant greening trend around 15 × 10−4 per year, leading the average LAI in China to increase from about 0.85 to 1.0.

To fully understand the spatial and temporal distribution of greenness among scenarios, we painted the LAI increasing value in two periods: 2025 to 2050 (25 years) and 2050 to 2100 (50 years). Please refer to Supplementary Figures 2, 3 for more information.

In Fig. 6, there is a huge gap between GCM LAI and F0.05D-LAI. According to some related research, the future greening trend of the Earth may not be as large as previously thought49, which means some systematic bias might exist in LAI projections. Similar overestimation may also exist in future scenarios according to the comparison in Fig. 7, and our data may be closer to the real situation in the future and have a rather high accuracy.

Fig. 7
figure 7

Discussion of overestimation in GCM LAI. The GCM LAI and F0.05D-LAI are the average data in 2050 of SSP-370. The GLASS LAI data are the average data in 2014. The shaded area in chart a.1 depicts the mean value ± standard error of the monthly averaged LAI in each year. Charts in the left column (b.1, c.1, d.1) are three sample areas in China with high overestimation. Charts on the center column (b.2, c.2, d.2) are other areas whose LAI is close to the GCM LAI of the left column. Charts on the right column (b.3, c.3, d.3) are the box plots of different sources of LAI. Column GCM is the box plot of GCM LAI in b.1, c.1 and d.1 in 2050. Column GLASS is the box plot of GLASS LAI in b.1, c.1 and d.1 in 2014. Column F0.05D-LAI is the box plot of F0.05D-LAI in b.1, c.1 and d.1 in 2050. Column CPR is the box plot of GLASS LAI in b.2, c.2, d.2 in 2014.

Full size image

The subfigure (a.1) in Fig. 7 shows that the F0.05D-LAI value is much closer to the GLASS LAI value. Since our result has a higher accuracy in the historical period, it is reasonable to infer that our data can depict the vegetation more precisely in future scenarios.

The subfigure (a.2) of Fig. 7 shows the overestimation areas which are distributed mainly in the Hengduan Mountains, Sichuan Basin, Loess Plateau, and southeast China. The three sample areas are selected from these overestimation areas. Sample Area (b.1) located in Loess Plateau, with LAI around 1. F0.05D-LAI shows that the vegetation will remain stable until 2050, but GCM LAI indicates that the average LAI will increase to about 2.5 by 2050, which is equal to the vegetation situation in the sample (b.2) located in the Daba Mountains in Hubei Province, central south China. Vegetation in (b.1) is the temperate shrublands, growing Vitex negundo var. heterophylla and Zizyphus jujuba var. spinosa, while vegetation in (b.2) is the subtropical forest and shrublands growing Quercus fabri Hance and Quercus glandulifera var. brevipetiolata Nakai50. Similarly, sample area (c.1) which is farmland growing wheat and rice will change to a subtropical Needleleaf Forests growing Pinus massoniana Lamb like Wuyi Mountain in (c.2)50, and sample area (d.1) which is subalpine grassland will change to a rainforest like Sumatra in (d.2). Therefore, we infer that F0.05D-LAI is a rather precise LAI projection data in future scenarios, which shows a rather slightly greening trend.

In another aspect, take the sample area (d.1) as an example. The yearly average temperature of (d.1) is about 10 °C, while the yearly average temperature of (d.2) is about 25 °C; the precipitation of (d.1) is about 800 mm per year, while the precipitation in (d.2) is more than 2500 mm up to 6000 mm per year51. However, the precipitation will only increase about 15–20% in the (d.1) area, and the temperature will only increase about 3–4 °C until the 2080s52. Likewise, the precipitation in the (b.1) area will increase from about 400 mm to 600 mm per year in the 2080s52, but there is still a large gap to the 1000 mm precipitation in (b.2).

Currently, many studies indicate that GCMs, which are designed for global-scale simulations, face challenges in accurately predicting future LAI at finer spatial resolutions49,53. In the northern hemisphere, some models tend to overestimate the annual mean LAI and the rate of increase in LAI, which may reflect systematic biases due to the models’ global focus53. This overestimation aligns with research suggesting that vegetation growth may be slower than previously modeled49. While GCMs excel in capturing large-scale climatic patterns9, they show greater variability and uncertainty when applied to fine-scale vegetation dynamics49. Therefore, our dataset can help to improve the accuracy of climate models at regional scales, bridging the gap between GCMs and local environmental needs.

Limitation and future work

This study downscaled the LAI data in future scenarios, providing data that can support further research in the mitigation and adaptation of climate change. We provided high-resolution and high-accuracy F0.05D-LAI dataset in both historical and future scenarios, and we demonstrated that our result is better than other existing downscaling methods. However, there are still some limitations in our data. In Fig. 4, although our model depicts a better spatial distribution of vegetation, some details in hills and basins still disappear. Figure 5 also indicates that projection from our model shows a relatively low accuracy in mountains in southern China and Mountain Hengduan. Besides, city-level data is still not very convincing after downscaling. Metropolises in Fig. 4 Sample Area 1, Chongqing and Chengdu show a relatively indeterminate vegetation structure in the downscaled result because smaller vegetation such as green lands and parks are not shown. Therefore, using our data to conduct inner-city research is still difficult. Besides, F0.05D-LAI data are only potential LAI, which are only based on four SSPs, and there are still many situations that cannot be covered by these scenarios. The complexity and unpredictability of future human activities may result in actual LAI being significantly different from predictions.

To minimize the limitations of the data, there are a few directions for future research that are worth considering. Firstly, using more variables with higher resolution may be useful to improve the final resolution. For example, we may consider using RCMs instead of GCMs to have a higher initial resolution and add other variables like wind speed or radiation to provide more information. Secondly, since China is a large country and the climate in different regions is controlled by different factors, we may split China into parts and do downscaling separately. For example, east China is mainly controlled by the monsoon, west-north China has a primarily continental climate, while the Qinghai-Tibet Plateau is influenced by its elevation. Splitting China into regions may allow the model to fit the regional climate with a higher accuracy. Besides, as different models have different advantages, comparison between models based on the PP method can provide more useful data and even correct some errors on some specific models. In addition, LAIDN might be generalizable to downscale other vegetation parameters. We have done a simple experimental downscaling to Gross Primary Productivity (GPP) and Net Primary Productivity (NPP) whose result is shown in Supplementary Figures 5, 6. We will conduct further research on downscaling vegetation parameters from different simulations and analyze future vegetation changes more accurately in the future.

Usage Notes

To show an application of our data, we evaluated the vegetation degradation risk in future scenarios in the Chengdu-Chongqing City Group. To distinguish the diverse levels of vegetation risk, we classify risk areas into three categories: High-Risk, Medium-Risk, and Low-Risk based on the significance level and decreasing range as factors. The classification method is shown in Table 3. We use the Mann-Kendall test to detect possible trends and use linear regression to calculate the slope. The decreasing range is calculated based on the average LAI in 2025–2035 and 2091–2100.

Table 3 Vegetation degradation risk classification.
Full size table

Figure 8 shows a resolution comparison between F0.05D-LAI and GCM LAI, highlighting the significance of downscaling. For example, some small risk areas in SSP-126 located in the southwest of the city group may not be detected through GCM data, since they are much smaller than a single pixel of GCM. The large risk area in SSP-126 has clear edges in F0.05D-LAI and different risk levels are shown. High-risk areas are at the Chengdu-Chongqing metropolis and the alluvial plain of Qingyi River, while low-risk areas are located at some mountains and hills. Another high-risk area under the SSP-585 scenario is also correctly detected. This area is on the edge of a very undulating mountain range, ecologically fragile, and shows a high vegetation risk under a high emission scenario with fast climate change. Therefore, F0.05D-LAI can detect smaller vegetation risk zones and may be helpful for urban planning and environmental assessment.

Fig. 8
figure 8

Vegetation risk area distribution in Chengdu-Chongqing city group from 2025 to 2100. The figure indicates the vegetation degradation risk in Chengdu-Chongqing City Group from 2025 to 2100. The meaning of each color in the map is the same as that in the bar charts. The grid in the figure is a latitude/longitude grid with 1° intervals, which has the same size as GCM pixels.

Full size image

The vegetation degradation risk detection method is also available in the whole of China, and we also provide a risk assessment map. Please refer to Supplementary Figure 4 for more information.