Background & Summary

The critical point (CP) refers to the volumetric soil water content at which evaporation transitions from being energy-limited to being water-limited. It separates the Stage-I evapotranspiration regime and the Stage-II evapotranspiration regime1,2,3. As evaporation proceeds, soil moisture decreases, eventually reaching a level at which it can no longer be absorbed or utilised by vegetation. This moisture level is termed the permanent wilting point (PWP)4,5,6. The PWP and CP are important soil hydraulic properties for global hydrological models7,8, biophysical models9,10, and agricultural irrigation11. However, due to the lack of large-scale estimates of CP, and PWP, these soil parameters often exist as unified constants in global hydrological models12. The hydraulic properties of soil affect vegetation growth and are also proven to play a role in intensifying extreme events such as floods13, droughts14, and heatwaves15. With the continuously increasing population16, food production demand, and water resource shortages, accurately estimating global soil hydraulic characteristics – thereby enhancing model accuracy – is of great significance in addressing the above issues17.

It is difficult to obtain soil hydraulic properties globally, as most of the existing data comes from field observations18. One traditional method for estimating PWP on a large scale is based on pedo-transfer functions (PTFs)9,12,16,17,18,19,20,21. This method requires a large number of field samples, but the accuracy of the results is still limited22,23. A more recent method uses machine learning (ML) to predict PWP. But these algorithms are based on input soil parameters such as soil porosity, sand content, clay content, etc24,25,26,27 meaning that they still rely on a large number of field samples for validation, which is time-consuming and labour-intensive28,29.

Recent advancements in satellite remote sensing techniques provide an efficient way to capture the global soil moisture drydown (SMD) curve and use this to determine information related to soil hydraulic characteristics. The underlying theory posits that there is a close relationship between SMD and the two soil hydraulic properties: The SMD is defined as a process with consistent soil moisture decrement following a precipitation event30,31. Initially, during the SMD process, the soil moisture decrease may be due to excess water in the soil being allocated to runoff and drainage until the soil becomes unsaturated. Subsequently, the soil moisture decrease will be due to evapotranspiration controlled by energy availability. When the soil moisture reaches the CP, evapotranspiration will instead be controlled by the water supply until soil moisture reaches PWP32. The critical range of SMD can, therefore, be used to infer CP and PWP.

The method of using remote sensing soil moisture data to estimate soil hydraulic properties has already been applied in previous studies. Field capacity, a commonly used soil hydraulic parameter, was estimated in Yang et al.33 using the Advanced Microwave Scanning Radiometer for EOS (AMSR-E) soil moisture data, where soil moisture values observed within 1-2 days following rainfall peaks were assumed to approximate field capacity. However, there are few existing products that represent the CP, a direct measure of water stress. In some previous studies34, CP has been considered to be the same as field capacity because the two points appeared very close together in time. However, in reality, CP may be slightly smaller than field capacity31,35,36. Recently, Fu et al.37 used the evaporative fraction-soil moisture (EF-SM) method to calculate global values of CP by combining satellite and ERA5-land reanalysis data, but their results may still be dependent on the model’s parameterization schemes. PWP is represented in products like Shangguan et al.’s Global Soil Dataset for use in Earth System Models (GSDE) dataset38,39 and Tomislav and Gupta’s (TG) global soil water content dataset40 by soil moisture values at 1500 kPa suction, since PWP is traditionally considered to be the water content measured at a matric potential of ≤-1500 kPa. While numerous PWP datasets, such as those mentioned above, do exist, most are derived from PTFs rather than from direct observational data. What is required is a global soil CP and PWP dataset derived solely from satellite soil moisture observations with robust data quality over time.

In previous studies31,36, the satellite SMD analyses were mainly conducted over short time spans but a recently developed soil moisture dataset, Neural Network-based Soil Moisture (NNsm), makes it possible to extend SMD analyses to a long temporal span so that temporal variability can be investigated. This dataset is generated using a soil moisture neural network algorithm developed by Yao et al.41. The training target is the Soil Moisture Active and Passive (SMAP) soil moisture product, with the brightness temperature from AMSR-E/2 serving as the input to produce long-term soil moisture data. This method is able to reproduce the spatiotemporal distribution of SMAP soil moisture with an accuracy comparable to SMAP soil moisture products, and superior to the input soil moisture products of AMSR-E and AMSR2. It has been verified that NNsm matches SMAP well with similar accuracy (Unbiased Root Mean Square Error, ubRMSE ≤ 0.04 m3/m3)42. Another major advantage of NNsm is that the use of daily resolution data means that the estimation of the short-term drydown process will be “truer” to the real situation36.

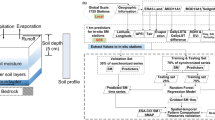
This study derived long-term satellite-based soil CP and PWP from SMD characteristics and analyzed their annual variability. The use of multi-year data may help to reveal differences in soil hydraulic parameters under different climatic conditions, which can lead to increased errors in land surface models. The CP and PWP obtained in this way are completely based on observational data, a unique advantage over the results of previous ML models, PTF analysis, or the EF-SM method. To demonstrate the applicability of NNsm in capturing SMD characteristics, the NNsm-based SMD events are compared with those estimated from SMAP during 2015–2020 and validated against 1334 in-situ stations from the International Soil Moisture Networks (ISMN). Additionally, the global median CP and PWP values are compared with Fu et al.’s global CP products37 (hereafter Fu), GSDE dataset38, and TG products40 to explore the advantages of this dataset. For future applications, this dataset can provide global scale estimates of CP and PWP, which can help with agricultural yield estimation20,43,44, irrigation strategy regulation45,46, soil health monitoring23,47,48, and providing important input parameters for ecohydrological models37,49,50. Additionally it can be expected that increasing understanding of soil moisture characteristics on a global scale will help to reduce the labor cost of field sampling.

Methods

Fitting soil moisture drydown

SMD is usually divided into three processes. The first of these, in which soil moisture decreases rapidly, is dominated by drainage and runoff. This process occurs on an hourly scale making it difficult for exponential decay models, suitable for monthly scale input data, to capture. Jahlvand et al.51 developed a method named “drainage from drydown” to estimate the coefficients of drainage, but it is only suitable for ground-based soil moisture observations. The second process of SMD is the first stage of evapotranspiration (ET-I) when soil moisture exceeds the field capacity but the rate of drydown is limited by energy. The third process is the second stage of evapotranspiration (ET-II) when the rate of SMD is limited by available water. Since the first process is far quicker than can be caught by remote sensing observation and of far shorter duration than the latter two processes, it is assumed that the first process can be neglected. McColl et al.36 developed a drying characterization method suitable for daily scale input data, which has been proven to be highly suitable for studying SMD when the input data is satellite soil moisture data. Therefore, McColl’s36 method is used to calculate drydown timescales in this study (Eq. (1)):

$$\frac{d\theta \left(t\right)}{dt}=\left\{\begin{array}{l}-\frac{\theta \left(t\right)-{\theta }_{w}}{{\tau }_{L}},{\rm{if\; P}}=0\,{\rm{in\; the\; interval}}[{\rm{t}}-\triangle {\rm{t}},{\rm{t}}]\\ -\frac{\theta \left(t\right)-\bar{\theta }}{{\tau }_{S}}+\varepsilon (t),{\rm{if\; P}} > 0\,{\rm{in\; the\; interval}}[{\rm{t}}-\triangle {\rm{t}},{\rm{t}}]\end{array}\right.$$
(1)

where \(\theta \left(t\right)\) is soil moisture (with units of m3/m3), \(t\) is time (day) and \({\theta }_{w}\) (m3/m3) is a minimum soil moisture value. \(\varepsilon \left(t\right)\) is the random error (m3/m3 day), \(\bar{\theta }\) is the mean soil moisture (m3/m3) and \({\rm{P}}\) is precipitation (mm/day). \({\tau }_{S}\) is the short-term timescale of drydown events (day), which reflects energy-limited soil hydrological processes (e.g., drainage and potential ET process). \({\tau }_{L}\) is the long-term timescale of drydown events (day), which reflects water-limited processes (e.g., the water-limited stage of ET). After simplification, \({\tau }_{S}\) and \({\tau }_{L}\) can be calculated from Eqs. (2) and (3), respectively.

$${\tau }_{S}=-\frac{\frac{\triangle t}{2}}{\log \left(\frac{\triangle z\bar{\triangle {\theta }_{+}}}{\alpha }\right)}=-\frac{\frac{\triangle t}{2}}{\log ({F}_{p})}$$
(2)
$$\theta \left(t\right)=\triangle \theta \,\exp \left(-\frac{t-\triangle {t}_{p}}{{\tau }_{L}}\right)+{\theta }_{w}$$
(3)

where \(\triangle {\theta }_{+}=\theta \left(t\right)-\theta \left(t-\triangle t\right)\), Δt is the temporal resolution of model outputs or satellite observations (day) and \(\triangle \theta \) is the drydown amplitude (m3/m3). \(t-\triangle {t}_{p}\) is defined as the time of the precipitation event (day), which is also the start of an individual drydown. \(\alpha \) is mean event precipitation (mm/day), \({F}_{p}\) is the stored precipitation fraction developed by McColl et al.36 and \(\triangle z\) is the depth of soil (mm).

In this algorithm, any event for which the decrease in soil moisture is less than 0.04 m3/m3 is not considered a drydown event, as such fluctuations may occur even in ground measurements.

Through this method, four parameters (see Table 1) reflecting either soil hydraulic properties (eg. the CP and PWP) or land-atmosphere feedback variables (\({\tau }_{S}\) and \({\tau }_{L}\)) are provided for both stages.

Table 1 Parameters of drydown characteristics.
Full size table

Soil moisture data

NNsm data ranging from 2002 to 2023 with daily resolution is used as soil moisture input for the primary analyses in this study. NNsm is a continuous and consistent global surface soil moisture dataset from 2002, with a resolution of 36 km on the daily scale. It is provided by the National Tibetan Plateau Data Center (http://data.tpdc.ac.cn)42. This dataset is a neural network-based product that utilizes multi-frequency brightness temperature data from AMSR2 and AMSRE, with the SMAP Level 3 passive daily surface soil moisture product as the training target. It does not directly use soil texture information but can accurately reproduce the SMAP surface soil moisture.

The soil moisture product from SMAP is used in this study for comparison with the SMD estimations from NNsm. Here, the SMAP Level-3 soil moisture product (SPL3SMP) was chosen since it has been evaluated intensively against ground observations and proven to have a high quality performance in characterizing surface hydrometeorological processes52. It can provide global soil moisture at a daily timescale with 36 km spatial resolution. Studies have shown that out of several available soil moisture satellite products (i.e., AMSR2/-E and The Soil Moisture and Ocean Salinity, SMOS), SMAP has shown the lowest ubRMSE against in-situ networks53. The SMAP data, which can be accessed at https://nsidc.org/data/spl3smp/versions/9/54, is available from 2015.04.01. Here, 5 annual cycles, with timespans overlapping the NNsm data, were chosen from within the period of 2015.04.01 – 2020.03.31. Areas with vegetation water content (VWC) greater than 5 kg/m2 were masked as the dense vegetation as these areas would interfere with soil moisture observations. Previous literature shows that in Earth System Models CP may be underestimated in arid regions, while PWP may be overestimated in humid regions33,37,50. Therefore, an experiment was designed to compare the mean square error (MSE) of PWP and CP with ISMN site results at different percentiles, and ultimately select the 10th percentile (MSE = 0.008) of PWP of all SMD events over 22 years to represent PWP in humid areas and the 79th percentile (MSE = 0.010) of CP to represent CP in hyper-arid and arid areas.

In-situ soil moisture data from 1334 stations in the ISMN (https://ismn.earth/en/)55,56 dataset are used for verification. This dataset provides open soil moisture data from across the world to enable users to easily validate and improve global satellite products as well as land surface, climate, and hydrological models57. The original sampling frequency (SF) of this dataset is 1 hour−1. The data have been aggregated to 1 day−1 and 1/3 day−1 to be consistent with NNsm and SMAP, respectively. To diminish the scale mismatch between in-situ stations and satellite pixels to the maximum degree, at each specific grid square, averaged soil moisture from all stations within the grid square is regarded as a representative value to compare with the remote sensing products. For quantifying the bias between other CP (i.e., Fu) and PWP (i.e., GSDE and TG) products, only grid squares containing more than two stations were selected.

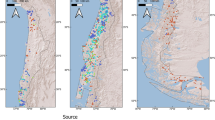
Data quality control procedures were followed to ensure the effectiveness of the analyses. In-situ stations with data records shorter than 1 year were excluded. Additionally, although ISMN provides in-situ soil moisture at depths from 0 to 100 cm, only data from the depth of 5 cm are used in this study to ensure consistency with the vertical depths of the NNsm and SMAP data, which are 3 cm and 5 cm, respectively. The locations of all stations and the global climate zones58 are displayed in Fig. 1.

Fig. 1
figure 1

Distribution of the selected ISMN stations. Red triangles indicate the selected ISMN stations. The background map shows the Köppen-Geiger (KG) Climate Classification.

Full size image

Ancillary data

Since the analyses of short-term drydown requires precipitation information, the contemporaneous hourly Global Precipitation Mission (GPM) product59 is used. The GPM data are aggregated into the same temporal and spatial resolutions as the NNsm data. In detail, GPM Level 3 IMERG Final Daily 0.1 degree \(\times \) 0.1 degree (GPM_3IMERGDF) derived from the half-hourly GPM_3IMERGHH was adopted in this study. The derived result represents the final estimate of the daily accumulated precipitation. The dataset is produced at the NASA Goddard Earth Sciences (GES) Data and Information Services Center (DISC) by accumulating the valid precipitation retrievals for the day in GPM_3IMERGHH and giving the result in the unit of mm.

To filter for the PWP and CP in humid, hyper-arid, and arid regions, ERA5 reanalysis data60 were used to calculate the Aridity Index (AI). According to the classification from the World Atlas of Desertification (https://wad.jrc.ec.europa.eu/patternsaridity), the global land is divided by AI into 5 categories: hyper-arid, arid, semi-arid, dry subhumid, and humid. Here the humid area (AI ≥ 0.65), hyper-arid, and arid area (AI < 0.2) are defined in Table 2.

Table 2 Climate classification and dryland subtypes based on the Aridity Index.
Full size table

To compare CP and PWP across different vegetation types and soil textures, land use data from MCD12Q1 (https://lpdaac.usgs.gov/products/mcd12q1v061/)61 spanning the period 2002 to 2023 and soil texture data from SoilGrids (https://www.isric.org/explore/soilgrids)62 were resampled to a 36 km resolution to align with the NNsm grid. Land cover types were classified according to the International Geosphere-Biosphere Programme (IGBP) classification scheme. Only non-waterbody and non-permafrost land types with more than 20% of their area remaining after excluding VWC values greater than 5 kg/m2 were retained for further analysis. Soil texture data, representing the mean values for the following parameters: clay content (g/100 g, %), sand content (g/100 g, %), and silt content (g/100 g, %), were derived from the 0–5 cm depth layer. All the datasets mentioned above are summarized in Table 3.

Table 3 Summary of the datasets used in this study.
Full size table

Data Records

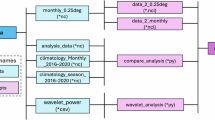
The data records63 contain a global dataset of yearly soil critical point (CP) and permanent wilting point (PWP) and are publicly available at https://doi.org/10.6084/m9.figshare.27969276. Using McColl’s36 method to calculate drydown timescales, the dataset includes four other parameters that are related to SMD at two SFs: global medians of estimated parameters (i.e., \({\tau }_{S}\), annual drydown times (\({n}_{{dd}}\)), \({\tau }_{L}\), and the fitting coefficient (\({R}^{2}\))) of the SMD curves. This dataset contains the global 36 km resolution soil characteristics from June 2002 to December 2023. There are 406 (latitude) \(\times \) 964 (longitude) grid points in each file. The file format is.mat. All files can be opened in MATLAB. Each file stores data for one year. SMD data are missing from October to December 2011 and January to June 2012, due to missing NNsm data. The spatial resolution is 36 km \(\times \) 36 km. The composition of the filename is: “Parameter”_“Sample frequency”_“Year”.mat. Full details of these filename components are given in Table 4.

Table 4 Composition of filename and corresponding meanings.
Full size table

Technical Validation

Spatial and temporal characteristics of soil CP and PWP

Figure 2 shows the mean values of CP and PWP in different climate zones from 2002 to 2023. Due to missing data from November 2011 to June 2012, the 2012 data is replaced with the mean of 2011 and 2013 values. It can be seen that the time series of CP and PWP have only small fluctuations for most climate zones, indicating that the method of extracting CP and PWP using SMD is very robust.

Fig. 2
figure 2

Mean value of (a) CP and (b) PWP based on Köppen-Geiger climate zones. The colored bars represent the mean values. Abbreviations in the legend represent different climate zones. A: equatorial, B: arid, C: warm temperate, D: snow, E: polar, W: desert, S: steppe, f: fully humid, s: summer dry, w: winter dry.

Full size image

Figure 3 shows the global median value and variation of CP and PWP. Areas with dense vegetation have been masked in advance. It can be seen that the global CP value (mode = 0.21) is higher than the PWP value (mode = 0.04). The range of PWP is very small (0–0.3 m3/m3). The coefficient of variation (CV) map clearly illustrates the low degree of temporal variability of CP (mean = 14%) and PWP (mean = 23%) over 22 years.

Fig. 3
figure 3

The global median value of (a) CP (in m3/m3) and (b) PWP (in m3/m3). The coefficient of variation (CV) of (c) CP (%) and (d) PWP (%). The subgraphs show the probability density function (PDF).

Full size image

Comparison with other CP and PWP products

Figure 4 shows the global distribution of the other CP and PWP products. Comparison with Fig. 3 reveals that the spatial pattern of CP and PWP in our new dataset is broadly similar to that of the other products. However, the PWP of our dataset is slightly lower than that of the other products in North America, Brazil, South Africa, and Australia, while our CP is slightly higher than Fu’s CP. The Fu results (mode = 0.15) are based on reanalysis data, while the GSDE results (mode = 0.11) are based on legacy site observations, and the TG results (mode = 0.13) are based on the estimation of PTFs. The variations in the data and methods used in these products from the statistical results based on satellite observations may cause the observed differences in the CP and PWP.

Fig. 4
figure 4

Spatial distribution of the (a) PWP from GSDE (%), (b) PWP from TG (%), (c) CP from Fu (m3/m3), (d) mean values by longitude based on PWP (m3/m3) calculated in this study and other PWP products, and (e) mean values by longitude based on CP (m3/m3) calculated in this study and CP of Fu. The subgraphs in panels a, b and c show the probability density function (PDF).

Full size image

Figure 5 shows scatter plots of CP and PWP from the different products against values from the ISMN sites. The correlation coefficient (r) and MSE are used to quantify the agreement between the two soil moisture datasets. The results show that, out of the three products, the PWP extracted based on NNsm is the closest to the site data. Although the r between the CP of Fu and the site data is slightly higher, it is found that the CP of our new dataset has a smaller MSE than that of Fu. Therefore, the CP and PWP based on long-term remote sensing observations of soil moisture have a higher accuracy compared to the other data products.

Fig. 5
figure 5

CP and PWP calculated using various products compared with values from ISMN sites. (a) PWP derived from NNsm. (b) PWP derived from GSDE. (c) PWP derived from TG. (d) CP derived from NNsm. (e) CP derived from Fu. The r in the upper left corner of each panel represents the correlation coefficient (p < 0.01). MSE is the mean square error.

Full size image

In 2015, 35 ISMN stations, distributed across different climate zones, were selected for calculation of their CP and PWP. These values were compared with those from Fu, TG, GSDE, and the dataset of CP and PWP created in this study. The CP and PWP values at these stations are presented in Fig. 6, along with comparisons to other products. Figure 6c shows that for 29 of the 35 stations, our CP values were closest to the ISMN station results. Due to the lower global grid point density of the Fu product compared to the CP grid points in our dataset, CP values could only be extracted from the Fu product for 21 out of 35 stations (60%). Therefore, in terms of data point validity, our dataset is more reliable.

Fig. 6
figure 6

CP and PWP in 2015 at 14 network sites and from different products. (a,b) show the boxplots of CP and PWP in different climate regions. Box edges are the 25th and 75th percentiles of the distribution bounding the median, and whiskers extend to extrema (maximum and minimum). (c,d) present the values of CP and PWP, respectively, as measured and derived from different products at the individual sites.

Full size image

For PWP, the station data exhibit a wide distribution range, indicating the large degree of variability in soil moisture characteristics across regions. The NNsm-derived PWP values have a closer alignment with the ISMN median in the Cfa, Cfb, and Dfc climate zones, as illustrated in Fig. 6b. In the Dfb and Dwc climate zones, the PWP medians from all products were relatively concentrated and closely matched the ISMN values, suggesting consistency in these regions. However, in some tropical and polar regions, there were insufficient valid data points to reliably validate the data.

Comparison of NNsm results with those from other soil moisture products

To demonstrate the applicability and advantages of the NNsm-based CP and PWP, their values and those calculated based on SMAP were compared and validated with those reported by ISMN sites worldwide.

Figure 7 shows the results of the comparison of CP and PWP based on both NNsm and SMAP with the data from the ISMN sites. It is apparent that the values of CP (r = 0.42, p < 0.01) and PWP (r = 0.37, p < 0.01) calculated based on NNsm are a better match to the site-based data than are the values of CP (r = 0.24, p < 0.01) and PWP (r = 0.13, p < 0.01) calculated based on SMAP. This better performance may be because NNsm’s soil moisture data is closer to ground observations: the result of NNsm’s ability to utilize daily soil moisture data, while SMAP’s data is only provided every 2–3 days. Many studies have shown that satellite remote sensing observation data shows soil moisture decreasing at a faster rate than shown by station data64,65, a fact that indicates that there are likely to be some differences in the results produced by different soil moisture products. However, there are several reasons why both of the satellite calculation results differ from the site-based calculation results and these are described below.

Fig. 7
figure 7

Scatter plots of NNsm and SMAP compared with ISMN for (a,b) CP and (c,d) PWP. The r in the upper left corner of each panel represents the correlation coefficient.

Full size image

First, the representativeness of the site space is limited. A site cannot capture all drydown events in a 36 km \(\times \) 36 km grid, and the remote sensing products contain errors caused by large scale meteorological disturbances. The second reason is the heterogeneity of detection depth. There is a mismatch between the sensing depth of soil moisture based on the L-band radiometer and the detection depth of 5 cm at the sites66. In some densely vegetated areas, the detection depth of the L-band may be less than 5 cm, but in some arid regions it may exceed this limit. There are also differences in site quality, and the variety of measurement methods used can result in differences. The effects of vegetation optical depth, climate type, surface roughness, and spatial heterogeneity need to be taken into account. According to Ma et al.67, the SMAP soil moisture products are similar to the site results under medium vegetation optical depth (VOD), small surface roughness, low heterogeneity conditions, and in temperate and frigid climate types. However, the product quality in high VOD, high roughness, or high terrain complexity and in tropical or desert areas needs to be improved. The above limitations are common issues for all satellite products, including SMAP and NNsm.

Distribution of CP and PWP under different vegetation types and soil texture conditions

As shown in Fig. 8, the CP and PWP of barren land had relatively low values. This was also the case in grassland and shrubland. In contrast, the CP and PWP of woody savannas and deciduous broadleaf forests were higher: a reasonable result as only sufficient precipitation can sustain the growth of vegetation with higher water demands. When the water requirements of the vegetation growing in a given area are higher, the CP and PWP also tend to be higher. Compared to other products, the median of CP extracted based on NNsm is closer to that extracted based on ISMN sites in woody savannas, cropland, and grassland. However, our PWP calculation performed poorly in woody savannas, exhibiting a large spread. This is possibly due to the excessive VWC of the woodland, which can interfere with L-band satellite observations of soil moisture. Despite this, the median PWP of this study is still close to that of TG in woody savannas. In other vegetation types, the PWP of this study was similar to the results of other products.

Fig. 8
figure 8

The relationship between CP and PWP and vegetation types. (a,b) show the boxplots of CP and PWP derived from NNsm in different vegetation types. (c,d) show comparisons of CP and PWP derived from NNsm with the values based on 35 ISMN sites and derived from other products. Box edges are the 25th and 75th percentiles of the distribution bounding the median, and whiskers extend to extrema (maximum and minimum).

Full size image

Figure 9 reveals a clear relationship between soil texture and both CP and PWP. Clay and silt fractions exhibit positive correlations with PWP (r = 0.18, p < 0.01 and r = 0.17, p < 0.01, respectively) and CP (r = 0.24, p < 0.01 and r = 0.13, p < 0.01, respectively), indicating that higher clay and silt content enhances the soil’s water retention capacity and the lower limit of plant-available water. In contrast, sand content shows a negative correlation with both PWP (r = −0.24, p < 0.01) and CP (r = −0.24, p < 0.01), suggesting that increased sand content reduces water retention due to its larger pore size and better drainage properties. These findings align with the results reported by Feldman et al.68 who also identified significant relationships between soil texture, vegetation type, and CP. Overall, the results underscore the importance of soil texture in determining soil hydraulic properties and their implications for vegetation growth.

Fig. 9
figure 9

The relationship between (a–c) CP and soil texture and (d–f) PWP and soil texture. Box edges are the 25th and 75th percentiles of the distribution bounding the median, and whiskers extend to extrema (maximum and minimum). Bin counts are all greater than 600.

Full size image

Limitations and future applications

Our approach to extracting CP and PWP has several limitations. First, in regions with weak land-atmosphere interactions and frozen areas, the water and energy limitation stages of SMD may not occur concurrently1 and therefore only one estimated parameter may hold valid in these regions. This limitation is due to an assumption made in the current SMD detection algorithm that requires further improvement in future studies. In addition, in some areas with high VWC, the observed soil moisture may be too high, leading to an overestimation of PWP. Users should be cautious when applying the data in the above areas. Second, the spatial resolution of our dataset is still too coarse to be implemented in regional hyper-resolution (e.g., <1 km) land surface simulations. Currently, very few global hyper-resolution soil moisture datasets exist. However, this is one promising direction for future studies as the framework proposed here has flexible applicability in terms of spatial resolution. It will be possible to release updated products of the derived CP and PWP parameters with higher resolution once the global soil moisture dataset is available. Users may also apply our framework to obtain their own estimates independently by using locally available soil moisture data.

Despite these limitations, our product has the ability to provide long-term, global-scale CP and PWP data. Compared to previous products, our dataset demonstrates improved accuracy when validated against ground station measurements, achieving results that align more closely with ISMN data. Our dataset is particularly valuable for large-scale global studies, as it provides comprehensive soil CP and PWP data across extensive spatial domains. Applications of this dataset include assessing multi-year dynamic changes in variables such as the timescale of drydown, CP, and PWP. These variables can serve as stable input parameters to advance the development of land surface models69. For this purpose, one recent study has already applied the preliminary version of our product to calibrating a global soil texture map and demonstrated the benefit of our product in improving land surface simulation accuracy70. Furthermore, researchers can utilize our dataset to monitor global soil moisture variations and identify regions where soil moisture falls below the PWP or CP, aiding the prediction of future drought trends37.