Introduction

Metamaterial is a man-made composite material with unique features not found in nature1. This structure consists of exotic effects and has inspired countless researchers to build an innovative contribution direction in almost all fields2. A single negative (SNG) structure has negative permeability or permittivity, but a double negative (DNG) or left-handed (LH) structure has both negative permittivity and permeability. In 1968, the principle of left-hand metamaterials was first explored by the Russian physicist Victor Veselago in19673. This unusual material can monitor the propagation of light when passed in waveguides and free space. As a result, electromagnetic (EM) wave manipulation has a wide range of applications, including holography, signal multiplexing, data processing, and so on. The MTM can be used in a variety of applications, including antenna design4,5, filters6, specific absorption rate (SAR) reduction7, invisibility cloaking8, superlenses9, absorber10,11, sensors12,13 etc. In addition, the MTM is also widely used in radar and satellite communication14,15.

Islam et al., proposed a new metamaterial architecture in16 for the satellite antenna. The defined MTM scheme was put on FR-4 substrate. The frequency spectrum 2 to 4 GHz was used for this simulation procedure. Shahidul et al., presented a crossed-line CSRR based epsilon negative (ENG) metamaterial in17 for tri-band microwave functions. The size of this MTM unit cell is 10 \(\times\) 10 mm2, and the EMR is low, only 4.5. Hossain et al. recommended a meta-atom in18 for an effective medium ratio (EMR) that would follow the meta-atom criteria and is applicable for multiband. The size is 12 × 12 × 1.6 mm3, and EMR is 10.55 of this MTM. Hasan et al., developed a DNG metamaterial in19, which is compactly miniaturized, modified Z-shaped and applicable for wideband operation. This MTM has only one frequency band (X- band), and EMR is low, only 4. Islam et al., presented an SNG metamaterial in15 for the application of gain enhancement of satellite and radar antenna. It has another feature i.e., near-zero indexes, the unit cell size and ERM are 8 × 8 mm2 and 14.37, respectively. in20, Cheng et al., introduced a seven-band metamaterial absorber that is ultra-thin, compact, and has a single resonator structure and has numerous prospective applications such as detection, sensing, and imaging. Chen et al., proposed single-layer graphene tunable broadband THz MTM absorber in21, which has important applications in tunable filtering, sensing, and modulators. Hossain et al., proposed a composite DNG metamaterial in22 for multiband applications. The presented MTM unit cell shape is double C, and its EMR is moderate. Zhou et al. developed a DNG metamaterial in23, which is a double Z-shape, its EMR is 4.80, and size is 8.5 × 8.5 mm2. Hoque et al., demonstrated a DNG metasurface absorber in24 for dual-band applications. The size of the metasurface unit cell is large, but EMR is low. Hossain et al., described an SRR based ENG metamaterials25 for multiband microwave functions. Islam et al. suggested an “H-shape” DNG metamaterial unit-cell in26 which size was very large 30 × 30 mm2, but EMR was very low, only 3.65. Cheng et al., presented a broadband MTM microwave absorber in27, which is an asymmetric and sectional resonator and it is applicable for energy harvesting and stealth technology. Kalraiya et al., designed a polarization-independent MTM absorber in28 for wideband applications. The unit cell size is 12.5 \(\times\) 12.5 mm2, which covers C-, and X- band. Zhou et al. described a 12 × 12 mm2 size of an SNG metamaterial unit cell in29 which was ‘‘S-shape’’, applicable for X- and Ku- bands and EMR was below 4. Islam et. al., also described an MTM sensor in30 for showing the sensitivity of the structure. The structure of metamaterial is meanderline, its sensitivity and EMR are -3 dB/mm and 7.2, respectively.

Thummaluru et al., developed an MTM absorber in31, which shape is four-fold symmetric, applicable only for C-band, and the cell size is very large 28.2 \(\times\) 28.2 mm2. Faruque et al., developed a DNG metamaterial in32 for dual-band microwave applications, but the unit cell structure is very large 25 \(\times\) 20 mm2. Islam et al., introduced a hexagonal SRR based MTM in33 for S-, and X-band applications. Its size is 10 \(\times\) 10 mm2, and the EMR of this structure is 8.40. Rao et al., presented an MTM inspired circularly polarized antenna34 for WiMAX and WLAN applications. The coverage band, EMR and size of the structure are 4, 9.95, and 9 × 9 mm2. The MTM was used in the coplanar waveguide (CPW) antenna to increase the bandwidth, but the antenna's gain is extremely low. Cheng et al., also presented a dual-band anisotropic metamaterial in35, which is circular polarization and applicable for radar, satellite, and remote sensing. Zhou et al., demonstrated a high gain and wideband patch antenna in36 using reflective focusing metasurface. The patch antenna's initial design consists of a slot planar patch radiating portion fed by a coplanar waveguide (CPW). The simulated average gain relative bandwidth is 4.5 dBi and 76%, respectively. Hossain et al., described an MTM37 for a multiband meta-atoms which is left-handed obeying EMR, but its size is 11 × 10 mm2. Hossain et al., developed a DNG metamaterial in38 for dual-band microwave applications. The shape of this design is “Modified H”, and its size is 9 \(\times\) 9 mm2. Kumari et al. demonstrated a polarization-insensitive MTM absorber in39, compact ultra-thin and applicable simply for X-band. The size of the MTM absorber is 10 \(\times\) 10 mm2, and EMR is very low. Almutairi et al. demonstrated a DNG metamaterial in40 whose size is 5.5 × 5.5 and applicable only for C-band and EMR is 7.44. Thummaluru et al. also presented a tunable MTM absorber in41, a wide-angle polarization controllable and circular sector. This structure is applicable only for C-band and it’ size is 9 \(\times\) 9 mm2. Rao et al., presented a circular-shaped metamaterial in42, which is applicable for multiband. This MTM was utilized to increase bandwidth in a CPW fed antenna, although the gain is relatively modest.

A DNG metamaterial has been developed by using an inverse double V inspired CSSRR resonator shape in this paper. This DNG MTM provides three resonance frequencies of 2.86, 5, and 8.30 GHz. The first resonance frequency, 2.86 GHz, covers S-band (2 to 4 GHz), the second resonance, 5 GHz, covers the C- band (4 to 8 GHz), and the third resonance, 8.3 GHz, covers X-band (8 to 12 GHz). The S-band is utilized in traffic control radar at airports, weather radar, and surface ship radar. The majority of marine, civil, military radars work on X- bands. The C-band, especially the 5 GHz band, is widely used in Wi-Fi for high bandwidth and high-speed applications. The DNG region has been found from 2.82 to 2.89, 5.04 to 5.23, and 8.36 to 8.46 GHz. The effective medium parameters, equivalent circuit, surface current, E-field, and H- field have been analyzed. Different parametric studies and arrays such as 1 \(\times\) 2, 2 \(\times\) 2, 3 \(\times\) 3, 4 \(\times\) 4, and 20 \(\times\) 25 have also been examined. The proposed inverse double V-shaped DNG metamaterial has an EMR value of 4.5, which defines smallness and appropriateness.

Design structure of the MTM unit cell

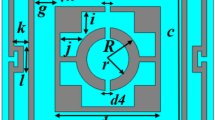
Figure 1a reveals the top view of the introduced inverse double V structure, imported from CST software43. Firstly, the presented structure consists of Rogers RO4350B dielectric substrate material of 8 \(\times\) 8 mm2 (length and width) with a thickness of 1.524 mm. The dielectric constant \((\varepsilon\)) and tangent loss (δ) of this material are 3.66 and 0.0037. The proposed structure comprises three square rings, which are complementary split-ring resonators and inside the inverse double V-shape resonator. These resonators consist of copper which thickness was 0.035 mm. The conductivity (σ) of the resonator is 5.8 × 107 S/m, which is annealed copper. The width of the first square ring is 0.4 mm, the second square ring is 0.30 mm, and the third one is 0.25 mm, where the width of the V-shape is 0.20 mm. The gap between the first and second rings is 0.40 mm, the second and third ring is 0.30 mm, and the third and inverse double V-ring is 0.20 mm. All split gaps of the proposed cell are equal to 0.25 mm. The perspective view of the recommended resonator on Rogers RO4350B is shown in Fig. 1b. The full-dimensional descriptions of the MTM configuration of the unit cell are stated in Table 1.

Figure 1
figure 1

(a) CST simulated top view, (b) Perspective view of the suggested structure. (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst- studio-suite)43.

Full size image
Table 1 Dimensional descriptions for the suggested MTM configuration.
Full size table

Methods and techniques

Figure 2 reveals the boundary form of the suggested MTM unit cell. The suggested resonator's electromagnetic response is examined using the CST-2019 software43 and the finite element method. The waveguide ports are put on the negative and positive z-axes, and the V-structure is located in the middle, which is afterwards motivated in the direction of the z-axis by the EM wave. The electric field boundary condition that sets the tangential component electric field to zero is the perfect electric conductor (PEC). The magnetic equivalent of PEC boundaries is known as the perfect magnetic conductor (PMC) boundary conditions. The PEC and PMC borders and two wave ports represent the source of plane wave excitation and show that unit cells can be repeated indefinitely along the x and y directions. EM wave sources are applied from port 1 to all modes. The planes parallel to xz and yz are assigned ideal electric and ideal magnetic borders. Combining the PMC, PEC, and open space conditions of each wall aids in observing the field properties of the resonance frequencies. The suggested V-shaped cell was simulated using a frequency-___domain solver with tetrahedral meshing in the frequency range of 2 to 10 GHz. From unit cell simulations in the proper frequency range, we got the complex scattering parameters S11 and S21.

Figure 2
figure 2

Boundary conditions are set up for the proposed structure.

Full size image

The Nicolson-Ross-Weir (NRW) approach, which is one of the most widely used EM characterization techniques44, is used to derive the effective medium parameters, i.e., relative permittivity (\(\varepsilon_{r}\)), permeability (\(\mu_{r}\)), refractive index \((n)\), and impedance (\(Z\)) from the simulated S-parameter. The NRW approach begins with the application of composite terms \(V_{1}\) and \(V_{2}\), which add and subtract scattering properties.

$$V_{1} = S_{{11}} + S_{{21}}$$
$${V_{2}} = {S_{21}} - {S_{11}}$$
$$T = X \pm \sqrt {X^{2} - 1}$$

Here, T is the interface reflection, the \(\varepsilon_{r}\), \(\mu_{r}\), \(n\) and \(Z\) features of MTM are calculated using the equations below.

$$S_{11} = \frac{{\left( {1 - Z^{2} } \right)T}}{{1 - T^{2} Z^{2} }}$$
(1)
$$S_{21} = \frac{{\left( {1 - T^{2} } \right)Z}}{{1 - T^{2} Z^{2} }}$$
(2)
$$\varepsilon_{r} = \frac{2}{{jk_{0} d}}\frac{{1 + S_{11} - S_{21} }}{{1 - S_{11} + S_{21} }}$$
(3)
$$\mu {}_{r} = \frac{{j2S_{11} }}{{jk_{0} d}} + \mu_{0}$$
(4)
$$n = \frac{2}{{jk_{0} d}}\sqrt {\frac{{\left( {S_{21} - 1} \right)^{2} - S_{11}^{2} }}{{\left( {S_{21} + 1} \right)^{2} - S_{11}^{2} }}}$$
(5)
$$Z = \sqrt {{\raise0.7ex\hbox{${\mu_{r} }$} \!\mathord{\left/ {\vphantom {{\mu_{r} } {\varepsilon_{r} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon_{r} }$}}}$$
(6)

Here \(k_{0}\) is the wave number and \(d\) is the substrate thickness.

Design procedure of the proposed metamaterial unit cell

We have analyzed the different designs of the MTM unit cell for selecting the intended design. Different design layouts for choosing the suggested unit cell are depicted in Fig. 3. The S11 and S21 results for the different design layouts are shown in Fig. 4(a, b). In design 1, two square split rings and inverse double V-shape resonators exist. Two resonance frequencies are obtained from it, the magnitudes of S11 are − 28.50, − 20.66 dB at 3.22, and 7.27 GHz, where the magnitudes of S21 are − 26.61, − 36.21 dB at 2.97, and 6.09 GHz, it covers S-, and C- bands. From design 2, two resonance frequencies are obtained; the magnitudes of S11 are − 28.13, − 15.77 dB at 4.86, and 7.12 GHz, where the magnitudes of S21 are − 37.39, − 13.01 dB at 3.59, and 7.01 GHz, it covers S-, and C-bands. From design 3, it is seen that the magnitudes of S11 are − 26.29, − 17.13 dB at 4.32, and 9.25 GHz, where the magnitudes of S21 are − 18.63, − 27.52 dB at 4.12, and 8.36 GHz, which also covers the S-, and C- bands. From design 4, it is seen that the magnitudes of S11 are − 27.07, 22.65, and − 13.65 dB at 3.21, 5.87, and 9.22 GHz, respectively, where the magnitudes of S21 are − 24.40, − 30.28, − 24.91 dB at 2.99, 5.22, and 8.86 GHz, and it covers S-, C-, and X- bands. The magnitudes of S11 are − 27.06, 22.66, − 13.66 dB at 3.27, 5.69, and 9.11 GHz, where the magnitudes of S21 are − 25.0, − 30.64, − 26.05 dB at 3.06, 5.22 GHz, and 8.54 GHz, which covers S-, C-, and X- bands for design 5. And the magnitudes of S11 are − 27.82, − 23.15, − 14.78 dB at 3.11, 5.67, and 8.74 GHz, where the magnitudes of S21 are − 26.86, − 31.24, − 26.16 dB at 2.86, 5, and 8.30 GHz, which covers S-, C-, and X-bands for the final design. The features of the final design are better than other designs since the desired resonance frequencies have gotten from it. Figure 4a,b demonstrates the S11 and S21 graphs for different design layouts.

Figure 3
figure 3

Different design layouts for selecting the final design. (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst- studio-suite)43.

Full size image
Figure 4
figure 4

Frequency versus (a) S11 and (b) S21 for different design layouts.

Full size image

Parametric analysis

Effect of substrate material on the MTM performance

Several types of substrate material have been used to justify the forms of the suggested MTM unit cell. Substrate materials are Rogers RO4350B, RT5880, and FR-4. Dielectric constant (DK), loss tangent (LT), and thickness are 3.66, 0.037, and 1.524 mm for Rogers RO4350B, 2.2, 0.009, 1.575 mm for Rogers RT5880 and 4.3, 0.025, 1.5 mm for FR-4, respectively. When Rogers RO4350B was used as a substrate, the magnitudes of S11 were − 27.81 dB at 3.13 GHz, − 23.15, − 14.78 dB at 5.69, 8.77 GHz and the amplitudes of S21 were − 26.86, − 31.24, − 26.16 dB, at 2.86, 5, 8.30 GHz, which covers three bands S-, C-, and X-. When RT5880 was used, the magnitudes of S11 were − 34.23 dB at 3.73 GHz, − 27.64 dB at 6.87 GHz, and the values of S21 are − 31.32, − 35.39 dB at 3.45, 6.02 GHz, which covers S-, and C- bands. When FR-4 was used as a substrate, the magnitudes of S11 were − 17.98 dB at 3.10 GHz, − 16.75, − 9.03 dB at 5.96, 9.46 GHz and the values of S21 were − 15.60, − 20.92, and − 16.55 dB at 2.86, 5.26, and 9 GHz, respectively, it covers three bands. Figure 5a,b signifies the frequency versus S11 and S21 curves for different substrate materials. Since the permittivity value of the material is directly proportional to the capacitance (C), and C is inversely proportional to the resonance frequency. Hence the resonance frequency differs for Rogers RO4350B, RT5880, and FR-4 due to the different permittivity values, indicating that the MTM's performance is dependent on the substrate material. The resonance frequency of the MTM is a shift to the higher value for the lower value of substrate permittivity and a shift to the lower value for the higher value of substrate permittivity. Since the features such as covering band, EMR, desired frequency and magnitude of S11 and S21 of the Rogers RO4350B are better than others, so Rogers RO4350B is finally selected as a substrate material.

Figure 5
figure 5

Frequency versus (a) S11 and (b) S21 curves for the different substrate materials.

Full size image

Effect of variations of split gap

The impact of split gap variations on transmission coefficient (S21) is exhibited in Fig. 6. In this analysis, five different split gap such as 0.2, 0.35, 0.4, 0.5, and 0.6 mm has been used to see the best performance of the MTM cell. The values of S21 are − 25.72, − 31.81, − 25.75 dB at 2.86, 4.99, and 8.27 GHz for 0.20 mm gap. The values of S21 for split gap 0.25 mm are − 26.86, − 31.24, − 26.16 dB at 2.86, 5 and 8.30 GHz, respectively. When the structure’s split gap is 0.40 mm, the magnitudes of S21 are − 26.75, − 32.26, − 27.24 dB at 2.93, 5.12 and 8.56 GHz, respectively. If the cell’s split gap is 0.50 mm, then the amplitudes of S21 are − 26.26, − 32.62, − 27.59 dB at 2.95, 5.17, and 8.67 GHz, respectively. The magnitudes of S21 are − 27.62, − 32.92, and − 28.18 dB at 2.98, 5.21, and 8.77 GHz for a 0.60 mm gap. The resonance frequency increases with increasing the split gap. We can see that the performance of the MTM unit cell for the gap of 0.50 mm is better than the other split gap. Finally, a 0.50 mm gap was selected for the proposed structure.

Figure 6
figure 6

Effect on S21 for changing the split gap.

Full size image

Effect of several types of conductor on transmission coefficient

Various conductor effects on the S21 is depicted in Fig. 7. We have used four different metal conductors such as nickel, gold, platinum, and copper. When the nickel is used as a patch on the substrate, the magnitudes of S21 are − 8.81, − 10.69, and − 7.78 dB at 2.77, 4.74, and 7.76 GHz, respectively. The magnitudes of S21 are − 25.53, − 31.53, and − 25.89 dB at 2.94, 5.10, and 8.39 GHz for gold. If the platinum is used as a patch, then the magnitudes of S21 are − 23.60, − 27.81, − 21.89 dB at 2.98, 5.13, and 8.43 GHz. When we used copper as a patch on the substrate, the magnitudes of S21 were − 26.86, − 31.24, and − 26.16 dB at 2.86, 5, and 8.30 GHz. Since the performance of the copper as a patch is better than others, finally, copper is selected as a patch.

Figure 7
figure 7

Effect on S21 for changing the conductor materials.

Full size image

Effect of structure dimension variations

Figure 8 shows the S21 curve for different sizes of the inverse double V-shaped unit cell. We have taken five different sizes of the MTM structure for delivering the best performance. The different sizes of the MTM cell are 6 \(\times\) 6, 7 \(\times\) 7, 8 \(\times\) 8, 9 \(\times\) 9, and 10 \(\times\) 10 mm2. If the unit cell size is 6 \(\times\) 6 mm2, the S21 are 3.90, 6.79 GHz with amplitude − 26.35 and 31.31 dB, respectively. The EMR 12.82 and including bands are S-, and C-. The S21 resonance frequencies are 3.29, 5.75, and 9.55 GHz, with magnitudes − 26.72, − 31.83, and − 26.25 dB respectively; EMR is 13.03 and including bands are S-, C-,and X- for the size of 7 \(\times\) 7. When the size is 8 \(\times\) 8 mm2, including bands are S-, C-, X-, magnitudes of S21 are − 26.86, − 31.24, and − 26.16 dB at 2.86, 5, and 8.30 GHz and the EMR is 13.11. The EMR is 12.87, covering bands S-, C-, magnitudes of S21 are − 27.03, − 31.81, and − 26.61 dB at 2.59, 4.52, and 7.48 GHz for the unit cell size 9 \(\times\) 9. The magnitudes of S21 are − 26.13, − 31.73, and − 27.09 dB at 2.43, 4.23, and 7.01 GHz; EMR is 12.35, covering bands S-, and C-, for the unit cell size 10 \(\times\) 10 mm2. After analysing the cell size, the number of resonance frequency, covering bands, desired frequency and high EMR value 13.11 were found for the 8 \(\times\) 8 mm2 size, which is better than the others. So the structure size 8 \(\times\) 8 mm2 has been fixed for this MTM structure.

Figure 8
figure 8

Effect on S21 for changing the unit cell size.

Full size image

Effect of different thicknesses of the substrate

Figure 9 symbolizes the impact of different thicknesses of the substrate on the transmission result (S21). We have taken four (4) different thicknesses of the substrate to investigate the response of the S21. Four (4) thicknesses are 0.762, 1.145, 1.524, and 2.286 mm. The amplitudes of S21 are − 27.97, − 31.29, and − 24.80 dB at 2.93, 5.15, and 8.57 GHz, respectively for 0.762 mm. The S21 amplitudes are − 26.22, − 31.97, and − 25.85 dB at 2.90, 5.07, and 8.43 GHz, respectively for the 1.145 mm. If the substrate thickness is 1.524 mm, then the amplitudes of S21 are − 26.86, − 31.24, and − 26.16 dB at 2.86, 5, and 8.30 GHz, respectively. When the substrate thickness 2.286 mm was taken, the magnitudes of S21 were − 26.09, − 31.35, and − 26.08 dB at 2.89, 5.01, and 8.31 GHz, respectively. In Fig. 9, the resonance frequency decreases with the increased thickness. Since the magnitude and desired resonance frequency for the substrate thickness of 1.524 mm is better than others, it is selected for the thickness of the substrate.

Figure 9
figure 9

Effect on S21 for changing the thickness of the substrate.

Full size image

Analysis of the axis of waveguide port

The MTM structure was also analyzed in the x- and y-axes to see how the results changed. Figure 10a,b depicts the simulation arrangement and scattering parameters in the x-axis wave propagation. Figure 10b shows that the reflection coefficient magnitudes are − 39.97, − 31.19 dB at 2.60, and 9.25 GHz, whereas the transmission coefficient magnitudes are − 22.91, − 14.74 dB at 2.84, and 8.31 GHz, respectively. When a wave propagates along the y-axis, the S11 magnitude values are − 13.58, − 11.80 dB at 5.70, and 8.88 GHz, whereas the transmission magnitude values are − 28.45, − 28.35, and − 24.34 dB at 2.92, 5.10, and 8.32 GHz, respectively. These two investigations revealed that neither of the wave propagations exhibits the appropriate resonance frequencies. In the meantime, superior results were obtained in the z-axis. As a result, the lack of resonance frequencies and distinct properties, x- and y-axes wave propagations were rejected.Fig. 11a represents the simulation configuration, and Fig. 11b depicts the S-parameters for the y-axis wave propagation in the suggested structure.

Figure 10
figure 10

Wave propagation in the x-axis: (a) Simulation structure (b) S-parameters. (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst- studio-suite)43.

Full size image
Figure 11
figure 11

Wave propagation in the y-axis: (a) Simulation arrangement (b) S-parameters.

Full size image

MTM array analysis

In general, a single unit cell MTM cannot function on its own; rather, it requires an array of unit cells to demonstrate acceptable exotic EM properties. On the other hand, an MTM containing electrically conductive parts is an array with sufficient capacitive and inductive properties. Figure 12 shows the simulation setup and fabricated design of a 4 \(\times\) 4 array of V-shaped MTM unit cells.

Figure 12
figure 12

The 4 \(\times\) 4 array (a) simulated arrangement (b) fabricated design.

Full size image

As shown in Fig. 13, several array arrangements were chosen for this parametric study, including 1 × 2, 2 × 2, 3 × 3, and 4 × 4 arrays. All four array cells delivered multi resonance frequencies in the S-, C-, and X-bands; the magnitude values and frequency deviated slightly from unit cell results. Table 2 represents the various features of the array.

Figure 13
figure 13

Effect on S21 for a different array of the V-shaped cell.

Full size image
Table 2 The transmission resonance frequency and its magnitude for different arrays.
Full size table

Equivalent circuit analysis

The equivalent circuit of the CST and HFSS simulated unit cell has been made by the Advanced Design System (ADS-2019) software45 shown in Fig. 14. In this designed equivalent circuit, inductances (L)and capacitances (C) are used to create the resonance point of transmission response (S21). The metal strip produces inductances, and capacitances are produced by the split gap of the designed unit cell46. The LC circuit is constructed the transmission resonance frequency to validate the CST and HFSS simulated transmission response of the MTM structure. The inverse double V-ring forms the inductances and capacitances L1, L2, C1, and C2. L3 and C4 are formed by the second square ring, where C3 is the coupling capacitance created by the gap between inverse double V and the second square ring. The third square ring forms L4 and C6; here, C5 is the coupling capacitance formed by the gap between the second and third square rings. L5 and C8 are created by the fourth square ring, where C7 is the coupling capacitance produced by the gap between third and fourth square rings. Individual inductance and capacitances are L1, L2, L3, L4, L5, and C1, C2, C3, C4, C5, C6, C7, and C8. The transmission resonance frequency (fr) can be stated by the equation.

$$f_{r} = \frac{1}{{2\pi \sqrt {LC} }}$$
(7)
Figure 14
figure 14

Equivalent circuit of the proposed structure. (Path Wave Advance Design System (ADS) https://www.keysight.com/sg/en/lib/resources/software-releases/pathwave-ads-2019.html)45.

Full size image

Here, C is the capacitance that is created by the split gap and can be expressed by the resulting equation

$$C = \varepsilon_{0} \varepsilon_{r} \frac{A}{d}(F)$$
(8)

where \(\varepsilon_{0}\)=\(8.854\times {10}^{-12}\) F/m, \(\varepsilon_{r}\) = relative permittivity, \(A\) and \(d\) are the area and distance of the split, respectively. And L is the inductance generated by the metal strip, which the equation can present

$$L\left( {nH} \right) = 2 \times 10^{ - 4} \left[ {\ln \left( {\frac{l}{w + t}} \right) + 1.193 + 0.02235\left( {\frac{w + t}{l}} \right)} \right]K_{g}$$
(9)

where \(K_{g}\) denote the adjustment factor, \(K_{g} = 0.57 - 0.145\ln \frac{{w^{\prime}}}{{h^{\prime}}}\) here \({w}^{^{\prime}}\) and \({h}^{^{\prime}}\) are the width and thickness of the substrate. Also,\(t\), \(l\), and \(w\) are the microstrip line thickness, length, and width correspondingly. To attain overall inductance, it's vital to accept both internal and external inductance in this equivalent circuit; the values of inductance and capacitance components are obtained by using the ADS software considering the desired response of S21. By tuning the component values in ADS, the values are so chosen that it provides similar resonances of S21 obtained from the CST and HFSS. To adjust the first transmission resonance frequency to 2.86 GHz, we tuned the inductor L3 and capacitor C4. When the second resonance 5 GHz is fixed, the inductor L4 and capacitors C6 has been tweaked. The inductor L5 and capacitor C8 are tuned to adjust the third resonance frequency 8.30 GHz. Finally, the CST, HFSS and ADS simulated transmission coefficient is presented in Fig. 15, where these three results are almost the same.

Figure 15
figure 15

Transmission coefficient (S21) graph for CST, HFSS, and ADS simulation.

Full size image

Surface current, E-field, and H-field analysis

The surface current of the produced MTM unit cell is described for different transmission resonance frequencies. Figure 16a shows the surface current pattern of three distinct resonances that occurred at frequencies of 2.86, 5, and 8.30 GHz, respectively. The current is distributed on the surface of the patch. For the first resonance frequency, 2.85 GHz, current follows equally in every metal ring which is mentioned by the red colour. The intensity of the surface current is high for the upper portion of the second ring and the lower portion of the third ring, as depicted in 5 GHz. The outer ring and opposite double V-shape resonator observed the lower intensity of the current. The inner ring feels the high intensity of the current, and the middle ring shows a moderate level of current for 8.30 GHz resonance frequency. The outer ring and V-ring noticed the minimum intensity of the current. The E-field and H-field can be described by the following equations47.

$$\nabla \times H = J + \frac{\partial D}{{\partial t}}$$
(10)
$$\nabla \times E = - \frac{\partial B}{{\partial t}}\;{\text{where}}\;\nabla = \left[ {\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z}} \right]$$
(11)
Figure 16
figure 16

Analysis of (a) Surface current (b) E-field and (c) H-field for the designed structure. (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst- studio-suite)43.

Full size image

Two more equations can be used to determine the electromagnetic field's interaction with materials48.

$$D(t) = \varepsilon (t) \times E(t)$$
(12)
$$B(t) = \mu (t) \times H(t)$$
(13)

The E-field and H-field distributions have been taken in absolute components with instantaneous plot attributes and CST simulation outside orientation at different frequencies. So, the z-component of E-field and H-field distributions (Ez and Hz) of the absolute of E-field and H-field distributions (|E| and |H|). Figure 16b shows the E-field of the aforementioned MTM unit cell at three distinct resonance frequencies. These frequencies are 2.86, 5 and 8.30 GHz. The E-field is almost equally noticeable around the different rings at the 2.86 GHz resonance frequency. The distribution of the E-field is more concentrated in the inner ring and slightly concentrated on the middle and outer ring of the cell for 5 GHz transmission resonance frequency. The lower portion of the middle ring and upper portion of the inner ring noticed a high charge, but the outer ring and double V-shape noticed a very small charge for 8.3 GHz resonance frequency. The break or gap in the resonator ring creates a capacitor, which accumulates electric charge and produces additional E-fields; the E-field strength is significant at certain points. At a reserver, the H-field around a wire follows the equation \(B = {{\mu I} \mathord{\left/ {\vphantom {{\mu I} {2\pi r}}} \right. \kern-\nulldelimiterspace} {2\pi r}}\); here \(\mu\) is the permeability of the free space. For all resonance frequencies, the H-field and E-field show nearly opposing excitation. The magnetic field is formed by the movement of electrical charges in general. As a result, maximal charge mobility boosts magnetic field strength, as evidenced by the magnetic field (also known as the H-field). Figure 16c represents the H-field distribution for three individual resonance frequencies. When a transverse EM wave propagates through a metamaterial for a specific frequency spectrum, an artificial magnetic dipole moment is introduced in a split ring resonator. The three different resonance frequencies are 2.86 GHz, 5, and 8.30 GHz, and for each resonance frequency, the H-field behaviour has been shown. The h-field are strong in the lower position of the outer and middle ring and surroundings of the inner ring. The opposite double V shape resonator noticed moderate field intensity for 2.86 GHz resonance frequency. It is also noticeable that the field intensity is moderate in the middle and inner ring, but it is low in the outer and V shape resonator for the resonance frequency 5 GHz. The intensity of the field is much visible in the most inner ring, but the so slight intensity is observed in the most outer, middle and V shape resonator for the resonance frequency 8.30 GHz.

Results and discussion

The S-parameter of the recommended unit cell is shown in Fig. 17. The reflection and transmission factor has three resonance frequencies. Three resonance frequencies of S11 are 3.07, 5.67, and 8.68 GHz with magnitudes of − 27.99, − 23.35, and − 14.72 dB, respectively. The − 10 dB bandwidth of S11 is 3.01 to 3.22, 5.51 to 5.94, and 8.61 to 8.77 GHz. Similarly, the three resonance frequencies of S21 are 2.86, 5, and 8.30 GHz with magnitudes of − 26.86, − 32.42, and –26.16 dB, respectively. The − 10 dB bandwidth of S21 is 2.80 to 2.91, 4.76 to 5.17, and 8.05 to 8.42 GHz.

Figure 17
figure 17

S-parameter graph of the suggested V-structure.

Full size image

The effective medium parameters \({\varepsilon }_{r}\), \({\mu }_{r}\), \(n\), and Z of the inverse double V-structure is derived from the scattering parameters using the NRW approach, which was addressed by Eqs. (3–6). The NRW based MATLAB code is used for obtaining the features of \({\varepsilon }_{r}\), \({\mu }_{r}\), \(n\), and Z49. The information extracted from these qualities using the NRW approach can be compared to CST findings. Figures 18a–d shows the extracted real and imaginary parts of the \({\varepsilon }_{r}\), \({\mu }_{r}, n\), and Z, from the MATLAB program. It is visible that the designed MTM unit cell shows the epsilon and mu negative, i.e., double negative. The frequency range of epsilon negative is 2.82 to 3.03, 5.04 to 5.62, and 8.36 to 8.68 GHz. From Fig. 18b, we can see that the negative region of relative permeability (real part) is 2.81 to 2.89, 4.89 to 5.23, and 8.24 to 8.46 GHz and the negative peaks are − 0.064 dB at 2.91 GHz, − 0.081 dB at 5.1 GHz, and − 0.061 dB at 8.34 GHz. Hence the double negative regions of the inverse double V-shaped MTM unit cell are 2.82 to 2.89, 5.04 to 5.23, 8.36 to 8.46 GHz. Refractive index (\(n\)) is also negative; these ranges are 2.84 to 2.99, 4.97 to 5.52, and 8.26 to 8.54 GHz, as presented in Fig. 18c. The impedance values are as well reported in this study, as seen in Fig. 18d. The suggested inverse double V structure had impedance values of 0.23, 0.12, 0.29, and 0.27 at 5.89, 7.70, 10.37, and 12.58 GHz, respectively. In the meantime, the real impedance values were kept positive across the whole simulated frequency range. To validate the simulation result, unit cell and array prototypes have been fabricated and taken the experimental results.

Figure 18
figure 18

Frequency versus: (a) Relative permittivity (b) Relative permeability(c) Refractive index and (d) Impedance.

Full size image

Figure 19a,b depicts the MTM unit cell measurement setup and the unit cell fabricated prototype. At first, the vector network analyzer (VNA model N5227A) of the PNA series was calibrated by the Agilent N4694-60001 calibration kit. The VNA is connected to the two waveguides by the coaxial cables. One waveguide acts as a transmitter, and another one acts as a receiver. To measure, the fabricated prototype is placed in between two waveguides using the close boundary condition. The waveguide models 340WCAS, 187WCAS, and 112WCAS were utilized for the frequency ranges of 2.20–3.30 GHz, 3.95–5.85 GHz, and 7.05–10 GHz, respectively and a total frequency range of 2–10 GHz. The values of S21 were taken from the VNA as a prn form, then we have processed the prn data and made the S21 graph. Figure 20 shows the measured and simulated S21 graph which has a close similarity to each other. The measured resonance frequencies of S21 are 2.87, 5.01, and 8.32 GHz with magnitudes of − 26.86, − 32.42, and − 26.16 dB, respectively. The measured − 10 dB bandwidth of S21 are 2.80 to 2.91, 4.76 to 5.17, and 8.05 to 8.42 GHz. The simulated and measured S21 results were slightly different for the following factors. The Agilent N5227A VNA's calibration inaccuracy is one of the causes for the differences between the two procedures. A little difference occurred during the production of the Rogers RO4350B substrate layer. Furthermore, the substrate material is significant in the production of S-parameters. Waveguides coupling effect, the permittivity of the dielectric substrate also influences the resonance frequency. Capacitance values alter as a result of the dielectric constant, which is also responsible for adjusting the resonance frequency.

Figure 19
figure 19

Unit cell (a) measurement setup (b) fabricated prototype size of 8 \(\times\) 8 mm2.

Full size image
Figure 20
figure 20

Simulated and measured transmission coefficient (S21) for the double inverse V-shaped unit cell.

Full size image

Figure 21a,b reveals the array of the MTM unit cell measurement setup and fabricated MTM 20 \(\times\) 25 array prototype. For the MTM array measurement, the developed prototype was placed in between two horn antennas, and these antennas were connected with VNA by the lossy coaxial cable. One horn antenna acts as a transmitter, and another one acts as a receiver. 2–10 GHz frequency range is used to take the S21 results of the array. When measured the array structure, we took 201 data points, i.e., in VNA, we set the number of data points to 201. The distance between the two horn antennas is 38 cm. For normal incidences, the wave propagates in the z-direction. Horn antennas were placed in an anechoic chamber to avoid the outer noise. The values of S21 were taken from the VNA as a prn form, then we have processed the prn data and made the S21 graph. Figure 22 shows the measured frequency versus S21 curve for the 20 \(\times\) 25 array of the structure. There are some additional resonance frequencies in the measurement data due to the mutual coupling effects of the unit cell architectures, the coupling capacitor effect of the prototype. Due to the long-extended wire from the horn antenna to the VNA, the prototype's restricted dimension relative to the horn antenna causes some measurement errors, and the measured data contain some noise and harmonics.

Figure 21
figure 21

MTM array (a) measurement setup (b) fabricated prototype size of 160 \(\times\) 200 mm2.

Full size image
Figure 22
figure 22

Transmission response (S21) for measured results of the 20 \(\times\) 25 array structure.

Full size image

The designed metamaterial structure provides three resonance frequencies are 2.86, 5, and 8.30 GHz, it covers S-, C-, and X-bands. Wi-Fi (wireless fidelity) is a widely used wireless networking protocol. Wi-Fi works in the same way as other wireless devices in that it sends signals between devices using radio frequencies. It works in 2.4 and 5 GHz frequency bands50. Wi-Fi network speeds are generally faster when frequencies in the 5 GHz band are used. The 5 GHz band has a smaller coverage area, but it delivers data quicker and has difficulty penetrating solid things. Higher frequencies allow data to be delivered quicker than lower frequencies; hence the 5 GHz band allows for faster uploading and downloading of information. Since the proposed structure provides a 5 GHz frequency band, the suggested MTM can be used in Wi-Fi for high bandwidth and high-speed applications. The marine radar is possibly the most important piece of equipment on the ship's bridge for the officer on watch (OOW) to keep a safe navigating watch. The X-band is extensively utilized in marine radars because it allows smaller antennas that fit on most boats and provides improved target resolution. A weather radar is a device that sends pulses of electromagnetic electricity into the ecosystem to locate precipitation, decides its movement and intensity, and discover the precipitation kind which includes rain, snow, or hail. The S-Band radar provides the ultimate long-range perspective, allowing to plan, forecast, and defend before severe weather. Since the designed cell provides more two resonance frequencies i.e., 2.86 GHz (S-band) and 8.30 GHz (X-band), so the proposed metamaterial could be used in weather radar and marine radar51.

The following steps can solve the loss problem of the radar and Wi-Fi. The power of the transmitter and the length of the MTM have an impact on the widest range of radar systems. The radar system's performance improves as transmission power and MTM size increase. The unavoidable noise appears as its input influences the receiver's ability to perform according to its specifications. Because of the noise generated by the gadget, the frequencies attributed to the microwave radar, for example, may go undetected. Frequency interference can potentially be resolved by altering the Wi-Fi router's channel. The broadcast frequency can usually be set for the channel. The more expensive and powerful routers can broadcast at a frequency of 5 GHz, which is fantastic.

EMR analysis

The effective medium ratio (EMR) is an important consideration in the MTM study. The EMR represents the metamaterial's smallness and effectiveness37. Many devices work in the low resonance frequency, but the low resonance frequency is challenged to achieve for the small size of metamaterial; the high EMR represents the perfectness and criteria fulfil of the MTM design. If the value of EMR is less than 4, then the criterion of subwavelength of metamaterial is not fulfilled. The frequency and size of the metamaterial are inversely proportional to each other, the small size of MTM provides a high resonance frequency which is not applicable for low-frequency devices. So, it is necessary to consider EMR when designing metamaterial. The EMR is the ratio between the wavelength and unit cell size, presented by the Eq. (14).

$$EMR= \lambda /L$$
(14)

\(\lambda\) = wavelength at the lower resonance frequency and \(L\)= length of the MTM unit cell.

The advantages of high EMR are small metamaterial size with low frequency, which is applicable for low-frequency devices. Furthermore, the high EMR demonstrates that the proposed design fulfils the MTM criteria. The proposed MTM unit cell has a high EMR of 13.1 for a size of 8 \(\times\) 8 \(\times\) 1.524 mm3 and a lower resonance frequency of 2.86 GHz. The suggested unit cell's EMR value of 13.11 increases its consistency while reducing its electrical dimensions without imposing fabrication constraints. The important advantages of the high EMR are: (i) enhanced uniformity of the properties, (ii) decreased electrical length without fabrication limit, and (iii) diminished effects of coupling with low transmission22.

Table 3 compares the proposed MTM unit cell structure with the existing unit cell structures. According to the research, the proposed unit cell structure covers the tri-band frequencies with double negative MTM properties. From the references19,23,24,28,29,31,32,33,38,39,41, it is seen that the unit cell size is large, covering frequency band, and EMR is lower than the proposed inverse double V-shaped unit cell. In addition, from the references17,22,42, we can see that the unit cell size is large, EMR is lower than the recommended unit cell, though the covering band is equal. Thus, the overall performance of the suggested unit cell is superior to that of the structure mentioned in Table 3.

Table 3 Comparison between suggested and existing work based on some aspects.
Full size table

Conclusion

In this article, a DNG metamaterial has been established and investigated numerically and experimentally for radar and Wi-Fi applications. The designed metamaterial delivers three transmission resonance frequencies such as 2.86, 5, and 8.30 GHz, covering S-, C-, and X-bands. The entire dimension of the suggested unit cell is 8 \(\times\) 8 \(\times\) 1.524 mm3, and a high EMR value of 13.11 is found from this structure. Since the proposed MTM is DNG, so the DNG region has been found from 2.82 to 2.89, 5.04 to 5.23, and 8.36 to 8.46 GHz. The S-band (2.86 GHz) is applied in, weather radar. The marine radar works in X- band (8.30 GHz). The C-band (5 GHz) is widely used in Wi-Fi for high bandwidth and high-speed applications. Wi-Fi was originally designed for mobile computing devices such as laptops, but it is now widely used in consumer goods such as televisions, DVD players, and digital cameras. Parametric tests on various lengths and widths with various structures have been used to determine the effective medium parameters. Different types of array structure 1 \(\times\) 2, 2 \(\times\) 2, 3 \(\times\) 3, 4 \(\times\) 4, and 20 \(\times\) 25 is analyzed and validated by the measured result. The simulated and measured result is a good deal for the inverse double V-shaped unit cell and an array of the cell. We got the indicated formation's whole performance better than the other structures mentioned in this paper. Since the proposed metamaterial unit cell size is small, provides desired resonance frequency, and gives a large frequency band and high EMR value; hence the suggested metamaterial can be effectively used in radar and Wi-Fi applications.