Abstract
In the current study, the fish farm model perturbed with time white noise is numerically examined. This model contains fish and mussel populations with external food supplied. The main aim of this work is to develop time-efficient numerical schemes for such models that preserve the dynamical properties. The stochastic backward Euler (SBE) and stochastic Implicit finite difference (SIFD) schemes are designed for the computational results. In the mean square sense, both schemes are consistent with the underlying model and schemes are von Neumann stable. The underlying model has various equilibria points and all these points are successfully gained by the SIFD scheme. The SIFD scheme showed positive and convergent behavior for the given values of the parameter. As the underlying model is a population model and its solution can attain minimum value zero, so a solution that can attain value less than zero is not biologically possible. So, the numerical solution obtained by the stochastic backward Euler is negative and divergent solution and it is not a biological phenomenon that is useless in such dynamical systems. The graphical behaviors of the system show that external nutrient supply is the important factor that controls the dynamics of the given model. The three-dimensional results are drawn for the various choices of the parameters.
Similar content being viewed by others
Introduction
There are many industries in our surroundings. The waste of these industries is not pesticide-free matter, which pollutes the water body, ecosystem, and whole wildlife surrounding the water. Water is a good solvent that dissolves most substances and we believe that water can dilute or absorb any substance. Lakes, rivers, or any water body can be polluted due to pesticide wastage by industries1. Here, our intention is on wildlife like fish farms because fish farms completely depend on organic food and pesticide-free feeds. If the water is polluted then the outside food will be harmful to the fish2. Due to the excess use of natural foods, there will deficiency of oxygen in the water, and the harmful waste of industries draw inadequate effects on agriculture and wildlife like mussels, shellfish, oyster gulfweed, and rockweed. All these types of species are used as biomass, biofuel, or bio-filter that feed extra-undissolved substances in the water body3. As a result, water will purify and filter. These species have positive effects to purify the water and particularly shellfish have characteristics to filter the water, food, and feeds. Nowadays, many fishers use mussels, oysters, and shellfish as bio-filters or biomass to make highly purified fish farms. These can work in the following ways: one is, it consumes undissolved substances and fish waste, and other, it can feed pesticide and artificial food4. Many works are based on a system of differential equations that deal with such models of the population in mathematics and analyze their numerical results through different methods.
The disease dynamics are widely discussed due to the importance of human life and living organisms. Recently, the Coronavirus disturbed the human community drastically. Butt et al. used the optimal control analysis for the Corona disease5, considered the bi-model dynamics Covid-19 model, and analyzed the results by using optimal control theory6, used the optimal control strategies to eradicate the Rubella disease7, considered the fractional epidemic model with Atangana–Baleanu derivative8. Rafiq et al. proposed an Ebola epidemic model and analyzed its different aspects9. Butt et al. considered the Covid-19 pandemic model and used mathematical techniques such as the unique existence of the solution and other techniques to minimize the effect of the disease on the human community10. Hanif et al. employed the numerical technique to find the solution of the Caputo-Fabrizio-fractional model of the coronavirus pandemic11. Authors considered the various epidemic models analyzed the disease dynamics12,13,14.
A great number of stochastic process models investigated comprise space and spatial variables15. Nevertheless, a couple of authors studied and observed fish farm dynamics models just as stochastic procedures due to undetermined stochastic terms or variables16. In 1998, Virtala et al.17 constructed such a model, which is consistent and formulated the reason for dead fish due to inevitable accidents. In addition, from 1990 to 2003 Harris et al.18 worked on stochastic models which are of fault damage zones that are generated by statistical properties for fault populations. Yoshioka et al.19 showed the art of the state of modeling, computation, and analysis of stochastic control science in environmental engineering and research areas related to these fields. Gudmundsson et al.20 gave their efforts on an age-structured system comprised of time and space and described the gap connecting biofuel and the age of the system.
Furthermore, Sullivan et al.21 and Lewy et al.22 appreciate stochastic procedure in their models and contemplate it emphatically reliable method. Schnute23 narrated such models that accommodate a bit of error and then appraise both stochastic process and stochastic PDEs to estimate errors. Stochastic PDEs own such properties and characteristics that enhance unpredictability and errors. León-Santana et al.24 figure out procedures to accomplish earthly and habitat models based on linear stochastic PDEs. Likewise, Nøstbakken25 numerically works out on stochastic PDEs for ecological systems and wildlife like fish farms. Additionally, Reed and Clarke26 collected optimum reaping rules for organic phenomena along with stochastic PDEs. As our model is substantial and earthly so, we convert the system of PDEs into stochastic PDEs because the substantial model can perform randomness in behavior at some particular stage and results may not be predicted27. In extension, stochastic has numerous applications in real life. The majority of the researchers and authors used the stochastic in their work and paper. So, we prefer stochastic PDEs instead of simple PDEs28.
The fish form model under the influence of time noise is given as,
with initial conditions
here u(x, t), v(x, t), and w(x, t) are the densities of nutrient, fish, and mussel population at a point (x, t) respectively. Also, there are four parameters present in the given model that is \(\phi\), \(\mu\), \(\alpha\), and \(\xi\) which describe the rate of external deposition of food, digestion rate of food of fish community and maximum digestion rate of food of mussel community respectively. These parameters have had a great effect on the ecosystem and its functioning. Here, \(\delta\), \(\gamma\), and \(\beta\) describe the death rate respectively, competition occurring within a species, and the proportion of food supply to biofuel of fish. In addition, \(\rho\) and \(\eta\) describe the death rate and transfer the ability of mussel. Thus, the external deposition of food does not be digested into fish biofuel so that it could reach oysters in the form of specific pesticide-free matter and mussels can easily absorb it. Moreover, \(d_u\), \(d_v\) and \(d_w\) be the coefficients of diffusion and \(\dot{B}_i\) be the standard Wiener one-dimensional processes, with \(\sigma _i\) that represent noisy strengths where \(i=1,2,3\) and it is a Borel functions29.
To work on stochastic is a challenging task especially when we have to deal with non-linear terms. Numerous researchers worked on SPDEs and their numerical solutions by two finite difference schemes and methods and proved the consistency and stability30. The stochastic procedure can be beneficial to demonstrate some of the unpredictable results in the accomplishment of the distinct objective because they handle the randomness in the model31. A stochastic method commonly used in various fields and has real-life applications in gaming theory, surveys, tracking ___location, and probability statistical analysis32. In extension, SPDEs are used in numerous models such as the substantial or physical system with time frame because it consists of a random variable that calls noise term calculated with the Wiener process which dominates the unpredicted behavior of random behavior33. Therefore, it is extensively in numerous mathematical models like echography, pictorial representation, ultrasonography, computational molecular biology, and financial markets like a trading floor that vary with time randomly34.
Chessari et al. considered the backward stochastic differential equations and employed various numerical methods35. Zheng et al. used the finite elements methods for the study of SPDEs36. Röckner et al. worked on the wellposedness of the SPDEs37. Gyöngy et. al. used the lattice approximation of the SPDEs perturbed by white noise on a bounded ___domain \(R^d\) for \(d=1,2,3\) and gained the convergence rates of the approximation38. The authors gained the numerical approximation of Bagley-Trovik and fractional Painleve equations by using the cubic B-spline method39. Arqub et al. worked on the numerical computing of the Singular Lane-Emden type model by using the reproducing Kernal discretization method40. Sweilam et al. worked on the numerical solution of a stochastic extended Fisher-Kolmogorov equation perturbed by multiplicative noise41.
The main contribution of this work is given below:
-
The classical models cannot represent the true behavior of nature. So, need of the hour to consider the classical model under the impact of some environmental noise.
-
The fish farm model is considered under the temporal noise.
-
The underlying is numerically investigated.
-
Two schemes are constructed and used for the numerical study.
-
Schemes are von Neumann stable and consistent.
-
Equilibrium points are successfully gained.
-
The graphical behavior of the state variables is explained from the biological point of view.
-
The MATLAB 2015a is used for the graphical behavior of the test problem.
Numerical methods
In order to analyze the given system of equations, we discretized the whole ___domain of space and temporal variables. The grid points \((x_l,t_m)\) are explained as
Here, M and \(N_1\) are the integers, and \(\Delta x=h\) and \(\Delta t= k\) are stepsizes of space and temporal respectively.
The proposed stochastic backward Euler(SBE) scheme of Eqs. (1), (2), (3) is
The Eqs. (5)–(7) are required proposed SBE scheme for Eqs. (1)–(3). The proposed stochastic Implicit finite difference (SIFD) scheme of Eqs. (1)–(3)
The Eqs. (8)–(10) are required SIFD scheme for Eqs. (1)–(3).
Here \(\lambda _1 = \frac{d_u\Delta t}{\Delta x^2}\) ,\(\lambda _2 = \frac{d_v\Delta t}{\Delta x^2}\), \(\lambda _3 = \frac{d_w\Delta t}{\Delta x^2}\). The numerical approximation of u(x, t), v(x, t) and w(w, t) is \(u_d^e, v_d^e, w_d^e\) at point \((d \Delta x,e \Delta t)\). The analysis of the scheme is discussed in the next sections.
Stability analysis
By Von-Neuman method of stability42,
where \(\hat{A}^n_m\) is a Fourier transformation of \(A^n_m\) which is given below,
Where \(\theta\) is a real variable. By substituting this value in finite schemes, we may get
The sufficient and necessary condition for Von Neumann the stability method is,
where \(\varrho\) is constant.
Theorem 1
The SBE scheme for u(x, t), v(x, t), and w(x, t) is von Neumann stable in the mean square sense.
Proof
Von Neuman stability criteria are used for linear equations. So non-Linear term can be linearized by taking \(v_d^e= \psi _1\) and \(w_d^e=\psi _2\) where \(\psi _1\), \(\psi _2\) and \(\phi\) are local constants so it can be set equal to zero. Thus, finite difference scheme for Eqs. (1) in (5) can be written as,
By amplification factor, Eq. (13) can be written as,
Now by using independent of Wiener process increment and amplification factor, we reached at
\(\left| \frac{1 -\Delta t \mu }{\left( 1+4\lambda _1 \sin ^2 \frac{\Delta x \theta }{2}\right) } \right| ^2\le 1\), then (15) becomes,
Here, \(\left| \frac{\sigma _1}{\left( 1+4\lambda _1 \sin ^2 \frac{\Delta x \theta }{2}\right) }\right| ^2 = \varrho _1\). According to the stability definition, we deduced that Eq. (1)is von Neumann stable.
Similarly, Eq. (6) is linearized as follows,
Now by using independent of Wiener process increment and amplification factor, we reached at
\(\left| \frac{1 -\Delta t \delta }{\left( 1+4\lambda _1 \sin ^2 \frac{\Delta x \theta }{2}\right) } \right| ^2\le 1\), then equation (20) becomes,
Here, \(\left| \frac{\sigma _2}{\left( 1+4\lambda _1 \sin ^2 \frac{\Delta x \theta }{2}\right) }\right| ^2 = \varrho _2\). According to the stability definition, we deduced that this scheme is von Neumann stable.
Similarly, Eq. (7) is linearized as follows,
Now by using independent of Wiener process increment and amplification factor, we reached at
\(\left| \frac{1 -\Delta t \rho }{\left( 1+4\lambda _3 \sin ^2 \frac{\Delta x \theta }{2}\right) } \right| ^2\le 1\), then (25) becomes,
Here, \(\left| \frac{\sigma _3}{\left( 1+4\lambda _3 \sin ^2 \frac{\Delta x \theta }{2}\right) }\right| ^2 = \varrho _3\). According to the stability definition, we deduced that this scheme is von Neumann stable.
Theorem 2
The SIFD scheme for u(x, t), v(x, t), and w(x, t) is von Neumann stable in the mean square sense.
Proof
Similarly, Eq. (8) is linearized as follows,
Now by using independent of Wiener process increment and amplification factor, we reached at
\(\left| \frac{1}{1+\Delta t \mu + 4\lambda _1 \sin ^2 \frac{\Delta x \theta }{2}} \right| ^2\le 1\), then (30) becomes,
Here, \(\left| \frac{\sigma _1}{1+\Delta t \mu + 4\lambda _1 \sin ^2 \frac{\Delta x \theta }{2}}\right| ^2 = \varrho _4\). According to the stability definition, we deduced that (8) is von Neumann stable.
Similarly, Eq. (9) is linearized as follows,
Now by using independent of Wiener process increment and amplification factor, we reached at
\(\left| \frac{1}{1+\Delta t\delta +4\lambda _2 \sin ^2 \frac{\Delta x \theta }{2}} \right| ^2\le 1\), then Eq. (35) becomes,
Here, \(\left| \frac{\sigma _2}{1+\Delta t\delta +4\lambda _2 \sin ^2 \frac{\Delta x \theta }{2}}\right| ^2 = \varrho _5\). According to the stability definition, we deduced that (9)is von Neumann stable.
Similarly, Eq. (10) is linearized as follows,
Now by using independent of Wiener process increment and amplification factor, we reached at
\(\left| \frac{1}{1+\Delta t\rho +4\lambda _3 \sin ^2 \frac{\Delta x \theta }{2}} \right| ^2\le 1\), then equation(39) becomes,
Here, \(\left| \frac{\sigma _3}{1+\Delta t\rho +4\lambda _3 \sin ^2\frac{\Delta x \theta }{2}}\right| ^2 = \varrho _6\). According to the stability definition, we deduced that equation(10)is von Neumann stable.
Consistency
A finite difference scheme \(L|_{(l,m)} u|_{(l,m)} = G|_{(l,m)}\) is consistent with SPDE \(LU=G\) at a point (x, t), if for any continuously differentiable function \(\phi (x,t) = \phi\) in mean square that is
\(E||(L\phi -G)|_{(l,m)}- [L|_{(l,m)}\phi |_{(lh, mk)}-G(l,m)]||^2 \rightarrow 0\), as \(h \rightarrow 0\), \(k\rightarrow 0\) and \((lh, (m+1)k)\) approaches to (x, t).
Theorem 3
The SBE scheme given in Eqs. (5)–(7) is consistent in the mean square with SPDE Eqs. (1)–(3).
Proof
The consistency of the proposed SBE scheme is given as By using the operator as \(F(u)=\int _{mk}^{(m+1)k} u dr\) on Eq. (1)
Hence, we conclude that
Now the square of It\(\hat{o}\) Integral gives us
\(E|F(u)|_d^e -F|_d^e(u)|^2\rightarrow 0\) as \((d,e)\rightarrow \infty\). So, the given scheme for state variable u is consistent.
Similarly, Consistency for Eq. (6) is as follows,
Hence, we conclude that
\(E|F(v)|_d^e - F_d^e(v)|^2\rightarrow 0\) as \((d,e)\rightarrow \infty\). So, the given scheme for state variable v is consistent.
Similarly consistency for Eq. (7) is ,
Hence, we conclude that
\(E|F(w)|_d^e -F|_d^e(w)|^2\rightarrow 0\) as \((d,e)\rightarrow \infty\). So, the given scheme for state variable w is consistent.
Theorem 4
The proposed SIFD scheme given in Eqs. (8)–(10) is consistent in the mean square with SPDE Eqs. (1)–(3).
Proof
Now, the consistency of the proposed SIFD scheme for Eq. (8) is,
Hence, we conclude that \(E|F(u)|_d^e -F|_d^e(u)|^2 \le\)
\(E|F(u)|_d^e-F|_d^e(u)|^2\rightarrow 0\) as \((d,e)\rightarrow \infty\). So, the given scheme for state variable u is consistent.
Similarly, consistency for the Implicit finite scheme for equation (9).
Hence, we conclude that
\(E|F(v)|_d^e-F|_d^e(v)|^2\rightarrow 0\) as \((d,e)\rightarrow \infty\). So, the given scheme for state variable v is consistent.
Similarly, consistency for the Implicit finite scheme for equation (10) is
Hence, we conclude that
\(E|F(w)|_d^e-F|_d^e(w)|^2\rightarrow 0\) as \((d,e)\rightarrow \infty\). So, the given scheme for state variable w is consistent.
Convergence
The convergence of the stochastic implicit scheme is analyzed in the means square sense.
Theorem 5
The stochastic implicit scheme is given by Eqs. (8)–(10) is convergent in the mean square sense.
Proof
as the scheme is consistent in the mean square sense i.e., \(L_d^{e}u_d^{e} \rightarrow L_d^{e}u\) as \(\Delta x \rightarrow 0, \Delta t \rightarrow 0\) and \((d\Delta x, e\Delta t,)\rightarrow (x,t)\),
also, scheme is stable, then \((L_d^{e})^{-1}\) is bounded. So, \(E\bigg |u_d^{e}-u \bigg |^2 \rightarrow 0\). Hence proposed scheme for u is convergent in the mean square sense. By doing the same practice, we can show that the scheme for v, w is convergent.
The convergence of another scheme can be deduced in a similar way.
Graphically representation
The initial conditions are \(u(x,0)=v(x,0)=w(x,0)=1\)43.
The equilibria of given equations are
Also, assume that \(\varsigma _1=\frac{\mu \delta }{\beta }\), \(\varsigma _2=\frac{\mu \rho }{\eta }\), \(\varsigma _3=\varsigma _2\bigg [1+\frac{\alpha \delta }{\gamma \mu }\bigg (\frac{\varsigma _2}{\varsigma _1}-1\bigg )\bigg ]\) In44, Gazi et al. analyzed the different dynamics of the Fish farm model. They worked on the local behavior of the Fish farm system of the equations and summarized the existence of equilibria as follows
\(\begin{array}{ccc} \text{ Equilibrium } \text{ point } &{} \text{ feasibility } \text{ condition } &{} \text{ stability } \text{ condition } \\ E_1 &{} always &{} \phi<\varsigma _1,\phi<\varsigma _2 \\ E_2 &{} \phi>\varsigma _1 &{} \phi<\varsigma _3 \\ E_3 &{} \phi>\varsigma _2 &{} \varsigma _2<\varsigma _1\\ E_4 &{} \varsigma _2>\varsigma _1,\phi >\varsigma _3 &{} always \end{array}\)
By concluding this brief discussion, equilibrium \(E_1\) is sable if \(\phi<\varsigma _1,\phi <\varsigma _2\) and becomes unstable if exterior nutrients exceed the value of \(\varsigma _1\). The equilibrium \(E_2\) goes stable if exterior nutrient between the value of\(\varsigma _1\) and \(\varsigma _3\) with \((\varsigma _1<\varsigma _3)\). The equilibrium point \(E_3\) is stable only if the feasibility condition, as well as stability condition, exists A. The given model is around the coexistence equilibrium if the exterior nutrient supply exceeds values \(\varsigma _3\) with \(\varsigma _1<\varsigma _2\). Thus, the given Fish form model is stable in various levels of exterior nutrient supply.
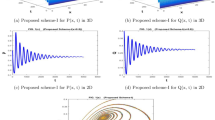
The values of the parameters that are given in Table 1 showed by the Figs. 1, 2, 3, 4, 5, 6, 7 and 8) . The Figs. 1, 2, 3 and 4) have noise strength 0.25 and the Figs. 4, 5, 6, 7 and 8 have noise strength 0.025. The BFD Scheme for external nutrient \(\phi =4\) is discussed in the Fig. 1 and \(E_1\) is a stable point nevertheless the graphical representation displays that state variable u(x, t) and v(x, t) have negative values and it is an imperfection in SBE scheme. Furthermore, the SIFD scheme for external nutrient \(\phi =4\) discussed in the Fig. 2 and \(E_1\) is a stable point nevertheless the graphical representation displays that state variable u, v, and w have positive values for the entire ___domain and this showed that this scheme is stable as well as keep the entire behavior. The SBE scheme for external nutrient \(\phi =10\) is discussed in the Fig. 3 and \(E_2\) is the stable point but the graphical representation displays that the state variable u(x, t) has negative values and it is insignificant for the population dynamics. Similarly, The IFD scheme for external nutrient \(\phi =10\) discussed in the Fig. 4 and \(E_2\) is a stable point nevertheless the graphical representation displays that entire state variable u, v, and w have positive values. Moreover, The BFD scheme for external nutrient \(\phi =100\) is discussed in Fig. 5 and \(\eta =10.75\), is not stable and the state variables have negative values along with divergent behavior. In addition, The IFD scheme for external nutrient \(\phi =100\) discussed in the Fig. 6 and \(\eta =10.75\), the equilibrium point \(E_3\) is stable as well as its graphical behavior display that all state variables own the positivity. The BFD scheme for external nutrient \(\phi =100\) is discussed in Fig. 7\(E_4\) is gained and the state variables keep the positivity. Similarly, The IFD scheme for external nutrient \(\phi =100\) discussed in the Fig. 8 and the \(E_4\) point is stable nevertheless the graphical representation displays that the entire state variable has positive values. MATLAB 2015a is manipulated for this discussion and analysis of the stated Fish Form model.
The fish farm models are population dynamics and necessarily their; solutions must be positive. We have used 2 schemes for the numerical approximation of the governing model. One technique fails to preserve the positive behavior while the other has positive and converges towards the true steady states. One of the most compelling reasons to consider this model with a numerical scheme is to construct and apply the scheme in a way that yields positive solutions. As the governing model is population dynamics and its minimum values can be zero but can never be negative. So its solution must preserve the positivity. The results of the stochastic implicit finite difference scheme resemble the positive steady states. As population dynamics have random behavior, it is better to use the continuous model with a random effect. Such random behavior is observed in every physical phenomenon at a certain level. So we incorporate diffusion as well as random behavior in the underlying model.
Conclusions
The fish farm model under the influence of the Wiener process is considered. The literature on numerical study for the stochastic partial differential equations is required. We have designed two novel and time-efficient numerical techniques for the computational study of the underlying model. The schemes are proposed stochastic backward Euler(SBE) and proposed stochastic Implicit finite difference(SIFD) scheme. The analysis of schemes is analyzed in the mean square sense. Both schemes are compatible with the given system of equations and the linear analysis of schemes is analyzed. The underlying model has four equilibrium points. When the SBE scheme is used for the study, equilibrium \(E_1\) is successfully gained but it also shows negative behavior, \(E_2\) is also obtained with negative behavior, \(E_3\) is not gained because it has divergent behavior, and \(E_4\) is obtained with positive behavior. On the other hand, when the SIFD scheme is applied, equilibrium point \(E_1\) is successfully attained with positive behavior \(E_2\) is attained with convergent and positivity, \(E_3\) also gained with positive behavior, and \(E_4\) is successfully obtained with positive behavior for the given values of the parameter. From the graphical behavior of the system, it is observed that the effect of external food is the main factor that controls the dynamics of the model. The simulations are drawn for various values of the parameters.The study of the SPDEs and their dynamics is the need of the hour. So, we will try to analyze its various aspects such as qualitative analysis of the model and use of optimal strategies to control the SPDEs.
Data availability
Data will be provided by corresponding author on reasonable request.
References
Chaudhry, F. N. & Malik, M. F. Factors affecting water pollution: A review. J. Ecosyst. Ecogr. 7(1), 225–231 (2017).
Wang, Q. & Yang, Z. Industrial water pollution, water environment treatment, and health risks in China. Environ. Pollut. 218, 358–365 (2016).
Neori, A. et al. Integrated aquaculture: Rationale, evolution and state of the art emphasizing seaweed biofiltration in modern mariculture. Aquaculture 231(1–4), 361–391 (2004).
Copertino, M. D. S., Tormena, T. & Seeliger, U. Biofiltering efficiency, uptake and assimilation rates of Ulva clathrata (Roth) J. Agardh (Clorophyceae) cultivated in shrimp aquaculture waste water. J. Appl. Phycol. 21, 31–45 (2009).
Butt, A. I. K., Ahmad, W., Rafiq, M., Ahmad, N. & Imran, M. Computationally efficient optimal control analysis for the mathematical model of Coronavirus pandemic. Expert Syst. Appl. 234, 121094 (2023).
Ahmad, W. et al. Analytical and numerical explorations of optimal control techniques for the bi-modal dynamics of Covid-19. Nonlinear Dyn. 112(5), 3977–4006 (2024).
Ahmad, W. et al. Developing computationally efficient optimal control strategies to eradicate Rubella disease. Phys. Scr. 99(3), 035202 (2024).
Butt, A. I. K., Ahmad, W., Rafiq, M., Ahmad, N. & Imran, M. Optimally analyzed fractional Coronavirus model with Atangana–Baleanu derivative. Results Phys. 53, 106929 (2023).
Rafiq, M., Ahmad, W., Abbas, M. & Baleanu, D. A reliable and competitive mathematical analysis of Ebola epidemic model. Adv. Differ. Equ. 2020, 1–24 (2020).
Butt, A. I. K., Rafiq, M., Ahmad, W. & Ahmad, N. Implementation of computationally efficient numerical approach to analyze a Covid-19 pandemic model. Alex. Eng. J. 69, 341–362 (2023).
Hanif, A., Kashif Butt, A. I. & Ahmad, W. Numerical approach to solve Caputo–Fabrizio-fractional model of corona pandemic with optimal control design and analysis. Math. Methods Appl. Sci. 46(8), 9751–9782 (2023).
Ahmad, W., Rafiq, M. & Abbas, M. Mathematical analysis to control the spread of Ebola virus epidemic through voluntary vaccination. Eur. Phys. J. Plus 135(10), 775 (2020).
Ahmad, W. & Abbas, M. Effect of quarantine on transmission dynamics of Ebola virus epidemic: A mathematical analysis. Eur. Phys. J. Plus 136(4), 1–33 (2021).
Ahmad, W., Abbas, M., Rafiq, M. & Baleanu, D. Mathematical analysis for the effect of voluntary vaccination on the propagation of Corona virus pandemic. Results Phys. 31, 104917 (2021).
Yasin, M. W. et al. Numerical scheme and analytical solutions to the stochastic nonlinear advection diffusion dynamical model. Int. J. Nonlinear Sci. Numer. Simul. 24, 467–487 (2021).
Newman, K. B. & Lindley, S. T. Accounting for demographic and environmental stochasticity, observation error, and parameter uncertainty in fish population dynamics models. N. Am. J. Fish. Manag. 26(3), 685–701 (2006).
Virtala, M., Kuikka, S. & Arjas, E. Stochastic virtual population analysis. ICES J. Mar. Sci. 55(5), 892–904 (1998).
Harris, S. D., McAllister, E., Knipe, R. J. & Odling, N. E. Predicting the three-dimensional population characteristics of fault zones: A study using stochastic models. J. Struct. Geol. 25(8), 1281–1299 (2003).
Yoshioka, H., Yaegashi, Y., Yoshioka, Y. & Tsugihashi, K. Non-renewable fishery resource management under incomplete information. In Progress in Industrial Mathematics at ECMI 2018 445–451. (Springer, 2019).
Gudmundsson, O., Davies, J. H. & Clayton, R. W. Stochastic analysis of global traveltime data: Mantle heterogeneity and random errors in the ISC data. Geophys. J. Int. 102(1), 25–43 (1990).
Sullivan, P. P., McWilliams, J. C. & Melville, W. K. The oceanic boundary layer driven by wave breaking with stochastic variability. Part 1. Direct numerical simulations. J. Fluid Mech. 507, 143–174 (2004).
Lewy, P. & Nielsen, A. Modelling stochastic fish stock dynamics using Markov Chain Monte Carlo. ICES J. Mar. Sci. 60(4), 743–752 (2003).
Schnute, J. T. & Richards, L. J. The influence of error on population estimates from catch-age models. Can. J. Fish. Aquat. Sci. 52(10), 2063–2077 (1995).
de Castro Santana, R., Sato, A. C. K. & Da Cunha, R. L. Emulsions stabilized by heat-treated collagen fibers. Food Hydrocoll. 26(1), 73–81 (2012).
Nøstbakken, L. Stochastic modelling of the North Sea herring fishery under alternative management regimes. Mar. Resour. Econ. 23(1), 65–86 (2008).
Reed, W. J. Optimal escapement levels in stochastic and deterministic harvesting models. J. Environ. Econ. Manag. 6(4), 350–363 (1979).
Yasin, M. W. et al. Reliable numerical analysis for stochastic reaction–diffusion system. Phys. Scr. 98(1), 015209 (2022).
McFadden, D. L. Revealed stochastic preference: A synthesis. In Rationality and Equilibrium: A Symposium in Honor of Marcel K. Richter 1–20. (Springer, 2006).
Román-Román, P. & Torres-Ruiz, F. A stochastic model related to the Richards-type growth curve. Estimation by means of simulated annealing and variable neighborhood search. Appl. Math. Comput. 266, 579–598 (2015).
Harris, C. M. On the optimal control of behaviour: A stochastic perspective. J. Neurosci. Methods 83(1), 73–88 (1998).
Chase, J. M. Drought mediates the importance of stochastic community assembly. Proc. Natl. Acad. Sci. 104(44), 17430–17434 (2007).
Gredler, M. E. Games and simulations and their relationships to learning. In Handbook of Research on Educational Communications and Technology 571–581. (Routledge, 2013).
Kac, M. A stochastic model related to the telegrapher’s equation. Rocky Mt. J. Math. 4(3), 497–509 (1974).
Schuss, Z. Theory and Applications of Stochastic Processes: An Analytical Approach Vol. 170 (Springer, 2009).
Chessari, J., Kawai, R., Shinozaki, Y. & Yamada, T. Numerical methods for backward stochastic differential equations: A survey. Probab. Surv. 20, 486–567 (2023).
Zheng, Z., Valdebenito, M., Beer, M. & Nackenhorst, U. A stochastic finite element scheme for solving partial differential equations defined on random domains. Comput. Methods Appl. Mech. Eng. 405, 115860 (2023).
Röckner, M., Shang, S., & Zhang, T. Well-posedness of stochastic partial differential equations with fully local monotone coefficients. Mathematische Annalen 1–51 (2024).
Gyöngy, I. & Martînez, T. On numerical solution of stochastic partial differential equations of elliptic type. Stoch. Int. J. Probab. Stoch. Process. 78(4), 213–231 (2006).
Shi, L. et al. The novel cubic B-spline method for fractional Painlevé and Bagley–Trovik equations in the Caputo, Caputo–Fabrizio, and conformable fractional sense. Alex. Eng. J. 65, 413–426 (2022).
Arqub, O. A., Osman, M. S., Abdel-Aty, A. H., Mohamed, A. B. A. & Momani, S. A numerical algorithm for the solutions of ABC singular Lane–Emden type models arising in astrophysics using reproducing kernel discretization method. Mathematics 8(6), 923 (2020).
Sweilam, N. H., ElSakout, D. M. & Muttardi, M. M. Numerical solution for stochastic extended Fisher–Kolmogorov equation. Chaos Solitons Fractals 151, 111213 (2021).
Iqbal, M. S. et al. Numerical simulations of nonlinear stochastic Newell–Whitehead–Segel equation and its measurable properties. J. Comput. Appl. Math. 418, 114618 (2023).
Sambath, M. & Balachandran, K. Laplace Adomian decomposition method for solving a fish farm model. Nonauton. Dyn. Syst. 3(1), 104–111 (2016).
Gazi, N. H., Khan, S. R. & Chakrabarti, C. G. Integration of mussel in fish farm: Mathematical model and analysis. Nonlinear Anal. Hybrid Syst 3(1), 74–86 (2009).
Acknowledgements
This research is funded by Researchers Supporting Project Number (RSPD2024R733), King Saud University, Riyadh, Saudi Arabia.
Author information
Authors and Affiliations
Contributions
All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yasin, M.W., Ahmed, N., Saeed, J. et al. Numerical study of diffusive fish farm system under time noise. Sci Rep 14, 14711 (2024). https://doi.org/10.1038/s41598-024-62304-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-62304-8