A gene selection algorithm for microarray cancer classification using an improved particle swarm optimization

The rapid growth of microarray knowledge in the previous decade has allowed researchers to analyze many genes instantaneously and find biological data for several determinations, particularly cancer classification. Microarray is used in clinics and research laboratories to understand the molecular procedures and effective treatment of many diseases. Cancer-related microarray genes have been determined through a gene selection algorithm, which is very useful in the biological cancer system. Several different microarray genes contain information about many disease samples. The number of genes has redundant data in other microarray data, so the current methods are not accurate for prediction¹. In microarray datasets, the matrix is a challenging problem. Gene expression plays a vibrant role in this regard. Many computational methods are unsuccessful in recognizing a small subset of significant genes in microarray data, which eventually raises the challenge of microarray analysis. Apart from the proposed approach, alternatively, there is another solution that unifies multiple models into a uniform model for the evolution of cellular functionality phenomena².

An improved whale optimization method is proposed, incorporating a pooling mechanism and three efficient search strategies: migrating, preferential selection, and enriched encircling prey. An evaluation is conducted to assess the performance of enhanced whale optimization algorithm (E-WOA), which demonstrates that E-WOA surpasses the versions of WOA. Following the successful performance of E-WOA, a binary version called BE-WOA was developed to specifically identify effective features, notably in medical datasets. The validation of the binary whale optimization algorithm (BE-WOA) algorithm involves the use of medical ailments datasets and a comparison with the most advanced optimization algorithms. The evaluation is based on criteria such as fitness, accuracy, sensitivity, precision, and the number of features.³. Another optimization algorithm, the quantum-based avian navigation optimizer algorithm (QANA) proposes a self-adaptive quantum orientation and quantum-based navigation with mutation strategies. It proposes a fast communication topology to share the information flow through the flocks. Also, the introduced long-term and short-term memories provide meaningful knowledge for partial landscape analysis, and the qubit-crossover operator produces the next generation. The experimental results prove that QANA is effective and scalable on test functions and real-world applications such as applied engineering problems⁴.

Different gene selection methods are categorized as filter, wrapper and embedded methods⁵. The filter methods exploit a gene's general properties and estimate every gene without the classification algorithm. But in the wrapper method, a pool of genes is created, and with the help of classification algorithms, we can attain the accurate gene pool sunset for solving the classification problems. Embedded methods achieved the properties of wrapper and filter methods. However many embedded methods plan with genes one by one, which takes a long time for microarray data⁶. Evolutionary methods are more appropriate and refined than wrapper gene selection because of their capability to refine solutions on complex spaces of potential solutions. These days, a lot of approaches use hybrid techniques such as genetic algorithm (GA)⁷, PSO^8,9 have been used progressively and proved to be good for microarray datasets^{10,11,12,13,14,15,16}. A binary PSO hybrid with a filter method is used to attain accurate gene subsets¹⁷. Genetic algorithm techniques have been used to improve the classification accuracy^13,14. The hybrid method of genetic algorithm (GA) and k- nearest neighbors (KNN) identifies the different classes of genes¹⁵. The deep learning method microarray optimized gene selection method for cancer classification has been introduced in¹⁶. Swarm intelligence algorithms in gene selection profiles based on the classification of microarray data were introduced¹⁷. In¹⁸, authors propose the Hybrid leader selection strategy for many objective particle swarm optimization to encounter the Mult objective problem effectively.

In terms of identifying both breast cancer subtypes and other cancer types, the IMS and FES employing the core gene set outperformed the other techniques. Additionally, the IMS may be repeated even with different gene expression data (i.e. RNA-seq and microarray)¹⁹. The study, conceptual discussion, and demonstration of the algorithmic behaviors—including convergence trends, mutation and crossover rate variations, and running time—showed that they were consistent with the results of the literature²⁰. Microarrays are motionless and one of the major methods employed to study cancer biology²¹. The effectiveness of minimum redundancy maximum relevance with imperialist competition algorithm (mRMR-ICA) is evaluated using ten benchmark microarray gene expression datasets. Comparing mRMR-ICA to the original ICA and other evolutionary algorithms, experimental results show an improvement in the precision of cancer classification and the number of useful genes²². The gene set that deep gene selection (DGS) chose has demonstrated greater effectiveness in the categorization of cancer. The number of genes in the original microarray datasets can be significantly decreased using DGS²³. Recognizing vigorous prognostic biomarkers to stratify colorectal cancer (CRC) has been proposed in²⁴. In DNA microarray technology, gene expression data have a high dimension with a small sample size. Consequently, the growth of well-organized and healthy feature selection approaches is crucial that classify a minor set of genes to attain better classification performance²⁵. An advanced bio-inspired multi-objective procedure is suggested for gene selection in microarray data classification specifically in the binary ___domain of feature selection²⁶.

This manuscript proposes a gene selection method based on a new variant of PSO. Microarray facilitates researchers to measure the expression levels of several genes concurrently. For the classification of microarray data gene selection provides a vital role. Microarray facilitates to determination of the expression ranks of numerous genes concurrently. The selection of a prognostic gene with a small redundancy is a great challenge for the researcher. A PSO-based gene selection technique has limitations which is why a new method of PSO is proposed in this manuscript. In the proposed algorithm, self-inertia weight adaptive particle swarm optimization with extreme learning machine (SIW-APSO-ELM) is utilized to achieve gene selection prediction accuracies. The extreme learning machine (ELM) had prearranged for selection procedure. The proposed method with the few discriminative genes as selected by the algorithm, attains high forecast accuracy on microarray datasets and shows the usefulness of the proposed method. The primary contribution of the aforementioned method is to achieve an appropriate balance between the exploration capabilities of the increased inertia weight adaptive particle swarm optimization and the exploitation. The SIW-APSO algorithm is employed for solution exploration. The SIW-APSO conducts an evolutionary process where each particle iteratively enhances its velocities and positions. The extreme learning machine (ELM) has been designed for the selection procedure. The proposed method has been used to identify several genes in the cancer dataset. The classification algorithm contains ELM, K- centroid nearest neighbor (KCNN), and support vector machine (SVM) to attain the high forecast accuracy as compared to the start-of-the-art methods on microarray cancer datasets.

The article's arrangement is as follows: Related work has been presented in section "Related work", which contains a study of ELM, SVM, and KCNN. Section "Proposed method" provides a methodology, which describes the development of the proposed improved PSO. Section "Experimental results and discussion" introduces the experimental work and the results and discussion, which includes comparative analysis studies. Section "Conclusions" concludes the article by providing its findings.

Extreme learning machine

The gradient-based learning algorithms have faced different problems. For hidden feedforward neural network’s extreme learning algorithm has been used¹⁹. This algorithm selects the input weights arbitrarily; the hidden layer logically controls the output weights of SLFN. This algorithm significantly improved the enactment of a faster learning speed than gradient-based algorithms^20,21. ELM has minor training bugs and minimal weights. The almost negligible weight in ELM shows the best performance. The parameters of SLFN are not tuned to obtain the analytical method. ELM converges very fast as compared to gradient-based algorithms.

Linear support vector machine

Support vector machine (SVM) is a machine learning algorithm²². The hypersphere around the part of feeding data is calculating the class problem which is handled by one class SVM. Inside the hypersphere are known as specific data points, and outside the hypersphere are called anomalous data points. For the one class SVM, \(\gamma\) and \(\nu\) are the hyper-parameters, wherever \(\gamma\) =\(\frac{1}{2\upsigma ^2}\) is used for the variance of the input. For the input data, variance is calculated for \(\gamma\). A lower \(\gamma\) value maps input data points near to each other. A higher \(\nu\) value accepts many outliers, whereas a low value shows data points outside the hyperspace. One class SVM provides the best result and the linear kernel achieves high accuracies^23,24.

K-nearest centroid neighbor (KNCN) Classifier

KNCN is a very popular classifier²⁵. It has been observed that this classifier is a valuable approach in the finite sample size. Let \(TS =\){\({\text{p}}_{\text{i}}\in {\mathbb{R}}^{\text{d}}{\}}_{\text{i}=1}^{\text{N}}\) be a training sample and \({c}_{i}\)∈ {\({\text{c}}_{1}\), \({\text{c}}_{2}\), . . . ,\({\text{c}}_{\text{M}}\)} means the class label for \({\text{p}}_{\text{i}}\) with M number of classes. The centroid of an assumed set of points \(Z = (z1 ,z2 , \dots zq)\) can be calculated as:

For a known query sample x, its unidentified class c can be projected by KNCN using the steps below:

1. 1.

   With the help of nearest centroid neighbor (NCN) search the nearest neighbor of X from Ts.

   $${TR}_{k}^{NCN}\left(x\right)= \{{p}_{ij}^{NCN}\in {\mathbb{R}}^{\text{d}}{\}}_{j=1}^{k}$$

   (2)
2. 2.

   Assign x to the class c, which the centroid neighbors in the set most frequently represent \({TR}_{k}^{NCN}\)(x).

   $$arg\underset{{c}_{j}}{\text{max}}\sum_{{p}_{ij}^{NCN}\in {TR}_{k}^{NCN}\left(x\right)}\delta ({c}_{j c =}{c}_{n}^{NCN})$$

   (3)

   where \({c}_{n}^{NCN}\) is the centroid neighbor \({p}_{in}^{NCN}\), and \(\delta \left(cj= {c}_{n}^{NCN}\right).\)

Hybrid gene selection algorithm

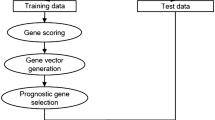
Gene selection is typically a two-step procedure. One must recognize related genes and be alike to choose the minor subsets from the related genes. SIWAPSO-ELM has been used to simplify the gene selection procedure. It has been used to select the smallest gene subset pool from the primary gene pool. An improved inertia weight PSO for the updating global combined with extreme learning has been proposed for the best selection of dense gene subsets from the accurate gene pool. The steps in the proposed method are shown in Fig. 1.

The framework of the proposed hybrid gene selection method.

Full size image

In the first step, the gene, and the dataset are separated into training and testing sets. Furthermore, in the first phase 150 to 300 genes were selected from the total dataset. Create a second-level initial gene pool. After training and testing 5–5-fold cross-validation is applied to each gene subset. After that, every gene subset perdition is determined with the help of fivefold cross-validation and with the help of ELM on the training sets classification accuracy obtained. An improved inertia weight PSO has been used to select the optimal gene after the validation pool. The \(ith\) particle \(Xi = (xi1, xi2, . . . , xiD)\)

Signifies an applicant gene subset. The measurement of the particles corresponds to the number of certain genes selected from the original gene pool. The Extreme Learning Machine (ELM) achieves higher accuracy when trained on specific gene subsets indicated by the \(ith\) particle. The proposed SIWAPSO is very accurate as compared to the traditional PSO.

It is far more effective for updating the best swarm position. The proposed method is also beneficial to decrease premature convergence of the swarm; SIW-APSO is implemented as an optimizer to revise the optimal ___location of the swarm. In the \((i+1)th\) generation, the velocity and position of the swarm, \(Pg\), are updated by Eqs. (6 and 7).

Fitness function

The value of X is assessed by a fitness function f. Fitness is determined by the genetic aptitude acquired within this subset. The fitness value is computed in the following manner:

wherever \({{\varvec{w}}}_{1}\) is a weight coefficient \([0,\boldsymbol{ }1]\) which handles the combination of both intentions, the number of genes the number of selected genes in X, and p the dimension of the vector X. The additional period promises the detail of favoring subsets with less number of genes. The goal is to exploit the function f. As the main objective is to find a subset of genes with maximum accuracy, we choose \({{\varvec{w}}}_{1}\) = 0.95. Where accuracy is calculated as follows:

An improved inertia weight PSO for the updating global combined with extreme learning has been proposed for best selecting compact gene subsets from the refined gene pool. The pseudocode of a proposed method is as follows:

• Step 1: In the first step, training and testing have been performed on the datasets.

  And from the total datasets, 150 to 300 genes were selected for testing and validation.

• Step 2: Determine the pbest Pb and gbest Pg.

• Step 3: Find the fitness function of every particle.

• Step 4: with the help of the fitness function, adjust the best Pb and gbest Pg.

• Step 5: Update the position of all particles accordingly.

• Step 6: Evaluate the fitness function and calculate accuracy with classifiers.

• Step 7: The process is recurrent till the aim is encountered or the maximum optimization is achieved, or else, go to Step 3.

Self-inertia weight adaptive particle swarm optimization (SIW-APSO)

Since the evaluation of particle swarm optimization (PSO) numerous researchers tried to explore the solution for the precise value of inertia weights. A self-adaptive inertia weight PSO is proposed for the optimization of the exploration and exploitation of the particles. SIW helps to improve the premature convergence in PSO. The proposed method is able to improve the premature convergence of the PSO. It is vital to find the position of the particle in the population for all set of given epochs. When using this approach, it is critical to determine the particle’s position in the population for all iterations. SIW-APSO initializes the random particles in the multidimensional search. A predetermine fitness function helps to evaluate the relative fitness function and for each iteration every particle in a randomized swarm indicated a point in feature space. However, SIW managed to attain the best solution. The Eqs. (4 and 5) determine the updates of velocity and position for each particle that moves around the dimensional search space. The Eqs. (6 and 7) provide the information about the iterative adaptive inertia weight as a function of iteration number, for each iteration the inertia weights update itself accordance to the improvement in the best fitness.

SIW-APSO improves the precocious convergence issue of PSO. The self-inertia weight is an adapted iteration of the PSO method. In this method, a random swarm of particles initializes. Every particle corresponds to a certain ___location inside the search space. A fitness function is derived from the pre-evaluated process, which greatly aids in achieving the desired optimal solution. The particles navigate inside a multidimensional solution space as a collective.

where \({Z}_{i}^{d}\) is the position of particle i,\({W}_{i}^{t+1}\) is the inertia weight of i^th at the iteration (t + 1)th, \({k}_{1}\)&\({k}_{2}\) are the constants, \({r}_{1}\)&\({r}_{2}\) the random functions and \("{p}_{b}^{d}\)” is the d^th best position particle i,\({p}_{g}^{d}\) is the d^th global best position founded by the whole swarm⁸?

According to the Eq. (6), The repetitive nature of inertia weight is highly beneficial for determining actual fitness.

where \({W}_{i}^{t+1}\) and \(f\left({Z}_{i}^{t}\right)\) represent the inertia weight and best fitness value at the t^th and t + 1^thiteration, respectively.

\(\frac{{(\beta f \left( {Z_{i}^{t + 1} } \right) {-} (\beta f \left( {Z_{i}^{t} } \right)}}{{(\beta f \left( {Z_{i}^{t + 1} } \right)}}\) Illustrate the improvement in the optimal fitness function that relies on the suggested inertia weight. The Eq. (6) shows the \(f ({Z}_{i}^{t}\)) and \(f{(Z}_{i}^{t-1}The)\), fitness function of the swarms at the t^th and t − 1^th repetitions, correspondingly. If \({W}_{i}^{t+1}\) = \({W}_{i}^{t}\), the particle is unable to find an optimal solution due to its limitations as \(f{(Z}_{i}^{t-1})\) = \(f\left({Z}_{i}^{t}\right)\) and there is no change in inertia weight. In the case of \(t>0\), as we can use in the above Eq. (6), then The variability in inertia weight is advantageous, leading to an improvement in fitness. The fitness function improves when the most optimal position is close to the other particles in the swarm.\({W}_{i}^{t}\) Will grow to \({W}_{i}^{t+1}\) at t − 1^th loop, it is advantageous for both exploration and exploitation. When \({W}_{i}^{t+1 }=0.9\) as described in Eq. (6) The inertia weight remains constant and functions similarly to a typical Particle Swarm Optimization (PSO). The oscillations exhibited a decline as the iterations progressed, an outcome of permissible modifications in the intended solution. SIW-APSO is capable of effectively augmenting the precision of PSO. The study reveals that the inertia weight becomes zero at certain phases and remains constant for multiple consecutive iterations, indicating that the swarm becomes stuck and unable to escape a local optimum. To adjust the range of inertia weight a linear function is used:

According to Eq. (6) The inertia weight for each swarm is modified autonomously at every iteration, utilizing the improvement in its own best fitness.²⁵. An indication of a change in fitness is present. When the individual fitness of a particle improves at any iteration. A particle undergoes a direction change; otherwise, its moment of inertia remains constant at zero. The particle begins its search locally and continues its global exploration until it acquires additional inertia and an improvement in inertia. According to the mentioned method, balancing global and local research improves diversity.

Datasets

In this manuscript, eight microarray datasets are utilized for various types of cancer: Leukemia, Brain Cancer, Colon Cancer, SRBCT (Small Round Blue Cell Tumors), Lung Cancer, brain cancer, Lymphoma, 11_Tumors, and Diffuse large B cell lymphoma (DLBCL). These datasets are publicly available and were sourced from the GEMS system (http://www.gems-system.org). which are listed in Table 2. The comprehensive explanation of the datasets is recorded in Table 2. Table 1 has defined the parameter settings. The selection of these datasets includes a diverse range of cancers, which helps in demonstrating the generalizability and robustness of the gene selection technique across different types of cancer. Each of these cancers has distinct gene expression profiles, making them ideal for evaluating the effectiveness of gene selection methods in identifying relevant biomarkers. fivefold cross-validation is used in this manuscript which is a good compromise between the bias and variance of the model. It helps in ensuring that the results are not overly optimistic (low variance) while still providing a sufficient number of training samples to maintain generalizability (low bias). Compared to leave-one-out cross-validation or higher k-fold values, fivefold cross-validation is computationally less intensive, making it suitable for large microarray datasets. fivefold cross-validation is a widely accepted method in bioinformatics and machine learning literature, providing a balance between reliability and computational demand.

The parameter tuning process for SIW-APSO involves setting and optimizing the values of key parameters to achieve optimal performance of the algorithm. Here is a detailed discussion of the parameter tuning process, how the parameters were optimized, and their impact on the performance of SIW-APSO which is shown and highlighted blue in Table 1. A swarm size of 30 is a common choice, balancing diversity and computational efficiency. For iteration, setting it to 100 aims to balance solution quality and computational time. C1 and C2 values are typically set to the same value (2) to balance exploration (C1) and exploitation (C2). If C1 is much larger than C2, the particles may explore too much without converging. Conversely, if C2 is much larger than C1, the particles may converge prematurely without exploring the search space adequately. An inertia weight of 0.9 favors exploration in the initial stages of the optimization process. Properly tuned velocity limits Vmax is 4 and Vmin is − 4 ensure that particles explore the search space effectively without oscillating too much.

The experimental study has been conducted on eight microarray datasets, including SRBCT, Lung cancer, Colon cancer, brain cancer, Leukemia, and Lymphoma, shown in Table 2.

The proposed method of self-inertia weight PSO with ELM is to classify the eight Microarray datasets to verify selected gene subsets. Every experiment is made 500 times and means accuracies and standard deviation are listed in Table 3.

The prediction ability of the selected gene subsets

The predictive accuracy of certain groups of genes is confirmed using the proposed SIW-APSO-ELM method. The experiments have been conducted 500 times, Std., and the accuracy is shown in Table 3. The proposed method has obtained high accuracy for brain cancer. The proposed method obtains 100%. SIW-APSO-ELM method on the colon obtains excellent accuracies. These results indicate that the SIW-APSO-ELM can select highly valuable prognostic genes. Table 4 shows the best accuracy of the proposed method SIW-APSO-ELM > using the 5-fold validation on the eight cancer datasets.

In Table 5. KCNN classification accuracy with different parameters is given. We achieved 97% on Colon and 100% on SRBCT which shows good results in terms of parameters used. We achieved 100% accuracy on Lymphoma while it was slightly reduced in 11_Tumors which is 97% approximately.

In Table 6. SVM classifier shows the classification accuracy with different parameters. We achieved 97% on Colon and 100% on SRBCT which shows good results when we applied BPSO-GCSELM. We achieved 100% accuracy on Lymphoma while it was slightly reduced in 11_Tumors which is 99% approximately when we applied SIW-APSOELM.

In Table 7. Different datasets provided different values and it shows the accuracy, sensitivity, and specificity with different parameters. We achieved 96%, 93%, and 92% on Colon accuracy sensitivity and specificity.

In Table 8. A comparison of the proposed method with a modified version of the Moth Flame algorithm is given. It shows Lung accuracy of 94%using MMFA while 97% using the SIW-APSO-ELM approach.

In Table 9. The proposed method with selected genes on the Colon dataset is given that shows the description of each selected gene.

In Table 10. The proposed method with selected genes on the Leukemia dataset is given that shows the description of each selected gene.

In Table 11. The proposed method with selected genes on the Lymphoma dataset is given that shows the description of each selected gene.

In Table 12. The proposed method with selected genes on the SRBCT dataset is given that shows the description of each selected gene. It is linked to sample classes. Table 4 presents the experimental results with the latest gene selection methods. It demonstrates that the proposed technique has outclassed the other PSO²⁶ variants and other standard gene selection approaches such as IBPSO, SVM²⁷, IG-GA²⁸, EPSO²⁹, BPSO-GCS-ELM³⁰, mABC³¹, because SIWAPSO-ELM has been used to simplify the genes selection procedure. It has been used to select the smallest gene subset pool from the primary gene pool which has been updating global position and extreme learning for the best selection of dense gene subsets from the accurate gene pool. From Table 3, the SIW-APSO-ELM chooses a nearly similar number of genes as the former approaches on Leukemia, SRBCT, and DLBCL. At the same time, it determines the maximum number of genes in the colon, brain, and lung data, amongst others. ELM attains 100% accuracy on the Leukemia, DLBCL, and SRBCT datasets compared to other state-of-the-art methods.

From Table 3, the SIW-APSO-ELM chooses a nearly similar number of genes as the former approaches on Leukemia, SRBCT, and DLBCL. At the same time, it determines the maximum number of genes in the colon, brain, and lung data, amongst others. ELM attains 100% accuracy on the Leukemia, DLBCL, and SRBCT datasets compared to other state-of-the-art methods. Figure 2 shows the fivefold CV accuracy on the training data versus the iteration number of a proposed algorithm. With the help, we verified that it improves the premature convergence of the proposed method. The graph in Fig. 2. further shows that the tendency of improving convergence rate for the four genes Brain Cancer, Lymphoma, 11_Tumors, and Colon is greatly impacted by the training examples and it improves over time as the model is trained.

Fold CV accuracy on the training data versus the iteration number of a proposed algorithm.

Full size image

Comparison with other classification models

The proposed approach has been evaluated against several state-of-the-art models, including IBPSO³², SVM³³, IG_GA³⁴, EPSO³⁵, BPSO-GCS-ELM³⁶, mABC³⁷, and intelligent models³⁸. This judgment was founded on the classification outcome and the number of genes irrespective of data dispensation and classification methods. The assessment outcomes on eight datasets are obtained in Table 4. From Table 3, the SIW-APSO-ELM method achieves 100% accuracy on the Leukemia, DLBCL, and SRBCT data with the genes selected by the other methods. Table 8 shows that the proposed algorithm performs much better as compared to the latest algorithm because the proposed algorithm has been used to simplify the gene selection procedure³⁹. It has been used to select the smallest gene subset pool from the primary gene pool which has been updating global position and extreme learning for the best selection of dense gene subsets from the accurate gene pool.

Comparison SIW-APSO- ELM method with the KCNN and SVM

The proposed method achieved stunning performance with the other gene selection methods, such as BPSO-GCS-ELM on public microarray data. The SIW-APSO- ELM is matched with the BPSO-GCS-ELM process on the eight data employing ELM and KCNN consistent results are recorded in Tables 5 and 6. From Tables 5 and 6, KCNN and SVM were obtained with a fivefold CV Accuracy of 100% on the Leukemia and SRBCT data. The accuracy of the KCNN and SVM models is higher when using the genes identified by the SIW-APSO-ELM technique compared to the BPSO-GCS-ELM method for both colon cancer and lung cancer data. In the case of brain cancer, the SIW-APSO-ELM technique achieves more accuracy than the BPSO-GCS-ELM method for ELM. Similarly, for KCNN, the SIW-APSO-ELM method also yields higher accuracy compared to the BPSO-GCS-ELM method. The findings presented in Tables 4 and 5 demonstrate that the suggested method surpasses the BPSO-GCS-ELM method, as well as other PSO variants, in terms of performance. In the context of brain cancer, the SIW-APSO-ELM technique achieves more accuracy than the BPSO-GCS-ELM method in ELM. Similarly, in KCNN, the SIW-APSO-ELM method also outperforms the BPSO-GCS-ELM method in terms of accuracy. The BPSO-GCS-ELM technique chooses a smaller number of genes compared to the proposed method when applied to the Colon, Brain cancer, and Lung, including 11_Tumors and DLBC datasets.

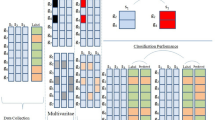
Table 7 shows the accuracy, sensitivity, and specificity of the eight datasets. From Tables 5 and 6, we can observe that the proposed method performs an outstanding performance compared to the BPSO-GCS-ELM. From Fig. 3, the classification accuracy of Leukemia, DLBCL, and SRBCT achieved 100%. Figure 4 shows the ranks of genes from five independent runs on the two data sets, DLBCL and 11-Tumor, to assess the proposed method's reproducibility.

Classification Accuracy of proposed datasets (a) leukemia, DLBCL, tumor, brain cancer (b) SRBT, lung, colon, lymphoma.

Full size image

Ranks of genes from five independent runs on the two data sets.

Full size image

Figure 3 shows the classification accuracy for different datasets of the proposed method. It shows that some of the selected genes are better converged than others. However, it also shows that these variations are due to different parameters for different datasets that can impact the convergence rate of the selected genes.

Biological analysis of the selected gene subsets

Biological experiments on different data have been conducted. The highest five often selected genes have been listed in Tables 9, 10, 11 and 12. Table 12 shows the top five frequently selected genes with the proposed method on SRBCT dataset. For classification, gene X03934 is very critical which is listed in Table 10. From Table 9, the genes H06524, H20709, T94579, T92451, and K03474 were also selected. From Table 11, the gene U66559_at is also an essential gene for anaplastic lymphoma kinase. Figure 4. Shows the ranks of selected genes by using 5 independent runs on the two different datasets.

In this research, the gene subset classification is performed using a new variant of PSO along with an extreme learning machine (ELM). The algorithm is based on the SIWAPSO variant of swarm optimization to perform gene selection. The selection of prognostic genes with a small redundancy is a great challenge as the main drawback of a PSO-based gene selection method is its complexity. Gene selection is typically a two-step procedure. In the first step, data is initialized whereas in the second step, an improved inertia weight PSO is used to select the optimal gene. In the proposed method, SIW-APSO-ELM is used to achieve the gene selection task. The proposed technique is more accurate in comparison to the traditional PSO. It updates the optimum position of the swarm. It is also an efficient technique as it decreases premature convergence of the swarm. The proposed method using the modified swarm optimization performs better than its counterparts with minimal error rates. The main algorithm contains an adaptive swarm optimization and an extreme machine learning method, which are more accurate and less complex than current state of the art methods. In the future, the ensemble learning and shallow deep learning frameworks with a few hidden layers may be employed to perform effective gene selection to reduce the processing time. The dataset may also be expanded to test the robustness of the proposed algorithm.