Introduction

WMR is widely used in the fields of logistics and transport, planetary exploration, emergency rescue, and agricultural plant protection due to its simple structure, stable motion, and height self-adaptation1,2,3,4,5.Stable and accurate trajectory tracking is the key for WMR to fulfil its mission. However, as a typical class of multiple-input multiple-output systems subject to nonholonomic constraints, WMR does not satisfy the brockett condition6,7, and thus the traditional linear system theory approach is difficult to address the WMR trajectory tracking problem8.Meanwhile the unavoidable disturbances and uncertainties in practical applications make the WMR trajectory tracking control problem extremely challenging9.

In recent years, many scholars have carried out a lot of research work on WMR trajectory tracking control, introducing nonholonomic constraints at the system kinematic level. Adaptive neural network approaches have been used to solve the problem of the difficulty of accurately obtaining the dynamic parameters of WMR systems10,11,12. Fuzzy logic is essential in handling the uncertainty and inaccuracy of WMR trajectory tracking, and the Literatures13,14 advocate the use of fuzzy control for the smooth control of WMR trajectory tracking.An adaptive sliding mode control method is used to develop a trajectory tracking controller for a mobile robot with differential driving in the presence of unknown parameter variations and external disturbances15.But it is clear that the above design of trajectory tracking controllers based purely on the kinematic model to achieve perfect tracking is impractical16. Therefore, more and more researchers are shifting their attention from the design of kinematic controllers to the integrated design of kinematic and dynamic controllers. There are two mainstream research schemes, the first is hierarchical control17,18,19,20, and the second is dual closed-loop control, which is significantly superior for nonlinear system control and is essentially a double feedback control structure21. A dual control scheme is used to solve the trajectory tracking control of WMR in the existence of external disturbances and unknown variables22,23. Literature24 combined the ideas of backstepping and sliding mode control to design a dual closed-loop control structure that improves the trajectory tracking accuracy of WMR on a right-angled road. It should be noted that most previous studies have ignored the physical limitations of the WMR itself, such as actuator saturation. In general, when the position error of the WMR is relatively large, or when it is subjected to violent disturbances, the controller will generate a large velocity in order to follow the reference trajectory as quickly and stably as possible, which will generate a sudden change in velocity and thus cause a sudden change in the torque of the driving motor. And when the actual position is close to the reference position, the change in vehicle velocity will be relatively large, causing the output torque of the drive motor to be unstable. Therefore, there is an urgent requirement to design a dual closed-loop control structure that can simultaneously consider the kinematics and dynamics of the WMR to fulfil effective handling of the WMR system constraints and perfect trajectory tracking.

Model predictive control (MPC) is an elegant approach to tackle constrained control problems and is now widely used for the control of autonomous unmanned systems, such as underwater unmanned aerial vehicles , autonomous surface vessels, autonomous unmanned aerial vehicles , and unmanned vehicles25,26,27,28. It is clear that MPC has an unrivalled innate advantage for the control of WMR, both in terms of control performance (optimality) and ability to handle constraints. Literature29 emphasises the problem of fast nonlinear MPC-based implementation of unmanned ground vehicles for tracking control in complex environments. Literature30 proposes a fuzzy MPC to improve the operational stability of WMR trajectory tracking. In31, a nonlinear distributed MPC is applied to the cooperative formation control of WMR. In32, the WMR trajectory tracking and obstacle avoidance task is solved in a single optimisation problem using a nonlinear MPC. It is worth mentioning that MPC requires the optimal control input sequence to be obtained by solving the optimal control project online in a finite time ___domain at each sampling instant and applying the first value of the sequence to the system. This implies a large amount of waste of limited computational resources, so how to reduce the computational amount of MPC has become an important research topic. A self-triggered MPC strategy is used to reduce the solving frequency of the MPC optimisation problem to some extent33. As a further research, an MPC scheme with adaptive prediction horizon and event triggering mechanism is proposed to reduce the computational burden of MPC in terms of reducing the number of solution times of the optimal control problem and lowering the prediction level34. However, it is clear that the previous studies did not consider the reduction of the complexity of the single optimisation solution, and for linear time-varying MPC, the computational complexity of the optimisation problem solution increases exponentially with the increase of the prediction horizon and the control horizon. Fortunately, the Laguerre functions allows the coefficients used in the MPC optimisation solution process to be reduced to a fraction of the coefficients required by the usual process35. Therefore, an improved MPC with Laguerre functions significantly reduces the number of optimisation variables and reduces the computational effort of MPC single optimisation solution while guaranteeing the performance of trajectory tracking for self-driving cars36. Therefore, we propose a motion controller based on the LMPC framework for the WMR outer-loop kinematic model to further design the optimised solution conditions and reduce the optimised solution frequency. A better trade-off between system control performance and computational resource saving is attained to satisfy the “fast” systems such as WMR.

It is well known that dynamic disturbances are an important part of control system design, such as the unavoidable ground friction disturbances to which WMR wheels are subjected, but unlike the nonholonomic problem, such ground friction disturbances are in the form of forces that are related to the dynamics model. Therefore, how to ensure attitude tracking accuracy under nonholonomic constraints and improve disturbances adaptivity at the same time, ESO-based dynamics controller design is not an elegant solution. As an important component of self-resilient control, ESO is often designed to estimate external and internal disturbances of nonlinear systems37. Literature38 developed a friction-compensated sliding mode control scheme for an omnidirectional mobile robot based on reduced-order ESO, designing the controller by means of a dynamics model with unknown friction; In39, a finite-time extended state observer has been investigated to improve the estimation performance, which can estimate all states and the total disturbances of the system. In particular, sliding mode control strategies are often combined with self-resilient control strategies to achieve good control performance for nonlinear systems40, as opposed to integral sliding mode control (ISMC), which avoids the shortcomings of the convergence phase of ordinary sliding mode control by solving for an appropriate initial position so that the system has only a sliding phase. Therefore, it is characterised by fast convergence, robust performance and high control accuracy41. Literature24 uses the integral sliding mode technique to design the dynamics controller and two ESOs to estimate the external disturbance. It should be emphasised that in most of the literature, the effectiveness of ESO is mostly based on third or higher order and its proof methods are cumbersome. It is also considered that simple control strategies can not combine tracking accuracy with immunity, while complex controllers consume too much energy42. Therefore, in the inner-loop, we try to propose a new second-order nonlinear ESO convergence theory, based on which we develop the force controller under the ISMC strategy, introducing an adaptive law to dynamically adjust the upper bound of the switching gain, thereby reducing the controller jitter and enabling it to accurately track the desired velocity.

Inspired by the above studies, this paper devises a dual closed-loop control structure to implement the trajectory tracking control of a nonholonomic WMR, where the outer-loop motion controller is used to internally produce the desired velocity, and the inner-loop force controller accurately tracks the desired velocity and produces the actual WMR driving torques, and the ESO performs the dynamic disturbances observation and feedback compensation. The main contributions of this paper can be summarised as follows:

  1. 1.

    A novel dual closed-loop control structure is developed for coordinated trajectory tracking control of motion/force subject to incomplete constraints WMR.

  2. 2.

    The introduction of the Laguerre functions to optimise the MPC for the outer- loop motion controller reduces the computational load of each step of the optimisation solution .The solution conditions of the optimisation problem are also specified in order to reduce the number of optimisation problem solutions.

  3. 3.

    A force controller based on second-order nonlinear ESO with AISMC strategy is designed to achieve perfect tracking of the desired velocity of the outer-loop and external integrated disturbances estimation.

The rest of the components of this paper are as follows. In “Preliminaries”, the kinematic and dynamic model of the WMR with the centre of mass coinciding with the geometric centre is developed and the dual closed-loop control structure designed in this paper is given. In “Motion controller”, the design of the outer-loop kinematic controller is carried out. In “Force controller” , the design of the ESO is given together with the design of the inner-loop force controller and the Lyapunov stability proofs are given. In “Experimental validation and discussion”, numerical simulations and practical experiments are performed. And in “Conclusion”, drawing conclusions and looking ahead to the future of research.

Preliminaries

Mathematical description of the WMR model

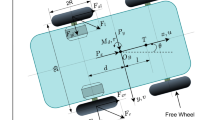
A typical WMR consists of two differential driving wheels and one driven omnidirectional wheel. In this paper, we consider the WMR with the centre of mass coinciding with the geometric centre as shown in Fig. 1.The vehicle coordinate system is denoted by \(\{ {\bar{x}},o,{\bar{y}}\}\),while the Cartesian coordinate system is denoted by \(\{ X,O,Y\}\).The centre of mass of the WMR and the midpoint of the line connecting the two driving wheels of the WMR are defined by o. The radius of the driving wheels and half the distance between the two driving wheels are defined by r and R, respectively, and \(\vartheta\) is the robot heading angle.

Figure 1
figure 1

Schematic diagram of WMR.

Full size image

Mark (x, y) as the coordinates of the centre of mass in the Cartesian coordinate system. Assuming that the wheeled mobile robot does not slip laterally, i.e. it can not move in the direction of the driving wheel axis, the robot’s velocity along the direction of the driving wheel axis is zero, and it satisfies the nonholonomic constraints of pure rolling and no sliding as follows:

$$\begin{aligned}{} & {} \dot{x}\sin \vartheta - \dot{y}\cos \vartheta = 0 \end{aligned}$$
(1)
$$\begin{aligned}{} & {} M(q)\ddot{q} + C(q,\dot{q})\dot{q} + F(\dot{q}) + G(q) + {\tau _d}= B(q)\tau - {A^{\textrm{T}}}(q)\lambda \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \dot{q} =\Psi (q,\eta ) = S(q)\eta \end{aligned}$$
(3)

where \(q = {(x,y,\vartheta )^{\textrm{T}}} \in {\Re ^{3 \times 1}}\) is the position vector of the WMR under \(\{ X,O,Y\}\) , \(\eta = {({v_a},{\omega _a})^{\textrm{T}}} \in {\Re ^{2 \times 1}}\) is the actual velocity vector \({v_a}\) is the actual linear velocity and \({\omega _a}\) is the actual angular velocity. \(\tau = {({\tau _l},{\tau _r})^{\textrm{T}}} \in {\Re ^{2 \times 1}}\) is the control torque vector , \({\tau _l}\) and \({\tau _r}\) are the control torques applied to the left and right wheels respectively. \(\lambda\) is the constraint force vector, and \({\tau _d}\) is the uncertain disturbance; \(M(q) \in {\Re ^{3 \times 3}}\) is the system inertia matrix, \(C(q,\dot{q}) \in {\Re ^{3 \times 3}}\) is the centripetal Coriolis matrix relating position and velocity, \(F(\dot{q})\) is the friction term, G(q) is the gravity vector, \(B(q) \in {\Re ^{3 \times 2}}\) is the input transformation matrix, \({A^{\textrm{T}}}(q)\) is the nonholonomic constraint matrix, and \(S(q) \in {\Re ^{3 \times 2}}\) is the Jacobi matrix that transforms the velocity of the WMR vehicle body coordinate system to the velocity of the Cartesian coordinate system. The above matrices take the following form: \(M(q) = \left[ {\begin{array}{*{20}{c}} m&{}0&{}0\\ 0&{}m&{}0\\ 0&{}0&{}J \end{array}} \right] ,C(q,\dot{q}) = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}} \right]\), \(B(q) = \frac{1}{r}\left[ {\begin{array}{*{20}{c}} {\cos \vartheta }&{}{\cos \vartheta }\\ {\sin \vartheta }&{}{\sin \vartheta }\\ R&{}{ - R} \end{array}} \right] ,{A^{\textrm{T}}}(q) = \left[ {\begin{array}{*{20}{c}} { - \sin \vartheta }\\ {\cos \vartheta }\\ 0 \end{array}} \right]\), \(S(q) = \left[ {\begin{array}{*{20}{c}} {\cos \vartheta }&{}0\\ {\sin \vartheta }&{}0\\ 0&{}1 \end{array}} \right]\). where m and J denote the mass and rotational inertia of the WMR, respectively. Derivation of Eq. (3) yields:

$$\begin{aligned} \ddot{q} = \dot{S}(q)\eta + S(q){{\dot{\eta }}} \end{aligned}$$
(4)

Bringing Eqs. (4) and (3) into the kinetic model (2), and at the same time for the elimination of the incomplete constraint term \({A^{\textrm{T}}}(q)\lambda\) , a simultaneous left-multiplication of \({S^{\textrm{T}}}(q)\) on both sides of the equation yields:

$$\begin{aligned} \begin{array}{l} {S^{\textrm{T}}}(q)M(q)\dot{S}(q)\eta + {S^{\textrm{T}}}(q)M(q)S(q){\dot{\eta }} + {S^{\textrm{T}}}(q)G(q) + {S^{\textrm{T}}}(q)({\tau _d} + F(\dot{q})) = {S^{\textrm{T}}}(q)B(q)\tau - {S^{\textrm{T}}}(q){A^{\textrm{T}}}(q)\lambda \end{array} \end{aligned}$$
(5)

For the plane-moving WMR, its gravitational potential energy remains unchanged, resulting in \(G(q) = 0\) . Additionally, there are \({S^{\textrm{T}}}(q)M(q)\dot{S}(q) = 0\) and \({S^{\textrm{T}}}(q){A^{\textrm{T}}}(q) = 0\) . This allows for a simplified dynamical model of the system to be obtained:

$$\begin{aligned} {\bar{M}}(q){\dot{\eta }} + {{\bar{\tau }} _d} = {\bar{B}}(q)\tau \end{aligned}$$
(6)

where \({\bar{M}}(q) = {S^{\textrm{T}}}(q)M(q)S(q)\) , \({\bar{B}}(q) = {S^{\textrm{T}}}(q)B(q)\), and \({{\bar{\tau }} _d} = {S^{\textrm{T}}}(q)({\tau _d} + F(\dot{q}))\), specifically, \({\bar{M}}(q) = \left[ {\begin{array}{*{20}{c}} m&{}0\\ 0&{}J \end{array}} \right] ,{\bar{B}}(q) = \frac{1}{r}\left[ {\begin{array}{*{20}{c}} 1&{}1\\ b&{}{ - b} \end{array}} \right]\) Equation (6) can be written as:

$$\begin{aligned} {\dot{\eta }} = {{\bar{M}}^{ - 1}}(q){\bar{B}}(q)\tau - {{\bar{M}}^{ - 1}}(q){{\bar{\tau }} _d} \end{aligned}$$
(7)

where \({{\bar{\tau }} _d} = {\left[ {\begin{array}{*{20}{c}} {{{\bar{\tau }}_{d1}}}&{{{{\bar{\tau }} }_{d2}}} \end{array}} \right] ^{\textrm{T}}}\).

Dual closed-loop control structure

To achieve coordinated trajectory tracking control of nonholonomic constrained WMR motion/force objective, this paper proposes a dual closed-loop control structure as shown in Fig. 2. This structure is essentially a dual-loop feedback control structure. The motion controller in the outer-loop generates the desired linear and angular velocities using an MPC strategy. In the inner-loop, an integral sliding mode strategy is used to design the force controller, while an ESO estimates the force from perturbations acting on the wheels and feeds forward the disturbance estimates for compensation. To enhance the timeliness of MPC calculation, the Laguerre functions are used to approximate the reconstruction of the MPC algorithm. This converts the optimised multiple control inputs into the optimised few Laguerre coefficients while designing the optimisation problem solving conditions. Additionally, the self-adaptive law is introduced to dynamically adjust the sliding mode switching gain. This reduces system jitter and ensures that the mobile robot can track the desired trajectory stably and reliably.

It is noteworthy that the desired velocity vector generated by the outer-loop is exactly the trajectory required by the inner-loop, and it is this desired velocity vector that establishes the link between the kinematics of the system and the dynamical system.

Figure 2
figure 2

Dual closed-loop control structure.

Full size image

Motion controller

MPC is a closed-loop optimal control strategy based on a model. It applies the idea of rolling computation in a finite horizon and uses feedback and prediction corrections. The optimal computation of a certain system performance indicator is used to determine the optimal control sequence in a control horizon. In order to ensure that the system has better dynamic performance, which often requires a longer control horizon, this paper applies the Laguerre functions, which are widely used in the field of system identification, to the design of model predictive controllers, which are able to use fewer parameters instead of the length of the control horizon in the original design, thus effectively reducing the amount of computation while ensuring the dynamic performance.

WMR tracking error model

Figure 3
figure 3

Schematic of WMR tracking error.

Full size image

The purpose of the motion controller design is to provide the WMR with the ability to generate the desired velocities, assuming that a virtual WMR exists under the Cartesian coordinate system asshown in Fig. 3, given a virtual global coordinate vector \({q_r} = {({x_r},{y_r},{\vartheta _r})^{\textrm{T}}}\), such that \({v_r}\) and \({\omega _r}\) are the virtual linear and angular velocities. Then its corresponding virtual kinematic model is

$$\begin{aligned} {\dot{q}_r} = \Psi ({q_r},{\eta _r}) = S({q_r}){\eta _r} \end{aligned}$$
(8)

where \({q_r} = {({x_r},{y_r},{\vartheta _r})^{\textrm{T}}} \in {\Re ^{3 \times 1}}\), \({\eta _r} = {({v_r},{\omega _r})^{\textrm{T}}} \in {\Re ^{2 \times 1}}\).

Assumption 1

The linear and angular velocities of the virtual WMR are not equal to zero simultaneously, i.e. the virtual WMR being tracked is always in motion or in rotation.

Using Taylor’s formula, the kinematic model (3) is unfolded at the reference point \(({q_r},{\eta _r})\) , ignoring the effect of its higher order terms. The MWR error system can be obtained by differentiating Eq. (3) from Eq. (8):

$$\begin{aligned} \dot{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q}} = A(t)\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} + B(t)\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \eta}\label{eq9}\end{aligned}$$
(9)

Where \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} = {q_r} - q = {\left[ {{e_x},{e_y},{e_\vartheta }} \right]^{\rm T}} = \left[ {\begin{array}{*{20}{c}} {{x_r} - x}\\ {{y_r} - y}\\ {{\vartheta _r} - \vartheta }\end{array}} \right] \in {\Re ^{3 \times 2}}\), \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \eta } = {\eta _r} - \eta = \left[ {\begin{array}{*{20}{c}} {{v_r} - {v_a}}\\ {{\omega _r} - {\omega _a}}\end{array}} \right] \in {\Re ^{2 \times 1}}\), \(A(t) = \left[ {\begin{array}{*{20}{c}} 0&{}0&{}{ - {v_r}\sin {\vartheta _r}}\\ 0&{}0&{}{{v_r}\cos {\vartheta _r}}\\ 0&{}0&{}0 \end{array}} \right] \in {\Re ^{3 \times 3}}\), \(B(t) = \left[ {\begin{array}{*{20}{c}} {\cos {\vartheta _r}}&{}0\\ {\sin {\vartheta _r}}&{}0\\ 0&{}1 \end{array}} \right] \in {\Re ^{3 \times 2}}\).

Obviously, the error system (9) is controllable. In order to carry out the design of the MPC controller, the error system (9) must be discretised for the sampling time h, and the discretised prediction model is obtained as follows:

$$\begin{aligned} \dot {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q}} (k + 1) = {A_{kh}}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q } (k) + {B_{kh}}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \eta } (k)\end{aligned}$$
(10)

where \({A_{kh}} = I + hA(t) = \left[ {\begin{array}{*{20}{c}} 1&{}0&{}{ - {v_r}\sin {\vartheta _r}h}\\ 0&{}1&{}{{v_r}\sin {\vartheta _r}h}\\ 0&{}0&{}1 \end{array}} \right] \in {\Re ^{3 \times 3}}\),\({B_{kh}} = hB(t) = \left[ {\begin{array}{*{20}{c}} {\cos {\vartheta _r}h}&{}0\\ {\sin {\vartheta _r}h}&{}0\\ 0&{}h \end{array}} \right] \in {\Re ^{3 \times 2}}\).

In this paper, we assume that the matrices \({A_{kh}}\) , \({B_{kh}}\) are time-invariant matrices, i.e., there are \({A_{kh}} = {A_h}\) , \({B_{kh}} = {B_h}\) at any moment. Define the augmented state matrix \(x(k) = \left[ {\begin{array}{*{20}{c}} {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} (k)}\\ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \eta } (k - 1)}\end{array}} \right] \in {\Re ^{5 \times 1}}\), from (10), the augmented state space model can be obtained:

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} {x(k + 1) = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}_{h}}x(k) +\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B}_{h}}{\Delta {\eta }} (k)\\ {y(k) = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }_{h}}x(k)} \end{array} \right. \end{aligned}$$
(11)

Where \({\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _h} = \left[ \begin{array}{*{20}{c}} {{A_h}}&{}{{B_h}}\\ {{0_{2 \times 3}}}&{}{{I_{2 \times 2}}} \end{array} \right] \in {\Re ^{5 \times 5}}\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} _{h} = \left[ \begin{array}{*{20}{c}} {{B_h}}\\ {{I_{2 \times 2}}} \end{array} \right] \in {\Re ^{5 \times 2}}\), \({\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} _h} = \left[ \begin{array}{*{20}{c}} {{I_{3 \times 3}}}&0 \end{array} \right] \in {\Re ^{3 \times 5}}\), \({\Delta {\eta }}\) denotes the system control input increment, while

$$\Delta {\textrm{H}}(k) = \left[ \begin{array}{*{20}{l}} {{\Delta {\eta }} (k)}&{{\Delta {\eta }} (k + 1)}&\cdots&{{\Delta {\eta }} (k + {N_c} - 1)} \end{array} \right] ^{\textrm{T}}$$

is defined as the sequence of future control input increments at time k , and \({N_c}\) is the control horizon.

Laguerre functions

Figure 4
figure 4

Laguerre network.

Full size image

The discrete-time Laguerre network is shown in Fig. 4. The z-transform of the discrete-time Laguerre network is as follows:

$$\begin{aligned} {\Gamma _n}(z) = \frac{{\sqrt{1 - {\alpha ^2}} }}{{1 - \alpha {z^{ - 1}}}}{\left( {\frac{{{z^{ - 1}} - \alpha }}{{1 - \alpha {z^{ - 1}}}}} \right) ^{n - 1}} \end{aligned}$$
(12)

where \(\alpha\) is the pole of the discrete Laguerre network and \(0 \le \alpha \le 1\); nis the rank of the discrete Laguerre network; \({\Gamma _n}(z)\) is the nth Laguerre network, the Laguerre function is defined as the inverse z-transform of the Laguerre network, and the sequence of the Laguerre function can be expressed in vector form as

$$\begin{aligned} L(k) = {\left[ {\begin{array}{*{20}{c}} {{l_1}(k)}&{{l_2}(k)}&\cdots&{{l_N}(k)} \end{array}} \right] ^{\textrm{T}}} \end{aligned}$$
(13)

where N is the number of functions used by the Laguerre network and \({l_j}(k)(j = 1,2, \ldots ,N)\) is the standard orthogonal Laguerre function. The sequence of Laguerre functions satisfies the following difference equation in state space form,

$$\begin{aligned} L(k + 1) = \textrm{A}{\textrm{I}_N}L(k) \end{aligned}$$
(14)

where

$$\textrm{A}{\textrm{I}_N} = \left[ {\begin{array}{*{20}{c}} \alpha &{}0&{} \cdots &{}0\\ {{\alpha _0}}&{}\alpha &{} \cdots &{}0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{{( - 1)}^{N - 3}}{\alpha ^{N - 3}}{\alpha _0}}&{}{{{( - 1)}^{N - 3}}{\alpha ^{N - 3}}{\alpha _0}}&{} \cdots &{}\alpha \end{array}} \right]$$

\({\alpha _0} = (1 - {\alpha ^2})\), \(L(0) = \sqrt{{\alpha _0}} \left[ {\begin{array}{*{20}{c}} 1&{ - \alpha }&\cdots&{{{( - 1)}^{N - 1}}{\alpha ^{N - 1}}} \end{array}} \right] ^{\textrm{T}}\).

In particular, the Laguerre function becomes a series of impulse functions when\(\alpha = 0\).

$$\begin{aligned} L(k) = {\left[ {\begin{array}{*{20}{c}} {\delta (k)}&{\delta (k - 1)}&\cdots&{\delta (k - N + 1)} \end{array}} \right] ^{\textrm{T}}} \end{aligned}$$
(15)

    Assuming that the impulse response of the discrete stabilised system at time k is P(k) , for a given parameter N , it can be expressed as

$$\begin{aligned} P(k) = {c_1}{l_1}(k) + {c_2}{l_2}(k) + \cdots + {c_N}{l_N}(k) \end{aligned}$$
(16)

where \({c_j}(j = 1,2, \ldots ,N)\)is the Laguerre coefficient. A further significant property is the standard orthogonality of the Laguerre function.

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {\sum \limits _{k = 0}^\infty {{l_i}(k){l_j}(k) = 0,i \ne j} }\\ {\sum \limits _{k = 0}^\infty {{l_i}(k){l_j}(k) = 1,i = j} } \end{array}} \right. \end{aligned}$$
(17)

Design of the LMPC controller

Performance indicator

Consider the increment of the control input after moment a as the impulse response of the stabilised system and express it in the following form:

$$\begin{aligned} {\Delta {\eta }} (k + i)= \left[ {\begin{array}{*{20}{l}}{\delta (i)}&{\delta (i - 1)}&\cdots&{\delta (i - {N_c} + 1)}\end{array}} \right] \Delta {\textrm{H}} \end{aligned}$$
(18)

where \(\delta (i)\) denotes the impulse function, i.e., when \(i = 0\) , \(\delta (i) = 1\) , otherwise \(\delta (i) = 0\) . According to (16) and (18) can be approximated as

$$\begin{aligned} {\Delta {\eta }} (k + i) = \sum \limits _{j = 1}^N {{c_j}(i){l_j}(k) = {L^{\textrm{T}}}(k)\mu } \end{aligned}$$
(19)

where \(\mu = {\left[ {\begin{array}{*{20}{l}} {{c_1}}&{{c_2}}&\cdots&{{c_N}} \end{array}} \right] ^{\textrm{T}}}\) is a parameter vector made up of N Laguerre coefficients. Therefore, the problem of solving the optimal control increment \({\Delta {\eta }} (k + i)\) is transformed into a problem of solving the parameter vector \(\mu\) . This reduces the number of parameters to be optimised by the controller, i.e. the optimisation variables are reduced from \({N_c}\) to N dimensions. From Eqs. (11) and (19) the state and output variables of the system at time after time are as follows:

$$\begin{aligned} x(k + m|k)&= {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} ^m_h}x(k) + \varsigma _1^{\textrm{T}}(m)\mu \end{aligned}$$
(20)
$$\begin{aligned} y(k + m|k)&={\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} _h}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} ^m_h}x(k) + \varsigma _2^{\textrm{T}}(m)\mu \end{aligned}$$
(21)

where \({\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}^m_{h}}\) is the mth power of the matrix \({\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _{h}}\) . \(\varsigma _1^{\textrm{T}}(m) = \sum \limits _{i = 0}^{m -1} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _{h}^{m - (i +1)}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B} }_{h}}{L^{\textrm{T}}}(i)\), \(\varsigma _2^{\textrm{T}}(m) = \sum \limits _{i = 0}^{m - 1} {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} }_h}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _{h}^{m - (i +1)}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{B}}_{h}}{L^{\textrm{T}}}(i)\) . Thus, the performance indicator of the system is given by the following equation

$$\begin{aligned} J = \sum \limits _{m = 1}^{{N_p}} {{x^{\textrm{T}}}(k + m|k)Qx(k + m|k)} + \Delta {\textrm{H}^{\textrm{T}}}R\Delta \textrm{H} \end{aligned}$$
(22)

where Q , R are the weight matrices of the state and control inputs of the system, respectively, R is an \({N_c}\)-dimensional diagonal matrix with diagonal elements a , and a is the number of normals. If the predicted horizon \({N_p}\) takes a sufficiently large value, it is obtained by substituting the \(\Delta \textrm{H}\) sequence and Eq. (19) into Eq. (22) based on Eq. (17):

$$\begin{aligned} J = \sum \limits _{i = 1}^{{N_p}} {{x^{\textrm{T}}}(k + i|k)Qx(k + i|k)} + {\mu ^{\textrm{T}}}{R_L}\mu \end{aligned}$$
(23)

Note that \({R_L}\) in Eq. (23) is a N-dimensional diagonal matrix with diagonal elements a , but with a different number of dimensions than R in Eq. (22). If Eq. (20) is substituted into Eq. (23), we obtain

$$\begin{aligned} J = {\mu ^{\textrm{T}}}\Omega \mu + 2{\mu ^{\textrm{T}}}\Upsilon x(k) + \sum \limits _{m = 1}^{{N_p}} {{x^{\textrm{T}}}(k){{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _h^{\textrm{T}})}^m}Q{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A}^m_h}x(k)} \end{aligned}$$
(24)

where \(\Omega = \sum \limits _{m = 1}^{{N_p}} {{\varsigma _1}(m)Q\varsigma _1^{\textrm{T}}(m) + {R_L}}\), \(\Upsilon = \sum \limits _{m = 1}^{{N_p}} {{\varsigma _1}(m)Q\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} _h^m}\).

It can be seen that the third term in Eq. (24) is independent of \(\mu\) . Therefore, minimising the performance indicator J is essentially minimising the sum of the first two terms, and the performance indicator can be rewritten as

$$\begin{aligned} {\bar{J}} = {\mu ^{\textrm{T}}}\Omega \mu + 2{\mu ^{\textrm{T}}}\Upsilon x(k) \end{aligned}$$
(25)

Constrained optimal solution

To avoid the problems of sudden torque change and unstable torque output of the driving motor caused by sudden velocity change during WMR motion, it is necessary to constrain the velocity and velocity increment during the control process, i.e. the following input constraints are introduced.

$$\begin{aligned} \begin{array}{l} \Delta {\eta _{\min }} \le {\Delta {\eta }} (k + m) \le \Delta {\eta _{\max }},\\ {\eta _{\min }} \le \eta (k + m) \le {\eta _{\max }},\\ m = 0,1, \ldots ,{N_c} - 1 \end{array} \end{aligned}$$
(26)

where \({\eta _{\min }}\), \({\eta _{\max }}\) are the minimum and maximum values of the control quantity and \(\Delta {\eta _{\min }}\) , \(\Delta {\eta _{\max }}\) are the maximum and minimum values of the control increment.

Without loss of generality, it follows from Eq. (19) and \(\eta (k) = \sum \nolimits _{i = 0}^{k - 1} {{\Delta {\eta }} (i)}\) that the constraints of Eq. (26) can also be introduced into the Laguerre functions, written as

$$\begin{aligned} \begin{array}{l} \Delta {\eta _{\min }} \le {M_1}\mu \le \Delta {\eta _{\max }}\\ {\eta _{\min }} \le {M_2}\mu + \eta (k - 1) \le {\eta _{\max }} \end{array} \end{aligned}$$
(27)

where \({M_1} = \left[ {\begin{array}{*{20}{c}} {L_1^{\textrm{T}}(m)}&{}{0_2^{\textrm{T}}}&{} \cdots &{}{0_m^{\textrm{T}}}\\ {0_1^{\textrm{T}}}&{}{L_2^{\textrm{T}}(m)}&{} \cdots &{}{0_m^{\textrm{T}}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {0_1^{\textrm{T}}}&{}{0_2^{\textrm{T}}}&{} \cdots &{}{L_m^{\textrm{T}}(m)} \end{array}} \right]\), \({M_2} = \left[ {\begin{array}{*{20}{c}} {\sum \limits _{i = 0}^{k - 1} {L_1^{\textrm{T}}(i)} }&{}{0_2^{\textrm{T}}}&{} \cdots &{}{0_m^{\textrm{T}}}\\ {0_1^{\textrm{T}}}&{}{\sum \limits _{i = 0}^{k - 1} {L_2^{\textrm{T}}(i)} }&{} \cdots &{}{0_m^{\textrm{T}}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {0_1^{\textrm{T}}}&{}{0_2^{\textrm{T}}}&{} \cdots &{}{\sum \limits _{i = 0}^{k - 1} {L_m^{\textrm{T}}(i)} } \end{array}} \right]\).

Up to this point, the quadratic programming problem for the error system (9) is solved by forming the MPC at the discrete sampling time k :

$$\begin{aligned} \begin{array}{l} {\mu ^*} = \mathop {\arg \min }\limits _\mu {\mu ^{\textrm{T}}}\Omega \mu + 2{\mu ^{\textrm{T}}}\Upsilon x(k)\\ s.t.\left[ {\begin{array}{*{20}{c}} {{M_1}}\\ { - {M_1}}\\ {{M_2}}\\ { - {M_2}} \end{array}} \right] \mu \le \left[ {\begin{array}{*{20}{c}} {\Delta {\textrm{H}_{\max }}}\\ { - \Delta {\textrm{H}_{\min }}}\\ {{\textrm{H}_{\max }} - {\textrm{H}_t}}\\ { - {\textrm{H}_{\min }} + {\textrm{H}_t}} \end{array}} \right] \end{array} \end{aligned}$$
(28)

where \(\Delta {\textrm{H}_{\max }}\), \(\Delta {\textrm{H}_{\min }}\), \({\textrm{H}_{\max }}\), \(\Delta {\textrm{H}_{\min }}\) are the set of maximum and minimum values of control increments and the set of maximum and minimum values of control quantities, respectively in the control horizon; and \({\textrm{H}_t} = {1_{{N_c}}} \otimes \eta (k - 1)\) , \({1_{{N_c}}}\) are the column vectors with rows of \({N_c}\) . \(\otimes\) is the Kronecker product.

The above quadratic programming problem can be solved by existing well-established algorithms by choosing \(\Omega\) to be a positive definite symmetric matrix of \(N \times N\) . The programming is a strictly convex quadratic programming problem, and if at least one of the vectors \(\mu\) satisfies the constraints and the feasible ___domain of the performance indicator \({\bar{J}}\) is lower bounded, then the quadratic programming problem has a globally unique minimum value \({\mu ^*}\).

Following Eqs. (18) and (19), the sequence of optimal control increments can be obtained at the sample time.

$$\begin{aligned} \begin{array}{l} \Delta {\textrm{H}^*} = {\left[ {\begin{array}{*{20}{l}}{\Delta {\eta ^*}(k)}&{\Delta {\eta ^*}(k + 1)}&\cdots&{\Delta {\eta ^*}(k + {N_c} - 1)} \end{array}} \right] ^{\textrm{T}}} \end{array} \end{aligned}$$
(29)

The conventional MPC applies the first value of Eq. (29) as the actual control increment to the system, performing the following feedback correction,

$$\begin{aligned} \eta (k) = \eta (k - 1) + \Delta {\eta ^*}(k) \end{aligned}$$
(30)

Repeating the above process as the control horizon and prediction horizon roll forward clearly only reduces the complexity of a single optimal solution. To further reduce the computational complexity of the MPC, assuming the existence of an upper bound on the difference between the actual state value \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} (\ell )\) and the optimal prediction \({\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} ^*}(\ell )\) of the system after the \(\ell\)-step control, we implement an optimisation solution condition to reduce the number of optimisation solutions34.

$$\begin{aligned} \left\| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} (k + \ell ) - {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} }^*}(k + \ell |k)} \right\| \ge \kappa {e^{\varpi h(\kappa - 1)}}\end{aligned}$$
(31)

where \(\kappa \in {_{ \ge 1}}\) is an adjustable parameter, and \(\varpi = \sqrt{2(v_{\max }^2 + {R^2}\omega _{\max }^2)}\). Notice that the optimal control increment obtained at moment k is used in subsequent moments to provide feedback corrections to the system.

$$\begin{aligned} {\textrm{H}^*} = \left[ {{\eta ^*}(k),{\eta ^*}(k + 1), \cdots ,{\eta ^*}(k + \ell )} \right] \end{aligned}$$
(32)

Since we are iterating over a nominal system in the optimisation problem, it is clear that for the system, \({\eta ^*}(k)\) is the optimal control input at moment k , but for \(k + 1\) and moments thereafter, although \({\eta ^*}(k + 1), \cdots ,{\eta ^*}(k + \ell )\) may not necessarily be the optimal solution, it must have the property of being suboptimal. Therefore, if Eq. (31) is not satisfied, the control sequence obtained at the current moment is applied to the system through feedback correction, and when the condition (31) is satisfied, an optimisation solution is performed to obtain a new control sequence. After obtaining the optimal sequence of increments, a feedback correction is performed based on the rule in Eq. (30) to obtain the desired velocity vector.

$$\begin{aligned} {\eta ^*}(k) = {\left[ {{v_c}(k),{\omega _c}(k)} \right] ^{\textrm{T}}} \end{aligned}$$
(33)

where the desired velocity vector \({\eta ^*}(k)\) contains both the desired linear velocity \({v_c}(k)\) and the desired angular velocity \({\omega _c}(k)\) . The optimisation process is then repeated in the next cycle to obtain the desired velocity of the WMR online.

Note 1: The system automatically optimises the solution during the initial moments k and \(k + {N_c}\) , as there is no control volume available in either case.

Stability assessment

The paper guarantees system stability through a reasonable terminal state, as stated in the following theorem.

Theorem 1

Develop a terminal state constraint \(x(k + {N_p}) = 0\) into the rolling horizon optimisation problem, which is generated by the control sequence\({\Delta {\eta }} (k + m)m = 0,1,2, \ldots ,{N_p}\). For each sampling moment k , there exists a Laguerre coefficient \(\mu\) that satisfies the inequality constraints and the terminal equation constraints, minimizing the performance indicator \(\bar{J}\).

Proof

The Lyapunov function should be chosen as follows:

$$\begin{aligned} V\left( {x(k),k} \right) =\sum \limits _{m = 1}^{{N_p}} {x_0^{\textrm{T}}(k + m|k)Q{x_0}(k + m|k)}+\sum \limits _{m = 0}^{{N_p} - 1} {{\Delta {\eta }} _0^{\textrm{T}}(k + m)R\Delta {\eta _0}(k + m)} \end{aligned}$$
(34)

where \({x_0}(k + m|k) = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} ^m_h{x_0}}(k) + \varsigma _1^{\textrm{T}}(m){\mu _0}\), \({\mu _0}\) is the optimal solution of the performance indicator J in Eq. (23) at the moment of k when both the inequality constraints and the equation constraints are satisfied, i.e.\(\Delta {\eta _0}(k + m) = {L^{\textrm{T}}}(m){\mu _0}\) . It is evident that the V(x(k), k) function is positive definite when \(x(k) \rightarrow \infty\) and \(V(x(k),k) \rightarrow \infty\) , as shown in Eq. (34). The Lyapunov function at moment is

$$\begin{aligned} \begin{array}{l} V\left( {x(k + 1),k + 1} \right) = \sum \limits _{m = 1}^{{N_p}} {x_1^{\textrm{T}}(k + 1 + m|k + 1)Q{x_1}(k + 1 + m|k + 1)}+ \sum \limits _{m = 0}^{{N_p} - 1} {{\Delta {\eta }} _1^{\textrm{T}}(k + 1 + m)R\Delta {\eta _1}(k + 1 + m)} \end{array} \end{aligned}$$
(35)

where the state variables are \({x_1}(k + 1 + m|k + 1) = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} ^m_h}{x_1}(k) + \varsigma _1^{\textrm{T}}(m){\mu _1}\), \({\mu _1}\) is the optimal solution of J at the moment \(k + 1\) satisfying all constraints, i.e. \(\Delta {\eta _1}(k + 1 + m) = {L^{\textrm{T}}}(m){\mu _1}\) . Assuming that all constraints are met at moment k , a feasible solution of \({\mu _1}\) for the initial state \(x(k + 1)\) in the rolling horizon is \({\mu _0}\) . Therefore, the feasible control sequence corresponding to the feasible solution \({\mu _0}\) at moment \(k + 1\) is \({L^{\textrm{T}}}(1){\mu _0},{L^{\textrm{T}}}(2){\mu _0}, \cdots ,{L^{\textrm{T}}}({N_p} - 1){\mu _0},0\) . As \({\mu _1}\) is an optimal solution, there is:

$$\begin{aligned} V\left( {x(k + 1),k + 1} \right) \le {\bar{V}}\left( {x(k + 1),k + 1} \right) \end{aligned}$$
(36)

where \({\bar{V}}\left( {x(k + 1),k + 1} \right)\) is obtained by replacing the control sequence of Eq. (35) with a feasible control sequence \({L^{\textrm{T}}}(1){\mu _0},{L^{\textrm{T}}}(2){\mu _0}, \cdots ,{L^{\textrm{T}}}({N_p} - 1){\mu _0},0\) . Let

$$\Delta {V_1} = V\left( {x(k + 1),k + 1} \right) - V\left( {x(k),k} \right)$$
$$\begin{aligned} \Delta {V_2} = {\bar{V}}\left( {x(k + 1),k + 1} \right) - V\left( {x(k),k} \right) \end{aligned}$$

Then there is:

$$\begin{aligned} \Delta {V_1} \le \Delta {V_2} \end{aligned}$$
(37)

and

$$\begin{aligned} \Delta {V_2}= & {} {x^{\textrm{T}}}(k + {N_p}|k)Qx(k + {N_p}|k)-{x^{\textrm{T}}}(k + 1)Qx(k + 1) - \Delta {\eta ^{\textrm{T}}}(k)R\eta (k) \nonumber \\ ~= & {} -{x^{\textrm{T}}}(k + 1)Qx(k + 1) - \Delta {\eta ^{\textrm{T}}}(k)R\Delta \eta (k) \end{aligned}$$
(38)

Equation (36) is carried over into Eq. (37):

$$\begin{aligned} \Delta {V_1} \le - {x^{\textrm{T}}}(k + 1)Qx(k + 1) - \Delta {\eta ^{\textrm{T}}}(k)R{\Delta {\eta }} (k) < 0 \end{aligned}$$
(39)

The Lyapunov function value is decreasing, indicating that the control system is asymptotically stable.\(\square\)

Force controller

In contrast to motion controller, force controller require online tracking of the desired velocity generated by the outer-loop. When constructing the force controller, the desired velocity is fitted as a smooth curve \({\eta _c} = {\left[ {{v_c},{\omega _c}} \right] ^{\textrm{T}}}\), where \({v_c}\) and \({\omega _c}\) are the desired linear velocity and the desired angular velocity, respectively, taking into account the optimal control increment at the current time and the control sequence at the previous time. Let \(- {{\bar{M}}^{ - 1}}(q){{\bar{\tau }} _d} = {({\tau _{dv}},{\tau _{d\omega }})^{\textrm{T}}}\) denotes the external disturbances to which the WMR is subjected, while \({\tau _{dv}}\) and \({\tau _{d\omega }}\) denote the disturbances acting on \({v_a}\) and \({\omega _a}\) , respectively. The dynamical model of the WMR can be rewritten as follows:

$$\begin{aligned} {\dot{v}_a}&=\frac{1}{{mr}}({\tau _l} + {\tau _r}) + {\tau _{dv}}\end{aligned}$$
(40)
$$\begin{aligned} {{\dot{\omega }} _a}&=\frac{R}{{Jr}}({\tau _l} - {\tau _r}) + {\tau _{d\omega }} \end{aligned}$$
(41)

Assumption 2

For the kinetic models (40) and (41) it is assumed that the external disturbances \({\tau _{dv}}\) and \({\tau _{d\omega }}\) are bounded and continuous, and also that their first-order derivatives are bounded.

It can be seen that Eq. (40) has a similar form to Eq. (41), so the controller designed for it also has a similar form, therefore the linear velocity dynamics (Eq. 40) is used as an example to design the inner-loop controller.

Design of ESO

In the kinetic model (40), let \({v_a} = {\chi _1}\) ,\(\frac{1}{{mr}} = {b_0}\), \({\tau _{dv}} = {\chi _2}\), \({\bar{\tau }} = {\tau _l} + {\tau _r}\) , Eq. (40) can be rewritten as

$$\begin{aligned} \begin{aligned} {{{\dot{\chi }} }_1}&= {b_0}{\bar{\tau }} + {\chi _2}\\ {{{\dot{\chi }} }_2}&= \varepsilon \end{aligned} \end{aligned}$$
(42)

By Assumption 2, the disturbance \({\tau _{dv}}\) is bounded and continuously integrable, so \({{\dot{\chi }} _2} = \varepsilon\) exists and holds.

Let \({e_1} = {{\hat{\chi }} _1} - {\chi _1}\), \({e_2} = {{\hat{\chi }} _2} - {\chi _2}\), \({e_0} = {\left[ {\begin{array}{*{20}{c}} {{e_1}}&{{e_2}} \end{array}} \right] ^{\textrm{T}}}\) denotes the observation error, \({\hat{\chi }_1}\) and \({{\hat{\chi }} _2}\) are the observations of \({\chi _1}\) and \({\chi _2}\) , respectively, then the ESO of system (42) can be designed as follows:

$$\begin{aligned} \begin{aligned} {\dot{ \hat{\chi }}}_1&= {\dot{ \hat{\chi }}}_2 - {\beta _1}{e_1} + {b_0}{\bar{\tau }} \\ {\dot{ \hat{\chi }}}_2&= - {\beta _2}fal({e_1},{\sigma _1},{\delta _2}) \end{aligned} \end{aligned}$$
(43)

where \({\beta _1} > 0\), \({\beta _2} > 0\) are two adjustable variables. Similarly, for systems (40) and (41), the adjustable variables of the ESO are denoted by \({\beta _{13}} = diag\left\{ {\begin{array}{*{20}{c}} {{\beta _1}}&{{\beta _3}} \end{array}} \right\}\) and \({\beta _{24}} = diag\left\{ {\begin{array}{*{20}{c}} {{\beta _2}}&{{\beta _4}} \end{array}} \right\}\) , respectively, and bringing Eq. (42) into Eq. (43), the observation error system is denoted by

$$\begin{aligned} \begin{aligned} {{\dot{e}}_1}&= {e_2} - {\beta _1}{e_1} \\ {{\dot{e}}_2}&=-{\beta _2}fal({e_1},{\sigma _1},{\delta _1})-\varepsilon \end{aligned} \end{aligned}$$
(44)

Note 2: \(fal({e_1},{\sigma _1},{\delta _1}) = \left\{ {\begin{array}{*{20}{c}} {|{e_1}{|^{{\sigma _1}}}sgn({e_1})\mathrm{{ }},\mathrm{{ }}|{e_1}| > {\delta _1}}\\ {\frac{{{e_1}}}{{{\delta _1}^{1 - {\sigma _1}}}}\mathrm{{ }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,\mathrm{{ }}|{e_1}| \le {\delta _1}} \end{array}}\right.\) is a non-linear function. The essence of Eq. (42) is a filtering structure, \({e_1}\) is a variable containing a time parameter, \({\sigma _1}\) is a coefficient between 0 and 1 . \({\delta _1} \ge 0\) is a constant that affects the filtering effect.

Note 3: For the angular velocity system (41), let \({\omega _a} = {\chi _3}\), \({\tau _{d\omega }} = {\chi _4}\) ; \({e_3} = {{\hat{\chi }} _3} - {\chi _3}\), \({e_4} = {{\hat{\chi }} _4} - {\chi _4}\) denote the observation errors, \({{\hat{\chi }} _3}\) and \({{\hat{\chi }} _4}\) are the observations of \({\chi _3}\) and \({\chi _4}\) , respectively.

Theorem 2

Let \({e_{21}} = {e_1}\), \({e_{22}} = {e_2} - {\beta _1}{e_1}\) for the observation error system (44), if \({\beta _1}\) satisfies \(|{e_{22}}| > \frac{{|{\varepsilon _1}|}}{{{\beta _1}}}\) , then the constructed ESO is valid, i.e. the observations \({{\hat{\chi }} _1}\) and \({{\hat{\chi }} _2}\) can converge to the actual states \({\chi _1}\) and \({\chi _2}\) respectively.

Proof

If \(\varepsilon > 0\) , by Theorem 2, the estimation error system (44) can be written as

$$\begin{aligned} \begin{aligned} {\dot{e}}_{21}&={e_{22}} \\ {\dot{e}}_{22}&= - {\beta _2}fal({e_{21}},{\sigma _1},{\delta _1}) - {\beta _1}{e_{22}} - \varepsilon \end{aligned} \end{aligned}$$
(45)

Choose a Lyapunov function as follows

$$\begin{aligned} {V_3} = \int _0^{{e_{21}}} {2{\beta _2}fal(\varsigma ,{\sigma _1},{\delta _1})} d\varsigma + e_{22}^2 \end{aligned}$$
(46)

Then, in the interval \({\varsigma _1} \in [0,{e_{21}}]\) , Eq. (44) can be written as

$$\begin{aligned} {V_3} = 2{\beta _2}fal({\varsigma _1},{\sigma _1},{\delta _1}){e_{21}} + e_{22}^2 \end{aligned}$$
(47)

Since \({\beta _2} > 0\) , and \(fal( \cdot )\) is an odd function, then

$$\begin{aligned} {V_3} = 2{\beta _2}fal(\varsigma ,{\sigma _1},{\delta _1}){e_{21}} + e_{22}^2 > 0 \end{aligned}$$
(48)

The derivation of Eq. (44) is as follows:

$$\begin{aligned} {{\dot{V}}_3}=2{e_{22}}{\beta _2}fal({e_{21}},{\sigma _1},{\delta _1}) +2{e_{22}}[ - {\beta _2}fal({e_{21}},{\sigma _1},{\delta _1}) - \varepsilon - {\beta _1}{e_{22}}]=- 2{e_{22}}({\beta _1}{e_{22}} + \varepsilon ) \end{aligned}$$
(49)

The conditioning gain \({\beta _1}\) satisfies the inequality \(|{e_{22}}| > \frac{\varepsilon }{{{\beta _1}}}\) and it follows that \({\dot{V}_3} < 0\) is constant. Similarly, if inequality \(|{e_{22}}| > - \frac{\varepsilon }{{{\beta _1}}}\) is met under condition \(\varepsilon < 0\), \({\dot{V}_3} < 0\) is constant.

In summary, if the gain meets the inequality \(|{e_{22}}| > \frac{{|\varepsilon |}}{{{\beta _1}}}\), then \({\dot{V}_3}\) is negative definite and \({e_{22}} = 0\) holds if and only if\({e_{22}} = 0\) . This demonstrates the feasible validity of the error system. \(\square\)

Design of the AISMC controller

The advantage of ISMC is that it ensures that the system state is on the sliding mode surface at the initial stage, which reduces the convergence time of the system, and at the same time avoids the steady-state error that occurs in conventional sliding mode control due to rebalancing by disturbance effects. Adaptive control is to make the state of the system more in line with the environment by adjusting the parameters online, and constantly adjusting the gain coefficients so that the system state far away has large gain coefficients and reduce the gain when close to the sliding mode surface to reduce the back and forth vibration of the system near the sliding mode surface. Therefore, this section designs the AISMC strategy to satisfy not only the achievability but also the smoothness. Let \(e = {v_c} - {v_a}\) denote the tracking error in \({v_c}\) and \({v_a}\) . Deriving the error e yields.

$$\begin{aligned} \dot{e} = {\dot{v}_c} - {b_0}{\bar{\tau }} - {\chi _2} \end{aligned}$$
(50)

Design the integral sliding mode surface as follows:

$$\begin{aligned} \Im (t) = e + p\int _0^{\textrm{T}} {fal\left( {e(\hbar ),{\sigma _2},{\delta _2}} \right) d\hbar } \end{aligned}$$
(51)

From Note 2, Eq. (51) is a segmented integral sliding mode surface, and \(p > 0\) is the sliding mode surface splitting constant obtained by its derivation:

$$\begin{aligned} {\dot{\Im }} (t) = {\dot{v}_c} - {b_0}{\bar{\tau }} - {\chi _2} + pfal(e,{\sigma _2},{\delta _2}) \end{aligned}$$
(52)

Assuming the existence of an upper bound \({\gamma _H}\) on the sliding mode switching gain, adaptive gain coefficients are designed to reduce jitter near the segmented sliding mode surface, so the gain coefficients are dynamically adjustable.

$$\begin{aligned} \dot{{\hat{\gamma }}} = \rho \Im {\textrm{sgn}} (\Im ) \end{aligned}$$
(53)

where \({\hat{\gamma }}\) is the estimated value of \({\gamma _H}\) and \(\rho > 0\) is a constant. The estimation error of the gain switching coefficient is

$$\begin{aligned} {\tilde{\gamma }} = {\hat{\gamma }} - {\gamma _H} \end{aligned}$$
(54)

Therefore, based on the ESO (43), the integral sliding mode surface (51) with the switching gain adaptive law (Eq. 53), the following form of inner-loop torque control law is developed:

$$\begin{aligned} {\bar{\tau }} = \frac{1}{{{b_0}}}\left( {{{\dot{v}}_c} - {{{\hat{\chi }} }_2} + pfal(e,{\sigma _2},{\delta _2}) + {\hat{\gamma }} {\textrm{sgn}} (\Im )} \right) \end{aligned}$$
(55)

Note 4. \(sgn( \cdot )\)denotes a symbolic function specifically for \({\textrm{sgn}} ( \cdot ) = \left\{ {\begin{array}{*{20}{c}} 1&{}{ \cdot > 0}\\ { - 1}&{}{ \cdot < 0} \end{array}} \right.\)

Theorem 3

Taking into account the segmented integral sliding mode surface (51) and the inner loop torque control rule (55), by selecting an appropriate positive parameter p , it is possible to cause the linear velocity tracking error e to approach an appropriately small interval in a limited time, and simultaneously to cause the actual linear velocity \({v_a}\) to track up to the desired linear velocity \({v_c}\) under the action of the adaptive rule (Eq. 53).

Proof

For the sectional integral sliding mode surface (Eq. 51), \(\dot{s} = 0\) is satisfied under an equation \(\dot{e} + pfal(e,{\sigma _2},{\delta _2}) = 0\) , i.e.

$$\frac{{de}}{{dt}} = - p{| e |{\bar{\lambda}} }{{\rm sgn}} (e)$$
(56)

If the initial tracking error e(0) is not in the linear interval \(\left[ { - {\delta _{_2}},{\delta _2}} \right]\) , integration of Eq. (56) leads to

$$t = \int_{{e_0}}^{{\delta _2}} {\left( { - \frac{{{{\left| e \right|}^{ - \bar{\lambda} }}}}{{p{{\rm sgn}} (e)}}} \right)de}= \frac{1}{{p(1 - \bar{\lambda} )}}\left( {{{\left| {{e_0}} \right|}^{1 - \bar{\lambda} }} - \delta _2^{1 - \bar{\lambda} }} \right) = {\bar T_{\max }}$$

As a result, the error e will converge within the linear interval \(\left[ { - {\delta _{_2}},{\delta _2}} \right]\) at the maximum time \({{\bar{T}}_{\max }}\) . Construct the Lyapunov function as follows:

$$\begin{aligned} {V_4} = \frac{1}{2}{\Im ^2} + \frac{1}{2}\frac{1}{\rho }{\tilde{\gamma } ^2} \end{aligned}$$
(57)

The derivation yields

$$\begin{aligned} \begin{aligned} {{\dot{V}}_4}&= \Im {\dot{\Im }} + \frac{1}{\rho }{\tilde{\gamma }} \dot{{\tilde{\gamma }} }\\&= \Im \left[ {{{\dot{v}}_{c} - {b_0}{\bar{\tau }} - {\chi _2} + pfal(e,{\sigma _2},{\delta _2})} }\right] + \frac{1}{\rho }{\tilde{\gamma }} \dot{{\tilde{\gamma }}} \\&= \Im \left[ {{{\hat{\chi }}}_{2} - pfal(e,{\sigma _2},{\delta _2}) - {\hat{\gamma }} \textrm{sgn}(\Im ) - {\chi _2} + pfal(e,{\sigma _2},{\delta _2})} \right] + \frac{1}{\rho }{\tilde{\gamma }} \dot{{\tilde{\gamma }}} \\&= \Im \left[ {{e_2} - {\hat{\gamma }} {\textrm{sgn}}(\Im )} \right] + \frac{1}{\rho }{\tilde{\gamma }} \dot{{\tilde{\gamma }}} \\&= \Im \left[ {{e_2} - ({\tilde{\gamma }} + {\gamma _H}){\textrm{sgn}}(\Im )} \right] + \frac{1}{\rho }{\tilde{\gamma }} \dot{{\tilde{\gamma }}} \\&= \Im \left[ {{e_2} - {\gamma _H}{\textrm{sgn}} (\Im )} \right] + {\tilde{\gamma }} \left[ {\frac{1}{\rho }{\dot{\tilde{\gamma }}} - {\textrm{sgn}} (\Im )\Im } \right] \end{aligned} \end{aligned}$$

Since there is an upper bound \({\gamma _H}\) on the switching gain of the sliding mode, we have, according to the adaptive law (53)

$$\begin{aligned} \frac{1}{\rho }{\dot{\tilde{\gamma }}} - {\textrm{sgn}} (\Im )\Im = 0 \end{aligned}$$
(58)

Thus, \({{\dot{V}}_4}\) can be written as:

$$\begin{aligned} {\dot{V}_4} = \Im \left[ {{e_2} - {\gamma _H}{\textrm{sgn}} (\Im )} \right] \end{aligned}$$
(59)

According to Assumption 2, \(\left| {{e_2}} \right|\) is bound, that is, there exists a positive real number \(\mathbb {R}\) such that \(\left| {{e_2}} \right| \le \mathbb {R}\) , hence

$$\begin{aligned} \begin{aligned} {{\dot{V}}_4}&\le \left| {{e_2}} \right| \left| \Im \right| - {\gamma _H}\left| \Im \right| \\&\le - \left( {{\gamma _H} - \mathbb {R} } \right) \left| \Im \right| \end{aligned} \end{aligned}$$
(60)

\({\dot{V}_4} \le 0\) holds if the upper bound of the sliding mode switching gain \({\gamma _H} \ge \mathbb {R}\) . That is, the adaptive law (Eq. 53) with ESO (Eq. 43) ensures that Eq. (60) is semi-negative definite and therefore \({V_4}(\Im ,{\tilde{\gamma }} )\) is a non-increasing function with respect to time t , i.e. for any \(t \ge 0\), \({V_4}\left( {\Im (t),{\tilde{\gamma }} (t)} \right) \le {V_4}\left( {\Im (0),{\tilde{\gamma }} (0)} \right)\) holds. Obviously, the integral sliding mode surface \(\Im \rightarrow 0\) , when\(\Im = 0\) , by Eq. (51), \(e = - p\int _0^{\textrm{T}} {fal\left( {e(\hbar ),{\sigma _2},{\delta _2}} \right) d\hbar } ,e(\infty ) \rightarrow 0\) is established, i.e.the actual linear velocity \({v_a}\) tracks the desired linear velocity \({v_c}\) . \(\square\)

Experimental validation and discussion

Numerical simulation experiments

To verify the effectiveness of the proposed control scheme, in this section we show the simulation results of tracking the reference trajectory in the WMR inertial coordinate system. First, the structural parameters of the WMR with the centre of mass coinciding with the geometric centre are given, \(m = 4\)kg , \(J = 2.5\) \({\hbox {kg} \cdot {m^2}}\), \(r = 0.1\) m, \(R = 0.4\) m. Provided that the three-petalled rose with reference trajectories \({x_r}(t) = {\kappa _1}\cos (3{\kappa _2}t)\cos ({\kappa _2}t)\), \({y_r}(t) = {\kappa _1}\cos (3{\kappa _2}t)\sin ({\kappa _2}t)\), where \({\kappa _1} = 3\) is the reference length of each petal and \({\kappa _2} = \pi /45\). Unlike simple circular or linear reference trajectories, the tracking behaviour of a three-petalled rose trajectory is more complex, with a time-varying reference velocity. In this experiment, the linear reference velocity is represented by \({v_r} = \sqrt{\dot{x}_r^2 + \dot{y}_r^2}\),\({w_r} = \pi /16\) m/s.

The WMR is assumed to have an initial position error \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over q} (0) = {\left[ {\begin{array}{*{20}{c}} {{e_x}(0)}&{{e_y}(0)}&{{e_\vartheta }(0)} \end{array}} \right]^{\rm T}} = {\left[ {\begin{array}{*{20}{c}} { - 0.5}&{0.5}&{0.1} \end{array}} \right]^{\rm T}}\), a state observer initial error\({\left[ {\begin{array}{*{20}{c}} {{e_1}(0)}&{{e_2}(0)}&{{e_3}(0)}&{{e_4}} \end{array}(0)} \right] ^{\textrm{T}}} = {\left[ {\begin{array}{*{20}{c}} 0&{0.5}&0&{0.5} \end{array}} \right] ^{\textrm{T}}}\), and it is also assumed that the external disturbances to the WMR are trigonometric polynomials consisting of a sine-cosine function, i.e. \({{\bar{\tau }} _{d1}} = {{\bar{\tau }} _{d2}} = 8\sin (0.5t) + 10\cos (0.5t)\). To further verify the robustness of the controller to external disturbances, a pulse disturbance of amplitude 10 is applied to the angular velocity system for 20s to simulate that the WMR is subjected to a violent shock during trajectory tracking, but taking into account the requirements of assumption 2; we approximate the pulse signal by a Gaussian function so that the disturbance has a continuous and conducting character, in the following form:

$$\begin{aligned} {\bar{\tau }} _{_{d2}}^* = F*\exp \left( { - \frac{{{{(t - {m_u})}^2}}}{{2*{m_p}^2}}} \right) \end{aligned}$$

where \({m_p} = 0.1\) is the standard deviation, \({m_u} = 30\) is the mean and \(F = 10\) is the magnitude.

In general, the LMPC controller needs to be given the sampling time h, the prediction horizon \({N_p}\) and the control horizon \({N_c}\), where the parameters \(h = 0.2s\), \({N_p} = 20\), and \({N_c} = 6\) are set in the LMPC. The choice of weight matrices Q and R can determine whether the system focuses more on position tracking or velocity tracking, set the elements \(a = 0.5\) in R, and \(Q = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C}^{\textrm{T}} _h{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{C} _h}\), thus the matrices \(\Omega\) and \(\Upsilon\) in the optimisation problem can be obtained, and take \(\kappa = 2\) in the optimisation solution condition according to Ref.34. In order to illustrate the ability of motion controllers to handle various constraints, the velocity and velocity increments of the WMR will be appropriately limited in this paper, taking into account its real-world mechanical structure with actual physical constraints. In the procedure it is assumed that the virtual WMR has \({\left| \omega \right| _{\max }} = 0.3\), \({\left| v \right| _{\max }} = 0.8\), \(\Delta {\eta _{\min }} = {\left[ {\begin{array}{*{20}{c}} { - 0.2}&{ - 0.5} \end{array}} \right] ^{\textrm{T}}}\), \(\Delta {\eta _{\max }} = {\left[ {\begin{array}{*{20}{c}} {0.2}&{0.5} \end{array}} \right] ^{\textrm{T}}}\), which is introduced to the optimisation problem (28) through Eq. (27). The second order nonlinear ESO with force controllers can be tuned parametrically by theorems 2 and 3: \({\beta _1} = {\beta _2} = 30\), \({\beta _3} = {\beta _4} = 255\), the sliding mode area division constants \({p_v} = 4\), \({p_\omega } = 6\), \(\rho = 0.01\), \({\delta _2} = 0.01\).

Figure 5
figure 5

Tracking of reference trajectories under two control strategies,

Full size image
Figure 6
figure 6

Trajectory tacking error on X axis.

Full size image
Figure 7
figure 7

Trajectory tacking error on Y axis.

Full size image

Figure 5 shows the actual tracking performance of WMR for a three-petalled rose curve under the control strategy of this paper and the Ref.30 strategy. Comparison can be seen, even in the case of a large initial error, the control strategy in this paper can make the WMR track on the reference trajectory within 8s, while the reference control strategy30 needs 11s, it is obvious that the control strategy of this paper has a superior timeliness. At 20s, the WMR will briefly deviate from the reference trajectory in the face of the suddenly applied intense impulse disturbance, but it can be adjusted in time under the control strategy in this paper and can quickly follow the reference trajectory, and its ability to overcome the external intense shock disturbance is better than that of the Ref.30.

Due to the WMR underdrive behaviour, the tracking errors presented in Figs.6, 7 and 8 are not asymptotically stabilised at zero, and there are some slight fluctuations, but from Fig. 5 these fluctuations are within an acceptable range. If a violent shock occurs at 20s, the tracking error will fluctuate slightly and then quickly converge to zero. The novel dual closed-loop control strategy is designed to be responsive and more robust to external disturbances and strong impulsive disturbances.

Figure 8
figure 8

Trajectory tacking error on \(\vartheta\) axis.

Full size image
Figure 9
figure 9

Desired vs. actual linear velocity and estimation of actual velocity.

Full size image
Figure 10
figure 10

Desired vs. actual angular velocity and estimation of actual velocity.

Full size image
Figure 11
figure 11

Actual linear velocity observation error.

Full size image
Figure 12
figure 12

Actual angular velocity observation error.

Full size image
Figure 13
figure 13

Control torque.

Full size image

In Figs. 9 and 10, the purple solid line shows the velocity constraints of the motion controller and it can be seen that the desired linear velocities generated by the outer-loop motion controller is limited within the constraints and no unpredictable velocity bursts occur. The maximum linear velocity of the WMR was limited to 0.8m/s and maintained between 5s and 7s. The angular velocity system is subjected to a strong impulse disturbance with a fluctuation of \({\omega _c}\) within a deviation value of 0.1, which is adjusted to the vicinity of the reference angular velocity \({\omega _r}\) within 3s. It is illustrated that the ESO developed in this paper is capable of better velocity estimation and obtaining velocity signals online for timely feedback to ensure that the inner-loop force controller can accurately track the generated desired velocity. Figs. 11 and 12 show the actual velocity observation error, Fig. 13 illustrates that the output torque of the inner- loop controller outputs are in the range of 20 \(\rm{N\cdot m}\) .

Figure 14
figure 14

Linear velocity system disturbance and estimation.

Full size image
Figure 15
figure 15

Angular velocity system disturbance and estimation.

Full size image
Figure 16
figure 16

Derivative of angular velocity system disturbance.

Full size image

Figures 14 and 15 illustrate estimation of the disturbance, where \(E = {\hat{\chi }} - \chi\) is defined as the absolute observer error, i.e. the difference between the disturbance observer and the true value. Given the presence of an initial error of 0.5 in the observer, it is clear that although the second-order nonlinear ESO designed in this paper has a relatively large absolute error value in the first 8s, it basically remains in the range of less than 0.1 in the following. In particular, there is a transient increase in the value of \({E_{d\omega }}\) when the angular velocity system is subjected to impulsive disturbance, but the immunity of the force controller to estimation errors allows the overall control performance not to be significantly affected, Fig. 16 verifies that the disturbance are consistent with those described in Assumption 2.

The Laguerre network is determined by the number of laguerre functions used N and the Laguerre pole \(\alpha\). Here, a minimum cost function \({{\bar{J}}_{\min }}\) is defined, namely the optimal control inputs of Eq. (32) are brought to the values obtained from Eq. (25). The effect of the Laguerre pole on the control performance of the LMPC is analysed by simulation, with the linear velocity taken as an example. This is shown in Fig. 17. It can be observed that the minimum cost function decreases with the increase of N. When the value of N is large, the optimal adjustment of the Laguerre pole \(\alpha\) will not affect the control performance of the LMPC. Conversely, in the case of a small value of N, an inappropriate selection of the Laguerre pole \(\alpha\) will result in a decrease in the control performance of the LMPC. Consequently, in this experiment, an N value of 8–10 and a \(\alpha\) value of 0.75–0.95 can be identified as optimal parameters for achieving a satisfactory control effect.

Figure 17
figure 17

The number of Laguerre functions and the minimum cost function corresponding to the Laguerre pole.

Full size image

In order to ascertain the impact of the introduction of the optimisation solution condition (31) on the MPC computation, \(\kappa = 0\) is designated as the regular cycle-sampling MPC, and \(\kappa = 2\) denotes the LMPC strategy with the introduction of the optimisation solution condition. The results are presented in Fig. 18, which illustrates that the incorporation of the optimisation solution condition renders the optimisation problem acyclical in comparison to the conventional cycle-sampling MPC approach. The solver is activated 98 times, whereas the conventional MPC solution necessitates 300 instances, thereby signifying a substantial reduction in computational burden.

Figure 18
figure 18

Optimisation problem solving moments.

Full size image
Figure 19
figure 19

Comparison of the actual running time of the simulation under the three strategies.

Full size image

In MATLAB/Simulink co-simulation, the “set_param(’filename’,’Profile’,’on’)” command is employed to obtain a report of the execution time of the program when tracking the trilobal rose curve in Fig. 5. Setting the simulation time to 60s, the actual running time of the system for MPC, LMPC and LMPC with optimised solution condition (31) is shown in Fig. 19. The results demonstrate that the LMPC reduces the system running time by 43.6% in comparison to the conventional MPC, while the introduction of the optimal solution condition reduces the system running time by 61.5%. Consequently, the proposed control strategy exhibits a significant advantage in terms of timeliness.

Practical experimental verification

To further validate the effectiveness and practicality of the dual closed-loop control structure proposed in this paper, it is necessary to verify the algorithm on a real physical system. The WMR prototype system equipped with LiDAR and inertial measurement unit (IMU) used for the experiments is shown in Fig. 20. The motor microcontroller STM32F429VET6 (180 MHz) is utilised to generate pulse width modulated (PWM) signals with varying duty cycles, thereby regulating the speed of the two drive wheels, which are driven by two DC motors. LIDAR and IMU are employed to acquire the position and orientation information of the WMR, and the WMR transmits the aforementioned information between the WMR and the ground workstation via a WiFi network.

Figure 20
figure 20

WMR system in practical experiments.

Full size image

The practical control system structure is shown in Fig. 21. Considering the problem of LMPC computation, in the proposed control algorithm, the outer-loop controller optimisation problem is run on a ground workstation (configured with a dual-core 2.4GHz Intel Core i5 CPU, 16GB RAM, 64-bit Windows 11 system), and the ESO is executed on the local device of the WMR with the inner-loop controller. The WMR status information is sent via Wifi to the PC ground station, which solves the optimisation problem to obtain the optimal control sequence and sends the desired speed signal to the WMR.

Figure 21
figure 21

Practical control system framework.

Full size image

The tracking task and controller parameter selection are identical to those employed in the simulation. The experiments are conducted on an unsmooth concrete pavement, with and without ESO, with the objective of validating the efficacy of ESO. The WMR position sampling trajectories are illustrated in Figs. 22 and 23. It can be observed that the sum trajectory tracking with ESO is superior to that without ESO, but Fig. 22 shows that the tracking error cannot be converged strictly to zero, the reason is that this WMR, as a special class of networked control system, is faced with packet loss, latency and other typical problems that cannot be avoided.

Figure 22
figure 22

Actual tracking trajectory with ESO.

Full size image
Figure 23
figure 23

Actual tracking trajectory without ESO.

Full size image

Conclusion

In this paper, the problem of nonholonomic constrained WMR trajectory tracking control in the presence of external disturbances is investigated and a dual closed-loop control structure is presented. The development of an advanced MPC motion controller based on the Laguerre functions for generating desired velocities in the outer-loop achieves higher tracking accuracy of the robot’s pose, and the construction of optimised solution conditions to improve the computational timeliness of the conventional MPC in two dimensions. In the inner-loop, the AISMC scheme with ESO is considered to track the desired velocity while estimating and compensating for the external disturbances in the inner-loop and outputting the control torques that actually operate on the WMR system. The proposed dual control structure can implement coordinated trajectory tracking control of motion/force. We consider introducing more complex nonlinear constraints in MPC and applying them to WMR trajectory tracking control under the dynamics model in the further work.