Introduction

As we known that optical bistability (OB) and optical multistability (OM) are essential element in photonic devices such as optical transistors, optical memories, optical logic gates, optical switches, and so on1. Response speed and the sensitivity of the optical devices depend on the threshold intensity and width of the OB. Therefore, one is always looking for solutions to control the threshold intensity and the width of the OB, so that the operating characteristics of optical devices can be changed as desired.

In fact, the OB or OM effect depends on the dispersion and absorption properties of the material, so to change the characteristics of OB requires that the dispersion and absorption properties be adjusted. Currently, a simple method to change the optical properties of materials is to use electromagnetically induced transparency (EIT)2. The simplest configuration of EIT is three-level atomic systems excited by a probe laser field and a coupling laser field according to lambda-, cascade- and V-type diagrams. According to these three-level configurations, a transparent spectral region (called the EIT window) is formed at the center of the absorption while on either side is the absorption maximum; at the same time, EIT window and dispersion are also easily changed by intensity and frequency coupling laser. In particular, to significantly change the probe response of the medium, one often introduce other external fields such as the magnetic field3, incoherent pumping field in the presence of spontaneously generated coherence (SGC)4 and so on. In the presence of the static magnetic field, the Zeeman effect separates the degenerate energy levels in the atomic levels and hence it shifts the EIT window into different frequency domains. This means that the response of the medium for the probe field can change from transparency to maximum absorption and thus the dispersion properties also change from normal dispersion to anomalous dispersion and vice versa.

By placing EIT materials with such variable absorption and dispersion properties in a ring cavity, one can easily create a low-threshold OB effect with the threshold intensity and width of the OB also being easily changed by external fields. Indeed, the first theoretical and experimental studies on the OB under EIT condition were performed in three-level atomic systems including three-level lambda-, V- and ladder-type configurations5,6,7,8,9. Because an EIT window is formed in three-level atomic configurations, the OB effect is also only present in a single spectral ___domain (single channel). Nevertheless, modern photonic systems require operation at multiple different frequency domains (multi-channel), so the operating medium of the devices is also required to respond at multiple frequency domains. To obtain OB at different frequency domains (multi-channel), one must use four-level or five-level atomic configurations with two or three EIT windows, respectively10. In particular, for such multi-level atomic media, one can easily obtain the OM effect in the presence of other combined effects such as SGC11,12,13, or external fields such microwave field14,15, degenerate field16, incoherent pumping field17 and static magnetic field18,19. Besides the atomic medium, the OB effect is also realized in semiconductor quantum well systems under Fano-type interference20,21. It is demonstrated that the threshold intensity and the hysteresis loop of the OB behaviors can be manipulated efficiently by tuning the coupling strength of the tunneling, the Fano-type interference, and the intensity and frequency detuning of the control field.

Among such methods controlling optical atomic properties, the method based on a static magnetic field is simpler and easier to perform in experiments, thus attracting the most attention from researchers. Recently, static magnetic field has been used to control absorption and dispersion22,23, light propagation24,25, Kerr nonlinearity26 and magneto-optical switching27,28. In this paper, we study the formation of two-channel OB and OM effects in a degenerate four-level atomic system under the presence of external magnetic field. The OB and OM effects can appear simultaneously at two different frequency domains and are controlled according to the laser parameters and the external magnetic field simply.

Theoretical model

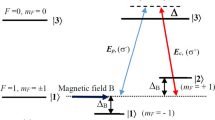
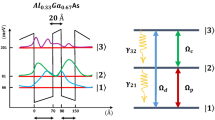
Figure 1 shows the schematic of a four-level inverted-Y atomic system that is excited by a probe laser field, a coupling laser field and a signal laser field. The atom is placed in a longitudinal magnetic field B parallel to the propagation direction of the laser fields that removes the degeneracy of the ground-state sublevels, where the magnetic field B shifts mF =  ± 1 levels by ± ΔB via the Zeeman effect. The left-circularly polarized probe field with Rabi frequency Ωp and angular frequency ωp drives the transition |1〉 (mF =  + 1) ↔|3〉 (mF = 0). The right-circularly polarized coupling field with Rabi frequency Ωc and angular frequency ωc is applied to the transition |2〉 (mF =  − 1) ↔|3〉 (mF = 0). The levels |3〉 (mF = 0) and |4〉 (mF = 0) are connected by the linearly polarized signal field with Rabi frequency Ωs and angular frequency ωs. The Zeeman shift of levels |1〉 and |2〉 is given by Ref.27 \(\hbar \Delta_{B} = \mu_{B} m_{F} g_{F} B\) where \(\mu_{B}\) is the Bohr magneton, \(g_{F}\) is the Landé factor. The spontaneous decay rate from the upper state to the lower state is denoted by γij.

Figure 1
figure 1

Degenerated four-level atomic system in an external magnetic field, where the state |1〉 is lowered while the state |2〉 is lifted by the same amount ΔB corresponding to the Zeeman shift.

Full size image

Using the electric dipole and the rotating-wave approximations, the total Hamiltonian of the system can be given by:

$$ H = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \Omega_{p}^{{}} } & 0 \\ 0 & {2\Delta_{B} } & { - \Omega_{c}^{{}} } & 0 \\ { - \Omega_{p}^{{}} } & { - \Omega_{c}^{{}} } & {\Delta_{p} + \Delta_{B} } & { - \Omega_{s}^{{}} } \\ 0 & 0 & { - \Omega_{s}^{{}} } & {\Delta_{p} + \Delta_{s} - \Delta_{B} } \\ \end{array} } \right]. $$
(1)

To describe the dynamical evolution of the proposed system, the density matrix approach is employed via Liouville equation:

$$ \frac{\partial \rho }{{\partial t}} = - \frac{i}{\hbar }\left[ {H,\rho } \right] + \Lambda \rho , $$
(2)

where the term Λρ represents the decay part in the atom, with Λ is the Liouvillian operator acting on the density matrix ρ. Using Eqs. (1) and (2), the density matrix equations of motion are written as:

$$ \dot{\rho }_{11}^{{}} = - \gamma_{21} (\rho_{11}^{{}} - \rho_{22}^{{}} ) + \gamma_{31} \rho_{33}^{{}} - \frac{i}{2}\Omega_{p}^{{}} \rho^{{}}_{31} + \frac{i}{2}\Omega_{p} \rho_{13}^{{}} , $$
(3a)
$$ \dot{\rho }_{22}^{{}} = - \gamma_{21} (\rho_{22}^{{}} - \rho_{11}^{{}} ) + \gamma_{32} \rho_{33}^{{}} + \frac{i}{2}\Omega_{c}^{{}} \rho_{23}^{{}} - \frac{i}{2}\Omega_{c}^{{}} \rho_{32}^{{}} , $$
(3b)
$$ \dot{\rho }_{33}^{{}} = - (\gamma_{32} + \gamma_{31} )\rho_{33}^{{}} + \gamma_{43} \rho_{44}^{{}} - \frac{i}{2}\Omega_{p}^{{}} \rho_{13}^{{}} + \frac{i}{2}\Omega_{p} \rho_{31}^{{}} - \frac{i}{2}\Omega_{c}^{{}} \rho_{23}^{{}} + \frac{i}{2}\Omega_{c}^{{}} \rho_{32}^{{}} - \frac{i}{2}\Omega_{s}^{{}} \rho_{43}^{{}} + \frac{i}{2}\Omega_{s}^{{}} \rho_{34}^{{}} , $$
(3c)
$$ \dot{\rho }_{44}^{{}} = - \gamma_{43} \rho_{44}^{{}} + \frac{i}{2}\Omega_{s}^{{}} \rho_{43}^{{}} - \frac{i}{2}\Omega_{s}^{{}} \rho_{34}^{{}} , $$
(3d)
$$ \dot{\rho }_{21}^{{}} = - {[}\gamma_{21} - i(\Delta_{p} - \Delta_{c} - 2\Delta_{B} ){]}\rho_{21}^{{}} + \frac{i}{2}\Omega_{p} \rho_{23}^{{}} - \frac{i}{2}\Omega_{c}^{{}} \rho_{31}^{{}} , $$
(3e)
$$ \dot{\rho }_{31}^{{}} = - [\gamma_{31} - i(\Delta_{p} - \Delta_{B} )]\rho_{31}^{{}} + \frac{i}{2}\Omega_{p} (\rho_{33}^{{}} - \rho_{11}^{{}} ) - \frac{i}{2}\Omega_{c}^{{}} \rho_{21}^{{}} - \frac{i}{2}\Omega_{s}^{{}} \rho_{41}^{{}} , $$
(3f)
$$ \dot{\rho }_{32}^{{}} = - {[}\gamma_{32} - i(\Delta_{c} { + }\Delta_{B} {)]}\rho_{32}^{{}} + \frac{i}{2}\Omega_{c} (\rho_{33}^{{}} - \rho_{22}^{{}} ) - \frac{i}{2}\Omega_{p}^{{}} \rho_{12}^{{}} - \frac{i}{2}\Omega_{s}^{{}} \rho_{42}^{{}} , $$
(3g)
$$ \dot{\rho }_{41}^{{}} = - [\gamma_{41} - i(\Delta_{p} + \Delta_{s} - \Delta_{B} )]\rho_{41}^{{}} + \frac{i}{2}\Omega_{p}^{{}} \rho_{43}^{{}} - \frac{i}{2}\Omega_{s}^{{}} \rho_{31}^{{}} , $$
(3h)
$$ \dot{\rho }_{42}^{{}} = - {[}\gamma_{42} - i(\Delta_{c} { + }\Delta_{s} { + }\Delta_{B} {)]}\rho_{42}^{{}} + \frac{i}{2}\Omega_{c}^{{}} \rho_{43}^{{}} - \frac{i}{2}\Omega_{s}^{{}} \rho_{32}^{{}} , $$
(3i)
$$ \dot{\rho }_{43}^{{}} = - {[}\gamma_{43} - i\Delta_{s} {]}\rho_{43}^{{}} + \frac{i}{2}\Omega_{p}^{{}} \rho_{41}^{{}} + \frac{i}{2}\Omega_{s}^{{}} (\rho_{44}^{{}} - \rho_{33}^{{}} ), $$
(3j)
$$ \rho_{nm} = \rho_{mn}^{*} , $$
(3k)
$$ \rho_{11} + \rho_{22}^{{}} + \rho_{33} + \rho_{44} = 1, $$
(3l)

where \(\Delta_{p} = \omega_{p} - \omega_{31}\) and \(\Delta_{c} = \omega_{c} - \omega_{32}\) are the frequency detuning of the probe and coupling beams, respectively. The Rabi frequencies are related to the corresponding electric field amplitude Ek (k = p, c or s) by \(\Omega_{p}^{{}} = \frac{{d_{31} E_{p} }}{\hbar }\), \(\Omega_{c}^{{}} = \frac{{d_{32} E_{c} }}{\hbar }\) and \(\Omega_{s}^{{}} = \frac{{d_{43} E_{s} }}{\hbar }\) with dij being the electric-dipole matrix element associated with the transition from the state |i〉 to the state |j〉.

In order to compute the linear susceptibility, we solve the density matrix Eqs. (3a)–(3l) under the steady-state condition \(\partial \rho /\partial t = 0\). We assume that initially the atomic population is in the ground states |1〉 and |2〉 with the same populations, namely, \(\rho_{11}^{(0)} \approx \rho_{22}^{(0)} \approx 1/2\), and \(\rho_{33}^{(0)} \approx \rho_{44}^{(0)} \approx 0\). Using the weak-probe approximation we found the solution of the matrix element ρ31 as:

$$ \rho_{31}^{{}} = \frac{{ - \frac{i}{4}\Omega_{p} }}{{\gamma_{31} - i(\Delta_{p} - \Delta_{B} ) + \frac{{\frac{1}{4}\Omega_{c}^{2} }}{{\gamma_{21} - i(\Delta_{p} - \Delta_{c} - 2\Delta_{B} )}} + \frac{{\frac{1}{4}\Omega_{s}^{2} }}{{\gamma_{41} - i(\Delta_{p} + \Delta_{s} - \Delta_{B} )}}}}. $$
(4)

It is well known that the response of the atomic medium to the probe field is governed by its polarization \(P = Nd_{31} \rho_{31} \equiv - \tfrac{1}{2}\varepsilon_{0} \chi_{31} E_{p}\), thus, we can obtain the probe susceptibility given by:

$$ \chi_{31} = - \frac{{Nd_{31}^{{}} }}{{\varepsilon_{0} E_{p} }}\rho_{31} , $$
(5)

with N being the atomic density. The absorption and dispersion coefficients are determined through the imaginary and real parts of \(\chi_{31}\), respectively.

Now we put a medium of length L composed of N atoms into a unidirectional ring cavity as shown in Fig. 2. Where, the reflection and transmission coefficients of mirrors M1 and M2 are R and T with R + T = 1. We assume that both mirrors M3 and M4 are perfect reflectors. In the ring cavity configuration, the probe field Ep is circulated in the ring cavity but nor the coupling field Ec.

Figure 2
figure 2

Unidirectional ring cavity with atomic sample of length L, where, mirrors M1 and M2 have the refection and transmission coefficients as R and T with R + T = 1, whereas mirrors M3 and M4 are perfect reflectors. \(E_{p}^{I}\) and \(E_{p}^{T}\) denote the incident and transmitted probe field, respectively. \(E_{c}^{{}}\) and \(E_{s}^{{}}\) represent the coupling and signal fields that are not circulated inside the cavity.

Full size image

The total electromagnetic field can be written as

$$ E = E_{p} e^{{ - i\omega_{p} t}} + E_{c} e^{{ - i\omega_{c} t}} + c.c. $$
(6)

Under the slowly varying envelop approximation, the dynamic response of the probe field governed by Maxwell equations as follows:

$$ \frac{{\partial E_{p} }}{\partial t} + c\frac{{\partial E_{p} }}{\partial z} = i\frac{{\omega_{p} }}{{2\varepsilon_{0} }}P(\omega_{p} ), $$
(7)

where \(P(\omega_{p} )\) is induced polarization by the probe field in the transition |1〉 ↔|3〉 and is given by:

$$ P(\omega_{p} ) = Nd_{31} \rho_{31} . $$
(8)

Substituting Eq. (8) into Eq. (7), we obtain the field amplitude relation in the steady state as:

$$ \frac{{\partial E_{p} }}{\partial z} = i\frac{{N\omega_{p} d_{31} }}{{2c\varepsilon_{0} }}\rho_{31} . $$
(9)

For a single circulation of the probe field in the cavity, we denote probe the field at the start and the end of the sample is Ep(0) and Ep(L), respectively (see Fig. 2). For a perfectly tuned cavity, the boundary conditions in the steady state for the incident (\(E_{p}^{I}\)) and transmitted (\(E_{p}^{T}\)) probe fields are given by:

$$ E_{p}^{{}} (L) = E_{p}^{T} /\sqrt T , $$
(10)
$$ E_{p}^{{}} (0) = \sqrt T E_{p}^{I} + RE_{p}^{{}} (L), $$
(11)

where R is the feedback mechanism from the mirror M2, which is essential for the generation of bistability. We note that no bistability occurs if R = 0. In the mean-field limit and using of the boundary conditions, we obtain the following input–output relation for the transmitted probe field as:

$$ Y = X - iC\rho_{31} , $$
(12)

where \(Y = d_{31} E_{p}^{I} /(\hbar \sqrt T )\), \(X = d_{31} E_{p}^{T} /(\hbar \sqrt T )\) are normalized input and output probe fields, respectively, and \(C = \frac{{N\omega_{p} Ld_{31}^{2} }}{{2c\varepsilon_{0} \hbar T}}\) is the cooperation parameter for atoms in the ring cavity. Thus, transmitted field depends on the incident probe field and the coherence term ρ31 via Eq. (12). Theorefor, the bistable behavior of medium can be determined by atomic variables through ρ31 which can be numerically solved from the density matrix Eqs. (3a)–(3l).

Results and discussion

In experimental performance, this configuration can be applied to the 87Rb atom with the states |1〉, |2〉, |3〉 and |4〉 can be chosen as \(5S_{1/2} (F = 1,\,\,m_{F} = + 1)\), \(5S_{1/2} (F = 2,\,\,m_{F} = - 1)\), \(5P_{1/2} (F = 1,\,\,m_{F} = 0)\) and \(5D_{3/2} (F = 2,\,\,m_{F} = 0)\), respectively. The atomic parameters are23,24: N = 4.5 × 1017 atoms/m3, γ31 = γ32 = 2π × 5.3 MHz, d31 = 1.6 × 10–29 C.m. The Landé factor gF = − 1/2, and the Bohr magneton μB = 9.27401 × 10–24 JT−1. For simplicity, all quantities related to frequency are given in units γ that is of the order of MHz for rubidium atom. In this approach, when the Zeeman shift ΔB is scaled by γ, then the magnetic field strength B should be in units of the combined constant \(\gamma_{c} = \gamma \hbar /(\mu_{B}^{{}} g_{F}^{{}} )\).

Firstly, we demonstrate that our model can obtain both OB and OM at different probe frequency regions with an appropriate magnetic field strength. Indeed, in Fig. 3 we have obtained the OB and OM curves at the probe frequency detunings Δp = 0 (a) and Δp = 2γ (b). From Fig. 3 it can be seen that the appearance of OB and OM depends on different values of the magnetic field. In terms of physical principles, the OB effect depends mainly on the dispersion of the material, while the threshold intensity and the width of OB depend mainly on the absorption. In Fig. 3c,d, therefore, to explain the appearance of OB and OM we plotted the variations of absorption (dashed) and dispersion (solid) according to magnetic field strength with the parameters are similar to those in Fig. 3a,b, respectively. In Fig. 3a corresponding to probe frequency detuning Δp = 0, we can see that when B = 0, OB does not appear because the dispersion of the material is very small (near zero); as increasing the magnetic field strength the dispersion also increases, so that OB has started to appear; as B = 1γc, the OB appears clearly but the strong absorption leads to a large threshold intensity; with B = 2γc, the absorption is significantly reduced due to the EIT effect, at the same time, the OM effect is formed. Similarly, in Fig. 3b with probe frequency detuning Δp = 2γ, OB does not appear with B = 1γc due to near-zero dispersion; OB appears when B = 0 or B = 0.5γc, while OM appears at B = 3γc. Thus, by adjusting the magnetic field strength, the threshold intensity and width of the OB is also changed and can be switched between OB and OM. We also note that the appearance of OM allows us to obtain many stable output intensities for a given input intensity, however, it is more difficult to occur than OB; in fact, the appearance of OM requires not only large dispersion but also small absorption, for example, in Fig. 3c when B increases from 0 to 1γc, the dispersion increases and OB is clearly established (see Fig. 3a), but the absorption also increases so the threshold intensity and the width of OB are also increased. If B continues to increase to a value of 2γc, OM can appear (see solid line in Fig. 3a). To illustrate these phenomena, a 3D graph of input–output intensity versus magnetic field strength B at the probe frequency detuning Δp = 0 is constructed as shown in Fig. 4. In this case, OB gradually appears and its width also increases with the growth of magnetic field strength B from 0 to 1γc, and then OM also begins to appear as B increases from 1γc to 2γc. If B is increased further, both OB and OM may disappear because the probe beam is detuned far away from the atomic resonance frequency so its nonlinear response also becomes too small. We also note that B = 2γc = 1.5 × 10−3 T ≡ 15G corresponds to the Zeeman shift ΔB = 2γ ~ 2 MHz, which is quite small in experiment.

Figure 3
figure 3

The appearance of OB and OM at two probe frequency regions: Δp = 0 (a) and Δp = 2γ (b) when Ωc = Ωs = 5γ, Δc = 0, Δs = 5γ and C = 100γ, while the magnetic strength is varied as indicated in the figures. Variations of absorption and dispersion versus the magnetic strength at two probe frequency regions: Δp = 0 (c) and Δp = 2γ (d) with other parameters similar to those in figures (a,b).

Full size image
Figure 4
figure 4

The 3D graph of input–output intensity versus magnetic field strength B for Δp = Δc = 0, Δs = 5γ, Ωc = Ωs = 5γ and C = 100γ.

Full size image

Next, in the following cases we fix the magnetic field strength at B = 2γc and study the influence of the intensity and the frequency of the laser fields on OB and OM behaviors in two different probe frequency regions Δp = 0 and Δp = 2γ. Specifically, the investigations in Fig. 5 describe the variation of OB with the intensity (Rabi frequency) of the signal laser field when the coupling laser parameters are fixed at Ωc = 5γ and Δc = Δs = 0. From Fig. 5a,b we can easily observe that OB can occur simultaneously at two different frequency regions of the probe laser field Δp = 0 and Δp = 2γ with the same set of laser parameters; however, at different values of signal laser intensity, the threshold strength and the width of the OB are also different. These phenomena are explained based on the absorption and dispersion varying with signal laser intensity as shown in Fig. 5c,d. In particular, the solid line in Fig. 5a corresponds to Ωs = 2γ, the threshold intensity and the width of OB are larger than the other cases, because at Ωs = 2γ the absorption is strongest, even though the dispersion is quite large (see Fig. 5c); the same phenomenon is also observed in Fig. 5b that the threshold intensity and the width of OB at Ωs = 0 are smaller than those at Ωs = 2γ because at Ωs = 0 dispersion is higher and absorption is smaller than that at Ωs = 2γ (see Fig. 5d). In addition, by comparing Fig. 5a,b we also see that the threshold intensity of the OB curves in Fig. 5b is smaller than that in Fig. 5a because the absorption in Fig. 5d (corresponding to Fig. 5b) is much smaller than the absorption in Fig. 5c (corresponding to Fig. 5a).

Figure 5
figure 5

The appearance of OB at two probe frequency regions: Δp = 0 (a) and Δp = 2γ (b) when Ωc = 5γ, Δc = Δs = 0, B = 2γc and C = 100γ, while the signal laser intensity is varied as indicated in the figures. Variations of absorption and dispersion versus the signal laser intensity at two probe frequency regions: Δp = 0 (c) and Δp = 2γ (d) with other parameters similar to those in figures (a,b).

Full size image

Figure 6 depicts the dependence of the OB and OM curves on the intensity (Rabi frequency) of the coupling laser field at the two probe frequency regions Δp = 0 and Δp = 2γ when fixing the parameters of the signal laser at Ωs = 5γ and Δs = 5γ. From the figure it can be seen that OM can be appeared in the probe frequency region Δp = 0, while OB can be appeared in the region Δp = 2γ. At the same time, the threshold intensity and the width of OB or OM curves also change significantly at different laser coupling intensities because of the variation of absorption and dispersion with the coupling intensity as shown in Fig. 6c,d.

Figure 6
figure 6

The appearance of OB and OM at two probe frequency regions: Δp = 0 (a) and Δp = 2γ (b). Other parameters are Δc = 0, Ωs = 5γ, Δs = 5γ, B = 2γc and C = 100γ, while the coupling laser intensity is varied as indicated in the figures. Variations of absorption and dispersion versus the coupling laser intensity at two probe frequency regions: Δp = 0 (c) and Δp = 2γ (d) with other parameters similar to those in figures (a,b).

Full size image

In Fig. 7, we investigate the impact of coupling frequency detuning on the formation of OB and OM in two probe frequency domains. The survey results show that OM easily occurs in the probe frequency ___domain Δp = 2γ, while OB appears in the probe frequency ___domain Δp = 0. We also notice that there are significant changes in the OB and OM curves at different coupling frequency detunings. In this case, we do not show absorption and dispersion graphs varying with coupling frequency detuning, however such changes in OB and OM are also caused by changes in absorption and dispersion (similar to the analysis above).

Figure 7
figure 7

The appearance of OB and OM at two probe frequency regions: Δp = 0 (a) and Δp = 2γ (b). Other parameters are Ωc = Ωs = 5γ, Δs = 5γ, B = 2γc and C = 100γ, while the coupling frequency detuning is varied as indicated in the figures.

Full size image

Finally, in Fig. 8 we study the dependence of the OB and OM curves on the signal frequency detuning at two probe frequency regions Δp = 0 (a) and Δp = 2γ (b). By changing the signal laser frequency detuning, we can find the OB and OM effects in the two probe frequency domains, and the threshold intensity and the width of OB are also changed according to the signal frequency detuning.

Figure 8
figure 8

The appearance of OB and OM at two probe frequency regions: Δp = 0 (a) and Δp = 2γ (b). Other parameters are Ωc = Ωs = 5γ, B = 2γc, Δc = 0 and C = 100γ, while the signal frequency detuning is varied as indicated in the figures.

Full size image

Conclusion

We have demonstrated the formation of OB and OM simultaneously at two different probe frequency regions in a degenerate four-level atomic system under an external magnetic field. By adjusting the magnetic field strength or the intensity and the frequency of laser fields, the absorption and dispersion properties of the atomic medium are also significantly changed, so that the threshold intensity and the width of OB and OM are also easily changed, and even the OB and OM effects can be converted. The model easily generates single- or two-channel OB and OM effects, which can be useful for experimental observations and applications such as multi-channel all-optical switches and logic-gate devices.