Introduction

In the agricultural sector, multi-task planning (MTP)1,2 are widespread, particularly in complex agricultural production scenarios. In agricultural operations, autonomous driving tractors are tasked with crop harvesting across multiple designated plots, while agricultural robots are responsible for tasks such as planting, fertilizing, and harvesting within specific areas. Additionally, they may also be required to undertake various common tasks like weeding and irrigation. However, as agricultural robot technology continues to advance and its application scope broadens, agricultural production faces new challenges that demand urgent attention. For example, achieving efficient planting and weeding in large-scale farms3. Therefore, proposing a rapid planning and optimization algorithm to address the challenges of multi-task sequence optimization and collision-free path planning is paramount for enhancing the efficiency and quality of agricultural production4.

Presently, research into path planning considering obstacle distribution has garnered considerable attention from scholars. Yang et al.5 have categorized this research into classical algorithms, intelligent optimization algorithms, and artificial intelligence algorithms. Classical algorithms such as the A* algorithm and RRT algorithm have been extensively studied, yet ensuring path optimality in large-scale complex environments remains challenging. Lin et al.6 addressed the issues of high memory consumption and lengthy operation associated with the traditional A* algorithm by enhancing heuristic functions. Zhang et al.7 introduced the Gaussian-fitted Smooth RRT*-Smart algorithm for global path planning, thereby enhancing the robot's performance during sharp turns. Intelligent optimization algorithms encompass ant colony optimization, genetic algorithms, and sparrow optimization, among others. In recent years, scholars have made notable progress in addressing common problems. Miao et al.8 integrated multi-objective performance metrics into an enhanced ant colony algorithm. They transformed the path planning problem into a multi-objective optimization problem, utilizing weighted evaluation criteria such as path length, safety, and energy consumption as constraints for the multi-objective function, thereby achieving comprehensive global optimization of path planning. Fu et al.9 introduced a quantum-inspired particle swarm algorithm, utilizing phase angle encoding to generate three-dimensional trajectories for unmanned aerial vehicles. The application of artificial intelligence techniques in mobile robot path planning represents a significant advancement. These techniques encompass a range of methods, including artificial neural networks, machine learning algorithms, deep learning algorithms, and fuzzy logic. Huang et al.10 introduced an algorithm that combines enhanced self-organizing map neural networks with novel velocity synthesis techniques for dynamic task allocation and path planning involving multiple autonomous underwater robots. Song et al.11 introduced a fuzzy logic ant colony optimization algorithm, dynamically seeking the optimal path for autonomous vehicles based on multiple criteria, including traffic flow, accident risk, and speed limits. Sangeetha et al.12 proposed a dynamic ant colony optimization algorithm based on fuzzy gain principles for dynamic path planning. This innovative approach provides conflict-free, smooth paths with several advantages, including optimized path length and minimal time consumption. Undoubtedly, the aforementioned works have enhanced the performance of path planning optimizers in complex environments involving static and moving obstacles. Planned paths typically involve two given points, namely the starting point and the destination. If these are viewed as tasks to be completed, the aforementioned optimizers can only accomplish two tasks, without addressing other tasks between the starting and ending points. This implies that both the mentioned models and optimizers are unable to handle the problem of robots completing multiple tasks.

Traveling Salesman Problem (TSP) problems primarily involve sequencing multiple tasks, without the need for conflict detection between task switches, and solutions to large-scale TSP13 problems are relatively well-developed . Wang et al.14 introduced a Hybrid Symbiotic Organism Search (HSOS) and Ant Colony Optimization (ACO) approach to address TSP. By adaptively optimizing ACO parameters with HSOS, the complexity of algorithm parameter allocation is reduced, and a straightforward local optimization strategy is employed to enhance the algorithm's convergence speed and solution quality. Khan et al.15 explored four traversal schemes for autonomous underwater vehicles while considering energy optimization. Pěnička et al.16 proposed Dubins-TSP, a variant of TSP in which the robot is treated as a Dubins vehicle operating in an obstacle-free environment, and the trajectories between the targets can be derived analytically in a short period of time. However, the path optimizers in previous studies only calculate the distance between two tasks without considering obstacles, which oversimplifies the problem and lacks practicality. In solving practical problems, MTP problems extend beyond TSP problems, involving the coupling of task sequence optimization and collision-free path planning. Many studies seek to simplify the problem under specified conditions17. Ye et al.18 proposed an innovative approach that integrates collision avoidance path planning using the Improved Probabilistic Roadmap method with delivery sequence optimization using the Improved Genetic Algorithm to solve MTP. Zacharia et al.19 introduced a genetic algorithm to simultaneously tackle collision-free motion planning and task sequence optimization. This method leverages concave-convex surface concepts, representing the entire robot environment by embedding three-dimensional B-spline surfaces in four-dimensional Euclidean space and employing a unique encoding method. Jaroslav et al.20 suggested a sampling-based planner combined with a hierarchical approach to MTP incorporating TSP. This setup requires defining costs between individual targets, and the sampling-based planner computes the shortest collision-free paths between targets on obstacle maps, ultimately finding high-quality solutions through TSP.

For addressing the MTP problem, we introduce a novel solving algorithm that decomposes the issue into two components: optimal collision-free path planning and task scheduling optimization. In terms of collision-free path planning, the task sequence optimization resembles the Traveling Salesman Problem21, while the optimal collision-free path planning problem falls within the realm of multi-path traversal sequence problems22. The primary innovations of this paper are outlined as follows:

  1. (1)

    This paper introduces an MTP hierarchical decoupling framework aimed at addressing complex issues and optimizing solutions. The problem under consideration encompasses both collision-free nature and task scheduling optimization, areas that have received relatively scant attention in the literature. Notably, the execution algorithms for these two problems can be tailored to fit practical scenarios.

  2. (2)

    Concerning collision-free path planning, we propose a 16-direction 24-neighborhood A* algorithm for generating asymmetric executable paths, with a focus on enhancing advantages in aspects such as path length, smoothness of turns, and amplitude.

  3. (3)

    In tackling the task scheduling optimization problem, we present a genetic algorithm based on elite evolution strategy to efficiently obtain task execution sequences with lower energy consumption costs.

The paper is organized as follows: Section "Description of the problem" describes the MTP problem and two typical algorithms. Section "MTP layered decoupling algorithm" presents our proposed hierarchical decoupling framework for MTP and the fusion algorithm flow. Section "Simulation results" discusses the experiments. Section "Conclusion" concludes the paper and discusses future work.

Description of the problem

Description of the agricultural environment

Given that A*, ACO, and other path planning algorithms operate as grid traversal search algorithms, our initial step involves constructing a grid model of the agricultural environment map using the grid method. This method divides the map into equally-sized adjacent grids. The size of these grids is contingent upon the dimensions of the robot, thereby influencing the efficiency and precision of the algorithm. The map model of the crop area with a length of 105 m and a width of 94 m is shown in Fig. 1, with the ___location coordinates of the robot's initial state at (20, 80) and the ___location coordinates of the goal state G at (75, 60). Each grid represents a state where the robot can stay, the green area is the crop impassable area, the black area is the obstacle impassable area, and the white area is the free exploration area.

Figure 1
figure 1

Description of the agricultural environment.

Full size image

Description of the multi-task planning problem

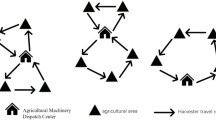
Figure 2 presents two distinct multi-task planning scenarios: Fig. 2a depicts the classical traveling salesman problem (TSP), while Fig. 2b illustrates the multi-target planning problem (MTP). The TSP represents the foundational problem, focusing solely on the sequencing of multiple tasks. Conversely, the MTP extends the TSP by integrating collision avoidance considerations along the paths.

Figure 2
figure 2

Different multitasking planning problems. (a) TSP, (b) MTP.

Full size image

The MTP problem applied to agricultural environments will be stratified and decoupled in the next section, and we will use the energy cost as the evaluation criterion. Assuming that the speed of the robot in the linear motion state is constant as \(v\), the energy consumption cost function \(Ecost\) is:

$$Ecost=\frac{1}{\frac{a}{l}+\frac{b}{n+0.01}+\frac{c}{{f}_{p}(l+\eta \times angle\times r)/v}}$$
(1)

where, \(l\) denotes the path length; \(n\) as the number of turning nodes of the path; \({f}_{p}\) is the robot motor power, \(\eta\) is the turning energy efficiency; \(angle\) is the cumulative turning angle of the path; \(r\) is the radius of the robot's wheels; \(a + b + c = 1\) is the weighting factor.

Below is the mathematical model description for MTP: Given a set of \(n\) task objectives \(G = \{ {G}_{1},{G}_{2},..., {G}_{n} \}\), the primary objective is to determine the optimal collision-free path that visits each target area exactly once while satisfying the constraints of Eq. (2) with minimal cost. Here, the energy cost \({Ecost}_{ij}\) between each target point is pre-solved through collision-free path planning algorithms.

Minimize:

$$mincost=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}{x}_{ij}{Ecost}_{ij}$$
(2)

Subject to:

$$\sum_{j=1}^{n}{x}_{ij}=1, i\in V*$$
(3)
$$\sum_{i=1}^{n}{x}_{ij}=1, j\in V$$
(4)
$$\sum_{j=s}\sum_{j\in s}{x}_{ij}\le |s|-1, \forall s\subset V and 2\le |s|\le n-1$$
(5)
$$x_{{ij}} = \left\{ {\begin{array}{*{20}l} {1,} & {if\,(i,j)\,in\,the\,path} \\ {0,} & {other} \\ \end{array} } \right.,$$
(6)

where, \(mincost\) represents the final cost of the collision-free path, while \(|V|\) denotes the number of target points in the region. Constraints (3–4) are utilized to define closed loops, ensuring that each point has precisely one path originating from it and one terminating at it concurrently. Constraint (5) is imposed to avert the emergence of small loops, guaranteeing the absence of any sub-circuit solutions. Within constraint (6), \({x}_{ij}\) denotes a binary variable that equals 1 only when a path exists. When \({C}_{ij}={C}_{ji}\) holds true, the problem is referred to as symmetric TSP; otherwise, it is a asymmetric TSP.

Algorithm description

Numerous studies have concentrated on MTP research, with the simplest approach to addressing such problems involving direct decoupling23, dividing them into two independent tasks. For instance, the A* algorithm can be utilized to determine collision-free path planning between tasks, followed by the application of a genetic algorithm to optimize the sequencing of these tasks.

A* algorithm

The A* algorithm is a heuristic search technique developed on the foundation of Dijkstra's algorithm and breadth-first search algorithm. As a classical heuristic approach, it finds widespread application in determining optimal paths. Throughout the search process, it calculates the actual cost value \(G(n)\) from the start node \(s\) to the expanded node \(n\), the heuristic value \(H(n)\) from the expanded node \(n\) to the target node \(g\), and the cumulative cost value \(F(n)\), which is the sum of the former two. The algorithm then selects the node \(n\) with the minimum corresponding \(F(n)\) value as the next expanded node. The expression for the evaluation function of the A* algorithm is as follows:

$$F(n)=G(n)+H(n)$$
(7)

where, the heuristic surrogate value \(H(n)\) is computed as can be manhattan distance, diagonal distance or Euclidean distance, which are computed as shown in the following equations, respectively:

$${d}_{M(n)}=\left|{x}_{n}-{x}_{g}\right|+\left|{y}_{n}-{y}_{g}\right|$$
(8)
$${d}_{E(n)}=\sqrt{{({x}_{n}-{x}_{g})}^{2}+{({y}_{n}-{y}_{g})}^{2}}$$
(9)
$${d}_{E(n)}=\sqrt{{({x}_{n}-{x}_{g})}^{2}+{({y}_{n}-{y}_{g})}^{2}}$$
(10)

where, \(({x}_{n},{y}_{n})\) denotes the coordinates of the current node and \(({x}_{g},{y}_{g})\) represents those of the target node. Unlike manhattan distance and diagonal distance, euclidean distance more accurately portrays the path's real-world scenario. Therefore, working with euclidean distance can provide rich heuristic information for the 24-neighborhood A* algorithm proposed in this paper.

Genetic algorithm

Genetic Algorithm (GA) is an optimization problem-solving approach that simulates the natural evolutionary process, drawing inspiration from biological evolution theory. By emulating biological evolution processes such as natural selection, genetic variation, and mutation, it explores candidate solutions in the solution space and iteratively improves them to discover the optimal or near-optimal solution. Key characteristics of the algorithm include direct manipulation of structural objects without the need for gradients or function continuity, inherent implicit parallelism, and superior global optimization capabilities. The fundamental operational process unfolds as follows:

Step 1 Encoding: Individuals are encoded based on the problem model, typically utilizing binary, floating-point, or symbolic encoding techniques.

Step 2 Initialization: The evolution generation counter is set to \(t=0\), with the maximum evolution generation \(T\) specified. \(M\) individuals are randomly generated to form the initial population \({P}_{0}\).

Step 3 Fitness Evaluation: The fitness of each individual in the population \(P(t)\) is computed.

Step 4 Selection Operation: Selection operators are applied to the population to select superior individuals for propagation to the next generation or to generate new individuals through crossover. Common selection operators include roulette wheel selection, random competition, elitism, and stochastic universal sampling.

Step 5 Crossover Operation: Crossover operators are applied to the population to promote the exchange of genetic information. Typical crossover operators include single-point, two-point, uniform, and arithmetic crossovers.

Step 6 Mutation Operation: Mutation operators are applied to the population to introduce random changes in individual genes, thereby preserving diversity. Common mutation operators include basic mutation, uniform mutation, boundary mutation, and non-uniform mutation.

Step 7 Termination Condition Evaluation: If \(t=T\), the individual with the highest fitness is outputted as the optimal solution, and the computation terminates.

MTP layered decoupling algorithm

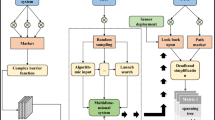
In this section, we provide a detailed description of a hierarchical decoupling algorithm designed to address collision-free MTP problems. The algorithm's primary framework is illustrated in Fig. 3. The complex collision-free MTP problem is decomposed into Collision-Free Path Planning (CPP) and Task Scheduling Optimization (TSO), each tackled separately. Initially, the A* algorithm is refined to traverse collision-free paths between pairs of target points while simultaneously optimizing path length, turning points, and corner angles. Subsequently, the multi-region path planning problem is reformulated as a discrete optimization challenge, where a genetic algorithm is applied to optimize the task sequence, aiming to determine the most efficient task execution order under energy constraints.

Figure 3
figure 3

MTP solving framework.

Full size image

Collision-free path planning

The conventional A* algorithm presents certain limitations when navigating through complex obstacle environments, including redundant path nodes, excessive turns, abrupt turning angles, and inefficiencies. These drawbacks directly impede the safety and responsiveness of rescue robots. To address these challenges, this paper introduces the 16-direction Safety A* algorithm (16S-A*). This algorithm aims to enhance search efficiency in free space areas, alleviate the search burden on obstacle-free regions, and optimize the heuristic function to reduce the number of search nodes. Consequently, it facilitates quicker discovery of initial paths, ultimately improving overall path planning efficiency.

16-direction 24-neighborhood security node expansion approach

Despite the diverse mobility options available to mobile robots in real-world scenarios, path planning algorithms based on grid-based map models, such as A* and ant colony optimization, are often constrained by the characteristics of the grid map. These algorithms' search directions are not entirely flexible but rather bound by pre-defined valid directions. Typically, they explore using neighborhood nodes in four directions (up, down, left, right) as illustrated in Fig. 4a, or eight directions (including diagonals) as depicted in Fig. 4b.

Figure 4
figure 4

Node expansion approach for A* algorithm.

Full size image

To enhance the flexibility and precision of path searching in the A* algorithm, it is worth considering the expansion of node exploration directions to widen the search scope. In this regard, this study extends the search directions to encompass 16 directions, utilizing a 24-neighborhood node expansion, as depicted in Fig. 4c. This extension encompasses not only the standard directions of up, down, left, right, and diagonal but also intermediate nodes along the diagonals. The beneficial effects of this approach are evident in Fig. 5, where the search cost for 4 directions is 4, for 8 directions is 3.4, and for 16 directions is 3.2.

Figure 5
figure 5

Path cost of different expansion methods.

Full size image

Expanding node exploration to 16 directions within a 24-neighborhood framework contributes to broadening the search coverage. However, it is crucial to mitigate the risk of traversing invalid paths to ensure the derivation of safe and efficient optimal paths. Therefore, careful consideration of several safety node expansion strategies illustrated in Figs. 6, 7, 8 and 9 is necessary. Note: In the figures, black lines indicate expandable directions, blue lines represent non-expandable directions within the visible range, and yellow grids denote non-expandable directions beyond the visible range.

  1. (1)

    Eight-neighborhood view: As depicted in Fig. 6, only the inner eight neighboring grids within the eight directions are taken into consideration. A node is included in the set of candidate nodes for expansion if there is no collision observed between the current position and the grid lines connecting to the eight neighboring grids within this view.

  2. (2)

    Sixteen-neighborhood view: As illustrated in Fig. 7, the outer sixteen grids in twenty-four directions are considered. A node is added to the set of candidate nodes for expansion if the node under consideration is not located on an obstacle, and the expansion direction does not result in any collisions with obstacles.

Figure 6
figure 6

Eight-neighborhood horizon.

Full size image
Figure 7
figure 7

Sixteen-neighborhood horizon.

Full size image
Figure 8
figure 8

Sixteen-neighborhood non-viewable type A.

Full size image
Figure 9
figure 9

Sixteen-neighborhood non-viewable type B.

Full size image

Subsequently, the set of candidate nodes for expansion is refined (excluding the invisible grids from the sixteen-neighborhood view) to ensure that the planned path does not traverse hazardous areas. Specifically, scenarios where obstacles obstruct the path between the current position and the grid lines within the outer range are eliminated. The yellow grids highlighted in Figs. 8 and 9 represent the invisible grids.

Improving the heuristic function

The heuristic function of the traditional A* algorithm, as depicted in Eq. (7) above, fails to consider the impact of obstacle density on the algorithm's search efficiency. The presence of obstacles between the starting and ending points increases the search space, reduces efficiency, and leads to the generation of numerous redundant nodes. In situations where obstacles are scarce, the heuristic function values closely approximate the actual distance values. In such cases, adjusting the weight of the heuristic function \(\text{h}(\text{n})\) proportionately can effectively decrease the search space, thus enhancing search efficiency. Conversely, in regions with complex obstacle distributions, the heuristic function values tend to be smaller than the actual distance values. In such scenarios, reducing the weight of the heuristic function can increase the number of expanded nodes, thereby expanding the algorithm's search space and improving its ability to find the optimal path to some extent.

We introduce Eq. (11) to calculate the obstacle density \(P\) within the rectangular region formed by the current node and the target node, which is then incorporated into the Eq. (12). The enhanced heuristic function \(f(n)\) dynamically adjusts its weight based on the obstacle density within different regions. The expression is as follows:

$$P=\frac{N}{(\left|{x}_{i}-{x}_{l}\right|+1)\times (\left|{y}_{i}-{y}_{l}\right|+1)}$$
(11)
$$f(n)=g(n)+(1+\frac{r}{R}+ln(e+P))\bullet h(n)$$
(12)

where, \(({x}_{i},{y}_{i})\) is the coordinates of the current node, \(N\) is the number of obstacles in the rectangular area formed by the current node and the target node, and \({x}_{l}\) and \({y}_{l}\) are the boundary lengths of the map, respectively.

The OPEN and CLOSED lists are still used by our improved A* algorithm to manage generated but unexamined nodes and examined nodes during the search process, and the algorithm pseudo-code is as follows:

Algorithm 1
figure a

16S-A*.

Full size image

Floyd path optimization

The paths generated by grid-based global planning algorithms consist of continuous grid lines. However, when navigating in close proximity to obstacles, these paths often exhibit excessive corners and large turning angles. Such characteristics do not align well with the movement patterns of agricultural robots and pose significant collision risks in practical scenarios. To mitigate path curvature and ensure the safe traversal of agricultural robots, this study proposes a strategy to diminish the turning angles of path nodes. This involves post-processing the paths planned by the 16S-A* algorithm, aiming to enhance both the feasibility and safety of the generated paths. The optimization outcomes are depicted in Fig. 10, with the specific steps outlined as follows:

Figure 10
figure 10

Floyd path optimization.

Full size image

Step 1 Key Node Extraction: Sequentially extract three consecutive nodes \({Node}_{i-1}\), \({Node}_{i}\), and \({Node}_{i+1}\) from the initial path. Compare the slope of line segment \(\overline{{{Node }_{i-1}Node}_{i}}\) with that of line segment \(\overline{{{Node }_{i}Node}_{i+1}}\). If the slopes are equal, delete node \({Node}_{i}\). Repeat this process for all nodes to eliminate all collinear nodes, resulting in a path sequence containing only the start point, key nodes, and end point.

Step 2 Redundant Node Removal: Let the path sequence obtained after Step 1 be \(\{{\text{P}}_{i},1\le \text{i}\le \text{n}\}\). Using Fig. 10 as an example, initially connect the start point \({P}_{1}\) to the end point \({P}_{4}\). If the distance \({d}_{2}\) of line segment \(\overline{{P }_{1}{P}_{4}}\) from the obstacle region exceeds the designated safety distance \(l\), connect \({P}_{1}{P}_{3}\). If the distance \({d}_{1}\) of line segment \(\overline{{P }_{1}{P}_{3}}\) from the obstacle is less than or equal to the designated safety distance, node \({P}_{2}\) is considered redundant and is removed from the path sequence. Finally, a path sequence containing \(\{{P}_{1}, {P}_{3}, {P}_{4}\}\) is generated.

Task scheduling optimization

In the task scheduling optimization process, we utilize an Elite Genetic Algorithm (EGA) to encode the task execution sequence of robots and evaluate scheduling schemes based on energy consumption using a fitness function. However, early applications of GA often encounter the issue of super individuals, which results in premature convergence to local optima. To mitigate this challenge, we introduce elite strategies and evolutionary reversals to preserve diversity and sustain the evolutionary capacity of the population. The pseudocode and workflow are outlined below.

Algorithm 2
figure b

EGA.

Full size image

Step1: code

We use the integer permutation coding method to encode the \(n\) target points to be visited by the robot as \(\text{1,2},3,... ,n\), For the MTP problem, the chromosome is defined as \(|k1|k2|\dots |kn|\). For example, if there are 10 task points, then |1|2|4|10|5|6|8|7|9|3| constitutes a valid chromosome. Consequently, we can represent the cost of the chromosome additively, where the cost of |1|2|4| is denoted by \({Cost}_{12}+{Cost}_{24}\).

For the acquisition of path cost, we obtain the asymmetric optimal paths between all the tasks to be accessed by the improved A* algorithm, so as to obtain the path length cost matrix \(Length\_Cost(n,n)\), the number of corners cost matrix \(Smoothing\_Cost(n,n)\), the corner magnitude cost matrix \(Transition\_Cost(n,n)\). As shown in Fig. 11, combined with the evaluation indexes will be quantified into the energy cost matrix \(Energy\_Cost(n,n)\), and ultimately through the GA to determine the lowest cost of the energy cost of the task scheduling sequence.

Figure 11
figure 11

Representation of the cost of multi-region connectivity paths.

Full size image

Step2: initialization of populations

After completing the chromosome encoding, it is imperative to generate an initial population to serve as the starting solution. Therefore, determining the number of individuals in the initial population is crucial. Typically, this number is determined based on empirical knowledge, and it varies depending on the size of the problem instance. Usually, it fluctuates between 50 and 300, reflecting the size of the task set.

Step3: the fitness function

Traditional genetic algorithm commonly utilize the reciprocal of the total path length as the criterion for evaluating the fitness function. However, factors influencing the efficiency of robotic tasks are multifaceted. Therefore, within the context of differential-drive robots, this paper integrates multiple evaluation metrics to formulate the following fitness function \(fit\):

$$fit=\frac{1}{Ecost}$$
(13)

where, \(Ecost\) represents the energy evaluation function provided by Eq. (1). A smaller value indicates lower costs for robot operations with this sequence of multiple task points, thereby reflecting a higher \(fit\) value. Consequently, a higher fitness value implies a greater likelihood of selecting this encoded path.

Step4: stochastic universal sampling

With a certain probability, optimized individuals are directly transmitted to the next generation, or new individuals are generated through pairwise crossover and subsequently passed on to the next generation. The selection process relies on evaluating individual fitness within the population. This selection operator is sometimes referred to as the reproductive operator. The higher an individual's fitness value, the greater its probability of selection. Taking the roulette wheel selection method as an example, the probability of selecting an individual is determined by its fitness value:

$${p}_{i}=\frac{{fit}_{i}}{\sum_{k=1}^{M}fit}$$
(14)

Once the probabilities for individual selection are determined, uniformly distributed random numbers are generated to decide which individuals participate in mating. If an individual has a higher selection probability, it has a greater chance of being chosen multiple times, leading to an expansion of its genetic representation in the population. Conversely, individuals with lower selection probabilities are more likely to be eliminated. In the process of roulette wheel selection, if \(N\) individuals need to be selected, the wheel must be spun \(N\) times. To address this, we employ Stochastic Universal Sampling (SUS). In SUS, if \(N\) individuals need to be selected, only \(N\) equidistantly spaced pointers are generated once, allowing the selection of \(N\) individuals. Suppose the total fitness value is \(F\) and the number of individuals to be selected is \(N\), the specific steps for SUS are as follows:

Step 4.1 Compute the spacing between pointers, denoted as \(P=F/N\).

Step 4.2 Generate a random number between 0 and \(P\) as the starting position for the pointer.

Step 4.3 Calculate the positions of each pointer, denoted as \(Pointers=[Start+i\bullet P]\), where \(i=[\text{0,1},...N-1]\).

Step 4.4 Based on the positions of the pointers, select \(N\) individuals.

Step 5: evolutionary matching crossover operation

Partial match crossover is employed, and only those with enhanced fitness values are retained for subsequent steps; otherwise, the crossover is considered ineffective. To determine the parents for the crossover operation, the parental samples are paired off, and the following steps are executed:

Step 5.1 Randomly select a pair of chromosomes and determine the start and end positions, designated as \(r1\) and \(r\) 2, respectively (the same positions are chosen for both chromosomes in the pair).

Step 5.2 Swap the positions of these two sets of genes.

Step 5.3 Conduct conflict detection. Establish a mapping relationship based on the exchanged gene pairs as shown in Fig. 12. For instance, in the mapping relationship 7-5-2, if there are two genes labeled 7 in the offspring resulting from the second step, they are transformed into gene 2 according to the mapping relationship, and this process continues until no conflicts persist. Ultimately, all conflicting genes are mapped, ensuring that the newly formed pair of offspring genes is conflict-free.

Figure 12
figure 12

Evolutionary matching crossover operation.

Full size image

Step6: evolutionary mutation operations

The mutation strategy involves randomly selecting two points and swapping their positions. Here, "evolution" refers to the unidirectionality of the evolution mutation operator, whereby only those mutations leading to an improved fitness value are accepted, while ineffective mutations are disregarded. As illustrated in Fig. 13, two random integers \(r1\) and \(r2\) are generated on the chromosome to determine the positions where their genes are exchanged.

Figure 13
figure 13

Evolutionary mutation operation.

Full size image

Step7: evolutionary reversal operation

To enhance the local search capability of the genetic algorithm, we introduced a series of consecutive evolutionary reversal operations following the selection, crossover, and mutation stages. Here, "evolution" refers to the unidirectionality of the evolutionary mutation operator, whereby only mutations resulting in an improved fitness value are accepted, while ineffective mutations are disregarded. As illustrated in Fig. 14, two random integers \(r1\) and \(r2\) are generated on the chromosome to determine the positions where their gene sequences are reversed and exchanged.

Figure 14
figure 14

Evolutionary reversal operation.

Full size image

Step8: cyclic operation

Determine whether the set maximum number of genetic generations is satisfied; if not, jump to the calculation of the fitness value; otherwise, end the genetic operation.

MTP layered decoupling algorithm flow

This section outlines a hierarchical decoupling algorithm for MTP, which employs 16S-A* and EGA to address the CPP and TSO problems, respectively. The algorithm's workflow is illustrated in Fig. 15. It is noteworthy that the implementation algorithms within our proposed MTP solving framework are interchangeable. For instance, in the CPP phase, global path planning algorithms such as A*, RRT, or ACO can be utilized. Similarly, in the TSO phase, optimization algorithms like GA, ACO, ABC, or PSO can be employed.

Figure 15
figure 15

MTP layered decoupling algorithm flow.

Full size image

Simulation results

The simulation experiments in this section further confirm the feasibility of the proposed approach. We designed experiments for both single-task and multi-task planning scenarios. Given the limited availability of relevant research references, our validation primarily relies on conducting ablation experiments and comparing against traditional methods to assess the performance of the 16S-A*-Floyd algorithm and the effectiveness of multi-task planning with the 16S-A*-Floyd hybrid EGA. All computations were performed on a computer equipped with an R7-5800H, 2.3 GHz CPU, and 16 GB RAM, using single-thread MATLAB implementation. The algorithm parameters were configured as follows: EGA population size of 100, 200 generations, crossover probability of 0.9, mutation probability of 0.05, turning energy efficiency of 0.8, robot motor power of 120, robot turning radius of 0.5, the speed is 1 and the energy consumption weighting factor is \(a=0.6\), \(b=0.2\), \(c=0.2\)。

Single-task planning experiment

In the single-task planning experiments, the results of the five algorithms are summarized in Table 1 and illustrated in Fig. 16. Among these, the 16-A* algorithm is an enhanced version of the traditional 8-neighborhood search A*, expanded to encompass 16 directions. The 16S-A* algorithm, built upon the 16-A* framework, incorporates safety considerations to circumvent traversing through diagonal obstacles and other non-optimal terrains. The 16S-IA* algorithm further refines this approach by integrating an optimized heuristic function, and following the inclusion of Floyd's post-optimization techniques, culminates in our 16S-IA*-Floyd algorithm. Notably, our proposed 16S-IA*-Floyd algorithm demonstrates a path planning time of 0.1261s, marking improvements of 49.72%, 35.63%, and 40.24% over A*, 16-A*, and 16S-A*, respectively. It is attributed to the fact that we have improved the search neighbourhood mechanism and heuristics of the A* algorithm with a view to reducing the ineffective node expansion directions and improving the path search efficiency. Furthermore, the 16S-IA* algorithm achieves a 13.00% reduction in path planning time compared to our method, owing to our additional focus on the Floyd optimization step. Regarding the number of traversed nodes, both our 16S-IA*-Floyd algorithm and the 16S-A* algorithm traverse 24 nodes, significantly outperforming the other algorithms. This underscores a distinct advantage of our method in minimizing memory overhead and augmenting path search efficiency, particularly in large-scale environment explorations. Our algorithm ultimately yields a path length of 61.8973 m, surpassing A*, 16-A*, and 16S-A* by 1.72%, 0.31%, and 0.68%, respectively. Notably, our method excels in path smoothness, exhibiting fewer path turning points and cumulative turning angles compared to the other algorithms, indicative of smoother paths planned, thus effectively ensuring the safety of agricultural robot operations.

Table 1 Results of single-task planning.
Full size table
Figure 16
figure 16

Single-task planning results. (a) A* algorithm, (b) 16-A* algorithm, (c) 16S-A* algorithm, (d) Ours.

Full size image

In summary, the 16S-IA*-Floyd algorithm presented in this study exhibits superior performance in comprehensive metrics compared to the methods used for comparison. Moreover, paths generated by the A* and 16-A* algorithms often collide with obstacle edges on the map. Through extensive experimentation, the advantages of the 16S-IA*-Floyd algorithm proposed in this paper have been convincingly demonstrated in terms of the overall cost of path execution within the entire robotic system, particularly in enhancing the search efficiency for multi-task CPP.

Multi-task planning experiment

In experiments of this nature, algorithm performance testing was conducted by incrementally increasing planning difficulty and map size. These encompassed open environments of 50 × 50 scale as depicted in Fig. 17, confined environments of 94 × 78 scale, and two categories of large-scale complex environments of 513 × 513 scale, each with 10, 20, 30, and 40 task points randomly distributed. Comparative experiments with A*-GA and A*-EGA fully demonstrated the effectiveness of our proposed 16S-IA*-Floyd hybrid EGA in solving CPP and TSO problems.

Figure 17
figure 17

Testing Map. (a) Open environment, (b) Narrow environment, (c) Large-scale complex environment I, (d) Large-scale complex environment II.

Full size image

Open environment experiment

In the expansive 50 × 50 environment, the outcomes of multi-task robot path planning are detailed in Table 2 and depicted in Figs. 18, 19 and 20. During the resolution of the CPP problem, both the A*-EGA and A*-GA algorithms exhibit similar metrics, owing to their common foundation in the A* algorithm. Distinctions primarily emerge during the TSO problem-solving phase, where EGA and GA implementations diverge. While our algorithm's performance advantages have been previously evident in single-task planning, they are now extended to the CPP problem involving traversal of multiple task points. Our algorithm traversed 1084 nodes, covering 43.4% of the map area, representing a substantial 90.97% enhancement over the other two algorithms. Regarding metrics such as path length, number of turning points, cumulative turning angles, and optimization time, our algorithm surpassed the other two algorithms by 6.59%, 71.43%, 88.51%, and 42.86%, respectively. In the TSO problem-solving phase, our algorithm exhibited advantages over the A*-EGA algorithm by 16.73%, 47.37%, and 56.38% in terms of path length, number of turning points, and cumulative turning angles, respectively, and over the A*-GA algorithm by 2.37%, 60%, and 55.39%, respectively. In terms of optimization time, our method rapidly identified the lowest-cost path combinations between multiple task points. Moreover, from the path performance iteration graph in Fig. 20, it can be observed that both the A*-EGA and our EGA-based methods optimized the path length metric and a composite metric (derived from Formula (1), which comprehensively considers path length, number of turning points, and cumulative turning angles), while the composite metric provides a more comprehensive assessment of path performance, which A*-GA lacks. The experimental value of the composite metric for our algorithm was 41.43, representing improvements of 42.09% and 48.66% over the A*-EGA and A*-GA algorithms, respectively.

Table 2 Experimental results in open environment.
Full size table
Figure 18
figure 18

CPP stage. (a) A*-GA, (b) A*-EGA, (c) Our.

Full size image
Figure 19
figure 19

TSO stage. (a) A*-GA, (b) A*-EGA, (c) Our.

Full size image
Figure 20
figure 20

Path performance iteration. (a) A*-GA, (b) A*-EGA, (c) Our.

Full size image

Furthermore, the experimental results depicted in Figs. 18 and 19 illustrate that the paths generated by our algorithm are more concise and clear compared to those produced by the other two algorithms, indicating superior path quality. In the path performance iteration graph presented in Fig. 20, it is observed that the composite metric value for A*-GA in Fig. 20a did not converge, while the metric curve for A*-EGA in Fig. 20b converged but was less effective than that of our method shown in Fig. 20c. Overall, our proposed algorithm demonstrates superior performance in both the CPP and TSO phases compared to the other two algorithms, highlighting the effectiveness and advantages of our approach in multi-task path planning in open environments.

Narrow environment experiment

Building upon the experimental groundwork established in open environments, we conducted thorough testing of the algorithms in larger-scale and more intricate narrow environments, with 20 task points randomly distributed to assess their adaptability to diverse and complex scenarios. The results are shown in Figs. 21, 22 and 23 and Table 3, during the CPP phase in narrow environments, both the A*-EGA and A*-GA algorithms exhibited similar performance metrics. However, our algorithm outperformed the others by 48.22%, 32.93%, and 44.77% in terms of traversed nodes, turning points, and cumulative turning angles, respectively. In the TSO phase, regarding the optimal paths obtained for task scheduling, our method surpassed the other two algorithms by 44.30% and 48.84% in terms of turning points. Concerning the cumulative turning angle metric, our algorithm achieved a value of 4236.16°, outperforming the other two algorithms by 59.14% and 58.34%, respectively. In both phases, due to the increased coupling among multiple path metrics in the context of multi-task points within narrow environments, although our algorithm slightly lagged behind the others in terms of path length, its comprehensive metric value of 180.23 surpassed that of the A*-EGA and A*-GA algorithms by 35.94% and 38.89%, respectively.

Figure 21
figure 21

CPP stage. (a) A*-GA, (b) A*-EGA, (c) Our.

Full size image
Figure 22
figure 22

TSO stage. (a) A*-GA, (b) A*-EGA, (c) Our.

Full size image
Figure 23
figure 23

Path performance iteration. (a) A*-GA, (b) A*-EGA, (c) Our.

Full size image
Table 3 Results of narrow environment experiment.
Full size table

Additionally, the path planning results illustrated in Figs. 21 and 22 reveal that our algorithm generates smoother paths compared to those produced by the other two algorithms, offering better suitability for robotic operations. Examining the path performance iteration graphs, we observe in Figs. 23b and c that while the path planning metrics in Fig. 23a have not yet fully converged, our algorithm exhibits slightly superior convergence values for path length compared to the A*-EGA algorithm. Notably, our algorithm demonstrates significantly lower convergence values in the comprehensive metric than the A*-EGA algorithm. Overall, our algorithm outperforms others in testing within complex and narrow environments.

Large-scale complex environment experiment

We further expanded our evaluation to include testing in two significantly larger environments, with 30 and 40 task points distributed randomly. This expansion aimed to verify the algorithm's applicability in more complex and diverse scenarios, offering valuable technical insights for real-world applications. For direct comparison, we transformed the path metrics traversed during the CPP phase into a comprehensive metric using Eq. (1). The results are shown in Figs. 24, 25, 26 and 27 and Table 4. In Environment I, our algorithm outperforms the A*-GA algorithm by 86.65%, 50.63%, and 78.45% in terms of traversed node count, CPP comprehensive metric, and TSO comprehensive metric, respectively. Similarly, in the results for Environment II, our algorithm surpasses the A*-GA algorithm by 85.77%, 49.97%, and 75.57% in the same metrics. Additionally, as depicted in Figs. 24, 25, 26 and 27, the path planning results of the A*-GA algorithm fail to converge in both Environment I and Environment II. In Environment I, our algorithm exhibits stable iteration cycles for path length and comprehensive metrics, with convergence values of approximately 70 iterations. Specifically, the convergence values for path length and comprehensive metrics are approximately 3800 and 226, respectively, both superior to those of the A*-GA algorithm. Similarly, in Environment II, our algorithm demonstrates stable iteration cycles for path length and comprehensive metrics, with convergence values of approximately 110 iterations. The convergence values for path length and comprehensive metrics are approximately 4000 and 271, respectively, both outperforming those of the A*-GA algorithm. Overall, in large-scale environments, our algorithm maintains high-quality path planning and stable search performance.

Figure 24
figure 24

A*-GA in environment I. (a) CPP stage, (b) TSO stage, (c) Path performance iteration.

Full size image
Figure 25
figure 25

Our method in environment I. (a) CPP stage, (b) TSO stage, (c) Path performance iteration.

Full size image
Figure 26
figure 26

A*-GA in environment II. (a) CPP stage, (b) TSO stage, (c) Path performance iteration.

Full size image
Figure 27
figure 27

Our method in environment II. (a) CPP stage, (b) TSO stage, (c) Path performance iteration.

Full size image
Table 4 Results of large-scale complex environment experiment.
Full size table

Conclusion

In addressing the multi-task path planning problem, this study proposes a solving framework that decomposes the problem into collision-free path planning and task scheduling optimization. For collision-free path planning, we introduce an enhanced extension of the traditional eight-neighbor search A* algorithm to a sixteen-direction twenty-four-neighbor search, capable of providing more alternative solutions efficiently. We incorporate considerations of path safety and length as optimization objectives to improve the A* algorithm. For task scheduling optimization, we enhance the A* algorithm to determine all asymmetric optimal paths between tasks to be visited. These paths are quantified into an energy cost matrix based on evaluation metrics. Finally, the proposed elite genetic algorithm is employed to determine the task scheduling sequence with the optimal energy cost. This strategy enhances the local search capability and solving efficiency of the traditional genetic algorithm. We conduct a series of experiments for both single-task and multi-task planning scenarios. Through ablation experiments and comparisons with other methods, we validate the performance of the 16S-A*-Floyd algorithm in single-task scenarios and the effectiveness of the hybrid approach of 16S-A*-Floyd combined with EGA in multi-task planning. Experimental results demonstrate the proposed method's good performance and robustness across various scenarios. Looking forward, the proposed method can be further developed for various applications in agricultural contexts, such as multi-region seeding tasks and weed control operations.

In this study, we focus on the environmental aspects concerning the global distribution of static obstacles, with a plan to gradually incorporate more complex factors such as non-flat terrain and dynamic obstacles in future work. Furthermore, we aim to extend our research to three-dimensional environments, leveraging sensor-collected data, including environmental models, complex maritime elements, and dynamic obstacle factors, to establish precise models, thereby enriching the content of multi-task path planning.