Introduction

Al alloy and carbon fiber are popular lightweight materials for aircraft and automotive applications. Often, the manufacturing of various lightweight composite components implies the use of welding technologies1. Friction stir welding (FSW) is an efficient join technology for lightweight materials2. This welding method exhibits pollution-free welding, high welding efficiency, high weld mechanical properties, and small heat distortion, which enables the welding structure of lightweight materials to have low deformation and dimensional stability3,4.

In recent years, FSW has been widely used in the joining of lightweight materials. Some researchers have suggested incorporating underwater welding techniques into FSW (UFSW) to enhance joint performance, reduce welding defects, and extend machine lifespan5,6. Venugopal et al.7 proposed to employ liquid (water) to optimize the FSW process to improve the performance of welded joints and discussed the reasons for the improvement of welded joint performance. Derazkola et al.8 designed a UFSW welding model for PC materials and verified it by experiments. Talebizadehsardari et al.9 achieved PC material UFSW by modeling and experimentation. Lader et al.10 improved the performance of Cu–Zn-Al welded joints by using UFSW. Rizzo et al.11 discussed the difficulties of underwater welding technology monitoring and the application of sensors. The water medium improves the flow and fusion of different materials during the welding process and enhances the strength of welded joints. However, it is not easy to monitor the welding status due to the welding environment in FSW being water.

In underwater monitoring methods, acoustic emission (AE) monitoring technology is employed to monitor and diagnose the defects in the FSW process by detecting elastic waves generated from the internal structure of materials. Dmitriev et al.12 used AE technology to detect FSW of dissimilar aluminum alloys and determine the parameters of the variance stir welding for obtaining a high-quality joint. Ambrosio et al.13 discussed the potential application of AE signals in UFSW and proposed a welding monitoring system. The AE signals are disturbed by underwater noise in different frequency bands, which leads to frequency band overlaps and hinders the qualitative and quantitative analysis of welding defects. It is necessary to design adaptive feature extraction algorithms for different frequency bands. Zheng et al.14 proposed an amplitude-duration-peak frequency-based AE signal filter to eliminate the impact of tidal effects on the AE signal. Bashir et al.15 have designed an AE sensing array to compensate for the noise caused by seawater.

Modal decomposition algorithms are employed for defect monitoring and life prediction of rotating machinery fault diagnosis, which limits the influence of noise on feature extraction by decomposing the feature frequency band16. Li et al.17 proposed a feature extraction method based on entropy theory, which can achieve effective recognition of ship-radiated noise signals. Moreover, the Hilbert–Huang transform is a powerful tool for analyzing and characterizing non-stationary and nonlinear signals by leveraging the advantages of adaptive modal decomposition18. Xu et al.19 applied the Hilbert Huang transform based on empirical mode decomposition to analyze the stability of dual pulse VP-GTAW. Artificial intelligence is increasingly applied in welding monitoring. Such as some intelligent models applied for the recognition and classification of welding status, with the aid of welding images or features of observation targets. Commonly used intelligent models include BP neural network20, SVM21, radial basis function neural networks (RBF)22, and convolutional neural networks (CNN)23. Jiao et al.24 designed an end-to-end machine learning model based on ResNet to achieve recognition of MIG welding penetration depth. The ResNet is applied in defect recognition and online monitoring as the fundamental model for CNN with its unique residual structure and global average pooling. It is a lightweight convolutional network with fewer layers, which limits underfitting in the case of fewer training samples25,26.

The time–frequency spectrum of HHT mainly depends on the decompose frequency band in modal decomposition27. However, the parameters of variational mode decomposition (VMD) are required to set decomposition level K and penalty parameters α before the signal decomposes. The over and under decomposition is caused by improper K values, and the frequency band information loss and redundancy are caused by the improper value of α, which needs to be optimized by optimization algorithms28. The beluga optimization algorithm (BWO) has global search and fast convergence speed, which can quickly solve the global optimal solution and compensate for the shortcomings of VMD29. Moreover, the AE signal is disturbed by noise from aqueous media during the welding process30. This requires a special HHT algorithm based on optimization algorithms and modal decomposition for defect monitoring in UFSW.

UFSW is a potential method for the dissimilar materials joining of Al alloy and CFRTP, which enhances the joint strength by the aqueous medium31. There are rare efficient monitoring methods published to extract features related to defects from the AE signal mingled with the noise from an aqueous medium. This paper proposed a UFSW defect monitoring method based on BWO–VMD–HHT and ResNet18 for the UFSW defect monitoring. The Hilbert Huang transform feature extraction method is optimized by Beluga Optimization and Variational Mode Decomposition (BWO–VMD–HHT) to address the noise interference of AE signals caused by an aqueous medium. The relationship between time–frequency features and welding defects is established by BWO–VMD–HHT, and the BWO–VMD–HHT spectral vector features at welding defects are extracted by PCA. Additionally, the UFSW defect recognition model has been established based on ResNet18 and compared with other time–frequency ___domain analysis methods and classification models, as well as the ability to resist intense noise.

The remainder of this paper is arranged below. Section II shows related experiment setups and mechanisms of UFSW. Section III presents the BWO–VMD–HHT defect prediction algorithm. In Section IV, the time–frequency features are extracted and related to the defects in UFSW. Also, the UFSW defect recognition model is trained by the BWO–VMD–HHT spectral features vector. Section V draws the conclusions.

Material and experimental procedure

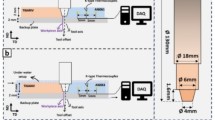
FSW experiment is performed on the HT-JM20 × 8/2 machine from aerospace engineering equipment Su Zhou Co. Ltd. The schematic diagram of UFSW defect monitoring is shown in Fig. 1. The Al alloy and CFRTP plates are placed in the container and clamped by fixture tooling. The AE sensor of R15a from PAC with the response frequency band between 50 Hz and 400 kHz is installed on the side 50 mm away from the edge of the test plate. The test plate is immersed in water, and the temperature of water is kept within an error of ± 2 ℃ by an electric heating.

Figure 1
figure 1

Schematic diagram of UFSW defect monitoring.

Full size image

The UFSW experiments of Al alloy and CFRTP are carried out, and the test plates are prepared in the same size with a length of 150 mm, a width of 100 mm, and a thickness of 2 mm. The pin tool is designed in a cylindrical thread shape. The diameter of the pin is 3 mm, the length is 2.5 mm, and the diameter of the shoulder is 10 mm. Before welding, the surfaces of the two kinds of plates are cleaned with sandpaper and ethanol to remove surface contaminants. In the UFSW experiments, the welding speed is 15 mm/min, the rotation speed is 1900 rpm, and the insertion depth is 2.5 mm. The water temperature is set to be 40 ℃ to 100 ℃ with increments of 20 ℃.

Principles and algorithm

BWO–VMD algorithm

The EMD in HHT is modified by the BWO–VMD algorithm, which enhances the noise resistance of the HHT. The BWO algorithm is introduced into VMD decomposition to improve VMD adaptive extraction of IMF, with \(K\) and \(alpha\) as optimization parameters and IMF entropy as evaluation indicators. The process of the algorithm is shown in Fig. 2. The VMD parameters (as a member of the BWO population) are determined as a base value, and the population range and maximum number of iterations for BWO are defined. The VMD algorithm is defined as:

$$imf(t)=VMD(K, alpha,tol)$$
(1)

where \(imf(t)\) is intrinsic mode function; \(K\) represents the number of decomposition layers, with values ranging from 3 to 20; \(alpha\) is penalty coefficient, with values ranging from 100 to 3000; \(tol\) is convergence tolerance, usually takes the value of \(1\times {10}^{-1} \sim 5\times {10}^{-1}\).

Figure 2
figure 2

Flow chart of VMD algorithm optimization by BWO.

Full size image

The BWO algorithm is defined as:

$${X}_{i\left(t+1\right)}= {X}_{i\left(t\right)}+ A \times {D}_{i} + B \times {C}_{i}$$
(2)

where \({X}_{i\left(t+1\right)}\) is the updated position of whale \(i\) at time \(t+1\). \({X}_{i\left(t\right)}\) is the current position of whale \(i\) at time \(t\). \(A\) and \(B\) are scalar coefficients for controlling the movement. \({D}_{i}\) represents the individual learning term based on the best-known solution within the neighborhood of whale \(i\). \({C}_{i}\) represents the social learning term based on the best-known solution within the population.

Then, the AE signal is decomposed by VMD with initialized parameters. The initial positions of all beluga whales are randomly generated within the search space, and the fitness values are obtained based on the objective function. The fitness function is defined by envelope entropy because it represents the noise characteristics of the IMF component in the AE signal compared to information entropy and sample entropy32. Next, the fitness values of the population are calculated by the fitness function, and the optimal individual is selected. Then, start the BWO main loop, the population is optimized by exploration and the whale fall phase. Finally, the best individual of the population will be found by BWO–VMD after several iterations.

The optimized IMF component is analyzed by the Hilbert time–frequency spectrum to obtain the BWO–VMD–HHT time–frequency spectrum. The Hilbert transform is defined as:

$$H[x(t)] = x(t) + i \times H\{[x(t)]\}$$
(3)

where \(H[x(t)]\) is the Hilbert Transform of \(x(t)\). \(i\) is the imaginary unit. \(H\{[x(t)]\}\) is the convolution of \(x(t)\) with the Hilbert kernel \((1/\pi t)\), and it is computed in the frequency ___domain.

Moreover, the average power of frequency component in the spectrum is defined as:

$${Mean}_{power} = \frac{\sum_{i=1}^{k}power(n)}{{\sum }_{i=1}^{n}power(n)}$$
(4)

where \(k\) is the number of defect feature frequency components. \(n\) is the number of frequency components in spectrum. \(power(n)\) is the power of the \(n\) th frequency components.

ResNet model

ResNet is a deep convolutional neural network architecture. The basic building module of ResNet is the residual block, which consists of multiple convolutional layers. The residual blocks are employed by ResNet to achieve high accuracy in small sample datasets with fewer network structure layers, which is suitable for lightweight real-time monitoring. Moreover, the ResNet is introduced into defect prediction methods and improved by 1D convolution and attention module to learn the welding defect feature frequency bands of the spectrum.

ResNet18 is an efficiently lightweight network of the ResNet architecture with reduced inference time and computational resource consumption. The residual block in ResNet18 can be expressed mathematically as follows:

$$y = F(x, \{{W}_{i}\}) + x$$
(5)

where \(x\) represents the input to the residual block. \(F(*)\) denotes the residual mapping, which consists of one or more convolutional layers. \(\{{W}_{i}\}\) represents the learnable weights of the convolutional layers, and \(y\) represents the output of the residual block.

ResNet18-attention is proposed for lightweight real-time monitoring based on ResNet18. The network structure of ResNet18-attention is shown in Fig. 3. The input and output dimensions of each layer in the network structure are shown in Table 1. ResNet18-attention is fine-tuned based on the ResNet18 network, which replaced the 3 × 3 convolution module with the 1 × 3 convolution module and performed convolutional learning on each frequency band, respectively. In addition, an attention module is set after the convolutional layer to increase the learning ability of the convolutional layers. The train hyperparameters of the ResNet18-attention prediction models are set to 1000 epochs, with a learning rate of 0.001 and an activation function of ReLU. It is far from scientific and comprehensive to evaluate an algorithm model only by the accuracy, so the precision, recall, and F1-Score, whose meaning are introduced to evaluate the model.

Figure 3
figure 3

The network structure of ResNet18-attention.

Full size image
Table 1 The dimension of each layer in ResNet18-attention.
Full size table

BWO–VMD–HHT algorithm

The BWO–VMD–HHT algorithm is designed to solve the Hilbert Huang transform (HHT) frequency band mixing caused by impact noise. The procedure of the defect monitoring method based on BWO–VMD–HHT and ResNet is shown in Fig. 4. Firstly, the two hyperparameters in the VMD are optimized by BWO, and then the intrinsic mode function (IMF) is extracted from the AE signal by optimized VMD. Additionally, the BWO–VMD–HHT time–frequency spectrum is calculated by Hilbert transform on the IMF, and the BWO–VMD–HHT features are extracted at weld defects. Then, the BWO–VMD–HHT features are reduced by principal component analysis (PCA) to build weld defect feature vectors, and welding labels are assigned in weld defect feature vectors to establish the BWO–VMD–HHT dataset. Finally, the ResNet18 prediction model is trained by the dataset and applied to the prediction and classification of UFSW.

Figure 4
figure 4

Procedure of BWO–VMD–HHT defect monitoring algorithm.

Full size image

Results and discussion

Time ___domain analysis

The Al-CFRTP UFSW joint surfaces and AE signals at water temperatures of 40, 60, 80, and 100 ℃ (marked T40, T60, T80, and T100.) are shown in Fig. 5. From the photo of welding surfaces, T80 has a neat surface compared with the other three cases. From the AE signals, the total time of the signal is 120 s during the welding. The whole process is divided into multiple zones according to the states of the welding surfaces, including the normal weld zone and surface crack zone. In the normal weld zone of four cases, the amplitude of the AE waveform remains stable around 2 V. In the surface crack zone of four cases, multiple impulse signals with an amplitude of 5 V appear in the AE signal, which reflects the position of surface defects.

Figure 5
figure 5

Time ___domain analysis of AE signal in T40 ~ T100.

Full size image

BWO–VMD–HHT analysis

A comparative experiment for FSW and UFSW on common HHT is carried out based on the T40 welding parameters. The AE signals are transformed by HHT with the time–frequency spectrum shown in Fig. 6. It is found that the HHT spectrum power of the AE signal in the FSW is concentrated at 22.5 kHz. For the UFSW, the power in the 22.5 kHz frequency band decreases by 30%, and the spectrum power is scattered in the range of 20 kHz to 25 kHz. The reason is that the empirical mode decomposition (EMD) algorithm in HHT is sensitive to noise, which leads to lower signal-to-noise ratio (SNR) and also modal mixing in the time–frequency spectrum.

Figure 6
figure 6

HHT spectrum of FSW and UFSW. (a) The HHT spectrum of FSW. (b) The HHT spectrum of UFSW.

Full size image

The EMD is substituted with the BWO–VMD in HHT to increase the SNR of time–frequency spectrum. Firstly, two hyperparameters in the VMD, \(K\) and \(alpha\), need to be evaluated by BWO. The envelope entropy function is employed as the evaluation criterion of the BWO algorithm, and the BWO hyperparameter is set to the size of populations is 1000 and the number of iterations is 100 epochs. The optimization result of T40 is shown in Fig. 7. It is found that the envelope entropy decreases from 8.99 to 8.955, the \(K\) increases from 3 to 10, and the \(alpha\) increases from 537 to 1563 during the optimization progresses. The best solution is found in 65 iterations when \(K\) is 10 and \(alpha\) is 1563 the envelope entropy of the decomposed IMF component is the smallest. Although the improvement appears to be little in the envelope entropy index, this is a comparison of the results of VMD decomposition between 10 and 3 layers.

Figure 7
figure 7

The result of BWO iteration and VMD decomposition.

Full size image

The time–frequency spectrum is calculated by BWO–VMD–HHT, which is shown in Fig. 8b. Compared to the spectrum from HHT in Fig. 8a, it is found that the main frequency components from BWO–VMD–HHT are concentrated in 20 kHz and 24 kHz, while the ones from HHT scatter in the range of 20 kHz ~ 25 kHz, and the power of the main frequency components from BWO–VMD–HHT is 30% higher than HHT. In addition, the average power of other frequency components (without 20 and 24 kHz) decreased by 60% from 0.03 dBm to 0.01 dBm. So, the BWO–VMD–HHT improves time–frequency resolution and the SNR of the time–frequency spectrum.

Figure 8
figure 8

HHT and BWO–VMD–HHT spectrum of T40. (a) The spectrum of HHT. (b) The spectrum of BWO–VMD–HHT.

Full size image

Time–frequency analysis based on BWO–VMD–HHT

The relation between time–frequency spectrum features by BWO–VMD–HHT and UFSW defects is studied. According to the power of the spectrum, the weld seam is divided into multiple zones. Combined with the microscopic photos of the joint cross-section, it includes the normal weld zone, surface crack defect zone, shallow hole defect zone, and deep hole defect zone. The BWO–VMD–HHT spectra and microscopic photos of the four cases are shown in Figs. 9, 10, 11, 12. It is found that the frequency components of T40, T60, and T80 are concentrated in the spectrum of 20 ~ 25 kHz. The frequency band of 22.5 kHz accompanies the whole welding process in the spectrum, which can be regarded as the main frequency band for AE signals in the UFSW process. There is another phenomenon worth noting that the spectrum of T100 is different from the other three cases, with its frequency components concentrated between 15 kHz and 22.5 kHz, and the power of 22.5 kHz is weak.

Figure 9
figure 9

BWO–VMD–HHT analysis of AE signal in T40.

Full size image
Figure 10
figure 10

BWO–VMD–HHT analysis of AE signal in T60.

Full size image
Figure 11
figure 11

BWO–VMD–HHT analysis of AE signal in T80.

Full size image
Figure 12
figure 12

BWO–VMD–HHT analysis of AE signal in T100.

Full size image

For T40 in Fig. 9, the welding process is divided into three stages according to the BWO–VMD–HHT spectrum. In the first stage, the frequency components are concentrated in the frequency bands of 22.5 kHz and 24 kHz. In the microscopic image, shallow hole defects are found in the joint cross-section located in the blue line. In the second stage, the frequency component is mainly concentrated at 22.5 kHz, and the power in the 24 kHz frequency band is lower than in the first stage. On the surface of the weld joint, surface crack defects are found. In the third stage, the power of 22.5 kHz and 24 kHz frequency bands has been reduced, and the frequency components are transferred to 15 kHz, 18 kHz, and 20 kHz. From the microscopic image, deep hole defects are found in the joint cross-section located in the green line. However, deep hole defects are accompanied by surface crack defects in the third stage, which lead to great power loss in the spectrum.

For T60 in Fig. 10, the welding process is divided into three stages according to the BWO–VMD–HHT spectrum, and shallow hole and surface crack defects similar to T40 are found in the first two stages of T60. The frequency component is concentrated at 22.4 kHz and 24 kHz in the first stage, while the second stage is concentrated at 24 kHz. In the third stage, the power of the frequency component is mainly concentrated at 22.5 kHz, and the power of other frequency bands is relatively weak. In the microscopic image, there is no welding defect but a dense mixture of Al alloy and CFRTP, which is located in the purple line.

For T80 in Fig. 11, the spectrum of T80 has similar features to T40 and T60, and the welding process also has three stages. The frequency component is concentrated at 22.4 kHz in the first and second stages, and the frequency components are concentrated at 22.4 kHz and 24 kHz in the third stage. Also, the surface crack defect is found in the first stage, and the dense mixture of Al alloy and CFRTP material is found on the cross-section of the joint located on the purple line in the second stage. In the third stage, shallow hole defects are discovered in the cross-section of the joint, which is located on the blue line.

For T100 in Fig. 12, the frequency components of the spectrum remain constant, which are concentrated at 15 kHz, 18 kHz, and 20 kHz. However, a frequency band transition phenomenon happened compared to T40, T60, and T80, which is transferred from 22.5 kHz and 24 kHz to 15 kHz, 18 kHz, and 20 kHz. The power of 15 kHz, 18 kHz, and 24 kHz are 0.05 dBm, 0.03 dBm, and 0.03 dBm, respectively. Meanwhile, the power of 22.5 kHz and 24 kHz are 0.02dBm and 0.01dBm, respectively. However, the power of the three frequency components of 15 kHz, 18 kHz, and 20 kHz is 60% higher than compared to T40 deep hole defects, which is because the surface of the T100 is neat and free of defects. In the microscopic image, deep hole defects are found in the joint cross-section, which keeps the whole weld seam. As a display of the deep hole defect in the middle part, it is located at the green line.

From the above results, there is a correlation between the welding defects and the BWO-VMD–HHT spectrum. Corresponding to shallow hole defects, the power of 22.5 kHz decreased from 0.05 dBm to 0.02 dBm, and the power of 24 kHz increased from 0.01 dBm to 0.04 dBm. This is because shallow hole defects create gaps inside the joint and the intense vibration of a thinner air column under the excitation of the pin tool. For the surface crack defect, the power of the 22.5 kHz decreased from 0.05 dBm to 0.02 dBm, and the power of the 24 kHz frequency band increased from 0.01 dBm to 0.03 dBm. This is because surface crack defects damage the surface of the joint, and AE signals are reflected multiple times on the surface, which will cause waveform superposition and mutual interference. This also results in the power transfer to 24 kHz under the excitation of the pin tool. However, the power of 24 kHz in the surface defect spectrum is lower than that of shallow hole defects. This phenomenon is caused by the high sensitivity of AE sensors with the internal stress vibration from lightweight materials. For the deep hole defect, the power of 22.5 kHz and 24 kHz is transferred to 15 kHz, 18 kHz, and 20 kHz. The power of each frequency band in deep hole defects with and without surface crack defects is 0.02 dBm and 0.05 dBm, respectively. The reason is that deep hole defects create gaps deep in the weld seam, and filled weld materials limit deep hole vibration.

Defect prediction and monitoring by BWO–VMD–HHT method

The feature vectors are constructed by BWO–VMD–HHT and PCA algorithms, which comprise the defect recognition model dataset. In BWO–VMD–HHT, the frequency channel is equally divided into 1024 parts in units of 48.5 Hz, and the time channel is divided equally into 15 k parts in units of 10 ms (1024 data points). This means that the dimension of each feature vector is 1024 × 1024. Then, the principal component analysis (PCA) is employed to reduce the feature vector. The covariance matrix of PCA is shown in Table 2. The selection rule of new feature vector is eigenvalues are higher than one, and the accumulated contribution rate is higher than 95% in the covariance matrix. According to the selection rule, the new feature vector dimension is 6 × 1024, including 22.5 kHz, 24 kHz, 20.6 kHz, 18.4 kHz, 15.6 kHz, and 17.3 kHz.

Table 2 The result of PCA and description of feature vectors.
Full size table

The dataset is built by feature vectors under row normalized. There are seven statuses, including four weld defect statuses, two weld stages statuses, and one normal weld status in the dataset, where the number of samples in each status is 20 k and the total number is 140 k. Each sample contains one feature vector with dimension 6 × 1024. The details of the dataset are shown in Table 3. One-hot encoding is applied to label the sample data, and the samples with the same label are randomly divided into three datasets such as the training set, the validation set, and the test set. For each weld state, 70% of the samples are randomly selected for model training, 20% are used for model validation, and 10% are left for model testing.

Table 3 The details of the dataset.
Full size table

The ResNet18-attention is employed for defect monitoring based on the dataset. The confusion matrix is introduced to show the prediction ability of the proposed model clearly, and the results are shown in Fig. 13, where the horizontal axis represents the type of weld defect predicted by the ResNet18-attention model, and the vertical axis represents the true type of weld defect. The seven classification results of the ResNet18-attention model have all reached approximately 90%, and the Precision, Recall, and F1-Score are 0.906, 0.899, and 0.902, respectively. It is concluded that the BWO–VMD–HHT algorithm can effectively extract AE signal features of UFSW welding defects, and the introduction of a one-dimensional band convolution and attention model enables the ResNet18-attention model to learn on the spectrum.

Figure 13
figure 13

Confusion matrix of ResNet18-attention model.

Full size image

Comparative analysis with other methods

The BWO–VMD–HHT is compared with the short-time Fourier transform (STFT), Mel frequency cepstrum (Mel), and continuous wavelet transform (CWT) to verify its effectiveness. The time–frequency features include STFT, Mel, and CWT, where STFT and CWT are feature vectors in the same frequency component as BWO–VMD–HHT, and Mel is the corresponding Mel frequency. Moreover, Muti-SVM, BP, and RBF models are designed with six inputs and seven outputs to verify the performance of the BWO–VMD–HHT dataset in different classification algorithms. The datasets are built by three time–frequency and BWO–VMD–HHT feature vectors and applied to classification algorithms. Also, the precision, recall, and F1-score are introduced to evaluate the ability of classification algorithms.

The prediction results of four models based on the STFT, Mel, CWT, and BWO–VMD–HHT (marked as BVH in Fig. 14) datasets are shown in Fig. 14. The results showed that the precision of models has improved by at least 10%, which are trained by BWO–VMD–HHT features vector. This means that BWO–VMD–HHT features can accurately describe UFSW welding defects and eliminate the influence of water vortex flow noise on AE signals. However, in terms of feature extraction calculation time, the STFT is the shortest only 1.2 s, Mel is 1.5 s, CWT is 124 s, and BWO–VMD–HHT is 3600 s or even longer. This means a lot of time is sacrificed in exchange for recognition accuracy by the BWO–VMD–HHT algorithm, but it is more difficult to apply online monitoring.

Figure 14
figure 14

The prediction results of STFT, Mel, CWT, and BWO–VMD–HHT in four models.

Full size image

The prediction results of BWO–VMD–HHT datasets are shown in Table 4. The precision of the ResNet18-attention model reaches about 90% and has been improved by 20%, 10%, 11%, 12%, 7%, and 6% in precision compared with Muti-SVM, BP, RBF, CNN33, Res-GCM26, and BiLSTM34, respectively. However, the model complexity of BiLSTM is about twice that of ResNet18-attention, and Res-GCM is 0.2 GFLOPs higher than it, which indicates that the ResNet18-attention has the best prediction precision with a not complex model. Additionally, the Gaussian noise with a signal-to-noise ratio of − 2 dB and − 10 dB is added to the test dataset to validate the anti-noise performance of ResNet18-attention. It is found that the precision of ResNet18-attention decreased by 2% and 30%, respectively. This indicates that ResNet18-attention has a certain resistance to noise.

Table 4 Prediction results of BWO–VMD–HHT datasets.
Full size table

Conclusion

The defect monitoring method based on BWO–VMD–HHT for Al-CFRTP UFSW is proposed to address the unclear features in AE signals caused by an aqueous medium. Compared with BWO–VMD–HHT and HHT algorithms, the power of the defect frequency band is higher than 30%, and the power of other frequency bands is reduced by 60%. Then, UFSW experiments are carried out, and four typical cases are analyzed based on the BWO–VMD–HHT algorithm. The analysis results indicate that the surface crack defects and shallow hole defects are accompanied by a frequency component transition from 22.5 kHz to 24 kHz, and the power of the 24 kHz in these two defects increases by 10% and 50%, respectively. The deep hole defect is accompanied by a transition phenomenon from 22.5 kHz to 15, 18, and 20 kHz, and the power of each frequency component with or without surface defects are 0.02 dBm and 0.05 dBm, respectively. The feature vectors are built by frequency components in the BWO–VMD–HHT spectrum, and the defect prediction model is built by ResNet18-attention. The test result indicates the average precision of ResNet18-attention is about 90%, and the average precision of models trained with BWO–VMD–HHT has improved by at least 10%. The improved HHT based on the BWO–VMD is an effective time–frequency analysis method for defect monitoring in UFSW. In future work, we’ll explore the employment of ultrasonic C-scan to detect defects in the entire welding joint and study defect monitoring algorithms based on the detection results, which will make the proposed method to locate defects macroscopically and accurately in the welding joint.