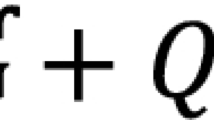Construction of improved comprehensive classes of estimators for population distribution function

In the literature on survey sampling, the use of auxiliary information progresses the precision of an estimators. The finest possible estimates of population metrics like mean, median, variance, standard deviation, etc. have previously been discovered by researchers. To achieve this goal, it is necessary to draw sample from the population; when the target population is uniform, a simple random sampling provide better result. When the study variable and the auxiliary variables have a high degree of association, then the rank of the auxiliary information is also associated to the study variable. The ratio and product estimators can enhance the accuracy of estimators when there is either a positive or negative association between the studied variable and the extra information. By consulting^{1,2,3,4,5,6,7}, the researcher can further investigate these findings using auxiliary variables.

There is a substantial amount of literature available on the topic of population parameter estimate using different sampling approaches. But research based on distribution function (DF) has received less attention compared to the many estimators for estimating distinct finite population parameters under diverse sampling procedures in the literature. In order to determine what percentage of values are less than or equal to the threshold value, it is necessary to estimate a finite population DF. As an example, a doctor would wonder what percentage of the population get at least 20% of their caloric intake from cholesterol in their food. A soil scientist is interested in learning the poverty rate in a developing nation. Initially the technique for estimating the population DF was proposed by⁸. Some essential resources for learning how to estimate population DF using auxiliary information are given in^{9,10,11,12,13,14,15,16}.

There is a substantial amount of literature available on the topic of population parameter estimate using different sampling approaches. But research based on distribution function (DF) has received less attention compared to the many estimators for estimating population parameters. In this paper we suggested improved classes of estimators for estimation of population DF using dual use of an auxiliary variables. Estimation of population DF is required when the percentage of particular values are less than or equal to the specific threshold. To check the robustness and generalizability we have utilized six real data sets and a simulation study.

The remaining of the article is designed as follows. In “Notation and symbols” section, the notations and symbols for the said work is given. The existing estimators were analyzed in “Existing estimators” section. In “Suggested estimators” section, we suggested two improved classes estimators for determining the DF. In “Numerical study” section, the empirical study are given. In “Simulation study” section, we also comportment a simulation study to test the efficacy of our proposed families of estimators using a simple random sample. In “Discussion” section, the numerical results are discussed. “Conclusion” section, provides conclusion of the article.

Let a population \(\Omega =\{1,2,\dots ,N\}\) consist of \(N\) separate and identifiable units, we take a sample of size n from \(\Omega\) using a SRSWOR. Let \(Y\) and \(X\) be the study variable and auxiliary variable. Consider \(Z\) is used for the rank of \(X\). Let \(I(Y\le y)\) signify the indicator variable for \(Y\), and \(I(X\le y)\) signify the display variable for \(X\).

\(\widehat{\mathcal{F}}(x)=\sum_{i=1}^{n}I({X}_{i}\le y)/n\), are the DF functions of \(Y\) and \(X\) for population and sample, respectively. Similarly,

\({\rho }_{12}={\sigma }_{12}/\left({\sigma }_{1}{\sigma }_{2}\right),{\rho }_{13}={\sigma }_{13}/\left({\sigma }_{1}{\sigma }_{3}\right),{\rho }_{23}={\sigma }_{23}/\left({\sigma }_{2}{\sigma }_{3}\right),{\rho }_{14}={\sigma }_{14}/\left({\sigma }_{1}{\sigma }_{4}\right),{\rho }_{24}={\sigma }_{24}/\left({\sigma }_{2}{\sigma }_{4}\right)\).

\({\sigma }_{12}=\sum_{i=1}^{N}\left\{(I({Y}_{i}\le y)-\mathcal{F}(y))(I({X}_{i}\le x)-\mathcal{F}(x))\right\}/(N-1),{\sigma }_{13}=\sum_{i=1}^{N}\left\{(I({Y}_{i}\le y)-\mathcal{F}(y))({X}_{i}-\overline{\mathcal{X} })\right\}/(N-1), {\sigma }_{23}=\sum_{i=1}^{N}\left\{(I({X}_{i}\le x)-\mathcal{F}(x))({X}_{i}-\overline{\mathcal{X} })\right\}/(N-1),{\sigma }_{14}=\sum_{i=1}^{N}\left\{(I({Y}_{i}\le y)-\mathcal{F}(y))({Z}_{i}-\overline{\mathcal{Z} })\right\}/(N-1),{\sigma }_{24}=\sum_{i=1}^{N}\left\{(I({X}_{i}\le x)-\mathcal{F}(x))({Z}_{i}-\overline{\mathcal{Z} })\right\}/(N-1),\)

where \(\lambda =(1/n-1/N)\).

let \({R}_{1.23}^{2}={\rho }_{12}^{2}+{\rho }_{13}^{2}-2{\rho }_{12}{\rho }_{13}{\rho }_{23}/\left(1-{\rho }_{23}^{2}\right)\). Similarly, \({R}_{1.24}^{2}={\rho }_{12}^{2}+{\rho }_{14}^{2}-2{\rho }_{12}{\rho }_{14}{\rho }_{24}/\left(1-{\rho }_{24}^{2}\right)\).

Here, we take some adopted existing for population DF, which is given by

1. 1.

   The usual estimator for DF, is given by:

   $$\widehat{\mathcal{F}}(y)=\frac{1}{n}\sum_{i=1}^{n}{Y}_{i}.$$

   (1)

   The variance of \(\widehat{\mathcal{F}}(y)\):

   $$\text{Var}(\widehat{\mathcal{F}}(y))=\lambda {\mathcal{F}}^{2}(y){C}_{Fy}^{2}.$$

   (2)
2. 2.

   Reference¹⁷ give a ratio estimator for estimating \(\mathcal{F}(y)\):

   $${\widehat{\mathcal{F}}}_{R}(\mathcal{Y})=\widehat{\mathcal{F}}(y)\left(\frac{\mathcal{F}(x)}{\widehat{\mathcal{F}}(x)}\right).$$

   (3)
   $$\text{Bias}({\widehat{\mathcal{F}}}_{R}(\mathcal{Y}))\cong \lambda \mathcal{F}(y)({C}_{Fx}^{2}-{\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}),$$

   and

   $$\text{MSE}({\widehat{\mathcal{F}}}_{R}(\mathcal{Y}))\cong \lambda {\mathcal{F}}^{2}(y)({C}_{Fy}^{2}+{C}_{Fx}^{2}-2{\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}).$$

   (4)
3. 3.

   Reference¹⁸ suggested a product estimator for \(\mathcal{F}(y)\):

   $${\widehat{\mathcal{F}}}_{P}(\mathcal{Y})=\widehat{\mathcal{F}}(y)\left(\frac{\widehat{\mathcal{F}}(x)}{\mathcal{F}(x)}\right).$$

   (5)
   $$\text{Bias}({\widehat{\mathcal{F}}}_{P}(\mathcal{Y}))=\lambda \mathcal{F}(y){\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}},$$

   and

   $$\text{MSE}({\widehat{\mathcal{F}}}_{P}(\mathcal{Y}))\cong \lambda {\mathcal{F}}^{2}(y)({C}_{Fy}^{2}+{C}_{Fx}^{2}+2{\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}).$$

   (6)
4. 4.

   The regression estimator of \(\mathcal{F}(y)\):

   $${\widehat{\mathcal{F}}}_{Reg}(\mathcal{Y})=\left[\widehat{\mathcal{F}}(y)+w(\mathcal{F}(x)-\widehat{\mathcal{F}}(x))\right]$$

   (7)

   where \(w\) is constant.

   $${w}_{(\text{opt})}={\rho }_{12}({\rho }_{Y}/{\rho }_{X}),$$
   $${\text{Var}}_{\text{min}}({\widehat{\mathcal{F}}}_{Reg}(\mathcal{Y}))=\lambda {\mathcal{F}}^{2}(y){C}_{Fy}^{2}(1-{\rho }_{12}^{2}).$$

   (8)
5. 5.

   Reference¹⁹ suggested a difference estimator, given by:

   $${\widehat{\mathcal{F}}}_{R,D}(\mathcal{Y})=\left[{w}_{1}\widehat{\mathcal{F}}(y)+{w}_{2}(\mathcal{F}(x)-\widehat{\mathcal{F}}(x))\right]$$

   (9)
   $$\text{Bias}({\widehat{\mathcal{F}}}_{R,D}(\mathcal{Y}))=\left[\mathcal{F}(y)({w}_{1}-1)\right]$$

   and

   $$\text{MSE}({\widehat{\mathcal{F}}}_{R,D}(\mathcal{Y}))\cong {\mathcal{F}}^{2}(y)({w}_{1}-1{)}^{2}+\lambda {\mathcal{F}}^{2}(y){C}_{Fy}^{2}{w}_{1}^{2}+\lambda {\mathcal{F}}^{2}(x){C}_{{F}_{x}}^{2}{w}_{2}^{2}$$
   $$-2\lambda \mathcal{F}(y)\mathcal{F}(x) {\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}{w}_{1}{w}_{2}.$$

   (10)

   where

   $${w}_{1\left(\text{opt}\right)}=\frac{1}{1+\lambda {C}_{Fy}^{2}\left(1-{\rho }_{12}^{2}\right)},$$
   $${w}_{2(\text{opt})}=\frac{\mathcal{F}(y){\rho }_{12}{C}_{{F}_{y}}}{\mathcal{F}(x){C}_{{F}_{x}}\{1+\lambda {C}_{Fy}^{2}(1-{\rho }_{12}^{2})\}},$$

   Using \({w}_{1\left(\text{opt}\right)}\), \({w}_{1\left(\text{opt}\right)}\) we got:

   $${\text{MSE}}_{\text{min}}({\widehat{\mathcal{F}}}_{R,D}(\mathcal{Y}))\cong \frac{\lambda {\mathcal{F}}^{2}(y){C}_{Fy}^{2}(1-{\rho }_{12}^{2})}{1+\lambda {C}_{Fy}^{2}(1-{\rho }_{12}^{2})}.$$

   (11)
6. 6.

   Reference²⁰ suggested exponential type estimators, given by:

   $${\widehat{\mathcal{F}}}_{BT,R}(\mathcal{Y})=\widehat{\mathcal{F}}(y)\text{exp}\left(\frac{\mathcal{F}(x)-\widehat{\mathcal{F}}(x)}{\widehat{\mathcal{F}}(x)+\mathcal{F}(x)}\right),$$

   (12)
   $${\widehat{\mathcal{F}}}_{BT,P}(\mathcal{Y})=\widehat{\mathcal{F}}(y)\text{exp}\left(\frac{\widehat{\mathcal{F}}(x)-\mathcal{F}(x)}{\widehat{\mathcal{F}}(x)+\mathcal{F}(x)}\right).$$

   (13)
   $$\text{Bias}({\widehat{\mathcal{F}}}_{BT,R}(\mathcal{Y}))\cong \lambda \mathcal{F}(y)\left(\frac{3{C}_{Fx}^{2}}{8}-\frac{{\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}}{2}\right),$$
   $$\text{MSE}({\widehat{\mathcal{F}}}_{BT,R}(\mathcal{Y}))\cong \frac{\lambda \mathcal{F}(y{)}^{2}}{4}(4{C}_{Fy}^{2}+{C}_{Fx}^{2}-4{\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}),$$

   (14)

   and

   $$\text{Bias}({\widehat{\mathcal{F}}}_{BT,P}(\mathcal{Y}))\cong \lambda \mathcal{F}(y)\left(\frac{{\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}}{2}-\frac{{C}_{Fx}^{2}}{8}\right),$$
   $$\text{MSE}({\widehat{\mathcal{F}}}_{BT,P}(\mathcal{Y}))\cong \frac{\lambda {\mathcal{F}}^{2}(y)}{4}(4{C}_{Fy}^{2}+{C}_{Fx}^{2}+4{\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}).$$

   (15)
7. 7.

   Reference²¹ suggested the following estimator, given by:

   $${\widehat{\mathcal{F}}}_{S}(\mathcal{Y})=\widehat{\mathcal{F}}(y)\text{exp}\left[\frac{\alpha (\mathcal{F}(x)-\widehat{\mathcal{F}}(x))}{\alpha (\mathcal{F}(x)+\widehat{\mathcal{F}}(x))+2\beta }\right]$$

   (16)

   The estimator \({\widehat{\mathcal{F}}}_{S}(\mathcal{Y})\) reduces to \({\widehat{\mathcal{F}}}_{BT,R}(\mathcal{Y})\) and \({\widehat{\mathcal{F}}}_{BT,P}(\mathcal{Y})\) when \((\alpha =1,\beta =0)\) and \((\alpha =-1,\beta =0)\), respectively.

   $$\text{Bias}({\widehat{\mathcal{F}}}_{S}(\mathcal{Y}))\cong \lambda \mathcal{F}(y)\left(\frac{3{\Theta }^{2}{C}_{Fx}^{2}}{8}-\frac{\Theta {\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}}{2}\right),$$

   and

   $$\text{MSE}({\widehat{\mathcal{F}}}_{S}(\mathcal{Y}))\cong \frac{\lambda {\mathcal{F}}^{2}(y)}{4}(4{C}_{Fy}^{2}+{\Theta }^{2}{C}_{Fx}^{2}-4\Theta {\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}),$$

   (17)

   where \(\Theta =\alpha \mathcal{F}(x)/(\alpha \mathcal{F}(x)+\beta ).\)

8. 8.

   Reference²² suggested a generalized ratio-type exponential estimator, given by:

   $${\widehat{\mathcal{F}}}_{GK}(\mathcal{Y})=\left\{{w}_{3}\widehat{\mathcal{F}}(y)+{w}_{4}(\mathcal{F}(x)-\widehat{\mathcal{F}}(x))\right\}\text{exp}\left[\frac{\alpha (\mathcal{F}(x)-\widehat{\mathcal{F}}(x))}{\alpha (\mathcal{F}(x)+\widehat{\mathcal{F}}(x))+2\beta }\right],$$

   (18)
   $$\text{Bias}({\widehat{\mathcal{F}}}_{GK}(\mathcal{Y}))\cong \mathcal{F}(y)-{w}_{3}\mathcal{F}(y)+\frac{3}{8}{w}_{3}{\Theta }^{2}\mathcal{F}(y)\lambda {C}_{Fy}^{2}+\frac{1}{2}{w}_{4}\Theta \mathcal{F}(x)\lambda {C}_{Fx}^{2}$$
   $$-\frac{1}{2}{w}_{3}\Theta \mathcal{F}(y)\lambda {\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}},$$

   and

   $$\begin{aligned}&\text{MSE}({\widehat{\mathcal{F}}}_{GK}(\mathcal{Y}))\cong {\mathcal{F}}^{2}(y)({w}_{3}-1{)}^{2}+{w}_{3}^{2}{\mathcal{F}}^{2}(y)\lambda {C}_{Fy}^{2}+{w}_{4}^{2}{\mathcal{F}}^{2}(x)\lambda {C}_{Fx}^{2}+{\Theta }^{2}{\mathcal{F}}^{2}(y)\lambda {C}_{Fx}^{2}{w}_{3}^{2}\\ &\quad +2{w}_{3}{w}_{4}\Theta \mathcal{F}(y)\mathcal{F}(x)\lambda {C}_{Fx}^{2}-\frac{3}{4}{w}_{3}{\Theta }^{2}{\mathcal{F}}^{2}(y)\lambda {C}_{Fx}^{2}-{w}_{4}\Theta \mathcal{F}(y)\mathcal{F}(x)\lambda {C}_{Fx}^{2}\\&\quad +{w}_{3}\Theta {\mathcal{F}}^{2}(y)\lambda {\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}-2{w}_{3}^{2}\Theta {\mathcal{F}}^{2}(y)\lambda {\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}\\&\quad -2{w}_{3}{w}_{4}\mathcal{F}(y)\mathcal{F}(x)\lambda {\rho }_{12}{C}_{{F}_{y}}{C}_{{F}_{x}}.\end{aligned}$$
   $${w}_{3(\text{opt})}=\frac{8-\lambda {\Theta }^{2}{C}_{Fx}^{2}}{8\{1+\lambda {C}_{Fy}^{2}(1-{\rho }_{12}^{2})\}}$$
   $${w}_{4(\text{opt})}=\frac{\mathcal{F}(y)\left[\lambda {\Theta }^{3}{C}_{Fx}^{3}+8{\rho }_{12}{C}_{{F}_{y}}-\lambda {\Theta }^{2}{\rho }_{12}{C}_{{F}_{y}}{C}_{Fx}^{2}-4\Theta {C}_{{F}_{x}}\{1-\lambda {C}_{Fy}^{2}(1-{\rho }_{12}^{2})\}\right]}{8\mathcal{F}(x){C}_{{F}_{x}}\{1+\lambda {C}_{Fy}^{2}(1-{\rho }_{12}^{2})\}},$$
   $${\text{MSE}}_{\text{min}}\left({\widehat{\mathcal{F}}}_{GK}(\mathcal{Y})\right)\cong \frac{\lambda {\mathcal{F}}^{2}(y)\{64{C}_{Fy}^{2}(1-{\rho }_{12}^{2})-\lambda {\Theta }^{4}{C}_{Fx}^{4}-16\lambda {\Theta }^{2}{C}_{Fy}^{2}{C}_{Fx}^{2}(1-{\rho }_{12}^{2})\}}{64\{1+\lambda {C}_{Fy}^{2}(1-{\rho }_{12}^{2})\}}.$$

   (19)

   Here, (19) may be written as

   $${\text{MSE}}_{{\min}}\left({\widehat{\mathcal{F}}}_{GK}(\mathcal{Y})\right)\cong {\text{Var}}_{{\min}}({{\widehat{\mathcal{F}}}_{st}^{*}}{}_{Reg}(\mathcal{Y}))-\frac{{\lambda }^{2}{\mathcal{F}}^{2}\left(y\right)\left\{{\Theta }^{2}{C}_{Fx}^{2}+8{C}_{Fy}^{2}\left(1-{\rho }_{12}^{2}\right)\right\}^{2}}{64\{1+\lambda {C}_{Fy}^{2}(1-{\rho }_{12}^{2})\}},$$

   (20)

By incorporating the auxiliary variables, the design and estimation stages of an estimator can take benefit. When the study variable is associated with the auxiliary variable, then rank of the auxiliary variable is also correlated with each other. Therefore, the rank of the auxiliary variable can be considered as an additional information, it helps to improve the estimator accuracy. To calculate an approximation of the population distribution function, we use more information regarding the sample means and the rank of the auxiliary variable, along with the sample distribution functions of F(y) and F(x).

First improved class of estimator

Taking motivation from \({\widehat{\mathcal{F}}}_{R,D}(y)\), \({\widehat{\mathcal{F}}}_{S}(y)\) and average of \({\widehat{\mathcal{F}}}_{BT,R}(y)\) and \({\widehat{\mathcal{F}}}_{BT,P}(y)\), our first proposed class of the estimator, is given by:

The estimator \({\widehat{\mathcal{F}}}_{P{r}_{1}}(\mathcal{Y})\), is expressed as:

By simplifying (21), we have

The bias and MSE of \({\widehat{\mathcal{F}}}_{P{r}_{1}}(\mathcal{Y})\), are given as

and

The optimum values for \({w}_{5}\), \({w}_{6}\) and \({w}_{7}\), determined (23) are given as:

and

where

Second modified class of estimator

Both the design and estimating stages of an estimator can benefit by incorporating of additional information. When the study variable is highly connected with the auxiliary variable, the rank of the auxiliary variable will also be connected with the study variable. That's why the rank of the auxiliary variable can serve as yet another piece of supplementary data. Using the idea of rank, we proposed a second modified class of estimator, given by:

The estimator \({\widehat{\mathcal{F}}}_{P{r}_{2}}(\mathcal{Y})\), can also be written as

The values of \({w}_{8}\), \({w}_{9}\) and \({w}_{10}\), are given by:

and

The MSE of \({\widehat{\mathcal{F}}}_{P{r}_{2}}(\mathcal{Y})\) at the values of \({w}_{8}\), \({w}_{9}\), and \({w}_{10}\), is given by:

where \({R}_{1.24}^{2}=\left[{\rho }_{12}^{2}+{\rho }_{14}^{2}-2{\rho }_{12}{\rho }_{14}{\rho }_{24}/\left(1-{\rho }_{24}^{2}\right)\right]\) (Table 1).

We take a numerical analysis to compare the existing and the suggested classes of estimators. Six actual data sets are used for this purpose. Tables 2, 3, 4, 5, 6 and 7 present aggregate statistics for the provided data. PRE of an estimator \({\widehat{\mathcal{F}}}_{i}(\mathcal{Y})\) concerning \(\widehat{\mathcal{F}}(y)\) is

Population-I: [Source:²³]:

\(Y\): Number of instructors,

\(X\): number of pupils,

Z: order of X.

Population-II: [Source:²³].

Y: number of an instructors,

X: number of classes,

Z: order of X.

Population III: [Source:²⁴].

Y: the number of fish caught in 1995,

X: The number of fish caught in 1994,

Z: order of X.

Population IV: [Source:²⁴]:

Y: the number of fish caught in 1995,

X: The number of fish caught in 1993,

Z: order of X.

Population V: [Source:²⁵].

Y: The eggs formed in 1990,

X: The amount of per dozen eggs in 1990,

Z: order of X.

Population VI: [Source:²⁶].

Y: The production of apple in 1999,

X: The number of apple plants in 1999,

Z: order of X.

We have generated three populations of size 1000 from a multivariate normal distribution with different covariance matrices. All the populations have different correlations i.e., the auxiliary variable (X) and study variable (Y) are negatively correlated in Population I, but the same variables are positively correlated in Population II, and strongly positive association in case of Population III correlation.

Population-I:

and

Population-II:

Population-III:

\({\rho }_{XY}=\) 0.902645.

The Percentage Relative Efficiency (PRE) is calculated as follows:

The results of MSE and PRE are given in Tables 16 and 17. Here we can only point out the best results of MSEs and PREs in these tables when \(\Theta =\frac{\alpha \mathcal{F}(x)}{\alpha \mathcal{F}(x)+\beta }\) if \(\alpha ={C}_{{F}_{x}}\text{ and }\beta ={\beta }_{2}\).

Table 1, include some elements of the existing and suggested classes of estimators. From the numerical results, which are presented in Tables 8, 9, 10, 11, 12, 13, 14 and 15, We want to bring back the fact that PRE varies for the different choices of a and b. For the data sets, if we use (\(\alpha =1\) and \(\beta ={\rho }_{12}\)), (\(\alpha ={C}_{{F}_{x}}\) and \(\beta ={\rho }_{12}\)) and (\(\alpha ={\beta }_{2}\) and \(\beta ={\rho }_{12}\)) we get the largest values of PRE of all families among different classes. Consequently, the ideal results from the families of estimators are attained by choosing and as the coefficients of variation, kurtosis, and correlation, respectively. It is also found that the second proposed class of estimators \({\widehat{\mathcal{F}}}_{P{r}_{2}}(\mathcal{Y})\) behaves slightly better than the first proposed family of estimators \({\widehat{\mathcal{F}}}_{P{r}_{1}}(\mathcal{Y})\), shown in Tables 8, 9, 10, 11, 12, 13, 14 and 15 which demonstrate the average gain inadequacies for the six populations, respectively, while the first suggested class of estimator \({\widehat{\mathcal{F}}}_{P{r}_{1}}(\mathcal{Y})\) performs better over the second suggetsed class of estimator \({\widehat{\mathcal{F}}}_{P{r}_{2}}(\mathcal{Y})\) with substantial normal improvement inadequacies for the second population. While from Tables 8, 9, 10, 11, 12, 13, 14 and 15 the PRE of all families are diminishing diagonally the values of (\(\alpha =1\) and \(\beta =N\mathcal{F}(x)\)).

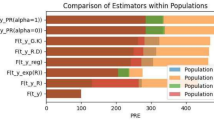
For visualization, we take population 1 and 4 respectively, in descriptions of these graphs we mention that what kind of trash holed we used for finding distribution function. The comparison of numerous estimators in terms of PRE for six populations is depicted in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. The length of a bar is directly associated with the efficiency of an estimator. However, it can be conditional that the suggested estimators, in our case shown by \({\widehat{\mathcal{F}}}_{P{r}_{1}}(\mathcal{Y})\) and \({\widehat{\mathcal{F}}}_{P{r}_{2}}(\mathcal{Y})\), have outperformed the other competitive estimators. Across the suggested class, it is observed that the second proposed class of estimator is more robust than the first proposed class of estimators, because of higher efficiency. Tables 16 and 17 show that the proposed estimators outperform all other estimators currently in use. When X and Y are highly positively correlated, the PRE demonstrates that the second family of estimators proposed in SRS provides a reliable estimate.

Percentage of relative efficiencies of existing and proposed estimators when \(\{x=\overline{{\mathcal{X}}},y=\overline{{\mathcal{Y}}}\}\), using Population 1.

Full size image

Percentage of relative efficiencies of existing and proposed estimators when \(\left\{x={Q}_{1}(x),y={Q}_{1}(y)\right\}\), using Population 1.

Full size image

Percentage of relative efficiencies of existing and proposed estimators when \(\left\{x=\widetilde{\mathcal{X}},y=\widetilde{\mathcal{Y}}\right\}\), using Population 1.

Full size image

Percentage of relative efficiencies of existing and proposed estimators when \(\left\{x={Q}_{3}(x),y={Q}_{3}(y)\right\}\), using Population 1.

Full size image

Percentage relative efficiencies of existing and proposed estimators when \(\{ x=\overline{{\mathcal{X}}},y=\overline{{\mathcal{Y}}}\}\), using Population 4.

Full size image

Percentage of relative efficiencies of existing and proposed estimators when \(\left\{x={Q}_{1}(x),y={Q}_{1}(y)\right\}\), using Population.

Full size image

Percentage relative efficiencies of existing and proposed estimators when \(\left\{x=\widetilde{\mathcal{X}},y=\widetilde{\mathcal{Y}}\right\}\), using Population 4.

Full size image

Percentage relative efficiencies of existing and proposed estimators when \(\left\{x={Q}_{3}(x),y={Q}_{3}(y)\right\}\), using Population 4.

Full size image

In this article, we have suggested two improved classes of estimators to estimate the finite population DF using dual auxiliary varaible. The bias and MSE of the suggested classes of estimators are derived up to the first order of approximmation. To observe the efficiency of estimators, six real data sets are used. Also To check the uniqueness and generalizability of the suggested classes of estimaators, we also employ a simulation study. Based on the numerical outcomes, it is observed that the suggested classes of estimators are more efficient than the exisitng estimators, for all the considered populations. The suggested modified classes of estimators \({\widehat{\mathcal{F}}}_{P{r}_{1}}(\mathcal{Y})\) and \({\widehat{\mathcal{F}}}_{P{r}_{2}}(\mathcal{Y})\) perform better as compared to all other considered estimators, although \({\widehat{\mathcal{F}}}_{P{r}_{2}}(\mathcal{Y})\) is the best. The current work can be extended to estimate population mean using calibration approach under stratified random sampling.