Introduction

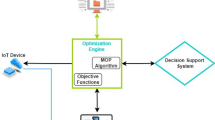
In the realm of service-oriented computing, Web Service Composition (WSC) involves amalgamating numerous web services to generate a novel, more intricate service offering enhanced functionality1. In other words, it is the process of aggregating different web services to establish a novel service that fulfills a particular need or solves a particular problem2. WSC allows developers to leverage the functionality of existing web services to create new services without having to build everything from scratch. By combining the capabilities of multiple web services, developers can create more powerful and flexible applications that can meet a wider range of user needs. Overall, WSC is an important aspect of modern web application development, as it allows developers to build more robust and powerful applications using existing services while taking into consideration various Quality of Service (QoS) attributes. The goal is to ensure that the resulting composite service meets the desired level of QoS requirements3. This is an NP-hard4 problem it includes nm possible solutions for a workflow that comprises n tasks and m web services assigned to each task. Figure 1 presents the WSC model.

QoS-aware WSC encompasses the process of selecting suitable web services according to their QoS characteristics, engaging in QoS agreement discussions between providers and users, and overseeing and controlling QoS levels throughout the service operation5. QoS-aware composition methodologies also take into account the influence of QoS on the total expense of the service composition, including Throughput (T), Reliability (R), Cost (C), and Response Time (RT). These four QoS characteristics are utilized in the present study.

QoS WSC is essential in service-oriented architectures, where multiple services are integrated to provide a more complex functionality. By incorporating QoS awareness into the composition process, the resulting composite service can provide improved performance, reliability, and security, which can lead to better user experience and increased trust in the service. The QoS WSC is a crucial component in developing high-quality web services and applications that meet the expectations of users while maintaining a high level of performance, reliability, and security. WSC is the process of producing more complex and useful services by combining multiple web services. Swarm Intelligence algorithms have the potential to be applied in WSC in order to discover the most efficient combination of web services that meet the needs of users6.

Swarm Intelligence represents the aggregate conduct of distributed, self-regulating systems, drawing inspiration from the actions observed in social insect communities like ant colonies and bee hives. Swarm Intelligence algorithms are optimization techniques that simulate the collective behavior of these social insect colonies to solve complex optimization problems7. In Swarm Intelligence algorithms, a group of simple agents, known as “particles” or “swarm members,” interact with each other and with their environment to find an optimal solution. The agents communicate with each other, exchange information, and adapt their behavior based on local and global feedback to reach a common goal. The most common Swarm Intelligence algorithms are Whale Optimization Algorithm (WOA), Particle Swarm Optimization (PSO), Bee Algorithm (BA), Artificial Bee Colony (ABC), and Ant Colony Optimization (ACO. These algorithms have been successfully applied in various fields, such as engineering, finance, robotics, and biology, to solve complex optimization problems that are difficult or impossible to solve with traditional optimization methods8.

Fig. 1
figure 1

The modelling of WSC problem.

Full size image

WSC involves the integration of various web services to establish a novel service that aligns with the needs of the user. It is a challenging task that requires the consideration of multiple parameters such as QoS. To address this challenge, researchers have proposed various optimization algorithms, including WOA. The WOA is a computational technique that draws inspiration from the collective actions of humpback whales in their natural environment. This algorithm operates on a population basis, simulating the social interactions observed in whale communities, including activities like bubble-net feeding and prey herding. Initially, WOA creates a set of potential solutions, referred to as “whales,” through a random process. These solutions are then iteratively refined using search procedures that are guided by the behaviors exhibited by whales in nature. One of the advantages of WOA is that it can efficiently handle the optimization of multiple objectives, which is a critical requirement for WSC. For instance, QoS parameters such as response time and throughput are typically conflicting objectives, and optimizing one objective may compromise the other. WOA possesses the capability to harmonize various objectives and ascertain a collection of ideal solutions that meet the criteria set forth by the user. Another advantage of WOA is that it can handle complex search spaces, which is common in WSC. The algorithm uses a set of search operators that can explore the search space efficiently and avoid local optima. In conclusion, WOA is a promising optimization algorithm for WSC due to its ability to handle multiple objectives and complex search spaces. The algorithm has the capability to enhance the performance of WSC systems and elevate the standard of service delivered to users.

The subsequent sections of this manuscript are structured as subsequent; Sect. 3 delivers a thorough examination of the current literature concerning the subject matter. Within Sect. 3, the investigator delineates the methodologies employed in carrying out the investigation. The outcomes section (Sect. 4) illustrates the discoveries of the inquiry. The ultimate segment of the document explicates the findings, deliberates on their consequences, and proposes avenues for prospective research endeavors.

Related work

In recent years, swarm intelligence algorithms have shown promising results in solving the WSC problem, and several studies have investigated their effectiveness in terms of solution quality, convergence speed, and scalability. This literature review aims to provide an overview of the existing research on using swarm intelligence algorithms for web services.

A hybrid Whale Optimization Algorithm (WOA) algorithm9 was suggested by the researcher, which integrates the principles of mutation, non-linear convergence factor, and chaos initialization. The proposed approach is named hybrid WOA (HWOA). Jin et al.10 introduced a refinement to the Whale Optimization Algorithm (WOA) by employing an eagle incorporating uniform mutation. The resultant method is denoted as the Modified Whale Optimization Algorithm (MWOA). This amalgamation of techniques aims to uphold an equilibrium between the exploratory and exploitative capacities of the eagle strategy and WOA. Kumar Mohit et al.11 introduce a resource allocation framework that prioritizes Quality of Service (QoS) using a specialized optimization technique called Fine-tuned Sunflower Whale Optimization Algorithm (FSWOA). This model identifies optimal resources for deploying microservices, meeting the needs of both users and service providers. Dahan Fadl12 proposed an enhanced version of the whale optimization algorithm (IWOA) designed to tackle intricate multi-objective optimization challenges. Its key advantage lies in its straightforward implementation requiring minimal control parameters. Katkam et al.13 introduce an improved version of the whale optimization algorithm aimed at supporting Quality of Service (QoS) in sessions. Nevertheless, their proposed EWOC method, while building upon the enhanced Whale optimization algorithm, neglects the QoS aspects. In addressing the service composition optimization challenge, a WOA-derived algorithm, known as iWOA, is introduced in14. It incorporates Analytic Hierarchy Process (AHP) and Simple Additive Weighting (SAW) techniques to validate parameters for the fitness function and employs tent map and OBL for population initialization. Teng et al.15 introduce the logarithmic energy whale optimization algorithm (LEWOA), which relies on aggregating potential energy and employing a logarithmic convergence factor. They demonstrate that LEWOA outperforms various swarm intelligence algorithms in terms of optimization capability and convergence speed. Gao et al.16 proposed an improved AHP approach to consistency verification and the subsequent ordering for an incomplete judgment matrix is proposed, which can deal with situations where information is insufficient, and inherits all the merits of the traditional AHP approaches. Zhang et al.17 proposed a novel approach to enable trustworthy service evaluation and invocation during the process of composition and can decentralizedly evaluate the trust degree of each service based on a lattice-based trust model to prevent data from being transmitted to untrustworthy counterparts.

Du and Miao18 introduced a novel hybrid service composition optimization method of beetle antenna search and ACO in cloud computing environments. The authors argue that their proposed Be-ACO algorithm is more effective in balancing exploration and exploitation and can generate better solutions. Shree et al.19 introduced a meta-heuristic optimization mechanism for QoS-based web service selection, integrating ACO and ABC algorithms. Yang et al.20 presented a dynamic ant colony genetic algorithm (DAGA) to optimize the cloud services composition. They proposed a framework that combines ACO and genetic algorithms (GA) to address the cloud service composition. The main objective is to search the optimal cloud services combination that meet the user’s preferences while minimizing the cost and maximizing the QoS. a multi-agent ant colony optimization algorithm was presented in21. The proposed method tailored to address the QoS-aware cloud service composition. The findings indicate its superiority over current methods in both solution quality and convergence speed. Shan and Li22 proposed an approach for optimizing the composition of express services using an improved ant colony algorithm. The authors introduce the concept of “express service composition” as a way to dynamically construct a path of service nodes to meet the requirements of express services. Wang et al.23 introduced an optimization algorithm for cloud manufacturing resource service composition. This algorithm is founded on enhancements to both genetic and ant colony algorithms. This algorithm is founded on enhancements to both genetic and ant colony algorithms. The algorithm aims to optimize the use of resources in cloud manufacturing by identifying the most efficient service composition for a given set of user requests. El-allali et al.24 introduced an ACO algorithm to address the problem of service composition. Asghari et al.25 introduced a unique and innovative method for cloud service composition utilizing an inverted ACO algorithm. The paper discusses the limitations of traditional ACO and proposes an inverted ACO algorithm as a solution to these limitations. Fadl Dahan26 suggested a methodology utilizing the Bat algorithm and integrating neighborhood search to enhance its overall performance. In27, a fresh hybridization of the firefly optimization algorithm is introduced within a cloud environment for ___location awareness, incorporating a fuzzy logic-based WSC model termed F3L-WSCM. A QoS-aware optimization model was proposed in28 and established QoS information awareness and quantification mechanisms, and the weights, identified by the variable precision Rough Set, which extracted evaluation indicators from past data, furnished a thorough ranking of service quality performance. In29, an efficient technique is employed to forecast QoS values of web services. This method calculates credibility evaluation by aggregating reputation and trustworthiness, and utilizes an automated approach for determining the weight of QoS attributes. A method combining agent-based and PSO approaches was suggested in reference30, wherein the agent-based technique is utilized for QoS parameter identification, followed by the application of PSO to choose optimal services. In their work, Ahmed and Majid31 presented an agent-based technique grounded on multi-criteria decision-making and Petri net. The trust-enabled service composition model proposed by Li et al.32 comprises three layers: customers, providers, and brokers. The introduction of cloud composition has played a key role in the advancement of service composition within the manufacturing cloud. Bouzary and Chen33 introduced a hybrid method merging grey wolf and genetic algorithms, employing crossover and mutation to prevent local stagnation in the grey wolf algorithm. Yang et al.34 suggested three enhancements to the grey wolf optimizer to effectively balance exploration and exploitation in search mechanisms. They improved exploration through a backward learning approach for initializing the initial population, enhanced the search strategy to promote leaders’ exploration, and optimized exploitation using a nonlinear adjustment strategy.

Evolutionary algorithms have been utilized to tackle this particular issue. Jatoth et al.35 introduced an adaptive genotypes approach based on genetic algorithms, incorporating the use of discrete uniform rank distribution and discrete uniform service rank distribution methods for assessing solution fitness. The optimal approach is suggested in36, along with the introduction of a clustering method to streamline the search space. The search for the most suitable services to meet the workflow requirements is conducted using two distinct methods - the non-dominated sorting genetic algorithm and the beam search strategy. Sangaiah et al.37 presented an effective biogeography-based optimization technique, serving as a practical algorithm with a limited number of control parameters. A combined evolutionary algorithm involving the shuffled frog leaping algorithm and genetic algorithm was recommended in38. A formal algorithm for the minimally unsatisfiable subset was put forth in39 for composing the workflow, with the utilization of a penalty-based genetic algorithm to explore near-optimal solutions.

The swarm-based algorithms mentioned above are constrained by their inability to ensure the optimal path for web services due to the random nature of their behavior. Moreover, the No-Free-Lunch theorem (NLF)40 asserts that these optimizers are incapable of adequately managing all optimization challenges. Consequently, the previously mentioned algorithms struggle to effectively tackle extensive datasets and suffer from diminished efficacy. This discourse serves as a catalyst for the development of novel optimization algorithms aimed at addressing the WSC, which introduces superior evaluation criteria encompassing efficiency and execution time40. In this study, our objective is to address these challenges, focusing particularly on the issue of diminished efficacy, through the distribution of the whale swarm among various agents, ensuring enhanced search efficiency alongside consistent monitoring.

Whale optimization algorithm (WOA)

The WOA algorithm, derived from the hunting behavior of humpback whales, is a metaheuristic optimization algorithm. Introduced by Mirjalili et al. in 201641, it presents a novel approach to handling optimization problems. Modeled after the movement patterns of whales during hunting, the WOA algorithm comprises three key phases: searching for prey, encircling prey, and attacking prey. These phases are utilized to create a population of potential solutions and enhance them through iterative processes.

In the WOA algorithm, each candidate solution is represented as a whale, and the position of the whale corresponds to a possible solution to the optimization problem. The algorithm maintains a population of these whales and iteratively updates their positions based on the three main phases of the whale hunting process.

During the searching phase (encircling prey phase), the whales move randomly in the search space to explore new solutions using Eq. (1) and Eq. (2). During the encircling phase, the whales converge to the best solution found so far and move around it to find a better solution using Eq. (5) and Eq. (6). Finally, during the attacking phase, the whales move directly towards the best solution found so far to refine it using Eq. (7).

$$\vec {D}=\left| {\vec {C}.\overrightarrow {{X_{rand}}} - \vec {X}} \right|$$
(1)
$$\vec {X}\left( {t+1} \right)= \, \overrightarrow {{X_{rand}}} - \vec {A}.\vec {D}$$
(2)

where Xrand is the position of the randomly generated search agent, A is a random number, and D is the distance between the current search agent and the randomly generated search agent.

The equation for updating the value of \(\:\overrightarrow{A}\) and \(\:\overrightarrow{C}\):

$$\vec {A}=2\vec {a}.\vec {r} - \vec {a}$$
(3)
$$\vec {C}=2.\vec {r}$$
(4)

where a is a parameter that decreases linearly from 2 to 0, and r is a random number between 0 and 1.

$$\vec {D}=\left| {\vec {C}. \overrightarrow {{X^{\text{*}}}} \left( t \right) - \vec {X}\left( t \right)} \right|$$
(5)
$$\vec {X}\left( {t+1} \right)= \, \overrightarrow {{X^{\text{*}}}} \left( t \right) - \vec {A}.\vec {D}$$
(6)

where D is the distance between the current position and the position of the best whale.

$$\vec {X}\left( {t+1} \right)= \, \overrightarrow {D^{\prime}} .{e^{bl}}. \cos \left( {2\pi l} \right)+\overrightarrow {{X^{\text{*}}}} \left( t \right)$$
(7)

where l is a random number between − 1 and 1, and b is a constant.

Fig. 2
figure 2

The MA-WOA architecture.

Full size image

The WOA algorithm efficacy has been demonstrated in addressing a diverse array of optimization issues, encompassing nonlinear, multimodal, and high-dimensional problems. Furthermore, its implementation is considered relatively straightforward, with minimal parameters requiring adjustment, rendering it a favored option for numerous optimization endeavors41.

Multi-agent whale optimization algorithm (MA-WOA)

The Multi-Agent Whale Optimization Algorithm (MA-WOA) represents a modification of the Whale Optimization Algorithm (WOA) which integrates multi-agent systems theory. In MA-WOA, a group of individual agents, each representing a candidate solution to the optimization problem, interact with each other and collectively search for the optimal solution42.

In MA-WOA, the agents are divided into several groups or subpopulations, and each subpopulation is considered as a swarm. Each agent in a swarm communicates with the other agents in its swarm and exchanges information about their positions and fitness values43. The information exchange helps the agents to collectively explore the search space and converge towards the optimal solution. MA-WOA also includes a social learning mechanism that allows agents from different swarms to share information with each other. This mechanism helps to prevent premature convergence and encourages the swarms to explore the search space to find new regions.

The architecture of the MA-WOA is illustrated in Fig. 2, where the agents used in the proposed method are: Synchronization Agent, Execution Agent, and Monitor Agent. The description of the agents’ functionality is illustrated in the following sections.

Synchronization agent (SA)

In MA-WOA, the synchronization agent is a special agent that is responsible for coordinating the behavior of the other agents in the group. The synchronization agent receives information from all the other agents about their current position and fitness and then calculates the average fitness and position of the group. Based on this information, the synchronization agent decides on the direction and speed of movement for each agent in the next iteration.

The main role of the synchronization agent is to promote diversity and avoid premature convergence of the algorithm. By continuously adapting the movement of the agents based on the average fitness and position of the group, the synchronization agent ensures that the agents explore different regions of the search space and do not get stuck in local optima.

In general, the coordination agent assumes a pivotal function within MA-WOA’s efficacy by enabling efficient information exchange and collaboration among agents while fostering an equilibrium between exploring and exploiting the search landscape.

The pseudocode for Algorithm 1 delineates the procedural flow of the SA’s functionality and its interrelationship with the other agents within the MA-WOA algorithm.

Algorithm 1
figure a

SA

Full size image

Execution agents (EA)

In MA-WOA, the execution agents are the individual agents (whales) that make up the group working together to solve the optimization problem. In each iteration, each execution agent has a search space position that updates along with its velocity based on a set of rules that are derived from the hunting behavior of humpback whales.

In MA-WOA, the execution agents communicate with each other by exchanging information about their current position and fitness. This communication helps the agents to coordinate their movements and avoid redundancy in their search. The execution agents are also influenced by the behavior of the synchronization agent, which helps to promote diversity and prevent premature convergence. The main role of the execution agents in MA-WOA is to explore the search space and locate promising areas for further exploration. In the search space, the agents move by adjusting their position and velocity according to the positions of the other agents and the fitness of their own position. By iteratively adjusting their movements, the agents converge toward a globally optimal solution.

In summary, the execution agents in MA-WOA are the individual agents that perform the search process. They communicate with each other, adapt their movements based on their own fitness and the behavior of the synchronization agent, and work together to converge towards the optimal solution of the optimization problem.

The pseudocode associated with Algorithm2 articulates the procedural framework governing the functionality of the EAs and elucidates its interconnection with the MA within the context of the MA-WOA algorithm.

Algorithm 2
figure b

EA

Full size image

Monitor agent (MA)

In MA-WOA, a monitor agent is an additional agent that can be added to the system to monitor the performance of the algorithm and provide feedback to the other agents. The monitor agent does not participate in the search process itself, but instead observes the behavior of the execution agents and the synchronization agent and provides information about the progress of the search process.

The main role of the monitor agent is to collect and analyze data about the behavior of the other agents, such as the convergence rate, diversity of the search space exploration, and the frequency of updates to the agents’ velocity and position. Based on this information, the monitor agent can identify potential issues or areas for improvement in the algorithm and provide feedback to the other agents to help guide their movements.

In addition to monitoring the performance of the other agents, the monitor agent can also assist with visualization and data analysis to help users understand the algorithm behavior and the search process progress. This can be especially useful for complex optimization problems where it may be difficult to interpret the behavior of the agents and the candidate solutions quality.

Algorithm 3
figure c

MA

Full size image

Overall, the monitor agent is an optional component that can be added to the MA-WOA algorithm to provide additional feedback and guidance for the other agents. It can help to improve the algorithm efficiency and effectiveness by identifying potential issues and guiding the movements of the other agents toward more promising search space areas.

The multi-agent approach utilization in MA-WOA offers numerous advantages in comparison to the original WOA algorithm. Specifically, it serves to augment the variability within the search procedure, diminishes the likelihood of becoming trapped in local optima, and amplifies the overall search capacity of the algorithm.

The pseudocode correlated with Algorithm3 delineates the systematic structure that underpins the operational mechanisms of the MA, while also clarifying its relationships with the SA and EA in the overarching framework of the MA-WOA algorithm.

Experimental settings and results discussion

We evaluate the efficacy of the MA-WOA algorithm with conventional WOA and state-of-the-art algorithms through a comparative analysis. The objective of this assessment is to substantiate the dominance of the MA-WOA methodology across diverse experimental dimensions. The ensuing sections elaborate on the specifics of the experimental configurations and outcomes.

Experimental settings

This research utilized two separate collections of data to confirm the competitive performance and demonstrate the superior effectiveness of MA-WOA compared to other competing methods. The first set originated from real-world datasets known as QWS 2.044, a widely recognized dataset featuring 2507 web services (WSs) with authentic quality of service (QoS) measurements. This set comprises small-sized datasets, maintaining a consistent task size while varying the number of WSs, totaling 20,000 WSs randomly selected with replacement.

Table 1 Details on the datasets.
Full size table

The second set was generated in a random manner through the utilization of the methodology presented in reference45, where the QoS limitation values spanned from 1 to 1000. This particular collection encompasses datasets of both moderate and significant sizes, sustaining a consistent count of Web Services (WSs) while modifying the range of services provided by individual tasks, resulting in a total of 52,000 WSs. The tabulated data in Table 1 offers comprehensive insights into the datasets, outlining the quantity of tasks and WSs assigned to each task. It is imperative to highlight that the study under consideration evaluates four distinct QoS restrictions: Throughput (T), Reliability (R), Cost (C), and Response Time (RT). Equation (8) presents the mathematical computation to evaluate each proposed solution with respect to these restrictions involves:

Fig. 3
figure 3

Box plots illustrating the average fitness values achieved by the analyzed algorithms when applied to datasets of small size.

Full size image
$${F_i}{\text{=}}\frac{{\mathop \prod \nolimits_{{{\text{j=1}}}}^{n} {{\text{T}}_{{\text{jb}}}}{\text{+}}\mathop \prod \nolimits_{{{\text{j=1}}}}^{n} {{\text{R}}_{{\text{jb}}}}}}{{\mathop \sum \nolimits_{{{\text{j=1}}}}^{n} {{\text{C}}_{{\text{jb}}}}{\text{+}}\mathop \sum \nolimits_{{j=1}}^{n} R{T_{jb}}}}$$
(8)

In the formula, \(\:F\) stands for the solution’s effectiveness for the ith whale, where n represents the task number, and b represents the web services.

In order to guarantee impartial and equitable experiments, all algorithms were executed on the Java operational platform with a standardized system configuration, which includes an Intel(R) Core (TM) i7-7500U CPU @ 2.70 GHz with 8.0GB RAM. The MA-WOA efficacy comparison was assessed in comparison to the Standard WOA and three cutting-edge swarm-based algorithms (WOA10, LEWOA15, and HWOA9).

In order to uphold experimental equity, the parameters for MA-WOA were established to be identical to those of WOA, whereas the parameters for LEWOA, MWOA, and HWOA were adjusted according to the preferences outlined in their individual sources. Ensuring uniformity across all algorithms, the common parameters were normalized with a maximum iteration count (Z) of 500 and a population size (P) of 100.

Moreover, the assessment criteria comprised of the optimal fitness values (BFV), mean execution duration (AET), mean fitness value, and standard deviation (STD) for every algorithm. The trials on every dataset were carried out autonomously 30 times. The value of mean fitness was computed for each iteration, and the time taken to identify the optimal fitness values was documented.

Results discussion

In this segment, we delve into the outcomes achieved by MA-WOA alongside four other algorithms. Figures 3, 4 and 5 depict the results across all algorithms concerning the average fitness solution. The scenarios encompass workflows with 10 abstract tasks in Fig. 3. For each abstract task, there are 200, 400, 600 and 800 candidate services. The scenarios encompass workflows with 30, 40, 50, 60, 70, 80, 90, and 100 abstract tasks in Figs. 4 and 5. For each abstract task, there are 100 candidate services. Table 2 demonstrates all the all algorithms’ results in terms of BFV, STD, and AET. In the table, the values highlighted in bold indicate the optimal performance results.

Fig. 4
figure 4

Box plots illustrating the average fitness values achieved by the analyzed algorithms when applied to the datasets of medium-size.

Full size image

We designed to sets of experiments to verify the capabilities of the MA-WOA in both local exploitation and global search when compared to other algorithms. The first set of experiments focused on small-sized datasets to demonstrate the proficiency of MA-WOA in local exploitation relative to its competitors46. This selection was made due to the small-dimensional search space of the initial group of datasets while maintaining a constant task size. In contrast, the second set of experiments targeted moderate to large dimensions datasets to exhibit the MA-WOA effectiveness compared to other algorithms in global search46. This choice was influenced by the diverse nature of task services they offer and the high-dimensional search space of the moderate to large dimensions datasets.

Local exploitation validation experiments

The experiments were formulated on small-scale datasets. The aim is to verify the effectiveness of the MA-WOA in exploiting local resources. Figure 3 presents the results of all algorithms in terms of average fitness values. The outcomes indicate that, overall, the MA-WOA shows a higher median value in comparison to its counterparts across all datasets. Moreover, the MA-WOA average fitness results display a certain level of concentration. It is worth noting that the absence of outlier values in the figure suggests greater stability in performance for the MA-WOA. The lack of overlapping notches observed between the MA-WOA boxplot and those of rival methods in all datasets presents strong evidence supporting the distinctiveness of the results produced by the MA-WOA. Additionally, the visual representation suggests that the MA-WOA consistently outperformed other methods with notably higher boxplot values across all datasets.

Fig. 5
figure 5

Box plots illustrating the average fitness values achieved by the analyzed algorithms when applied to datasets of large size.

Full size image

Table 2 demonstrates that the MA-WOA algorithm displays significant competitiveness and stability in comparison to other algorithms across various small-size datasets. The MA-WOA demonstrates superior performance compared to its competitors in terms of optimal fitness values and standard deviation. These results highlight the effective performance of MA-WOA, characterized by notable competitiveness and stability. In addition, WOA algorithm attains the lowest values of average execution time, with MA-WOA ranking third after LEWOA and WOA.

Thus, the MA-WOA demonstrates a markedly enhanced efficiency in comparison to the other algorithms. This can be attributed to the effective integration of agents during the optimization phases, along with the role of the MA in directing the EAs toward novel search domains by keeping better solutions for next iterations, thereby facilitating the MA-WOA’s convergence towards the optimal solution. These findings further indicate that, in terms of achieving the optimal solution, MA-WOA exhibits greater stability relative to its algorithmic counterparts. The MA-WOA displays a heightened concentration concerning the distributions of solutions. This phenomenon arises from the MA-WOA’s adeptness in circumventing premature convergence issues through the employment of MA, which effectively monitors the advancement of solutions.

Global search validation experiments

The experiments were formulated on moderate to large dimensions datasets. The aim is to validate the effectiveness of the MA-WOA in performing comprehensive exploration. Figures 4 and 5 depict the mean fitness values achieved by various algorithms over 30 independent iterations. The findings show that, in general, the MA-WOA presents a higher median value compared to its counterparts across all datasets. Additionally, the algorithm’s performance in terms of mean fitness values shows a certain level of consistency. It is noteworthy that the figures indicate the absence of outliers in the MA-WOA results, suggesting a more stable performance.

The lack of overlapping notches between the MA-WOA boxplot and those of rival algorithms across all datasets presents compelling evidence of significant differences in the results achieved by the MA-WOA. Moreover, the graphical representation suggests that the MA-WOA consistently outperformed other algorithms with notably higher boxplots across all datasets.

Analysis of Table 2 reveals the impressive competitiveness and stability of the MA-WOA algorithm in comparison to other algorithms in datasets of medium and large sizes, outperforming them in terms of optimal fitness values and standard deviation. These findings underscore the efficient performance in terms of competitiveness and stability of the MA-WOA algorithm. In relation to average execution time, the WOA algorithm demonstrates the shortest durations, with the MA-WOA algorithm ranking third, following LEWOA and WOA.

Table 2 MA-WOA performance compared to WOA, MWOA, LEWOA, and HWOA.
Full size table

Thus, the MA-WOA exhibits a significantly superior level of efficiency when compared to alternative algorithms. This superiority can be ascribed to the proficient integration of agents throughout the optimization processes, coupled with the function of the MA in steering the EAs toward unexplored search areas in case of not finding new good solutions, thereby promoting the MA-WOA’s exploring the search space efficiently towards the optimal solution. These results further suggest that, with respect to attaining the optimal solution, the MA-WOA demonstrates enhanced stability in relation to its algorithmic peers. The MA-WOA reveals an increased focus concerning the distributions of solutions. This phenomenon stems from the MA-WOA’s proficiency in avoiding premature convergence dilemmas through the utilization of MA, which adeptly oversees the progression of solutions.

Conclusion

This study introduces a decentralized approach incorporated into the WOA algorithm to address the WSC problem. This specific approach is designed to distribute the exploration of the WOA within a framework involving multiple agents, wherein each agent contributes to the exploration of the solution space. The SA plays a pivotal role in coordinating the activities of the different agents within a collective. The EA are tasked with exploring novel solutions within sub-populations using diverse initialization strategies. Meanwhile, the MA oversees these agents, reallocates populations in favor of superior agents, and assists the algorithm in mitigating premature convergence. The outcomes of the experiments demonstrate the enhanced effectiveness and stability of MA-WOA in comparison to four contemporary state-of-the-art algorithms. Through a comparison with 12 datasets of varying sizes, it was further evidenced that the computational efficiency of the MA-WOA surpasses that of its competitive counterparts.

The proposed algorithm is expected to be effectively utilized in diverse optimization problems in future scenarios, showcasing promising results specifically in the context of the WSC problem. Moreover, as a potential avenue for further investigation, the strategies proposed could be extended to address challenges related to premature convergence in a variety of swarm-based algorithms.