Introduction

Vanadium dioxide (VO2) is a phase change material (PCM) that exhibits a sharp structural lattice change from a monoclinic phase, characterized by a semiconducting state, to a tetragonal (rutile) phase, exhibiting metallic behavior. This phase change occurs at a relatively low transition temperature (TC), i.e. around 68 °C1,2,3,4. Furthermore, by doping vanadium dioxide, for example with tungsten, it is possible to tune the phase transition temperature, bringing it to values close to room temperature5,6. During the semiconductor-to-metal phase transition (SMT) and back, the dispersion law of the complex refractive index n + ik gets strongly modified, leading to abrupt changes of the optical properties7,8,9,10. Being a very efficient thermochromic material, VO2 has been extensively studied in the seek for active control of thermal emission, attracting interest in applications in infrared optical systems, smart windows, “smart” blackbody devices for spacecraft, light modulators, and photonic crystals11,12,13,14,15,16,17. Thermally induced SMT in VO2 can be nowadays obtained with nanoscale heaters18, while the optically induced SMT allows for femtosecond timescale19, opening new potentialities in ultrafast optical switching20,21.

As micro/nanotechnology advances, tuneable properties of VO2 are being used in combination with nanostructured media, thus allowing for numerous degrees of freedom in electromagnetic manipulation. An asymmetric Fabry–Perot (FP) cavity based on an ultra-thin VO2 was discovered to lead to almost perfect SMT switching of absorption at 11.75 μm22, while its combination with Au microresonators led to both FP and metamaterial infrared resonances23. Different metamaterial geometries combined with VO2 have been explored since: split ring resonators,24,25 periodic gratings and cylinders,26 Al circular patch arrays,27 sub 10-nm gap metamaterials resonating in the near-infrared28 etc. Furthermore, patterning of VO2 into metasurfaces has enabled smart thermal emitters for thermal management, which is of great importance for both terrestrial and space radiative cooling applications29,30. Metal–insulator-metal (MIM) designs were proposed for multiple resonance tuning in the near-infrared range31, and for tunable emission of magnetic dipolar emitters at 1.54 μm32.

In a more complex configuration33, we designed a plasmonic metamaterial hybridized with VO2, with the optimized resonant absorption behavior in the 3–5 μm, i.e. Mid-wave infrared range (MWIR) range. Specifically, the investigated metamaterial design consists of a thin layer of VO2 sandwiched between an Au ground layer and the Au nanodisks metamaterial. This structure displays MIM resonance when VO2 is in its semiconductor, i.e. cold state. The resonant behavior disappears when the VO2 layer is heated to the transition temperature: metallic VO2 becomes reflective as the underlying Au layer. Several factors such as disk dimensions and periodicity can be adjusted in order to achieve almost unitary absorption in the desired spectral range, which can be switched to zero absorption by changing the VO2 phase. Such behavior can be applied in thermal camouflage systems34,35, thus the need for the experimental confirmation of our numerical proposal.

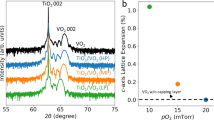
Pulsed laser deposition (PLD) is a very versatile and low-cost deposition technique which has been widely used to produce high quality VO2 thin films without the need for a post-growth annealing step36,37. Beside deposition parameters such as temperature and oxygen pressure, VO2 films optical properties depend also on films thickness. In particular, optical properties such as IR emissivity, show a dynamic range dependent on the films thickness due to a correlation with the crystalline grain size.37.

Following the numerical study and inspired by our previous experimental results,4,5 we here experimentally investigate a structure composed by a thin VO2 layer, deposited by PLD, with a specially designed metamaterial. The present design is based on the tunable resonant absorption achievable in the MIM switchable structure. We experimentally demonstrate a monotonical tuning of the absorption intensity and resonance in the 3–5 μm range as a function of temperature. Finally, we employ detailed numerical modelling to highlight how resonances are affected by the phase transition and how they depend on the fraction of the transitioned part of VO2.

Results and discussion

Sample design

Our sample is based on the resonant absorption in the MIM type of the designs38,39. The metamaterial design consists of a thin layer of VO2 inserted between a 2D matrix of gold nanodisks and a thin continuous gold film, as schematically depicted in the Fig. 1a; the whole metamaterial sits on a CaF2 substrate. This structure provides a typical MIM resonance when VO2 layer is in its semiconductor state (i.e., at room temperature). Several parameters such as metamaterial periodicity p, nanodisk radius r, nanodisk height h, VO2 film and Au ground layer thicknesses, can be optimized to get tuning of the MIM resonance position within the range of interest. When the VO2 layer is heated above the transition temperature, it turns into a metallic state thus it becomes reflective, as the underlying Au layer. Therefore, we can expect a resulting increase of the reflectivity with respect to the resonant state. Moreover, at intermediate temperatures where VO2 has not completely transitioned, it will be possible to exploit a continuous spectral tuning of the resonance, as we show in the following paragraph in the experimental section.

Fig. 1
figure 1

(a) 3D schematic of the unit cell of the metamaterial on CaF2 substrate. (b) SEM image of the sample.

Full size image

For what concerns the Au metamaterial design, the absorption contrast due to SMT in the infrared range was investigated using full-wave 3D electromagnetic simulations based on finite difference time ___domain (FDTD) commercially available solver by Lumerical40. The details of the simulation procedure are given in Methods; the optimization of the MWIR contrast was done in the parameter space of the design geometry30,31,41 The fabrication details are given in Methods, while Fig. 1b shows a representative micrograph of the fabricated device.

Experimental and numerical investigation

Spectral IR reflectivity (R) measurements of the VO2/Au based metamaterial were performed using a Bruker VERTEX 70v FTIR spectrometer coupled with the Hyperion microscope at the INFN-LNF Dafne-Light facility in Frascati. The IR source was a globar while the detector was a liquid nitrogen-cooled mercury − cadmium − telluride photovoltaic element. Concerning with measurement reproducibility, for each measurement a total number of 64 interferograms were acquired, with a spectral resolution of 4 cm−1. The spectral averaging of obtained scans was applied when calculating the reflectivity to improve the signal-to-noise ratio. The sample was placed onto a stabilized heat source (Linkam THMS600 Heating and Freezing stage system) and a control thermocouple was placed in contact with the sample surface to monitor the actual temperature evolution of the sample during measurements. Spectra were collected at different temperatures, ranging from room temperature (26 °C) to 100 °C. Finally, the obtained measurement data were normalized to the spectra of a gold reference mirror. The absorption was calculated as 1-R.

In Fig. 2a, we show the different spectra of the VO2-based hybrid metamaterial obtained when it is heated from room temperature to 100 °C. Experimental results show that there is an efficient tuning of the resonance with increasing temperature. First evidence from Fig. 2a is a large dip in reflectance for the room-temperature (RT) curve at 4.72 μm, which corresponds to the plasmonic gap resonance due to the Au nanodisks metamaterial. This mode is red-shifted as the temperature increases due to the modified dielectric constant of the VO2 layer as a function of the temperature. The observed wavelength tuning range is continuous and broadband since the reflectance dip reaches 5.43 μm at 66 °C, spanning for more than 0.5 μm while the reflection dip becomes shallower. We also assessed the reversibility by cooling the sample down to room temperature and checked the reestablishment of the dip at 4.72 μm even after repeatedly heating/cooling cycles. Although stable and reproducible, the obtained experimental values differ from the designed (ideal) dynamic range (as studied in ref.33), which was expected to be higher (about 1) when the VO2 switches to metallic state.

Fig. 2
figure 2

(a) Experimental spectra showing the resonance tuning of the metamaterial with the temperature. (b) Simulation using Bruggeman formalism and Looyenga mixing rule; f is the fitting parameter which represents the fraction of metallic VO2 during the heating.40,41.

Full size image

To shed light on such effects, we present the numerical fitting procedure which allows us to reconstruct the electromagnetic metamaterial behavior at the micro/nanoscale as the temperature changes. Starting from the fabricated geometric parameters, our goal was to match the simulated absorption spectra with the experimental data at both the highest and lowest temperatures, as well as in the intermediate states. We first used effective-medium approach combined with Bruggeman formalism to retrieve the refractive indices of VO2 during the transition9,42,43 by assuming that in the intermediate states both semiconductor and metallic domains coexist. The best fitting value for the starting (semiconductor-like) state of the VO2 was found to be ncold = 2.7 + 0.6i. Meanwhile, the optimal fit of the VO2 state at the highest temperature (metal-like) was found to be nℎot = 3.4 + 0.7i. These parameters were then used as constant, while we introduced a volume filling factor f as the fraction of the metallic phase which increases with the temperature T: f changes the effective complex refractive index of VO2 according to Looyenga mixing rule.9,44 By using f as a fitting parameter, the resulting fitting process yielded theoretical curves that closely match the experimental results, as reported in Fig. 2b. However, we note the extracted complex refractive indices differ from the ones previously reported by both our4 and other groups9,25, suggesting a potentially incomplete SMT.

In Table 1, we further report the experimentally measured wavelengths of the absorption peaks and the corresponding absorption for different temperature values. In the last column, the absorption at a fixed wavelength, corresponding to the room temperature “semiconductor” absorption peak (@4.72 μm) is shown. We note that the fabrication parameters were obtained following an optimization process with initial refractive indices values reported in ref.4. Using such optimized parameters, we predicted a dynamic absorption range of 0.8 at around 4.3 μm. Moreover, in previous numerical investigation of such design, the dynamic absorption range was proven to be robust to variations of VO2 thickness as high as 10%.33 However, in the experiment, we observed that at room temperature, the peak is positioned at approximately 4.72 μm, and it results in significantly lower dynamic absorption range.

Table 1 Experimental values obtained for the resonant wavelengths and corresponding absorption values.
Full size table

The main reasons for the observed discrepancies could be ascribed to the inhomogeneity, in terms of density and optical parameters (e.g., refractive index), of the very thin VO2 film, which are different than those of thicker films having a different growth regime; such effects were recently experimentally demonstrated in ref.37. This means that the optical parameters of the 60 nm-thick VO2 film, extrapolated by our measurements, may be slightly different than those expected, which refer typically to fully formed VO2 films.

Our results provide a proof of concept of the wavelength and intensity tunability using a hybrid metamaterial based on VO2 phase change. Strategies to overcome technological issues and obtain enhanced/optimized performances will be considered in further work.

In thermodynamic equilibrium, the tuning of the absorption corresponds to the tuneable emissivity. Therefore, in Fig. 3a, we focus on the absorption intensity tuning at the resonant wavelength of the semiconductor-like state (at 4.72 μm); the calculation details for absorption density ρabs and total absorption are given in Methods. When the fraction f of the metallic VO2 phase is increased, the absorption peak gradually becomes lower, following an almost linear trend, as it can be seen on the left axis in Fig. 3a. A similar trend can be seen in experimentally extracted values of absorption at the same wavelength for the different temperatures, reported on the right y-axis of Fig. 3a. Blue, green and red stars on the graph represent the total simulated absorption when the fitting factor f is equal to 0 (semiconductor-like), 0.6 (intermediate) and 1 (metal-like).

Fig. 3
figure 3

(a) Simulated and experimental absorption intensity at the resonant wavelength for the purely semiconductor VO2. Blue, green and red stars on the graph represent the total simulated absorption when the fitting parameter f is equal to 0 (semiconductor-like), 0.6 (intermediate) and 1 (metal-like). Heating increases reflection, hence decreasing absorption, as shown in (b): 3D distribution of the absorption density at f = 0, f = 0.6 and f = 1. (c) Magnetic field intensity as a function of the volume parameter f; the strong magnetic field at the resonant wavelength and f = 0, is gradually switched off as f increases.

Full size image

In Fig. 3b, we further visualize 3D distribution of ρabs in the unit cell, calculated for f = 0, f = 0.6 and f = 1. The obtained results highlight that for f = 0 (i.e. semiconductor-like state), there is a strong absorption between the two metallic layers, due to the plasmonic gap resonances. The absorption decreases as f increases. When the filling factor reaches the unity value, at f = 1, we notice much lower absorption due to the red-shift of the resonant wavelength for the metal-like VO2 state. In Fig. 3c, we highlight the plasmonic gap resonances generating an extremely strong magnetic field in the VO2 layer. Furthermore, the magnetic resonance can be temperature-controlled since heating of the VO2 leads to the increase in the reflectivity, and subsequently switches off the resonance. This feature can be harnessed for several magnetic-dipole based applications.20,31,45

Finally, we show the tuning of the absorption peak resonance as a function of both theoretically calculated filling factor, and the measured temperature. In Fig. 4a, simulated filling factor values (continuous line) show a linear behavior as a function of the fitting parameter f: the resonance is red-shifted with increasing metallic phase content. The blue and the red stars represent the simulated resonant wavelength for the fitting parameter f = 0 (semiconductor-like state) and f = 1 (metal-like state). On the other hand, the experimental values of resonant wavelengths are shown as a function of the temperature (right y-axis). While there is a good agreement for the resonant wavelength in the lower temperature range, there is a discrepancy for the behavior at temperatures above 60 °C since the resonant wavelength stabilizes around 5.43 μm. As already mentioned, we attribute these differences to the complex fabrication process leading to material modifications with respect to ideal VO2. Another issue is the fact that we used two average refractive indices for the semiconducting and metallic VO2 phases, i.e. for f = 0 and f = 1 respectively. In order to better match experimental results with the theoretical calculated values, one would need the ellipsometric characterization for VO2 fabricated with the same procedure and under same conditions. Nevertheless, in the low-temperature range, this device can tune the absorption peak wavelength without drastically altering its absolute value (Table 1). Accordingly, the electromagnetic fields, as it can be appreciated in Fig. 4b, show similar distributions at increasing resonant wavelengths, i.e. when factor f increases. Finally, at resonant wavelengths for f = 0 (4.72 μm) and f = 1 (5.96 μm), the resonant magnetic field is largely concentrated in the VO2 gap between the Au nanodisk and the Au ground layer, Fig. 4c.

Fig. 4
figure 4

(a) Simulated and experimental results for the resonant wavelength as a function of the fitting parameter f (simulation, left axis) and temperature (experiment, right axis), respectively. The blue and the red stars represent the simulated resonant wavelength for the fitting parameter f = 0 (semiconductor-like state) and f = 1 (metal-like state). (b) Distribution of the electric field in the xy-plane positioned 10 nm above the Au nanodisk: resonant wavelengths and the enhancement red-shift with the increase of the factor f. (c) xz-monitor of the simulated magnetic field intensity at resonant wavelengths for f = 0 (4.72 μm) and f = 1 (5.95 μm).

Full size image

Conclusion

In conclusion, we fabricated a VO2-based hybrid metamaterial and experimentally demonstrated the infrared tuning of the resulting gap plasmon resonance. Heating the metamaterial from 26 to 100 °C results into the reversible resonance shift from 4.72 to 5.34 μm. Finally, we have employed numerical modelling to retrieve the effective refractive indices of the VO2 binary system, composed by semiconductor and metallic phases, during the heating process. Numerical calculations highlight that strongly confined magnetic field at the resonant wavelength can be tuned in both intensity and wavelength by temperature control. Even though the total semiconductor-to-metal phase transition was not achieved, the observed tuning is found to be reconfigurable and highly repeatable. We are confident that the investigated design can be refined and improved for optimal tunable absorber applications in the infrared, paving the way for applications where strong absorption contrast over a broad wavelength range is required.

Methods

Numerical simulations

FDTD ___domain surrounds the MIM structure with Bloch boundary conditions (BBCs) in the xy-plane, and the Perfectly Matched Layers (PMLs) in the z-direction. We performed convergence testing to ensure simulation stability in terms of PML properties and distance from the structure (at least one maximum wavelength). The structure is then excited by a linearly polarized plane-wave in the 2–8 μm range coming from the air side. The absorption density in each point of the unit cell is calculated from 3D electric field E and complex permittivity ε monitors at frequency ω as: ρabs = -0.5‧ω‧│E2│‧imag(ε); the total absorption is then calculated integrating ρabs over the unit cell volume. The refractive indices of CaF2 substrate and Au are taken from the Lumerical database, while the initial (pre-fabrication) modelling of VO2 was based on our experimental results from ref.4. Specifically, the best fitting parameters in that study provided average refractive indices for the MWIR for metallic and semiconductor phases of VO2. The optimization was performed by switching the material properties of VO2 layer from semiconductor to metallic and then monitoring the resulting optimal contrast between the two states. The optimization procedure leads to the resulting optimal nanodisk parameters of h = 60 nm, r = 345 nm, and periodicity p = 900 nm, while the optimized thicknesses for VO2 and Au background layers was calculated to be 60 nm and 80 nm, respectively.

Fabrication of the VO2-hybridized metasurface

The device was realized starting from a 1 mm-thick CaF2 substrate. It underwent a cleaning process using an ultrasonic bath containing acetone, isopropyl alcohol (IPA), and distilled water (2 min for each step). Harsh impurities were removed by using oxygen plasma cleaning for 3 min. Subsequently, an 80 nm thick gold layer was grown on the sample using electron beam physical vapor deposition (e-beam PVD), followed by a 60 nm-thick VO2 layer obtained by PLD. On top of the VO2 film, a poly(methylmethacrylate) (PMMA) electron-sensitive resist was spin-coated at 1800 rpm for 1 min and dried on a hotplate at 180 °C for 7 min. The PMMA was then patterned by electron beam lithography at 20 kV with a dose of 500 μC/cm2 and developed in a solution of Methyl isobutyl ketone (MIBK) and IPA (1:3 in volume) at 4 °C for 30 s, stopped in IPA for 30 s and dried with a nitrogen flow. The sample was finally covered with 60 nm of Au by e-beam PVD, and then immersed in hot acetone to remove via lift-off the unexposed resist.