Introduction

Recently, there has been a growing interest in distributed cooperative control of multi-agent systems due to its various advantages over traditional centralized approaches. These advantages include increased flexibility, decentralization, and stronger robustness1. As a result, this field has given rise to numerous research topics, such as consensus2,3, tracking4,5, distributed formation control6,7, containment8, and flocking9. However, most existing literature in this area focuses on systems with single- or double-integrator dynamics and Lipschitz-type dynamics. Although these dynamics are suitable for many applications, the use of such models may not be sufficiently rigorous for networked robotic systems, which are typical examples of multi-agent systems. Instead, employing Euler–Lagrange dynamics provides a more accurate representation of real-world robotic systems and their interactions. This distinction highlights the need for more specialized and precise control strategies of networked robotic systems.

Fig. 1
figure 1

Cluster formation tracking control scenario of NPRS.

Full size image

Therefore, many researchers have been directing their effort toward the collaborative control of networked robotic systems with Euler–Lagrange dynamics10,11,12. However, the existence of actuator input deadzone, parametric uncertainties, and external perturbations is inevitable in networked perturbed robotic systems (NPRSs). These deadzone characteristics often arise in practical robotic systems due to factors such as friction, backlash, and mechanical wear, which introduce nonlinearities and can significantly impair system performance13,14. In addition, NPRSs exhibit inherent characteristics, such as nonlinearity, susceptibility to uncertainties, and inter-joint couplings, further complicating their analysis and control. To address these difficulties, several control algorithms have been developed, including adaptive control15, fuzzy control16, robust control17, and sliding mode control18. In particular, sliding mode control has gained significant attention due to its potential for achieving finite convergence19,20,21/fixed-time convergence22,23,24,25,26,27and robustness in the presence of uncertainties. While finite-time stability ensures convergence within a time frame that depends on the system’s initial conditions, fixed-time stability guarantees convergence regardless of these initial conditions. This key difference enhances system predictability and performance reliability, making fixed-time stability particularly useful in time-critical applications. Significantly, under the framework of finite-time control for switched nonlinear systems with multiple objective constraints, an adaptive finite-time controller based on a multi-dimensional Taylor network is proposed, ensuring constraint compliance and avoiding singularity21. Polyakov et al. have utilized theorems on Lyapunov functions for fixed-time stability analysis to design nonlinear control laws for the robust stabilization of a chain of integrators24. Based on the framework of input-output linearization, the challenge of fixed-time stabilization for nonlinear systems with a full relative degree has been addressed by developing homogeneous feedback laws27. However, achieving fixed-time stability for NPRSs remains an open problem.

Moreover, constructing appropriate equivalent terms to approximate the lumped uncertainty terms of a system is particularly challenging. These uncertainty terms include actuator input deadzone, external perturbations, and parametric uncertainties. Recently, interest in utilizing radial basis function (RBF) neural networks for approximating unknown nonlinear functions has been increasing28,29. In the context of multi-agent systems, the neural network approach presumes that the uncertainties within the system can be accurately approximated by a neural network with adequate capacity and training data. It also presupposes that the dynamics of the multi-agent system can be accurately represented by the neural network to capture the nonlinear characteristics of these uncertainties. Under the neural network-based control strategy, the challenge of fixed-time formation control in nonlinear multi-agent systems has been addressed30. Within the framework of backstepping and utilizing predefined-time stability, the predefined-time adaptive neural tracking control problem for nonlinear multi-agent systems is investigated in31. Hierarchical control strategies, in particular, offer considerable advantages for managing multi-agent systems by enhancing robustness and scalability32,33. By breaking down a global problem into smaller sub-problems, hierarchical framework reduce computational complexity and enhance overall system stability and coordination. Building on this interest, we propose a novel hierarchical fixed-time neural adaptive (HFNA) control algorithm that combines the fixed-time algorithm that uses a hierarchical framework with an RBF neural network. This innovative approach aims to enhance steady-state performance compared with that of conventional methods.

Meanwhile, existing research on cooperative control has focused on cooperative tracking25 and formation tracking34,35,36,37,38, where all robots converge to a single stable state or formation. Specifically, Cheng et al. have investigated single time-varying formation control for heterogeneous multi-agent systems, addressing actuator faults, uncertainties, and perturbations34. Under an adaptive fuzzy control approach combined with a periodic adaptive event-triggered control scheme, single fixed-time formation control for multi-agent systems facing actuator failures is achieved35. Based on a low-complexity control framework ensuring prescribed performance, single formation tracking for networked underactuated surface vessels in a fully quantized environment has been addressed in38. However, these results are not directly applicable to scenarios wherein networked robotic systems are required to perform multiple tasks simultaneously. This motivation has led to research on group consensus39 and multi-tracking40. However, most of the aforementioned studies primarily address state coordination problems in networked robotic systems. By contrast, the current study focuses on the cluster formation tracking (CFT) problem, which involves coordinating the output of subnetworks in an NPRS to form multiple desired formations in local coordinates. Each chosen reference point follows a predefined trajectory in global coordinates while maintaining the formation. In the CFT control task scenario of NPRSs, as shown in Fig. 1, it becomes indispensable to study the fixed-time problem in CFT of NPRSs. This is particularly important when considering actuator input deadzone, external perturbations, and parametric uncertainties, as it addresses a fundamental challenge in the control of networked robotic systems.

Motivated by the aforementioned discussions, this paper introduces the HFNA control algorithm, specifically crafted to address the intricate challenges of fixed-time CFT in NPRSs. By focusing on key issues such as parametric uncertainties, external perturbations, and actuator input deadzone, the HFNA algorithm aims to enhance the robustness and effectiveness of multi-robot coordination. The following are the main contributions of this paper.

  • In contrast with prior research on the finite-time stability of NPRSs, where error states typically reach the origin within a finite time that is dependent on the initial condition19,20,21, we propose a novel HFNA control algorithm that achieves fixed-time stability independent of the initial condition, ensuring a controllable convergence time, which enhances the predictability and reliability of the system’s performance.

  • The proposed HFNA control algorithm provides a comprehensive framework for fixed-time CFT under directed graphs, addressing key challenges in existing studies34,36,38,41 by systematically managing parametric uncertainties, external perturbations, and actuator input deadzone.

  • Different from the conventional fixed-time control algorithms for networked robotic systems26,27, the HFNA control algorithm effectively addresses lumped uncertainty terms while exhibiting minimal chattering by utilizing RBF neural networks to approximate the lumped uncertainty.

The remaining sections are organized in the following sequence. Section Preliminaries provides preliminaries on graph theory, stability theory, neural networks, function approximation, systems, and problems. Section Major results describes the designed HFNA control algorithm with the corresponding convergence analysis. Section Simulations presents the simulation results. Eventually, a concise summary of conclusions is provided in Section Conclusion.

Notations: Let \({{\mathbb {R}}^{d}}\) be the d-dimensional Euclidean space. \({{\mathbb {R}}^{d \times d}}\) represents a \({d \times d}\) real matrix. \(\otimes\) denotes the Kronecker product. \(\mathbf{{1}}_{d}\) refers to a d-dimensional vector with elements equal to 1. The symbols \(\max \{\cdot \}\) and \(\min \{\cdot \}\) denote maximum and minimum magnitudes, respectively. \({\left\| \cdot \right\| _p}\) represents the p-norm. Moreover, the column vectors \(a \cdot b = \mathrm{{col}}({a_1}{b_1},{a_1}{b_1}, \ldots ,{a_1}{b_1})\), \(\forall a = \mathrm{{col}}({a_1},{a_1}, \ldots ,{a_d}) \in {{\mathbb {R}}^d}\), and \(b = \mathrm{{col}}({b_1},{b_2}, \ldots ,{b_n}) \in {{\mathbb {R}}^d}\). For the provided \(\varsigma = \textrm{col}({\varsigma _1}, {\varsigma _2},\ldots ,{\varsigma _N})\) and \(\rho > 0\), it follows that \(\textrm{sig}(\varsigma )^\rho = \textrm{col}(\textrm{sgn}({\varsigma _1})|{\varsigma _1}|^\rho \! , \textrm{sgn}({\varsigma _2})| {\varsigma _2}|^\rho \!,\ldots , \textrm{sgn}({\varsigma _N})|{\varsigma _N}|^\rho \!)\) and \(\textrm{diag}(\varsigma ) = \textrm{diag}({\varsigma _1}, {\varsigma _2},\ldots ,{\varsigma _N})\).

Preliminaries

Graph theory

In this paper, we consider a NPRS comprising N robots. The communication topology in NPRS is crucial, as it defines how robots exchange information. This topology forms the foundation for both the formulation of the control problem and the control design. To represent these interactions, we introduce a directed graph \({{\mathscr {G}}} = \left\{ {{{\mathscr {V}}},{{\mathscr {E}}},{{\mathscr {A}}}} \right\}\), where \({{\mathscr {V}}}\) denotes the set of vertices representing the robots, \({{\mathscr {E}}} \subset {{\mathscr {V}}} \times {{\mathscr {V}}}\) is the edge set, and \({{\mathscr {A}}} = \left[ {{a_{ij}}} \right] \in {{\mathbb {R}}^{N \times N}}\) is the adjacency matrix. \({e_{ij}} \in {{\mathscr {E}}}\) represents the direct information flow from robot j to robot i. More precisely, we establish \({a_{ij}} > 0\) to represent cooperation between robot i and robot j; \({a_{ij}} < 0\) to indicate competition; otherwise, \({a_{ij}} = 0\) signifies no interaction. In addition, the directed graph \({{\mathscr {G}}}\) is acyclic, i.e., \({a_{ii}} = 0\). \({{{\mathscr {N}}}_i} = \left\{ {j \in {{\mathscr {V}}}\left| \ {{e_{ij}} \in {{\mathscr {E}}} } \right. } \right\}\) denotes the neighbor set of robot i. The Laplacian matrix \({{\mathscr {L}}} = \left[ {{l_{ij}}} \right] \in {{\mathbb {R}}^{N \times N}}\) of \({{\mathscr {G}}}\) is defined such that \({l_{ij}} = - {a_{ij}}\) and \({l_{ii}} = \sum \nolimits _{j \in {{{\mathscr {N}}}_i}} {{a_{ij}}}\) for \(i \ne j \in {{\mathscr {V}}}\). Moreover, \({{\mathscr {G}}}\) can be partitioned into \({\mathscr {K}}\) subnetworks denoted by \({{\mathscr {G}}}_k = \left\{ {{{\mathscr {V}}}_k,{{\mathscr {E}}}_k,{{\mathscr {A}}}_k} \right\}\) with each comprising \(n_k\) robots, where \(k \in \{1, 2, \ldots ,{{\mathscr {K}}}\}\), \({{\mathscr {V}}}_k \cap {{\mathscr {V}}}_m = \emptyset\) for all \(k \ne m \in \{1, 2, \ldots ,{{\mathscr {K}}}\}\), \(\sum \nolimits _{k = 1}^{{\mathscr {K}}} {{{{\mathscr {V}}}_k}} = {{\mathscr {V}}}\) and \(\sum \nolimits _{k = 1}^{{\mathscr {K}}} {{n_k}} = N\). Specifically, \({{{\mathscr {V}}}_k}=\{ 1 + \sum \nolimits _{i = 1}^k {{n_{i - 1}}} , \ldots ,\sum \nolimits _{i = 1}^k {{n_i}} \}\) is utilized to describe the nodes of the kth subnetwork with \(n_0 = 0\). Besides, each subnetwork has \({\mathscr {K}}\) corresponding virtual leaders. The interactions among robots and virtual leaders are captured by the diagonal weighted matrix \({{\mathscr {B}}}=\textrm{diag}\left( {{b_1},{b_2},\ldots ,{b_N}} \right)\). When the ith robot is able to receive information from its virtual leader, we have \(b_i > 0\); otherwise, \(b_i = 0\). Let \({{\mathscr {B}}}_k\) represent the diagonal weighted matrix associated with \({{\mathscr {G}}}_k\). Then, \({{\mathscr {B}}}=\textrm{diag}\left( {{{{\mathscr {B}}}_1},{{{\mathscr {B}}}_2},\ldots ,{{{\mathscr {B}}}_{{\mathscr {K}}}}} \right)\).

Assumption 1

The directed graph \({{\mathscr {G}}}\) can be partitioned into a sequence \(\{{{\mathscr {V}}}_1, {{\mathscr {V}}}_2, \ldots , {{\mathscr {V}}}_{{\mathscr {K}}}\}\) such that no cycles occur within this partition. Within each subnetwork, the information of the virtual leader is accessible to all individuals globally.

Assumption 2

For any given \(i \in {{\mathscr {V}}}_k\) and \(k \ne m \in \{1, 2, \ldots ,{{\mathscr {K}}}\}\), the sum of the connection weights between robot i and the robots in subnetwork m is equal to zero to ensure that the interaction in subnetwork m is balanced in terms of its influence on NPRS, i.e., \(\sum \nolimits _{j = {\varsigma _k}}^{{{{\tilde{\varsigma }} }_k}} {{l_{ij}}} = 0\), where \({\varsigma _k} = 1 + \sum \nolimits _{i = 1}^k {{n_{i - 1}}}\) and \({{{\tilde{\varsigma }} }_k} = \sum \nolimits _{i = 1}^k {{n_i}}\).

Remark 1

Unlike previous work on single formation34,36,37,38, which may not explicitly enforce an acyclic structure within a partition, Assumption 1 ensures that information from the virtual leader is accessible to all individuals globally within each subnetwork. Assumption 2 means that the sum of connection weights between robot i and robots in subnetwork m equals zero, not requiring the sum of weights within each subnetwork to be zero. Negative edge weights represent inhibitory constraints on interactions among robots. They are included to illustrate scenarios where interactions within a subnetwork offset each other, resulting in a neutral effect on a specific robot’s behavior.

Finite- and fixed-time stability

Imagine a differential system in the following manner:

$$\begin{aligned} \dot{z} = f(z, t), z(0) = z_0, \end{aligned}$$
(1)

where \(z \in {{\mathbb {R}}^d}\) represents the system state, \(f( \cdot )\) denotes a nonlinear function, and \(z_0 \in {{\mathbb {R}}^d}\) is the initial state.

Definition 1

10 System (1) is considered to exhibit finite-time stability if it satisfies the conditions of Lyapunov stability and there exists a settling time function \({{\mathscr {T}}}({z_0})\) such that \(\left| {{\Phi _z}(t,{z_0})} \right| =0\) for \(t \in [{{\mathscr {T}}}({z_0}), + \infty ]\). Unlike autonomous systems, the Lyapunov function V(z, t) and the stability conditions explicitly depend on time, incorporating additional terms to reflect this time dependency.

Definition 2

22 System (1) is characterized as fixed-time stability if it satisfies the conditions of finite-time stability and a settling time function \({{\mathscr {T}}}(z_0)\) that is bounded by a constant exists. In simpler terms, there exists a maximum settling time \({{{\mathscr {T}}}{\max }} > 0\) such that \(f(z(t))=0\), \(\forall t \ge {{{\mathscr {T}}}{\max }}\) and \(\forall {{\mathscr {T}}}({z_0}) \le {{{\mathscr {T}}}{\max }}\), \({z_0} \in {{\mathbb {R}}^d}\).

Lemma 1

22 Given a system described as system (1), if a continuous positive-definite function V(z) satisfies the condition

$$\begin{aligned} \frac{{\partial V}}{{\partial z}}f(z,t) \le - \sigma {V^{\frac{{{\ell _1}}}{{{\gamma _1}}}}}(z) - \eta {V^{\frac{{{\ell _2}}}{{{\gamma _2}}}}}(z), \end{aligned}$$

where \(\sigma >0\), \(\eta >0\), \(\ell _1\), \(\gamma _1\), \(\ell _2\), and \(\gamma _2\) are positive odd integers that satisfy \(\ell _1> \gamma _1\) and \(\ell _2<\gamma _2\). In such case, the origin of the system is a globally fixed-time stable equilibrium, with the settling time function \({{\mathscr {T}}}\) limited by

$$\begin{aligned} {{\mathscr {T}}} \le {{{\mathscr {T}}}_{\max }}= \frac{1}{\sigma }\frac{\gamma _1}{{\ell _1 - \gamma _1}} + \frac{1}{\eta }\frac{\gamma _2}{{\gamma _2 - \ell _2}}. \end{aligned}$$

Furthermore, if \(\theta \buildrel \Delta \over = [{\gamma _2}({\ell _1} - {\gamma _1})]/[{\gamma _1}({\gamma _2} - {\ell _2})] \le 1\), we can obtain a less conservative estimate of the time function\({{\mathscr {T}}}\)as

$$\begin{aligned} {{{\mathscr {T}}}} \le {{{\mathscr {T}}}_{\max }}= \frac{{{\gamma _2}}}{{{\gamma _2} - {\ell _2}}}\left( {\frac{1}{{\sqrt{\sigma \eta } }}{{\tan }^{ - 1}}\sqrt{\frac{\sigma }{\eta }} + \frac{1}{{\sigma \theta }}} \right) . \end{aligned}$$

Neural network principle

Fig. 2
figure 2

RBF neural network.

Full size image

As depicted in Fig. 2, the RBF neural network is typically characterized by the neural structure that consists of an input layer, a hidden layer, and an output layer. The primary purposes of these layers are as follows: the input layer is responsible for receiving external information, the hidden layer performs nonlinear transformations, and the output layer provides the final output information. RBF neural networks are a suitable choice in this scenario due to their capability to estimate unknown nonlinear functions effectively23. Therefore, we employ RBF neural networks to estimate a nonlinear function \(g( \cdot ) : {{{\mathbb {R}}}^b} \rightarrow {{{\mathbb {R}}}^d}\).

The RBF neural network approximates the function g(z) as follows:

$$\begin{aligned} g(z) \approx \hat{g}(z) = K^T \varphi (z) + \varepsilon , \end{aligned}$$

where the weight matrix \(K \in {{{\mathbb {R}}}^{m \times d}}\) consists of the weights of m neurons, and the input data vector is denoted as \(z \in {{{\mathbb {R}}}^b}\). The approximation error of a RBF neural network is represented by \(\varepsilon \in {{{\mathbb {R}}}^d}\). To derive this, consider the basis function \(\varphi = {\left[ {{\varphi _j}(z)} \right] _{m \times 1}} \in {{{\mathbb {R}}}^m}\), defined as:

$$\begin{aligned} {\varphi _j}(z) = \exp \left[ { - \frac{1}{{2{\iota _j}}}\left\| {z - {\rho _j}} \right\| } \right] , \ \forall j \in \{ 1,2, \ldots ,m\}, \end{aligned}$$

where \({\rho _j} \in {{{\mathbb {R}}}^b}\) is the center of the jth neuron and \(\iota _j\) represents the width of this neuron. A practical rule for choosing the width \(\iota _j\) for each neuron based on the distance between the centers can be expressed as:

$$\begin{aligned} \iota _j=\frac{1}{m}\sum _{k=1}^m\Vert \rho _j-\rho _k\Vert . \end{aligned}$$

The width of a neuron remains a positive constant when the neuron is a hidden neuron. This ensures that each neuron’s receptive field overlaps with its neighbors, providing smooth transitions and improved approximation capabilities.

The RBF network’s output is a linear combination of these basis functions weighted by the matrix K. This can be expressed as:

$$\begin{aligned} \hat{g}(z) = \sum _{j=1}^m K_j \varphi _j(z), \end{aligned}$$

where \({K_j} \in {{{\mathbb {R}}}^b}\) is the weight vector associated with the jth neuron.

By minimizing the approximation error \(\varepsilon\) between the actual function g(z) and the observed function \(\hat{g}(z)\), the weights K are adjusted to ensure that the RBF neural network can approximate g(z) as accurately as possible. This is typically done through a learning algorithm such as gradient descent.

System statement

In this scenario, we examine an example that involves a NPRS that consists of N robots. The dynamics and kinematics of the ith robot can be represented by

$$\begin{aligned} {H_i}({q_i}){{\ddot{q}}_i} + {C_i}({q_i},{{\dot{q}}_i}){{\dot{q}}_i} + {G_i}({q_i}) + {d_i}(t)= \psi ({\tau _i}), \end{aligned}$$
(2)

where the position, velocity, and acceleration vectors of the robot are denoted as \({q_i}, {{\dot{q}}_i}\), and \({{\ddot{q}}_i} \in {{\mathbb {R}}^d}\), respectively. \({H_i}({q_i}) \in {{\mathbb {R}}^{d \times d}}\) represents the robotic inertia matrix. \({C_i}({q_i},{{\dot{q}}_i}) \in {{\mathbb {R}}^{d \times d}}\) denotes the Coriolis centrifugal matrix. \({G_i}({q_i})\) represents the gravitational torque. \(d_i(t)\) represents external perturbations that affect the robot. \({\tau _i} \in {{\mathbb {R}}}^d\) includes the calculated control signals. \(\psi ({\tau _i}) \in {{\mathbb {R}}}^d\) is the deadzone function of the input torque, i.e.,

$$\begin{aligned} \psi ({\tau _i}) = \left\{ {\begin{array}{*{20}{l}} {{u_h}({\tau _i} - {\delta _h}{\textbf{1}_d}),\left\| {{\tau _i}} \right\| \ge {\delta _h}},\\ {0,\;\;\;\;\;\;\;\;\;\;\;\;{\delta _l}< \left\| {{\tau _i}} \right\| < {\delta _h}},\\ {{u_l}({\tau _i} - {\delta _l}{\textbf{1}_d}),\; \; \left\| {{\tau _i}} \right\| \le {\delta _l}}, \end{array}} \right. \end{aligned}$$

where the constants \({\delta _l}\) and \({\delta _h}\) represent the bounds of the deadzone. In addition, \({u_l}( \cdot )\) and \({u_h}( \cdot )\) refer to the uncertain deadzone functions. Furthermore, to account for parametric uncertainties, the unknown \(\psi ({\tau _i})\) can be decomposed into two components: \(\psi ({\tau _i}) \buildrel \Delta \over = {\tau _i} - \Delta {\tau _i}\), where \(\Delta {\tau _i}\) denotes an unknown continuous error function. Accounting for the presence of parametric uncertainties, the dynamical terms take the form of

$$\begin{aligned}&{H_{{i}}}({q_i}) = {{H}_{{i0}}}({q_i}) + \Delta {H_{{i}}}({q_i}), \\&{C_i}({q_i},{{\dot{q}}_i}) = {{C}_{i0}}({q_i},{{\dot{q}}_i}) + \Delta {C_i}({q_i},{{\dot{q}}_i}), \\&{G_i}({q_i}) = {G_{i0}}({q_i}) + \Delta {G_i}({q_i}), \end{aligned}$$

where the terms \({H}_{{i0}}({q_i})\), \({C}_{i0}({q_i},{{\dot{q}}_i})\), and \({G_{i0}}({q_i})\) are known and provided by the user, directly usable for control design. By contrast, \(\Delta {H_i}({q_i})\), \(\Delta {C_i}({q_i},{{\dot{q}}_i})\), and \(\Delta {G_i}({q_i})\) are uncertain terms that arise due to inevitable measurement errors in practical applications. Consequently, System (2) can be reformulated as follows:

$$\begin{aligned} {H_{i0}}({q_i}){{\ddot{q}}_i} + {C_{i0}}({q_i},{{\dot{q}}_i}){{\dot{q}}_i} + {G_{i0}}({q_i}) = {\tau _i} + {F_i}(t), \end{aligned}$$
(3)

where the consideration of lumped uncertainty terms \({F_i}(t) = - \Delta {H_{i}}({q_i}){{\ddot{q}}_i} - \Delta {C_i}({q_i},{{\dot{q}}_i}){{\dot{q}}_i} - \Delta {G_i}({q_i})\)\(- d_i(t) - \Delta {\tau _i}\) encompasses the effects of parametric perturbations \(\Delta {H_{i}}({q_i})\), \(\Delta {C_i}({q_i},{{\dot{q}}_i})\), and \(\Delta {G_i}({q_i})\), as well as external disturbances \(d_i(t)\), and actuator input deadzone \(\Delta {\tau _i}\). Utilizing RBF neural networks, \({F_i}(t)\) can be represented as follows:

$$\begin{aligned} {F_i}(t) = K_{i}^T{\varphi _i}({z_i}) + {\varepsilon _i}, \end{aligned}$$
(4)

where \({K_i} \in {{{\mathbb {R}}}^{m \times d}}\) represents the weight matrix associated with m neurons. The input vector is denoted as \({z_i} \in {{{\mathbb {R}}}^b}\). Furthermore, \({\varepsilon _i} \in {{{\mathbb {R}}}^d}\) represents the neural network approximation error, assumed to be bounded, i.e., \(\left\| {{\varepsilon _i}} \right\| \le {\varpi _i}\), \({\varpi _i}\) is a positive constant. In this case, \({\varphi _i}({z_i}) = {\left[ {{\varphi _{ij}}(z_i)} \right] _{m \times 1}}\) represents the Gaussian function associated with the RBF neural network, and

$$\begin{aligned} {\varphi _{ij}}({z_i}) = \exp \left[ { - \frac{1}{{2{\iota _j}}}\left\| {{z_i} - {\rho _j}} \right\| } \right] , \ \forall j \in \{ 1,2, \ldots ,m\}. \end{aligned}$$

\({\rho _j} \in {{{\mathbb {R}}}^b}\) represents the center of the jth neuron, while \(\iota _j\) denotes the width of the same neuron.

Subsequently, NPRS (3) can be reformulated as follows:

$$\begin{aligned} {H_{i0}}({q_i}){{\ddot{q}}_i} + {C_{i0}}({q_i},{{\dot{q}}_i}){{\dot{q}}_i} + {G_{i0}}({q_i}) \!=\! {\tau _i} \!+\! K_{i}^T{\varphi _i}({z_i}) \!+\! {\varepsilon _i}. \end{aligned}$$
(5)

Notably, the following salient properties distinctly characterize the model of NPRS (2).

Property 1

The inertia matrix \({H_i}({q_i})\) is known to possess the properties of symmetry and positive definiteness.

Property 2

The matrix \({{\dot{H}}_i}({q_i}) - 2{C_i}({q_i},{{\dot{q}}_i})\) exhibits the property of skew-symmetry.

Furthermore, with regard to the kth subnetwork, the dynamics of the virtual leader’s trajectory are given by

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{0,k} = v_{0,k},\\ \dot{v}_{0,k} = a_{0,k}, \end{array} \right. \end{aligned}$$

where \(x_{0,k}, v_{0,k}\), and \(a_{0,k} \in {{\mathbb {R}}^d}\) represent the position, velocity, and acceleration vectors of the kth virtual leader, respectively, \(\forall k \in {{\mathscr {K}}}\). Here, we present a justifiable assumption that concerns the virtual leaders.

Assumption 3

Acceleration \(a_{0,k}\) is bounded by a nonnegative constant \({{ \delta }_{0,k}}\), such that \(\left\| {{a_{0,k}}} \right\| \le {{ \delta }_{0,k}}\).

Remark 2

RBF networks are particularly advantageous for our application due to their universal approximation capabilities, enabling accurate approximation of continuous functions with sufficient neurons in the hidden layer. This makes them effective for modeling and compensating for system nonlinearities and uncertainties. Additionally, RBF networks are well-suited for capturing complex, nonlinear disturbances that are challenging for observer techniques. Their effectiveness in similar applications has been demonstrated in previous studies23,28,29, further supporting our choice.

Remark 3

The NPRS (2) can be extended to form a mobile manipulator when integrated with a mobile platform. This system comprises a nonholonomic mobile base and a holonomic manipulator. Specifically, consider a two-wheel-driven mobile platform operating under non-slip conditions. When factoring in parametric uncertainties, the system’s dynamics can be written as:

$$\begin{aligned} \left\{ \begin{array}{l} {H_{i022}}{{\ddot{q}}_{ia}} + {C_{i022}}{{\dot{q}}_{ia}} + {G_{i0a}} + {f_{ia}} = {\tau _{ia}},\\ {H_{i011}}{{\ddot{q}}_{ib}} + {C_{i011}}{{\dot{q}}_{ib}} + {G_{i0b}} + {U_{ib}} = {B_{ib}}{\tau _{ib}} - A_{ib}^\mathrm{{T}}{\vartheta _i}, \end{array} \right. \end{aligned}$$

where \({q_i} = \textrm{col}({q_{ia}},{q_{ib}})\), \({\tau _{i}} = \textrm{col}({\tau _{ia}},{\tau _{ib}})\), \({d_{i}} = \textrm{col}({d_{ia}},{d_{ib}})\), \({H_i} = [{H_{i11}},{H_{i12}};{H_{i21}},{H_{i22}}],\)\({C_i} = [{C_{i11}},{C_{i12}};{C_{i21}},{C_{i22}}]\), \({f_{ia}} = \Delta {H_{i22}}{{\ddot{q}}_{ia}} + \Delta {C_{i22}}{{\dot{q}}_{ia}} + \Delta {G_{ia}} + {d_{ia}} + {H_{i21}}{{\ddot{q}}_{ib}} + {C_{i21}}{{\dot{q}}_{ib}}\), \({U_{ib}} = \Delta {H_{i11}}{{\ddot{q}}_{ib}} + \Delta {C_{i11}}{{\dot{q}}_{ib}} + \Delta {G_{ib}} + {d_{ib}} + {H_{i12}}{{\ddot{q}}_{ia}} + {C_{i12}}{{\dot{q}}_{ia}}\) with \(A_{ib}\) denoting the constraint matrix, \(B_{ib}\) as the transformation matrix, and \(\vartheta _i\) representing the Lagrange multiplier.

Problem formulation

The primary focus is to investigate the fixed-time CFT problem of NPRSs described below. The following form of problem definition is provided using the principle of fixed-time stability.

Definition 3

The achievement of the fixed-time CFT problem of NPRSs is determined by the existence of a settling time \({{\mathscr {T}}}_{\max }\), which remains independent of the initial condition, such that

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{\lim }_{t \rightarrow {{{\mathscr {T}}}_{\max }}}}\left\| {{q_i}(t) - {r_i} - {x_{0,k}}(t)} \right\| = 0,}\\ {{{\lim }_{t \rightarrow {{{\mathscr {T}}}_{\max }}}}\left\| {{\dot{q}_i}(t) - {v_{0,k}}(t)} \right\| = 0,}\\ {\left\| {{q_i}(t) - {r_i}- {x_{0,k}}(t)} \right\| = 0,\forall t \in [{{{\mathscr {T}}}_{\max }},\infty ),}\\ {\left\| {{\dot{q}_i}(t) - {v_{0,k}}(t)} \right\| = 0,\forall t \in [{{{\mathscr {T}}}_{\max }},\infty ),} \end{array}} \right. \end{aligned}$$

where \({q_i}(t)\) and \({{\dot{q}}_i}(t) \in {{\mathbb {R}}^d}\) are the robot’s position and velocity defined in formula (2), and \({r_i} \in {{\mathbb {R}}^d}\) denotes the ith robot’s formation offset.

Remark 4

In the practical application of CFT for the NPRS, uncertain factors, such as device precision, actuator limitations, and variations in operating conditions, inevitably result in negative effects, such as reduced control accuracy and difficulties in determining the time when the system becomes stable. Consequently, considering actuator input deadzone, parametric uncertainties, and external perturbations, becomes of paramount importance.

Major results

This section introduces a new HFNA control algorithm tailored to address the CFT problem for NPRSs while ensuring fixed-time convergence capability. Additionally, the effectiveness of the algorithm is verified by the following stability analysis.

HFNA control algorithm

In this subsection, we present the HFNA control algorithm for NPRSs. Before proceeding further, we define \({{{\hat{e}}}_i} = {q_i} - {r_i}-{{{\hat{x}}}_i}\), \({{\dot{{\hat{e}}}}_i} = {\dot{q}_i} - {{{\hat{v}}}_i}\), and \({{\ddot{{\hat{e}}}}_i} = {\ddot{q}_i} - {{{\hat{a}}}_i}\), where \({{{\hat{x}}}_i}\), \({{{\hat{v}}}_i}\), and \({{{\hat{a}}}_i}\) are the observations of \({q_i}\), \({\dot{q}_i}\), and \({\ddot{q}_i}\), respectively. Moreover, we design a fixed-time sliding vector as follows:

$$\begin{aligned} {{{\hat{s}}}_i} = {{{\hat{e}}}_i} + {\left( {\hbar _i^{ - 1} \cdot {{\dot{{\hat{e}}}}_i}} \right) ^{{n_4}/{m_4}}}, {\hbar _i} = {\sigma _0}{\hat{e}}_i^{{m_3}/{n_3} - {m_4}/{n_4}} + {\eta _0}{\textbf{1}_d}, \end{aligned}$$

where \({{{\hat{s}}}_i} \in {{\mathbb {R}}}^{d}\), \(m_3\), \(n_3\), \(m_4\), and \(n_4\) are positive odd integers that satisfy \(m_3 > n_3\), \(m_4< n_4 < 2 m_4\), and \({{m_3}/{n_3} - {m_4}/{n_4}} > 0\). \({\sigma _0}\) and \({\eta _0}\) are positive constants.

In this manner, let \({{{\hat{\xi }} }_i} = \mathrm{{col(}}{{{\hat{x}}}_i},{{{\hat{v}}}_i},{{{\hat{a}}}_i}\mathrm{{)}} \in {{{\mathbb {R}}}^{3d}}\) and \({\gamma _{0,k}} = \mathrm{{col}}({x_{0,k}},{v_{0,k}},{a_{0,k}}) \in {{{\mathbb {R}}}^{3d}}\). In the presence of actuator input deadzone, parametric uncertainties and external perturbations, the HFNA control algorithm is formulated in the following manner:

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} {\tau _i} \ \ & = {\tau _{i,1}} + {\tau _{i,2}}\\ {\tau _{i,1}} & = {{C_{i0}}}{{\dot{q}}_i} + {G_{i0}} - {\hat{K}}_i^T{\varphi _i} - {{{\hat{\varpi }} }_i} - {\beta _i}\mathrm{{sig}}({{{\hat{s}}}_i})\\ {\tau _{i,2}} & = {H_{i0}}{{{\hat{a}}}_i} - {H_{i0}}{{\dot{q}}_i} - {H_{i0}}({\Gamma _i} \cdot \dot{{\hat{e}}}_i^2 \cdot \hbar _i^{ - 1}) \\ & \ \ \ - \frac{{{m_4}}}{{{n_4}}}{H_{i0}}{\hbar _i} \cdot {(\hbar _i^{ - 1} \cdot {{\dot{{\hat{e}}}}_i})^{\frac{{{m_4}-{n_4}}}{{{m_4}}}}} \cdot ({{\dot{{\hat{e}}}}_i} + {\delta _i})\\ {{\dot{{\hat{K}}}}_i} & = {\alpha _1}{\varphi _i}{\hat{s}}_i^T, {{\dot{{\hat{\varpi }}}}_i} = {\alpha _2}\left\| {{{{\hat{s}}}_i}} \right\| , \end{aligned} \end{array} \right. \end{aligned}$$
(6)
$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} {{\dot{{\hat{\xi }} }}_i} =& \left( {\sum \limits _{j \in {{{\mathscr {N}}}_i}} {{a_{ij}} + {b_i}} } \right) ^{ - 1} \left[ \sum \limits _{j \in {{{\mathscr {N}}}_i}} {{a_{ij}}{{\dot{{\hat{\xi }} }}_j}} + {b_i}{{{\dot{\gamma }} }_{0,k}} \right. \\ & - \left( {P \otimes {I_d}} \right) \textrm{sig}( {\sum \limits _{j \in {{{\mathscr {N}}}_i}} {{a_{ij}}({{{\hat{\xi }} _i} - {{\hat{\xi }} _j}}) + {b_i}({{{\hat{\xi }}}_i} - {\gamma _{0,k}})} } )^{\frac{m_1}{n_1}}\\ & \left. - \left( {Q \otimes {I_d}} \right) \textrm{sig}( {\sum \limits _{j \in {{{\mathscr {N}}}_i}} {{a_{ij}}({{{\hat{\xi }} _i} - {{\hat{\xi }} _j}}) + {b_i}({{{\hat{\xi }}}_i} - {\gamma _{0,k}})} } )^{\frac{m_2}{n_2}} \right] \\ P =& \ diag({\sigma _1},{\sigma _2},{\sigma _3}), Q = diag({\eta _1},{\eta _2},{\eta _3}), \end{aligned} \end{array} \right. \end{aligned}$$
(7)

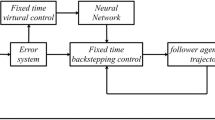
where \({\delta _i} = {\sigma _4}{\hat{s}}_i^{{{{m_3}} /{{n_3}}}} + {\eta _4}{\hat{s}}_i^{{{{m_4}} / {{n_4}}}}\), \({\Gamma _i} = - {\sigma _0}[({m_3}/{n_3}) - ({m_4}/{n_4})]{\hat{e}}_i^{({m_3}/{n_3}) - ({m_4}/{n_4}) - 1}\), \({\sigma _4}\), and \({\eta _4}\) are positive constants, and \({\beta _i}\) is given as a scalar gain. \({\alpha _1}\), and \({\alpha _2}>0\), \({\varphi _i}\) is given by the expression in (4). The hierarchical framework of the proposed HFNA control algorithm is illustrated in Fig. 3, providing a clear depiction of its structure.

Remark 5

The control algorithm given in (6) demonstrates considerable physical significance. To elaborate further, \({\tau _{i,1}}\) represents the robust control term for addressing the challenges posed by actuator input deadzone, parametric uncertainties, and external perturbations. \({\tau _{i,2}}\) corresponds to an equivalent control designed for NPRSs to process known information. Additionally, the update laws \({{\dot{{\hat{K}}}}_i} \!=\! {\alpha _1}{\varphi _i}{\hat{s}}_i^T\) and \({{\dot{{\hat{\varpi }}}}_i} \!=\! {\alpha _2}| {{{{\hat{s}}}_i}} |\) in the neural adaptive control serve as effective approximations for dealing with the complexities introduced by the actuator input deadzone, parametric uncertainties, and external perturbations.

Remark 6

The proposed HFNA control algorithm consists of a local control layer (i.e., (6)) and a distributed observer layer (i.e., (7)). Its hierarchical architecture decomposes the control task into multiple levels, allowing each layer to handle specific aspects of the control problem. This structured decomposition enables smoother transitions between control actions, minimizing abrupt control signal changes, which helps reduce the high-frequency switching that typically leads to chattering in conventional sliding mode control. Furthermore, the adaptive neural network components continuously adjust control parameters in response to real-time system dynamics. This adaptability enables more precise and gradual modifications, mitigating the need for aggressive switching and further reducing chattering. Together, the hierarchical design and adaptive neural network enhance the robustness of the control strategy against parametric uncertainty and external perturbations, ensuring stable and reliable performance.

Fig. 3
figure 3

Hierarchical control framework for NPRSs.

Full size image

Analysis for the distributed observer

In this subsection, we validate the performance of the proposed distributed observer algorithm in addressing the fixed-time CFT problem.

Theorem 1

Under the assumptions of Assumption 1-3, and with the proposed distributed observer algorithm (7), if the conditions are satisfied as

$$\begin{aligned} & \sigma _{\min }> 0, \eta _{\min } > 0, \end{aligned}$$
(8)
$$\begin{aligned} & \ m_1 > n_1, \ m_2 < n_2, \end{aligned}$$
(9)

where \(\sigma _{\min } = \min \{\sigma _1, \sigma _2, \sigma _3 \}\), and \(\eta _{\min } = \min \{\eta _1, \eta _2, \eta _3 \}\). Then, the states of the virtual leaders are effectively observed within a fixed time \(t \le {{\mathscr {T}}}_e\), i.e.,\({\lim _{t \rightarrow {{{\mathscr {T}}}_e}}}\Vert {{{{\tilde{\xi }}}_{i}}} \Vert = 0\), and \(\Vert {{{{\tilde{\xi }}}_{i}}} \Vert = 0\), when\(t > {{{\mathscr {T}}}_e}\), \(\forall i \in {{\mathscr {V}}}\).

Proof

First, the distributed observer tracking error vectors for \(i, j \in {{\mathscr {V}}}\) are defined as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {{{\tilde{x}}}_i} = {{{\hat{x}}}_i} - {x_{0,k}},\\ {{{\tilde{v}}}_i} = {{{\hat{v}}}_i} - {v_{0,k}},\\ {{{\tilde{a}}}_i} = {{{\hat{a}}}_i} - {a_{0,k}}. \end{array} \right. \end{aligned}$$

Let \({{{\tilde{\xi }} }_i} = \mathrm{{col(}}{{{\tilde{x}}}_i},{{{\tilde{v}}}_i},{{{\tilde{a}}}_i}\mathrm{{)}} \in {{{\mathbb {R}}}^{3d}}\), the compact representations of \({{\tilde{x}}}_i\) , \({{\tilde{v}}}_i\), and \({{\tilde{a}}}_i\) are as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\tilde{x}} = \mathrm{{col}}({{{\tilde{x}}}_1}, {{{\tilde{x}}}_2}, \ldots ,{{{\tilde{x}}}_N})\\ {\tilde{v}} = \mathrm{{col}}({{{\tilde{v}}}_1}, {{{\tilde{v}}}_2}, \ldots ,{{{\tilde{v}}}_N})\\ {\tilde{a}} = \mathrm{{col}}({{{\tilde{a}}}_1}, {{{\tilde{a}}}_2}, \ldots ,{{{\tilde{a}}}_N}) \end{array} \right. \end{aligned}$$

Thus, we can obtain the compact form \({{\tilde{\xi }} } = \textrm{col}({{{\tilde{x}}}},{{{\tilde{v}}}},{{{\tilde{a}}}})\). Furthermore, substituting the proposed HFNA control algorithm (6), (7) into (5) obtains the cascade closed-loop system as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} {{\dot{{\hat{s}}}}_i} & = {{\dot{{\hat{e}}}}_i} + \frac{{{n_4}}}{{{m_4}}}{(\hbar _i^{ - 1} \cdot {{\dot{{\hat{e}}}}_i})^{\frac{{{n_4}-{m_4}}}{{{m_4}}} }}({\Gamma _i}\cdot \dot{{\hat{e}}}_i^2 \cdot \hbar _i^{ - 2} + \hbar _i^{ - 1} \cdot {{\ddot{{\hat{e}}}}_i}),\\ \dot{{\tilde{\xi }}} & = {[({{\mathscr {L}}} \!+\! {{\mathscr {B}}}) \otimes {I_{3d}}]^{ - 1}}\{ - P\mathrm{{sig}}{([({{\mathscr {L}}} \!+\! {{\mathscr {B}}}) \otimes {I_{3d}}]{\tilde{\xi }} )^{\frac{{{m_1}}}{{{n_1}}}}}\\ & \qquad - Q\mathrm{{sig}}{([({{\mathscr {L}}} \!+\! {{\mathscr {B}}}) \otimes {I_{3d}}]{\tilde{\xi }} )^{\frac{{{m_2}}}{{{n_2}}}}} \!+\! ({{\mathscr {B}}} \otimes {I_{3d}}){{{\dot{\gamma }} }_0}\} \!-\! {{{\dot{\gamma }} }_0}, \end{aligned} \end{array} \right. \end{aligned}$$
(10)

where \({\gamma _0} = \mathrm{{col}}\left( {{x_0},{v_0},{a_0}} \right)\),

$$\begin{aligned} {x_0} \! =&\mathrm{{col}}( {\underbrace{{x_{0,1}}, \ldots ,{x_{0,1}}}_{{n_1}},\underbrace{{x_{0,2}}, \ldots ,{x_{0,2}}}_{{n_2}}, \ldots ,\underbrace{{x_{0,{{\mathscr {K}}}}}, \ldots ,{x_{0,{{\mathscr {K}}}}}}_{{n_{{\mathscr {K}}}}}} ),\\ {v_0} \! =&\mathrm{{col}}( {\underbrace{{v_{0,1}}, \ldots ,{v_{0,1}}}_{{n_1}},\underbrace{{v_{0,2}}, \ldots ,{v_{0,2}}}_{{n_2}}, \ldots ,\underbrace{{v_{0,{{\mathscr {K}}}}}, \ldots ,{v_{0,{{\mathscr {K}}}}}}_{{n_{{\mathscr {K}}}}}} ),\\ {a_0} \! =&\mathrm{{col}}( {\underbrace{{a_{0,1}}, \ldots ,{a_{0,1}}}_{{n_1}},\underbrace{{a_{0,2}}, \ldots ,{a_{0,2}}}_{{n_2}}, \ldots ,\underbrace{{a_{0,{{\mathscr {K}}}}}, \ldots ,{a_{0,{{\mathscr {K}}}}}}_{{n_{{\mathscr {K}}}}}} ). \end{aligned}$$

In the closed-loop system (10), given that \({\dot{{\tilde{\xi }}}}\) is defined, taking linear transformations \({\tilde{\Phi }} = [({{\mathscr {L}}} + {{\mathscr {B}}}) \otimes {I_{3d}}]{\tilde{\xi }}\) yields

$$\begin{aligned} {\dot{{\tilde{\Phi }}}} =&\, [({{\mathscr {L}}} + {{\mathscr {B}}}) \otimes {I_{3d}}]{\dot{{\tilde{\xi }}}} \nonumber \\ =&\! - \! P\mathrm{{sig}}{([({{\mathscr {L}}} \! + \! {{\mathscr {B}}}) \otimes {I_{3d}}]{\tilde{\xi }} )^{\frac{m_1}{n_1}}} \nonumber \\&- Q\mathrm{{sig}}{([({{\mathscr {L}}} \! + \! {{\mathscr {B}}}) \otimes {I_{3d}}]{\tilde{\xi }} )^{\frac{m_2}{n_2}}} \nonumber \\&+ ({{\mathscr {B}}} \otimes {I_{3d}}){{{\dot{\gamma }} }_0} - [({{\mathscr {L}}} + {{\mathscr {B}}}) \otimes {I_{3d}}]{{{\dot{\gamma }} }_0}. \end{aligned}$$
(11)

It’s worth noting that \(({{\mathscr {B}}} \otimes {I_{3d}}){{{\dot{\gamma }} }_0} = [({{\mathscr {L}}} + {{\mathscr {B}}}) \otimes {I_{3d}}]{{{\dot{\gamma }} }_0}\). Then, it can be derived that

$$\begin{aligned} {\dot{{\tilde{\Phi }}}} = - P\mathrm{{sig}}{({\tilde{\Phi }})^{\frac{m_1}{n_1}}} - Q\mathrm{{sig}}{({\tilde{\Phi }})^{\frac{m_2}{n_2}}}. \end{aligned}$$
(12)

Consider the positive-definite Lyapunov function candidate defined as

$$\begin{aligned} V({\tilde{\Phi }} ) = \mathrm{{sig}}{\mathrm{{n}}^T}({\tilde{\Phi }} ). \end{aligned}$$
(13)

Further, taking the derivative of the function \(V({\tilde{\Phi }} )\), it can be derived that

$$\begin{aligned} \dot{V}({\tilde{\Phi }} ) \le&- \Vert P \Vert _1 \Vert {{\tilde{\Phi }} } \Vert _1^{\frac{m_1}{n_1}} - \left\| Q \right\| _1 \Vert {{\tilde{\Phi }} } \Vert _1^{\frac{m_2}{n_2}} \nonumber \\ =&- \left\| P \right\| _1 {V^{\frac{m_1}{n_1}}}({\tilde{\Phi }} ) - \left\| Q \right\| _1 {V^{\frac{m_2}{n_2}}}({\tilde{\Phi }} ). \end{aligned}$$
(14)

Thus, \({{{\tilde{\xi }} }_i} = 0\) when fixed-time \(t \ge {{\mathscr {T}}}_e\) and \({{\mathscr {T}}}_e\) is bounded by

$$\begin{aligned} {{{\mathscr {T}}}_e} \le {{{\mathscr {T}}}_{e\max }} {=} \frac{1}{\sigma _{\min }}\frac{n_1}{{m_1 - n_1}} + \frac{1}{\eta _{\min }}\frac{n_2}{{n_2 - m_2}}. \end{aligned}$$
(15)

In addition, if \({\theta }_1 \buildrel \Delta \over = [{n_2}({m_1} - {n_1})]/[{n_1}({n_2} - {m_2})] \le 1\), a less conservative approximation can be derived as follows:

$$\begin{aligned} {{{{\mathscr {T}}}_e}} \! \le \! {{{\mathscr {T}}}_{e \max }} \!= \! \frac{{{n_2}}}{{{n_2} \!-\! {m_2}}}\! \left( {\frac{1}{{\sqrt{{\sigma _{\min }} {\eta _{\min }} } }}{{\tan }^{ - 1}} \! \sqrt{\frac{{\sigma _{\min }} }{\eta _{\min }}} \! +\! \! \frac{1}{{{\sigma _{\min }} {\theta }_1}}} \right) . \end{aligned}$$

\(\square\)

Remark 7

The result from Theorem 1, \({\lim _{t \rightarrow {{{\mathscr {T}}}_e}}}\Vert {{{{\tilde{\xi }}}_{i}}} \Vert = 0\), and \(\Vert {{{{\tilde{\xi }}}_{i}}} \Vert = 0\), when \(t > {{{\mathscr {T}}}_e}\), and \({{{\tilde{\xi }} }_i} = \mathrm{{col(}}{{{\tilde{x}}}_i},{{{\tilde{v}}}_i},{{{\tilde{a}}}_i}\mathrm{{)}} \in {{{\mathbb {R}}}^{3d}},\) can be easily obtained \({\lim _{t \rightarrow {{{\mathscr {T}}}_e}}}\left\| {{{{\tilde{x}}}_{i}}} \right\| = 0\), \({\lim _{t \rightarrow {{{\mathscr {T}}}_e}}}\left\| {{{{\tilde{v}}}_{i}}} \right\| = 0\), \({\lim _{t \rightarrow {{{\mathscr {T}}}_e}}}\left\| {{{{\tilde{a}}}_{i}}} \right\| = 0\) and \(\left\| {{{{\tilde{x}}}_{i}}} \right\| = 0\), \(\left\| {{{{\tilde{v}}}_{i}}} \right\| = 0\), \(\left\| {{{{\tilde{a}}}_{i}}} \right\| = 0\).

Analysis of fixed-time CFT

In this subsection, we demonstrate the effectiveness of the presented algorithm in solving the fixed-time CFT problem, building upon the result established in Theorem 1.

Theorem 2

By applying the proposed HFNA control algorithm (6)–(7) to the system (5), and under the condition that

$$\begin{aligned} {\beta _i} \ge \left\| {{\tilde{K}}_i^T{\varphi _i} + {{{\tilde{\varpi }} }_i}} \right\| , \forall i \in {{\mathscr {V}}}, \end{aligned}$$
(16)

where \({{{\tilde{K}}}_i} = {K_i} - {{{\hat{K}}}_i}\) and \({{{\tilde{\varpi }} }_i} = {\varpi _i} - {{{\hat{\varpi }} }_i}\), the fixed-time CFT problem (Definition3) in NPRSs is successfully solved.

Proof

The theorem demonstrates that \(q_i\) and \(\dot{q_i}\) can track their corresponding observer terms \(\hat{x}_i\) and \(\hat{v}_i\) within a fixed time. First, the distributed tracking errors are defined as \(\hat{e}_i = q_i - r_i - \hat{x}_i\) and \(\dot{\hat{e}}_i = \dot{q_i} - \hat{v}_i\). The analysis then focuses on the convergence of the fixed-time sliding vector \(\hat{s}_i\). To facilitate this analysis, a Lyapunov function candidate is introduced, followed by a detailed convergence analysis.

$$\begin{aligned} {V_i}({{{\hat{s}}}_i}) = \frac{1}{2}{\hat{s}}_i^T{{{\hat{s}}}_i}, \forall i \in {{\mathscr {V}}}. \end{aligned}$$
(17)

Consider that \({{\dot{{\hat{s}}}}_i}\) is defined in the closed-loop system (10), the derivative of \(V_i\) can be expressed as follows:

$$\begin{aligned} \dot{V}_i({{{\hat{s}}}_i}) =&{\hat{s}}_i^T{{\dot{{\hat{s}}}}_i}\nonumber \\ =&\, {\hat{s}}_i^T[{{\dot{{\hat{e}}}}_i} + \frac{{{n_4}}}{{{m_4}}}{(\hbar _i^{ - 1} \cdot {{\dot{{\hat{e}}}}_i})^{({n_4}/{m_4}) - 1}}({\Gamma _i} \cdot \dot{{\hat{e}}}_i^2 \cdot \hbar _i^{ - 2} \nonumber \\&+ \hbar _i^{ - 1} \cdot {{\ddot{{\hat{e}}}}_i})], \nonumber \\&= {\hat{s}}_i^T\{ {{\dot{{\hat{e}}}}_i} + \frac{{{n_4}}}{{{m_4}}}{(\hbar _i^{ - 1} \cdot {{\dot{{\hat{e}}}}_i})^{({n_4}/{m_4}) - 1}}\{ {\Gamma _i} \cdot \dot{{\hat{e}}}_i^2 \cdot \hbar _i^{ - 2} \nonumber \\&+ \hbar _i^{ - 1} \cdot [{H_{i0}}^{ - 1}({\tau _i} + K_i^T{\varphi _i} + {\varepsilon _i} \nonumber \\&- {{C_{i0}}}{{\dot{q}}_i} - {{G_{i0}}}) - {{{\hat{a}}}_i}]\} \} \end{aligned}$$
(18)

where \({\Gamma _i} = - {\sigma _0}[({m_3}/{n_3}) - ({m_4}/{n_4})]{\hat{e}}_i^{({m_3}/{n_3}) - ({m_4}/{n_4}) - 1}\). Then, (18) can be rewritten as

$$\begin{aligned} \dot{V}_i({{{\hat{s}}}_i}) =&\frac{{{n_4}}}{{{m_4}}}{(\hbar _i^{ - 1} \cdot {{\dot{{\hat{e}}}}_i})^{({n_4}/{m_4}) - 1}}{\hat{s}}_i^T[{H_{i0}}^{ - 1}\hbar _i^{ - 1} \cdot (K_i^T{\varphi _i} \nonumber \\&+ {\varepsilon _i} - {\hat{K}}_i^T{\varphi _i} - {{{\hat{\varpi }} }_i} - {\beta _i}\mathrm{{sig}}({{{\hat{s}}}_i}))] - {\hat{s}}_i^T{\delta _i} \nonumber \\ \le&\, {\hat{s}}_i^T[{H_{i0}}^{ - 1}\hbar _i^{ - 1} \cdot (K_i^T{\varphi _i} + {\varpi _i} - {\hat{K}}_i^T{\varphi _i} - {{{\hat{\varpi }} }_i} \nonumber \\&- {\beta _i}\mathrm{{sig}}({{{\hat{s}}}_i}))] - {\hat{s}}_i^T{\delta _i} \nonumber \\ \le&\, {\hat{s}}_i^T[{H_{i0}}^{ - 1}\hbar _i^{ - 1} \cdot ({\tilde{K}}_i^T{\varphi _i} + {{{\tilde{\varpi }} }_i} - {\beta _i}\mathrm{{sig}}({{{\hat{s}}}_i}))] \nonumber \\&- {\hat{s}}_i^T{\delta _i}, \end{aligned}$$
(19)

where \(\left\| {{\varepsilon _i}} \right\| \le {\varpi _i}\) is defined in (4). In accordance with (16), we obtain that

$$\begin{aligned} \dot{V}_i({{{\hat{s}}}_i})&\le - {\hat{s}}_i^T{\delta _i}\nonumber \\&\le - {\hat{s}}_i^T({\sigma _4}{\hat{s}}_i^{{{{m_3}} / {{n_3}}}} + {\eta _4}{\hat{s}}_i^{{{{m_4}} / {{n_4}}}}) \nonumber \\&\le 0, \end{aligned}$$
(20)

where \({\delta _i} = {\sigma _4}{\hat{s}}_i^{{{{m_3}} / {{n_3}}}} + {\eta _4}{\hat{s}}_i^{{{{m_4}} / {{n_4}}}}\) is defined in (6). The inequality above indicates that \(\dot{V}_i({{{\hat{s}}}_i})\) is negative definite, ensuring the convergence of \({{\hat{s}}}_i\) for all \(i \in {{\mathscr {V}}}\). Alternatively, the selected Lyapunov function candidate is as follows for the neural adaptive laws:

$$\begin{aligned} V_i({{{\tilde{K}}}_i},{{{\tilde{\varpi }} }_i}) = \frac{1}{2}\mathrm{{tr(}}{\tilde{K}}_i^T\alpha _1^{ - 1}{{{\tilde{K}}}_i}\mathrm{{) + }}\frac{1}{2}\alpha _2^{ - 1}{\tilde{\varpi }} _i^2. \end{aligned}$$
(21)

Given the positive constants \({\alpha _1}\) and \({\alpha _2}\), the function \(V_i({{{\tilde{K}}}_i},{{{\tilde{\varpi }} }_i})\) is positive definite. Furthermore, we can deduce from (6), (16), and the previous analysis that \({{{\tilde{K}}}_i}, {{{\tilde{\varpi }} }_i} \in {L_2} \cap {L\infty }\) and \({{\dot{{\tilde{K}}}}_i},{{\dot{{\tilde{\varpi }} }}_i} \in {L\infty }\). The derivative of \(V_i({{{\tilde{K}}}_i},{{{\tilde{\varpi }} }_i})\) is then expressed as follows:

$$\begin{aligned} \dot{V}_i({{{\tilde{K}}}_i},{{{\tilde{\varpi }} }_i}) = - \mathrm{{tr(}}{\tilde{K}}_i^T({\varphi _i}{\hat{s}}_i^T\mathrm{{)) - }}{{{\tilde{\varpi }} }_i}\left\| {{{{\hat{s}}}_i}} \right\| . \end{aligned}$$
(22)

Thus, it follows that

$$\begin{aligned} {\ddot{V}}_i({{{\tilde{K}}}_i},{{{\tilde{\varpi }} }_i}) \!=\! \mathrm{{tr(}}{\alpha _1}{{{\hat{s}}}_i}\varphi _i^T({\varphi _i}{\hat{s}}_i^T\mathrm{{)}}) \!+\! \mathrm{{tr(}}{\tilde{K}}_i^T({{\dot{\varphi }}_i}\dot{{\hat{s}}}_i^T\mathrm{{)}} \!+\! {\alpha _2} \Vert {{{\dot{{\hat{s}}}}_i}} \Vert . \end{aligned}$$
(23)

On the basis of the analysis of (19) and (20), which shows that \({{{\hat{s}}}_i} \in {L_2} \cap {L_\infty }\), and considering the closed-loop dynamics (10), we can conclude that \({{\dot{{\hat{s}}}}_i} \in {L_\infty }\). Additionally, the boundedness of \({{{\dot{\varphi }} }_i}\) defined in (4) implies that \({\ddot{V}}_i({{{\tilde{K}}}_i},{{{\tilde{\varpi }} }_i}) \in {L_\infty }\). By applying Barbalat’s lemma10 and combining it with the previous analysis, we further deduce that \({{{\tilde{K}}}_i} \rightarrow 0\) and \({{{\tilde{\varpi }} }_i} \rightarrow 0\) as \(t \rightarrow \infty\). This finding demonstrates the effectiveness of the neural adaptive law, allowing the use of smaller \({\beta _i}\) and reducing the chattering phenomenon.

With regard to (16), obtaining knowledge of \({{{\tilde{\varpi }} }_i}\) may be challenging in practical applications. In such scenarios, a practical solution is to choose a suitably large \({\beta _i}\) to ensure the stability condition. This solution results in the following reformulation of (19):

$$\begin{aligned} \dot{V}_i({{{\hat{s}}}_i}) \le&- {\hat{s}}_i^T({\sigma _4}{\hat{s}}_i^{{{{m_3}} /{{n_3}}}} + {\eta _4}{\hat{s}}_i^{{{{m_4}} / {{n_4}}}}) \nonumber \\ \le&- {\sigma _4}{\hat{s}}_i^{({m_3} + {n_3})/{n_3}} - {\eta _4}{\hat{s}}_i^{({m_4} + {n_4})/{n_4}} \nonumber \\ \le&- {\sigma _4}{2^{({m_3} + {n_3})/2{n_3}}}V_i{({{{\hat{s}}}_i})^{({m_3} + {n_3})/2{n_3}}} \nonumber \\&- {\eta _4}{2^{({m_4} + {n_4})/2{n_4}}}V_i{({{{\hat{s}}}_i})^{({m_4} + {n_4})/2{n_4}}}. \end{aligned}$$
(24)

By utilizing Lemma 1 and the expression in (24), the distributed tracking errors \({{{\hat{e}}}_i} = {q_i} - {r_i}-{{{\hat{x}}}_i}\) and \({{\dot{{\hat{e}}}}_i} = {\dot{q}_i} - {{{\hat{v}}}_i}\) evidently reach the manifold \({{{\hat{s}}}_i}\) within the fixed time \(t \le {{{\mathscr {T}}}_{l,1}}\). Then, \({{{\mathscr {T}}}_{l,1}}\) is defined as follows:

$$\begin{aligned} {{{\mathscr {T}}}_{l,1}} \le {{{\mathscr {T}}}_{l\max ,1}} = \frac{{{2^{({n_3} - {m_3})/2{n_3}}}}}{{{\sigma _4}}}\frac{{{n_3}}}{{{m_3} - {n_3}}} + \frac{{{2^{({n_4} - {m_4})/2{n_4}}}}}{{{\eta _4}}}\frac{{{n_4}}}{{{n_4} - {m_4}}}. \end{aligned}$$
(25)

Drawing upon the preceding analysis and fixed-time sliding mode control theory22, a conclusion can be readily drawn that \({{{\hat{e}}}_i}\) and \({{\dot{{\hat{e}}}}_i}\) achieve convergence to the origin within the fixed time \({{{\mathscr {T}}}_l} \le {{{\mathscr {T}}}_{l\max ,1}} + {{{\mathscr {T}}}_{l\max ,2}}\). In particular, it follows from (25) that

$$\begin{aligned} {{{\mathscr {T}}}_l} \le&\, {{{\mathscr {T}}}_{l\max ,1}} + {{{\mathscr {T}}}_{l\max ,2}} \nonumber \\ =&\, {{{\mathscr {T}}}_{l\max ,1}} + \frac{1}{{{\sigma _0}}}\frac{{{n_3}}}{{{m_3} - {n_3}}} + \frac{1}{{{\eta _0}}}\frac{{{n_4}}}{{{n_4} - {m_4}}} \nonumber \\ =&\frac{{{n_3}}}{{{m_3} - {n_3}}}\left( {\frac{{{2^{({n_3} - {m_3})/2{n_3}}}}}{{{\sigma _4}}} + \frac{1}{{{\sigma _0}}}} \right) \nonumber \\&+ \frac{{{n_4}}}{{{n_4} - {m_4}}}\left( {\frac{{{2^{({n_4} - {m_4})/2{n_4}}}}}{{{\eta _4}}} + \frac{1}{{{\eta _0}}}} \right) . \end{aligned}$$
(26)

In addition, if \({\theta _2} \buildrel \Delta \over = [{n_4}({m_3} - {n_3})]/[{n_3}({n_4} - {m_4})] \le 1\), a less conservative bound can be obtained as

$$\begin{aligned} {{{\mathscr {T}}}_l} \le&\frac{{{n_4}}}{{{n_4} - {m_4}}}\left( {\frac{1}{{\sqrt{{\sigma _0}{\eta _0}} }}{{\tan }^{ - 1}}\sqrt{\frac{{{\sigma _0}}}{{{\eta _0}}}} + \frac{1}{{{\sigma _0}{\theta _2}}}} \right. \nonumber \\&\left. { + \frac{1}{{\sqrt{{\sigma _4}{\eta _4}} }}{{\tan }^{ - 1}}\sqrt{\frac{{{\sigma _4}}}{{{\eta _4}}}} + \frac{{{2^{ - ({n_3} + {m_3})/2{n_3}}}}}{{{\sigma _4}{\theta _2}}}} \right) . \end{aligned}$$
(27)

The second step validates the successful resolution of the fixed-time CFT problem. Before proceeding, let \({e_i} = {q_i} - {r_i} - {x_{0,k}}\) and \({{\dot{e}}_i} = {{\dot{q}}_i} - {v_{0,k}}\), where \({e_i}\) and \({{\dot{e}}_i}\) represent the position and velocity tracking errors of the robots, respectively. Applying the Triangle Inequality, it can be obtained that

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow {{{\mathscr {T}}}_f}} \left\| {{e_i}} \right\| =&\mathop {\lim }\limits _{t \rightarrow {{{\mathscr {T}}}_f}} \left\| {({q_i} - {r_i} - {{{\hat{x}}}_i}) + ({{{\hat{x}}}_i} - {x_{0,k}})} \right\| \\ \le&\mathop {\lim }\limits _{t \rightarrow {{{\mathscr {T}}}_f}} \left\| {{{{\hat{e}}}_i}} \right\| + \mathop {\lim }\limits _{t \rightarrow {{{\mathscr {T}}}_f}} \left\| {{{{\tilde{x}}}_i}} \right\| \\ \le&0,\\ \mathop {\lim }\limits _{t \rightarrow {{{\mathscr {T}}}_f}} \left\| {{{\dot{e}}_i}} \right\| =&\mathop {\lim }\limits _{t \rightarrow {{{\mathscr {T}}}_f}} \left\| {({{\dot{q}}_i} - {{{\hat{v}}}_i}) + ({{{\hat{v}}}_i} - {x_{0,k}})} \right\| \\ \le&\mathop {\lim }\limits _{t \rightarrow {{{\mathscr {T}}}_f}} \left\| {{{\dot{{\hat{e}}}}_i}} \right\| + \mathop {\lim }\limits _{t \rightarrow {{{\mathscr {T}}}_f}} \left\| {{{{\tilde{v}}}_i}} \right\| \\ \le&0, \end{aligned}$$

where \({{{\mathscr {T}}}_f} \le {{{\mathscr {T}}}_e} + {{{\mathscr {T}}}_l}\). Therefore, the problem defined in Definition 3 is effectively resolved, concluding the proof. \(\square\)

Remark 8

We choose \({{{\mathscr {T}}}_f} \le {{{\mathscr {T}}}_e} + {{{\mathscr {T}}}_l}\) to represent the total time required for system convergence, which includes the time \({{{\mathscr {T}}}_e}\) associated with the distributed observer layer and the time \({{{\mathscr {T}}}_l}\) related to the local control layer. This approach ensures that the cumulative nature of the convergence times across different stages is fully considered, encompassing all phases of the convergence process. By contrast, using \(\mathscr {T}_f \le \max (\mathscr {T}_e, \mathscr {T}_l)\) would imply that the convergence time is determined solely by the longer duration of either the distributed observer layer or the local control layer. This choice assumes that one stage completes immediately after the other, disregarding potential overlaps or the possibility of collaborative convergence between the stages.

Simulations

This section depicts the efficacy of the HFNA control algorithm outlined in Algorithm 1 through simulation.

Algorithm 1
figure a

HFNA control

Full size image
Fig. 4
figure 4

Directed graph \({\mathscr {G}}\) representing the NPRS network.

Full size image

The NPRS comprises ten identical follower robots (2-DOF) and three virtual leaders (simplified leader representations). Moreover, the interactions of the NPRS are illustrated in Fig. 4. The Laplacian matrix \({{\mathscr {L}}}\) can be computed as

$$\begin{aligned} {{\mathscr {L}}} \!=\!\! \left[ {\begin{array}{*{20}{c}} 2& 0& { - 2}& 0& 0& 0& 0& 0& 0& 0\\ { - 1}& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ { - 2}& 0& 2& { - 4}& 0& 4& 0& 0& 0& 0\\ 0& 0& 0& 1& { - 1}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 3& 0& { - 3}& 0& 0& 0\\ 0& 0& 0& { - 2}& 0& 3& { - 1}& 0& 0& 0\\ 0& 0& 0& 0& { - 3}& 0& 3& { - 2}& 0& 2\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& { - 1}\\ 0& 0& 0& 0& 0& 0& 0& { - 2}& 2& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& { - 1}& 1 \end{array}} \right] . \end{aligned}$$

Additionally, the physical parameters of the NPRS are selected in Table 1. The observations of the physical parameters of the NPRS are selected in Table 2. The dynamics descriptions is given by

$$\begin{aligned}&\left[ {\begin{array}{*{20}{c}} {{H_{i11}}}& {{H_{i12}}}\\ {{H_{i21}}}& {{H_{i22}}} \end{array}} \right] \! \left[ {\begin{array}{*{20}{c}} {{{\ddot{q}}_{i1}}}\\ {{{\ddot{q}}_{i2}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{C_{i11}}}& {{C_{i12}}}\\ {{C_{i21}}}& {{C_{i22}}} \end{array}} \right] \! \left[ {\begin{array}{*{20}{c}} {{{\dot{q}}_{i1}}}\\ {{{\dot{q}}_{i2}}} \end{array}} \right] \\&\ \ + \left[ {\begin{array}{*{20}{c}} {{G_{i1}}}\\ {{G_{i2}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{d_{i1}}}\\ {{d_{i2}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\psi ({\tau _{i1}})}\\ {\psi ({\tau _{i2}})} \end{array}} \right] . \end{aligned}$$

In more detail, \({{H}_{i11}}={{\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i1}} + 2{\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i2}}\cos ( {{{\dot{q}}_{i2}}} )}\), \({{H}_{i12}}={{H}_{i21}}={\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i3}} + 2{\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i2}}\cos ( {{{\dot{q}}_{i2}}} )\), \({{H}_{i22}}={\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i2}}\), \({C}_{i11}= - {\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i2}}\sin ( {{{\dot{q}}_{i2}}} ){{\dot{q}}_{i2}},\)\({C}_{i12}= - {\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i2}}\sin ( {{{\dot{q}}_{i2}}}) ( {{\dot{q}}_{i1}} + {{\dot{q}}_{i2}} )\) \({C}_{i21}= - {\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i2}}\sin ( {{{\dot{q}}_{i2}}}){\dot{q}}_{i1}\), \({C}_{i22} = 0\), \({{G}_{i1}}= g {\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i4}}\cos ( {\dot{q}}_{i1} ) + g{p_{i5}}\cos ( {\dot{q}}_{i1} + {\dot{q}}_{i2} ),\)\({{G}_{i2}}= g{\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i5}}\cos ( {\dot{q}}_{i1} + {\dot{q}}_{i2} )\). We select the standard gravitational torque as \(g = 9.8 \phantom {i} \mathrm{m/{s^2}}\). Furthermore, the detailed description of the corresponding parameters is provided below. \({\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i1}}\) to \({\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i5}}\) are given as \({\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i1}} = {{m}_{i1}}\chi _{i1}^2 + {{m}_{i2}}( {l_{i1}^2 + \chi _{i2}^2} ) + {I}_{i1} + {I}_{i2}\), \({\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i2}} = {{m}_{i2}}{{l}_{i1}}{{\chi }_{i2}}\), \({\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i3}} = {{m}_{i2}}\chi _{i2}^2 + {{I}_{i2}}\), \({\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i4}} = {{m}_{i1}}{{\chi }_{i1}} + {{m}_{i2}}{{l}_{i1}}\), \({\bar{\phantom {n}}\hspace{-10.0pt}\lambda _{i5}} = {{m}_{i2}}{{\chi }_{i2}}\), and \({{I}_{i1}} = \frac{1}{3}{{m}_{i1}}l_{i1}^2\), \({{I}_{i2}} = \frac{1}{3}{{m}_{i2}}l_{i2}^2\).

Table 1 Physical parameters of the robot.
Full size table
Table 2 The observations of the physical parameters.
Full size table

Under Assumption 3, the trajectory of the virtual leaders, labeled as \(L_1\), \(L_2\), and \(L_3\), are selected as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{x_{0,1}} = \mathrm{{col}}(0.9 + 0.4\sin (0.4t),1.0 + 0.4\cos (0.4t)),}\\ {{v_{0,1}} = \mathrm{{col}}({{0.4}^2}\cos (0.4t),\; - {{0.4}^2}\sin (0.4t)),}\\ {{a_{0,1}} = \mathrm{{col}}( - {{0.4}^3}\sin (0.4t),\; - {{0.4}^3}\cos (0.4t)),} \end{array}} \right. \\ \left\{ {\begin{array}{*{20}{l}} {{x_{0,2}} = \mathrm{{col}}(2.6 + 0.5\cos (0.5t),1.4 + 0.5\sin (0.5t)),}\\ {{v_{0,2}} = \mathrm{{col}}( - {{0.5}^2}\sin (0.5t),\;{{0.5}^2}\cos (0.5t)),}\\ {{a_{0,2}} = \mathrm{{col}}( - {{0.5}^3}\cos (0.5t),\; - {{0.5}^3}\sin (0.5t)),} \end{array}} \right. \\ \left\{ {\begin{array}{*{20}{l}} {{x_{0,3}} = \mathrm{{col}}(1.6 + 0.3\sin (0.3t),2.6 + 0.3\cos (0.3t)),}\\ {{v_{0,3}} = \mathrm{{col}}({{0.3}^2}\cos (0.3t),\; - {{0.3}^2}\sin (0.3t)),}\\ {{a_{0,3}} = \mathrm{{col}}( - {{0.3}^3}\sin (0.3t),\; - {{0.3}^3}\cos (0.3t)).} \end{array}} \right. \end{aligned}$$

Furthermore, we present the parameters used in the HFNA control algorithm (6)–(7). To ensure the establishment of (8) and (9), the following parameter values are used: \({\sigma _{\min }} = 8\) (\({\sigma _{1}} = 8\), \({\sigma _{2}} = 9\), \({\sigma _{3}} = 10\)), \({\eta _{\min }} = 8\) (\({\eta _{1 }} = 8\), \({\eta _{2}} = 9\), \({\eta _{3}} = 10\)), \({m_1} = 2\), \({n_1} = 1\), \({m_2} = 1\), and \({n_2} = 2\). Besides, the parameters of the neural adaptive laws are specified as \({\alpha _1} = 0.1\) and \({\alpha _2} = 1.01\). The neural networks \({\hat{K}}_i^T{\varphi _i}\) comprise 10 neurons, where the centers \({\rho _i}\) are evenly distributed in the range \([-2\pi , 2\pi ]\), with widths \(\iota _i = 20\). We choose \({\sigma _0} = 1,{\eta _0} = 1,{\sigma _4} = 1,{\eta _4} = 1\), \({m_3} = 9,\)\({n_3} = 5\), \({m_4} = 7\) and \({n_4} = 9\), \({\beta _i} = 50\) to make (16) holds. Furthermore, the external perturbations is chosen as \({d_i}(t) = - 0.1\mathrm{{col}}(\cos t,\;\sin t)\). Besides, the formation offsets are set to \({r_1} = \mathrm{{col}}(0,{2 / 9})\textrm{m}\), \({r_2} = \mathrm{{col}}({{ - \sqrt{3} } / 9},{{ - 1} / 9})\textrm{m},\)\({r_3} = \mathrm{{col}}({{\sqrt{3} } / 9},{{ - 1} / 9})\textrm{m}\), \({r_4} = \mathrm{{col}}( - 0.16,0.15)\textrm{m}\), \({r_5} = \mathrm{{col}}(0.15,0.15)\textrm{m}\), \({r_6} = \mathrm{{col}}(0.15, - 0.15)\textrm{m}\), \({r_7} = \mathrm{{col}}( - 0.15, - 0.15)\textrm{m}\), \({r_8} = \mathrm{{col}}(0,{1 / 4})\textrm{m}\), \({r_9} = \mathrm{{col}}({{ - \sqrt{3} } / 8},{{ - 1} / 8})\textrm{m}\), \({r_{10}} = \mathrm{{col}}({{\sqrt{3} } / 8}, {{ - 1} / 8})\textrm{m}\). Here, the input deadzone function of the robotic manipulator is denoted as

$$\begin{aligned} \psi ({\tau _i}) = \left\{ {\begin{array}{*{20}{l}} {{\tau _i} - \textrm{col}(10,10), \ \ \, \, \left\| {{\tau _i}} \right\| \ge 10},\\ {0,\;\;\;\;\;\;\;\;\;\;\;\; \ \, - 10< \left\| {{\tau _i}} \right\| < 10},\\ {{\tau _i} + \textrm{col}(10,10),\;\left\| {{\tau _i}} \right\| \le - 10}. \end{array}} \right. \end{aligned}$$

The initial states \({q_i}\left( 0 \right)\) and \({{\dot{q}}_i}\left( 0 \right)\) are randomly assigned within the ranges of \([-5,5]\) and \([-0.2,0.2]\), respectively.

Fig. 5
figure 5

Trajectories of NHRS with a constant cluster formation configuration under different initial conditions. Note: The intersections of the trajectories in this figure do not occur simultaneously. The robots do not occupy the same position at the same time, hence avoiding any potential collisions.

Full size image
Fig. 6
figure 6

(a, b) Illustrate the evolution of the error term (\(q_i-r_i\)), representing the difference between the actual and reference trajectories. (c, d) display the evolution of the observed state \({\hat{x}}_i\), showing how the state observation evolves over time.

Full size image
Fig. 7
figure 7

(a, b) Show the overall position error \(e_i\), illustrating the deviation between the actual and desired positions. (c, d) describe the evolution of the state observation error \({{{\tilde{x}}}_i}\) in the distributed observer layer. Finally, (e, f) display the evolution of the position error \({\hat{e}}_i\) in the local control layer.

Full size image
Fig. 8
figure 8

(a, b) Illustrate the velocity errors associated with cluster formation tracking, highlighting the discrepancies between the desired and actual velocities of the robots throughout the formation process.

Full size image
Fig. 9
figure 9

(a, b) Illustrate the neural adaptive parameters of the 1st subnetwork. (c, d) display the neural adaptive parameters of the 2nd subnetwork. (e, f) present the neural adaptive parameters of the 3rd subnetwork.

Full size image
Fig. 10
figure 10

(a, b) illustrate the convergence of the RBF neural network approximation error \(\varepsilon _i\) during the approximation of \(F_i(t)\) for coordinates 1 and 2.

Full size image
Fig. 11
figure 11

(a) Control input torque \(\tau _{i}\) for coordinates 1 and 2 of the first robot without considering actuator input deadzone compensation. The comparison algorithm applied in the figure (a) is derived from reference23. (b) Control input torque \(\tau _i\) for coordinates 1 and 2 of the first robot while considering actuator input deadzone compensation.

Full size image
Table 3 Comparison of related literature.
Full size table

Remark 9

The comparative analysis provided in Table 3 offers a thorough evaluation of our proposed control algorithm in relation to several established methods20,33,34,37,38. This analysis emphasizes the advantages of our approach, particularly in key performance areas such as convergence time, hierarchical control, deadzone compensation, uncertainty treatment, and formation task. By highlighting these aspects, we demonstrate the practical benefits of our method, ensuring a more comprehensive understanding of its effectiveness in addressing complex control challenges.

\(\textbf{Simulation}\) \(\textbf{results}\) are presented in Figs. 5, 6, 7, 8, 9, 10 and 11, depicting the fixed-time CFT trajectories of the NPRS on the XY plane for 10 robots (Fig. 5). The efficacy of the proposed HFNA control algorithm (6)–(7) in achieving excellent fixed-time CFT performance of the NPRS is evident from the outcomes. In detail, from (c)–(d) in Figs. 6 and 7, the position observers \({\hat{x}}_i\) converge to \(x_{0,k}\) for all \(i \in {{\mathscr {V}}}_k, k \in { 1,2,3}\) within the fixed time \({{{\mathscr {T}}}_e}\). Additionally, (a)–(b) in Figs. 6 and 7 reveal the attainment of fixed-time convergence of \(q_i\), \(i \in {{\mathscr {V}}}\), through the designed HFNA control algorithm. Using the parameters we set, the fixed settling time of the distributed observer layer \(t \le {{{\mathscr {T}}}_e}=0.38 \textrm{s}\) (based on (15)), and the fixed settling time of the local layer \(t \le {{{\mathscr {T}}}_l}=9.36\,\textrm{s}\) (based on (26)). Therefore, the total fixed-time convergence is \({{{\mathscr {T}}}_f} \le {{{\mathscr {T}}}_e} + {{{\mathscr {T}}}_l}=9.74\,\textrm{s}\). Meanwhile, from Fig. 7, \(e_i\) for \(i \in {{\mathscr {V}}}\) are bounded within the range of \([-0.1, 0.1]\) in a fixed time \(t \approx 4.50\,\textrm{s} < {{{\mathscr {T}}}_f}\). Similarly, Fig. 8 demonstrates the tracking performance of the velocities. Additionally, Fig. 9 provides evidence of the stability of the neural adaptive parameters. Figure 10 illustrates the evolution of the RBF neural network approximation error. As shown, the neural network approximation error \(\varepsilon _i\) gradually converges to zero. This result demonstrates that the RBF network effectively approximates the lumped uncertainties, thereby ensuring the accuracy of the control algorithm and the stability of the overall system. In Fig. 11b, the control input torque \(\tau _1\) for the 1st robot is bounded, minimizing the impact of minor input fluctuations and resulting in smoother control inputs as well as improved overall system performance. Overall, the simulation results validate the effectiveness and accuracy of the HFNA control algorithm.

Conclusion

The fixed-time CFT control problem in NPRSs was successfully addressed by considering actuator input deadzone, parametric uncertainties, and external perturbations. To address this challenging problem, a novel HFNA control algorithm, which comprised a distributed observer algorithm and a neural-adaptive fixed-time controller in the local control layer, was proposed. The simulation results demonstrated that the robots in a NPRS effectively achieved the fixed-time CFT control task, validating the feasibility of the HFNA control algorithm. Furthermore, the bipartite CFT control problem of NPRSs, which incorporates cooperative and antagonistic interconnections, can handle more complex control tasks. Consequently, our future work will be dedicated to exploring the CFT control for bipartite consensus and mobile manipulators.