Introduction

In the coming decades, coal will remain the most important energy source, so coal mining is crucial. In recent years, the number of accidents in the coal mine and the death rate of one million tons have continued to decline, but there are still huge safety problems, and gas explosion is dangerous accidents in the coal mine1,2,3. Statistical data reveals that 36% of gas explosion accidents occur in the excavation face, as reported by Li et al.4. Due to the complexity of ventilation and equipment in excavation face, the restart or failure of ventilation equipment will lead to insufficient ventilation volume, which will lead to gas accumulation in the excavation roadway and lead to accidents5,6,7,8. Therefore, it is very important to study the law of gas explosion propagation in excavation face.

Mine gas explosion is a very complex process. Previous studies on mine gas explosion mainly used experimental and numerical simulation methods to study the propagation characteristics of gas explosion in small tunnels or pipelines. The research factors involved mainly include initial gas temperature, methane characteristics, i.e., (concentration, distribution), obstacle configurations, such as shape, number, and ___location, initial turbulence degree, initial pressure. Some research found that the higher the initial temperature of methane/air mixtures, the higher explosion temperature9,10,11. Gao et al.12 revealed the relationship between flame diffusion distance and gas concentration at low gas concentrations. Cao et al.13 and Bao et al.14 analyzed the relationship between methane concentration and the number of explosion peaks. The study found that when the methane concentration is between 7.5% and 13%, the explosion pressure curve will have two peaks. Li et al.15 analyzed the influencing factors of specific flame forms and revealed the causes of flame instability.

For the influences of obstacles on gas explosion propagation, Gao et al.16 studied the impacts of staggered and neatly arranged obstacles on gas explosion propagation law by means of OpenFOAM and found that the staggered obstacles has a certain promotion effect on the flame acceleration and flame speed. Dong et al.17 conducted the influences of the ignition points and obstacle number by the experience. Zheng et al.18 conducted a study on methane concentration and obstacle blocking rate. Andrews et al.19 and Wu et al.20 explored the influence of the ___location of obstacles on the law of explosion propagation. Wang et al.21 studied the effect of obstacle shape on the propagation law of explosion through numerical simulation and experiment, and explained the mechanism of flame acceleration. Nguyen et al.22 studied the effects of obstacle shape, turbulence model and fire point ___location on flame propagation of methane explosion by two-dimensional Chen et al.23 established a prediction function of methane air explosion pressure for sudden expansion of pipeline area, which can accurately predict explosion overpressure and time change curve. Zhu et al.24 and Niu et al.25 studied the laws of methane explosion propagation in complex pipe networks. Additionally, the attenuation equation of explosion overpressure with explosion propagation distance was obtained by fitting experimental data. Gao et al.26 studied the influence of flexible obstacles in roadway on gas explosion by means of numerical simulation, and found that flexible obstacles (ventilation system and cable, etc.) have a certain impact on gas explosion.

Moreover, some studies have found that gas parameters such as initial turbulence intensity, gas distribution, gas density, initial pressure will also affect the gas explosion propagation law. Many scholars have revealed the detailed mechanism of the effect of turbulence intensity enhancement on explosion characteristics6,21,27,28,29,30,31,32. Gao et al.33 studied the influence of TBM on gas distribution in roadway through simulation, and pointed out that TBM has a non-negligible influence on gas concentration distribution and gas density. Wu et al.20, Huang et al.34 and Xiu et al.35 experimentally studied the effect of non-uniform methane concentration on explosion pressure. Leo et al.36 and Li et al.37 reveal the effect of initial pressure on flame characteristics and explosion pressure. Yang et al.38 believes that the maximum flame propagation velocity increases with an increase in initial pressure, and the explosion overpressure fluctuates more significantly.

Due to the complexity of the experimental system, it is very difficult to carry out the explosion experiment of real roadway39. However, many scholars have found that there is scale effect between large and small experiments40,41,42,43, so only small experiments can not accurately reflect the propagation law of real large roadway gas explosion. Therefore, numerical simulation is of great significance for studying the propagation law of large roadway gas explosion. In addition, in previous studies, the roadway is usually simplified as a pipeline, and the influence of TBM on the gas explosion propagation law is ignored. In actual situations, the existence of TBM has an impact on the gas explosion propagation law that cannot be ignored. Therefore, using Fluent software, this paper conducts a three-dimensional numerical simulation of gas explosions with varying gas concentrations and accumulation lengths to investigate the propagation law in the excavation roadway. Various parameters representing gas explosion characteristics are analyzed. The research results will provide guidance for the prediction of gas explosion losses and play an important role in the investigation of coal mine gas explosion accidents.

Numerical simulation setup

Basic assumptions

A one-step irreversible reaction of methane with air is adopted to simplify the reaction mechanism. Methane/air mixtures and the gas generated by the reaction adhere to the ideal gas equation of state, as well as the conservation principles of mass, momentum and energy. The walls of the physical model are rigid adiabatic walls, ensuring no slip or heat transfer. In the gas accumulation area, methane and air form a uniform mixture.

For calculation settings, the RNG k-ε turbulence model is selected, along with the Finite-Eddy combustion rate model. The PISO algorithm is used for pressure–velocity coupling calculation. First-order upwind discrete methods are applied to turbulent kinetic energy and turbulent dissipation rate, while second-order upwind discrete methods are used for the remaining parameters. The continuity, the velocity components in each direction, and residuals of each components are less than 0.00001. The time step is set to 0.0001 s, and each time step is calculated over 30 iterations. The computer is equipped with an AMD EPYC 7643 32-Core Processor, featuring a total of 128 threads and 256 GB memory.

Physical model and boundary condition settings

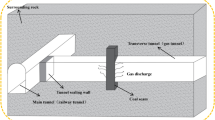
The excavation roadway and Tunnel Boring Machine are reasonably simplified to establish a physical model. The left end of the excavation roadway is closed while the right end is open. The excavation roadway has dimensions: length (L) of 50 m, width (K) of 5 m, and height (H) of 2 m. Its top is semi-circular with a diameter of 5 m.

The dimensions of the TBM are 13.18 m in length and 3.22 m in width. Within the mine environment, methane gas (CH4) is assumed to be present, accumulating only at the left end of the roadway over a length of 5 m. The ignition event occurs locally, initiating at a point with dimensions of 0.5 m in length, 1 m in height, and a radius of 0.025 m, reaching a high temperature of 2500 K. Monitoring points are set behind the boring machine and at distances of 25 m, 35 m and 45 m from the left side, labeled as M1, M2, and M3, respectively. The diagram is shown in Fig. 1.

Fig. 1
figure 1

Physical model and monitoring settings.

Full size image

In the roadway, the atmosphere temperature is set to 300 K, except at the ignition point. The pressure is standardized to 1 atm, and the outlet is configured as a pressure outlet. The turbulence intensity at the pressure outlet is specified as 5%. Different gas accumulation lengths (Lgas) ranging from 4 to 7 m are investigated within the gas accumulation zone. This region is filled with a methane/air mixtures characterized by different methane volume concentrations, ranging from 7 to 14% and beyond. The initial conditions in the roadway involve a methane volume fraction of 0%, with oxygen composing 22% and nitrogen accounting for 78%. The mass fractions of each parameter are detailed in Table 1.

Table 1 Data of each component at different methane concentrations.
Full size table

Mathematical model

In this paper, continuity equation (Eq. 1), energy conservation equation (Eq. 2), momentum conservation equation (Eq. 3) and transport equation for the RNG k-ε turbulence model (Eq. 4 and Eq. 5) are used.

$$\begin{array}{*{20}c} {\frac{\partial \rho }{{\partial t}} + \frac{\partial }{{\partial x_{j} }}\left( {\rho \tilde{u}_{j} } \right) = 0} \\ \end{array}$$
(1)
$$\begin{array}{*{20}c} {\frac{\partial }{\partial t}\left( {\rho \tilde{h}_{{\text{s}}} } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho \tilde{u}_{i} \tilde{h}_{{\text{s}}} } \right) - \frac{{\partial \overline{p}}}{\partial t} - u_{j} \frac{{\partial \overline{p}}}{{\partial x_{i} }} - \frac{\partial }{{\partial x_{i} }}\left( {\lambda \frac{{\partial \tilde{T}}}{{\partial x_{i} }}} \right) = \frac{\partial }{{\partial x_{j} }}\left[ {\rho \left( {u_{i} \tilde{h}_{{\text{s}}} - \tilde{u}_{i} \tilde{h}_{{\text{s}}} } \right)} \right]} \\ \end{array}$$
(2)
$$\begin{array}{*{20}c} {\frac{\partial }{\partial t}\left( {\rho \tilde{u}_{j} } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho \tilde{u}_{i} \tilde{u}_{j} } \right) = \frac{{\partial \sigma_{ij} }}{{\partial x_{i} }} - \frac{{\partial \overline{p}}}{{\partial x_{i} }} - \frac{{\partial \tau_{ij} }}{{\partial x_{j} }}} \\ \end{array}$$
(3)
$$\begin{array}{*{20}c} {\frac{\partial }{\partial t}\left( {\rho k} \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho ku_{i} } \right) = \frac{\partial }{{\partial x_{j} }}\left( {\alpha_{k} \mu_{eff} \frac{\partial k}{{\partial x_{j} }}} \right) + G_{k} + G_{b} - \rho \varepsilon - Y_{M} + S_{k} } \\ \end{array}$$
(4)
$$\begin{array}{*{20}c} {\frac{\partial }{\partial t}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho \varepsilon u_{i} } \right) = \frac{\partial }{{\partial x_{j} }}\left( {\alpha_{\varepsilon } \mu_{eff} \frac{\partial \varepsilon }{{\partial x_{j} }}} \right) + C_{1\varepsilon } \frac{\varepsilon }{k}\left( {G_{k} + C_{3\varepsilon } G_{b} } \right) - C_{2\varepsilon } \rho \frac{{\varepsilon^{2} }}{k} - R_{\varepsilon } + S_{\varepsilon } } \\ \end{array}$$
(5)

To evaluate \(G_{k}\) in a manner consistent with the Boussinesq hypothesis,

$$\begin{array}{*{20}c} {G_{k} = \mu_{t} S^{2} } \\ \end{array}$$
(6)

The turbulent (or eddy) viscosity, \(\mu_{t}\), is computed by combining \(k\) and \(\varepsilon\) as follows: \(C_{\mu } = 0.0845\)

$$\begin{array}{*{20}c} {\mu_{t} = \rho C_{\mu } \frac{{k^{2} }}{\varepsilon }} \\ \end{array}$$
(7)

where \(S\) is the modulus of the mean rate-of-strain tensor, defined as:

$$\begin{array}{*{20}c} {S \equiv \sqrt {2S_{ij} S_{ij} } } \\ \end{array}$$
(8)

The generation of turbulence due to buoyancy is given by Eq. 9:

$$\begin{array}{*{20}c} {G_{b} = \beta g_{i} \frac{{\mu_{t} }}{{{\text{Pr}}_{t} }}\frac{\partial T}{{\partial x_{i} }}} \\ \end{array}$$
(9)

In the case of the RNG \(k\)-\(\varepsilon\) model, \({\text{Pr}}_{t} = 1/\alpha\), where \(\alpha\) is given by: where \(\alpha_{0} = 1/Pr = k/\mu c_{p}\)

$$\begin{array}{*{20}c} {\left| {\frac{\alpha - 1.3929}{{\alpha_{0} - 1.3929}}} \right|^{0.6321} \left| {\frac{\alpha + 2.3929}{{\alpha_{0} + 2.3929}}} \right|^{0.3679} = \frac{{\mu_{{\text{mol }}} }}{{\mu_{{\text{eff }}} }}} \\ \end{array}$$
(10)

The coefficient of thermal expansion, \(\beta\), is defined as:

$$\begin{array}{*{20}c} {\beta = - \frac{1}{\rho }\left( {\frac{\partial \rho }{{\partial T}}} \right)_{p} } \\ \end{array}$$
(11)

\(R_{\varepsilon }\) is given by Eq. 12: where \(\eta \equiv Sk/\varepsilon\), \(\eta_{0} = 4.38\),\(\beta = 0.012\).

$$\begin{array}{*{20}c} {R_{\varepsilon } = \frac{{C_{\mu } \rho \eta^{3} \left( {1 - \eta /\eta_{0} } \right)}}{{1 + \beta \eta^{3} }}\frac{{\varepsilon^{2} }}{k}} \\ \end{array}$$
(12)

\(Y_{M}\) is given by Eq. 13: where \(a\left( { \equiv \sqrt {\gamma RT} } \right)\)

$$\begin{array}{*{20}c} {Y_{M} = 2\rho \varepsilon M_{t}^{2} } \\ \end{array}$$
(13)
$$\begin{array}{*{20}c} {M_{t} = \sqrt {\frac{k}{{a^{2} }}} } \\ \end{array}$$
(14)

\(C_{3\varepsilon }\) is given by Eq. 15:

$$\begin{array}{*{20}c} {C_{3\varepsilon } = tan{\text{h}}\left| \frac{v}{u} \right|} \\ \end{array}$$
(15)

where ui, uj is the speed component (m/s), ρ is the density of the gas mixture (kg/m3), t is the time (s), hs is the apparent enthalpy (J), λ is the thermal conductivity (W/mK), σij is the stress tensor component (N/M3); τij is the subgrid scale stress (N/M3), “−” Indicates physical space filtering, Quantity, “~” indicates the quality weight filtering amount. T is temperature (K), k is the turbulence kinetic energy (m2/s2); ε is the dissipation rate of turbulence kinetic energy (m2/s3); i and j are the indicator signs of the tensors; μeff is the effective dynamic viscosity coefficient (N·s/m2) ; GK and Gb are the generation of turbulence kinetic energy and buoyancy, respectively (m2/s3); YM is the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate (m2/s3); Sk and Sε are the turbulent kinetic energy term and turbulent dissipative source term, respectively (m2/s3); αk = αε = 1.393, αk and αε are the Prandtl numbers of turbulent kinetic energy and turbulent dissipation rate, respectively; C1ε, C2ε, and C3ε are the empirical constants inherent; Rε is an additional term in the ε equation, which serves to adapt the parameter to the rapid change in the curvature of the flow line to meet the needs of the calculation.

Model validation

The appropriate mesh size is determined by comparing the peaks of overpressure and flame propagation speed under the condition of WCH4 = 10% and Lgas = 5 m. Each set of simulations was repeated three times to eliminate the effects of systematic errors and ensure the accuracy and repeatability of the simulation. During mesh generation, the TBM is locally encrypted, and the method of restricting the maximum element length is employed for mesh division. The minimum orthogonal mass less than 0.15 is not suitable for calculation, so the maximum element length greater than 0.2 m should be selected to divide the mesh. As shown in Fig. 2a and b, it is apparent that using a maximum mesh cell length of 2 m results in a significant deviation in the calculation results. Conversely, employing maximum mesh cell lengths of 0.3 m, 0.6 m, and 1 m maintains the calculation error within acceptable range. Table 2 provides additional metrics including the minimum orthogonal mass of the mesh, mesh count, and computational time, enabling a comprehensive evaluation. Taking into account the above factors, the maximum mesh cell length is ultimately selected as 1 m for mesh subdivision. The resultant mesh division configuration is depicted in Fig. 3.

Fig. 2
figure 2

Mesh independence verification.

Full size image
Table 2 Mesh partition parameter.
Full size table
Fig. 3
figure 3

Meshing result.

Full size image

Numerical simulation results and analysis

Pressure propagation law in roadway

According to Fig. 4a and b, the explosion overpressures at points M1, M2, and M3 have increased by 30.9 kPa, 36.6 kPa, and 27.6 kPa, respectively, in the presence of the tunneling machine compared to its absence, representing approximately 2.2 times, 3.0 times, and 3.2 times increases, respectively. Additionally, the time to reach the peak explosion overpressure has been advanced by 310 ms, 341 ms, and 300 ms, respectively. These findings indicate that the presence of the tunneling machine significantly enhances the explosion overpressure, thereby increasing the risk of gas explosions. The propagation of explosion shock wave is roughly divided into four stages in Fig. 5: pressure rise stage, pressure drop stage, pressure negative increase stage, pressure recovery stage. Subsequently, the pressure of explosion shock wave goes through four stages and gradually attenuates.

Fig. 4
figure 4

Pressure comparison diagram with and without TBM.

Full size image
Fig. 5
figure 5

Overpressure time curve under different methane concentrations.

Full size image

The most intense stoichiometric concentration for methane combustion reaction is identified as 9.5%. As depicted in Fig. 6a, the explosion overpressure at methane concentration of 10% and 11% is close to the peak value observed at a methane concentration of 9.5%. However, the time to reach the peak overpressure value increases. This occurs because methane exhibits a partial premixed state in the roadway, causing gas in the burned area to diffuse to the non-gas accumulation area under pressure wave action during explosion reaction. Consequently, the gas concentration in the gas accumulation area decreases to the exact methane/air reaction concentration, causing the three explosion overpressure peaks to be close to each other, and extending the time to reach the peak explosion overpressure. In Fig. 6b, With the increase of gas accumulation, the explosion overpressure increases gradually, and the time to reach the peak explosion overpressure increases first and then decreases. Consequently, excavation roadway with larger methane accumulation lengths pose a greater risk of explosion. In Fig. 6c, at a methane concentration of 9.5%, the maximum pressure rise rate is higher compared to other methane concentrations, and the time to reach the maximum pressure rise rate is shortest. In Fig. 6d, the maximum pressure rise rate does not increase with the increase of methane accumulation length, instead, it reaches its peak when the methane accumulation length is 5 m, which is related to the position of methane accumulation in the TBM. The time to reach the maximum explosion pressure rise rate gradually increases with the length of gas accumulation. This occurs because the volume of methane increases, resulting in increase in the total reaction time.

Fig. 6
figure 6

The pressure parameters and the time to peak vary with WCH4 and Lgas.

Full size image

As shown in Fig. 7a–d. As the accumulation length of the gas increases, the peak value of the main peak also increases, while the peak values of other peaks decrease. This indicates that the rate of decay of explosion pressure increases with the increase of gas accumulation length. Furthermore, there are differences in the decay rates of the three monitoring points, with faster decay rates closer to the explosion source. Figure 8 shows the pressure cloud diagrams at different times when the methane concentration is 9.5%. At the start of the explosion, the pressure propagates from the explosion source to the surrounding areas, reflecting off the left wall and the TBM structure, and then propagating toward the rear of the TBM. Around 0.47 s, the pressure increases sharply. By 0.535 s, the pressure reaches the right exit, after which the pressure inside the tunnel gradually decreases.

Fig. 7
figure 7

Different Lgas explosion overpressure time curves.

Full size image
Fig. 8
figure 8

Overpressure cloud diagrams.

Full size image

Speed propagation law in roadway

Figure 9a depicts the flame speed-time graphs for monitoring points M1, M2, and M3 with and without the presence of TBM. It can be seen from the figure that there is a large difference in the flame propagation speed between the two situations. The variations in speed magnitude are due to differences in flame turbulence intensity., In the presence of TBM, when the explosion flame contacts the surface of TBM, the flame is hindered by the TBM. The flame wrinkles and is elongated and the flame area increases, which in turn causes the turbulence intensity to further increase. In Fig. 9b, with TBM present, the peak flame propagation speeds at points M1, M2, and M3 are higher compared to when TBM is absent. Additionally, the time taken to reach these peak speeds is reduced. The results demonstrate that the presence of TBM accelerates flame propagation to a certain extent. In Fig. 10a and b, the flame propagation speed peek increases first and then decreases with the increase of methane concentration. Compared to methane concentration at 7%, the flame propagation speed peek corresponding to M1, M2, and M3 increased by 139.9 m/s, 166.69 m/s, and 166.2 m/s, respectively, when the methane concentration was at 9.5%. Meanwhile, the time to reach the peak speed decreased by 721 ms, 763 ms, and 839 ms. The increase in methane concentration significantly enhanced the flame propagation speed and shortened the time to reach the peak flame propagation speed. This is because the pressure generated by the explosion increases with the increase of methane concentration, and due to the obstruction of TBM, The flame is stretched as it travels, so the turbulence degree of the premixed gas increases during the explosion process, which leads to the increase of the flame stretching speed, the increase of the energy release rate and the flame propagation speed peak, and the shortening of the presentation time to the flame propagation speed peek.

Fig. 9
figure 9

Flame propagation speed comparison with and without TBM.

Full size image
Fig. 10
figure 10

The speed parameters vary with WCH4 and Lgas.

Full size image

Figure 10c shows that when the methane accumulation length is 4m, the flame propagation speed peek at M1, M2 and M3 increases by 33.0%, 54.4% and 66.6%, respectively, when the methane accumulation length is 7 m. The results indicate that increasing the length of gas accumulation increases the flame propagation speed. For Fig. 10d the time for the three monitoring points to reach the flame propagation speed peek first increases and then decreases with the increase of gas accumulation length. When the methane accumulation length is 4 m, the flame propagation speed peek is lower than that when the methane accumulation length is 5 m, resulting the time to reach the flame propagation speed peek is shorten. Compared to the methane accumulation length of 5 m, the flame propagation speed peek of 6 m and 7 m methane accumulation length increases. Moreover, as the length of methane accumulation increases, the propagation speed of the flame correspondingly increases, so the time to reach the flame propagation speed peek is shortened. Figure 11 illustrates the flame propagation speed cloud diagram. During the explosion flame propagation, due to the obstruction caused by the TBM’s baffle and the TBM itself, the flame propagation speed is higher above the baffle, while low-speed regions form behind the baffle and at the rear of the TBM. As the explosion reaction progresses, the extent of these low-speed regions further increases.

Fig. 11
figure 11

Flame speed cloud diagrams.

Full size image

The average flame propagation speed is computed by \(\overline{V} = \frac{{x_{n} - x_{n - 1} }}{{\Delta_{t} }}\) (\(X_{n}\) is the x-coordinate from the beginning of calculation to the n time step, \(X_{n - 1}\) is the x-coordinate from the beginning of calculation to the n−1 time step, ∆t is the length of the time step). Figure 12a shows the effect of methane concentration on the average flame propagation speed. When the flame spreads to the baffle part, due to the obstruction of the baffle part, the flame propagation cross-sectional area decreases, and deflagration occurs at the same time, resulting in a significant increase in the average propagation speed of the flame. When the flame passes through the rear end of the TBM, the increase of the cross section of the flame leads to the decrease of the average flame propagation speed. Then, with the further increase of the flame propagation speed, the flame speed decreases rapidly when it reaches the exit section, which is due to the increase of the flame propagation cross-sectional area near the exit. When the methane concentration is 9.5%, the flame front propagation speed increases nearly six times compared to before the flame passes through the baffle, which is much greater than the increase in flame front propagation speed for other methane concentrations. It shows that when the methane concentration is 9.5%, TBM has the greatest impact on the flame front propagation speed. Figure 12b shows the variation of the average flame front propagation speed with distance under different methane accumulation lengths. When the methane accumulation length is 7 m, after the flame passes through the baffle, its speed is twice that of when the methane accumulation length is 4 m. This shows that the greater the length of methane accumulation, the greater the impact of TBM on its explosion, and the more serious the consequences.

Fig. 12
figure 12

The average flame propagation speed varies with distance.

Full size image

Temperature change in roadway

The results from Fig. 13a and b show that the presence of the TBM has minimal effect on the peak explosion temperature but does affect the time it takes to reach the peak temperature. In Fig. 14a, as the explosion flame propagates, the flame temperature at M1 experiences a sudden increase followed by a stable trend, after the flame front passes M1, the temperature decreases and then fluctuates. This occurs due to the reflection and blocking effects of the wall and the shell of the boring machine, resulting in increased turbulence and subsequent temperature fluctuations. When the methane concentration is 9% and 13%, it is observed that the temperature exhibits a downward trend after 1.5 s, attributable to the air backflow leading to a decrease in the roadway temperature. When the methane concentration is 7%, the temperature at M1 starts to increase from 1.45 s, and the heating rate is significantly lower than other conditions, because the flame front arrives at M1 only at 1.45 s, and its heating rate is positively correlated with the methane combustion reaction rate. Figure 14b indicates that the maximum flame temperature also decreases with the increase of propagation distance during flame propagation. Compared to other methane concentrations, when the methane concentration is 9%, the temperature at M1 is the largest, and the temperature at M3 is the smallest, indicating that the temperature dissipation is the largest in the explosion propagation process.

Fig. 13
figure 13

Temperature comparison with and without TBM.

Full size image
Fig. 14
figure 14

The temperature parameters vary with WCH4 and Lgas.

Full size image

Figure 14c and d shows that increasing the methane accumulation length has minimal effect on the maximum flame temperature at M1 and M2 in the roadway but does elevate it at M3. Increasing the methane accumulation length results in an earlier heating time for the roadway. Figure 15 depicts the fluctuation of flame temperature within the roadway. Initially, at the onset of the explosion, the flame expanded spherically, contacting the left wall and the cutting mechanism of the TBM, then subsequently extending towards the upward baffle. At 440 ms, the explosive flame started spreading along the baffle towards its rear. However, as it passed through the baffle, ignition of the gas behind it occurred first, resulting in disruptions at the flame front. At 517 ms, the flame crossed the baffle, causing a faulting phenomenon and continued forward propagation. Simultaneously, a faulting phenomenon also occurred at the rear of the boring machine, promoting the forward spread of the flame. The merging of the two flames drove their forward propagation, forming a cryogenic zone behind the TBM baffle. As the explosion flame spread, the low-temperature region dissipated, eventually making contact with the right exit at 730 ms and expanding outward.

Fig. 15
figure 15

Flame temperature propagation in roadway.

Full size image

Methane dissipation process

Figure 16 is the methane reaction and diffusion cloud diagram, and Fig. 17 is the methane concentration time series curve at each monitoring points. The monitoring points are arranged in the parallel position of the baffle plate, 1m to 10m away from the left working face, and each monitoring point is 1 m apart. When the explosion occurs, methane reacts with air to form a hollow spherical reaction area in the middle. With the progress of the reaction, the explosion pressure is reflected by the header and the left working face, and the reaction between methane and air is also accelerated. As shown in Fig. 17, the methane concentration at the monitoring points P1, P2, P3 and P4 in the reaction area drops rapidly. Until it is fully involved in the reaction and exhausted. The methane in the unreacted region diffuses towards the rear side of the baffle, and its concentration gradually decreases. At the same time, the methane concentration of P6, P7, P8, P9 and P10 at the monitoring points behind the baffle increased successively at about 0.4 s. Interestingly, methane diffusion was affected by the obstruction effect of the TBM, and the explosion center shifted, so the methane near the monitoring point P8 first participated in the reaction until it was exhausted, and the methane concentration at the P5 monitoring point increased again under the influence of the explosion force around 0.5 s, and was finally completely reacted around 0.6 s.

Fig. 16
figure 16

Diagram of methane propagation process in roadway.

Full size image
Fig. 17
figure 17

Methane dissipation curve at monitoring point.

Full size image

Conclusions

This paper investigates how the presence of TBM affects the propagation laws of methane/air explosions in drivage roadways. It analyzes the effects of different methane concentrations and gas accumulation lengths on explosion characteristics, including overpressure, overpressure rise rate, temperature, and flame propagation speed variations. The research findings are summarized as follows:

  1. (1)

    The existence of TBM will increase the explosion overpressure, accelerate the flame propagation speed, and change the flame propagation mode. The existence of tunneling machine is a crucial factor in the study of the law of gas explosion propagation in roadway.

  2. (2)

    Methane concentration and gas accumulation length have certain effects on the peak value of explosion overpressure, the rate of overpressure rise, the speed of flame propagation, etc. These two factors have different degrees of influence on the risk of gas explosion.

  3. (3)

    Under the influence of the TBM, the methane diffusion in the methane/air reaction zone shows a unique shape, and the diffusion of the unreacted area to the back of the baffle will lead to the transfer phenomenon of the explosion center.