Introduction

Oceanic mesoscale eddies and fronts, characterized by scales from tens to hundreds of kilometers, are ubiquitous in the global ocean1. By venting large amounts of heat and moisture associated with the sea surface temperature (SST) variability, these oceanic mesoscale processes have been suggested to shape the intensity of air-sea fluxes and the movement of the overlying atmosphere2,3,4,5. Based on satellite observations and model simulations, it is found that ocean mesoscale fronts and eddies drive substantial variabilities in local surface wind and associated vertical motions increase within the marine atmospheric boundary layer (MABL)2,6,7,8,9,10,11,12,13. This favors the cloud formation14,15,16 and precipitation2,10,17, and fuels the mid-latitude storm tracks2,5,11,18,19,20 and atmospheric rivers21. The impacts of these ocean features are not confined to the local area and can propagate to the upper troposphere10 or remote regions by forcing planetary waves22,23.

Two physical mechanisms that may lead to the variability of the atmosphere overlying the oceanic mesoscale SST signals are pressure adjustment and vertical mixing. The pressure adjustment mechanism involves a response in the local sea level pressure (SLP) to SST anomalies6,10,22,23,24 and has been invoked to explain the troposphere response to the Gulf Stream10 and Kuroshio12: a cold (warm) SST anomaly generates a positive (negative) anomaly in the local SLP, which further modulates the surface wind across the SST gradient. The vertical mixing mechanism involves changes in the atmospheric vertical mixing in response to SST anomalies7,8,11,12,13,20,25,26: a warm SST anomaly destabilizes the atmosphere, enhances vertical mixing, and favors vertical momentum flux.

These previous studies have significantly improved our knowledge of the response of the atmosphere to mesoscale SST signals. However, with the accumulation of observation data, it is realized that the SST change across the front or eddy edge is not uniformly distributed within tens to hundreds of kilometers, but is usually confined to a narrow space with a scale of less than 10 km27,28,29. This suggests a much larger SST gradient than those found in the current theoretical studies that are based on a uniform mesoscale front5,23,25,26, which cannot be resolved by the climate model with a resolution equal to or coarser than 10 km. The air-sea interaction and atmospheric response are sensitive to the SST gradient. Transient disturbances directly contribute to the time mean vertical motion and meridional flow, while the SST gradient of the Gulf Stream can significantly impact the regional atmospheric frontal frequency30,31. Fine-mesh large-eddy simulation shows that the convective structure of the marine atmospheric boundary layer, secondary circulations, and turbulent fluxes are clearly modulated by different magnitude of SST horizontal gradient32. Given the findings highlight significant influences of SST gradients that are not fully captured in current studies, the impacts of the discrepancy between observations and current studies should be estimated carefully. While our previous research has quantitatively analyzed the impacts of submesoscale fronts on the overlying atmosphere30, the influence of the temperature gradient intensity near the edge of ocean eddies, which exhibit strong diabatic heating effects, on air-sea exchange processes remains unknown. Here, based on high-resolution model simulations, we show that submesoscale SST gradients on the edge of an eddy drive much stronger air-sea exchanges and vertical mixing compared to mesoscale gradients, with significant implications for MABL changes, cloud distributions, and precipitation. Our results highlight the potential importance of considering submesoscale processes in air-sea interactions for future climate models to more accurately capture atmospheric responses to ocean variability.

High-resolution observations

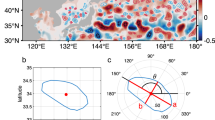
On April 10th, 2016 (14:21–16:48 UTC), we conducted a high-resolution observation at the edge of an anticyclonic mesoscale eddy detaching from the Kuroshio Extension (Fig. 1a; see section “Shipboard observations” in Method). The warm-core eddy encounters the cold and fresh Oyashio water from the subarctic gyre, resulting in large temperature and salinity gradients. During the two-hour observation, there is a prevailing northerly wind and the eddy is also approximately steady without significant changes. Shipboard temperature measurements indicate a sharp decrease in SST from 14 to 2 °C within 5 km across the eddy edge (blue line in Fig. 1b), which cannot be revealed from the satellite observations. Overlying, the surface air temperature (SAT) changes in line with SST and experiences a plummet from 9 °C inside the eddy to 5 °C outside the eddy within several kilometers (red line in Fig. 1b). Surface wind speed decreases from 8.5 m s−1 inside the eddy to 5 m s−1 outside. Turbulent heat flux spikes to over 200 W m−2 within the eddy but drops essentially to zero outside. MABL thickness expands to 8 km inside the eddy versus only 1.5 km outside, consistent with convective adjustment of the boundary layer to the SST pattern. More details about the structure of the submesoscale front and its impact on the atmosphere near the sea surface can be found in our previous studies30,31.

Fig. 1
figure 1

Temperature gradient across the eddy edge. (a) Satellite-observed SST anomaly (color shadings) and sea level anomaly (black contours) in the Kuroshio Extension region on April 11th, 2016. (b) Shipboard SST and SAT across the eddy edge along the green line in (a). (c) Model SST and SAT across the northern edge of the eddy in SubMesoE. Observations reveal a temperature plummet across the eddy edge.

Full size image

Intense air-sea interaction across the eddy edge

To compare the dynamics and impacts between submesoscale and mesoscale air-sea interactions on the eddy edge, two sets of regional atmospheric simulations at 1-km horizontal resolution are conducted based on the Weather Research and Forecasting Model (WRF) version 3 (see section “High-resolution atmosphere model” in Method): submesoscale SST gradients experiment (SubMesoE) and mesoscale SST gradients experiment (MesoE). In SubMesoE, the SST increases across the edge of eddy from 2 to 14 °C in 4 km (see Supplementary Fig. S1a), representing a submesoscale SST change (Fig. 1b). In comparison, the cross-edge SST increase occurs over 40 km in MesoE (see Supplementary Fig. S1b), which is designed to mimic the misrepresentation of find-scale SST fronts in low-resolution satellite observations or climate models. As such, a comparison between them allows us to compare the impacts of oceanic submesoscale and mesoscale SST gradients on the overlying air.

Figure 2a,b,d,e compare the horizontal distributions of 8-day-average surface heat flux (SHF; sensible heat flux and latent heat flux) and surface moisture flux (SMF) from two runs. Compared to MesoE, the presence of a much larger SST gradient in SubMesoE induces more rapid changes in SHF and SMF between the eddy and the surrounding waters (Fig. 2g–i). Notably, the intensity of air-sea exchange is enhanced at the eddy edge with a maximum increase of ~ 250 W m−2 in SHF and ~ 7 × 10−5 kg m−2 s−1 in SMF. When integrated over the eddy (148–152° E, 39–41° N), the SHF and SMF in SubMesoE are ~ 14% larger than MesoE. This enhanced air-sea flux suggests a stronger vertical mixing efficiency above the submesoscale SST gradients, which can be inferred from the air-sea transfer coefficient (see section “Air-sea transfer coefficient” in Method; Fig. 2c,f,i). Across the edge into the eddy, the abrupt change in the air-sea temperature difference destabilizes the atmosphere and leads to a larger heat release and stronger mixing overlying the eddy (see section “Diabatic heating rate” in Method and Supplementary Fig. S2). This enhanced mixing causes the air-sea transfer coefficient to peak just on the eddy edge in SubMesoE, especially on the northeastern edge where the cold atmosphere meets the warm SST (Fig. 1c). In comparison, the eddy in MesoE forces a more gradual cross-front change in the atmosphere. These results clearly demonstrate that the mesoscale and submesoscale SST transition scales can lead to significant differences in air-sea interaction.

Fig. 2
figure 2

Air-sea interaction differences between two experiments. Horizontal distribution of (a) surface heat flux (SHF), (b) surface moisture flux (SMF), and (c) air-sea transfer coefficient (Ch) in SubMesoE experiment. (d–f) are same as (a–c) but for MesoE experiment. (g–i) show their differences (SubMesoE-MesoE). Gray stripes denote significant values at 95% confidence level based on the Student’s t test. The freedom is calculated based on Satterthwaite’s approximation33. Submesoscale edge induces the stronger air-sea interaction above the eddy.

Full size image

To explore the mechanism that causes different atmospheric responses, we perform the budget analysis of meridional momentum (v), potential temperature (θ) and water vapor ratio (q) equation (see section “Budget analysis” in Method). For all these three variables, the budget on the eddy edge shows a primary balance between mixing (Mix) and advection (Adv) effects (see Supplementary Fig. S3). The sign of the mixing term at 1000 hPa is positive as the wind passes the eddy edge, suggesting that the ocean accelerates, heats, and moistens the atmosphere, consistent with the patterns of surface fluxes (Fig. 2). Figure 3a–d compare the budget of v at 1000 hPa between SubMesoE and MesoE. The key difference lies in Adv and Mix, whereas Cori and Pres are almost identical between the two experiments. Further examination reveals that the advection terms are dominated by horizontal components, consistent with previous estimations32. A comparison of Mix in the θ and q tendency equation also exhibits a similar pattern, with pronounced positive signals over the southwestern edge of the eddy (Fig. 3e–h). This implies that the SST transition on mesoscale and submesoscale at the eddy edge would force distinct intensities of turbulent mixing, thereby impacting the overlying atmosphere differentially.

Fig. 3
figure 3

Budget analysis of two experiments. Difference (SubMesoE-MesoE) of (a) Adv, (b) Cori, (c) Pres and (d) Mix in Eq. (4) at 1000 hPa. (e–h) are the same as (a) and (d) but for Eqs. (5) and (6), respectively. Grids with shading denote that the difference has past the Student’s t-test at 95% confidence level. Turbulent mixing accounts for the significant differences in air-sea interaction between the two experiments.

Full size image

In addition to affecting the surface air-sea interaction, the intensity of SST gradient on eddy edge could also leave footprints on atmospheric processes in the vicinity of MABL. In this study, the height of MABL is calculated based on the bulk Richardson number34:

$$ Ri_{B} = \frac{gz[\theta (z) - \theta (0)]}{{\theta (0)[u(z)^{2} + v(z)^{2} ]}} $$
(1)

Here, θ(z), u(z), and v(z) represent potential temperature, zonal and meridional wind velocity at height z, respectively; and g is the gravitational parameter. The MABL height is defined as the height where RiB is equal to 0.2534. An increase of MABL height is observed beyond the eddy region in both experiments, with the maximum height reaching 900 hPa (Figs. 4 and S4). This corresponded to the altered boundary layer structure attributed to a strong heating effect within the eddy of warm SST (see Supplementary Fig. S5). We further compare the meridional section of zonal-mean θ and q from 148.5 to 151.0° E, which reveals a clear difference across the MABL. Specifically, θ is higher (q is lower) within the MABL in the SubMesoE experiment, while above the MABL the patterns are opposite for θ and q with the maximum difference around 700–850 hPa (Fig. 4a,b). The vertical structures in these patterns can be well explained by the difference in mixing intensities between the two experiments as shown in Fig. 4c,d. The averaged θ (q) mixing intensity between 700 and 850 hPa is 1.3 times stronger in SubMesoE compared to MesoE experiment.

Fig. 4
figure 4

Vertical sections of temperature and moisture differences. Differences (SubMesoE-MesoE) of (a) θ, (b) q, and (c, d) their mixing terms between 148.5° E and 151.0° E. Black lines denote the height of MABL. Gray stripes denote significant values at 95% confidence level based on the Student’s t test. Mixing differences have a similar vertical pattern to the temperature and moisture differences.

Full size image

Besides, the θ and q changes will inevitably affect cloud distributions. In both experiments, we observe the high relative humidity and low dew point differences between 800 and 900 hPa above the eddy at the downwind direction within 39–40° N (Figs. 5a and S6), which is accompanied by the formation of middle cloud generally located between 2000 and 6000 m. Figure 5b shows that a large amount of the middle cloud is only distributed over the southwestern sector of the eddy. While chaotic signals can be seen in the budget analysis within the localized region of 149–150° E, 39–40° N near the sea surface (Fig. 3), they are not statistically significant when integrated over the longitudinal range of 148.5–151.0° E (Fig. 4c,d). Additionally, the differences observed along the southwestern edge of the eddy do not extend to heights above 2000 m (800 hPa), which are important for middle cloud formation. On day 4, both two experiments record a rainfall event occurring along the eddy edge below the middle cloud (Fig. 5c), which persists for only one day with no additional rainfall for other days. Although the two experiments are nearly identical in the ___location of the middle cloud and rainfall, there are substantial differences in cloud fraction and precipitation amount. Compared to those in MesoE experiment, the lower θ and higher q above the MABL in SubMesoE lead to an increase in relative humidity at the same height (Fig. 6a), which favors the formation of middle cloud. As shown in Fig. 6b, more middle cloud is generated over the southwestern sector of the eddy in the SubMesoE experiment, whose fraction magnitude is approximately two times larger than that in the MesoE experiment. Quantificationally, the 8-day-accumulated precipitation amount over the ___domain in the SubMesoE is 0.8 mm, 10 times greater than that in the MesoE (Fig. 6c). Overall, the enhanced middle cloud formation and rainfall in the SubMesoE case suggest that submesoscale SST features can significantly impact atmospheric moisture levels and precipitation by modifying vertical mixing and thermodynamic profiles.

Fig. 5
figure 5

Cloud and precipitation above the eddy. (a) Vertical section of 8-day-mean relative humidity in SubMesoE between 148.5° E and 151.0° E. Horizontal distribution of (b) 8-day-mean middle cloud formation and (c) 8-day-accumulated precipitation in SubMesoE. Middle cloud and rainfall are formed over the southwestern sector of the eddy.

Full size image
Fig. 6
figure 6

Cloud and precipitation differences between two experiments. (a) Relative humidity differences (SubMesoE-MesoE) between 148.5° E and 151.0° E. Black lines denote the height of MABL. Horizontal distribution of (b) 8-day-mean middle cloud fraction and (c) 8-day-accumulated precipitation differences (SubMesoE-MesoE). In (a), gray stripes denote significant values at 95% confidence level based on the Student’s t test. In (b) and (c), grids with shading denote that the difference has past the Student’s t-test at 95% confidence level. Submesoscale SST transition causes an increase in the middle cloud and precipitation account.

Full size image

Summary and implications

This study uses high-resolution atmospheric model experiments to examine how atmospheric response differs between the mesoscale (40 km) and submesoscale (4 km) SST gradients on an idealized oceanic mesoscale eddy. The difference between the two experiments could potentially inform future climate projections on the impact of spatial resolutions on resolving climate-critical air-sea processes. Surface heat/moisture fluxes and air-sea transfer coefficients are found to be substantially enhanced at the eddy edge under the 4 km SST transition case compared to the 40 km case. Budget analyses reveal that stronger turbulent mixing acts as the primary mechanism producing the distinct atmospheric responses. Impacts extended upwards, with potential temperature and water vapor vertical profiles as well as middle cloud formation differing between the experiments. The cloud amount and precipitation were two times and an order of magnitude larger for the submesoscale case, respectively.

Our finding in this study has profound implications for climate and weather projections. In the presence of sharp SST change on their edges, the oceanic mesoscale eddies and fronts could release more heat and moisture into the atmosphere, which drives stronger local convection systems, including vertical motions and precipitation, that can hardly be reproduced by the current mesoscale-resolving climate models35,36,37,38. Moreover, the energetic storm tracks and atmosphere rivers are largely maintained by the heat and moisture released by mesoscale eddies and fronts18,21,39,40,41,42,43,44,45. A proper representation of the SST structure of these oceanic mesoscale processes in climate models may avoid a misestimation of those extreme atmospheric events, providing a potential pathway by reducing the biases in the projection of their occurrence and intensity.

Methods

Shipboard observations

On April 10th, 2016 (14:21–16:48 UTC), we carried out a transect across a submesoscale front at the northern edge of a warm eddy, which was shed from the northward-intruding Kuroshio–Oyashio Extension meandering. High-resolution measurements were made along the transect. SST is obtained from a shipboard temperature recorder; surface air temperature and surface wind are measured by the vessel monitoring system. Please also refer to Yang et al.30 and Zhu et al.31 for more details.

High-resolution atmosphere model

To examine the different mechanisms between submesoscale and mesoscale air-sea interactions on the eddy edge, two sets of high-resolution regional atmospheric simulations are conducted based on the Weather Research and Forecasting Model (WRF) version 3.4. The WRF model is developed by the National Center for Atmospheric Research and is configured on the Arakawa-C grid at 1 km horizontal resolution with 30 vertical levels. The model output is saved every 3 h.

In SubMesoE and MesoE, the model ___domain is 800 km × 800 km (Fig. S1). The initial and lateral boundary conditions (horizontal velocity magnitude, temperature, and relative humidity) are area- and time-mean values of ERA5 data over 36–44° N, 146–154° E during December 2015. In particular, the initial wind velocity is northerly, and the bottom boundary condition is an idealized warm eddy with an SST of 14 °C that is surrounded by water of 2 °C (Fig. S1). By identifying the ___location of the Oyashio Extension front, we find that the observational site is locates at ~ 40 km to the south of the front. However, the satellite-observed SST gradient at the site is over 2.5 times of the gradient of the OE front, indicating the eddy-induced SST gradient dominates locally. Given this strong eddy influence evident in the observations, we simplified the background SST field in the model to be uniform.

During the model runs, both the lateral and bottom boundary conditions are kept constant. In SubMesoE, the SST increases across the eddy edge from 2to 14 °C in 4 km, close to the observation (Fig. 1b). In comparison, the cross-edge SST increase occurs over 40 km in MesoE. Both SubMesoE and MesoE reach steady states in 6 h with a persistent northeasterly flow, judged by changes in the total kinetic energy, and the data from model days 3–10 are used for analysis.

Air-sea transfer coefficient

Due to the dominant role of latent heat in air-sea exchanges, the transfer coefficient (Cd) is parameterized following the formulation of Fairall et al.46:

$$ C_{d} = \frac{LH}{{V_{10m} \left( {\frac{{q_{s} }}{RH} - q_{s} } \right)}}, $$
(2)

where LH is the latent heat flux at the sea surface, V10m the wind speed at 10 m, qs the water vapor mixing ratio and RH the relative humidity at 2 m. The initial wind field in the WRF simulations is set up with northerly winds.

Diabatic heating rate

Following Yanai and Tomita47, the diabatic heating rate (Q) can be estimated as:

$$ Q = c_{p} \left( {\frac{p}{{p_{0} }}} \right)^{{\frac{{R_{d} }}{{c_{p} }}}} \left( {\frac{\partial \theta }{{\partial t}} + {\mathbf{V}}_{{\mathbf{h}}} \cdot \nabla \theta + w\frac{\partial \theta }{{\partial p}}} \right), $$
(3)

where cp is the air specific heat capacity at constant pressure, p is the pressure with p0 = 1000 hPa, Rd is the dry air gas constant, θ is the potential temperature, Vh = (u,v) is the horizontal wind vector, ∇ is the 2D gradient operator, and w is the vertical velocity in pressure coordinates.

Budget analysis

The budget of meridional momentum (v), potential temperature (θ), and water vapor ratio (q) can be expressed as follows:

$$ \underbrace {{\frac{\partial v}{{\partial t}}}}_{Tend} = \underbrace {{ - \left( {u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} + w\frac{\partial v}{{\partial p}}} \right)\underbrace { - fu}_{Cori}}}_{Adv}\underbrace {{ - \frac{\partial \Phi }{{\partial y}}}}_{\Pr es} + \underbrace {{F_{v} }}_{Mix}, $$
(4)
$$ \underbrace {{\frac{\partial \theta }{{\partial t}}}}_{Tend} = \underbrace {{ - \left( {u\frac{\partial \theta }{{\partial x}} + v\frac{\partial \theta }{{\partial y}} + w\frac{\partial \theta }{{\partial p}}} \right)}}_{Adv} + \underbrace {{F_{\theta } }}_{Mix}, $$
(5)

and

$$ \underbrace {{\frac{\partial q}{{\partial t}}}}_{Tend} = \underbrace {{ - \left( {u\frac{\partial q}{{\partial x}} + v\frac{\partial q}{{\partial y}} + w\frac{\partial q}{{\partial p}}} \right)}}_{Adv} + \underbrace {{F_{q} }}_{Mix}, $$
(6)

where u, v, and w are three-dimensional velocities of the atmosphere, f is the Coriolis parameter, Φ is the geopotential, and p is the air pressure. Fv, Fθ and Fq represent forcing terms associated with turbulent mixing and surface fluxes. In particular, the surface fluxes (wind stress, SHF and SMF), are involved in these forcing terms as bottom boundary conditions. To estimate the role of vertical mixing in F terms, we calculate the spatial correlation between them. As shown in Fig. S7, the spatial distributions of the residual term in the water vapor ratio (q) equation resemble that of vertical gradients of q with the spatial correlation coefficient of 0.5. This consistency suggests that F is primarily governed by vertical mixing, as the effect of vertical mixing is to enable movement across isentropic surfaces. Therefore, the four terms on the right-hand side of Eq. (4) represent the advection effect (Adv), Coriolis force (Cori), pressure gradient (Pres), and mixing terms (Mix) of meridional momentum. It is noted that the Adv and Mix terms of Eqs. (5) and (6) are exact opposites under steady state conditions. Here, the WRF simulations save all the 3 h-mean terms except for the forcing terms that are computed as a residual, so that a detailed budget analysis can be performed. Results of budget analysis for these equations at 1000 hPa are shown in Supplementary Fig. S3.