Introduction

Urbanization is a global phenomenon surging at an unprecedented rate1. By 2030, urban populations are projected to make up 60.4% of the world’s total population, with China already exceeding 65% in 20222. While urbanization brings economic prosperity and better quality of life, it also leads to challenges like resource depletion, flooding, reduced biodiversity, and air pollution3,4. Economic growth, alongside increasing environmental pressures, threatens our ability to achieve sustainable development in ecologically fragile urban agglomerations. Addressing these challenges necessitates exploring potential policies for safeguarding the environment5. There exists a dynamic and complex relationship between socioeconomic development and environmental protection6. Rapid industrialization and economic growth can lead to increased pollution, which may degrade environmental quality, ultimately impacting public health and economic productivity. To improve environment, governments implement various policies to intervene and adjust economic activities7. However, excessive protective policies may hinder the sustainable development of society and the economy8. Analyzing the interaction between economic development and environmental protection is crucial for seeking policy recommendations for sustainable development.

The Yangtze River Delta Region (YRDR), one of the most vibrant, open and innovative city clusters in China, is acknowledged as a demonstration area for high-quality and sustainable development9. Despite covering less than 4% of China’s land area, it is home to about 17% of the population and contributes nearly a quarter of the country’s economic output10. The YRDR integration development strategy, introduced in 2018, aims to coordinating inter-regional efforts for high-quality socioeconomic growth while preserving the environment. Despite significant economic development and population growth, the YRDR faces environmental challenges such as air pollution, wastewater discharge, and land degradation11. Understanding the relationship between socioeconomic development and environmental protection in the YRDR is therefore essential for guiding integrated development and informing decision-making for sustainable urban development.

Literature review

The concept of coupling coordination

Socioeconomic development and environmental protection have a symbiotic relationship where each aspect reinforces and supports the other. The coupling and coordination of these systems reflect their intricate dynamics. To account for spatial-temporal dynamics and complex interactions between socioeconomic development and environmental protection, coupling coordination degree (CCD) is introduced into the analytical framework12. The concept of coupling coordination is derived from physics and describes the change relationship between the interactions and mutual effects of two or more systems. Coupling refers to the phenomenon where two or more systems interact closely in various ways13,14. Coordination reflects the degree of coherence between subsystems, and the extent to which the system tends toward the desired order15,16. Therefore, CCD measures the synergies among interacting subsystems, determining the trajectory of an integrated socioeconomic-environmental system from disorder to order17. The coupling coordination mechanism between the economy and the environment highlights their interdependent relationship, where each system enhances the other. Economic activities, such as investments in renewable energy, drive environmental protection by reducing emissions, while a healthy environment provides vital resources for economic growth. Technological innovations improve resource efficiency, and aligned policies ensure that economic objectives support sustainability. This dynamic interaction fosters a balanced approach to sustainable development, integrating economic growth with ecological integrity7,12. The concept of CCD has been widely applied in various fields, such as water system18, tourism17,19, the water-energy-carbon nexus20, financial development21, the power industry22, and more. These successful applications demonstrate that the mutual impacts of subsystems can be quantified through CCD trend and factor analysis, aiding in the development of policies for system collaboration23,24.

Study on CCD evaluation

The CCD model is a valuable tool used to analyze the interaction between the eco-environment and socio-economy, effectively describing the coupling relationship between these two elements. This model has gained recognition from numerous scholars for its applications across various scales, including city13,25,26, provincial27,28, regional[l4,16,29, and global30 levels. These studies focused on establishing environmental index subsystem and economic index subsystem, each containing several indicators reflecting the features of the subsystems. Evaluating CCD model metrics usually requires a prior evaluation of the development level of the subsystems by calculating the weighted sum of scores of different indicators8. The accuracy of the evaluation results largely depends on the rational indicator weights. Previous studies have employed subjective (e.g., analytic hierarchy process, AHP) and objective methods (e.g., entropy, coefficient of variance) weighting methods. For instance, Lu et al.28 applied hesitant fuzzy preference and entropy methods to elucidate the urbanization city-industry integration level. Zhao et al.30 utilized AHP to quantify urbanization and eco-environment indices. Zhang et al.31 employed entropy weight TOPSIS for quantifying the new-type urbanization and ecological well-being performance. Han et al.32 used the criteria importance through intercriteria correlation (CRITIC) weighted evaluation model to measure urban resilience assessment.

Study on the factors influencing coordination

Regarding the relevant factors affecting coordination, scholars have used various methods, such as regression analysis, obstacle analysis, and machine learning. For instance, Zhang et al.26 used Tobit regression to explore factors influencing the coordinated development of economy and environment in YRDR cities. Liu et al.33 developed an exponential regression model to identify key factors influencing coupling coordination between urbanization and atmospheric environment security system, highlighting industrial emission reductions and structure optimization. Liang et al.34 employed a geographical detector model to study the relationship between eco-economic coupling coordination and factors like regional topography, nature, transportation, and landscape. Sun et al.35 introduced an obstacle classification to identify factors influencing CCD of Chinese county territory, emphasizing the significant roles of development level and construction situation.

Recently, machine learning methods have been used to analyze the main driving factors, offering new insights into understanding CCD36. For example, Han et al.12 created a diagnostic model using boosted regression trees to explain coupling interactions, accounting for over 90% of CCD changes. Lu et al.28 employed a particle swarm optimization backpropagation artificial neural network to pinpoint factors affecting urbanization city-industry integration, highlighting low development levels and slow industry growth rates as significant constraints. Yang et al.36 introduced the random forest algorithm to to study the impact of low-carbon multivariate coupling systems, identifying industrial pollutant emissions, foreign direct investment, and economic output as key drivers of low-carbon levels.

Research gap and contribution

Despite the profound findings in the existing literature, some shortcomings remain. Firstly, most studies use a single weighting method for comprehensive evaluation of CCD. Each method has its advantages and disadvantages, subjective method is too artificial and objective method is too dependent on statistical data. As a result, a single weight method may lead to bias and arbitrariness37. Secondly, most approaches assume CCD is a function of indicators, especially for regression-based models. However, explicit functional expressions for conventional statistical methods do not exist. Thirdly, the factors affecting the coupling coordination are complex and diverse, and the interaction between indicators can be as significant as individual impact factors, which few studies have addressed38.

To address the aforementioned challenges, this study aims to develop a novel game theory stepwise-cluster factorial coupling coordination model (GSFCM) to identify the socioeconomic and environmental coordination in the YRDR. In response to the shortcomings of the single weighting method, the combination weighting method can realize the unification of subjective and objective and improve the scientific rationality of weighting decisions. Game theory, a mathematical discipline that studies strategic decision-making, helps players optimize outcomes by seeking consensus or compromise39. When applied to weight combination, game theory can not only consider the subjective factors of expert assessments but also involve some objective assessments through Nash equilibrium40,41. The game theory equilibrium idea has demonstrated successful applications in weight combinations in fields such as flood resilience assessment37, water resource spatial equilibrium42, and power system analysis43. These successes further validate the potential of game theory in optimizing weight combinations within environmental and socioeconomic systems.

Stepwise cluster analysis (SCA) and factorial analysis (FA) have recently gained attention due to their superior capability in analyzing complex environmental management problems, such as water policy analysis38, climate downscaling44,45, and water-carbon nexus management46. SCA is a multivariate automatic interaction detection algorithm capable of handling discrete or continuous, linear or non-linear variables without assuming a functional relationship45,47. FA is skilled in examining the individual and interactive effects of multiple factors through experimental design and variance analysis48. Integrating SCA and FA help researchers identify the most influential factors and their interactions. However, few studies have combined SCA and FA in analyzing mechanisms contributing to CCD.

The marginal contributions of this study can be concluded as: (1) avoiding inaccuracies brought by a single weighting method by introducing game theory into coupling coordination analysis, (2) capturing the complex and nonlinear relationships between socioeconomic and environmental indicators and CCD with a stepwise cluster tree, and (3) examining the individual and interactive effects of indicators on CCD through factorial analysis. The expected findings are expected to provide insights and recommendations for policymakers to improve CCD and achieve more balanced and sustainable development in the YRDR.

Materials and methods

Study area overview

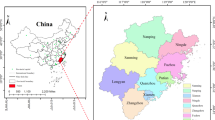
The YRDR (27°02′-35°20′N, 114°54′-123°10′E) is situated on the alluvial plain where the Yangtze River meets the East China Sea, encompassing Shanghai, Jiangsu, Zhejiang, and Anhui provinces, totaling 41 cities (as depicted in Fig. 1). The region features a subtropical monsoon climate, diverse land cover, and a complex ecosystem. It has undergone rapid urbanization, with an annual population growth rate of 3.0% and urbanization growth rate of 9.2%. Economic development and urbanization levels in the YRDR display spatial disparities, with the highest levels in the east gradually declining towards the western regions49.

Fig. 1
figure 1

The map of the Yangtze River Delta Region.

Full size image

Index system construction

To examine the coordination relationship between socioeconomic system (SES) and environmental system (ENS), an evaluation index system is established based on several fundamental principles, including criterion alignment for socioeconomic and environmental indicators, extensive literature reviews13,21,26,50,51 and expert consultations. The indicators are chosen for relevance, measurability, and comparability, ensuring the scientific validity of the system. This system, with 9 indicators for each subsystem (as shown in Table 1), provides a new perspective for promoting integrated socioeconomic and environmental development.

Table 1 The index system for coupling coordination analysis between socio-economy and environment.
Full size table

The SES is assessed based on economic output, return, development environment, and well-being26,52. GDP per capita provides an average economic output per person and is used to compare the economic performance and living standards of different cities. Economic return is measured by income per unit land area, where higher values indicate higher efficiency and economic benefit of land use. The economic development environment is reflected by the proportion of the added value of tertiary industry, import and export value per capita and population density, representing industrial structure, trade and openness, and labor forces, respectively. Well-being is indicated by Engel’s coefficient, urbanization rate of permanent residence, number of hospital beds, and number of college students. Engel’s coefficient measures food affordability and income inequality, with a higher values indicating lower income levels. Other indicators assess access to amenities, infrastructure, and services like education and healthcare.

The level of ENS development is evaluated based on the criteria of environmental pressure, status, and response25,53. Environmental pressures include industrial wastewater discharge, fine particulate matter (PM2.5) concentration, and energy consumption, which negatively impact environmental quality. The status of ecological and environmental health is described by the numbers of days with good air quality, per capital area of public green space, and forest coverage rate, with higher values indicating better conditions. Response actions to environmental challenges are measured by the utilization rate of non-hazardous industrial solid waste, centralized treatment rate of domestic sewage, and the greenery coverage in built-up areas, all of which contribute positively to environmental quality.

Data collection and pre-processing

This study uses panel data from 41 cities between 2015 and 2020 to study changes in socioeconomic and environmental coordination during China’s 13th Five-Year Plan, during which the YRDR integration development strategy was proposed. Data on socioeconomic and environmental indicators were gathered from various sources, including websites, expert consultations, Environmental Bulletins of the 41 cities, and Statistical Yearbooks (such as the Shanghai, Jiangsu, Zhejiang, Anhui Statistical Yearbooks, and the China Urban Construction Statistical Yearbook) for 2006 and 2021. Missing values were filled using adjacent year averages. The 2006 and 2021 yearbooks were used due to they recorded the data in 2015 and 2020.

Given the varying dimensions and magnitudes of each of the selected indicators, it is necessary to normalize the data before conducting game theory analysis. Indicators are categorized into positive and negative types: a greater value a positive indicator benefits system development, whereas a greater value for negative indicator is detrimental. Indicators are then transformed into non-dimensional values using normalization equations:

$$\text{Positive indicator: }{r_{ijk}}={{\left( {I{N_{ijk}} - \hbox{min} \left\{ {I{N_k}} \right\}} \right)} \mathord{\left/ {\vphantom {{\left( {I{N_{ijk}} - \hbox{min} \left\{ {I{N_k}} \right\}} \right)} {\left( {\hbox{max} \left\{ {I{N_k}} \right\} - \hbox{min} \left\{ {I{N_k}} \right\}} \right)}}} \right. \kern-0pt} {\left( {\hbox{max} \left\{ {I{N_k}} \right\} - \hbox{min} \left\{ {I{N_k}} \right\}} \right)}}$$
(1)
$$\text{Negative indicator: }{r_{ijk}}={{\left( {\hbox{max} \left\{ {I{N_k}} \right\} - I{N_{ijk}}} \right)} \mathord{\left/ {\vphantom {{\left( {\hbox{max} \left\{ {I{N_k}} \right\} - I{N_{ijk}}} \right)} {\left( {\hbox{max} \left\{ {I{N_k}} \right\} - \hbox{min} \left\{ {I{N_k}} \right\}} \right)}}} \right. \kern-0pt} {\left( {\hbox{max} \left\{ {I{N_k}} \right\} - \hbox{min} \left\{ {I{N_k}} \right\}} \right)}}$$
(2)

where i is the year, j is the city, k is the indicator, rijk is the normalized value, INijk is the original value, and max{INk} and min{INk} represent the maximum and minimum value of the indicator k in all of the years and cities studied. All the index values are within the scope of [0,1] after treatment.

The framework of GSFCM

The proposed GSFCM (as illustrated in Fig. 2) comprises four key components: game theory-based weight calculation method, CCD model, SCA method, and FA technique. Each technique can enhance the capability of the coupling coordination analysis and driver identification. In detail, game theory is utilized to balance the indicator weights calculated by both subjective and objective methods. Subsequently, the values of socioeconomic index (SI) and environmental index (EI) are derived from the weighted sum of normalized indicators. The CCD model is then employed to analyze the socioeconomic and environmental coordination. The SCA method is implemented to describe the complex relationships between the indicators and the CCD. Finally, FA is conducted to identify the individual and interactive effects of the indicators, providing policy implications for achieving high-level protection and high-quality development.

Fig. 2
figure 2

The framework of GSFCM.

Full size image

The game theory based system index evaluation

The central idea of game theory-based weight combination is Nash equilibrium, which is used to predict a strategy profile for a given game, or interaction among decision-makers. In a decision-making game, players have the option of adopting a mixed strategy that is a probabilistic distribution of the player’s strategies54. A Nash equilibrium in mixed strategies embodies a state of strategic interdependence where each player’s probabilistic strategy maximizes their expected payoff given the mixed strategies of other players, resulting in a stable outcome where no player has an incentive to unilaterally alter their strategy for higher payoffs55.

In this study, Nash equilibrium is used to coordinate conflicts and maximize benefits by considering the relationship between indicators, balancing subjective and objective weights, and optimizing indicator weight values37,56. Five weighting methods are employed as strategies in the game theory framework, they are AHP, entropy, coefficient of variance (CoV), independent weight coefficient method (IWM), and CRITIC. The detailed information of these individual methods can be found in published literature32,57,58,59,60. Individual weight vector w(θ) can be obtained by when the individual weight methods are conducted, which can be presented as:

$$w(\theta )=\left[ {{w_{\theta 1,}}{w_{\theta 2,}},\ldots,{w_{\theta m}}} \right], \;\; \theta =1,2,\ldots,5;\;\; m=1,2,\ldots,9$$
(3)

where wθℎ(ℎ=1,2,…,m) is the weight of indicator ℎobtained by using the θth weighting method. m is the indicator in each subsystem; nine indicators can be treated as nine players that pursue the optimal mixed strategies through Nash equilibrium. The mixed strategies can be expressed as the linear combination of five weight vectors as follows:

$$w=\sum\limits_{{\theta =1}}^{5} {{\alpha _\theta }w_{\theta }^{{\text{T}}}} ,\;\; {\alpha _\theta }>0$$
(4)

where w represents the set of possible weight vectors, aθ is the linear combination coefficient (i.e. probability of each strategy) of individual weights. Since probabilities are continuous, there are infinitely many mixed strategies available to all decision-makers. However, a Nash equilibrium is a set of strategies for which no player has an incentive to deviate from their current strategy61. Accordingly, the combined weight W can be converted into an optimization process to minimize the smallest possible deviation between each strategy and mixed strategy, which can be defined as follow62,63:

$$\hbox{min} {\left\| {\sum\limits_{{\theta =1}}^{5} {{\alpha _\theta }w_{\theta }^{T} - w{{\left( \theta \right)}^T}} } \right\|^2},\;\; \theta =1,2,.,5$$
(5)

According to the matrix differential property, the optimization model is transformed into linear equations as shown in Eq. (6):

$$\sum\limits_{{\theta =1}}^{5} {{a_\theta }{w_\hbar }w_{^{-}\!\!\!\lambda }^{T}={w_\hbar }w_{\hbar }^{T},\;\; \hbar =1,2,\ldots,5} ;\;\;^{-}\!\!\!\lambda =1,2,\ldots ,5$$
(6)

Weight coefficient are obtained by solving Eq. (6), and then the most satisfactory combined weights are calculated as:

$$w_{{}}^{*}=\sum\limits_{{\theta =1}}^{5} {a_{\theta }^{*}} w_{\theta }^{{\text{T}}},\;\; a_{\theta }^{*}={{a_{\theta }^{{}}} \mathord{\left/ {\vphantom {{a_{\theta }^{{}}} {\sum\limits_{{\theta =1}}^{5} {a_{\theta }^{{}}} }}} \right. \kern-0pt} {\sum\limits_{{\theta =1}}^{5} {a_{\theta }^{{}}} }}$$
(7)

where aθ* is the normalized coefficient of the optimal weight w*. Figure 3 provides the calculated weights for the selected indicators. Based on the standardized values and weights of the evaluation indicators, the comprehensive scores of SI and EI are calculated using this weighted summation model:

$$S{I_{ij}}=\sum\limits_{{k=1}}^{9} {w_{{SI}}^{*} \times } r_{{ijk}}^{{SI}};\;\; E{I_i}=\sum\limits_{{k=1}}^{9} {w_{{EI}}^{*} \times } r_{{ijk}}^{{EI}}$$
(8)

where SIij and EIij are the values of SI and EI in ith year and jth city.

Fig. 3
figure 3

Indicators’ weights under different methods.

Full size image

Coupling coordination degree model

The coupling degree model describing the relationship between a pair of parameters is widely applied to analyze the interaction between ecological environment and economic development. The degree of coupling coordination can reflect the trend of order and disorder between SES and ENS. The CCD model includes three components: coupling degree, comprehensive evaluation index and coupling coordination degree. The level of coupling degree indicates the strength of the interaction between systems, and a higher degree indicates a greater extent of interaction, which is calculated as follows26:

$$C=2*{\left[ {\frac{{{\text{EI}} \times {\text{SI}}}}{{\left( {{\text{EI+SI}}} \right)^{2}}}} \right]^{1/2}}$$
(9)

where EI and SI are the evaluation index of SES and ENS, respectively. C is the coupling degree that ranges from 0 to 1, and the larger the C value, the higher the coupling degree of system, and vice versa. Resonance coupling between subsystems is benign, which will tend to a new orderly structure. At C = 0, the coupling degree is extremely low, and subsystems are in a state of irrelevance. The coupling degree emphasizes the interaction strength between subsystems, which cannot reflect the development level or the overall function of subsystems. To this end, the coupling coordination degree model is introduced, constructed based on the coupling degree model and used to reflect the virtuous circular relationship19.

$$U=\alpha \times EI+\beta \times SI$$
(10)
$$CCD=\sqrt {C \times U}$$
(11)

where U is the outcome of a comprehensive evaluation of the SES and ENS that reflects the full advantages and levels of the two subsystems, and α and β are undetermined coefficients, whose values are given equal weights as they are equally important. CDD represents the coupling coordination degree.

Stepwise cluster analysis

SCA is a multivariate analysis tool that divides the sample sets of predictors and predictands into different sub-clusters through a series of cutting and merging operations48. The essence of stepwise cluster is, based on given criteria (i.e. Wilk’s statistic), to cut the sample of dependent variables into two, and to merge two sets into one, step by step, in classify samples and sieve variables44. According to Wilk’s likelihood-ratio criterion, if the cutting point is optimal, the value of Wilk’s \(\Lambda\) (\(\Lambda ={{\left| W \right|} \mathord{\left/ {\vphantom {{\left| W \right|} {\left| {W+H} \right|}}} \right. \kern-0pt} {\left| {W+H} \right|}}\)) should be the minimum, where W and H are the within and between groups matrix respectively. The symbol of |•| means the determinant of a matrix. If cluster ψ (containing nψ samples) could be cut into two sub-clusters e and f (e and f contain ne and nf samples, respectively). The H and W can be given by45:

$$W=\sum\limits_{{\zeta =1}}^{{{n_e}}} {\left( {{e_\zeta } - \bar {e}} \right){{\left( {{e_\zeta } - \bar {e}} \right)}^{\text{T}}}} +\sum\limits_{{\xi =1}}^{{{n_f}}} {\left( {{f_\xi } - \bar {f}} \right){{\left( {{f_\xi } - \bar {f}} \right)}^{\text{T}}}}$$
(12)
$$H=\frac{{{n_e}{n_f}}}{{{n_e}+{n_f}}}\left( {\bar {e} - \bar {f}} \right)\left( {\bar {e} - \bar {f}} \right)$$
(13)

where \(\bar {e}\) and \(\bar {f}\) is the sample mean of set of e and f, respectively. By Rao’s F-approximation, an exact F test is possible based on the Wilk’s criterion can be converted as:

$$F\left( {P,{n_\psi } - P - 1} \right)=\frac{{1 - \Lambda }}{\Lambda } \cdot \frac{{{n_\psi } - P - 1}}{P}$$
(14)

Therefore, the criteria of cutting and merging clusters become to make a number of F tests. If F < 1-p is satisfied, then cluster ψ can be cut into two sub-clusters. If F > 1-p is satisfied, clusters e and f can be merged into a new cluster ψ. Step by step, the sample will finally enter a tip cluster that can no longer be further cut or merged. Let \(e^{\prime}\) be the tip cluster where the new sample enters. Then the predicted dependent variables \(\left\{ {{y_i}} \right\}\) are:

$${y_i}=y_{i}^{{{{(e^{\prime})}}}} \pm R_{i}^{{{{(e^{\prime})}}}}$$
(15)

where \(y_{i}^{{{{(e^{\prime})}}}}\) is the mean of dependent variable i in sub-cluster \({e^{\prime}}\), and \(R_{i}^{{{{(e^{\prime})}}}}\) is the radius of yi in cluster.

Factorial analysis method

Factorial analysis is commonly used to assess factors and interactions in experiments. Two-level factorial designs are often used in experiments with multiple factors and interactions64. However, dealing with many factors can require too many experiments. To address this, a two-level fractional factorial design can be used to identify significant factors with fewer experiments, providing similar advantages65. Fractional factorial analysis uses variance analysis (ANOVA) to calculate effects by separating variability into identifiable sources. In ANOVA, the total sum of squares can be expressed as46:

$$S{S_{total}}=S{S_{treatments}}+S{S_{error}}$$
(16)
$$S{S_{total}}=\sum\limits_{{s=1}}^{S} {\sum\limits_{{t=1}}^{T} {\left( {{\Upsilon _{{\text{st}}}} - \left( {{1 \mathord{\left/ {\vphantom {1 {\sum\limits_{{{\text{t}}=1}}^{T} {{n_j}} }}} \right. \kern-0pt} {\sum\limits_{{{\text{t}}=1}}^{T} {{n_j}} }}} \right)\sum\limits_{{t=1}}^{T} {\sum\limits_{{s=1}}^{S} {I{N_{st}}} } } \right)} }$$
(17)
$$S{S_{treatments}}=\sum\limits_{{s=1}}^{S} {\sum\limits_{{t=1}}^{T} {\left( {\left( {{1 \mathord{\left/ {\vphantom {1 {{n_t}}}} \right. \kern-0pt} {{n_t}}}} \right)\sum\limits_{{s=1}}^{S} {{X_{st}}} - \left( {{1 \mathord{\left/ {\vphantom {1 {\sum\limits_{{t=1}}^{T} {{n_t}} }}} \right. \kern-0pt} {\sum\limits_{{t=1}}^{T} {{n_t}} }}} \right)\sum\limits_{{s=1}}^{S} {\sum\limits_{{t=1}}^{T} {I{N_{st}}} } } \right)} }$$
(18)
$$S{S_{error}}=\sum\limits_{{s=1}}^{S} {\sum\limits_{{t=1}}^{T} {\left( {I{N_{st}} - \left( {{1 \mathord{\left/ {\vphantom {1 {{n_t}}}} \right. \kern-0pt} {{n_t}}}} \right)\sum\limits_{{s=1}}^{S} {I{N_{st}}} } \right)} }$$
(19)

where s is the of factor level, t is the factor, T is the number of factors and S is the number of factor levels, INst is the tth indicator value at level s.

Result analysis

Spatial-temporal characteristics of socioeconomic system

Figure 4 illustrates the changes in SI from 2015 to 2020. The mean SI for the entire region increased from 0.276 to 0.359, indicating an overall socioeconomic improvement. All provinces experienced SI enhancements, with Shanghai showing the largest increment (0.136), followed by Anhui (0.093), Jiangsu (0.083), and Zhejiang (0.080). City-level SI ranged from 0.100 (Bozhou) to 0.617 (Shanghai) in 2015, and from 0.180 (Lu’an) to 0.754 (Shanghai) in 2020. Significant SI increments were in Wenzhou, Hefei, and Shanghai. Cities like Huangshan, Ma’anshan, Wuhu, Bengbu, and Chuzhou in Anhui ranked the fourth to eighth in terms of SI increment, indicating Anhui’s economic progress during the 13th Five-Year Plan period, largely due to the integration development strategy of YRDR. This strategy facilitated economic cooperation between Anhui and its more developed neighboring regions, leading to rapid industrial upgrades, expanded trade activities. Conversely, Tongling, Xuzhou, Jinhua, and Huainan had slower SI growth, likely due to reliance on resource-based industries and industrial transition challenges.

Fig. 4
figure 4

Spatial distributions and associated temporal changes in SI.

Full size image

Spatially, cities such as Shanghai, Suzhou (in Jiangsu), Nanjing, Hangzhou, Wuxi, and Hefei had higher SIs than other regions, indicating higher socioeconomic levels in the provincial capital cities and areas surrounding Shanghai.These regions benefit from higher GDP, better economic development environments, and superior well-being indicators. In contrast, cities like Lu’an, Fuyang, Bozhou, and Suzhou (in Anhui) had lower SIs. These cities situated on the periphery of the YRDR have larger areas; however, due to low public infrastructure and economic development levels, they cannot retain their populations, causing many people to move to more developed areas and thus exacerbating the gap in regional socioeconomic levels with trade values, and fewer college students. Besides, these cities are also agriculture-dominated areas with lower income per unit land area, hindering their socioeconomic development.

Spatial-temporal characteristics of environmental system

Figure 5 illustrates the spatial distributions and temporal changes in the EI across the YRDR. Darker colors presents higher EIs, with the mean EI for the YRDR rising from 0.488 in 2015 to 0.615 in 2020, suggesting an improvement in environmental quality. Zhejiang Province showed the highest EI growth (0.172), followed by Shanghai (0.135), Jiangsu (0.109), and Anhui (0.103). At the city level, Bozhou and Chizhou experienced slight declines in EI (-0.006 and − 0.005, respectively), while the remaining 39 cities showed improvements. Notable increases were observed in Shaoxing (0.214), Huzhou (0.209), Hangzhou (0.208), and Jinhua (0.196), highlighting Zhejiang’s enhanced environmental quality. Zhejiang’s success is largely attributed to its innovative and effective protection policies. As China’s first ecological province, Zhejiang has focused on pollution prevention and control, green and low-carbon development, and urban ecological protection. From 2015 to 2020, Zhejiang reduced PM2.5 concentration by 34.4%, increased the number of good air quality days by 20.63%, and promoted centralized domestic sewage treatment by 8.0%.

Fig. 5
figure 5

Spatial distributions and associated temporal changes in EI.

Full size image

The EI spatial distribution reveals that Huangshan led in environmental quality, with its EI rising from 0.779 in 2015 to 0.932 in 2020. Lishui, Quzhou, and Taizhou in Zhejiang also exceeded an EI value of 0.80 in 2020, indicating high environment quality clustered in the southern YRDR, including southern Anhui and most of Zhejiang. These areas have mountainous terrain, high forest coverage rates (nearly 80%) and strong air-purifying capabilities, resulting in lower PM2.5 concentrations and more days of good air quality. In contrast, the northern YRDR, particularly northern Anhui and Jiangsu, exhibited relatively lower EIs. Huainan had the lowest EI (below 0.40). largely due to its reliance on coal resources and sluggish responses to pollution treatment.

The characteristics of coupling coordination degree

Figure 6 presents the comprehensive evaluation index and coupling degree of SES and ENS. The comprehensive evaluation index reveals an upward trend, with the mean index climbing from 0.382 in 2015 to 0.478 in 2020, indicating robust environmental protection and socioeconomic development in the region. Shanghai led with a 2020 score of 0.639, followed by Zhejiang, Jiangsu, and Anhui. Regarding the temporal change, Ma’anshan exhibited the most obvious rise, followed by Shaoxing, Wenzhou, Huangshan, and Hefei. Conversely, Chizhou, Huainan, Bozhou, Tongling, and Xuzhou experienced minimal changes. Spatially, high index values were clustered around Hangzhou Bay (including Zhoushan, Hangzhou, Shanghai, and Ningbo), as well as Huangshan and Nanjing. This clustering demonstrates the successful integration of environmental protection and economic advancement in these areas. In contrast, lower values were concentrated in Bozhou, Huainan, Fuyang, Suzhou (in Anhui), Huaibei, and Xuzhou, primarily located in the northern Anhui and Jiangsu. These cities are located on the periphery of the YRDR, dominated with resource-based or agriculture-dominated economies. Their environment management was relatively extensive, and they faced greater challenges in achieving balanced development of environment and socio-economy.

Fig. 6
figure 6

Comprehensive evaluation degree and coupling degree between SES and ENS.

Full size image

The coupling degree was between 0.78 and 1 in 2015, and between 0.83 and 1 in 2020. These high values of coupling degree indicate that socioeconomic development and the promotion of environmental quality has an obvious interactive driving effect in relation to one another. Besides the average value increased from 0.871 in 2015 to 0.955 in 2020, signifying strengthened regional-scale integration between high-quality socio-economy and high-level environment. Despite this overall positive trend, 16 cities experienced declines in their coupling degrees. Eight of these cities are located in Zhejiang (e.g., Huzhou, Jinhua, Lishui, Quzhou, Shaoxing). This is perheps due to the fact that the environmental promotion trend is more rapid than the socioeconomic trend, leading to a weakened interaction between SES and ENS. This implies a need for these cities to prioritize measures to balance economic development with environmental protection. Additionally, nine out of the top ten cities with the largest increments were situated in Anhui, highlighting the province’s dedication in promoting sustainable development. Since all the cities of Anhui were involved into the YRDR since 2018, it has actively strengthened cooperation with other cities, undertaken industrial transfer, upgraded the economic structure, which has resulted in an increased investment in environmental protection, fostering progress in the relationship between the socio-economy and environment.

Figure 7 depicts the spatiotemporal distributions of the CCD and its associated classification. The CCD reflects the coherence and sustainability of the composite system, with high values indicating synergies and between environmental protection and socioeconomic development. Results show that the CCD fluctuated between 0.46 and 0.71 in 2015, and between 0.55 and 0.79 in 2020. The regional mean value increased from 0.594 to 0.677, indicating a strengthening of synergistic development between ENS and SES. From 2015 to 2020, the number of barely coordinated cities decreased from 17 to 6, the primary coordinated cities increased from 18 to 21, and the intermediate coordinated cities expanded from 3 to 14. This indicates that the cities in YRDR achieved better balances between ENS and SES. Ma’anshan experienced the largest CCD increment among the 41 cities, with an increment of 0.133. The possible reason is that Ma’anshan seized the opportunity provided by the integration development strategy of the YRDR. In the early stage of its development, the steel industry was the leading industry of economic development, which had a negative impact on the environment. With the deepening of YRDR’s integration and high-quality developement, the government has tried to promote the development of light industry and service industry and transfer the socio-economy into a greeny and lower-emssion development. This has resulted in a more sustainable and coordinated development between socio-economy and environment. Huangshan, Bengbu, Chuzhou, and Wenzhou are cities that have experienced significant improvements in CCD following Ma’anshan. Due to Huangshan deepening cooperation with Hangzhou, Chuzhou integrating into the Nanjing metropolitan coordinating region, and Wenzhou being included among the core cities of the YRDR, these cities have focused on industrial development, urban construction, ecological protection, and environmental governance in recent years. This demonstrates that regional integration policies have promoted regional cooperation and driven CCD growth.

Fig. 7
figure 7

Spatiotemporal distributions and classifications of CCD.

Full size image

There is a clear spatial heterogeneity in the CCD due to disparities between the SI and EI. Results show that the higher CCD values were mainly clustered around the Hangzhou Bay area (including Hangzhou, Shanghai, Ningbo, and Zhoushan), as well as cities near Shanghai like Suzhou(in Jiangsu), Wuxi, Nanjing. This further indicates that the characteristics of Shanghai are not only better than those in other regions but also have a certain radiation effect on the surrounding cities. Lower CCD values were mainly concentrated in Bozhou, Fuyang, Huaibei, Suzhou (in Anhui), Lu’an, and Huainan. These results are further verified by Fig. 8, which shows that higher CCD values are mainly associated with higher SIs or relatively high and equal SIs and EIs. Conversely, lower CCD values were mostly spread across cities with both low SIs and EIs. For example, Hangzhou had the highest CCD, followed by Shanghai. This is primarily attributable to Hangzhou’s higher degree of economic development, increasing emphasis on the development of clean, efficient, low-carbon energy sources, and greater expenditure on preventing environmental damage. This was consistent with the comprehensive evaluation index values, which also highlighted Hangzhou Bay as a region with elevated CCD values. Meanwhile, Zhoushan ranked the third in CCD due to its close alignment in environmental and socioeconomic development. Conversely, Bozhou, Suzhou (in Anhui), and Fuyang ranked the lowest in terms of CCD. These cities were both socioeconomically and environmentally lagging. Their CCD values were relatively low due to problems such as the rapid depletion of resources, degradation of green spaces, serious air and water pollution, and their economy dominated by agriculture and heavy industries.

Fig. 8
figure 8

The relationship plot among SI, EI and CCD.

Full size image

For further exploring the spatial pattern of SI, global Moran’s I value25 was calculated to test spatial auto-correlation. The results find that the Moran’s I values were 0.434 in 2015 and 0.391 in 2020, indicating that SI had positive spatial auto-correlation. This means that cities close to cities with a high CCD also tend to have a high CCD, and cities with a low CCD are close to low-CCD cities, reflecting a clustering phenomenon of similar-level cities driven by the extrinsic spatial correlation. However, the Moran’s I value showed decline, indicating a generally dispersed trend of high-high or low-low clusters and a more evenly distributed trend of CCD. The potential reason for this phenomenon is the integration development strategy of YRDR proposed in 2018. Since then, connections between various cities have been strengthened, transportation has become more convenient, and cities have emphasized collaboration in economic development and environmental protection.

Main factors affecting CCD

In this study, the stepwise cluster analysis method was utilized to establish the non-linear and complex relationship between CCD and its influencing factors. With 18 indicators treated as input variables and CCD as the output, a cluster tree (as shown in Fig. 9) was generated under the condition of p < 0.05. In this cluster tree, three indicators (i.e., numbers of college students among 10 thousand people, utilization rate of non-hazardous industrial solid waste, and greenery coverage in built-up areas) were automatically excluded due to their non-significance. The remaining 15 indicators underwent factorial factor design, combining two levels (5% and 95% confidence of the distributions) through 64 experiments. These combinations were then forced into the cluster tree to generate new outputs. The square errors of the outputs were calculated to analyze the effects of the indicators according to Eqs. (16–19).

Fig. 9
figure 9

The stepwise cluster tree of CCD.

Full size image

Figure 10 shows the standardized effects of the input indicators and their interactions, ranked in descending order based on their contributions. Overall, individual effects accounted for 79.02% of the total, while two-factor interactions contributed 20.88%. Socioeconomic indicators made up 82.98% of the effects, environmental indicators contributed 11.05%, and the interaction between the two systems constituted 5.92%. This underscored the predominant influence of the SES on coupling coordination. Cities with higher levels of socioeconomic development tended to exhibit higher CCD values. Results show that GDP (X1) was the major factor, contributing 53.81% to CCD, followed by the proportion of the added value of tertiary industry to GDP (X4) at 12.95%, and PM2.5 concentration (Y2) at 10.94%. These findings highlight GDP, industrial structure, and PM2.5 as critical links between socioeconomic and environmental coordination. The reasons for such phenomena may be that GDP is vitally indicative to economic returns, and a well-developed tertiary sector can support the growth in other industries while minimizing environmental harm through efficient resource utilization and technology advancement. PM2.5, an environmental pressure indicator, indirectly reflects the industrial structure and green economic development level due to its potential sources from energy and transport. This comprehensive analysis sheds light on the interplay between economic returns, industrial structure, and environmental pressures in shaping CCD in the YRDR, offering valuable insights for sustainable development research.

Fig. 10
figure 10

The standardized effects and contributions of indicators on CCD.

Full size image

Interactions between factors on CCD

Figure 11 visualizes the interactive plot of indicators’ effects on CCD. Parallel curves indicate no interactive effects, while intersecting lines suggest interactive effects The intersecting lines of X1*X4, X1*X5, X1*Y2, X3*X8, X3*Y1, and X5*Y2 imply interactive effects, meaning the effect of one indicator changed with the levels of another. X1 (GDP)*X4 (proportion of the added value of the tertiary industry to GDP) was identified as the most significant combination affecting CCD, with a contribution of 12.9%. When X1 was low, X4 hardly influenced CCD; when X1 was high, higher X4 led to higher CCD, and vice versa. A higher GDP indicates increased economic activities and demands for goods and services. Promoting the tertiary industry’s development could mitigate environmental impacts by encouraging cleaner and more sustainable service-oriented economic activities. The interaction between X1 (GDP) and Y2 (PM2.5) significantly contributed 3.43% to CCD. The interaction indicates that as thePM2.5 concentration level changed, CCD varied more at a low GDP level than that at a high GDP level. This is due to the fact that economics with higher GDP levels have more resources to invest in pollution control technologies, environmental regulations, and treatment infrastructures, accompanying with a shift towards cleaner and more sustainable industries, and thus reducing the impact of PM2.5 on CCD. Besides, At higher PM2.5 concentration levels, the effect of GDP on CCD was more pronounced. High PM2.5 concentration levels could negatively affect productivity and quality of life, promoting stricter environmental regulations and impacting economic performance. Thus, the influence of GDP on environmental and economic coordination became more visible.

Fig. 11
figure 11

The interactive plot of indicators’ effects on CCD.

Full size image

Additionally, the interaction between X3 (Engel’s coefficient) and X8 (number of hospital beds per 10 thousand people) reflect the combined effects on CCD. Higher income levels (low Engel’s coefficient) and greater number of hospital beds improve the living life quality and healthcare access, leading to better social and economic development. In contrast, higher Engel’s coefficient indicates limited resources and infrastructure constraints, undermining living life quality and negatively impacting coordination. Results also suggest that at a low Engel’s coefficient, the industrial wastewater discharge (Y1) negatively affected CCD; at high Engel’s coefficient, Y1 had a positive effect. Higher income levels and low low expenditure on basic necessities posed greater emphasis on environmental protection, sustainability, and regulatory compliance, and thus, higher discharge of industrial wastewater was perceived as detrimental to the environment and economic coordination. Conversely, lower income levels might prioritize economic growth and industrial development over environmental concerns, perceiving as synchronization between wastewater discharge and economic output. In summary, the observed interactions underscored the complex dynamics between socioeconomic and environmental factors, and their implications for coordination. Understanding these interactions can inform policy decisions and strategies aimed at promoting sustainable environmental protection and socioeconomic development.

Discussion

Comparison with other studies

In this study, the GSFCM was constructed to calculate the CCD between socio-economy and environment, as well as identify associated drivers and interactions in the YRDR from 2015 to 2020. The developed model incorporated ensemble weighting through game theory to enhance the accuracy compared to single methods like entropy or AHP30,32. Besides, SCA and FA were the fist time in analyzing CCD driver. Due to their ability in tackling discrete or continuous, linear or non-linear relationships, as well as identifying factor interactions, they are superior to traditional regression models with function assumption26,28, and machine learning inability of analyzing indicators’ interaction12,26. While some studies utilized geographic detectors to identify the interactions between driving factors, it is limited as it couldn’t quantify the direction of interaction and required transforming factors into categorical data, introducing uncertainty and subjectivity34.

The application of GSFCM in the YRDR revealed an upward trend in CCD, basically aligning with previous literature26,49,66,67 related to socioeconomic and environmental coupling coordination in the region. Higher CCD values were mainly concentrated around Hangzhou Bay and cities around Shanghai, while lower values clustered in the north Anhui like cities of Bozhou, Fuyang, Huaibei. This distribution pattern was consistent with Zhang et al.26, where found the coordinated development levels of those cities in the central coastal region of YRDR like Shanghai and Hangzhou were better than others. Dong et al.49 also revealed that Shanghai lead the largest CCD, followed by Jiangsu, Zhejiang and Anhui. Hu et al.68 proved that unbalanced cities are located in areas where urbanization is relatively lagging. Such spatial distributions of CCD indicated that cities with better economic development would be more coordinated and advanced.

Factors such as GDP and the proportion of the added value of the tertiary industry emerged as critical drivers of CCD, consistent with findings from other studies. For example, Zhao et al.30 found that the income levels remained an important determinant to coordination coupling relationship and higher level indicated better CCD. Dong et al.49 revealed that the proportion of tertiary industry in GDP, and retail sales of consumer goods per capita are critical to the coordinated development of the economy-society-environment system. Zhang et al.65 concluded that the architecture of industrial distribution should be further adjusted to improve the urban environment for economic development in South Jiangsu, Anhui Province and the area from Hangzhou to Ningbo. The positive correlation between GDP, the proportion of the added value of the tertiary industry and CCD, along with the interactive effects, reflects a common trend observed in studies linking economic growth to environmental coordination. While some factors like population density11, and technical aspects66, have been identified in other studies, the difference could be attributed to variations in indicators, time scales, and methods. In general, the similarities and consistencies with existing studies reinforced the credibility and robustness of the developed GFSCM method in assessing CCD in the YRDR.

Limitations and extension

This study presents valuable insights into the interplay between socioeconomic factors and environmental conditions in the YRDR, offering important implications for regional development and policy-making. However, it is essential to acknowledge and address several limitations within this research. Firstly, the study’s reliance on data spanning only two years may limit the comprehensive analysis of CCD, potentially overlooking long-term dynamics and weakening the temporal precedence required for rigorous causal analysis. To enhance robustness, future research should consider extending the period to causally analyze evolving trends. Secondly, the multifaceted nature of indicators influencing CCD necessitates further investigation to provide a more nuanced and holistic understanding the dynamics at play. This deeper investigation is crucial for optimizing strategies aligned with initiatives such as the Beautiful China Construction, aiming to harmonize economic development with environmental preservation effectively. Thirdly, it is important to recognize that indicators impacting CCD may vary significantly across different scales, from regional to provincial, city, and county levels. Exploring these multi-scale perspectives will be instrumental in crafting targeted and tailored policies that address specific challenges and opportunities within each administrative unit. while this study forms a foundational framework for comprehending socioeconomic and environmental coordination in the YRDR, future research endeavors should prioritize addressing the identified limitations. By extending the study period, delving into the complexities of indicator analyses, and embracing multi-scale perspectives, researchers can refine the understanding of CCD dynamics and contribute to more effective policy-making for sustainable regional development.

Conclusions and policy implications

Main findings

In this study, GSFCM was developed to examine the interplay between socio-economy and environment. Game theory was utilized to evaluate the SI and EI accurately. The CCD model was used to quantify the mutual relationship between SES and ENS. Additionally, SCA and FA were employed to identify key factors and interactions impacting CCD in the YRDR from 2015 to 2020. The key findings are summarized as follows:

  1. (1)

    The YRDR exhibited positive trajectory in SI, with cities like Shanghai, Suzhou (in Jiangsu), Nanjing, Hangzhou, Wuxi, and Hefei leading the region, while cities in norther Anhui showed lower SI levels.

  2. (2)

    The EI in the YRDR demonstrated an an upward trend, driven primarily by significant growth in Zhejiang province. In 2020, Huangshan recorded the highest EI, followed by Zhejiang’s cities like Lishui, Quzhou, and Taizhou.

  3. (3)

    The number of cities in coordination increased from 38 to 41, indicating a more balanced relationship between ENS and SES. CCD showed spatial disparities, with Hangzhou, Shanghai, and Zhoushan ranked the highest, while Bozhou, Suzhou (in Anhui), and Fuyang had the lowest levels.

  4. (4)

    The driving factors identification reveals the CCD variation mechanisms, which shows that socioeconomic factors, particularly GDP and the proportion of the added value of the tertiary industry, significantly positively influenced CCD. The complex interactions between GDP and the proportion of the added value of the tertiary industry, GDP and PM2.5 concentration, as well Engel’s coefficient and industrial wastewater discharge impacted the intricate dynamics between socioeconomic and environmental systems.

Policy implications

The analysis of the socioeconomic and environmental coordination in the YRDR provides valuable insights for enhancing regional development and environmental protection. Based on the findings, the following policy recommendations can be derived:

  1. (1)

    Strengthen regional collaboration. The disparities in CCD underscored the critical role of proactive leadership from key cities in driving economic development and environmental protection. Key cities like Shanghai, Hangzhou, and Nanjing should spearhead efforts to enhance regional cooperation to stimulate economic advancement in peripheral and underdeveloped regions like Bozhou, and Lu’an. Municipal administrations should proactively enhance their integration development strategies by establishing collaboration platforms, sharing technological innovations and addressing common environmental challenges such as air pollutants like PM2.5, which can bridge existing disparities in CCD and promote sustainable growth.

  2. (2)

    Upgrade the industry and promote economic development. Policy makers can exploit the positive synergies between GDP and the industry to foster economic growth by technological innovation tailored to each city’s unique characteristics. Cities like Suzhou (in Jiangsu), Wuxi, Nanjing, Hangzhou, and Hefei should prioritize technological advancements to diversify industrial structures and establish novel industrial pillars through the integration of modern service industries with cutting-edge manufacturing clusters. Agricultural cities like Bozhou, Suzhou (in Anhui), Fuyang, and Lu’an should cultivate modern agricultural practices and optimize agricultural frameworks to maximize economic gains. Resource-based industrial cities such as Huainan, Chizhou, Xuzhou, and Ma’anshan should enhance the efficiency of natural energy utilization by upgrading highly polluting and energy-intensive enterprises to mitigate environmental impact.

  3. (3)

    Invest in environmental infrastructure. The interactions between GDP and PM2.5, and between Engel’s coefficient and industrial wastewater discharge imply economic progress in enhancing living standards, investing environmental infrastructure, and reducing pollutant emissions. Increasing investments in environmental infrastructure, including air and water quality monitoring systems, waste management facilities, and green spaces, are imperative to enhance public health and environmental quality. Supporting sustainable practices within industries, reducing pollutants, and implementing efficient treatment technologies are integral steps to mitigating the adverse impacts of industrial discharges.

In general, these findings emphasize the importance of enhancing regional cooperation, industrial upgrades, and investment in environmental infrastructure to reconcile economic growth with environmental safeguarding. They serve as a valuable foundation for future researches and policy-making aimed at ensuring the region’s long-term sustainability.