Introduction

The dust problem in mine production is becoming more and more serious. And there is no technical method to solve it. The coal seam water injection technology plays a good role in mine dust control, coal mine gas prevention, rock burst and other disaster prevention1,2,3,4. The stress conditions in the deep stratum restrict the effect of coal seam water injection on dust reduction and disaster prevention5,6,7,8,9. Therefore, it is particularly important to study the influence of time effect of alternating hydraulic pressure on coal permeability10,11,12,13,14.

In recent years, many experts have carried out in-depth research on water injection in deep coal seams and put forward many technical means, such as hydraulic fracturing, hydraulic punching, hydraulic slitting, hydraulic blasting etc.15,16. Lu17 proposed the high-pressure pulse water jet assisted drilling and seam cutting technology to improve the permeability and gas extraction rate of soft coal seams, and carried out field test research in high gas and low permeability coal mines. Lin18,19,20 put forward the alternating hydraulic pressure relief and permeability increasing technology to improve the gas drainage efficiency of coal seams. During the research process, the pulsating hydraulic fracturing experiment was conducted on the briquette samples with different pressure and frequency conditions as variables. Zhu21,22,23 put forward the technology of alternating hydraulic pressure to enhance transparency, and studied the damage and deformation characteristics of coal and rock, the principle of pulsating water injection, and the initiation and propagation process of fatigue cracks under pulsating water pressure from the microscopic mechanism. Zhao24 proposed a frequency conversion pulse type coal seam water injection method in order to improve the water injection effect in coal seams. Zhang25 studied the mechanism of coal seam water injection to prevent rockburst in view of the influence of water on the mechanical properties of coal. The analysis shows that coal seam water injection will change the mechanical parameters of coal, thus playing a role in preventing rockburst. Cheng26,27 used MTS815.03 rock mechanics experimental control system to test the permeability of Coal Seam 3 # in the east working face of Xingcun Coal Mine. The experimental results show that it is difficult to inject water into coal seams with low permeability. Sun28 studied the generation and propagation of pulsating stress wave and its damage mechanism to coal and rock mass in the process of high alternating hydraulic pressure by combining theoretical research.

Chen29 analyzed the influence of the coupling of alternating hydraulic pressure parameters and confining pressure on the propagation of existing fractures and the fatigue damage of coal by measuring the fluid pressure. Li30,31 explored the influence of pulsating frequency on the fracture and extension of hydraulic fractures, believed that low-frequency fracturing has lower starting pressure, more complex fractures, and high alternating hydraulic pressure has faster fracture. Lu32,33 established a numerical model for the dynamic and static stress response of coal seams by using numerical calculation methods, and studied the influence of engineering parameters and geomechanical parameters on the stress disturbance effect of coal rock radial well pulsating hydraulic fracturing. Hu34 used the high alternating hydraulic pressure hammer generator to conduct pulsating water injection test on the hard to extract coal seams in the 1562 (3) working face of Pansan Coal Mine. The test proved that the pulsating high pressure water injection technology effectively improved the permeability of the coal seams and increased the gas extraction volume. Labus35,36 injected pulsating high-pressure water into the coal seam to change the water injection pressure so that the water can penetrate into different fractures and pores.

In summary, the study have less research on the injection time, especially the relationship between injection time and permeability and deformation is not clear. Therefore, using coal rock multi-field seepage simulation experimental system to carry out alternating hydraulic pressure test, and study on the influence law of hydraulic injection time on permeability and deformation. The results of the research for the deep coal seam water injection dust reduction as well as rockburst prevention and control to provide theoretical support.

Test introduction

Sample preparation

The coal samples used for the test were all φ50mm × 100mm cylindrical raw coal samples prepared in accordance with international mechanical rock standards, and the end-parallelism of all the coal samples made were within 0.02mm. All coal samples taken from Xinglongzhuang coal mine, six coal samples were selected for the alternating hydraulic pressure injection test. To ensure the internal homogeneity and uniformity of the selected coal samples, CT scans of cross-section and longitudinal section were performed firstly, and then ultrasonic monitoring was carried out on all coal samples during the selection process. Table 1 shows the ultrasonic testing results of the screened coal samples, Fig. 1 shows the coal sample testing equipment, and Fig. 2 shows the results of CT scan.

Table 1 Ultrasonic test results.
Full size table
Fig. 1
figure 1

Testing equipment.

Full size image
Fig. 2
figure 2

CT scan results.

Full size image

Experimental system

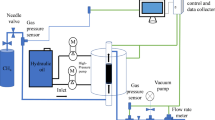
The experiments are conducted in the coal rock multi-field seepage simulation experimental system, comprising the experimental chamber, confining pressure and axial pressure loading system, control system, high-pressure water injection pump system. The schematic diagram of the equipment is shown in Fig. 3.

Fig. 3
figure 3

Coal rock multi-field seepage simulation experimental system.

Full size image

Because of the high accuracy of permeability testing using the steady-state method, this experiment utilizes the steady-state method for permeability calculation. Using the relevant data automatically collected by the coal rock multi-field seepage simulation experimental system, the permeability k value of coal samples was calculated as shown in Eq. 1.

$$k = - \frac{Q}{A}\frac{\Delta L}{{\Delta p}}u$$
(1)

where, k-permeability, Darcy, Q-Percolation volume per unit time through the sample, m3/s, A-Area of the sample cross-section, m2, ΔL-The height of the sample, m, ΔP-Pressure difference between the two ends of the sample, Pa, u-Fluid viscosity coefficient, Pa-s.

Experimental scheme

The experimental conditions selected for this study are based on the actual on-site working conditions. The subject of the research is coal seam water injection, which is employed for the purposes of dust reduction and the prevention of rockburst disasters. The alternating hydraulic pressure waveform and stress path are illustrated in Fig. 4. A constant stress cyclic injection percolation test was conducted, in which the alternating hydraulic pressure waveform was rectangular. The hydraulic pressure variation parameters were Pmin = 1 MPa, Pmax = 9 MPa, and the wave amplitude ΔP = 8 MPa. Each alternating hydraulic pressure time was 2 min, with 10 alternating hydraulic pressures constituting one cycle.

Fig. 4
figure 4

Stress path and alternating hydraulic pressure waveform.

Full size image

Table 2 presents the parameters of the alternating hydraulic test. The specific experimental plan comprises a constant confining pressure of 10 MPa, a constant axial pressure of 25 MPa, and a constant pressure hydraulic injection for 30 min between each cycle. The permeability of the coal sample is determined by means of the steady-state method. The numbering system for the coal samples is as follows: 1# and 2# have 15 cycles, 3# and 4# have 30 cycles, and 5# and 6# have 45 cycles.

Table 2 Alternating hydraulic pressure injection test parameters.
Full size table

Results

Deformation law of coal sample

In the process of alternating hydraulic pressure injection, the primary focus is on understanding the deformation law of the coal sample. Deformation parameters provide a visual representation of the impact of different cycle numbers during the cyclic water injection process. Both the radial strain and axial strain of the coal change when the pressure environment is altered. By considering the volume strain (the sum of two times the radial strain and one axial strain), we can comprehensively analyze the deformation of the coal using these three parameters.

Prior to initiating the alternating hydraulic pressure injection, the coal sample did not exhibit any deformation. Throughout the entire hydraulic injection cycle, an externally installed Linear Variable Differential Transformer (LVDT) extensometer was used to monitor and record the axial and radial deformation of the coal sample. Subsequently, the axial strain and radial strain were calculated. Since the alternating hydraulic pressure injection test was conducted with constant axial pressure and confining pressure, the overall deformation amplitude of the coal sample was significantly reduced compared to that caused solely by hydraulic pressure-induced stress. The corresponding deformation data were obtained through calculations, and the deformation laws of the six samples were plotted, as illustrated in Fig. 5.

Fig. 5
figure 5

1#, 2# coal samples deformation law.

Full size image

The axial and radial strains demonstrated fluctuating upward trends throughout the course of the alternating hydraulic pressure test. This is due to the fact that the volume strain was calculated by adding together the axial strain and radial strain, which resulted in a comparable trend in the volume strain. Nevertheless, the variation in radial strain was markedly less pronounced in comparison to that of axial strain. The impact of hydraulic pressure on the deformation of coal samples during the cycling process was predominantly evident in the axial direction. An analysis of the deformation patterns exhibited by the 1# and 2# coal samples reveals that the alternating hydraulic pressure test has a promotional effect on the deformation of coal samples. While the overall deformation is relatively minor, it does nevertheless increase consistently with each cycle of hydraulic pressure injection.

Figure 6 illustrates the deformation behaviour of coal samples labelled 3 and 4#. During the experiment, when the confining pressure remains constant and the hydraulic pressure gradually increases, the effective stress rises, resulting in the compression of the coal skeleton and a reduction in fissure volume. Consequently, there is an increase in negative strain and a decrease in the permeability of the coal volume. When the surrounding pressure is maintained at a constant level and the pore pressure declines gradually, the effective stress rises, resulting in the contraction of fissures. This results in an increase in negative strain and a reduction in the permeability of the coal volume. Furthermore, desorption results in contraction of the coal matrix, which in turn leads to an increase in fissure volume, negative strain, and permeability of the coal volume. The volumetric strain index is particularly illustrative of this deformation effect. Moreover, a specific hydraulic pressure value has been identified at which the permeability reaches its minimum. As the hydraulic pressure declines, the permeability of the coal initially decreases, then increases.

Fig. 6
figure 6

3#, 4# coal samples deformation law.

Full size image

The hydraulic alterations observed in coal samples are intrinsic to the deformation attributes and permeability modifications of coal. Fluctuations in hydraulic pressure during the seepage process result in deformation of the coal. The pressure of water represents a change in force, and changes in force affect alterations in coal pores and fractures, which in turn affect changes in coal sample permeability. When coal remains intact, this deformation is observed at the macroscopic level as volumetric strain and at the microscopic level as changes in crack size and matrix volume. Macroscopic strain can be understood as representing the cumulative effect of microscopic deformation, which is influenced by changes in hydraulic pressure.

Figure 7 illustrates the deformation behaviour of coal samples 5 # and 6 #, which exhibit relatively mild characteristics. However, the overall trends of axial strain, radial strain, and volumetric strain remained consistent, with more significant changes occurring in the initial stage of the cycle. The magnitude and pattern of these changes are analogous to those observed in coal samples 3 # and 4 #. Subsequently, the rate of change decelerated and the growth rate diminished between 15 and 30 cycles. It is noteworthy that the fluctuations in the later stages of the cycle were more pronounced. The primary cause of these fluctuations is the impact of hydraulic pressure, which has resulted in the clear development of internal pores and fractures within the coal sample. The fluctuations are primarily attributable to an apparent periodic opening and closing phenomenon. By the conclusion of the experiment, the deformation patterns exhibited a consistency with those observed in coal samples 3 # and 4 #, displaying a decelerating trend and a decline in growth between 15 and 30 cycles.

Fig. 7
figure 7

5#, 6# coal samples deformation law.

Full size image

The fundamental deformation observed across the three experiments exhibited slight discrepancies, with the level of strain change remaining relatively low throughout the entirety of the testing process. In conditions of constant axial and circumferential pressure, alternating hydraulic pressure exerts mechanical effects on coal samples, resulting in deformation. Although the deformation is relatively minor, the strain increases due to the cumulative damage caused by continuous alternating hydraulic pressure in the coal sample. The fluctuations observed during the experiment are primarily attributable to alterations in hydraulic pressure, which can be conceptualized as a change in force. This consequently gives rise to alterations in the distribution of internal pores and fractures in coal, which in turn affects parameter fluctuations.

Permeability change law

To visually analyze the permeability evolution pattern of the six coal sample samples during the alternating hydraulic pressure test, Figs. 8, 9, 10 illustrate the permeability change characteristics of the coal samples during the test in three different cycle periods.

Fig. 8
figure 8

1#, 2# coal samples permeability evolution law.

Full size image
Fig. 9
figure 9

3#, 4# coal samples permeability evolution law.

Full size image
Fig. 10
figure 10

5#, 6# coal samples permeability evolution law.

Full size image

Figure 8 reveals that when the stress state is held constant, the permeability change is not pronounced in the first six cycles. The increase in permeability from the third to the sixth cycle is approximately 10%, with only minor fluctuations. However, a noticeable increase in permeability occurs between the sixth and fifteenth cycles, with all increases exceeding 20%. These results indicate that the native microcracks and pores within the sample gradually expand throughout the entire cycle under the influence of alternating hydraulic pressure, resulting in an increasing trend in permeability. When comparing the permeability under two hydraulic pressure states (1 MPa and 9 MPa), it is evident that the 9 MPa hydraulic pressure significantly improves the permeability of the coal sample. Initially, during the early stages of alternating hydraulic pressure, the difference in permeability measured under 1 MPa and 9 MPa hydraulic pressure was not significant. However, as the cyclic water injection test progressed, this difference became apparent, thus confirming the enhancement mechanism of multi-alternating hydraulic injection pressure on the permeability of coal samples.

According to Fig. 9, the permeability of both coal samples exhibited an increasing trend with the rise in alternating hydraulic pressure cycles. However, at certain intervals, the permeability of the coal samples showed a slight decrease. For instance, when measuring the permeability of the 4# coal sample at 9 MPa injection pressure, the permeability of the 12th cycle was smaller than that of the 9th cycle, indicating a decreasing trend. Similar situations were observed for the 3# coal sample during the 21st and 24th cycles at 9 MPa injection pressure. Upon analysis, it was found that the cyclic water injection had a positive effect on increasing permeability throughout the testing process. At a certain point in time, the primary cause of the observed reduction in permeability is the damage caused by alternating hydraulic pressure, which may result in the closure and blockage of internal cracks. Prior to the complete destruction of the coal by hydraulic pressure, the continuous alteration in hydraulic pressure results in a shift in the force acting upon the coal. This will impact the regular expansion and closure of pores and fractures, resulting in a reduction in permeability. The most significant increase in permeability occurred between cycles 9 and 15, with an overall increase of over 20%. In the other stages, the increase in permeability was not as prominent, remaining relatively stable between cycles 15 and 30 without any sharp spikes in increase.

Figure 10 illustrates the permeability change law of the 45 cycles for 5# and 6# coal samples. The 6# coal sample exhibited more noticeable changes in the first 15 cycles, with a 16% increase in permeability compared to the initial cycle. On the other hand, the permeability of the 5# coal sample remained relatively stable. During the first 30 cycles, the permeability of both samples ranged from 0.6 × 10–4 mD to 0.8 × 10–4 mD. However, starting from the 30th cycle, there was a significant increase in permeability. For instance, the 6# coal sample experienced a 42% increase in the last cycle compared to the 30th cycle. This indicates that the effect of hydraulic pressure cycles on the permeability properties of coal samples becomes prominent after the 30th cycle.

The alternating hydraulic circulation process has been demonstrated to effectively enhance the permeability of coal samples. The initial 30 cycles resulted in a gradual enhancement in permeability. Subsequently, the repeated compression damage caused by alternating hydraulic pressure resulted in an enhanced continuity of the coal sample, thereby facilitating an accelerated increase in permeability. Furthermore, the cumulative damage caused by alternating hydraulic pressure affects the pore and fracture structure of the coal sample, thereby affecting its strength, increasing the wetting degree of water injection, and weakening the original strength of the coal.

Permeability change rate study

In order to study the specific effects of different alternating hydraulic pressure cycles on the magnitude of permeability change of coal rock under stress state, the concept of permeability change rate ∆k is introduced here based on the experimental data, and the ratio of the difference between the permeability of the two cycles before and after the interval cycle, this ratio constant is the permeability change rate ∆k. The algorithm of permeability change rate ∆k is shown in Eq. 2.

$$\frac{{D_{{{\text{after}}}} { - }D_{{{\text{before}}}} }}{{T_{{{\text{after}}}} { - }T_{{{\text{before}}}} }}$$
(2)

where, ∆k-permeability rate of change, Dbefore-previous cycle permeability value, Darcy, Dafter-the latter cycle permeability value, Darcy, Tbefore-the number of the previous cycle, Tafter-The number of the latter cycle.

The permeability change rate ∆k is calculated from the data, because there is a decrease in permeability during the cycle, so there is a situation where ∆k is negative, in order to reduce the impact of data errors, the permeability of two samples with the same hydraulic pressure at each stage is taken as the average value for calculation, the specific permeability change rate of each cycle stage is shown in Figs. 11, 12, 13.

Fig. 11
figure 11

1#, 2# coal samples permeability change rate law.

Full size image
Fig. 12
figure 12

3#, 4# coal samples permeability change rate law.

Full size image
Fig. 13
figure 13

5#, 6# coal sample spermeability change rate law.

Full size image

In the initial circulation stage, a relatively large increase in permeability change rate is easy to occur, such as region 1 and region 2 of coal samples 1# and 2# in Fig. 11, and region 1 in Fig. 12, all of which appear in the first 12 cycles; while a significant decrease in permeability change rate mostly appears in the middle and late stages, such as region 2 in Fig. 13, and region 5 in Fig. 13.

The fluctuation in permeability change rate reflects the influence mechanism of the entire water injection cycle process on the coal sample. The initial cycle’s hydraulic pressure has a notable effect on the permeability growth, primarily when the pore fracture structure inside the coal sample is relatively stable. As the alternating hydraulic pressure cycle continues, the effect on permeability increase diminishes in the middle stage due to the stabilized structure, resulting in a decrease or lesser rise in permeability change rate. In the later stages, the impact of previous increases tends to limit significant further increases. Overall, this pattern aligns with the overall change in permeability discussed in the previous section.

Discussion

Mathematical relationship analysis of coal sample permeability

Based on the test data, a significant correlation between cycle period and permeability change was observed. Therefore, a fitting analysis was performed to determine the relationship between the two variables. The permeability data of two coal samples in each stage, under the same hydraulic pressure conditions, were averaged for analysis. The specific mathematical relationship is presented in Figs. 14, 15, 16.

Fig. 14
figure 14

1#, 2# coal sample permeability mathematical relationship.

Full size image
Fig. 15
figure 15

3, 4# coal sample permeability mathematical relationship.

Full size image
Fig. 16
figure 16

5, 6# coal sample permeability mathematical relationship.

Full size image

Figure 14 and 15 demonstrate a clear linear relationship between permeability and cycle period for both 1 MPa hydraulic pressure and 9 MPa hydraulic pressure, particularly within the initial 30 cycle periods. The permeability increase during the first 30 cycles is relatively consistent, and the linear fitting accurately represents the relationship between cycle period and permeability observed in the initial test.

A linear relationship between cycles and permeability is observed in the first two stages, as depicted in Fig. 16. However, during the late stage of the third test, starting around 30 cycles and particularly evident at the onset of 33 cycles, the change in permeability deviates significantly from the earlier stages. At this point, the growth of permeability is no longer linear but instead exhibits a clear non-linear pattern. This indicates that the influence of alternating hydraulic pressure on the permeability of coal samples varies across different periods, with a relatively stable growth rate in the initial period and an accelerated growth phenomenon in the later stages of the cycle.

During the alternating hydraulic pressure test, continuous fluctuation damage leads to an accelerated expansion of internal fractures, connectivity within the coal rock, expansion of primary fractures, and generation of new fractures. Consequently, the permeability of the coal increases significantly. In the later stages of the cycle, the cumulative effect of circulating hydraulic pressure further enhances the coal’s permeability performance.

Study of the deformation-permeability relationship

The porosity and permeability, represented in the differential equation of seepage, change due to the stress field, reflecting the coupling effect between seepage and stress. Therefore, establishing the intrinsic relationship between seepage and stress coupling in the analysis of seepage and stress coupling is crucial. The strain encompasses the combined effect of effective stress and the mechanical properties of the rock itself, regardless of the deformation being linear or nonlinear, elastic or elastic–plastic. By considering volumetric strain, an applicable intrinsic structural relationship between seepage and stress coupling can be established. Figure 17 presents a schematic diagram of the seepage phenomenon observed in the coal sample injection process.

Fig. 17
figure 17

Schematic diagram of coal sample injection seepage.

Full size image

Volumetric strain is the change in volume per unit volume of a rock during deformation. Its mathematical equation is:

$$\varepsilon_{{\text{v}}} = \frac{{\Delta V_{{\text{b}}} }}{{V_{{\text{b}}} }} = \varepsilon_{{\text{x}}} + \varepsilon_{{\text{y}}} + \varepsilon_{{\text{z}}}$$
(3)

In the equation, Vb is the total volume of the rock, ∆Vb is the volume change of the rock, \(\varepsilon_{{\text{v}}}\) is the volume strain, \(\varepsilon_{{\text{x}}}\), \(\varepsilon_{{\text{y}}}\), \(\varepsilon_{{\text{z}}}\) is the positive strain in x, y and z directions.

Porosity is the ratio of the sum of the volume of all pore spaces in a rock sample to the volume of that rock sample, expressed as a percentage. It is called the total porosity of the rock, and it indicates the size of the pore space in the rock. From a practical perspective, only the connected pores are of practical significance. Volume strain refers to the ratio of the volume change of a material under external load to its original volume. Volume strain is one of the mechanical properties of a material, and its magnitude provides a reference for material selection in applications. The relationship between porosity and volume strain can be deduced from the definitions of porosity and volume strain. The equation for calculating porosity is as follows:

$$\phi = \frac{{V_{{\text{p}}} }}{{V_{{\text{b}}} }}$$
(4)

In the equation, Vp is the rock pore volume.

The porosity reaches the present state from the initial state through the volume strain then the equation of porosity versus volume strain can be derived.

$$\phi = \frac{1}{{1 + \varepsilon_{{\text{v}}} }}\left( {\phi_{0} + \varepsilon_{{\text{v}}} } \right)$$
(5)

The relationship between permeability and volume strain can be derived from the Kozeny-Carman equation, which has the following equation.

$$k = \frac{\phi }{{k_{z} S_{p}^{2} }}$$
(6)

kz is about 5, It is Kozeny’s constant and Sp is the specific surface area, which can be obtained from the following equation.

$$S_{p} = \frac{{A_{s} }}{{V_{p} }}$$
(7)

In the equation, As is the total surface area of the rock particles.

The permeability starts from the initial state and gradually increases through the effect of volume strain during water injection. Then the equation of permeability and volume strain is as follows.

$$k = k_{0} \frac{{\left[ {1 + {{\varepsilon_{v} } \mathord{\left/ {\vphantom {{\varepsilon_{v} } {\phi_{0} }}} \right. \kern-0pt} {\phi_{0} }}} \right]^{3} }}{{1 + \varepsilon_{{\text{v}}} }}$$
(8)

In the equation: k is the permeability; k0 is the initial permeability; \(\varepsilon_{{\text{v}}}\) is the volume strain; \(\phi_{0}\) is the initial porosity.

Some scholars37,38 founded that the permeability decreases when the rock volume is in compression with increasing stress, while the volume expands after damage and destruction of the rock and the permeability increases accordingly. Through the study, it is known that there is a close relationship between permeability and volume strain at different stages of the loading process (compression-density section, yield section, and damage section), and the equation of permeability and volume strain is established based on the Kozeny-Carman Equation.

$$k = \left\{ \begin{gathered} k_{0} \frac{{\left( {1 + {{\varepsilon_{v} } / {\phi_{0} }}} \right)^{3} }}{{1 + \varepsilon_{v} }} \hfill \\ \xi k_{0} \frac{{\left( {1 + {{\varepsilon_{v} } \mathord{\left/ {\vphantom {{\varepsilon_{v} } {\phi_{0} }}} \right. \kern-0pt} {\phi_{0} }}} \right)^{3} }}{{1 + \varepsilon_{v} }} \hfill \\ \xi^{\prime} k_{0} \frac{{\left( {1 + {{\varepsilon_{v} } / {\phi_{0} }}} \right)^{3} }}{{1 + \varepsilon_{v} }} \hfill \\ \end{gathered} \right.$$
(9)

In the equation, \(\xi\) and \(\zeta^{\prime}\) are the sudden jump coefficients in the yielding and damage stage.

Wang39 founded that the evolution pattern of permeability with volume strain has significant similarity and that volume expansion is a major cause of permeability evolution in rocks during the creep phase, which can be fitted with an exponential function related to volume strain.

$$k = k_{0} {\text{e}}^{{A\varepsilon_{{\text{v}}} + B}}$$
(10)

where: k is the permeability; k0 is the initial permeability; \(\varepsilon_{{\text{v}}}\) is the volume strain; A and B are constants.

Based on the research of various scholars, it was found that permeability is closely related to volumetric strain. Therefore, the change in permeability with volume strain during the whole cycle of alternating hydraulic injection experiments was plotted. To ensure data accuracy, permeability data from three different stages were considered, and volume strain data were treated as independent variables. The mean value of each stage was taken as the reference variable to eliminate the problem of multiple independent variables within the same group. After data processing, a fitted relationship was obtained (Fig. 18), and the corresponding functional equation is as follows.

Fig. 18
figure 18

Permeability-volume strain relationship.

Full size image

The corresponding function fitting equation is obtained.

$$k = e^{{\left( {a + b\varepsilon_{v} + c\varepsilon_{v} } \right)}}$$
(11)

where: k is the permeability; \(\varepsilon_{{\text{v}}}\) is the volume strain; A, B, and C are constants.

The above equation represents the fitting of the permeability response to volumetric strain. It shows an exponential relationship between volumetric strain and permeability. Since the initial permeability of the coal rock was not collected in this study, the first permeability at the beginning of the experiment was considered as the initial permeability. The relationship between permeability and volume strain was fitted and analyzed, resulting in the following fitted equation:

$$\left\{ \begin{gathered} k = k_{0} e^{{a\varepsilon_{v} }} \hfill \\ k = ak_{0} e^{{b\varepsilon_{v} + {\text{c}}}} \hfill \\ \end{gathered} \right.$$
(12)

Where: k is the permeability; k0 is the initial permeability; \(\varepsilon_{{\text{v}}}\) is the volume strain; A,B, and C are constants.

The fitted functional Equation (Eq. 12) was compared with the research results of Brace and Wang, among others. The relationship between permeability and volume strain is exponential when the initial porosity parameter is not considered. The form of the functional equation is essentially the same, which verifies the accuracy of the relationship between permeability and volume strain in this study.

Conclusion

(1) The alternating hydraulic injection process has been demonstrated to enhance the permeability of coal. The permeability demonstrates a gradual increase in line with the rise in the number of alternating cycles. The initial alternating hydraulic pressure has a more pronounced impact on permeability growth. During the midpoint of the cycle, the impact of alternating hydraulic pressure on the coal sample is minimal, as the internal pores and cracks have adapted and stabilized. The regions exhibiting the most notable alterations in permeability are primarily concentrated in the experimental and final stages.

(2) In the initial and intermediate phases of alternating hydraulic pressure, a linear correlation is observed between permeability and the number of cycles. The permeability demonstrates a gradual enhancement in conjunction with the cyclic water injection test. However, in the late stage of the cycle (after 30 cycles), the relationship between permeability and cycle period undergoes a transformation from linear to non-linear, with a notable increase in permeability. This serves to corroborate the phenomenon of permeability exhibiting a sudden increase in the late stage of the test.

(3) The mathematical relationship between volume strain and permeability during alternating hydraulic pressure injection was discussed based on a data analysis. A mathematical model was constructed to establish the relationship between the two variables, and the corresponding coefficients were optimised.

The present study offers a theoretical foundation for the implementation of water injection techniques in coal mines. The findings have significant implications for the management of dust and rockbursts in underground engineering sites.