Abstract
Red mudstone has significant hydrophilicity, that is hard at low water contents and soft and unstable at high water contents, and understanding the whole range of water content on the shear behavior of red mudstone is critical for evaluating red beds landslide stability. However, the deterioration mechanism of red mudstone in the process of gradual humidification is not clear in the whole range of water content. In this study, a series of mechanical and microscopic tests were carried out in the whole range of water content. A mechanical behavior prediction model for the entire process under the coupling of initial damage and load damage was constructed. The results show that the deterioration of shear strength, elastic modulus and strength parameters conforms to the “logistic model” curve with the increase of water content in the whole range of water content. In addition, the water sensitivity of cohesion was higher than the internal friction angle, and it gradually stabilized as water content increased. The weakening mechanism of the mechanical strength in the accelerated decline stage is the initiation and propagation of microcracks caused by mineral expansion, which leads to the corresponding shear behavior. Finally, the constructed damage model can be transformed into different yield conditions through parameter changes. The introduction of coupling damage enables the model to more accurately describe and predict the accelerated attenuation stage of red mudstone in the process of gradual humidification in the whole range of water content.
Similar content being viewed by others
Introduction
The term red beds refers to the red rock series deposited throughout geological history1, and such rocks are widely distributed all over the world2,3. Large-scale red beds in China were formed during the Meso-Cenozoic era4, and the total area of such red beds is more than 800,000 square kilometers. Their main lithology is red mudstone, siltstone, and sandstone (Fig. 1a)5,6. However, special attention should be paid to the high content of clay minerals in red mudstone7,8, which has strong disintegration, expansibility, and rheology after encountering water. Water–rock coupling has caused a large number of geological disasters9, seriously affecting urban construction, safe operation of roads and tunnels in the red beds (Fig. 1b–e). Such as, the red mudstone landslide triggered by rainfall in Jungong, Qinghai Province, which destroyed the 400 m highway10. The occurrence of the above geological disasters is often due to the transformation of red mudstone from low water content to high water content. It is necessary to study the mechanical behavior of red mudstone in the whole range of water content in order to effectively control and solve these geological disasters.
a Distribution of red beds in China and sampling site, b–e Red beds geological disasters. The map was drawn using ArcGIS 10.5 (https://www.esri.com/).
Water has always been considered an important factor that weakens the mechanical properties of rocks11,12,13,14,15,16, scholars have conducted extensive research on water–rock coupling14,17,18,19,20,21,22,23,24,25,26. At present, the research on the influence of water on red mudstone mainly focuses on different water content14,27, different humidity environment28,29, dry and wet cycle30,31, disintegration and expansion under the water action32,33,34. However, little attention has been paid to the deterioration behavior of red mudstone in the process of gradual humidification in the whole water content range, and its deterioration mechanism is still unclear. In addition, the study of the mechanical prediction model of the whole range of water content is the most lacking. In previous studies, the researchers usually assume that the rock material is composed of microstructure units35,36. Under load, the units with the lowest strength are destroyed first. Assuming that the micro element strength of mudstone under water follows a certain distribution, statistical methods can be used accordingly37,38. Following this, yield criterion can be selected based on the assumption of strain equivalence, and the stress–strain relationship can be obtained using Hooke’s theory39,40. However, due to the strong hydrophilicity of red mudstone, the damage of water to red mudstone cannot be ignored. Therefore, a new mechanical prediction model needs to be further studied.
Based on the degradation mechanism of red mudstone in the process of gradual humidification is not clear in the whole range of water content, and the lack of corresponding mechanical behavior prediction model, the self-made equipment in this paper overcomes the problem of sample disintegration in water and accurately prepares samples with different water contents. On this basis, the indoor mechanical test and microscopic test were carried out. The attenuation model of mechanical parameters in the whole range of water content is revealed, and the relationship between mineral composition, pore fissure and shear characteristics of red mudstone after hydration is analyzed. Finally, the unified damage prediction model of the whole process is proposed, which considers the coupling effect of hydration damage and load damage. The problem of prediction accuracy of mechanical prediction model of red mudstone under whole range of water content is solved. The above research results can provide a theoretical basis for the prevention and control of red mudstone landslide disasters.
Material and testing procedures
Engineering background and sample preparation
Samples were taken from the Gaojiawan red mudstone landslide in the Upper Yellow River in China, as shown in Fig. 1. The Gaojiawan landslide is located in Ledu District, Haidong City, Qinghai Province, China in the eastern section of the Huangshui River tectonic basin, between Laji Mountain and Daban Mountain. The landslide is a giant loess mudstone landslide, which is 1800 m long, 1300 m wide, and 110 m thick on average, with a plane area of about 2.4 km2 and 2a total volume of about 2.9 × 108m3. This landslide is composed of two parts; the upper part is loess, and the lower part is mudstone. The Gaojiawan loess-mudstone landslide led to the destruction of the Zhangjiazhuang tunnel that ran through the mudstone layer, the interruption of the Lanzhou-Xinjiang Railway, the serious deformation of houses, and an economic loss of about 2.25 billion yuan. The landslide also directly threatened the safety of 650 people in Gaojiawan Village.
The samples consisted of neogene red mudstone that exhibits argillaceous cementationin and has the additional characteristics of softening and disintegration in water and shrinkage and cracking after water loss. In order to maintain its natural water content and density, plastic film was used to wrap the samples on site. According to the International Society of Rock Mechanics (ISRM) specifications, the sample was then processed into a standard cylindrical sample with a diameter of 50 mm and a height of 100 mm. The parallelism of the sample was kept within ± 0.02 mm, and the maximum deviation between the end face and the axis was kept to less than 0.25 degrees. In order to avoid the influence of water on the mechanical properties of mudstone samples, no water was involved in the preparation process. In addition, before the start of the test, the appearance of the rock sample was initially checked to eliminate samples with obvious defects, and the RSM-SY5 (T) nonmetallic acoustic detector was used to test the ultrasonic rebound. In order to reduce the discreteness of the mechanical test results, only samples with acoustic wave velocity concentrated in 2.8–3.1 km/s were used for subsequent tests.
Experimental procedure
Whole range of water content testing
The processing flow of samples of red mudstone with different water content is shown in Fig. 2. The specific operation was as follows:
-
(1)
Each sample was numbered, and an electronic balance with a sensitivity of 0.01 g was used for weighing.
-
(2)
Each sample was placed in an electric blast drying box and dried at a constant temperature of 105° for 24 h, then placed in a drying container and cooled to room temperature before being weighed and recorded. The natural water content was then calculated according to Eq. (1).
$$\omega_{0} = \frac{{m_{0} - m_{d} }}{{m_{d} }} \times 100$$(1) -
(3)
w = 4.5% samples were prepared by gaseous water evaporation. The instrument used for this purpose was composed of a humidifier, a thermometer and a closed container. The natural water content samples were prepared by measuring their weight only. Finally, all samples were placed in a desiccator to ensure that the water content in the sample was uniform (Fig. 2a).
-
(4)
A self-made device that can record the weight of the sample in real time was used for the preparation of w = 9% samples. This instrument was composed of a lifting device, a water tank, a sample hanging basket, and a tension meter, and a computer was connected to the tension meter. The sample was placed in a \(\phi 50\;{\text{mm}}\; \cdot \;100\;{\text{mm}}\) saturator for protection, and the change in mass during the water absorption process was recorded in real time. After reaching the required weight for water content, the sample was placed in a sealed bag to ensure that the water content in the sample was uniform (Fig. 2b).
-
(5)
Preparation of saturated water content sample: First, each dried sample was wrapped with gauze and placed in a saturator. Then the sample was placed in a saturated cylinder, and the water surface was higher than the height of the sample. The sample was saturated in a vacuum environment of −0.1 MPa for 24 h. The vacuumized sample was placed in the original container and allowed to stand at atmospheric pressure for 4 h. Finally, the weight was measured, and the saturated water content was calculated.
Triaxial testing
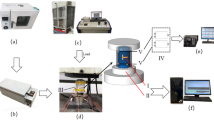
After the preparation of each sample, triaxial testing was carried out on four different water content samples, w = 0% (dry), w = 4.5%, w = 9%, and w = 14% (saturated water content). According to a sliding surface depth of 100–120 m, the confining pressure was set to 0 MPa, 1 MPa, 2 MPa, or 3 MPa, and an RTX-1000 rock triaxial testing machine was used to carry out the mechanical tests as shown in Fig. 3. The instrument was composed of a loading frame and a continuous axial loading double pump, a confining pressure continuous loading double pump, a high pressure chamber, axial and radial measuring devices, a digital servo controller, and acquisition software.
During the test, the sample had the upper and lower end force transmission columns sealed by heat shrinkable tube, and the end of the heat shrinkable tube was sealed again by waterproof tape to prevent the influence of oil leakage on the mechanical properties of the mudstone during the test. Then, two axial sensors and a radial sensor were installed. The confining pressure was subsequently applied to a predetermined value at a loading rate of 0.5 MPa/min and kept constant throughout the test. The axial force loading rate was set to 2 KN/min, and the end condition of the test was set to strain control.
XRD testing and CT testing
D/max-2500 X-ray powder diffraction was used for XRD testing. In order to ensure the accuracy of the test results, four samples with the same water content were selected, and 3-5g of mudstone powder was extracted from each sample for testing.
Computer tomography (CT) recognition technology is the most advanced nondestructive recognition technology currently available. It can obtain microscopic images without damaging a rock sample. In order to study the characteristics of the changes in porosity of the red mudstone under water, an industrial CT machine was used to test the mudstone samples with different water contents.
Results and analysis
Triaxial mechanical behavior analysis
Shear behavior in the whole range of water content
The deviatoric stress–strain curve and the results data are shown in Fig. 4 and Table 1. With confining pressure as a variable, the stress–strain relationship exhibits the following characteristics: (1) From a macroscopic perspective, each stress–strain curve shows strain softening. (2) Under lower confining pressure, the stress–strain curve is divided into four stages41,42: compaction, linear elastic, yield, and post-failure. However, the pore fracture compaction stage of the sample is not significant when confining pressure and water content increase. (3) The confining pressure is positively correlated with the shear strength. When the water content is constant, with the increase of confining pressure, the shear strength and residual strength of mudstone increase, the radial and axial peak strains increase, the brittleness of mudstone decreases, and the ductility increases43. The reason for this is that with an increase in confining pressure, the sample structure becomes denser, which weakens the lubrication, softening and argillization of water44.
Taking water content as a variable, the stress–strain relationship exhibits the following characteristics: (1) Under the same confining pressure, water content is negatively correlated with shear strength and residual strength, and this relationship is nonlinear. The deterioration of shear strength and elastic modulus conforms to the “logistic model” curve with the increase of water content in the whole range of water content. The change trend of mudstone strength with local water content conforms to the exponential form in the reference14,15, which is obviously different from the change trend of peak strength with water content in the whole range of water content in this paper. The research results of this paper further supplement the deterioration mode of water on red mudstone. (2) The curve after the peak becomes gentler with increasing water content. Taking confining pressure of 3MPa as an example, when the water content was w = 0%, 4.5%, 9% and 14%, the ratio of residual strength to peak strength was 0.51, 0.59, 0.94, and 0.99 respectively. The difference between residual strength and peak strength also decreased obviously, indicating that the plasticity of the mudstone increased with water content45.
Brittleness-ductility
‘Rock brittleness’ is the phenomenon where a rock breaks rapidly after loading to its peak without having experienced obvious deformation. When this happens the rock undergoes crack propagation and eventually forms a failure surface in a process known as brittle failure. ‘Rock ductility’ is the term for the phenomenon where a rock experiences relatively large deformation during loading but does not break immediately after peak loading, and the relatively soft rock is prone to ductile failure. In the case of red mudstone brittle-ductile characteristics are obviously transformed under wet conditions. Therefore, the index B that considers the post-peak and energy release ratio was selected to analyze the brittle-ductile characteristics of our mudstone samples46. The expression for B is as follows:
where \(\sigma_{{\text{r}}}\) and \(\sigma_{{\text{p}}}\) are residual strength and peak strength respectively, and \(\varepsilon_{{\text{r}}}\) and \(\varepsilon_{{\text{p}}}\) are residual strain and peak strain respectively. Figure 5 shows the variation in the characteristics of this mudstone brittleness index for different water content. The brittleness index decreases significantly with an increase in water content. There are evidently two stages in the downward trend: the rapid decline stage and the steady decline stage. The results show that the deformation and failure of the red mudstone under water action is a dynamic transformation process of brittleness and ductility.
Figure 6 shows images of the mudstone after deformation and failure under different water contents and confining pressures. The fracture surface is readily apparent, the failure mode transitions from brittle failure to ductile failure as water content increases47. During the uniaxial test of w = 0% and w = 4.5%, the larger lateral expansion of the sample was due to the lack of lateral deformation constraints and thus was mainly tensile fracture that caused the rock to become severely broken. Additionally, due to the effect of internal tensile stress, the rock also exhibits signs of brittle fracture failure. Moreover, due to the effect of confining pressure, the lateral deformation was suppressed in the triaxial test, and since the maximum shear stress was generated on the slope with an angle of 45° to the axial direction. Thus, the relative shear slip between the lattices in the material caused damage of a typical compression-shear failure nature. With an increase in confining pressure, the fracture surface was more and more flat48, and there was powder produced by strong friction on the shear fracture surface. The sample showed obvious ductility in the case of high confining pressure, and the fracture surface was more and more smooth with increasing water content.
Deterioration mode of elastic modulus
The deformation modulus of a specimen is a variable when the stress–strain curve is nonlinear, and the relationship between the elastic modulus and water content is shown in Fig. 7. The elastic modulus gradually decreased with the increase of water content17,18, and the decrease rate slowed down with the increase of confining pressure, indicating that confining pressure slowed down the deterioration of elastic modulus by water15.
The relationship between water content and elastic modulus can be fitted by the improved logistic function as follows:
The elastic modulus of mudstone is thus B + A / (C + 1) when the water content is 0. The parameter values obtained by genetic algorithm are shown in Fig. 7.
The strength parameters deterioration
The strength parameters of cohesion c and internal friction angle φ in this paper are obtained by drawing Mohr circle, as shown in Fig. 8. The relationship between strength parameters and water content takes an inverse ‘S’ shape (Fig. 9). Compared to the dry sample, the cohesion decreased by 19%, 92%, and 96%, respectively, a significant decreasing trend. Similarly, the internal friction angle decreased by 4%, 46%, and 48%, respectively, but the decrease rate was significantly lower than that of cohesion. This phenomenon shows that the influence of water on the strength of the red mudstone is mainly reflected in its cohesion, especially the red mudstone that contains more clay minerals. Most of the cemented substances were destroyed and reach the equilibrium state with an increase in water content, resulting in the cohesion not becoming fully reduced to 014.
According to the relationship between the water content and the Mohr–Coulomb strength envelope in Fig. 10, it can be found that the strength envelope shrinks with the increase in water content. The strength envelopes of the four water contents are divided into two groups, and the trend in the Mohr–Coulomb strength envelope changes between them. Therefore, it is necessary to determine the specific relationship between rock strength and the whole range of water content prior to landslide stability analysis or engineering design.
Weakening effects by water
The effects of water on mineral composition
The mineral composition and content of red mudstone with different water contents were measured and analyzed by mineral x diffraction testing (Fig. 11). It can be seen that the main mineral components of red mudstone samples included quartz, plagioclase, calcite, illite, chlorite, and analcime. Under the action of water, no new mineral composition was formed in the red mudstone, but the total amount of water-sensitive clay minerals decreased significantly with an increase in water content (32.7% > 30.1% > 28.7% > 27.3%) (Fig. 12). The decrease of clay mineral content may be due to its expansion in water, which leads to the formation of cracks in red mudstone, thus the loss of clay minerals in water. The expansion characteristics of red mudstone are mainly due to illite and chlorite. Illite is a mineral that contains hydrated aluminosilicate, and there are adsorption sites such as hydrogen bonds in its structure that can absorb surrounding water and interact with water molecules. This causes the lattice structure to change, resulting in volume expansion of minerals. Chlorite reacts with water similarly to illite. Chlorite is a layered silicate mineral that contains hydroxide ions (OH-), and its strong reaction with water is mainly due to the interaction between hydroxide ions and water molecules in the layered structure of chlorite. In addition, red mudstone is a kind of sedimentary rock, and its red color is dues to the presence of hematite (Fe2O3) and other iron oxides. Water reacts with iron oxides to form water-soluble iron ions. Thus, under water action, the structure of red mudstone becomes weakened due to the water reaction of water-sensitive clay minerals and the dissolution of iron oxides49.
The effects of water on microstructure
The CT scanning grayscale images of samples with different water contents are shown in Fig. 13, in order to improve the accuracy of CT calculation, the image is cropped to remove the contrast difference between the top and bottom caused by the ray source. In addition, the noise reduction method is used to process the CT image, and the watershed algorithm is used for binarization analysis. Each pixel of the grayscale image has a grayscale value, which is usually represented by a number. Different numbers represent different colors, where 0 is black, 255 is white, and the numbers in between represent different gray levels. These gray values reflect the relative absorption level of X-rays when passing through rock samples: higher gray values indicate higher X-ray absorption, which is presented as a brighter area on the image, and lower gray value indicates lower absorption, which is presented as a darker area. Different structures and minerals in the rock have different degrees of X-rays absorption50. Figure 13 shows that the grayscale images with different water contents can be divided into two categories. The mudstone samples with w = 0% and w = 4.5% have good integrity, no cracks, and compact structure. For w = 9%, w = 14%, however, the pores of the sample increased and cracks appeared inside. The reason may be that the water-sensitive clay minerals expand during the infiltration of water, resulting in the formation of cracks.
In order to analyze the influence of water on the porosity of mudstone samples further, firstly, the contrast between skeleton and pore was increased by image preprocessing. By performing pixel analysis on these images, the total volume of the pore regions could be calculated and then divided by the total volume of the entire sample to obtain the porosity, as shown in Fig. 14. It can clearly see that the total porosity and the connected porosity increased with water content51,52. The main reason is that water causes clay minerals to expand, migrate and the dissolution of iron oxides, resulting in changes in pores. In addition, compared to the sample with w = 0%, the growth rate of connected porosity rose, but the growth rate of total porosity declined. Water thus increases the connectivity of mudstone pores, and the connected pores are more active in the presence of water. In addition, according to Fig. 14, it can be found that when the water content is from 4.5% to 9% in the whole range of water content, the pore growth rate is the largest, the microstructure deterioration at this stage is the most significant, and the stability of the red mudstone is the most affected.
Strength deterioration analysis
The deterioration effects of water on rock can be categorized into mechanical effects and physical and chemical effects53,54. The conventional triaxial test in this paper was performed under undrained conditions. During shearing at constant water content, however, volume changes, which causes a change in (negative) pore-water pressure and thus shear strength.
The physical and chemical effects of water on rocks include lubrication, softening and argillization, particle exchange, dissolution, hydrolysis, and redox50. Water–rock coupling is that the dissolved substances in water affect the microstructure of mudstone through dissolution and precipitation reactions. For red mudstone specifically, water reacts with illite, chlorite, and iron oxides, which causes hygroscopic expansion of mineral particles and dissolution of iron oxides17,55. The resultant increase in pore connectivity, and the deformation space of mudstone increases so that the mudstone has greater plastic deformation during the loading process.
In addition, water as a medium can fill the pores and particle gaps of mudstone, resulting in the reduction of molecular tension on the surface of the shrinkage film on the water–air interface. Moreover, water has a certain lubricating effect on the particles of mudstone, changing the cementation state between the particles and weakening the internal cementation of the mudstone structure, which is a major reason for the decrease in cohesion. However, most of the cements are destroyed when the mudstone is exposed to a high enough water content. Further increase in water content after this point will not significantly change the relationship between particles, so the cohesion changes little under high water content, not decrease to zero56. Based on the above analysis of macro and micro test results, the deformation behavior and strength deterioration characteristics of mudstone are closely related to the continuous adjustment of its microstructure under water action.
Mechanical behavior prediction
The prediction model
Damage theory was proposed by Kachanov in 1958. Here, the stress–strain relationship after material damage is expressed by the concepts of continuity factor and effective stress. The study of damage mechanics follows certain steps, in which the selection of damage variables in the first step is extremely important for the accuracy of the results. Generally speaking, area, volume, elastic modulus, wave velocity and void ratio are selected as damage variables. According to the existing research, the porosity is used to construct the initial damage model in this paper57. The expression damage is as follows:
where \(P\) is the initial porosity, and \(p^{\prime}\) is the porosity after damage under the water action.
The rock is abstracted into two parts: damaged and undamaged materials and assume that the stress on the rock is shared by these two parts58. According to Lemaitre’s59 strain equivalence hypothesis, we have the rock water damage model given by:
where \(\sigma\) is the nominal stress of rock, \(\sigma^{ * }\) is the effective stress of rock, \(\sigma_{r}\) is the residual strength, and \(D\) is the coupling damage variable of rock, as shown in Eq. (6). When \(D = 0\), the material is in a undestroyed state or an initial state. When \(D = 1\), the material is in a completely damaged state.
where \(D_{{1}}\) is the damage to the rock caused by water (Eq. 4), and \(D_{{2}}\) is the damage to the rock caused by load.
According to the deformation compatibility of damaged and undamaged materials in rock, after combining Eq. (5) and the generalized Hooke’s law, the rock damage model can be obtained:
where \(\nu\) is Poisson’s ratio, and \(E\) is the rock elastic modulus. Combined with Eq. (3), the damage model that also considers water content is:
In the above formula, \(D\) is unknown. In this paper, an abstract damage variable is used to describe the damage to the rock caused by load. First, we assume that the rock under load is composed of numerous infinitesimal elements. According to the damage mechanics of such continuous media, the damage to a rock under load is defined as the ratio of the failure number n of micro-elements to the total number N of micro-elements without damage, and its value is on the interval [0, 1].
Considering that rock material undergoes a continuous damage process during loading, it is assumed that Hooke’s law is obeyed before the failure of rock micro-element60. Under the action of increasing load, the micro-element damage of each force is therefore random with some known distribution for convenience. In practice, the Weibull distribution reflects the response characteristics of rock mechanics well61, its internal parameters are few and easy to calculate, and the physical meaning is clear. Thus, it is assumed that the known distribution of micro-element damage is Weibull with probability density function:
where \(F_{0}\) and \(m\) represent the proportional parameter and the shape parameter, respectively. When loaded to a certain level F, the number of broken units is given by Eq. (11).
and the statistical damage variable can be further obtained as follows:
where F is the rock micro-unit strength.
There are many widely-used geotechnical yield criteria, including the Mohr–Coulomb criterion, Von-Mises criterion, Tresca criterion, Drucker-Prager criterion, and Zienkiewice-Pande criterion. Many scholars have carried out extensive research on statistical damage using the Mohr–Coulomb criterion62 and Drucker-Prager criterion63 have not given a unified statistical damage model. In this model, the unified yield condition is obtained by further extending the general formula of Zienkiewice’s yield function. By changing the coefficient value, a variety of yield conditions can be obtained, including the Tresca condition, Mises condition, Mohr–Coulomb condition (nonassociation rule), and Drucker-Prager condition. The expression is as follows:
Here \(p = \sigma_{1}^{ * } + \sigma_{2}^{ * } + \sigma_{3}^{ * } ,J_{2} = \frac{1}{6}\left[ {(\sigma_{1}^{ * } - \sigma_{2}^{ * } )^{2} + (\sigma_{1}^{ * } - \sigma_{3}^{ * } )^{2} + (\sigma_{2}^{ * } - \sigma_{3}^{ * } )^{2} } \right]\).
The following parameters values were selected for the yield condition:
where \(c\) is cohesion, and \(\varphi\) is internal friction angle. From the above formula, the statistical damage of the soft rock can be obtained as follows:
Since the stress measured in the triaxial test is the nominal stress, according to the generalized Hooke’s law, from using Eq. (5) we have:
and using the above formula we can obtain \(p\) and \(J_{2}\) as follows:
Here \(\sigma_{r}\) is the axial residual stress of the damaged part of the rock, which obeys the Mohr–Coulomb criterion. Combined with Eq. (16), the expression for \(\sigma_{r}\) is:
in addition, when the geotechnical material reaches its residual strength, the axial force does not change significantly with increases in deformation39. Usually, the residual strength is related to the confining pressure. Based on the assumption of Cao et al.64, the residual strength in our model is thus given by:
When \(\sigma_{2} = \sigma_{3}\), and combining the above with Eqs. (13), (14) and (17), the rock micro-element strength F under unified yield conditions can be obtained.
According to Eq. (7) and Eq. (15), the constitutive equation of coupled damage based on unified yield conditions can be obtained as follows:
Model parameters
The mechanical behavior prediction model of rock material has six parameters: elastic modulus \(E\), Poisson’s ratio \(\nu\), cohesion \(c\), and internal friction angle \(\varphi\), which can be obtained by conventional rock test, and \(m\) and \(F_{0}\) , which are obtained according to the extreme points of the stress–strain curve. The following relationships exists for the extreme points:
where \(\sigma_{p}\) is the peak stress, and \(\varepsilon_{p}\) is the strain related to the peak stress.
The partial derivative of Eq. (21) is as follows:
Combining the above two equations,\(m\) and \(F_{0}\) are thus:
where \(F_{p}\) can be obtained by substituting \(\sigma_{p}\) and \(\varepsilon_{p}\) into Eq. (20), that is, the partial derivative of \(F_{p}\) with respect to \(\varepsilon_{p}\) is as follows:
Substituting \(\sigma_{p}\) and \(\varepsilon_{p}\) into Eq. (21) and likewise in Eq. (22), the expression for \(D\) is given by:
Prediction model validation
In order to verify the rationality of the statistical mechanical behavior prediction model of rock damage softening proposed in this paper, the relationship between deviatoric stress and deviatoric strain in section "Triaxial mechanical behavior analysis" is transformed according to the following formula65.
where \(\sigma_{{\text{l}}}^{\prime }\) and \(\varepsilon_{{\text{l}}}^{\prime }\) are deviatoric stress and deviatoric strain, respectively. The parameters required for the mechanical behavior prediction model according to our test results, are shown in Table 2.
Substituting the above parameters into the mechanical behavior prediction model, the theoretical curve of the model can be obtained, as shown in Fig. 15.
Figure 15 shows that compared to the mechanical behavior prediction model without considering initial damage and residual strength (WCIDR) (red scatter in Fig. 15), the improved model (green scatter in Fig. 15) in this paper can better predict the mechanical behavior of red mudstone under the action of water, especially peak strength. The damage model can be transformed into different yield conditions by parameter changes, which has great flexibility and is convenient for engineering applications. However, the model in this paper only considers elasticity before the peak, which cannot describe the viscous and plastic deformation stages well. Therefore, the viscoelastic-plastic model considering coupling damage needs to be further studied in the subsequent research.
Parameter sensitivity analysis
As mentioned above, parameters \(m\) and \(F_{0}\) are obtained by mathematical method, and the influence of parameters \(m\) and \(F_{0}\) on peak strength is further studied by control variable method. As shown in Fig. 16 and Fig. 17, the stress–strain curves under different \(m\) and \(F_{0}\) are shown. The increase of \(m\) and \(F_{0}\) improves the peak strength, which is consistent with the results of reference38. In addition, through Pearson correlation analysis, it is found that the correlation between parameter \(F_{0}\) and peak strength is significant, and the control of parameter \(F_{0}\) on peak strength is greater than that of \(m\).
Conclusion
In this study, a combination of laboratory tests and theoretical methods was used to carry out mechanical and microscopic tests of red mudstone under the whole range of water content, and a mechanical behavior prediction model for this process under the coupling of initial damage and load damage was constructed. Our main conclusions are as follows:
-
(1)
In the whole range of water content, the deterioration of red mudstone has obvious stage attenuation mode. The deterioration of shear strength and elastic modulus conforms to the “logistic model” curve with the increase of water content.
-
(2)
The influence of water on the strength of the mudstone is reflected in its cohesion. The rate of decrease of internal friction angle was lower than that of cohesion. When approaching saturated water content, most of the cements in the mudstone are destroyed, resulting in a steady downward trend in strength parameters.
-
(3)
The expansion and migration of clay minerals increase the pore connectivity and lead to the deterioration of mudstone structure. In particular, the appearance of cracks leads to the accelerated deterioration of red mudstone. The mechanical behavior of the mudstone is thus essentially the result of continuous adjustment and changes in microstructure under loading and humidification conditions.
-
(4)
Predicted values from the mechanical behavior prediction model of the entire process under the coupling of initial damage and load damage agreed with the experimental results, the problem of the influence of microstructure damage on the accuracy of prediction results is solved. The model provides new ideas for evaluating the stability of red mudstone landslides under water action.
Data availability
Data availability All data generated or analysed during this study are included in this published article.
References
Peng, H., Ren, F. & Pan, Z. X. A review of Danxia landforms in China. Z. Geomorphol. 59, 19–33. https://doi.org/10.1127/zfg_suppl/2015/S-00173 (2015).
Handrij, H., Václav, C. & Andrew, J. Sandstone landscapes. Nakladatelství Academic Praha, Czech Republic 2007, 12–125 (2007).
Allan, P. The weathering rates of some sand stone cliffs central weald. Earth Surf. Process Landf 16, 83–91 (1991).
Pan, Z. X. & Peng, H. Comparative study on the global distribution and geomorphic development of red beds. Sci. Geogr. Sin. 35, 1575–1584 (2015).
Zhang, Z. P. et al. Effect of rainfall pattern and crack on the stability of a red bed slope: a case study in Yunnan Province. Adv. Civ. Eng. 2021, 211. https://doi.org/10.1155/2021/6658211 (2021).
Zhou, C. Y. et al. Classification of red-bed rock mass structures and slope failure modes in South China. Geosciences 9, 273. https://doi.org/10.3390/geosciences9060273 (2019).
Huang, K. et al. Relationship between capillary water absorption mechanism and pore structure and microfracture of red-layer mudstone in central Sichuan. B Eng. Geol. Environ. 82, 100. https://doi.org/10.1007/s10064-023-03115-5 (2023).
Yin, Y. P. & Hu, R. L. Engineering geological characteristics of purplish-red mudstone of middle tertiary formation at the three gorges reservoir. J. Eng. Geol. 12, 124–135 (2004).
Xu, Q. & Tang, R. Study on red beds and its geological hazards. Chin. J. Rock Mech. Eng. 42, 28–50. https://doi.org/10.13722/j.cnki.jrme.2022.0012 (2023).
Cheng, K. L., Bai, H. L. & Fang, H. Y. Study on deformation and failure characteristics and mechanism of Jungong landslide in Qinghai Province. Gansu Water Resour. Hydrop. Technol. 57, 45–51. https://doi.org/10.19645/j.issn2095-0144.2021.01.011 (2021).
Song, C. et al. Progressive failure characteristics and water-induced deterioration mechanism of fissured sandstone under water-rock interaction. Theor. Appl. Fract. Mec. 128, 104151. https://doi.org/10.1016/j.tafmec.2023.104151 (2023).
Zhao, K. et al. Effect of water content on the failure pattern and acoustic emission characteristics of red sandstone. Int. J. Rock Mech. Min. 142, 104709. https://doi.org/10.1016/j.ijrmms.2021.104709 (2021).
Zhao, Y. L. et al. Mechanical properties and energy evolution and the applicability of strength criteria of sandstone under hydro-mechanical coupling. J. China Coal Soc. 48, 3323–3335. https://doi.org/10.13225/j.cnki.jccs.2022.1387 (2023).
Huang, K. et al. Experimental and numerical simulation study on the influence of gaseous water on the mechanical properties of red-layer mudstone in central Sichuan. Rock Mech. Rock Eng. 56, 3159–3178 (2023).
Liu, C. D. et al. Experimental study on the effect of water on mechanical properties of swelling mudstone. Eng. Geol. 295, 106448. https://doi.org/10.1016/j.enggeo.2021.106448 (2021).
Iyare, U. et al. Water-weakening effects on the failure behavior of mudstones. Rock Mech. Rock Eng. 56, 1–15 (2023).
Erguler, Z. & Ulusay, R. Water-induced variations in mechanical properties of clay-bearing rocks. Int. J. Rock Mech. Min. 46, 355–370 (2009).
Chen, F., Sun, X. M. & Lu, H. Influence of water content on the mechanical characteristics of mudstone with high smectite content. Geofluids 2022, 9855213. https://doi.org/10.1155/2022/9855213 (2022).
Li, J. D. et al. Effect of water on the rock strength and creep behavior of green mudstone. Geomech Geophys Geo 9, 101. https://doi.org/10.1007/s40948-023-00638-9 (2023).
Douma, L. A. N. R., Dautriat, J., Sarout, J., Dewhurst, D. N. & Barnhoorn, A. Impact of water saturation on the elastic anisotropy of the Whitby Mudstone, United Kingdom. Geophysics 85, Mr57–Mr72. https://doi.org/10.1190/Geo2019-0004.1 (2020).
DeReuil, A. A., Birgenheier, L. P. & McLennan, J. Effects of anisotropy and saturation on geomechanical behavior of mudstone. J. Geophys. Res.-Sol. Ea 124, 8101–8126. https://doi.org/10.1029/2018jb017034 (2019).
Wu, Q. et al. Experimental study of the influence of wetting and drying cycles on the strength of intact rock samples from a red stratum in the three gorges reservoir area. Eng. Geol. 314, 107013. https://doi.org/10.1016/j.enggeo.2023.107013 (2023).
Li, H. Z., Liao, H. J., Kong, L. W. & Leng, X. L. Experimental study on stress-strain relationship of expansive mud-stone. Yantu Lixue (Rock Soil Mech.) 28, 107–110 (2007).
Sun, X.-M. et al. Microscopic mechanisms and acoustic emission characteristics of sandy mudstone under different water saturations. KSCE J. Civ. Eng. 28, 1–13 (2023).
Liu, Z., Liao, J., Xia, C., Zhou, C. Y. & Zhang, L. H. Micro-meso-macroscale correlation mechanism of red-bed soft rocks failure within static water based on energy analysis. Acta Geotech https://doi.org/10.1007/s11440-023-01893-6 (2023).
Yi, Q. Y., Pu, H., Preusse, A., Bian, Z. F. & Wu, J. Y. Effect of dry-wet cycles on dynamic mechanic and microstructure of cemented broken mudstone. Constr. Build Mater. 357, 129347. https://doi.org/10.1016/j.conbuildmat.2022.129347 (2022).
Chen, K. et al. Effect of water content on stiffness degradation and microstructure of red mudstone fill material. Rock Soil Mech. 45, 1976–1986. https://doi.org/10.16285/j.rsm.2023.1231 (2024).
Yu, F. et al. Experimental study on gaseous moisture absorption and swelling of red-bed mudstone in central Sichuan, China under different relative humidity environments. Sustain.-Basel 15, 12063. https://doi.org/10.3390/su151512063 (2023).
Yu, F. et al. Experimental study of the dehydration-shrinkage characteristics of red-bedded mudstone in central Sichuan under different humidity gradients. B Eng. Geol. Environ. 83, 118. https://doi.org/10.1007/s10064-024-03614-z (2024).
Yu, F. et al. Multi-scale deformation characteristics and mechanism of red-bed mudstone in dry-wet environment. Front. Earth. Sc-Switz 10, 974707. https://doi.org/10.3389/feart.2022.974707 (2022).
Zhou, M. L. et al. Impact of water-rock interaction on the pore structures of red-bed soft rock. Sci. Rep-Uk 11, 7398. https://doi.org/10.1038/s41598-021-86815-w (2021).
Luo, T. Y. et al. Experimental study on the disintegration behavior and mechanism of red-bed mudstone in guangxi, China. Front. Mater. 11, 1357116. https://doi.org/10.3389/fmats.2024.1357116 (2024).
Guan, H. et al. Microstructure and water-swelling mechanism of red-bed mudstone in the Xining region, Northeastern Tibetan Plateau. J. Rock Mech. Geotechn. Eng. 16, 2537–2551. https://doi.org/10.1016/j.jrmge.2023.11.0311674-7755 (2024).
Huang, K. et al. Swelling behaviors of heterogeneous red-bed mudstone subjected to different vertical stresses. J. Rock Mech. Geotechn. Eng. 16, 1847–1863. https://doi.org/10.1016/j.jrmge.2023.08.004 (2024).
Li, H. Z., Liao, H. J. & Sheng, Q. Study on statistical damage constitutive model of softRock based on unified strength theory. Chin. J. Rock Mech. Eng. 25, 1331–1336 (2006).
Zhang, C. et al. Statistical damage constitutive model of rock brittle-ductile transition based on strength theory. Chin. J. Rock Mech. Eng. 42, 307–316. https://doi.org/10.13722/j.cnki.jrme.2022.0278 (2023).
Krajcinovic, D. & Silva, M. A. G. Statistical aspects of the continuous damage theory. Int. J. Solids Struct. 18, 551–562 (1982).
Shen, P., Tang, H., Ning, Y. & Xia, D. A damage mechanics based on the constitutive model for strain-softening rocks. Eng. Fract. Mech. 216, 106521 (2019).
Ding, X. L., Fan, X. T., Huang, S. L., Yu, P. Y. & Zhang, J. X. Statistical damage model of mudstone considering hydration and swelling and its verification. Chin. J. Rock Mech. Eng. 42, 2601–2612. https://doi.org/10.13722/j.cnki.jrme.2023.0155 (2023).
Geng, D. D., Qi, X. Y., Ke, T. & Xu, M. Z. Study on damage test and constitutive model of layered shale under water degradation. China Civ. Eng. J. 08, 1–11. https://doi.org/10.15951/j.tmgcxb.23060524 (2023).
Eberhardt, E., Stead, D. & Stimpson, B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. 36, 361–380 (1999).
Cai, M. et al. Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations. Int. J. Rock Mech. Min 41, 833–847 (2004).
Liu, Y. et al. Deformation behavior and damage-induced permeability evolution of sandy mudstone under triaxial stress. Nat Hazards 113, 1729–1749. https://doi.org/10.1007/s11069-022-05366-z (2022).
Liu, Y. D. & Wang, D. P. Research on the failure mechanisms and strength characteristics of deeply buried mudstone under the interaction of water and stress. Processes 11, 1231. https://doi.org/10.3390/pr11041231 (2023).
Liu, H. L., Zhang, D. S., Zhao, H. C., Chi, M. B. & Yu, W. Behavior of weakly cemented rock with different moisture contents under various tri-axial loading states. Energies 12, 1563. https://doi.org/10.3390/en12081563 (2019).
Xia, Y. J. et al. A new method to evaluate rock mass brittleness based on stress–strain curves of class I. Rock Mech. Rock Eng. 50, 1123–1139 (2017).
Jiang, Y. J. et al. Mechanical properties and acoustic emission characteristics of soft rock with different water contents under dynamic disturbance. Int. J. Coal. Sci. Techn. 11, 36. https://doi.org/10.1007/s40789-024-00682-0 (2024).
Zhang, C. X. et al. Effect of confining pressure on shear fracture behavior and surface morphology of granite by the short core in compression test. Theor. Appl. Fract. Mech. 121, 103506. https://doi.org/10.1016/j.tafmec.2022.103506 (2022).
Zhou, C. Y., Tang, X. S., Deng, Y. M., Zhang, L. M. & Wang, J. H. Research on softening micro-mechanism of special soft rocks. Chin. J. Rock Mech. Eng. 24(3), 394–400 (2005).
Lu, Y. L., Wang, L. G., Sun, X. K. & Wang, J. Experimental study of the influence of water and temperature on the mechanical behavior of mudstone and sandstone. B Eng. Geol. Environ. 76, 645–660. https://doi.org/10.1007/s10064-016-0851-0 (2017).
Huang, H. W. & Che, P. Research on micro-mechanism of softening and argillitization of mudstone. J. Tongji Univ. Natl. Sci. 35, 866–870 (2007).
Zhou, C. Y., Liang, N. & Liu, Z. Multifractal characteristics of pore structure of red beds soft rock at different saturations. J. Eng. Geol. 28, 1–9 (2020).
Baud, P., Zhu, W. & Wong, T. F. Failure mode and weakening effect of water on sandstone. J. Geophys. Res. Solid Earth 105, 16371–16389 (2000).
Wang, L. L. et al. The mechanisms of deformation and damage of mudstones: A micro-scale study combining ESEM and DIC. Rock Mech. Rock Eng. 48, 1913–1926. https://doi.org/10.1007/s00603-014-0670-1 (2015).
Morrow, C., Moore, D. E. & Lockner, D. The effect of mineral bond strength and adsorbed water on fault gouge frictional strength. Geophys. Res. Lett. 27, 815–818 (2000).
Zhang, S., Xu, Q. & Hu, Z. M. Effects of rainwater softening on red mudstone of deep-seated landslide. Southwest China Eng. Geol. 204, 1–13. https://doi.org/10.1016/j.enggeo.2016.01.013 (2016).
Jia, H. L., Liu, Q. B., Xiang, W., Zhang, W. L. & Lang, L. Z. Damage evolution model of saturated sandstone under freeze-thaw cycles. Chin. J. Rock Mech. Eng. 32(2), 3049–3055 (2013).
Cao, W. G., Zhang, S. & Zhao, M. H. Study on a statistical damage constitutive model with conversion between softening and hardening properties of rock. Eng. Mech. 23, 110–115 (2006).
Lemaitre, J. How to use damage mechanics. Nuclear Eng. Des. 80, 233–245 (1984).
Cao, W. G. & Zhang, S. Study on the statistical analysis of rock damage based on Mohr-coulomb criterion. J. Hunan Univ. (Natl. Sci.) 32, 43–47 (2005).
Zeng, C. L. et al. Research on soft rock damage softening model and roadway deformation and failure characteristics. Materials 15, 5886. https://doi.org/10.3390/ma15175886 (2022).
Chen, S., Qiao, C. S., Ye, Q. & Deng, B. Composite damage constitutive model of rock mass with intermittent joints based on Mohr-Coulomb criterion. Rock Soil Mech. 39, 3612–3622. https://doi.org/10.16285/j.rsm.2017.0184 (2018).
Cao, W. G., Yang, S. & Zhang, C. A statistical damage constitutive model of rocks considering the variation of the elastic modulus. Hydrogeol. Eng. Geol. 44, 42–48. https://doi.org/10.16030/j.cnki.issn.1000-3665.2017.03.07 (2017).
Cao, W. G., Zhao, H., Li, X. & Zhang, L. A statistical damage simulation method for rock full deformation process with consideration of the deformation characteristics of residual strength phase. China Civ. Eng. J. 45, 139–145. https://doi.org/10.15951/j.tmgcxb.2012.06.001 (2012).
Cao, W. G., Lin, X. T., Zhang, C. & Yang, S. A statistical damage simulation method of dynamic deformation process for rocks based on nonlinear dynamic strength criterion Chin. J. Rock Mech. Eng. 36, 794–802. https://doi.org/10.13722/j.cnki.jrme.2016.0755 (2017).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No.42041006, No.42102317) and the National Key R&D Program of China (No. 2023YFC3008404).
Author information
Authors and Affiliations
Contributions
Qingyu Xie: Methodology, Validation, Writing–original draft. Qiangbing Huang: Conceptualization, Methodology, Resources, Supervision, Funding acquisition, Writing—review & editing. Xiaosen Kang: Validation. Shaoyan Wu: Validation. Hengxing Lan: Supervision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
The paper follows scientific ethics.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xie, Q., Huang, Q., Kang, X. et al. Study on the effect of water on the shear behavior and microstructure of red mudstone. Sci Rep 14, 29858 (2024). https://doi.org/10.1038/s41598-024-78710-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-78710-x