Introduction

Traditional longwall coal mining operations typically require two mining roadways. In China, the primary method for protecting the main roadway involves setting sectional coal pillars. There are three proposed methods for coal pillar retention: wide coal pillars, narrow coal pillars, and no coal pillars. Using wide coal pillars results in significant coal resource waste and can potentially induce rock bursts. On the other hand, adopting a non-pillar method can lead to safety risks such as gangue intrusion, air leakage, water seepage, and elevated gas concentrations1,2,3. Narrow coal pillars provide a balanced solution, overcoming the drawbacks of both wide and non-pillar methods while ensuring roadway protection4.

The investigation of optimal coal pillar dimensions can not only diminish roadway deformation and maintenance requirements but also enhance coal recovery rates, decrease coal resource losses, and yield substantial economic benefits for mining operations. Historically, both Chinese and international academics have predominantly concentrated on fundamental theoretical research related to coal pillar preservation. This theoretical groundwork is primarily rooted in specific theories, dependent on theoretical analysis, and provides corresponding formulas for determining coal pillar width, thereby constructing a theoretical framework for ascertaining the appropriate coal pillar dimensions. In terms of fundamental theoretical research, European and American experts and scholars have contributed extensively to theories concerning the rational retention of coal pillars due to early studies on mine pressure in Europe and the United States. Chinese scholars have subsequently refined these theories, incorporating adjustments based on the theoretical foundations established by foreign scholars and the practical production circumstances in China5.

The effective area theory posits that each coal pillar bears the weight of the overlying strata and evenly shares the upper section of the goaf with neighboring coal pillars. This approach is employed to assess coal pillar damage and ascertain the appropriate width of the coal pillar6,7. While this theory is straightforward and commonly applied in coal pillar design, especially in the primary development roadways8,9,10, its applicability is restricted to scenarios characterized by extensive excavation areas, consistent coal pillar spacing, and uniform distribution of coal pillars.

As per the pressure arch theory, the creation of a pressure arch above the roadway and goaf results in only a fraction of the overlying strata load impacting the immediate roof, with the rest being transferred to the coal pillars on both sides11,12,13. The internal width of the pressure arch is primarily influenced by the thickness and depth of mining of the overlying strata, while the external width is predominantly affected by the internal composite structure of the overlying strata14,15. When the mining width exceeds the internal width of the pressure arch, the load distribution becomes more intricate, leading to instability in the pressure arch. Even if the mining width is smaller than the internal width of the pressure arch, its stability varies over time due to the complex and time-dependent nature of load distribution. Consequently, the theory provides a method for estimating coal pillar dimensions16,17,18.

Wilson’s theory is grounded in the three-dimensional strength properties of coal pillars. It scrutinizes the stability of these pillars and prescribes their optimal width based on these three-dimensional strength properties19,20,21. This theory effectively addresses the deficiencies of alternative methodologies, rendering it more practical and dependable. Consequently, it has garnered widespread adoption. Nonetheless, the theory is not devoid of limitations. For instance, its reliance on empirical algorithms and the value of tgβ constrain its applicability beyond the confines of the United Kingdom22,23,24.

The theory of uneven core strength correlates the strength of the coal pillar’s core area with the actual stress, thereby determining the strength distribution within the core area. This theory emphasizes the significance of the coal pillar’s dimensions and shape, asserting that the strength of its core area varies spatially. Even when the average stress within the coal pillar’s core area surpasses the threshold, complete collapse may not occur due to friction between fractured blocks. However, it may compromise the connectivity between the core area and the surrounding roof and floor, potentially leading to coal pillar bursts or movement of adjacent strata25. While the theory of uneven core strength boasts rigorous theoretical underpinnings and precise calculation methods, it operates under idealized assumptions, neglecting the heterogeneity of geological and mining conditions. The complexity and inaccessibility of the theoretical calculation formula, along with the difficulty in acquiring parameters, constrain its widespread application.

The limit equilibrium theory utilizes a three-dimensional model analysis method within elastic mechanics26,27, alongside the stress differential equilibrium equation, to ascertain both the stress along the coal seam interface and the width of the stress limit equilibrium zone within the coal body. Subsequently, the minimum width of the coal pillar is determined. The primary criterion for coal pillar stability necessitates that, following plastic deformation on both sides of the coal pillar, it remains within an elastic stress state at the pillar’s center, thereby maintaining a specific width of the elastic core area. Typically, adopting a width equal to twice the height of the roadway is deemed more reasonable28,29.

Wilson’s theory and the theory of unequal strength of the nuclear zone both operate on the premise that the coal pillar can be partitioned into two distinct regions: the yielding zone and the nuclear zone. While the nuclear zone is bounded by the yielding zone and possesses its own logical components and application conditions, they share a common flaw—failure to consider the influence of cohesion and internal friction angle at the contact interface between the coal pillar and the roof and floor. Consequently, Wu Lixin and others introduced the “platform load method” principle, building upon the aforementioned framework and deriving the coal pillar width calculation formula accordingly30.

Niu et al. studied the instability of coal pillar in fully mechanized caving face, and studied the ultimate failure energy of elastic zone of coal pillar, the stress distribution of side abutment of coal pillar and the ultimate energy distribution of elastic zone of coal pillar31,32,33,34. The stress of side abutment of coal pillar presents convex distribution, and the elastic energy of coal pillar presents bimodal distribution. The criterion of instability of elastic zone of coal pillar and two kinds of instability forms of coal pillar, local impact and large-scale chain impact, are put forward35,36.

The preceding research primarily focuses on stress analysis, with limited attention to the investigation of coal pillar instability resulting from the accumulation of energy due to bending deformation of the main roof. This study centers on the coal pillar within the 3−1 coal seam of Nanliang Coal Mine. Theoretical analysis, simulation, and field measurements are employed to examine the bending deformation energy of the main roof and the factors influencing coal pillar instability from an energy perspective. By establishing a mechanical model of the roadway’s main roof near the goaf side, we derive a calculation formula for the bending elastic energy of the main roof and analyze the influencing factors and distribution patterns of this energy. Utilizing the stress distribution characteristics of the coal pillar’s side abutment, we calculate the distribution expression of the pre-yield elastic energy within the coal pillar’s elastic zone along its width. Additionally, we propose a criterion for coal body instability energy within the elastic zone of the coal pillar. The aim is to address coal pillar instability issues and offer theoretical insights to facilitate safe and efficient mining practices.

Analysis of bending elastic energy of main roof and elastic energy of coal pillar near goaf side

Calculation of bending elastic energy and analysis of influencing factors of main roof near goaf side

Mechanical model design of main roof

The structure of the overlying strata near the goaf-side roadway is depicted in Fig. 1. The main roof in proximity to the goaf undergoes bending and deformation due to the load from the overlying strata. However, owing to the high strength and considerable thickness of the main roof, the supporting force exerted by the caving gangue in the goaf is minimal. Consequently, the load from the overlying strata is transmitted onto the coal pillar through the exposed main roof, leading to stress concentration, yielding deformation, crushing, and plastic zones within the coal pillar, as well as deformation in the adjacent roadway.

Figure 1
figure 1

Mechanical model of main roof of roadway near goaf side.

Full size image

In accordance with the structural features of the overlying strata near the goaf-side roadway, the main roof of the roadway is treated as a continuous structure. It sustains the entire load and experiences elastic deformation, with no consideration for discontinuous plastic failure. Thus, it is simplified as a cantilever beam structure with fixed hinges at the left end, free at the right end, and subjected to a uniform load q. Based on this premise, the mechanical model of the main roof near the goaf-side roadway is established, as illustrated in Fig. 1. To characterize the stress distribution of the roadway roof, a rectangular coordinate system is established. The critical position of the elastic–plastic zone on the solid coal side serves as the coordinate origin, with the width direction of the coal pillar designated as the x-axis and the height direction of the coal pillar as the y-axis.

Calculation of bending elastic energy of main roof near goaf side

The mechanical model of the main roof near the goaf-side roadway illustrates that the load q from the overlying strata applies to the main roof, resulting in bending and deformation, and accumulating bending elastic energy UW. The calculation formula is provided in Eq. (1).

$$U_{{\text{W}}} = M\varphi /2$$
(1)

In the formula, UW is the main roof bending elastic energy, J; M is the bending moment of the main roof, N·m; φ is the rotation angle of the main roof bending subsidence, °.

For the main roof at the edge of the goaf, M and φ are respectively

$$M = \frac{1}{2}qL^{2}$$
(2)

In the formula, q represents the maximum load of the overlying strata on the main roof, Pa; L is the main roof length of bending deformation, m.

$$\varphi = \frac{{qL^{3} }}{2EI}$$
(3)

In the formula, E is the elastic modulus of the main roof, GPa; I is the section inertia moment of the main roof, m4. I = bh3/12, b is the width of the main roof, m. here the value is 1; h is the thickness of the main roof, m.

In the mining of longwall working face, according to the yield theory of the plate, the hanging length L of the main roof of the bending deformation is related to the periodic weighting step L1 and the length L2 of the working face, which can be calculated by Formula (4).

$$L = \frac{{2L_{1} }}{17}\left[ {\sqrt {\left( {10\frac{{L_{1} }}{{L_{2} }}} \right)^{2} + 102 - 10\frac{{L_{1} }}{{L_{2} }}} } \right]$$
(4)

In the formula, L1 is the periodic weighting step, m; L2 working face length, m.

$$L_{1} = h\sqrt {\frac{{R_{t} }}{3q}}$$
(5)

In the formula, Rt is the main roof tensile strength, MPa.

By substituting formula (2 ~ 5) into formula (1), the bending elastic energy UW of the main roof can be calculated.

$$U_{W} = \frac{{3q^{{2}} }}{{{2}Ebh^{3} }}\sqrt {\left[ {\frac{{4h^{2} R_{t} }}{867q}\left( {\frac{{100h^{2} R_{t} }}{{3qL_{2}^{2} }} + 102 - \frac{10h}{{L_{2} }}\sqrt {\frac{{R_{t} }}{3q}} } \right)} \right]^{5} }$$
(6)

Analysis of influencing factors of bending elastic energy of main roof near goaf side

Range analysis stands out as the most frequently employed technique for univariate sensitivity analysis. Its appeal lies in its simplicity of calculation, visual intuitiveness, and ease of comprehension. This method assesses primary and secondary factors by computing the average range for each factor. A wider range indicates a more pronounced influence of the factor on the test index, signifying higher sensitivity. The range analysis procedure unfolds as follows.

  1. 1.

    Calculate the index Xij corresponding to the factor of column j at the level of i.

  2. 2.

    Calculate the average value (\({\overline{X} }_{ij}\)) of Xij.

    $$\overline{X}_{ij} = X_{ij} /r$$

In the formula, r is the number of times the j-th column factor occurs at the i level.

  1. 3.

    Calculate the range Rj of the j-th column factor.

    $$R_{j} = \max (\overline{X}_{ij} ) - \min (\overline{X}_{ij} )$$

In the formula, max (\({\overline{X} }_{ij}\)) and min (\({\overline{X} }_{ij}\)) are the maximum and minimum values of the factors in the jth column at each level, respectively.

  1. 4.

    According to Rj, the sensitivity of factor j to the test index is judged, and the key of the factor is determined.

  1. 1.

    Scheme design

Formula (6) establishes the relationship between the bending elastic energy of the main roof and five key influencing factors. These factors include the maximum load q of the overlying strata on the main roof, elastic modulus E, thickness h, working face length L2, and tensile strength Rt. Utilizing an origin function fitting manager, Formula (6) is formulated, enabling the analysis of single-variable sensitivity to the bending elastic energy of the main roof under various overlying load conditions. This analysis aids in identifying the primary influencing factors. The calculation parameters for the example are provided in Table 1.

Table 1 Calculation parameters of bending elastic energy of main roof.
Full size table
  1. 2.

    Sensitivity analysis of influencing factors

Each example listed in Table 1 is input into the model for execution, generating variation characteristic curves depicting the bending elastic energy of the main roof, as illustrated in Fig. 2. Based on the calculation outcomes for each example, the sensitivity of individual parameters to the bending elastic performance of the main roof is evaluated using the range analysis method, and the results are tabulated in Table 2. The magnitude of the range indicates the degree of sensitivity of each influencing factor, thus facilitating the assessment of each factor’s sensitivity to the test index based on the size of Rj. The sensitivity ranking of each factor concerning the bending elastic energy of the main roof, from highest to lowest, is as follows: (1) the tensile strength of the main roof Rt, (2) the thickness of the main roof h, (3) the elastic modulus of the main roof E, and (4) the length of the working face L2.

Figure 2
figure 2

Variation characteristics of bending elastic energy of main roof.

Full size image
Table 2 Range analysis results of bending elastic energy of main roof.
Full size table

According to Fig. 2, it is evident that the tensile strength Rt of the main roof significantly influences its bending elastic energy. When the tensile strength of the roof is higher, the span of the main roof increases, resulting in an increase in its bending elastic energy. Conversely, when other conditions remain constant, a higher load q from the overlying strata on the main roof, as indicated by formulas (4 and 5), leads to a reduction in the span L of the main roof. This reduction in span subsequently decreases the bending elastic energy of the main roof.

The secondary factors influencing the bending elastic energy of the main roof include two parameters: the main roof thickness h and the elastic modulus E. As the thickness of the main roof increases, so does its bending elastic energy. A greater thickness results in a longer suspension length, consequently boosting the main roof’s bending elastic energy. Conversely, as the elastic modulus decreases, the variation in elastic energy accumulated by the main roof increases, albeit to a lesser extent compared to the tensile strength. This is because a decrease in the elastic modulus leads to increased bending subsidence of the roof, thereby elevating its bending elastic energy. Since the working face length L2 has minimal impact on the lateral hanging length of the main roof, an increase in L2 from 220 to 260 m hardly affects the bending elastic energy of the main roof.

Pre-yield elastic energy calculation and stability analysis of coal pillar

Stress distribution of side abutment of coal pillar

With the advancement of mining in the panel, the coal body originally supporting the roof load is excavated, leading to stress concentration in the coal pillar. This pillar delineates into a broken zone, a plastic zone, and an elastic zone, progressing from the exterior to the interior. The stress distribution within the coal pillar is illustrated in Fig. 3.

Figure 3
figure 3

Side abutment stress calculation model of coal pillar.

Full size image

The sides of the coal pillar are bordered by the goaf and the roadway, respectively. The side abutment stress primarily comprises two factors: (1) the friction f generated by the relative motion of the roof, floor, and the coal pillar; and (2) the lateral pressure F exerted by refuse on the coal pillar in the goaf. In cases where the coal seam is nearly horizontal, the roof rock layer finds support from the coal pillar, resulting in minimal caving refuse at the pillar’s edge. Consequently, the lateral pressure exerted by the refuse on the coal pillar can be disregarded. Thus, it is assumed that the lateral side of the coal pillar is primarily influenced by the friction f formed during the relative motion process of the roof, floor, and coal pillar. Moreover, the tangential stress on the coal pillar varies between the limit equilibrium zone and the elastic zone. Specifically, the tangential stress in the limit equilibrium zone is shown in formula (7).

$$\tau_{{{\text{yx}}}} = - \left( {C_{0} + \frac{{P_{x} \tan \varphi_{0} }}{\lambda }} \right)e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }x}}$$
(7)

In the formula, C0 is the cohesion of coal seam, Pa; φ0 is the internal friction angle of coal seam, °; Px is the support resistance of the pillar rib side, Pa; λ is the lateral pressure coefficient; m is the thickness of coal seam, m.

The stress calculation model for the side abutment in the elastic zone of the coal pillar is depicted in Fig. 3. In the figure, the coordinate origin O corresponds to the midpoint of the width direction of the coal pillar, with l representing half the width of the coal pillar, and x1 denoting half the width of the elastic zone. The stress distribution within the elastic zone of the coal pillar adheres to the constant body force compatibility equation.

$$\left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)\left( {\frac{{\partial^{2} \Phi }}{{\partial x^{2} }} + \frac{{\partial^{2} \Phi }}{{\partial y^{2} }}} \right) = 0$$
(8)

In the formula, Ф is the stress function.

The principal stress in x direction is shown in formula (9).

$$\sigma_{x} = \frac{{\partial^{2} \Phi }}{{\partial y^{2} }} - f_{x} x = 0$$
(9)

In the formula, fx is the volume force in the x direction.

There is no volume force in the x direction, that is, fx = 0, for the y integral in formula (9).

$$\frac{\partial \Phi }{{\partial y}} = f(x)$$
(10)
$$\Phi = yf(x) + f_{1} (x)$$
(11)

In the formula, f(x), f1(x) are undetermined functions of x.

Substituting Formula (11) into the compatibility Eq. (8), we get

$$y\frac{{{\text{d}}^{4} f(x)}}{{{\text{d}}x^{4} }} + \frac{{{\text{d}}^{4} f_{1} (x)}}{{{\text{d}}x^{4} }} = 0$$
(12)

Solving the differential Eq. (12).

$$\left\{ \begin{gathered} f(x) = Ax^{3} + Bx^{2} + Dx \hfill \\ f_{1} (x) = Ex^{3} + Gx^{2} \hfill \\ \end{gathered} \right.$$
(13)

In the formula, A, B, D, E, G are undetermined coefficients; the constant term of f(x), the constant term of f1(x) and the first-order term do not affect the isotropic stress component, so they can be omitted.

Substitute formula (13) into formula (11).

$$\Phi = y\left( {Ax^{3} + Bx^{2} + Dx} \right) + Ex^{3} + Gx^{2}$$
(14)

The shear stress component is obtained from the stress function.

$$\tau_{xy} = - 3Ax^{3} - 2Bx - D$$
(15)

According to the boundary conditions, the coal pillar stress satisfies the axisymmetric distribution, so B = 0. When x = 0, the shear stress between the coal pillar and the roof is 0, and D = 0 can be obtained by substituting it into Formula (15). At the boundary of the elastic–plastic zone x = x1, Px = 0, the tangential stress can be obtained by substituting it into Formula (7).

$$\tau_{{x_{1} }} = - C_{0} e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}}$$
(16)

Substituting the boundary conditions into the formula (15) can obtain A.

$$A = \frac{{C_{0} e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}} }}{{3x_{1}^{2} }}$$
(17)

The tangential stress in the elastic zone is obtained.

$$\tau_{yx} = - x^{2} \frac{{C_{0} e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}} }}{{x_{1}^{2} }}$$
(18)

The side abutment stress per unit length in the elastic zone of coal pillar is equal to the integral of tangential stress in the width direction.

$$\sigma_{3} = \int_{x}^{{x_{1} }} {\tau_{yx} {\text{d}}x} + \int_{x}^{{x_{1} }} {C_{0} e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}} {\text{d}}x}$$
(19)

The stress of side abutment in elastic zone is obtained.

$$\sigma_{3} = - \left[ {\frac{{C_{0} }}{{3x_{1}^{2} }}e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}} \left( {x_{1}^{3} - x^{3} } \right) + \frac{{m\lambda C_{0} }}{{2\tan \varphi_{0} }}\left( {e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}} - 1} \right)} \right]$$
(20)

In the formula, x ∈ (0, x1). The stress distribution of the coal pillar side abutment is shown in Formula (21).

$$\sigma_{3} = \left\{ \begin{gathered} - \frac{{m\lambda C_{0} }}{{2\tan \varphi_{0} }}\left( {e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}} - 1} \right),(x_{1} \le x < l) \hfill \\ - \left[ {\frac{{C_{0} }}{{3x_{1}^{2} }}e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}} \left( {x_{1}^{3} - x^{3} } \right) + \frac{{m\lambda C_{0} }}{{2\tan \varphi_{0} }}\left( {e^{{\frac{{2\tan \varphi_{0} }}{m\lambda }\left( {l - x_{1} } \right)}} - 1} \right)} \right],(0 \le x < x_{1} ) \hfill \\ \end{gathered} \right.$$
(21)

Analysis of pre-yield elastic energy in elastic zone of coal pillar

Under specific geological conditions, internal factors such as elastic modulus and internal friction angle, which affect the strength of the coal, generally remain constant. However, coal pillars of varying sizes experience different stress environments at various positions within them, leading to variations in the pre-yield elastic energy of the coal. Below, we analyze the relationship between pre-yield elastic energy and lateral stress of coal pillars.

The elastic energy Ee stored in unit volume of coal pillar is related to its stress state, and the analytical formula is shown in (22).

$$E_{{\text{e}}} = \frac{{\sigma_{1}^{2} + \sigma_{2}^{2} + \sigma_{3}^{2} - 2\mu (\sigma_{1} \sigma_{2} + \sigma_{1} \sigma_{3} + \sigma_{2} \sigma_{3} )}}{{2E_{{0}} }}$$
(22)

In the formula, E0 is the elastic modulus of coal, MPa; μ is the Poisson ratio of coal; σ1 is the first principal stresses, MPa.σ2 is the second principal stresses, MPa. σ3 is the third principal stresses, MPa.

When the shear failure of coal pillar occurs, the stress relationship conforms to the Mohr–Coulomb criterion.

$$\sigma_{1} = \frac{{1 + \sin \varphi_{{0}} }}{{1 - \sin \varphi_{{0}} }}\sigma_{3} + \frac{{2C_{{0}} \cos \varphi_{{0}} }}{{1 - \sin \varphi_{{0}} }}$$
(23)

Because the length of the coal pillar is much larger than the width, and the length direction is constrained without strain. Therefore, the coal pillar can be regarded as a plane strain problem, and the stress distribution satisfies the formula (24).

$$\sigma_{2} = \mu (\sigma_{1} + \sigma_{3} )$$
(24)

When the shear failure occurs in the coal pillar, the energy required is the pre-yield elastic energy Es, and Es can be obtained by combining Formulas (23 and 24).

$$E_{s} = \frac{{\alpha \sigma_{3}^{2} + 2\beta \sigma_{3} + 2C_{{0}}^{2} \cos \varphi_{{0}} (1 - \mu^{2} )}}{{E_{{0}} (1 - \sin \varphi_{{0}} )^{2} }}$$
(25)

In the formula, \(\alpha = - 2\mu^{2} + \mu (\sin^{2} \varphi_{{0}} - 1) + 1 + \sin^{2} \varphi_{{0}}\), \(\beta = C_{{0}} \cos \varphi_{{0}} \left[ { - 2\mu^{2} + \mu \left( {\sin \varphi_{{0}} - 1} \right) + 1 + \sin \varphi_{{0}} } \right]\).

According to the formula (25), the pre-yield elastic energy Es at any point in the elastic zone of the coal pillar is a quadratic function of the stress σ3 of the side abutment. The coefficient of the quadratic term and the coefficient of the first term are both quadratic functions of μ; because μ ∈ (0, 0.5), according to the knowledge of quadratic function, α and β are greater than 0 ; therefore, Es increases with the increase of σ3. When σ3 is 0, Es = (1−μ)Ec, Ec is the pre-yield elastic energy under uniaxial condition. Combined with the formulas (20) and (25), the distribution expression of the pre-yield elastic energy of the elastic zone of the coal pillar along the width direction of the coal pillar is obtained.

$$\begin{aligned} E_{s} & = \frac{{\alpha \left[ {\frac{{C_{0} }}{{3x_{1}^{2} }}e^{{\frac{{2\tan \varphi _{0} }}{{m\lambda }}\left( {l - x_{1} } \right)}} \left( {x_{1}^{3} - x^{3} } \right) + \frac{{m\lambda C_{0} }}{{2\tan \varphi _{0} }}\left( {e^{{\frac{{2\tan \varphi _{0} }}{{m\lambda }}\left( {l - x_{1} } \right)}} - 1} \right)} \right]^{2} }}{{E_{0} (1 - \sin \varphi _{0} )^{2} }} \\ & \quad + \frac{{2\beta \left[ {\frac{{C_{0} }}{{3x_{1}^{2} }}e^{{\frac{{2\tan \varphi _{0} }}{{m\lambda }}\left( {l - x_{1} } \right)}} \left( {x_{1}^{3} - x^{3} } \right) + \frac{{m\lambda C_{0} }}{{2\tan \varphi _{0} }}\left( {e^{{\frac{{2\tan \varphi _{0} }}{{m\lambda }}\left( {l - x_{1} } \right)}} - 1} \right)} \right] + 2C_{0}^{2} \cos \varphi _{0} (1 - \mu ^{2} )}}{{E_{0} (1 - \sin \varphi _{0} )^{2} }} \\ \end{aligned}$$
(26)

When the bending deformation of the main roof above the coal pillar and the accumulation of bending elastic energy UW is greater than the pre-yield elastic energy Es of the elastic zone of the coal pillar, the coal pillar is unstable, that is, the energy criterion of coal instability in the elastic zone of the coal pillar is shown in formula (27).

$$U_{{\text{W}}} > E_{{\text{s}}}$$
(27)

Analysis of influencing factors of pre-yield elastic energy in elastic zone of coal pillar

  1. 1.

    Scheme design

According to Formula (26), the pre-yield elastic energy of the elastic zone of the coal pillar is influenced by nine factors: (1) Poisson ratio of coal (μ); (2) internal friction angle of coal seam (φ0); (3) cohesion of coal seam (C0); (4) width of elastic zone of coal pillar (x1); (5) width of coal pillar (l); (6) thickness of coal seam (m); (7) position of coal pillar (x); (8) lateral pressure coefficient (λ); and (9) elastic modulus of coal seam (E0). Formula (26) is derived using the origin function fitting manager. Considering various factors, the pre-yield elastic energy at any position x within the elastic zone of the coal pillar is analyzed, and the sensitivity of each influencing factor is determined. The calculation parameters for the example are listed in Table 3.

Table 3 Example calculation parameters of pre-yield elastic energy of elastic zone of coal pillar.
Full size table
  1. 2.

    Sensitivity analysis of influencing factors

The data from Table 3 is inputted into the model for analysis, generating a curve depicting the variation in pre-yield elastic energy within the elastic zone of the coal pillar, as illustrated in Fig. 4. Utilizing the calculation outcomes, the range analysis method is employed to assess the sensitivity of each parameter to the pre-yield elastic energy of the coal pillar’s elastic zone. The findings are tabulated in Table 4. Sensitivity is evaluated based on the magnitude of Rj, with a larger range indicating higher sensitivity of the influencing factors. The sensitivity ranking of each factor concerning the pre-yield elastic energy of the coal pillar’s elastic zone is as follows: (1) internal friction angle of the coal seam (φ0); (2) width of the coal pillar (l); (3) elastic modulus of the coal seam (E0); (4) lateral pressure coefficient (λ); (5) cohesion of the coal seam (C0); (6) width of the elastic zone of the coal pillar (x1); (7) thickness of the coal seam (m); (8) Poisson ratio of the coal (μ).

Figure 4
figure 4

Distribution characteristics of pre-yield elastic energy in elastic zone of coal pillar.

Full size image
Table 4 Analysis results of pre-yield elastic energy range in elastic zone of coal pillar.
Full size table

According to Table 4, it is evident that the internal friction angle (φ0) of the coal seam, the width of the coal pillar (l), and the elastic modulus (E0) of the coal seam significantly influence the pre-yield elastic energy within the coal pillar’s elastic zone. A larger φ0, l, and a smaller E0 result in increased pre-yield elastic energy within the coal pillar’s elastic zone.

Following these factors, the lateral pressure coefficient (λ), coal seam cohesion (C0), and the width of the coal pillar’s elastic zone (x1) have a notable impact. As λ and x1 increase, the pre-yield elastic energy within the coal pillar’s elastic zone gradually decreases. Conversely, an increase in C0 leads to a gradual rise in the pre-yield elastic energy within the coal pillar’s elastic zone.

Lastly, the thickness (m) and Poisson ratio (μ) of the coal seam exert minimal influence on the pre-yield elastic energy within the coal pillar’s elastic zone. As m and μ increase, the pre-yield elastic energy within the coal pillar’s elastic zone decreases.

Engineering background

Project profile

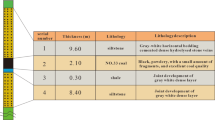
The Nanliang Coal Mine is situated in the Shenfu mining area of the Jurassic coalfield in northern Shaanxi. The 3−1 coal seam lies at a shallow depth, with the 2−2 coal seam serving as the overlying strata. The average thickness of coal at the panel 30,208 measures 2.16 m, with a coal seam dip angle ranging from 0° to 2°, rendering it relatively stable. The coal seam’s depth ranges from 0 to 144 m, and its floor elevation varies from 1250 to 1259 m. The mining roadway boasts a rectangular section, measuring 5.0 m in width and 2.5 m in height, supported by anchor cables. At present, the coal pillar size in the 3−1 coal seam of the Nanliang Coal Mine spans 15 m. The coal strata histogram is depicted in Fig. 5.

Figure 5
figure 5

Coal seam and rock stratum histogram.

Full size image

Supporting method of gateroad

Bolt support parameters

The selected bolt type and specifications are as follows: MSGLW-335/20 × 2200 mm non-longitudinal rib rebar bolts. Each bolt is anchored using MSCK2350 resin anchoring agent. The mesh employed is made of Φ6 mm steel with dimensions of 4400 × 1100 mm. Plate accessories for the anchor bolts consist of 150 × 150 × 10 mm steel plates. Installation angles for the roof bolts near the roadway side are set at + 15° with respect to the vertical line, while the remaining bolts are vertically positioned (90°). Bolt arrangement involves a row spacing of 1100 × 1000 mm, with five bolts per row. The minimum bolt pullout force is specified at 60 kN, while the anchor torque should not be less than 120 N m.

Anchor support parameters

The anchor cable specifications entail the use of a Φ21.8 × 6000 mm steel strand. Each anchor cable is outfitted with two MSK2850 resin anchoring agents. Supporting the anchor cable, a 300 × 300 × 12 mm tray and KM22-1860 lock fastening anchor cable are employed. Anchor cables are arranged in a single row along the roadway’s middle line, spaced at intervals of 3000 mm. The minimum pullout force requirement for the anchor cable is set at 150 kN. The layout of the roadway support is depicted in Fig. 6.

Figure 6
figure 6

Roadway support layout diagram.

Full size image

On-site monitoring of coal pillar stress

When the panel 30,208 progresses to the 1480 m mark, eight borehole stress meter monitoring stations labeled A–H are positioned along the 150 m headgate of the advancing working face. Their purpose is to monitor the vertical stress variations within the coal pillar, as depicted in Fig. 7. Borehole stress gauges were installed along the side of the coal pillar at depths of 1 m, 2 m, 4 m, 6 m, 8 m, 10 m, 12 m, and 14 m. The installation height is 1 m from the floor.

Figure 7
figure 7

Vertical stress monitoring layout of coal pillar.

Full size image

Figure 8 depicts the stress variation curve of the coal pillar along the strike direction of the panel. The stress evolution within the coal pillar is associated with its spatial position, which manifests in two distinct stages.

Figure 8
figure 8

Coal pillar stress distribution curve along the strike.

Full size image

Stage I: Unaffected by mining activities. At distances exceeding 37.5 m from the working face, the coal pillar experiences minimal disturbance from mining operations. Stress values at each measurement point remain relatively stable, with marginal fluctuations. The maximum stress registers between 8.9 and 16.6 MPa, with negligible changes observed in borehole stress values.

Stage II: Advanced impact phase. Within the vicinity of 0–37.5 m ahead of the panel, borehole stress values exhibit a rapid increase as the coal pillar becomes subject to advancing abutment pressure. Notably, the stress elevation is most pronounced at 1 m depth. When the working face advances to the 0 m station, the maximum stress reaches 16.3 MPa, exceeding the uniaxial compressive strength of the coal by 16.1 MPa, with a stress concentration factor of 1.83.

Figure 9 illustrates the stress distribution curve of the coal pillar along its trend. Following the evolution law of vertical stress within the coal pillar, stress changes can be categorized into two regions: 1–2 m and 12–14 m represent stress escalation zones, while 2–12 m signifies the original rock stress area. Proximity to the working face correlates with heightened side abutment stress. At a distance from the panel, coal pillar stress exhibits characteristics favoring the goaf side over the roadway side. As the working face advances continuously, roadway-measured stress values surge rapidly, indicating minimal influence from mining operations on coal pillar goaf measurements. Within the 0–7.5 m range from the panel, borehole stress meter readings at 1 m and 2 m depths increase notably as the distance diminishes. The stress at a depth of 1 m increased rapidly from 12.9 to 16.3 MPa, exceeding the uniaxial compressive strength of the coal by 16.1 MPa. Additionally, the stress within the center of the coal pillar was lower than that in the shallow coal near the two walls. Notably, the coal pillar’s elastic core area does not migrate to its center, preventing mid-pillar stress from exceeding shallower stress levels. The plastic zone width occupies approximately 15.4% of the elastic core area, leaving ample space for coal pillar width reduction. A coal pillar width exceeding 9 m is advisable when the elastic core area comprises over 50% and the safety factor stands at 1.5.

Figure 9
figure 9

Coal pillar stress tendency distribution curve.

Full size image

Calculation of reasonable coal pillar width

The calculation formula for the bending elastic energy UW of the main roof near the goaf is given in Eq. (6), while the formula for the pre-yield elastic energy Es of the elastic zone of the coal pillar along its width is provided in Eq. (26). These objective functions, Eqs. (6 and 26), were implemented using Origin C language and compiled using the custom fitting function manager. The objective functions were then solved using the working face of the No. 3−1 coal seam at Nanliang Coal Mine as the engineering context. The calculation parameters for determining the reasonable coal pillar width of the No. 3−1 coal seam are listed in Table 5.

Table 5 Example calculation parameters of pre-yield elastic energy of elastic zone of coal pillar.
Full size table

The distribution characteristics of the pre-yield elastic energy Es within the elastic zone of a 15 m wide coal pillar were calculated. Additionally, the local values of the bending elastic energy UW of the main roof under different overburden loads q were determined, as shown in Fig. 10. According to field monitoring data from Nanliang Coal Mine, the maximum load from the overlying strata on the main roof is q = 16.5 MPa, with a corresponding bending elastic energy of Es = 0.56 MJ.

Figure 10
figure 10

The bending elastic energy and the pre-yield elastic energy.

Full size image

Analysis indicates that the coal pillar of the No. 3−1 coal seam at Nanliang Coal Mine can remain stable when the width of the elastic zone exceeds 7.8 m. Field investigations further show that the width of the plastic zone of the coal pillar is 1 m. Therefore, the total width of the coal pillar for the No. 3−1 coal seam should be greater than 8.8 m to ensure stability.

Similar simulation verification of coal pillar width

In geotechnical engineering research methods, physical simulation offers high fidelity, ease of operation, and clear visualization of deformation processes and results in surrounding rock. As such, it finds extensive application. This study focuses on the 30,210 mining face and 30,208 heading face of Nanliang Coal Mine, conducting physical simulation tests. It investigates the structural changes resulting from lateral main roof rock beam fractures in the goaf post-mining of the panel 30,210, tracks the overburden rock migration patterns, and analyzes pressure distribution under varying sizes of retained coal pillars. The study aims to determine the optimal coal pillar width based on stability criteria.

Physical simulation scheme design

Model design

The physical model shown in Fig. 11 is constructed using the borehole histogram of the 3−1 coal seam in Nanliang Coal Mine as a reference. Based on the overlying strata conditions and laboratory model frame parameters, a plane stress model is selected for the physical simulation experiment. The model frame dimensions are 2000 × 1200 × 200 mm (length × height × width). To accurately depict the deformation and failure characteristics of the surrounding rock in the mining roadway under various coal pillar sizes, the model’s laying height is carefully considered. The actual laying height is set at 120 cm, with the remaining thickness simulated using iron bricks to apply pressure. The resulting geometric similarity ratio is 1:50, stress and strength similarity ratio is 1:80, time similarity ratio is 1:4, and mechanical similarity ratio is 1:200,000. Additionally, dimensionless physical quantities such as internal friction angle, strain, Poisson ratio, and friction coefficient maintain a similarity ratio of 1.

Figure 11
figure 11

Physical simulation model design diagram.

Full size image

The aggregate used is river sand, while the cementing materials include calcium carbonate and gypsum. Mica powder is applied between coal and rock layers to simulate bedding. Layered laying is employed during model construction to mitigate size effects associated with whole layer laying. The similar simulated coal-rock ratio scheme is determined based on comparable conditions, as outlined in Table 6. For coal pillar pressure monitoring, an LY-350 pressure sensor is utilized, with pressure data collected using an AD-36 pressure computer data acquisition instrument. Data analysis is conducted using a 128-channel data analysis system. The displacement monitoring system comprises a PENTAXR-322 NX optical total station and a model surface measuring line. Five roof displacement observation lines, denoted as R1 through R4, are set up for this test.

Table 6 The matching scheme of coal seam and rock stratum in similar simulation.
Full size table

Design of test excavation scheme

In order to accurately simulate the migration characteristics of the overburden structure above the panel 30,210 of Nanliang Coal Mine and its influence on the stress and stability of the coal pillar, test excavation is conducted in three steps, as follows:

The first step involves simulating the 2−2 coal goaf above the panel 30,210 of Nanliang Coal Mine. To ensure accuracy, the model’s left boundary is excavated to the right by 10 cm, with an excavation step distance of 50 mm. Stress data, fracture development characteristics, and other relevant data are recorded after each excavation cycle. Upon reaching the right boundary, a 2−2 coal goaf is formed.

In the second step, semi-infinite mining is employed at the model’s left boundary to advance to the right. This excavation spans a total length of 120 cm, resulting in the formation of the goaf 30,210. The excavation step remains at 50 mm. Throughout this process, displacement and stress data of the overlying strata, as well as fracture characteristics and crack distribution patterns, are meticulously recorded.

The third step involves excavating the tailgate 30,208, located 40 cm from the model’s right boundary. The excavation dimensions are 10 cm in width and 5 cm in height, resulting in the formation of a 30 cm (actual width of 15 m) coal pillar. Data regarding overburden displacement, pressure variations, fracture characteristics of overlying strata, and crack distribution are recorded. To determine the optimal coal pillar size, excavation is carried out on the left side of the tailgate 30,208 to simulate coal pillar optimization, with an excavation step of 2 cm (actual width of 1 m). Simulated supports are utilized to replace rock in the original excavation area, ensuring accurate roadway width. Optimization ceases when the coal pillar becomes unstable.

Analysis of overburden rock tendency fracture law

Mining simulation of No.2−2 coal seam

The post-mining caving features of overlying strata in the No. 2−2 coal seam are depicted in Fig. 12. During face advancement, the immediate roof collapses freely, fracturing under the weight of the overlying strata, with individual rock blocks remaining disconnected. Over time, as the working face progresses, compaction gradually occurs.

Figure 12
figure 12

Caving characteristics of overlying strata after No.2−2 coal seam mining.

Full size image

As the working face advances to distances of 60.2 cm, 74.0 cm, 89.5 cm, 103.7 cm, 120.9 cm, 138.2 cm, 159.0 cm, and 180.0 cm, the main roof periodically collapses. The broken blocks typically measure between 13.8 and 21.0 cm in length, with a caving angle averaging approximately 73°. Fracture development height increases with advancing distance. Large caving blocks are observed, with inclined fault blocks at the goaf’s edge and horizontally distributed remaining fault blocks, which interconnect with each other.

Mining simulation of No.3−1 coal seam

  1. 1.

    Mining simulation of panel 30,210

During the excavation of the panel 30,210, the immediate roof collapses due to the mining action of the overlying strata. At an advancement of 60 cm, part of the main roof is damaged, and cracks develop in the main roof behind the slope. By the time the working face reaches 80 cm, fractures extend through the intervening strata between the No.2−2 coal seam and the No.3−1 coal seam. At advancements of 60 cm, 100 cm, and 120 cm, the main roof experiences three periods of tendency fractures, with broken block lengths measuring 46.9 cm, 33.1 cm, and 27.5 cm, respectively. Figure 13 illustrates the caving characteristics of the overlying strata following the excavation of the panel.

Figure 13
figure 13

Caving characteristics of overlying strata after mining in panel 30,210.

Full size image

Through analysis, it is evident that the main roof at the right end of the panel 30,210 exhibits a masonry beam structure model, comprising four rock blocks along its tendency. Each block is interconnected, with block B and block C demonstrating nearly identical fracture lengths. Block B is inclined at the goaf’s edge, while the remaining crucial blocks are horizontally distributed. The spatial configuration of these blocks delineates the shape of the overlying strata and the stress distribution characteristics of the coal body along the goaf’s periphery.

  1. 2.

    Simulation analysis of coal pillar width optimization

When optimizing the coal pillar width from 30 to 18 cm, no significant deformation is observed in either the coal pillar or its overlying strata, indicating good stability. The tailgate 30,208 is positioned within the lower stress reduction zone of the “cantilever beam” structure (block A), supported by coal pillars and solid coal. This positioning effectively reduces the degree of deformation and failure in the surrounding rock of the roadway, as depicted in Fig. 14a–c ~ .

Figure 14
figure 14

Caving characteristics of overlying strata after optimization of coal pillar width.

Full size image

When the coal pillar width is reduced to 16 cm, insufficient to support the overlying strata load, the pillar collapses post-roadway excavation. This collapse induces rotary deformation in rock block A, subsequently affecting rock block B. Consequently, the stable A-B-C rock block structure is compromised, leading to overall rotation and sinking of the overlying strata. The immediate roof of the 30,210 goaf collapses, disrupting the A-B-C hinged rock beam structure of the main roof. Notably, during deformation, rock block A fractures atop the roadway, resulting in the formation of rock blocks A’ and A’'. Synchronous rotary deformation between rock block A’ and rock block B creates a new structure, A''-A'-B. This movement induces asymmetric roadway deformation, with greater deformation observed on the auxiliary side than the main side. Transverse cracks develop in the overlying strata of the roadway, accompanied by significant convergence of the roof and floor, as depicted in Fig. 14d.

The movement patterns of overlying strata significantly impact the pressure exerted on coal pillar protection roadways, which experience the entire process of strata movement. Coal pillars inevitably endure the effects of multiple mining operations. When pillars are small, despite the roadway potentially residing in a stress-reduced zone, their diminutive size makes them susceptible to roof rotation deformations. Consequently, pillars may fracture easily, leading to reduced load-bearing capacity and severe surrounding rock deformation. Hence, when the coal pillar width falls below 18 cm, its strength becomes inadequate to withstand overlying strata pressure. Therefore, the optimal coal pillar size is determined to be 18 cm (with an actual width of 9 m).

Displacement distribution characteristics of overlying strata

Figure 15 illustrates the displacement distribution along the four measuring lines (R1–R4) of the overlying strata. The abscissa represents the relative position of each measuring point to the left boundary of the model. Initially, during the mining of the panel 30,210 (0–30 cm), only some measuring points on the R4 line above the goaf exhibit displacement, with minimal roof subsidence. By the time the working face progresses to 40 cm, displacement is observed in certain measuring points along both the R3 and R4 lines above the goaf. Upon advancement to 60 cm, displacement is evident in all measuring points along the R1–R4 lines above the goaf. It is apparent from the figure that the excavation of the working face predominantly impacts the overlying rock within a 40 cm range to the left side of the working face.

Figure 15
figure 15

Measurement line displacement distribution characteristics of overlying strata.

Full size image

When optimizing the width of the coal pillar within the range of 30 cm to 18 cm, there is minimal change in displacement along each measurement line, and the displacement distribution characteristics of the measuring points closely resemble those of the panel 30,210 up to 100 m. However, upon optimizing the coal pillar width to 16 cm, significant subsidence occurs in the overburden rock due to coal pillar instability. The subsidence primarily spans from 50 to 146 cm (rock blocks A’ and B). Notably, the most substantial subsidence, approximately 4.2 cm, occurs at 100 cm from the left boundary. Asymmetric deformation of the roadway roof is evident, with greater deformation observed on the coal pillar side compared to the solid coal side.

Stress field evolution of coal pillar

During the optimization process of the coal pillar width, the stress distribution characteristics of coal pillars with varying widths are illustrated in Fig. 16. For a coal pillar width of 15 m, the stress curve within the pillar exhibits a “double hump” distribution, with maximum stress observed at the coal pillar goaf side. Specifically, the peak stress at the goaf side of the panel 30,210 is approximately 3 m away from the coal wall, reaching 16.7 MPa. Meanwhile, on the tailgate 30,208 side, the peak stress occurs approximately 1 m away from the coal wall, measuring 9.13 MPa. Notably, the stress distribution pattern within the coal pillar closely aligns with the field-measured values.

Figure 16
figure 16

Stress distribution characteristics of coal pillar.

Full size image

When optimizing the width of the coal pillar from 15 to 9 m, the stress within the coal pillar exhibits an overall increasing trend, with a significant growth value. Specifically, the peak stress of the coal pillar on the goaf 30,210 side rises to 20.0 MPa, while that of the tailgate 30,208 side increases to 12.8 MPa. Moreover, the stress concentration area gradually shifts towards the middle of the coal pillar, leading to a gradual increase in stress within this region. Consequently, the stress distribution transitions from a “double hump shape” to a “single hump shape”.

When the coal pillar width is 8 m, the stress concentration areas of both the goaf 30,210 side and the tailgate 30,208 side intersect within the coal pillar. This intersection leads to an overall concentration of stress within the coal pillar, maintaining the peak stress at approximately 20.7 MPa. The stress concentration area adopts a 'single hump shape’, with a stress concentration factor (k) of 2.4.

Field application effect evaluation

Since mining has commenced at the 30,208 working face, and the coal pillar in this section is 15 m wide, optimization of the section pillar is not feasible for this face. Therefore, the engineering practice was conducted on the 30,207 working face. To verify the stability of the surrounding rock when the coal pillar width is optimized to 9 m, a 100 m long section of the roadway in the tailgate of the 30,207 working face was selected for field testing. A set of measuring points was strategically placed 200 m ahead of the panel in the tailgate, utilizing a cross distribution method to track surface displacement of the roadway. Measuring instruments, including wooden wedges and measuring nails, were vertically installed in the middle of the roadway roof and horizontally positioned at the sides. Over a 12 day period, the surface displacement of the roadway was continuously monitored, culminating in the generation of a deformation curve depicting the surrounding rock’s behavior on the roadway surface. The monitoring scheme of roadway surrounding rock deformation is shown in Fig. 17.

Figure 17
figure 17

Roadway surrounding rock deformation monitoring scheme.

Full size image

Figure 18 shows the deformation curve of surrounding rock on the roadway surface. Analysis of the monitoring data reveals the deformation of the surrounding rock can be delineated into three distinct stages.

  1. 1.

    During the Deformation Acceleration Stage, occurring 13.8 m ahead of the working face, the roof and floor experience a maximum displacement of 149.9 mm, marking a 32.3% reduction compared to the original condition. Similarly, the maximum displacement of the sides measures 55.2 mm, reflecting a 29.5% decrease under support conditions. This support configuration effectively mitigates roadway separation and failure deformation, maintaining the internal stability of the surrounding rock.

  2. 2.

    The Deformation Deceleration Stage, spanning from 13.8 to 31.0 m ahead of the advancing working face, witnesses a gradual slowdown in the deformation rate of the roof, floor, and sides, accompanied by a reduction in overall deformation.

  3. 3.

    Beyond the 31.0 m mark of the advancing panel lies the Undisturbed Stage, characterized by a notable reduction in roadway deformation. Both the roof and floor exhibit a maximum displacement of 31.5 mm and 30.8 mm, respectively, with significantly decreased deformation rates compared to earlier stages.

Figure 18
figure 18

Surrounding rock deformation curve of roadway surface.

Full size image

Conclusions

  1. 1.

    By considering the structural characteristics of the overlying strata near the goaf side, a mechanical model is established for the main roof of the nearby roadway, and a calculation formula for its bending elastic energy is derived. Through the application of the range analysis method, the influencing factors and distribution patterns of this energy are examined. Results indicate that the tensile strength of the main roof emerges as the primary factor affecting its bending elastic energy. Specifically, higher tensile strength corresponds to reduced overlying strata load, increased thickness, and larger elastic modulus, all of which contribute to higher bending elastic energy in the roof.

  2. 2.

    By analyzing the stress distribution characteristics of the side abutment of the coal pillar, we derive the expression for the distribution of pre-yield elastic energy along the width direction of the coal pillar’s elastic zone. Furthermore, an energy criterion is proposed for coal instability within this elastic zone. Our findings indicate significant impacts of the internal friction angle, coal pillar width, and elastic modulus of the coal seam on the pre-yield elastic energy of the coal pillar’s elastic zone. Specifically, a larger internal friction angle, wider coal pillar, and smaller elastic modulus result in higher pre-yield elastic energy within the coal pillar’s elastic zone. Additionally, the lateral pressure coefficient, coal seam cohesion, and width of the coal pillar’s elastic zone have notable but secondary influences on its pre-yield elastic energy. Increasing the lateral pressure coefficient and the width of the elastic zone of the coal pillar leads to a gradual decrease in its pre-yield elastic energy. Conversely, higher coal seam cohesion corresponds to a gradual increase in the pre-yield elastic energy of the coal pillar’s elastic zone. Lastly, the thickness and Poisson’s ratio of the coal seam exhibit the least influence on the yield elasticity of the coal pillar’s elastic zone.

  3. 3.

    Taking the No.3−1 coal seam working face in Nanliang Coal Mine as the engineering background, calculations indicate that the coal pillar width should exceed 8.8 m to ensure stability. Physical simulation results demonstrate that with a coal pillar width of 8 m, it fails under the strain of overlying strata, leading to reduced bearing capacity and severe deformation of surrounding rock in the roadway. Hence, the optimal coal pillar size is determined to be 9 m. Field monitoring confirms that under this scheme, the maximum displacement of roof and floor is 149.9 mm, with the sides experiencing a maximum displacement of 55.2 mm. Notably, roadway separation and failure deformation are minimal, preserving the internal stability of the surrounding rock.