Introduction

Axial-flow pumps are widely chosen because of their large discharge, low head, and high specific rotating speed. They are used in fields including irrigation and drainage in agriculture, urban water supply and drainage, water-jet propulsion for ships, and water transfer in large river basins1,2,3. CFD has the advantages of low calculation cost, short calculation time, high precision, safety, and good repeatability. It has worked well in many aspects4,5,6,7. As the central part of the axial-flow pump, the design of the impeller directly impacts the capability of the pump8,9,10.

The water flow in an axial pump is complex three-dimensional unsteady turbulence during operation. The phenomenon of secondary backflow and unsteady turbulent flow of the axial-flow pump occur due to the distortion of the shape of the blade. As a result, the internal energy dissipation of the pump will increase and the pump efficiency will be reduced11,12,13. As a crucial geometric parameter of the axial-flow pump impeller, the cascade density directly affects the pump efficiency and cavitation capability14,15. The entropy generation method visualizes the ___location and distribution of dissipation. It is significant to explore the energy dissipation mechanism of the flow-passing parts of the axial-flow pumping device under different operating conditions16,17,18. Ma et al.19 examined the influence of cascade density on the capability of bidirectional axial-flow pumps. When the cascade density increases, the relative pressure distribution of the blades becomes more uniform, the efficiency increases, and the optimum operating point drifts to a small discharge condition. Yu et al.20 researched the changes in the internal flow characteristics of axial-flow pumps by adapting the angle of attack and cascade density. The results demonstrated that increasing the cascade density or reducing the inlet angle of attack can improve the pump efficiency and internal flow. Yang et al.21 studied the internal and external characteristics of multiblade axial-flow pump impellers under different cascade density schemes and drew some conclusions. They concluded that increasing the cascade density can effectively increase the minimum pressure on the suction side of the impeller blades then significantly improve the cavitation performance of the blades. All of the aforementioned scholars have investigated the effect of cascade density on axial-flow pumps; the difference lies in the types of pumps studied and the factors affecting the pumps. Similarly, other scholars have conducted research in a related field. Zhao et al.22 optimized the impeller and volute of a multistage double suction centrifugal pump with energy-saving as the design objective. The results revealed that improving the matching condition between rotor and stator can improve the pump performance. Osman et al.23 investigated the effects of different turbulence models on the hydraulic performance and internal flow characteristics of a vertical fire pump. The results show that SST k-ω is the best performing turbulence model for such applications. Gu et al.24 utilized a computational fluid dynamics approach to fully analyze a multi-stage centrifugal pump and verified the results with tests. The results show that the pressure fluctuations, efficiency and head coefficient show periodic variations with the frequency of the axial oscillation of impeller. Shi et al.25 elaborated the link between the effects of cavitation and the energy conversion characteristics of helical axial multiphase pump. They discovered that as the cavitation number σ became smaller and smaller, the cavitation following a streamline direction on the blade, extended from the suction side of the blade to the pressure side of the blade. Jiao et al.26 investigated the positive and negative disconnection processes of a bidirectional full-flow pump through numerical simulations and model tests. And they discovered that the entropy generation rate of the negative disconnection process was significantly larger than that of the positive disconnection process. Deng et al.27 found that the entropy generation in the main flow regions was critical in hydraulic loss, and that turbulent dissipation in the main flow regions of the impeller and volute casing play a dominant role in pump efficiency. The near-wall entropy generation of the impeller was positively correlated with the flow velocity but had little effect on the volute casing. Pei et al.28 employed the Rortex analysis method and Entropy analysis parameters to study the energy dissipation mechanism of a double-suction centrifugal pump. The results showed that the local shear plays a decisive role in energy dissipation in the pump. In related research on the cascade density of axial-flow pumps, the cascade density changes monotonously and linearly from the shroud to the hub. Simultaneously, the variation of cascade density is essential for the analysis of the impact of pump performance under a wide range of operating conditions.

These related studies illustrate the effect of cascade density on pumps, but there is still a lack of combining experiments to explore the effect of different cascade density schemes on the performance of axial-flow pumps. The purpose of this paper is to investigate the effects of different cascade density schemes on the energy and cavitation characteristics of the axial-flow pump, and to improve the efficiency of axial-flow pumps. Based on the abovementioned research results, this paper intends to optimize the design of the axial-flow pump impeller. Meanwhile, combined with computational fluid simulation and experiments, the functions of cascade density on the hydraulic performance of pump as well as the internal energy dissipation loss of the optimized scheme are mainly analyzed.

Numerical calculations

Numerical setup

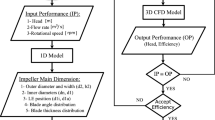
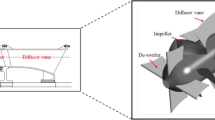
The axial-flow pump consists of inlet pipe, impeller, guide vane, and outlet pipe. Figure 1 shows the four flow sections model of the pump. Table 1 shows the main characteristic data of the pump. This paper mainly studies the functions of different cascade density on the performance of pump, the research results can be a reference for the optimization of axial-flow pump impellers.

Fig. 1
figure 1

3D model of axial-flow pump. (1) Inlet pipe; (2) Impeller; (3) Guide vane; (4) Outlet pipe with 60°ellow.

Full size image
Table 1 Main data of the axial-flow pump.
Full size table

Governing equations and turbulence model

The flowing medium inside the axial-flow pump is a continuous incompressible fluid, and the water flow is energized by the rotation of the impeller. Since the temperature of the fluid has no change, the energy equation can be ignored. Therefore, the continuity equation finally solved by CFD is shown in the following formula: (1) The momentum equation is shown in Formula (2) below.

The continuity equation is:

$$\frac{{\partial \rho }}{{\partial t}}+\frac{\partial }{{\partial {x_{\text{j}}}}}\left( {\rho {u_{\text{j}}}} \right)=0$$
(1)

The conservation of momentum is:

$$\frac{{\partial \rho {u_{\text{i}}}}}{{\partial t}}+\frac{\partial }{{\partial {x_{\text{j}}}}}\left( {\rho {u_{\text{i}}}{u_{\text{j}}}} \right) - \frac{\partial }{{\partial {x_{\text{j}}}}}\left[ {\mu \left( {\frac{{\partial {u_{\text{i}}}}}{{\partial {x_{\text{j}}}}}+\frac{{\partial {u_{\text{j}}}}}{{\partial {x_{\text{i}}}}}} \right)} \right]= - \frac{{\partial p}}{{\partial {x_{\text{i}}}}} - \frac{\partial }{{\partial {x_{\text{j}}}}}\left( {\rho \overline {{u_{{\text{i}}}^{{{\prime }}}u_{{\text{j}}}^{{{\prime }}}}} } \right)+{S_{\text{M}}}$$
(2)

Among:

$$- \rho \overline {{u_{{\text{i}}}^{{{\prime }}}u_{{\text{j}}}^{{{\prime }}}}} ={\mu _{\text{t}}}\left( {\frac{{\partial {u_{\text{i}}}}}{{\partial {x_{\text{j}}}}}+\frac{{\partial {u_{\text{j}}}}}{{\partial {x_{\text{i}}}}}} \right) - \frac{2}{3}\left( {\rho k+{\mu _{\text{t}}}\frac{{\partial {u_{\text{k}}}}}{{\partial {x_{\text{k}}}}}} \right){\delta _{{\text{ij}}}}$$
(3)

Where ρ represents fluid density, kg/m3; ui and uj represent the sections of the Reynolds time-average velocity, m/s; xi and xj represent the components of the Cartesian-coordinates, m; \(\:\stackrel{-}{p}\:\)represents the time average pressure, Pa; µ represents the dynamic viscosity, Pa· s; \(\:-\rho\:\stackrel{-}{{u}_{i}^{{\prime\:}}{u}_{j}^{{\prime\:}}}\:\text{i}\text{s}\:\text{t}\text{h}\text{e}\:\)Reynolds stress, Pa; and t is the physical time, s; \(\:{\mu\:}_{\text{t}}\) is the turbulent viscosity, pa·s; SM is the sum of the body forces, kg/m2·s2; and δij is the “Kronecker function”.

Near the wall, the SST k-ω turbulence model retains the original k-ω model, and away from the wall, the SST k-ω turbulence model applies the k-ε turbulence model. The model corrects the turbulent viscosity formula, which can better transfer the shear stress at the wall. At the same time, this helps to predict the flow of water near the wall and the separation of the fluid under a reverse pressure gradient.

Therefore, in this paper, the SST k-ω turbulence model is chosen to close the governing equation. Finally, the Reynolds averaged Navier-Stokes (RANS) equation and the SST k-ω turbulence model are used to simulate and predict the flow field and performance of the pump.

The k equation and the ω equation are as follows:

$$\frac{{\partial \left( {\rho k} \right)}}{{\partial t}}+\frac{{\partial \left( {\rho {u_{\text{i}}}k} \right)}}{{\partial {x_{\text{i}}}}}=\frac{\partial }{{\partial {x_{\text{j}}}}}\left[ {\left( {\mu +\frac{{{\mu _{\text{t}}}}}{{{\sigma _{k3}}}}} \right)\frac{{\partial k}}{{\partial {x_{\text{j}}}}}} \right]+{p_{\text{k}}} - {\beta ^{\prime}}\rho k\omega$$
(4)
$$\frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}}+\frac{{\partial \left( {\rho {u_{\text{i}}}\omega } \right)}}{{\partial {x_{\text{i}}}}}=\frac{\partial }{{\partial {x_{\text{j}}}}}\left[ {\left( {\mu +\frac{{{\mu _{\text{t}}}}}{{{\sigma _{\omega 3}}}}} \right)\frac{{\partial \omega }}{{\partial {x_{\text{j}}}}}} \right]+2\left( {1 - {F_1}} \right)\rho \frac{1}{{\omega {\sigma _{\omega 2}}}}\frac{{\partial k}}{{\partial {x_{\text{j}}}}}\frac{{\partial \omega }}{{\partial {x_{\text{j}}}}}+{\alpha _3}\frac{\omega }{k}{p_k} - {\beta _3}\rho {\omega ^2}$$
(5)

where σk3 can be solved using a weighted function by rewriting the corresponding terms in the k-ε and k-ω models. The function is as follows:

$$\frac{1}{{{\sigma _{{\text{k3}}}}}}={F_1}\frac{1}{{{\sigma _{{\text{k1}}}}}}+\left( {1 - {F_1}} \right)\frac{1}{{{\sigma _{{\text{k2}}}}}}$$
(6)

The eddy viscosity is defined as:

$${\mu _{\text{t}}}=\rho \cdot \frac{{{\alpha _1}}}{{\hbox{max} \left( {{\alpha _1}\omega ,S{F_2}} \right)}}$$
(7)

where S is an strain rate invariant, s-1; and Pk is the turbulence generation due to viscous forces, which is modeled using:

$${P_{\text{k}}}={\mu _{\text{t}}}\left( {\frac{{\partial {u_{\text{i}}}}}{{\partial {x_{\text{j}}}}}+\frac{{\partial {u_{\text{j}}}}}{{\partial {x_{\text{i}}}}}} \right)\frac{{\partial {u_{\text{i}}}}}{{\partial {x_{\text{j}}}}} - \frac{2}{3}\frac{{\partial {u_{\text{k}}}}}{{\partial {x_{\text{k}}}}}\left( {3{\mu _{\text{t}}}\frac{{\partial {u_{\text{k}}}}}{{\partial {x_{\text{k}}}}}+\rho k} \right)$$
(8)

For incompressible flow, \(\:\left(\partial\:{u}_{\text{k}}/\partial\:{x}_{\text{k}}\right)\) is small and the second term on the right side of Eq. (8) produces little effect on the generation.

The blending functions is the key to the success of the method. They are calculated based on the distance to the nearest surface and on the flow variables.

$${F_1}=\tanh \left( {\arg _{1}^{4}} \right)$$
(9)
$${\arg _1}=\hbox{min} \left[ {\hbox{max} \left( {\frac{{\sqrt k }}{{{\beta ^{\prime}}\omega y}},\frac{{500\nu }}{{\omega {y^2}}}} \right),\frac{{4\rho {\sigma _{\varvec{\upomega}2}}}}{\text{k}}{{C{D_{{\text{kw}}}}{y^2}}}} \right]$$
(10)
$$C{D_{{\text{k}\varvec{\upomega}}}}=\hbox{max} \left( {2\rho \frac{1}{{\omega {\sigma _{{{\varvec{\upomega}2}}}}}}\frac{{\partial k}}{{\partial {x_{\text{j}}}}}\frac{{\partial \omega }}{{\partial {x_{\text{j}}}}},1.0 \times {{10}^{ - 20}}} \right)$$
(11)

where y is the distance to the nearest wall, m; υ is the kinematic viscosity, m2/s; and k is the turbulent kinetic energy, m2/s2.

The SST k-ω turbulence model corrects the eddy viscosity coefficient by modifying its form as follows:

$${F_2}=\tanh \left( {\arg _{2}^{2}} \right)$$
(12)
$${\arg _2}=\hbox{max} \left( {\frac{{2\sqrt k }}{{{\beta ^{\prime}}\omega y}},\frac{{500\upsilon }}{{\omega {y^2}}}} \right)$$
(13)

The data coefficients for the equations are as follows:β’ = 0.09; σk1 = 1.176; σk2 = 1.0; σω3 = 2; σω2 = 1.1682; α3 = 0.44; β3 = 0.0828; α1 = 5/9.

Entropy generation theory

There is always a certain amount of mechanical energy lost through dissipation and friction in the axial-flow pump, which is converted into internal energy and can no longer be used, this process is irreversible, and leads to an increase in entropy. Entropy (s) is a state variable, when its transport equation in a single-phase incompressible flow is as follows:

$$\rho \frac{{Ds}}{{Dt}}= - \nabla (\frac{{\vec {q}}}{T})+\frac{{{\varvec{\Phi}}}}{T}+\frac{{{{{\varvec{\Phi}}}_{{\varvec{\uptheta}}}}}}{{{T^2}}}$$
(14)

where s is the instantaneous quantity, and the instantaneous quantity is divided into two parts, the average and the fluctuation part, by the Reynolds averaged Navier–Stokes (RANS) turbulence method:

$$s=\overline {s} +s^{\prime}$$
(15)
$$u=\overline {u} +{u^{\prime}}$$
(16)

The above Formulas (15) and (16) are substituted into Formula (14) to obtain the following entropy balance Eq. (17).

$$\rho (\frac{{\partial \overline {s} }}{{\partial t}}+\overline {U} \cdot \nabla \overline {s} )= - \overline {{\nabla (\frac{{\vec {q}}}{T})}} -\rho \nabla (\overline {{U^{\prime}s^{\prime}}} )+\overline {{\left( {\frac{{{\varvec{\Phi}}}}{T}} \right)}} +\overline {{\left( {\frac{{{\Phi _\theta }}}{{{T^2}}}} \right)}}$$
(17)

\(\:\stackrel{-}{{\varPhi\:}_{{\uptheta\:}}/{T}^{2}}\) do not calculate (In incompressible fluids, the fluid path of the pump is almost isothermal); The dissipation entropy yield comprises two parts: the direct dissipation rate (\(\:{S}_{\stackrel{-}{\text{D}}}\)) due to the average flow field and the turbulence dissipation rate (\(\:{S}_{{\text{D}}^{{\prime\:}}}\)) due to the pulsation velocity.

$$\frac{{\overline {\Phi } }}{T}={S_{\bar {{\text{D}}}}}+{S_{{\text{D}}^{\prime}}}$$
(18)

According to the Gouy-Stodola theorem, the entropy generation rate SD can be expressed by the following formula:

$${S_{\text{D}}}=\frac{{\dot {Q}}}{T}=\frac{{\overline {\Phi } }}{T}$$
(19)

where \(\:\dot{Q}\) is the energy transfer rate, W·m-3; and Φ is the dissipation function, W·m-3.

Therefore, the principle of entropy generation is essentially consistent with the Gouy-Stodola theorem.

$${S_{\overline {{\text{D}}} }}=\frac{{2{\mu _{{\text{eff}}}}}}{T}\left[ {{{\left( {\frac{{\partial \overline {u} }}{{\partial x}}} \right)}^2}+{{\left( {\frac{{\partial \overline {u} }}{{\partial y}}} \right)}^2}+{{\left( {\frac{{\partial \overline {u} }}{{\partial z}}} \right)}^2}} \right]+\frac{{{\mu _{{\text{eff}}}}}}{T}\left[ {{{\left( {\frac{{\partial \overline {u} }}{{\partial y}}+\frac{{\partial \overline {v} }}{{\partial x}}} \right)}^2}+{{\left( {\frac{{\partial \overline {u} }}{{\partial z}}+\frac{{\partial \overline {w} }}{{\partial x}}} \right)}^2}+{{\left( {\frac{{\partial \overline {v} }}{{\partial z}}+\frac{{\partial \overline {w} }}{{\partial y}}} \right)}^2}} \right]$$
(20)
$${S_{{\text{D}}^{\prime}}}=\frac{{2{\mu _{{\text{eff}}}}}}{T}\left[ {{{\left( {\frac{{\partial u^{\prime}}}{{\partial x}}} \right)}^2}+{{\left( {\frac{{\partial v^{\prime}}}{{\partial y}}} \right)}^2}+{{\left( {\frac{{\partial w^{\prime}}}{{\partial z}}} \right)}^2}} \right]+\frac{{{\mu _{e{\text{ff}}}}}}{T}\left[ {{{\left( {\frac{{\partial u^{\prime}}}{{\partial y}}+\frac{{\partial v^{\prime}}}{{\partial x}}} \right)}^2}+{{\left( {\frac{{\partial u^{\prime}}}{{\partial z}}+\frac{{\partial w^{\prime}}}{{\partial x}}} \right)}^2}+{{\left( {\frac{{\partial v^{\prime}}}{{\partial z}}+\frac{{\partial w^{\prime}}}{{\partial y}}} \right)}^2}} \right]$$
(21)
$${\mu _{e{\text{ff}}}}=\mu +{\mu _{\text{t}}}$$
(22)

where µeff is the effective dynamic viscosity, pa·s ; µ is the dynamic viscosity, pa·s; and µt is the turbulent viscosity, pa·s.\(\:\:\stackrel{-}{u}\), \(\:\stackrel{-}{v}\), and \(\:\stackrel{-}{w}\), respectively, represent the sections of the time-averaged velocity in the x, y, and z directions, m/s.\(\:{u}^{{\prime\:}}\), \(\:{v}^{{\prime\:}}\), and \(\:{w}^{{\prime\:}}\), respectively, represent the components of the pulsating velocity in the x, y, and z directions, m/s.

The pulsation velocity component is not available when using the Reynolds mean method. Based on Kock et al.29 and Mathieu et al.30, \(\:{S}_{{\text{D}}^{{\prime\:}}}\) in Eq. (21) above can be calculated by turbulence model. The \(\:{S}_{{\text{D}}^{{\prime\:}}}\) of the SST k-ω turbulence model can be given by:

$${S_{{\text{D}}^{\prime}}}={\beta ^{\prime}}\frac{{\rho \omega k}}{T}$$
(23)

whereβ’ is an empirical constant in the SST k-ω model, approximately equal to 0.0931; k is the turbulent kinetic energy, m2/s2; and ω is the turbulence eddy frequency, s-1.

Considering the high velocity gradient at the wall, additional turbulent dissipation losses are unavoidable. The wall entropy generation is calculated as follows:

$${S_{\text{W}}}=\frac{{\vec {\tau } \cdot \vec {v}}}{T}$$
(24)

where\(\:\overrightarrow{\:\tau\:}\) is the wall shear stress, Pa; and \(\:\overrightarrow{v}\) is the center velocity vector of the first layer mesh at the wall, m/s.

The entropy generation energy dissipation of each part can be obtained by volume integration of each local entropy generation rate. The wall entropy generation can be obtained by surface integration of the wall entropy generation rate. The entropy generation equation for each part is as follows:

$${S_{{\text{gen,}}\overline {{\text{D}}} }}=\int_{V} {{S_{\overline {{\text{D}}} }}} dV$$
(25)
$${S_{{\text{gen,D}}^{\prime}}}=\int_{V} {{S_{{\text{D}}^{\prime}}}} dV$$
(26)
$${S_{{\text{gen,W}}}}=\int_{A} {{S_{\text{W}}}} dA$$
(27)

where\(\:{\:S}_{\text{g}\text{e}\text{n},\stackrel{-}{\text{D}}}\:\)(EGDD) is the direct entropy generation caused by the time-average velocity;\(\:{\:S}_{\text{gen},{\text{D}}^{{\prime\:}}}\)(EGTD) is the turbulent entropy generation caused by the pulsating velocity; and \(\:{S}_{\text{g}\text{e}n,\text{W}}\)(EGWS) is the wall entropy generation caused by the wall velocity gradient.

In conclusion, the total entropy generation (\(\:{S}_{\text{g}\text{e}\text{n}}\)) of the convective flow field is equal to the sum of EGDD, EGTD, and EGWS.

$${S_{{\text{gen}}}}={S_{{\text{gen,}}\overline {{\text{D}}} }}+{S_{{\text{gen,D}}^{\prime}}}+{S_{{\text{gen,W}}}}$$
(28)

Considering that the temperature of the fluid in the axial-flow pump remains constant during the flow process, Formula (29) determines the hydraulic loss calculated according to the entropy generation Formula (28).

$${h_{{\text{gen}}}}=\frac{{T \cdot {S_{{\text{gen}}}}}}{{\mathop m\limits^{ \cdot } g}}$$
(29)

where, \(\:\dot{m}\) is the mass discharge rate of the pump, L/s; and T is the temperature, K.

Mesh independence and convergence analysis

The impeller and guide vane are structured meshed in the turbo-grid to meet the quality requirements. The inlet pipe with the water guide cone and the outlet pipe with the motor shaft are structured in ICEM CFD and the mesh quality is above 0.4, which is good quality. Figure 2 below shows the grid drawing of the impeller, guide vane, inlet pipe, and outlet pipe.

Fig. 2
figure 2

Grid model of each section of the axial-flow pump.

Full size image

Verification of grid independence is intended to reduce or eliminate the influence of the number and size of grids on the calculation results. The impeller is a rotating part, and the other parts are stationary, so it is necessary to verify the number of the impeller grids to ensure the accuracy of the calculation. Under the design operating conditions, eight different impeller grid number schemes are utilized to evaluate impeller grid independence. Figure 3 demonstrates that as the number of impeller grids increases from 651,152 to 710,444, the change of pump efficiency slows down significantly and the efficiency values growth rate is less than 2%. Therefore, the total number of impeller grids is approximately 651,152, and the grid count for the entire axial-flow pump is approximately 4.5 million.

Fig. 3
figure 3

Verification analysis of impeller grid independence.

Full size image

The grid quality has a significant impact on the results of numerical simulations. It is important to ensure grid convergence to strike a balance between computational resources and the numerical calculations accuracy. The GCI (Grid Convergence Index) criterion of the Richardson extrapolation method is used to verify the convergence of the mesh. Finally, three groups of fine mesh N1 = 4,511,756, medium mesh N2 = 1,316,776, and coarse mesh N3 = 573,075 are used to research the mesh convergence of pump. The grid refinement coefficients are all greater than 1.3. Then, the efficiency parameters of the pump are analyzed by discretization error analysis. Refer to the GCI calculation program of Yang et al.32. Table 2 shows the calculation results. The convergence index GCI21 is 0.154%, and the discretization error is small. Therefore, the final grid number is 4,511,756.

Table 2 Calculation of mesh discretization error.
Full size table

Numerical settings

The discretization of governing equations adopts a finite volume method which is based on finite elements, and the convective terms are implemented in a high-resolution format. The flow field solution uses a fully implicit multi-grid coupled solution technique, coupling the continuity and momentum equations. Table 3 below shows the boundary conditions set for the computational ___domain of the pump. The maximum number of iteration steps is set to 2000 in the solver control.

Table 3 Boundary condition settings.
Full size table

Design of different axial-flow pump impeller schemes

To investigate the effect of different cascade densities on the axial-flow pump, based on the selected airfoil, the airfoil placement angle, the maximum airfoil camber ratio, and the maximum airfoil thickness ratio are kept constant. By changing the tip cascade density, the effect of different cascade density on the performance of the axial-flow pump is studied.

In designing the impeller, the impeller blades are divided into eleven airfoil sections. R is the distance from each airfoil section to the center of rotation of the impeller. Figure 4a demonstrates the cross-sectional schematic diagram of the impeller airfoil. According to formulas (30) and (31), when each airfoil Section R is determined, the cascade distances t’ and r(i) remain unchanged. Figure 4b shows a schematic diagram of the two-dimensional leaf channel.

$${t^{{\prime }}}=\frac{{2\pi R}}{Z}$$
(30)
$${r_{\left( {\text{i}} \right)}}=\frac{{{R_{\left( {\text{i}} \right)}}}}{D}$$
(31)

where i = 1, 2, 3…11, 1 represents the shroud, and 11 represents the hub.

Fig. 4
figure 4

Axial-flow pump airfoil cross-section and 2D cascade schematic diagram.

Full size image

The cascade density of the airfoil section between the impeller hub and the shroud adopts the law of equal strength, so the cascade density of each airfoil section can be controlled by the two parameters σ1 and Zm, precisely according to the following formulas: (32), (33), (34), and (35). To explore the influence of σ1 on the performance of the axial-flow pump, Zm=1.433 is kept constant. By changing σ1, the effect of different cascade densities on the performance of the pump is studied.

$${\lambda _{\text{2}}}=\frac{{{d_{\text{h}}} \cdot \left( {{Z_{\text{m}}} - 1} \right) \cdot {\sigma _{\text{1}}}}}{{1 - {d_{\text{h}}}}}$$
(32)
$${\lambda _{\text{1}}}={\sigma _{\text{1}}} - \lambda {}_{{\text{2}}}$$
(33)
$${\sigma _{\left( {\text{i}} \right)}}={\lambda _{\text{1}}}+\frac{{{\lambda _{\text{2}}}}}{{{r_{\left( {\text{i}} \right)}}}}$$
(34)
$${Z_{\text{m}}}=\frac{{{\sigma _{{\text{11}}}}}}{{{\sigma _{\text{1}}}}}$$
(35)

where Zm is the multiple of cascade density, σ1 is the cascade density at the shroud, σ11 is the cascade density at the hub, σ(i) is the cascade density of each airfoil section of the blade, and dh is the hub ratio.

The values of σ1 are 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, and 1.0, for a total of seven schemes, among which the σ1 = 1.0, Zm=1.433 scheme is the initial scheme (OS) during the test; Table 4 demonstrates the cascade density for different schemes. Table 5 displays the sectional data of each airfoil under different schemes.

Table 4 Cascade density of each airfoil section under different schemes.
Full size table
Table 5 Sectional data of each airfoil under different schemes.
Full size table

Experiment test and validation

The experiment was conducted to verify the external characteristics of the pump. Figure 5 shows the test installation, including the inlet tank, pressure outlet tank, voltage stabilizing rectifier, electromagnetic flow meter, and control valve. Utilize CNC machining to produce the brass material impeller for the axial-flow pump, and through welding techniques, use the welded steel material to construct the guide vane. Figure 6 depicts a model of the main components of the axial-flow pump. Figure 7 is a comprehensive characteristic curve diagram of the pump. After the experimental system uncertainty calculation, the calculation results meet the accuracy requirements of the pump model and pumping device model acceptance test protocol (SL 140–2006), indicating that the experimental results are reliable.

Fig. 5
figure 5

Diagram of test pump. (1) inlet tank, (2) axial-flow pump, (3) pressure outlet tank, (4) bifurcated tank, (5) regulating gate valve, (6) voltage stabilizer rectifier, (7) electromagnetic flow meter, (8) control gate valve, (9) auxiliary pumping device, (10) differential pressure gauge.

Full size image
Fig. 6
figure 6

Model pump.

Full size image
Fig. 7
figure 7

Comprehensive characteristic curve of axial-flow pump.

Full size image

Figure 8 compares the model test and numerical simulation results of the pump. The impeller used in the axial-flow pump test is the impeller data of the initial scheme (OS). By comparing the data of experiment and initial protocol (OS), it can be found that the efficiency curve of the numerical simulation is in good agreement with the experiment under the large discharge condition. An unavoidable error in the small discharge condition may be due to the particular disturbance at the inlet of the pump. Under the design operating conditions, the experiment test efficiency is 84.22%, and the head is 6.076 m. In comparison, numerical simulation calculates an efficiency of 84.24% with a head of 5.95 m. The efficiency error is 0.024%, and the head error is 2.07%, both of which fall within the acceptable error range and satisfy the calculation accuracy requirement. Furthermore, by comparing the scheme (S4) and the initial scheme (OS), the pump efficiency increases, the efficiency of scheme (S4) is 0.99% higher than that of scheme (OS) under the design discharge condition and 3.87% higher than that of scheme (OS) under the large discharge condition. And the range of the high-efficiency zone expands by optimizing the density of the tip cascade. Finally, comparing numerical simulation and test results further demonstrates the dependability of numerical simulation and tests.

Fig. 8
figure 8

Comparison of experimental and numerical simulations.

Full size image

Results and discussions

Comparison of hydraulic characteristic under different schemes

Figure 9a, b show the head-discharge and efficiency-discharge characteristic curves of the axial-flow pump of different schemes. This indicates that the variation range of the head between different σ1 values is larger for small discharge conditions (Q ≤ 340 L/s) than for large discharge conditions (Q ≥ 380 L/s), indicating that the variation of σ1 affects the axial-flow pump more under small discharge conditions than under large discharge conditions. Simultaneously, under small discharge conditions, with an increase in σ1, the pump head gradually increases, and the efficiency gradually decreases. This is because the longer the cord at the impeller shroud, the more the impeller will work and the higher the head will be. However, the corresponding friction area between the blade and the fluid will increase, resulting in a decrease in the pump efficiency. In general, for the axial-flow pump, if Zm remains constant, although increasing σ1 can increase the pump head, it leads to a decrease in the pump efficiency and narrows the high-efficiency area of pump operating conditions. There σ1 should not be too large and should be kept within reasonable limits.

The density multiplier of the impeller cascade of the pump remains unchanged. As the σ1 decreases, the twist degree of the axial-flow pump blade decreases, the maximum displacement of the tip increases, and the maximum structural stress reduces. Therefore, reducing the tip cascade density improves the structural performance of the pump and ensures the efficient, safe, and stable operation of the pump station.

Fig. 9
figure 9

Performance curve of the axial-flow pump under different schemes.

Full size image

Figure 10a, c, show the head-discharge and efficiency-discharge characteristic curves, respectively, of the impeller for different schemes. The figure shows that the larger σ1 is under different discharge conditions, the greater the slope of the impeller’s head-discharge characteristic curve is. The change in σ1 has a significant effect on the impeller head under small discharge conditions, whereas it has no effect under the large discharge conditions. In contrast, under small discharge conditions, σ1 has little influence on the impeller efficiency. Under large discharge conditions, as σ1 increases, the impeller efficiency decreases gradually.

Figure 10b is the relationship curve between the head of the impeller and the head of the initial scheme minus ΔH1 and σ1 under different discharge conditions. This reveals that with the gradual decrease in σ1, the head drop ΔH1 of the impeller is greater. Similarly, a different σ1 has little influence on the impeller under large discharge conditions. The magnitude of the influence is greater under small discharge conditions. Figure 10d is the relationship curve between the impeller efficiency under different schemes and the efficiency of the initial scheme minus Δη1 and σ1 under different discharge conditions. This illustrates that Δη1 fluctuates under small discharge conditions; however, the design operating condition has almost no effect. Under large discharge conditions, the greater the increase in σ1 is, the greater the efficiency drop Δη1 of the impeller.

Fig. 10
figure 10

Effect of different σ1 values on the performance of the impeller.

Full size image

Figure 11 illustrates the relationship curve between the hydraulic loss of the pipeline and discharge. Under different schemes, the hydraulic loss in the pipelines decreases and then increases with increasing discharge, and there is a minimum value near the design operation conditions. The hydraulic loss of pipelines under different schemes is the same, under large discharge conditions. However, the hydraulic loss also increases gradually with the σ1 increasing under the small discharge conditions, which is consistent with the result that the larger σ1 is for axial-flow pump under small discharge conditions, the lower efficiency is.

Fig. 11
figure 11

Change curves of pipeline hydraulic loss under different schemes.

Full size image

Comparison of cavitation performance under different schemes

This paper selects S1, S4, the initial scheme (OS), and the suction-side pressure of the blade to predict the NPSHre (NPSH required) of the pump under the design operating conditions. The formula for the calculation is as follows:

$$NPS{H_{{\text{re}}}}=\frac{{{P_{\text{0}}}}}{{\rho g}} - \frac{{{P_{{\text{min}}}}}}{{\rho g}}+0.24$$
(36)

where P0 is the inlet total pressure, 1 atm, and Pmin is the suction side minimum pressure value of the blade.

According to many tests on axial-flow pumps, the cavitation of impellers often occurs near the shroud on the suction surface of the blade and close to 10–20% of the inlet width. Therefore, in CFD, the suction side span of the blade is taken as = 0.9, and the minimum pressure of the blade width at the airfoil section; is approximately 10–20% away from the blade inlet.

Figure 12 depicts the NPSHre of the impeller for different schemes. It reveals that along the streamlined direction, the suction side pressure of the impeller decreases firstly and then increases when the span is between 0.1 and 0.75. The maximum NPSHre for the pump in S1 is 7.36 m, the NPSHre for the pump in S4 is 6.55 m, and the minimum NPSHre for the pump in the OS is 6.1 m. The smaller the necessary NPSHre of the impeller is, the greater the cavitation margin and the lower the probability that the pump will cavitate. Both the OS and S4 can satisfy the requirements.

Figure 13 is the suction side pressure cloud diagram of the pump blade. This demonstrates that as σ1 increases, the pressure gradient at the blade suction side becomes more uniform, the range of the low-pressure region decreases, and the range of the inlet low-pressure region at the impeller suction side close to the blade suction side accounts for approximately 20% of the blade width, which is agreement with the results reflected in Fig. 8.

Fig. 12
figure 12

NPSHre of the axial-flow pump under different schemes.

Full size image
Fig. 13
figure 13

Pressure contour diagram of the blade suction side under different schemes.

Full size image

Entropy generation analysis of the axial-flow pump

In this section, three typical working conditions are selected in S4: small discharge conditions (Q = 280 L/s), design operation conditions (Q = 360 L/s), and large discharge conditions (Q = 420 L/s) for an axial-flow pump. Entropy generation in axial-flow pumps can be divided into local and overall entropy generation.

Analysis of local entropy generation

As the inlet part of pump, the inlet pipe is used to provide good inflow conditions for the inlet of the axial-flow pump. Figure 14 represents the ratio of entropy generation under different working conditions of the inlet pipe. Under each operating condition of the inlet pipe, EGWS accounts for approximately 70% and EGTD accounts for 30%, indicating that the inlet pipe is primarily affected by wall entropy generation. However, the percentage of EGDD for each operating condition is approximately equal to 0%, which is negligible and therefore not reflected in the figure. The wall shear force and shear velocity significantly impact the inlet pipe.

Fig. 14
figure 14

Entropy generation ratio diagram of the inlet pipe.

Full size image

The pump impeller is a rotating part that is entirely different from the rest of the stationary parts. It is meaningful to study the proportion of internal entropy generation and the distribution position of high entropy generation. Figure 15 shows the ratio of entropy generation of the impeller under different operation conditions. As discharge increases, the EGTD in the impeller firstly decreases and then increases, but the EGWS increases firstly and then decreases. The EGWS reaches a maximum of 57%, and the EGTD reaches a minimum of 42% under design operating conditions. EGTD and EGWS are nearly the same. This illustrates that although the EGTD due to the strong impeller rotation accounts for a particular proportion, the local loss caused by the wall shear force is also a more nonnegligible part of the impeller loss.

Fig. 15
figure 15

Entropy generation ratio diagram of the impeller.

Full size image

Figure 16 represents the EGWS at the impeller hub. The entropy generation on the surface of the hub is mainly distributed at the upper end under small discharge conditions (Q = 280 L/s). In contrast, under the design and large discharge conditions, most entropy generation occurs in the center of the hub. This could be due to the local high entropy generation caused by the secondary return flow at the outlet of impeller hub under small discharge conditions. Figure 17 depicts the EGWS at the impeller shroud, and the EGWS at the impeller shroud is the smallest under design operation condition. In general, when the pump is operated under the design conditions, the Sgen produced by the impeller is the smallest, the functional ability of the impeller is the strongest, and the pump efficiency is the highest.

Fig. 16
figure 16

Distribution of entropy generation of the impeller hub.

Full size image
Fig. 17
figure 17

Distribution of entropy generation of the impeller shroud.

Full size image

The function of the guide vane is to eliminate the velocity cycling of the water flow at the impeller outlet and to convert the velocity energy into pressure energy. Figure 18 shows the ratio of entropy generation of the guide vane under different working conditions. The EGTD of the guide vane occupies the central part under each discharge condition, which suggests that the guide vane reduces the turbulence and vortex inside the pump. As discharge increases, the EGTD of guide vane decreases firstly and then increases, and the EGWS increases first and then decreases. Under design operating conditions, EGWS reaches a maximum of 40%, and EGTD reaches a minimum of 59%. Figures 19 and 20 demonstrate that under small discharge conditions, the entropy generation of the guide vane is mainly distributed on the blade pressure side. The suction side is where the majority of guide vane blade entropy generation occurs under the design and large discharge operating conditions. Under different operating conditions, the high entropy generation of guide vane is largely distributed at the front end of guide vane inlet, which may be because of the influence of static and dynamic interference at the junction of the impeller and the guide vane.

Fig. 18
figure 18

Entropy generation ratio diagram of the guide vane.

Full size image
Fig. 19
figure 19

Entropy generation distribution of the guide vane hub and blades.

Full size image
Fig. 20
figure 20

Entropy generation distribution of the guide vane shroud.

Full size image

The outlet pipe is the outlet part of the pump, and its function is to further recover the velocity circulation at the guide vane outlet. Figure 21 shows the ratio of entropy generation under different working conditions of the outlet pipe. The EGTD of outlet pipe under different operating conditions also occupies a significant proportion, which indirectly shows the ability of the outlet pipe to maximize the recovery of water kinetic energy at the outlet of the guide vane. With increasing discharge, the EGTD of the outlet pipe first decreases and then increases, and the EGWS firstly increases and then decreases. Under design operating conditions, the EGWS reaches a maximum of 35%, and EGTD reaches a minimum of 65%. The percentage of EGDD is approximately equal to 0% at all operating conditions. Figure 22 reveals that the high entropy generation area is largely concentrated on the inlet of outlet pipe. This is because the flow is kept circulating at a certain velocity after passing through the guide vane. After flowing into outlet pipe, the strong rotation of the water flow driven by the rotation of the motor shaft concentrates on the inlet section of the pipe.

Fig. 21
figure 21

Entropy generation ratio diagram of the outlet pipe.

Full size image
Fig. 22
figure 22

Distribution of entropy generation inside the outlet pipe.

Full size image

Analysis of total entropy generation

Figure 23a, b depict the total entropy generation (Sgen) and the proportion of entropy generation of each over-water flow component for different operating conditions of S4. The Sgen of the inlet pipe increases as the discharge increases, but the proportion is negligible and can be ignored. The Sgen of the impeller, guide vane, and outlet pipe decreases first with increasing discharge. It increases after being small, and there is a minimum value under the design operating conditions. Meanwhile, under the design operating condition, the entropy generation of impeller is the largest among all the over-water flow components, which is 3.37 W/K, accounting for 47% of the total entropy generation, which is nearly half. This indicates that under the design conditions, impeller is the central area of energy dissipation of the pump, which also suggests that the workability of impeller is enhanced. The axial-flow pump has the highest efficiency.

Fig. 23
figure 23

Total entropy generation and proportion of each flow-passing component.

Full size image

Hydraulic loss comparison between entropy generation and pressure difference

The hydraulic loss of each over-water flow section is calculated utilizing the pressure difference method, as shown in Formula (30). R is defined as the ratio of the hydraulic loss calculated using the entropy generation method to the hydraulic loss calculated using the differential pressure method, and Formula (42) is used to calculate R:

$${h_{\text{p}}}=\frac{{{p_{{\text{in}}}} - {p_{{\text{out}}}}}}{{\rho g}}$$
(37)

where, Pin is the total pressure at the pump inlet, Pa, and Pout is the total pressure at the pump outlet, Pa.

$$R=\frac{{{h_{{\text{pro}}}}}}{{{h_{\text{p}}}}}$$
(38)

This paper selects S4 to explore the relationship between the R of each over-water flow section and each discharge condition, and Fig. 24 displays the results. Under each discharge condition, the R of the water inlet pipe is 1.3, the R of impeller and guide vane ___domain increases firstly and then decreases with increasing discharge, and the R of the impeller ___domain fluctuates between 0.595 and 0.686. The guide vane ___domain ratio fluctuates between 0.5 and 0.64, and the R of outlet pipe fluctuates between 0.83 and 1.1.

Fig. 24
figure 24

Ratio R of each flow-passing component.

Full size image

The R of impeller to guide vane ___domain and outlet pipe fluctuates and is small because the high-velocity rotating water flow inside the impeller ___domain retains high rotational strength after flowing into guide vane. Likewise, the rotating flow of water after guide vane enters outlet pipe causes a specific disturbance. In general, the hydraulic loss calculated by entropy generation method is highly consistent with which calculated by differential pressure method, and it is reliable within a specific error range.

Conclusions

This study compares the results of numerical simulation and experimental validation and therefore verifies the reliability of numerical simulation. The effects of different tip cascade density on the axial-flow pump performance and internal flow dissipation mechanism are studied and the following conclusions are drawn:

  1. (1)

    The highest efficiency of the axial-flow pump reached 86.15% for all optimization schemes. The pump head increases gradually with an increase in σ1 under the full discharge condition, while the efficiency gradually decreases. The variation range of large discharge rate is less obvious than that of small discharge rate. The high-efficiency zone of the pump widens as σ1 decreases. There is a minimum value of the hydraulic loss of pipelines near the design operation condition.

  2. (2)

    The pressure gradient on the blade suction side turns increasingly uniform as σ1 increases under the design operating conditions. The size of low-pressure area gradually decreases, NPSHre of the axial-flow pump gradually decreases, and the cavitation performance of the pump gradually improves as σ1 increases. The minimum NPSHre of the impeller for the scheme 4 is 6.55 m.

  3. (3)

    The EGDD is minimal and negligible in each over-water flow section. In the axial-flow pump impeller, EGTD and EGWS are close under each discharge condition. However, in the guide vane and outlet pipe, EGTD is greater than EGWS. The Sgen of the impeller, guide vane, and outlet pipe firstly decreases and then increases with increasing discharge. The impeller has the highest entropy generation among the over-water flow components under the design operating conditions, accounting for 47% of the Sgen. Impeller is the central area of energy dissipation. The hydraulic loss results of entropy generation are consistent with those of pressure difference calculation.