Task offloading for multi-server edge computing in industrial Internet with joint load balance and fuzzy security

The industrial Internet serves as a cornerstone for the next industrial revolution by elevating the intelligence level of traditional manufacturing industries^1,2. The industrial Internet necessitates strong computing power as a support to meet the challenges of real-time product optimization, large-scale data processing, intelligent decision-making, etc. The primary focus of industrial terminals is manufacturing, and their computing power is relatively weak due to constraints such as space, heat dissipation, and cost, which results in insufficient computational capabilities to support the industrial Internet adequately. Several computing paradigms, such as cloud computing, fog computing, and edge computing (EC), have been developed to serve as computing platforms that offer computational resources for impoverished terminals. Task offloading enables the migration of tasks to external platforms, resulting in the enhancement of terminal capabilities³. Unfortunately, as a mature computing paradigm, cloud computing fails to address the computational challenges faced by the industrial Internet due to its inherent characteristics of long-backhaul latency, lower security in data transmission through public networks, and significant bandwidth consumption⁴. Fog computing utilizes computing power on network nodes for processing during data transmission, necessitating transmission over public networks and where the computational capabilities of network nodes are very limited⁵. Edge servers are typically positioned within a one-hop distance from industrial terminals, offering the potentiality for low latency, bandwidth efficiency, and enhanced security⁶. EC provides a compliant computational platform for the industrial Internet, enabling the offloading of industrial computing tasks to edge servers⁷.

The decision regarding which tasks should be offloaded to edge servers has a significant impact on the EC performance and is the primary challenge that EC must address⁸. The partial offloading allows tasks to be proportionally offloaded to edge servers for execution, providing a finer granularity compared to binary offloading (the task is either fully offloaded or not offloaded at all). Improper task offloading not only hinders the full potentiality of EC but also suppresses its performance due to the additional data transmission overhead, ultimately rendering EC incapable of supporting the industrial Internet⁹.

Additionally, latency and security constitute two pivotal requirements for EC task offloading in the industrial Internet. Many manufacturing processes necessitate low latency for real-time processing of their data^10,11. For example, in the manufacturing process of large-scale precision mechanical components, such as ship propellers, lathes dynamically adjust their parameters based on the shape and size of the components in real-time. The prolonged latency would impede the timely adjustment of cutting parameters on lathes, leading to the inability to achieve the desired specifications of the components and resulting in defective products. EC in the industrial Internet faces elevated security challenges as a result of the inclusion of industrial computing tasks, which frequently involve trade-sensitive information, such as mechanical size parameters and material recipes. Concerns regarding the possible disclosure of trade secrets may lead factory owners to exhibit hesitancy in adopting EC. Furthermore, EC entails the distributed deployment of a substantial number of edge servers, which inherently possess limited resources compared to cloud data centers. The isolated utilization of a single edge server falls short of fully leveraging the potentiality of EC. To fully exploit the benefits of EC, it is imperative to employ multiple edge servers in a collaborative manner¹². Therefore, EC task offloading in the industrial Internet is characterized by the coupling of latency, security, and multi-server considerations.

When considering multiple edge servers, the importance of load balancing cannot be overstated. Without proper load balancing, there is a risk of tasks from terminals being disproportionately offloaded to specific edge servers, resulting in an uneven distribution of load and the potentiality for network congestion among edge servers. Consequently, this imbalance can adversely impact the overall load distribution and resource utilization efficiency of the entire system, leading to a decrease in system throughput^13,14,15. The detrimental consequences of performance degradation or service interruption due to server overload can be effectively mitigated through the equitable distribution of tasks among multiple edge servers.

Furthermore, in real-life industrial Internet scenarios, assessing task security risks often involves multiple uncertainties, such as data gaps, subjective judgments, and fuzzy boundaries^16,17. Traditional binary evaluation methods provide only two discrete outcomes: risky or risk-free. This simplistic categorization may overlook the complexity and subtle variations of task risks, leading to potential information loss in the evaluation process. Task risks are typically continuous and progressive, and binary methods fail to capture these nuances accurately. In practice, industrial task risks often exist at varying levels and degrees, making binary classification insufficient. Fuzzy numbers provide a more flexible and adaptive approach to handling the uncertainty and variability of task risks¹⁸. The fuzzy evaluation method allows for customization based on specific circumstances and requirements by adjusting the parameters and boundaries of fuzzy numbers. Compared to traditional binary methods, fuzzy numbers offer a more comprehensive spectrum of risk levels, enabling a more accurate representation of task risk gradations. Through fuzzy sets and membership functions, fuzzy logic can better express the various levels and subtle variations in task risks, providing a more precise and adaptable evaluation method.

The motivation of this paper is to tackle the latency-aware multi-server partial EC task offloading problem in the industrial Internet, emphasizing the integration of joint load balancing and security protection to optimize resource allocation and ensure the confidentiality of sensitive industrial data. To achieve this goal, we present an innovative task offloading approach that includes a novel task offloading model and a novel bi-layer offloading algorithm. To formulate the task offloading problem, we establish a task offloading model that enables partial offloading, leading to reduced latency, task offloading across various edge servers with load balancing, and consideration of fuzzy task risks. The established model is formulated as a three-objective constrained mathematical optimization model that targets the reduction of latency, load balancing, and mitigation of security risks. After formalizing the problem, we provide a proof demonstrating that the formulated model is NP-hard. Unfortunately, due to the inherent complexity of NP-hard problems, exact solutions cannot be obtained in polynomial time. Nevertheless, an alternative approach using evolutionary algorithms can be employed to efficiently approximate solutions. Evolutionary algorithms, drawing inspiration from natural processes such as human activities, swarm intelligence, and physical phenomena, exhibit the capacity to efficiently identify global optimum solutions. This efficacy is characterized by reduced computational time, a harmonious blend of exploration and exploitation, and the delivery of precise results^19,20,21. Therefore, we propose a bi-layer offloading algorithm with joint load balance and fuzzy security, which is based on the adaptive genetic algorithm and simulated annealing particle swarm optimization, to solve the established model. Our offloading algorithm decomposes the established model into two layers for solution. The upper-layer algorithm determines which edge server the task should be offloaded to, while the lower-layer algorithm determines the ratio of task offloading. The main contributions of this paper are summarized as following:

1. (1)

   We establish a latency-aware partial task offloading model for multi-server EC in the industrial Internet with joint load balancing and security protection. The established model supports fine-grained multi-server task offloading, allowing tasks to be offloaded proportionally. Moreover, this model employs fuzzy numbers to represent task risks and balances the load among multiple edge servers. We formulate this model as a constrained mixed integer optimization problem and prove its NP-hardness.

2. (2)

   We propose a bi-layer offloading algorithm with joint load balance and fuzzy security, which is based on the adaptive genetic algorithm and simulated annealing particle swarm optimization, to solve the offloading strategy from the established model. Our offloading algorithm decomposes the model into two layer for solution, and constructs the offloading strategy as a composite of offloading ___location and ratio. We employ the adaptive genetic algorithm in the upper-layer algorithm to determine the offloading ___location, and utilize simulated annealing particle swarm optimization in the lower-layer algorithm to optimize the offloading ratio based on the obtained offloading ___location.

3. (3)

   We conduct extensive experiments to validate the established offloading model and evaluate the effectiveness of the proposed offloading algorithm. These experiments comprehensively investigate the influence of diverse system parameters on the optimization objective. Additionally, we perform a comparative analysis of our offloading algorithm against five existing algorithms to assess its efficiency and performance.

The remainder of this paper is organized as follows. The second section summarizes the related work. The third section describes the system model, the problem formulation, and the proof of NP-hardness. The fourth section illustrates the proposed offloading algorithm. In the fifth section, the established model and proposed offloading algorithm are evaluated. Finally, the sixth section concludes this paper.

As a new paradigm that can support the industrial Internet, EC integrates various domains including communication, Internet of things (IoT), and automation, and has garnered significant attention as a prominent research area. Task offloading, as a primary challenge in the realm of EC, has garnered considerable attention and witnessed substantial research endeavors. We categorize existing relevant work into the following three classes for summarization and analysis.

Basic task offloading

You and Tang²² studied the task offloading problem in industrial IoT and proposed a particle swarm optimization-based task offloading strategy. They employed their strategy to offload tasks from resource-constrained terminals to edge servers, with the objective of reducing latency, energy consumption, and task execution cost. Zhou et al.²³ studied the task offloading problem in the healthcare IoT and formulated the offloading problem as an adversarial multi-armed bandit model. They proposed a ultra reliable and low latency communication-aware scheme to minimize the long-term energy consumption under latency requirements. Jiao et al.²⁴ studied the the online offloading problem in industrial IoT to optimize the tradeoff of the task accomplishing time and energy consumption. They proposed a time-energy trade-off online offloading algorithm called TETO to solve the online offloading problem. Deng et al.²⁵ proposed two partial offloading strategies based on the reinforcement learning to optimize the latency in industrial IoT. Liu et al.²⁶ studied the task offloading problem in the ultra-dense network and formulated this problem as a Markov decision process model that aims to minimize the latency and energy consumption in the long term. They proposed an attention-based double deep Q network to solve their offloading model. Dai et al.²⁷ investigated the collaborative task offloading problem to achieve latency reduction while avoiding network congestion. They proposed a collaborative task offloading framework and a learning-based algorithm for collaborative task offloading to minimize the system cost (i.e., task latency and offloading cost). Guo et al.²⁸ studied the task offloading problem in the industrial Internet and formulated it as a mixed integer non-linear programming model. They proposed a heuristic algorithm based on greedy policy to minimize the system overhead caused by task offloading. Saleem et al.²⁹ provided an integrated partial offloading and interference management framework using the orthogonal frequency division multiple access scheme. They formulated the task offloading problem as a mixed integer nonlinear programming model and proposed a scheme named JPORA to minimize the task execution latency. Sun et al.³⁰ proposed a Lyapunov-based task offloading algorithm for 5G-enabled Internet of vehicles scenarios to maximize the average profit of mobile EC providers through optimal task offloading decisions. Sun et al.³¹ addressed the task scheduling problem in space-air-ground integrated networks and proposed an algorithm named PFAPPO that combines proportional fairness-aware auction with deep reinforcement learning to optimize resource allocation and task offloading, thereby maximizing the system profit and ensuring load balancing. Sun et al.³² proposed a game-theoretic framework for joint mode selection and power adaptation in 5G vehicular networks to maximize the network throughput and improve energy efficiency while meeting the delay requirements of multi-priority vehicular services.

Task offloading with joint load balance

Mondal et al.³³ proposed an economic and non-cooperative game-theoretic model for load balancing among competitive cloudlets. They formulated the problem as a generalized Nash equilibrium model and designed a variational inequality based algorithm to compute the pure-strategy Nash equilibrium. Chen et al.³⁴ studied the task offloading problem with joint load balancing in the ultra-dense network and proposed a load estimation algorithm based on user load prediction. Xu et al.³⁵ studied the edge server selection and task allocation problem, and formulated this problem as an online linear programming model with the objective of minimizing task execution and transmission make-spans. They proposed an online deep reinforcement learning-based simultaneous multi-server offloading algorithm to solve their model. Lu et al.³⁶ proposed a workload balancing scheme for multi-road side units, which dynamically adapts to varying task popularity in dynamic environments. This scheme aims to prevent resource wastage caused by offloading duplicate tasks, thereby optimizing resource utilization. In order to improve the overall system utility, Yan et al.³⁷ studied the task offloading problem in unmanned surface vehicles network and proposed an algorithm based on deep reinforcement learning for optimizing load balancing in task offloading. Their proposed algorithm enables the selection of the most suitable edge server or cloud server for efficient offloading, thereby improving the overall system performance. Lu et al.³⁸ proposed a task offloading strategy based on deep reinforcement learning, which improves the deep Q-network algorithm by incorporating an long short-term memory network layer and a candidate network set. The objective of their strategy is to optimize latency, energy consumption, and load balancing. Hossain et al.³⁹ proposed a task offloading management scheme based on fuzzy decision-making, which takes into account both vertical and horizontal task offloading scenarios to cater to diverse user requirements. Their scheme prioritizes the balancing of network and computational resources when making offloading decisions, ensuring optimal utilization of available resources.

Task offloading with joint security

Nguyen et al.⁴⁰ formulated the joint optimization problem of task offloading and privacy preservation as a Markov decision process model. They proposed a reinforcement learning-based task offloading algorithm specifically designed for a dynamic blockchain network. Samy et al.⁴¹ propose a framework based on the blockchain technology for secure task offloading, ensuring guaranteed performance in terms of execution latency and energy consumption. They formulated the joint task offloading model as an NP-hard model and proposed a deep reinforcement learning-based algorithm to address it. Xu et al.⁴² proposed a task offloading method for video surveillance in the Internet of vehicles, aiming to reduce time costs, maintain load balancing of edge nodes, and enhance privacy protection. They formulated the joint problem as a multi-objective optimization model and employed the technique for order preference by similarity to ideal solution (TOPSIS) to solve it. Wei et al.⁴³ investigated the problem of personalized privacy-aware task offloading in the industrial IoT. They proposed an approach based on local differential privacy and deep reinforcement learning to address this challenge. Lingayya et al.⁴⁴ introduced a privacy-preserving framework based on Petri nets, encompassing techniques such as synchronization, sequential execution, concurrency, and conflict resolution. They employed a multi-agent-based cohesion approach to ensure consistent protection of user privacy and secure services in the face of the challenges posed by diverse tasks and global data management. Dai et al.⁴⁵ proposed a learning-based vehicle-to-vehicle offloading algorithm, which achieves low-latency and high-efficiency task offloading in dynamic vehicular networks by comprehensively evaluating the computational capacity and privacy risk of server vehicles.

Brief summary

The task offloading problem is commonly formulated as an optimization model, aiming to optimize various indicators such as latency, cost, energy consumption, and other relevant factors. The basic task offloading focuses solely on making reasonable offloading decisions to optimize EC indicators within, without incorporating any supplementary mechanisms^{22,23,24,25,26,27,28,29,30,31,32}. In scenarios involving task offloading across multiple edge servers, the need for load balancing becomes evident and imperative. By balancing the workload across the available edge servers, the system can avoid resource bottlenecks, and prevent overloading of specific servers^{33,34,35,36,37,38,39}. Although EC holds strong potentiality in terms of security, unreasonable task offloading will undermine this potentiality, leading to the risk of task information leakage^46,47. Therefore, it is imperative to implement requisite measures to ensure the security of EC⁴⁸. Security concerns associated with task offloading have garnered significant attention, compelling researchers to actively address and incorporate security protection measures within their offloading solutions^{40,41,42,43,44,45}.

Comparison of the related work is illustrated in Table 1. The existing work on basic task offloading predominantly concentrates on establishing optimization models for different scenarios and optimizing some indicators, often neglecting the incorporation of supplementary mechanisms to further enhance performance and address specific challenges. The basic task offloading lacks the utilization of collaborative capabilities among multiple edge servers, fails to adapt to the latency and security requirements of industrial Internet, and does not fully harness the maximum potentiality offered by EC. While some studies have incorporated load balancing into task offloading, their focus primarily lies within civil scenarios, lacking in-depth exploration of the key aspects pertaining to the industrial Internet. Existing task offloading approaches that incorporate security protections primarily rely on encryption algorithms and blockchain technology, which introduce additional overhead and potentially hinder the efficiency of EC task offloading.

Different from existing work, this paper focuses on the problem of latency-aware multi-server EC partial task offloading in the industrial Internet. We integrate load balancing and fuzzy security protection mechanisms to optimize the utilization of edge server resources and provide a more precise characterization of task risks. Furthermore, we leverage a partial offloading mode to facilitate task offloading at a fine-grained level. To address the composite offloading strategy derived from the established model, we propose a bi-layer offloading algorithm with joint load balance and fuzzy security, which is based on the adaptive genetic algorithm and simulated annealing particle swarm optimization. In contrast to existing work, our proposed approach offers the support for latency-aware multi-server EC partial task offloading in the industrial Internet with joint load balancing and fuzzy security, which has not been extensively explored before.

Scenario description

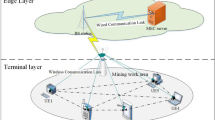
The system architecture, as depicted in Fig. 1, comprises a collection of industrial terminals and a set of edge servers. Let N represent the number of industrial terminals, and M denote the number of edge servers in the system. Due to their primary responsibility in manufacturing operations and the constraints imposed by the manufacturing environment, industrial terminals exhibit a significantly limited resource capacity in terms of computing power. Under the system architecture illustrated in Fig.  1, tasks on the industrial terminals can be partially offloaded to edge servers via wireless networks, thereby expanding the available computing resources of the industrial terminals. The system comprises multiple edge servers available for selection by industrial computing tasks. When offloading tasks from industrial terminals to edge servers, decisions need to be made regarding which server to offload to and the proportion of tasks to be offloaded for execution on the destination edge server. Additionally, it is necessary to consider the load balancing across multiple servers, ensuring that task execution meets the requirements of low latency and security. The task offloading decisions are orchestrated by the control server situated at the macro base station (MBS). The notations used in this paper are summarized in Table 2.

The system architecture.

Full size image

System model

Computation model

Let \(H_{i}=(D_{i},C_{i},\widehat{{\textbf{S}_i}})\) denote the computing task on the ith ( \(1\le i\le N\) ) industrial terminal. \(D_{i}\) represents its data size, \(C_{i}\) (in CPU cycles per bit) represents the number of CPU cycles required to compute one bit of data, and \(\widehat{\textbf{S}}_i\) represents its fuzzy security level. The offloading strategy for task \(H_i\) is composed of two distinct components. One component is the offloading ratio, denoted as a continuous variable \(x_i\) (\({x_i} \in [0,1]\)). \(x_i\) denotes the proportion of task \(H_i\) that is offloaded to the edge server for execution. As the value of \(x_i\) increases, a greater amount of computing overload will be offloaded to the edge server. Another component is the offloading ___location, represented by a binary variable \(y_{ij}\) (\(y_{ij} \in \{0,1\}\)). \(y_{ij}\) indicates whether task \(H_i\) is offloaded to the jth (\(1 \le j \le M\)) edge server \(E_j\) or not. \(y_{ij}=1\) means that task \(H_i\) is offloaded to edge server \(E_j\), while \(y_{ij}=0\) means that task \(H_i\) is not offloaded to edge server \(E_j\).

Although the computing power of industrial terminals is limited, they also have the possibility to perform a certain proportion of tasks. Let \(f_i^{l}\) denote the CPU frequency of the ith industrial terminal. When a fraction of the task is executed locally at the ith industrial terminal, the computation latency \(t_i^l(x_i)\) is expressed as

in which \(C_i^l(x_i)=(1-x_i)D_iC_i\).

Let \(f_j^e\) denote the the CPU frequency allocated from edge server \(E_j\). When a portion of the task is offloaded to edge server \(E_j\) for execution, the computation latency \(t_{ij}^e\big (x_i,y_{ij}\big )\) is expressed as

in which \(\beta _{ij}(x_{i},y_{ij})=x_{i}y_{ij}D_{i}C_{i}\).

Communication model

During the process of task offloading to edge servers, wireless networks are utilized for transmitting data between industrial terminals and edge servers. However, this data transmission introduces communication latency, which should be counted into the overall latency of task offloading in addition to the computation latency. The presence of additional communication latency significantly influences the efficacy of task offloading. Excessive communication latency can potentially negate the advantages of task offloading and may even yield adverse outcomes, leading to inferior task offloading performance compared to local execution on industrial terminals.

The transmission latency required to offload task \(H_i\) to edge server \(E_j\) is

in which \(r_{ij}\) represents the wireless network rate between the ith industrial terminal and edge server \(E_j\). According to Shannon’s theory⁴⁹, \(r_{ij}\) is expressed as

in which \(b_i\) represents the wireless bandwidth allocated to the ith industrial terminal, \(p_{ij}\) represents the transmission power of the ith industrial terminal when transmitting data to edge server \(E_j\), \(g_{i}\) represents the gain of the channel used to transmit data from the ith industrial terminal, and \(\zeta\) represents the noise power.

Load balance model

In the endeavor of load balance, CPU, bandwidth, and memory are chosen as the target resources to be balanced, as they serve as pivotal factors influencing system performance and task execution⁵⁰. By considering these three resources, we aim to optimize resource utilization, elevate overall system efficiency, and ensure effective task offloading and execution. We define the load level of edge server \(E_j\) as

in which \(\psi _j(y_{ij})\), \(\lambda _j(y_{ij})\) and \(\omega _j(y_{ij})\) represent edge server \(E_j\)’s resource utilization of CPU, bandwidth, and memory, respectively. \(\alpha _1\sim \alpha _3\) denote their weights and are constrained by \(\alpha _1+\alpha _2+\alpha _3=1\). \(\psi _j(y_{ij})\), \(\lambda _j(y_{ij})\) and \(\omega _j(y_{ij})\) are expressed as follows, with the constraint that their values do not exceed 1.

\(f_j^e\) represents the allocated CPU resources from edge server \(E_j\), \(b_i\) represents the wireless bandwidth allocated to the ith industrial terminal, and \(m_i\) represents the memory allocated to the ith industrial terminal. \(\Psi _j\) and \(\Omega _j\) represent the CPU capacity and memory capacity of edge server \(E_j\), respectively. \(\Lambda\) represents the wireless bandwidth capacity.

Let \(\overline{\Gamma _j}(y_{ij})\) denote the average load level of M edge servers, expressed as

Load variance is a measure of the variability of load distribution among different edge servers through the concept of variance. When the load is unevenly distributed, the variance value of edge server load will be more significant, reflecting the task offload imbalance. This imbalance may cause some edge servers to be overloaded while others are lightly loaded, thus affecting the performance and stability of the entire system. Let \(\Phi (y_{ij})\) denote the load variance, expressed as

Fuzzy security model

The triangular fuzzy number is utilized to effectively characterize the security level associated with the industrial task. To assess the security level of a task comprehensively, it is necessary to consider multiple perspectives. In this paper, we employ set \(\{u_1,u_2,u_3\}=\{\text {Task data, Task type, Terminal lifecycle}\}\) to represent the viewpoint for measuring task security level. To facilitate the comprehensive evaluation of the security level, we employ an evaluation set \(\{\text {High, Medium, Low}\}\), whose assessment scoring levels are shown in Table 3.

For example, from the perspective of task type (\(u_2\)), a triangular fuzzy number (0.28, 0.65, 0.86) can be assigned by a factory expert to represent the security level of task \(H_i\). In this example, the value 0.28 represents the lower bound of the security level assessment, indicating the expert’s minimum evaluation within the given task type. The value 0.65 represents the expert’s most probable assessment considering the task type. Lastly, the value 0.86 denotes the upper bound of the security level assessment, reflecting the expert’s highest evaluation based on the given task type.

We assume that L factory experts evaluate the task security level from different perspectives (\(u_1\), \(u_2\), and \(u_3\)). Let \(\widehat{S}_{li}^{(k)}=\left( \underline{s}_{li}^{(k)},s_{li}^{(k)},\overline{s}_{li}^{(k)}\right)\) denote the task security level assessment result given by the lth expert from the perspective of \(u_k\). Since experts have different working experiences, a weight matrix \(\mathbf {\varepsilon }=\left[ \varepsilon _l\right] _L\) is set for each expert’s evaluation in the overall evaluation. The evaluation result of the security level of N tasks from the perspective of \(u_k\) by L experts is expressed

in which \(\widehat{S}_i^{(k)}=\left( \underline{s}_{i}^{(k)},s_{i}^{(k)},\overline{s}_{i}^{(k)}\right)\) represents task \(H_i\)’s fuzzy security level from the perspective of \(u_k\). Correspondingly, security level \(\widehat{\textbf{S}}_i\) of task \(H_i\) can be expressed as \(\widehat{\textbf{S}}_i = \left[ \widehat{S}_i^{(k)}\right] _{k = 1}^3\). \(\underline{s}_{i}^{(k)} =\sum \nolimits _{l = 1}^L {{\varepsilon _l}{\underline{s}} _{li}^{(k)}}\) represent the lower bound of the weighted evaluation result for \(H_i\) from the perspective of \(u_k\). Similarly, \(s_{i}^{(k)} = \sum \nolimits _{l = 1}^L {{\varepsilon _l}s_{li}^{(k)}}\) denotes the most possible value of the weighted evaluation result for \(H_i\) from \(u_k\), while \(\overline{s}_{i}^{(k)} = \sum \nolimits _{l = 1}^L {{\varepsilon _l}{\overline{s}} _{li}^{(k)}}\) signifies the upper bound of the weighted evaluation result from \(u_k\).

The fuzzy transformation method is a viable approach for converting a triangular fuzzy number into a single value. Let \({\textbf{S}^{(k)}} = [S_1^{(k)},...,S_i^{(k)},...,S_N^{(k)}]\) represent the converted matrix from \(\widehat{\textbf{S}}^{(k)}=\left[ \underline{s}_{1}^{(k)},s_{1}^{(k)},\overline{s}_{1}^{(k)},\underline{s}_{2}^{(k)},s_{2}^{(k)},\overline{s}_{2}^{(k)},...,\underline{s}_{N}^{(k)},s_{N}^{(k)},\overline{s}_{N}^{(k)}\right]\), where each element is determined using the transformation method proposed by Dong et al.⁵¹ The transformed element, denoted as \(S_i^{(k)}\), is expressed as

Considering that different \(u_k\) may have varying degrees of influence, distinct weights are employed to account for their respective impacts. Let \(\eta _k\) denote the weight of \(u_k\), where \(\eta _k\ge 0, \sum _{k=1}^{3}\eta _{k}=1\). In summary, the security level of N tasks is expressed as

whose element \(S_i=\eta _{1}{S}_{i}^{(1)}+\eta _{2}{S}_{i}^{(2)}+\eta _{3}{S}_{i}^{(3)}\) represents task \(H_i\)’s security level.

We use security risks to quantitatively evaluate the security degree during task offloading process. The security risk of task \(H_i\) is expressed as

in which \(\theta\) represents the security threshold. In the case where the task security level exceeds the predetermined threshold, a security risk is present. An increasing trend in security risks is associated with a decreasing task security level. Conversely, when the security level is below or equal to the threshold, the security risk is assigned a value of 0. The security risk of task \(H_i\) in the offloading process is expressed as

Problem formulation

The problem formulation provides a mathematical description of the latency-aware partial task offloading problem for multi-server EC in the industrial Internet with joint load balancing and security protection. This formulation lays the foundation for quantitatively addressing the optimal composite offloading strategy. This paper strives to achieve three key objectives: minimizing latency, mitigating security risks, and reducing load variance.

The latency incurred during task offloading encompasses the transmission latency and the computation latency introduced by the edge server, in addition to the inherent latency associated with local computation latency. The offloading latency of task \(H_i\) is calculated by

in which \(t_{i}^{l}(x_{i})\) represents task \(H_i\)’s local computation latency, \(t_{ij}^{tr}(x_{i},y_{ij})\) represents the transmission latency of task when it is offloaded to edge server \(E_j\), and \(t_{ij}^{e}(x_{i},y_{ij})\) represents the computation latency of task when it is offloaded to edge server \(E_j\). The total execution latency of N tasks is expressed as

in which \(\textbf{X} = {[{x_i}]_{N}}\), and \(\textbf{Y} = {[{y_{ij}}]_{N \times M}}\). The normalized latency \(T(\textbf{X},\textbf{Y})\) is calculated by \(T(\textbf{X},\textbf{Y}) = {{{T^{total}}(\textbf{X},\textbf{Y})} / {{T_{\max }}}}\), in which \(T_{\max }\) represents the maximum latency. The total security risk of N tasks is expressed as

The normalized security risk \(\xi (\textbf{X},\textbf{Y})\) is calculated by \(\xi (\textbf{X},\textbf{Y}) = {{{\xi ^{total}}(\textbf{X},\textbf{Y})} / {{\xi _{\max }}}}\), in which \(\xi _{\max }\) represents the maximum security risk. Since the load variance is calculated based on resource utilization, which is already normalized, we integrate these three optimization objectives into a single objective function using the linear weighting method. The objective function \(F(\textbf{X},\textbf{Y})\) is expressed as

in which \({\delta _1}\sim {\delta _3}\) represent the weights of latency, security risk, and load variance.

Our objective is to simultaneously optimize latency, security risk, and load variance by adjusting the composite offloading strategy composed of offloading ___location and offloading ratio. The task offloading problem is formulated as objective function (20) with constraints (6–8,21–23):

      s.t.

Formula (20) represents the minimization of the objective function, in which the offloading ratio \(\textbf{X}\) and the offloading ___location \(\textbf{Y}\) are independent variables, while the objective function F, composed of latency, security risk, and load variance, serves as the dependent variable. Constraint (6) guarantees that the CPU capacity of edge server \(E_j\) remains unexceeded. Constraint (7) ensures that the bandwidth of edge server \(E_j\) remains within the specified limit. Constraint (8) ensures that the memory capacity of edge server \(E_j\) will not be surpassed. Constraint (21) ensures that the offloading ratio \(x_i\) for task \(H_i\) remains a continuous value between 0 and 1. Constraint (22) enforces that the offloading ___location \(y_{ij}\) can only be binary values of 0 or 1. Constraint (23) guarantees that the summation of the three weights equals 1.

Solution space analysis of the system model

The offloading problem is formulated as a constrained combinatorial optimization model, as shown in formulas (6–8, 20–23). This model is hybrid in nature, incorporating both offloading ratios \(\textbf{X}\) and offloading locations \(\textbf{Y}\). In terms of offloading locations, for each task, there are \(M+1\) possible locations (including M edge servers and the option for local execution). Therefore, for N tasks, the total number of possible solutions is \((M+1)^N\). As a result, the solution space of the optimization model is \((M+1)^N\), indicating that the solution space grows exponentially with the number of tasks and increases idempotently with the number of edge servers. The complexity of the system model is quite high, posing significant challenges in solving it.

As the number of tasks and edge servers increases, the solution space expands rapidly, leading to a combinatorial explosion that must be accounted for. Although the idempotent increase in the number of edge servers is less dramatic than the exponential growth in the number of tasks, it still adds significant computational burden to the task offloading optimization process. This rapid expansion leads to substantial computational challenges, making exhaustive searches of the entire solution space infeasible in most practical scenarios. Therefore, as the solution space grows, it becomes critical to employ efficient offloading algorithms that balance solution quality with computational efficiency.

NP-hardness proof of the system model

Theorem 1

The established task offloading optimization model is NP-hard.

Proof

The knapsack model is a classical combinatorial optimization model, in which a subset of items is chosen from a given set, with the objective of optimizing the objective value while respecting the capacity constraint of the knapsack. The knapsack model has been proven to be an NP-hard model⁵², indicating that it cannot be solved in polynomial time. Specifically, the 0-1 knapsack problem is a variant of the knapsack problem where each item is restricted to either being selected or not selected for inclusion in the knapsack. The knapsack has a fixed capacity, and the total weight of the chosen items must not exceed this capacity limit. Suppose there is a set of N items, where the ith (\(1 \le i \le N\)) item has the corresponding value \(v_i\) and weight \(w_i\). The mathematical formulation of the backpack model can be described as follows:

      s.t.

\(f(\textbf{Z})=\sum \nolimits _{i = 1}^N {{v_i}{z_i}}\) represents the objective function. \(z_i\) is the element of \(\textbf{Z} = {[{z_i}]_N}\) and indicates whether the ith item is selected to be placed in the backpack or not. Constraint (25) ensures that the value of \(z_i\) is binary. The binary variable \(z_i\) is assigned a value of 1 to indicate the selection of the ith item for placement in the knapsack, while a value of 0 signifies that the ith item is not chosen for inclusion in the knapsack. Constraint (26) guarantees that the total weight of the selected items does not exceed the capacity limit W of the knapsack.

We conduct an analysis on a simplified version of our task offloading optimization model, focusing solely on latency, a single edge server, and binary offloading mode. In the simplified task offloading optimization model, the objective is to efficiently offload suitable tasks to the edge server with the aim of minimizing latency. By regarding N tasks as N items and perceiving the edge server as the knapsack, the simplified model can be analogized to a knapsack scenario, where the objective entails selecting (offloading) the appropriate items (tasks) for inclusion within the knapsack (edge server). Since the simplified model has only one edge server, the number of edge servers \(M=1\), and the offloading ___location strategy degenerates from \(\textbf{Y}={[{y_{ij}}]_{N \times M}}\) to \(\textbf{Y}={[{y_i}]_N}\). Simultaneously, due to the simplification of partial offloading to binary offloading within the simplified model, the offloading ratio strategy \(x_i\) and the offloading ___location strategy \(y_i\) become equivalent. The simplified objective function can be expressed as

Define an objective function \(t(\textbf{Y})\) as

Let \(t_i^e\) denote the computation latency when task \(H_i\) is executed on the edge server. Let \(T^e\) denote the computation latency of executing N tasks on the edge server. Then, the simplified task offloading optimization model can be formulated as

         s.t.

Formula (29) presents the objective function formulated to minimize the latency. Constraint (30) imposes binary restrictions on the variables, ensuring that their values can only be 0 or 1. Constraint (31) ensures that the latency resulting from offloaded tasks executed on the edge server does not exceed the overall latency incurred by executing all tasks solely on the edge server. Formulas (29)–(31) mathematically convert the simplified task offloading optimization model into the knapsack model. Our complete task offloading optimization model extends the simplified model by incorporating multiple edge servers, partial offloading mode, load balancing, and fuzzy security. This extension significantly increases the complexity compared to the simplified model, which is mathematically transformed into the NP-hard knapsack model presented in formulas (29)–(31). Henceforth, the established task offloading optimization model is demonstrated to be NP-hard.□

Overview

Accurately solving NP-hard problems within the polynomial time is infeasible, as algorithms designed to solve such problems often exhibit exponential time complexity. Evolutionary algorithms, such as genetic algorithm and particle swarm optimization, offer efficient alternatives to exhaustive search by exploring the solution space in an adaptive manner. These algorithms can provide near-optimal solutions within a reasonable time, which makes them suitable for addressing the computational challenges of task offloading in multi-server EC environments. In this paper, we propose a bi-layer offloading algorithm with joint load balance and fuzzy security, which is based on the adaptive genetic algorithm and simulated annealing particle swarm optimization, to solve the established NP-hard model.

The genetic algorithm is a widely-used evolutionary algorithm inspired by the process of natural selection. It is particularly effective in solving discrete optimization problems by simulating evolution through operators such as selection, crossover, and mutation. In task offloading, it optimizes the offloading ___location by assigning tasks to the most appropriate edge server based on resources and network conditions⁵³. On the other hand, particle swarm optimization is well-suited for continuous optimization problems, such as the offloading ratio decision. It mimics the social behavior of birds flocking, where each particle adjusts its position based on its own experience and that of its neighbors, ultimately converging to an optimal or near-optimal solution²². These methods are foundational in our proposed bi-layer offloading algorithm, with the genetic algorithm handling the discrete assignment of tasks to edge servers and particle swarm optimization determining the offloading ratio.

Given the inherent coupling between the offloading ratio decision and the offloading ___location decision within the established optimization model, our approach decomposes the offloading problem into bi-layer to effectively address this interdependence. The upper layer is responsible for determining the task’s offload ___location (i.e., which edge server will handle the task), while the lower layer focuses on optimizing the offloading ratio (i.e., the proportion of the task to be offloaded). The upper layer uses a discrete decision variable \(y_{ij}\), representing the assignment of the offloaded task to a specific edge server. In contrast, the lower layer uses a continuous variable \(x_{ij}\), representing the proportion of task i to be offloaded to server j once the ___location is determined.

The proposed offloading algorithm employs adaptive genetic algorithm and simulated annealing particle swarm optimization in the upper and lower layers, respectively. The key idea revolves around utilizing an adaptive genetic algorithm to address the discrete offloading ___location strategy within the upper layer, while employing a simulated annealing particle swarm algorithm to tackle the continuous offloading ratio strategy within the lower layer. The optimized offloading ratio from the lower-layer algorithm is fed back to the upper-layer algorithm to refine subsequent task allocation decisions. The pseudo-codes for the upper-layer and lower-layer algorithms are presented in Algorithms 1 and 2, respectively.

Upper-layer algorithm based on the adaptive genetic algorithm

The upper-layer algorithm

Full size image

Initialization

Initialization plays a crucial role in the upper-layer algorithm as it sets the foundation for the subsequent evolutionary process. Its primary objective is to generate an initial population of candidate individuals (chromosomes), which serves as a representation of the starting search space. We randomly generate an initial population based on the size of the genetic population, which is an input to the upper-layer algorithm. Random initialization allows for the exploration of a wide range of possible solutions, promoting diversity within the initial population. This diversity helps to prevent premature convergence to sub-optimal solutions and encourages the upper-layer algorithm to explore different regions of the search space.

Fitness function

The fitness function assesses the quality of individuals within the population, serving as a means to quantify the suitability of solutions for survival and reproduction during the evolutionary process in the upper-layer algorithm. Its principal objective is to assign a fitness value to each individual, reflecting its performance and guiding the search process. We define the fitness function as

which equates the minimization of the objective function to the maximization of fitness value. The rationale behind this transformation lies in the need to harmonize the upper-layer algorithm with the genetic algorithm framework, thereby fostering the evolutionary process and facilitating subsequent selection operations for the preferential reproduction of individuals with superior fitness.

Selection

The selection operation determines which individuals from the current population will be chosen as parents for the creation of offspring in the next generation. Its primary objective is to favor individuals with higher fitness values, thereby promoting the propagation of favorable traits and driving the population towards improved solutions. By favoring individuals with higher fitness, the upper-layer algorithm enhances the probability of identifying the optimal offloading ___location. The roulette wheel selection algorithm, employed in this paper, is based on the principle of proportional selection. It simulates a roulette wheel where each individual’s fitness value corresponds to a portion of the wheel’s circumference. The algorithm assigns a probability of selection to each individual that is proportional to its fitness value relative to the total fitness of the population. The probability of the ith individual \(\textbf{Y}[i]\) being selected is calculated by

in which \({{f_u}(\textbf{X},\textbf{Y}[i])}\) (\({{f_u}(\textbf{X},\textbf{Y}[j])}\)) is the fitness of the ith (jth) individual. A random number \(\pi \in (0,1)\) is generated to select the individual. The first individual \(\textbf{Y}[i]\) that satisfies condition \(\sum \nolimits _{j=1}^i {{P_j}} \ge \pi\), is selected.

Crossover

Selected parent individuals contribute their genetic information to create offspring individuals by crossover. The crossover process entails the exchange of genetic segments between parent individuals, resulting in the generation of novel combinations within the offspring individuals. The crossover facilitates the exploration of the solution space by generating offspring individuals that inherit advantageous traits from both parent individuals. The crossover operation initially identifies a gene segment comprised of one or more contiguous genes from each parent individual. Subsequently, this gene segment is inserted into the corresponding position within the opposite parent individual.

To determine whether a crossover operation should be performed, a random number within the range of 0 to 1 is generated and compared against the crossover probability \(P_c\). A higher \(P_c\) contributes to increased diversity and exploration, aiding the upper-layer algorithm in discovering a greater number of possible solutions. However, a higher \(P_c\) may result in a slower convergence speed. A lower \(P_c\) can make the upper-layer algorithm more susceptible to getting trapped in local optima, consequently limiting its exploration capability. \(P_c\) serves as a critical parameter that substantially influences the performance of the upper-layer algorithm. Regrettably, the conventional \(P_c\) is fixed and lacks the ability to adapt to the iterations of the upper-layer algorithm.

Consequently, this paper incorporates an adaptive \(P_c\) expressed as

in which \(P_{c1}\) and \(P_{c2}\) (\(P_{c1} > P_{c2}\)) are two constants, \(f_u^h\) denotes the higher fitness value among the two parent individuals, \(f_u^{avg}\) represents the average fitness value of the population, and \(f_u^{\textit{max}}\) signifies the maximum fitness value within the population. In contrast to the conventional constant \(P_c\), the adaptive \(P_c\) takes the shape of a right-angled trapezoid. This adaptive form reduces the probability of crossover when the fitness of the parent individuals is high, thereby effectively preserving individuals with superior fitness and promoting the retention of advantageous traits within the population.

Mutation

Mutation serves as a mechanism to maintain genetic variability within the population, preventing premature convergence to sub-optimal solutions. Through the mutation operation, a small random perturbation is applied to the genetic information of individuals, leading to the creation of new genetic variants. The mutation operation involves the selection of genes with a probability denoted as \(P_m\), and a random number is generated within the range of 0 to 1 to determine the occurrence of gene mutation. Similarly, inappropriate \(P_m\) will also suppress the performance of upper-layer algorithm. A larger \(P_m\) facilitates enhanced exploration of the search space, introducing novel gene variants to the upper-layer algorithm. However, it may result in a slower convergence rate. Conversely, a smaller \(P_m\) will weaken the exploration capability of the upper-layer algorithm, leading to a propensity for local optima. Adaptive \(P_m\) is calculated by

in which \(P_{m1}\) and \(P_{m2}\) (\(P_{m1} > P_{m2}\)) are two constant values, while \(f_l\) denotes the fitness of the parent individual. The remaining parameters remain consistent with those outlined in Equation (34).

Lower-layer algorithm based on the simulated annealing particle swarm optimization

The lower-layer algorithm

Full size image

Initialization and fitness function

The initialization of particle swarm optimization provides a suitable starting point for the subsequent iterative search of the lower-layer algorithm. The particle swarm optimization utilizes the movement of particles within a defined range to search for the optimum solution, making it particularly suitable for continuous optimization problems involving the offloading ratio at the lower layer. The initialization process involves the initialization of particle positions and particle velocities. This paper employs the random initialization method to generate the initial particle population and initial velocities. The particle position is constructed as N-dimensional to represent the offloading ratios of N tasks. The velocity of each particle is also N-dimensional, representing the rate of movement in each dimension for the particle.

The fitness function evaluates the quality of solutions in lower-layer algorithm by mapping each particle to a numerical value. It serves the purpose of assessing the quality of solutions. The fitness function of the lower-layer algorithm is defined as

A smaller fitness function value of a particle indicates a higher quality of its represented solution.

Update of individual and global best positions

The evaluation results of the fitness function are utilized to determine the individual best position for each particle and the global best position for the population. The individual best position corresponds to the solution associated with the historical extremum of the individual fitness, while the global best position corresponds to the solution associated with the historical extremum of the population’s fitness. By updating the individual and global best positions, the lower-layer algorithm is able to progressively optimize solutions within the search space, enabling individuals and the entire particle swarm to approach their optimums gradually. This updating mechanism guides particles to search in more favorable solution spaces, thereby enhancing the convergence and search efficiency of the lower-layer algorithm.

When updating the individual best position, a comparison is made between the current solution’s fitness and the historical individual best fitness value to determine whether an update is necessary. Let \({\textbf{X}^{pb}}[j]\) represent the individual best position of the jth particle, and \(\textbf{X}(iter)[j]\) denote the position of the jth particle in the iterth iteration. If \(f_l\left( \textbf{X}(iter)[j],\textbf{Y}\right) < f_l\left( \textbf{X}^{pb}[j],\textbf{Y}\right)\), it signifies that the current position of the particle is better than its historical best position, prompting an update from \(\textbf{X}^{bp}[j]\) to \(\textbf{X}(iter)[j]\). The purpose of updating the individual best position is to ensure that each particle maintains tracking of its individual optimal solution and performs more targeted searches in subsequent iterations.

When updating the global best position, the comparison between the best fitness value of the current population and the historical global best fitness value is performed to determine whether an update to the global best position is required. Let \({\textbf{X}^b}\) denote the global best position, and \(\textbf{X}^b(iter)\) represent the best position of the population in the iterth iteration. If \(f_l\left( \textbf{X}^b(iter), \textbf{Y} \right) < f_l\left( \textbf{X}^b, \textbf{Y} \right)\), it indicates that the best position of the current population is better than the historical global best position, thereby triggering an update from \(\textbf{X}^b\) to \(\textbf{X}^b(iter)\). The purpose of updating the global best position is to maintain tracking of the optimal solution for the entire particle swarm and provide guidance throughout the entire search process.

Update of particle velocity and position

The purpose of velocity updating is to guide particles in exploring the search space and encourage them to approach their individual best position and the global best position, thereby assisting the lower-layer algorithm in obtaining superior solutions. When updating the velocity, the current velocity, individual best position, and global best position are taken into account. Subsequently, the particle’s velocity is updated by applying appropriate factors such as the inertia factor, learning factor, and random factor. This integration of factors facilitates a balanced adjustment that considers the particle’s inherent motion tendency, the guidance provided by both the individual and global best positions, and the introduction of controlled randomness to enhance the overall search capability. Through the comprehensive utilization of these factors, particles are able to conduct targeted exploration within the search space, with the ultimate goal of discovering superior solutions. Velocity of the jth particle in the iterth iteration is updated by

in which \(\chi (iter)\) denotes the inertia factor, \(\vartheta _1\) and \(\vartheta _2\) are random numbers between 0 and 1, \(c_1\) and \(c_2\) are learning factors. The inertia factor serves as an indicator of particles’ inherent motion tendency, while the learning factor is utilized to facilitate behavioral adjustments based on the individual and global best positions. Furthermore, the random factor introduces a controlled level of stochasticity to enhance the global search capability of the lower-layer algorithm. Position of the jth particle in the iterth iteration is updated by

The inertia factor reflects the influence of the previous iteration’s velocity on the current particle velocity. A higher value of the inertia factor strengthens the global optimization capability of the lower-layer algorithm while weakening the local optimization capability. Conversely, a lower value of the inertia factor weakens the global optimization capability and enhances the local optimization capability of the lower-layer algorithm. This paper employs a dynamic inertia factor, expressed as

in which \(\chi _1\) represents the maximum inertia factor, \(\chi _2\) represents the minimum inertia factor, iter represents the current number of iterations, and Iter represents the maximum number of iterations. The dynamic inertia factor offers a greater flexibility for the lower-layer algorithm. As the number of iterations increases, the dynamic inertia factor progressively decreases. Consequently, the lower-layer algorithm exhibits a strong global search capability in the early stages, enabling exploration of previously unexplored regions. In the later stages, it demonstrates a strong local optimization capability and enables a fine-grained search.

A decision criterion based on simulated annealing is utilized to determine the necessity of performing updates. Simulated annealing introduces a mechanism for escaping local optima by allowing occasional acceptance of worse particles. This promotes exploration of the search space and prevents premature convergence to sub-optimal solutions.

in which \(f_l^{'}\) denotes the fitness of the new particle position, \(f_l\) denotes the fitness of the current particle position, \(T_{iter}\) denotes the current temperature. A random number \(\pi \in (0,1)\) is generated and compared with \({P_{sa}}(f_l^{'},{f_l})\). If \(\pi < {P_{sa}}(f_l^{'},{f_l})\), the new particle position is accepted and updated to become the latest position of the particle.

The experiments were conducted on a PC equipped with the Intel Core i5 CPU (2 cores, 2.3 GHz), 16 GB of RAM, and a 64-bit operating system. The algorithms were implemented in Java using the JDK 1.8 development environment. To ensure the robustness of our evaluations, the experimental parameters were generated randomly within specified ranges rather than using fixed values. This approach captures the variability in system parameters and allows for testing under a wide range of scenarios, providing a comprehensive assessment of the established offloading model and the proposed offloading algorithm. In this study, we utilized synthetic datasets specifically designed to simulate realistic industrial Internet tasks, encompassing a wide range of resource demands and execution constraints. The synthetic data were carefully crafted based on extensive practical experience to ensure they accurately reflect real-world conditions. By randomly generating the experimental parameters within specified ranges, we covered various potential operational conditions, thereby enhancing the reliability of our evaluations.

The evaluation of the system model section first analyzes the impact of varying system parameters on the objective values, as solved by the proposed offloading algorithm. This provides insight into how different system configurations affect the performance of the established model. Following this, in the evaluation of the offloading algorithm section, we conduct a performance comparison between our offloading algorithm and other offloading algorithms to assess its effectiveness. The default experimental parameter settings used for these evaluations are summarized in Table 4.

Evaluation of the system model

We first evaluate the impact of different offloading modes on the task execution performance. According to the system architecture, there are three offloading modes:

1. (1)

   Edge: All tasks are offloaded to edge servers for execution.

2. (2)

   Local: All tasks are executed on the industrial terminals.

3. (3)

   Local-Edge: The execution of tasks can be performed either locally on industrial terminals or offloaded to edge servers. The offloading strategy is provided by the approach presented in this paper.

Objective values under different offloading modes.

Full size image

Figure 2 shows the objective values under different offloading modes. It can be observed that the objective value of Local-Edge mode is the minimum, while the objective value of Local mode is the maximum, with the objective value of Edge mode falling between the two extremes. This phenomenon signifies that offloading tasks to external platforms has the possibility to improve task execution efficiency. However, the achievement of such gains necessitates the implementation of precise offloading strategies. Incorrect offloading strategies can lead to misguidance in the task offloading process, consequently yielding unfavorable outcomes. In comparison to Edge and Local modes, the objective value of Local-Edge mode exhibits reductions of 27% and 46%, respectively. It is evident that blindly offloading all tasks to edge servers is not the optimal strategy. The underlying reason is that offloading tasks to edge servers introduces additional consumptions attributed to task data transmission. In the absence of precise offloading decisions, the potential decrease in objective value achieved by task offloading may be offset by the overhead incurred from data transmission.

Latencies under different offloading modes.

Full size image

The objective function comprises three sub-objectives: latency, security risk, and load variance. Figure 3 demonstrates the optimization effect of the sub-objective of latency, serving as an example to illustrate the performance improvement of the sub-objectives. The results reveal that the latency of the Local mode exhibits the highest value, reaching 820ms. The Edge mode demonstrates a slight reduction in latency, with a measured value of 774ms. The Local-Edge mode yields the lowest latency, recorded at 667ms. Compared to the Local mode and Edge mode, the Local-Edge mode achieves reductions in latency of 18.7% and 13.8%, respectively. The results indicate that task offloading indeed contributes to the reduction of task execution latency. Our model will offload tasks to appropriate locations for execution based on the optimization objective. However, it is crucial to emphasize that the accuracy of offloading strategy significantly impacts the offloading performance.

Figure 4 shows objective values under different numbers of edge servers. The observed trend reveals a gradual decrease in the objective values as the number of edge servers increases. The reduction in objective values from 3 edge servers to 9 edge servers is 13.22%. This indicates that scaling up the edge server quantity positively impacts the offloading performance. The decreasing trend in objective values can be attributed to the distribution of tasks among a larger number of edge servers, resulting in a more balanced load and efficient execution of tasks. The availability of additional edge servers enhances the system’s capability to offload tasks efficiently, thereby reducing both latency and load variance. However, the decrease in objective values demonstrates diminishing returns as the number of edge servers increases. For example, the reduction in objective values from 3 edge servers to 5 edge servers is 6.9%, while the decrease from 5 edge servers to 7 edge servers is 4.84%, and finally, the decrease from 7 edge servers to 9 edge servers is only 1.95%. This phenomenon indicates that increasing the number of edge servers does not lead to an infinite improvement in task offloading performance. The underlying reason is that when a sufficient number of edge servers are available, the limiting factor for offloading performance shifts away from the availability of edge resources.

Objective values under different numbers of edge servers.

Full size image

Figure 5 shows latencies under different numbers of edge servers. It can be observed that there is a decreasing trend in the task execution latencies as the number of edge servers increases. This suggests that increasing the number of edge servers has a positive impact on the system’s performance in terms of reducing task execution latency. Specifically, as the number of edge servers increases from 3 to 9, there is a 19.02% decrease in latency. The substantial reduction in task execution latency indicates that utilizing more edge servers leads to significant improvements in task processing efficiency. As the number of edge servers increases, the available resources for task execution also increase. The proposed offloading approach can avoid the pressure of resource capacity constraints, allowing for optimized task offloading with minimized latency. This finding provides experimental evidence and reference for enhancing the efficiency of EC systems and ensuring timely task execution.

Latencies under different numbers of edge servers.

Full size image

Figure 6 illustrates the comparison of objective values with and without load balancing. The results demonstrate that the final objective value is 0.628 without load balancing, whereas with load balancing, the final objective value is reduced to 0.537. In the absence of load balancing, offloading tasks among edge servers may be uneven, leading to resource overutilization or underutilization. The presence of load imbalance will lead to the non-offloading of some tasks, thereby increasing the objective value. This discrepancy can lead to a decline in EC performance and may potentially diminish the effectiveness of task execution. Load balancing plays a crucial role in offloading the tasks evenly across multiple edge servers. The experimental results indicate that the load balancing in our model effectively mitigates this issue.

Objective values with and without load balancing.

Full size image

Figure 7 shows objective values under different numbers of industrial terminals. The results demonstrate an increasing trend in the objective value with an increase in the number of industrial terminals. Specifically, when the number of industrial terminals increased from 60 to 120, there is a 25% growth in the objective value. The fundamental cause of this phenomenon is attributed to the escalating number of industrial terminals, which consequently escalates both the task and resource demand. The availability of resources is relatively higher when the number of industrial terminals is small, enabling the system to better meet the offloading requirements of tasks, resulting in lower objective values. However, as the number of industrial terminals increases, the availability of resources decreases, intensifying the competition among tasks and leading to an increase in the objective value. The constrained task offloading and the subsequent rise in objective values stem from the system’s limited resources, which hinder the simultaneous fulfillment of all task requirements.

Objective values under different numbers of industrial terminals.

Full size image

Figure 8 shows load variances under different numbers of industrial terminals. It can be observed that with the increase in the number of industrial terminals, the load variance on edge servers gradually increases. As the number of industrial terminals increases from 60 to 140, there is an upward trend in the load variance, rising from 0.208 to 0.280. With the increase in the number of industrial terminals, the competition for edge server resources becomes more pronounced. Under the constraint of a fixed number of edge servers, the availability of edge resources is limited, and the system needs to prioritize the execution of a greater number of tasks. As the number of industrial terminals continues to rise, edge servers experience an increased load pressure. This results in a wider distribution of the edge server load and a gradual increase in load variance. The experiment demonstrates that, alongside load balancing, as the number of industrial terminals continues to increase, the addition of edge servers should also be considered to uphold EC efficiency.

Load variances under different numbers of industrial terminals.

Full size image

Figure 9 shows objective values under different wireless network rates. It can be observed that as the wireless network rate increases, the objective value continuously decreases. When the wireless network rate increases from 6M/s to 15M/s, the objective value decreases by 15.19%. This suggests that higher wireless network rates contribute to the improved performance and efficiency in achieving the desired objective. In order to achieve an improvement in task offloading performance, it is necessary for the data transmission consumption during offloading process to be lower than the execution consumption after the tasks are offloaded. As the wireless network rate increases, the data transmission consumption consistently decreases, thereby amplifying the reduction in objective value resulting from task offloading. This experiment highlights the significance of wireless networks in task offloading and further demonstrates the positive impact of fast network rates on the objective value.

Objective values under different wireless network rates.

Full size image

By adjusting the weights of three sub-objectives, the effect of different weights on the objective value can be observed. The results are shown in Fig. 10. It can be seen that the objective value exhibits the smallest value for the first set of weights (\(\delta _1=0.2,\delta _2=0.5,\delta _3=0.3\)), an intermediate value for the second set of weights (\(\delta _1=0.3,\delta _2=0.2,\delta _3=0.5\)), and the largest value for the third set of weights (\(\delta _1=0.5,\delta _2=0.3,\delta _3=0.2\)). The first set of weights is characterized by a higher proportion of security risks, the second set of weights exhibits a higher proportion of load variance, and the third set of weights is associated with a higher proportion of latency. This observation indicates that the value of latency sub-objective is relatively large. As the weight assigned to sub-objective latency becomes larger, it contributes more heavily to the calculation of the weighted objective value. The experimental findings suggest that our model enables users to freely adjust weights, allowing for customized task offloading based on their individual needs.

Objective values under different weights.

Full size image

Evaluation of the offloading algorithm

In this section, we present a comparative evaluation for the proposed offloading algorithm against existing offloading algorithms to validate its performance. The conducted experiments in this section encompass the assessment of six distinct offloading algorithms: (1) our proposed bi-layer offloading algorithm with joint load balance and fuzzy security (BOALBFS), which is based on the adaptive genetic algorithm and simulated annealing particle swarm optimization; (2) the offloading algorithm based on the genetic algorithm and particle swarm optimization (GAPSO); (3) the offloading algorithm based on the simulated annealing and particle swarm optimization (SAPSO); (4) the offloading algorithm based on the hill climbing and particle swarm optimization (HCPSO); (5) the offloading algorithm based on the grey wolf optimization and particle swarm optimization (GWOPSO); (6) the offloading algorithm based on the improved whale optimization and particle swarm optimization (IWOPSO).

Performance comparison of offloading algorithms under different numbers of iterations.

Full size image

Figure 11 shows the performance comparison of offloading algorithms under different numbers of iterations. The results demonstrate that with an increasing number of iterations, offloading algorithms converge to their stable objective values. Evidently, the final objective value of BOALBFS is the smallest, indicating its superior performance compared to other offloading algorithms. In contrast, HCPSO demonstrates the highest final objective value, indicating its comparatively poorer performance among the evaluated offloading algorithms. In terms of quantitative analysis, BOALBFS achieves a reduction in the objective value compared to algorithms HCPSO, SAPSO, GWOPSO, GAPSO, and IWOPSO, with respective decreases of 28.04%, 22.24%, 14.16%, 10.34%, and 7.80%. The utilization of a local optimization heuristic algorithm in the upper layer of HCPSO prevents it from performing global search, resulting in being trapped in local optima and ultimately leading to a higher objective value. The observations reveal that IWOPSO and GAPSO exhibit premature convergence, while SAPSO and GWOPSO show relatively slower convergence but lower search efficiency. Although IWOPSO, GAPSO, SAPSO, and GWOPSO possess the capabilities for global optimization, their achieved objective values surpass that of HCPSO but are inferior to BOALBFS. This disparity arises due to the augmented global optimization ability of AGAPSO, which benefits from the integration of adaptive mechanism, simulated annealing, genetic algorithm, and particle swarm optimization.

Comparison of the running time of offloading algorithms.

Full size image

Figure 12 presents a comparison of the running time among different offloading algorithms. It is evident that HCPSO demonstrates the shortest running time, with values that are a mere fraction of BOALBFS, GAPSO, SAPSO, GWOPSO, and IWOPSO. Specifically, HCPSO’s running time is only 27.63%, 25.54%, 22.57%, 24.20%, and 26.44% of the running times of BOALBFS, GAPSO, SAPSO, GWOPSO, and IWOPSO. This phenomenon can be attributed to the absence of iterative search in the upper-layer algorithm of HCPSO. The non-iterative nature of HCPSO’s upper-layer algorithm allows it to make faster decisions, resulting in a significant reduction in the overall computational effort required to end the running process. However, as depicted in Fig. 11, HCPSO exhibits the lowest accuracy. The running time of BOALBFS is found to be higher than that of HCPSO but lower than the running times of GAPSO, SAPSO, GWOPSO, and IWOPSO. This observation highlights the advantage of BOALBFS, which achieves the highest level of accuracy with a comparatively lower running time. While BOALBFS achieves the highest accuracy, there are scenarios where faster running speed takes precedence over precision. In such cases, BOALBFS offers flexibility by reducing the number of iterations, enabling quicker results with minimal impact on accuracy. This adaptability makes it suitable for real-world applications where timely decisions are crucial, such as in time-sensitive industrial processes. Additionally, algorithms like HCPSO, with naturally shorter running times, can be employed when speed is the priority. Though HCPSO sacrifices some accuracy, its fast execution makes it ideal for tasks where approximate solutions are acceptable, such as in emergencies or high-priority operations.

Latencies of offloading algorithms in different scenarios.

Full size image

To thoroughly validate the proposed offloading algorithm, a comprehensive comparison is conducted with existing algorithms across various scenarios. In these scenarios, the wireless network rate changes from 4M/s to 10M/s. Table 5 presents the latencies of offloading algorithms across different scenarios, while their performance is visually depicted using box plots in Fig. 13. The results reveal that BOALBFS consistently achieves the minimum latency compared to other algorithms, indicating its superior performance across various scenarios. This consistent minimization of latency underscores the robustness and efficiency of BOALBFS in handling diverse operational conditions. In relation to BOALBFS, GAPSO, SAPSO, HCPSO, GWOPSO, and IWOPSO exhibit relative errors of 5.90%, 9.32%, 13.25%, 3.94%, and 2.82% respectively. The presence of positive error values signifies BOALBFS’s higher degree of accuracy, thus affirming its efficacy in optimizing task offloading. The substantial reduction in latency is attained exclusively when the offloading algorithm demonstrates a sufficiently high level of accuracy. In contrast, inaccurate offloading algorithms compromise the system performance and fail to achieve significant improvements in latency reduction. Consistent with the outcomes depicted in Fig. 9, the observations reveal a discernible trend where the reduction in latency is consistently observed with the progressive improvement of wireless network rates. The underlying reason for this phenomenon remains consistent, as the continuous increase in wireless network rate effectively reduces data transmission latency, consequently leading to a reduction in the overall latency of task offloading.

This paper aims to address the problem of latency-aware multi-server partial task offloading for EC in the industrial Internet by integrating joint load balancing and security protection. A novel task offloading model and a bi-layer offloading algorithm were presented. We established a constrained optimization model to mathematically formalize the task offloading problem for EC in the industrial Internet, providing a quantitative foundation for investigating it. The NP-hardness of the established model was rigorously demonstrated through a formal proof. To solve the composite offloading strategy, comprising both the offloading ___location and offloading ratio derived from the NP-hard model, we proposed a bi-layer offloading algorithm with joint load balance and fuzzy security, which is based on the adaptive genetic algorithm and simulated annealing particle swarm optimization. The upper-layer algorithm was responsible for determining the appropriate edge server to which the task should be offloaded, while the lower-layer algorithm determined the optimal ratio of task offloading. Drawing upon extensive experimental results, it was found that the evaluation outcomes of the established model aligned with the expected results. The proposed offloading algorithm was shown to outperform existing algorithms in terms of solution accuracy, demonstrating its superior performance. In the future, collaboration among multiple industrial terminals and competition among multiple edge servers will be considered based on this work. The expanded problem will allow tasks to be offloaded among industrial terminals and will support games among edge servers. To address this problem, a game theory-based model incorporating “terminal-to-terminal offloading” and “terminal-to-edge offloading” will be established, while accounting for interest competition among edge servers. This model will be more complex and challenging to solve, and parallel offloading algorithms will be explored to efficiently address its computational complexity.