Introduction

As critical lifeline infrastructure, power tower systems are susceptible to collapse and failure under extreme conditions1, directly affecting people’s productivity and daily life. Therefore, the research on the ultimate capacity of towers has become increasingly important. The incremental nonlinear finite element method (INFEM) is the commonly used numerical method for ultimate capacity, which is nonlinear iterative and time-consuming in calculation. In recent years, the Elastic Modulus Reduction Method (EMRM), an efficient and highly accurate linear elastic iterative method, has been developed and applied in various structures2,3,4,5. Generalized yield criteria (GYC) (i.e., interaction relationships) and homogenization play a crucial role in the EMRM. Equal-leg angle steel is a common member in towers. As illustrated in Fig. 1, the centroid (C) and shear center (S) of equal-leg angles do not coincide, making them singly symmetric. The legs of angles are prone to local buckling, and stability design is conducted based on parallel axes (y1, z1 axes) when there are continuous lateral torsional restraints along the length of members; otherwise, it is performed along the principal axes (y, z axes).

Fig. 1
figure 1

Section parameters of equal-leg angle.

Full size image

Numerous studies have explored GYCs for angle sections. Vayas et al.6 proposed a brief GYC that included both normal force and bi-axial bending. Cho et al.7 established an improved GYC by considering the position between the neutral axis and the legs. Based on both of the above, Charalampakis8 improved the exponential relationship of the function to eliminate errors, which occur when the neutral axis intersects one leg at a small angle.

However, these GYCs for angle sections mainly focus on strength safety, excluding stability and buckling factors such as initial bending, initial eccentricity of loads, and residual stress. Many studies have shown that these stability factors accelerate the deformation of angle steel tower members and significantly reduce their ultimate capacities9,10,11,12,13,14,15,16. Trahair et al.17,18,19,20 proposed a second-order elastic-torsional analysis and established an implicit GYC for bi-axial bending. Aydin et al.21,22 created an invisible GYC for both normal force and bi-axial bending, considering lateral-torsional and local buckling. Behzadi-Sofiani et al.23,24 modified the stability coefficient of the GYC in Eurocode 3 (EC3)25. Rasmussen26,27 improved expressions for the effective width and centroid of angle sections in AS/NZS 460028, overcoming the influence of effective eccentricity.

Currently, different design codes25,28,29,30,31,32,33 all use explicit expressions of GYCs that consider stability effects. GB50017-201729, DL/T5154-201230, ASCE 10-201531, and AISC 360-0532 introduce stability coefficients or reduction factors for normal force. ANSI/AISC 360-1633 considers both normal force and bi-axial bending effects but involves complex calculations using critical section points to establish angle steel GYC. AS/NZS 460028 provides GYC for both normal force and bi-axial bending, accounting for the influence of effective eccentricity (1/1000 of the length) based on the characteristic of single-angle steel members.

The GYCs for the stability of angle sections provided in the literature and codes are either implicit expressions and complex, or insufficient internal forces. Moreover, the internal forces in these criteria are non-proportionally loaded. Homogenization is necessary for the GYF to analyze effectively the stability ultimate capacity of equal-leg angle steel towers using linear elastic iterative methods.

In this paper, an efficient linear elastic iterative method is proposed for the stability ultimate capacity of equal-leg angle steel towers. Firstly, the angle steel stability GYC from the literature27,28 is selected from current design codes, which focus on the influence of stability factors and consider both normal force and bi-axial bending. Furthermore, the GYF is derived based on the GYC of equal-leg angle members using dimensionless expressions. The HGYFs with different orders are developed by regression analysis with 4421 fitting points uniformly distributed on the yield surface. The GYF includes two parameters in addition to the internal forces, which complicates the process of selecting polynomials for regression analysis.

From the HGYFs, a simple and high-accuracy HGYF through quantitative and qualitative analysis is selected. Based on the HGYF, the element load ratio is proposed as a dynamic threshold for distinguishing high-stress and low-stress elements in equal-leg angle elements. Then, an adaptive elastic modulus adjustment strategy is proposed for the linear elastic iterative analysis of the stability ultimate capacity of equal-leg angle steel towers. Finally, a single-span angle steel beam with analytical and traditional incremental nonlinear finite element methods (i.e., INFEM) and a tower with INFEM are adopted as benchmarks to demonstrate the accuracy and efficiency of the HGYF and the linear elastic iterative method.

Generalized yield criteria

GYC in different design codes

Table 1 shows the summary and comparison of GYCs for angle sections from different design codes that all consider stability factors. However, many codes, such as GB50017-201729, DL/T5154-201230, ASCE 10-201531, and ANSI/AISC 360-0532, use simplified interaction relationships that focus only on normal force and ignore bi-axial bending. ANSI/AISC 360-1633 establishes GYC based on critical points and involves complex calculations. EC325 covers both axial force and bi-axial bending while requiring excessive parameters and complex formulations. AS/NZS 4600-201828 incorporates both normal force and bi-axial bending with simple calculations and clear formulations.

Table 1 GYC for angle steel in different design codes.
Full size table

For equal-leg angle steel (with leg width B and leg thickness T) subjected to normal force N and biaxial bending (My0, Mz0), its stability GYC is as shown in Eq. (1), which is selected from the literature27,28. Equation (1) considers the influence of stability factors through NP, αy and αz.

$$\frac{N}{{N_{P} }} + \frac{{e_{y} N + M_{y0} }}{{\alpha_{y} M_{Py} }} + \frac{{e_{z} N + M_{z0} }}{{\alpha_{z} M_{Pz} }} \le 1$$
(1)
$$e_{y} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\quad \lambda_{{\text{p}}} = \sqrt {\frac{{f_{y} }}{{f_{{{\text{cr}}}} }}} \le 1.22} \hfill \\ {\frac{5b}{{16\sqrt 2 }} \cdot \frac{{\lambda_{{\text{p}}} - 1.22}}{{\lambda_{{\text{p}}} - 0.22}},} \hfill & {\quad \lambda_{{\text{p}}} = \sqrt {\frac{{f_{y} }}{{f_{{{\text{cr}}}} }}} > 1.22} \hfill \\ \end{array} } \right.$$
(2)
$$f_{{{\text{cr}}}} = \frac{{k_{{\text{c}}}\uppi ^{{2}} E}}{{12\left( {1 - \nu^{2} } \right)}}\left( \frac{T}{b} \right)^{2} ,\;\;k_{{\text{c}}} = \frac{{6\left( {1 - \nu } \right)}}{{\uppi ^{{2}} }},\;\;b = B - \frac{T}{2}$$
(3)
$$N_{P} = \rho Af_{y}^{\prime} = 2\rho bTf_{y}^{\prime} ;\;\;M_{Py} = \frac{\sqrt 2 }{2}f_{y0} b^{2} T;\;\;M_{Pz} = \frac{\sqrt 2 }{4}f_{y0} b^{2} T$$
(4)
$$\alpha_{y} = 1 - \frac{N}{{N_{{{\text{E}}y}} }};\;\;\alpha_{z} = 1 - \frac{N}{{N_{{{\text{E}}z}} }};\;\;N_{{{\text{E}}y}} = \frac{{\pi^{2} {\text{E}}A}}{{\lambda_{y}^{2} }};\;\;N_{{{\text{E}}z}} = \frac{{\pi^{2} {\text{E}}A}}{{\lambda_{z}^{2} }}$$
(5)
$$\rho = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\quad \lambda \le 0.673} \hfill \\ {\left( {1 - {{0.22} \mathord{\left/ {\vphantom {{0.22} \lambda }} \right. \kern-0pt} \lambda }} \right),} \hfill & {\quad \lambda > 0.673} \hfill \\ \end{array} } \right.,\;\;\lambda = \sqrt {\frac{{f_{y}^{\prime} }}{{f_{{{\text{cr}}}} }}} ,$$
(6)
$$\begin{aligned} f_{yY}^{\prime} & = \left\{ {\begin{array}{*{20}l} {0.658^{{\lambda_{cY}^{2} }} f_{y0} ,} \hfill & {\quad \lambda_{cY} \le 1.5} \hfill \\ {\frac{0.877}{{\lambda_{cY}^{2} }}f_{y0} ,} \hfill & {\quad \lambda_{cY} > 1.5} \hfill \\ \end{array} } \right.,\;\;\lambda_{cY} = \sqrt {\frac{{f_{y} }}{{f_{eY} }}} ,\;\; f_{eY} = \frac{{\pi^{2} E}}{{\lambda_{y}^{2} }},\;\; f_{y0} = {{f_{y} } \mathord{\left/ {\vphantom {{f_{y} } {1.1}}} \right. \kern-0pt} {1.1}}, \\ f_{yZ}^{\prime} & = \left\{ {\begin{array}{*{20}l} {0.658^{{\lambda_{cZ}^{2} }} f_{y0} ,} \hfill & {\quad \lambda_{cZ} \le 1.5} \hfill \\ {\frac{0.877}{{\lambda_{cZ}^{2} }}f_{y0} ,} \hfill & {\quad \lambda_{cZ} > 1.5} \hfill \\ \end{array} } \right.,\;\;\lambda_{cZ} = \sqrt {\frac{{f_{y} }}{{f_{eZ} }}} ,\;\; f_{eZ} = \frac{{\pi^{2} E}}{{\lambda_{z}^{2} }},\;\;f_{y}^{\prime} = \min \left( {f_{yY}^{\prime} ,f_{yZ}^{\prime} } \right) \\ \end{aligned}$$
(7)

Where ey and ez are the effective eccentricities for the strong axis (y-axis) and the weak axis (z-axis), and ez equals 0 for equal-leg angles26. The Poisson’s ratio ν is commonly taken as 0.3. The parameters above are represented by Eqs. (2)–(7).

Generalized yield function

The GYC is equal to 1 when the angle steel member reaches the plastic limit failure. The GYC of equal-leg angle sections under normal force and bi-axial bending is shown below:

$$f\left( {n,m_{y} ,m_{z} } \right) = 1,$$
(8)

Where \(f\) represents the GYF, and its specific expression reads:

$$f\left( {n,m_{y} ,m_{z} } \right) = n + \frac{{a_{{{\text{E}}y}} b_{{{\text{E}}y}} n}}{{1 - a_{{{\text{E}}y}} n}} + \frac{{m_{y} }}{{1 - a_{{{\text{E}}y}} n}} + \frac{{m_{z} }}{{1 - a_{{{\text{E}}z}} n}}$$
(9)

Where the dimensionless internal forces (i.e., n, my and mz) are given by Eq. (10), and the other parameters are represented as shown in Eq. (11). For an equal-leg angle, aEz is 4 times as large as aEy.

$$n = \frac{N}{{N_{{\text{P}}} }},\;\;m_{y} = \frac{{M_{y0} }}{{M_{{{\text{P}}y}} }},\;\;m_{z} = \frac{{M_{z0} }}{{M_{{{\text{P}}z}} }}$$
(10)
$$a_{{{\text{E}}y}} = \frac{{N_{P} }}{{N_{{{\text{E}}y}} }},\;\;a_{{{\text{E}}z}} = \frac{{N_{P} }}{{N_{{{\text{E}}z}} }},\;\;b_{{{\text{E}}y}} = \frac{{e_{y} N_{{{\text{E}}y}} }}{{M_{{{\text{P}}y}} }}$$
(11)

Let aE = aEy and bE = bEy, Eq. (9) is simplified as follows:

$$f\left( {n,m_{y} ,m_{z} } \right) = n + \frac{{a_{{\text{E}}} b_{{\text{E}}} n + m_{y} }}{{1 - a_{{\text{E}}} n}} + \frac{{m_{z} }}{{1 - 4a_{{\text{E}}} n}},\;\;{\text{and}}\;\;f = 1$$
(12)

Homogeneous generalized yield function

The GYF for angle members in Eq. (12) is a non-homogeneous function that does not satisfy the proportionality condition for plastic limit analysis2. Therefore, it is necessary to homogenize the GYF to establish an equivalent Homogeneous GYF (HGYF). It is worth noting that, the GYF in Eq. (12) includes parameters aE and bE in addition to the internal forces, which complicates the process of selecting polynomials for homogenization.

Selection of fitting points

The dimensionless internal forces (i.e., n, my and mz) all are in the range of 0–1 from the definition. The yield strength of commonly used steel is within Q235-Q460. The slenderness ratio (λ) selected for angle members is between 30 and 150. Based on Eq. (11), the range for aE is in the range of 0.02–0.2, as shown in Table 2. bE takes the value 0 when λp is not greater than 1.22, while it takes values ranging from 0 to 0.7 based on Eqs. (2) and (11) when λp is not less than 1.22.

Table 2 Calculation of aE.
Full size table

It is necessary to use sufficient sample points for regression analysis to achieve a good fit. The screening steps of sample points are as shown below:

  1. (1)

    Equidistant points are selected with an interpolated step of 0.02 within the scope of aE.

  2. (2)

    For each point of aE obtained in the previous step, equidistant points are taken in the range of bE with an interpolated step of 0.1 to obtain each set of (aE, bE).

  3. (3)

    For each set of (aE, bE), equidistant points are arranged in the range of n with an interpolated step of 0.1 to obtain each set of (aE, bE, n). The selection for equidistant points (aE, bE, n, my) follows a similar process.

  4. (4)

    Finally, the combination above, (aE, bE, n, my), is substituted into the GYF determined by Eq. (12) to obtain the values of mz. Filter values of mz in the range of 0 to 1 to determine all the fitting points, (aE, bE, n, my, mz), for the non-homogeneous GYF.

At this point, 4421 fitting points have been selected and uniformly distributed on the yield surface, as defined by Eq. (12).

Form of homogeneous generalized yield function

A homogeneous polynomial is established corresponding to Eq. (12), as shown in Eq. (13).

$${\overline{f}}_{{S_{1} }} \left( {n,m_{y} ,m_{z} } \right) = \sum\limits_{i = 0}^{{S_{1} }} {\sum\limits_{j = 0}^{{{\text{S}}_{1} - i}} {c_{q} n^{i} m_{y}^{j} m_{z}^{{(S_{1} - i - j)}} } } ,\quad q = 1,2, \ldots ,\frac{{\left( {S_{1} + 2} \right)\left( {S_{1} + 1} \right)}}{2}$$
(13)

Where \(\overline{f}_{{{\text{S}}_{1} }} \left( {n,m_{y} ,m_{z} } \right)\) is the HGYF. S1 is the highest degree of \(\overline{f}_{{S_{1} }} \left( {n,m_{y} ,m_{z} } \right)\). For the following three cases, cq = 1: (1). i = S1 and j = 0; (2). i = 0 and j = S1; (3). i = j = 0. For all other cases, cq is as follows:

$$c_{q} = a_{q} b_{q}$$
(14)
$$a_{q} = \sum\limits_{i = 0}^{{S_{{\text{a}}} }} {k_{{q\left( {i + 1} \right)}} a_{{\text{E}}}^{i} } = k_{q1} a_{{\text{E}}}^{0} + k_{q2} a_{{\text{E}}}^{1} + \ldots k_{{q\left( {S_{a} + 1} \right)}} a_{{\text{E}}}^{{S_{{\text{a}}} }} ,\;\;b_{q} = \sum\limits_{i = 0}^{{S_{{\text{b}}} }} {l_{{q\left( {i + 1} \right)}} b_{{\text{E}}}^{i} } = l_{q1} b_{{\text{E}}}^{0} + l_{q2} b_{{\text{E}}}^{1} + \ldots l_{{q\left( {S_{b} + 1} \right)}} b_{\text{E}}^{{S_{{\text{b}}} }}$$
(15)

Where Sa is the highest degree of \(a_{E}^{i}\), Sb is the highest degree of \(b_{E}^{i}\), \(k_{{q( {i + 1} )}}\) and \(l_{{q( {i + 1} )}}\) are coefficients to be determined.

Undetermined coefficients in homogeneous generalized yield functions

Regression analysis is carried out to determine the coefficients (i.e., \(k_{{q( {i + 1})}}\) and \(l_{{q( {i + 1} )}}\) in Eq. (15)) based on the selected fitting points, and then HGYF of different orders (2nd, 3rd and 4th) can be obtained. There are six homogeneous polynomials for different combinations of Sa and Sb from cq, namely: (1) Sa = 1 and Sb = 1; (2) Sa = 1 and Sb = 2; (3) Sa = 2 and Sb = 1; (4) Sa = 2 and Sb = 2; (5) Sa = 3 and Sb = 1; (6) Sa = 3 and Sb = 2. Due to limited space, only the HGYFs and their corresponding coefficients in different orders (2nd, 3rd, and 4th order) at Sa = 1 and Sb = 1 are presented here, and denoted as \(\overline{f}_{2} ,\overline{f}_{3} ,\overline{f}_{4}\), as shown in Eqs. (16)–(18).

$$\mathop {f_{2} }\limits^{-\!\!-} = c_{1} m_{y}^{2} + c_{2} m_{z} m_{y} + c_{3} m_{z}^{2} + c_{4} nm_{y} + c_{5} nm_{z} + c_{6} n^{2}$$
(16)

Where \(c_{1} = c_{3} = c_{6} = 1\), and the others are as follows:

$$\begin{aligned} c_{2} & = \left( { - 0.329 - 2.051a_{{\text{E}}} } \right)\left( { - 5.519 - 0.719b_{{\text{E}}} } \right), \\ c_{4} & = \left( { - 3.193 + 0.970a_{{\text{E}}} } \right)\left( { - 0.640 + 0.028b_{{\text{E}}} } \right), \\ c_{5} & = \left( {0.811 + 1.736a_{{\text{E}}} } \right)\left( {2.238 + 0.526b_{{\text{E}}} } \right). \\ \end{aligned}$$
$$\begin{aligned} \overline{f}_{3} & = c_{1} m_{y}^{3} + c_{2} m_{z} m_{y}^{2} + c_{3} m_{z}^{2} m_{y} + c_{4} m_{z}^{3} + c_{5} nm_{y}^{2} + c_{6} nm_{z} m_{y} + c_{7} nm_{z}^{2} + c_{8} n^{2} m_{y} \\ & \quad + c_{9} n^{2} m_{z} + c_{10} n^{3} \\ \end{aligned}$$
(17)

Where \(c_{1} = c_{4} = c_{10} = 1\), and the others are as follows:

$$\begin{aligned} c_{2} & = \left( {2.017 + 0.436a_{{\text{E}}} } \right)\left( {1.439 + 0.069b_{{\text{E}}} } \right),\;\;c_{3} = \left( {0.689 - 0.022a_{{\text{E}}} } \right)\left( {4.408 - 0.053b_{{\text{E}}} } \right), \\ c_{5} & = \left( {1.636 + 0.209a_{{\text{E}}} } \right)\left( {2.052 - 0.227b_{{\text{E}}} } \right),\;\;c_{6} = \left( {3.241 + 7.048a_{{\text{E}}} } \right)\left( {1.921 - 0.076b_{{\text{E}}} } \right), \\ c_{7} & = \left( {2.324 + 9.070a_{{\text{E}}} } \right)\left( {1.246 + 0.083b_{{\text{E}}} } \right),\;\;c_{8} = \left( {0.988 + 5.243a_{{\text{E}}} } \right)\left( {2.035 + 1.562b_{{\text{E}}} } \right), \\ c_{9} & = \left( {0.430 + 5.597a_{{\text{E}}} } \right)\left( {5.245 + 1.327b_{{\text{E}}} } \right). \\ \end{aligned}$$
$$\begin{aligned} \overline{f}_{4} & = c_{1} m_{y}^{4} + c_{2} m_{z} m_{y}^{3} + c_{3} m_{z}^{2} m_{y}^{2} + c_{4} m_{z}^{3} m_{y} + c_{5} m_{z}^{4} + c_{6} nm_{y}^{3} + c_{7} nm_{z} m_{y}^{2} + c_{8} nm_{z}^{2} m_{y} \\ & \quad + c_{9} nm_{z}^{3} + c_{10} n^{2} m_{y}^{2} + c_{11} n^{2} m_{z} m_{y} + c_{12} n^{2} m_{z}^{2} + c_{13} n^{3} m_{y} + c_{14} n^{3} m_{z} + c_{15} n^{4} \\ \end{aligned}$$
(18)

Where \(c_{1} = c_{5} = c_{15} = 1\), and the others are as follows:

$$\begin{aligned} c_{2} & = \left( {1.259 - 0.193a_{{\text{E}}} } \right)\left( {3.262 - 0.144b_{{\text{E}}} } \right),\;\;c_{3} = \left( {2.043 - 0.248a_{{\text{E}}} } \right)\left( {3.027 - 0.054b_{{\text{E}}} } \right), \\ c_{4} & = \left( {2.706 + 0.360a_{{\text{E}}} } \right)\left( {1.425 + 0.044b_{{\text{E}}} } \right),\;\;c_{6} = \left( {1.517 + 3.517a_{{\text{E}}} } \right)\left( {2.231 + 0.722b_{{\text{E}}} } \right), \\ c_{7} & = \left( {1.503 + 8.605a_{{\text{E}}} } \right)\left( {5.241 + 2.958b_{{\text{E}}} } \right),\;\;c_{8} = \left( {1.862 + 8.214a_{{\text{E}}} } \right)\left( {5.887 + 0.657b_{{\text{E}}} } \right), \\ c_{9} & = \left( {1.588 + 4.327a_{{\text{E}}} } \right)\left( {3.209 - 0.453b_{{\text{E}}} } \right),\;\;c_{10} = \left( {3.324 - 2.212a_{{\text{E}}} } \right)\left( {2.651 - 1.122b_{{\text{E}}} } \right), \\ c_{11} & = \left( {3.113 + 2.163a_{{\text{E}}} } \right)\left( {6.091 - 2.481b_{{\text{E}}} } \right),\;\;c_{12} = \left( {0.442 + 11.214a_{{\text{E}}} } \right)\left( {4.489 + 3.921b_{{\text{E}}} } \right), \\ c_{13} & = \left( {0.651 + 11.00a_{{\text{E}}} } \right)\left( {1.743 + 3.689b_{{\text{E}}} } \right),\;\;c_{14} = \left( {0.462 + 8.099a_{{\text{E}}} } \right)\left( {6.702 + 1.598b_{{\text{E}}} } \right). \\ \end{aligned}$$

The coefficients are shown above for HGYFs with Sa = 1 and Sb = 1 in different orders. The coefficients for others can be seen in Appendix B (i.e., Tables 10, 11, 12, 13, 14 and 15) for details.

Comparison between homogeneous generalized yield functions and generalized yield functions

The accuracy of the established HGYFs can be compared to the original GYF from quantitative and qualitative perspectives in this section.

Quantitative analysis

The fitting accuracies of different orders (2nd, 3rd, and 4th order) of HGYFs for the six homogeneous polynomials are listed in Table 3. RMSE refers to Root Mean Square Error and RC refers to the related coefficient.

Table 3 Fitting accuracy of different orders.
Full size table

It can be observed that overall, the RMSEs of HGYFs in different orders with different Sa and Sb are around 2% with RCs approaching 1, indicating that the six HGYFs all are high-accuracy.

Specifically, first, the RMSEs decrease slightly and the RCs increase slightly with the increase of Sa when HGYFs have the same order and Sb. For example, for the 3rd order HGYF with Sb = 1 and different Sa, the RMSEs are 1.97%, 1.82% and 1.82%, respectively, and the RCs are approximately 0.996.

Secondly, the increase of Sb does not significantly affect the RMSEs and the RCs when HGYFs have the same order as Sa. For example, for the 2nd order HGYF with Sa = 1 and different Sb, both RMSEs are 2.41%, and both RCs are 0.995.

In addition, there is a decreasing trend in RMSEs with the increase of the order when HGYFs have the same Sa and Sb, but the difference is not significant. For example, the RMSEs of the 2nd, 3rd and 4th orders with Sa = 3 and Sb = 1 are 2.40%, 1.82% and 1.62%, respectively, and the RCs are 0.995, 0.997 and 0.998, respectively. The same patterns above are observed in other cases.

In conclusion, the fitting accuracies of HGYFs are consistently high with minor differences for different combinations.

Qualitative analysis

3D yield surfaces of GYF vs. HGYF

The 3D yield surfaces of HGYF in different order with aE = 0.1 and bE = 0.2 are illustrated in Fig. 2 versus the original GYF (f). It should be noted that only the cases of aE = 0.1 and bE = 0.2 are given for the comparison due to limited space. The legend, \(\overline{f}_{432}\), represents the 4th-order HGYF yield surface with Sa = 3, Sb = 2. And others are similar.

Fig. 2
figure 2

3D yield surfaces of GYF vs. HGYF.

Full size image

It can be observed that the 3D yield surfaces from HGYFs with different Sa and Sb exhibit similar fusion properties versus GYF when the order of HGYF is the same. Slight separation is observed with approximately equivalent levels of overlap in the enlarged views, which aligns with the fitting accuracy in Table 3. The uniformity of fusion in the 3D yield surfaces from GYF and HGYFs slightly increases as the order of HGYF increases, with the separation slightly decreasing in the enlarged view. Overall, 3D yield surfaces from GYF and HGYFs are well fused, that is to say, 3D yield surfaces from the six HGYFs maintain high accuracy and consistency with GYF.

Slices of GYF vs. HGYF with different S a and S b

Slices of 3D yield surfaces of HGYFs with aE = 0.1 and bE = 0.2 are illustrated in Fig. 3 versus the ones of the original GYF. There are six different combinations of Sa and Sb for each order, namely Sa = 1, 2, and 3, as well as Sb = 1 and 2. The legend, \(\overline{f}_{432}\), represents the slices of the 4th-order HGYF yield surface with Sa = 3, Sb = 2. And others are similar.

Fig. 3
figure 3

Slices of GYF vs. HGYF with different Sa and Sb.

Full size image

Locally, the shapes of \(\overline{f}_{{S_{1} 11}} ,\overline{f}_{{S_{1} 21}}\) and \(\overline{f}_{{S_{1} 31}}\) (S1 = 2, 3, 4) are basically overlapping and also show a high degree of agreement with GYF in each subgraph of Fig. 3, indicating that the influence of different Sa on HGYF is minimal when HGYFs have the same order and Sb. Furthermore, the fitting accuracy (i.e., RMSE and RC in Table 3) also supports the same conclusion.

Globally, when the order of HGYF is the same, such as in Fig. 3a and b for 2nd-order HGYF, the HGYF with different Sa and Sb matches well with GYF. Their quantitative fitting accuracy is similar, with the RMSE of about 2.4% (as shown in Table 3). Similar patterns are observed for the 3rd-order comparisons in Fig. 3c and d, as well as the 4th-order comparisons in Fig. 3e and f. Therefore, it can be concluded that the influence of different Sa and Sb on HGYF is negligible when the order is the same.

Slices of GYF vs. HGYF with different a E and b E

Based on the above comparisons, slices of 3D yield surfaces of HGYFs with Sa = 1 and Sb = 1 are shown in Fig. 4 versus the ones of the original GYF, with six different combinations selected for aE and bE, i.e., aE = 0.05, 0.1, and 0.2, as well as bE = 0.2 and 0.6.

Fig. 4
figure 4

Slices of GYF vs. HGYF with different aE and bE.

Full size image

Locally, 2nd, 3rd, and 4th order HGYFs can match the GYF to a high degree when HGYFs have the same aE and bE in each subgraph of Fig. 4. This observation holds true for all subgraphs, indicating that different orders have minimal impact on the accuracy of HGYF.

Globally, most of the slices from different orders show good agreement with GYF, as demonstrated in Fig. 4a–e where HGYF and GYF largely overlap. In some individual cases, such as Fig. 4f at n = 0.5, there is a slight deviation when my = 0. The vertical axis mz of each HGYF is relatively consistent, about 0.298 and the value of GYF is 0.261, and the deviation is 0.037. The deviation is not severe and has little impact on the subsequent structural calculations, so it can be ignored. It can be seen that the HGYFs match well with the GYF within all the range values of aE and bE. All the observations above align with the results from Table 3.

The fitting accuracies from different combinations are similar and fall within an acceptable range. Hence, the 2nd order HGYF (\(\overline{f}_{211}\)) with Sa = 1 and Sb = 1 is chosen for simplicity in this paper, as given in Eq. (16).

Stability ultimate capacity analysis

According to the theory of plastic limit analysis, the lower limit value of the ultimate capacity can be determined through the linear elastic iterative method to identify the failure mode. Depending on the original GYF (i.e., \(f\left( {n,m_{y} ,m_{z} } \right)\) in Eq. (12)) and the selected 2nd order HGYF (i.e., \(\overline{f}_{211}\) in Eq. (16)) of the equal-leg angle section, the linear elastic iterative method for stability ultimate capacity of equal-leg angle towers is presented in this section.

The linear elastic iteration method defines the element bearing ratio (EBR) through a homogeneous generalized yield function (HGYF). EBR is used to characterize the development state of the plastic region on the control section of the component element and measure the degree of plastic yield near the full section of the component. If a single internal force acts on an element section, the EBR is equal to the ratio of that internal force to the corresponding section strength. If the element is subjected to the combined action of multiple internal forces, the HGYF established by the linear elastic iteration method can be used to define the EBR.

The EBR, \(r_{k}^{e}\), of angle members under axial force and bi-axial bending may be determined by the GYF and the HGYF respectively, as shown in Eqs. (19) and (20):

$$r_{k}^{e} = \sqrt[{S_{1} }]{{f\left( {n,m_{y} ,m_{z} } \right)}}\;$$
(19)
$$r_{k}^{e} = \sqrt[2]{{\overline{f}_{211} }}\;$$
(20)

Where k is the iterative step, and e is the element number. \(S_{1}\) is a constant determined by \(f\left( {n,m_{y} ,m_{z} } \right)\). When a member is discretized into multiple elements, \(r_{k}^{e}\) takes the maximum value.

\(r_{k}^{e}\) defined by Eq. (20) maintains the same proportional variation with the external load, satisfying the proportional conditions of plastic limit analysis2,3,4. This is crucial for ensuring the stability of the linear elastic iterative method calculation.

According to the principle of conservation of deformation energy, the elastic modulus adjustment strategy for each element of equal-leg angles can be determined as follows:

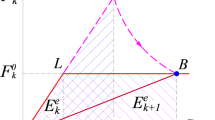
$$E_{k + 1}^{e} = \left\{ {\begin{array}{*{20}l} {E_{k}^{e} \frac{{2\left( {r_{k}^{0} } \right)^{2} }}{{\left( {r_{k}^{e} } \right)^{2} + \left( {r_{k}^{0} } \right)^{2} }},} \hfill & {\quad r_{k}^{e} > r_{k}^{0} } \hfill \\ {E_{k}^{e} ,} \hfill & {\quad r_{k}^{e} \le r_{k}^{0} } \hfill \\ \end{array} } \right.$$
(21)

Where \(E_{k}^{e}\) and \(E_{k + 1}^{e}\) are the elastic moduli of element e in the kth and (k + 1)th iterations, respectively. \(r_{k}^{e}\) and \(r_{k}^{0}\) are the EBR and the reference EBR, respectively. And \(r_{k}^{0}\) is an adaptive dynamic threshold for identifying high bearing elements:

$$r_{k}^{0} = r_{k}^{{{\max}}} - \left( {r_{k}^{{{\max}}} - r_{k}^{{{\min}}} } \right)d_{k}$$
(22)
$$d_{k} = \frac{{\overline{r}_{k} + r_{k}^{\min } }}{{\overline{r}_{k} + r_{k}^{\max } }};\;\;\overline{r}_{k} = \frac{1}{{N_{e} }}\sum\limits_{e - 1}^{{N_{e} }} {r_{k}^{e} }$$
(23)

Where \(d_{k}\) denotes the uniformity of the EBR. \(r_{k}^{\min }\) and \(r_{k}^{\max }\) are the minimum EBR and maximum EBR of all elements, respectively. \(N_{e}\) is the number of all elements. \(\overline{r}_{k}\) is the mean value of all EBRs.

At each iterative step, the linear elastic finite element analysis is used to obtain the stability ultimate capacity, where the maximum element bearing ratio (Max-EBR) of all members, \(r_{{\text{k}}}^{{{\max}}}\), can measure the bearing and damage states of the entire tower. The stability ultimate capacity of the iterative step can be determined as:

$$P_{{\text{k}}}^{L} = {{P_{0} } \mathord{\left/ {\vphantom {{P_{0} } {r_{{\text{k}}}^{{{\max}}} }}} \right. \kern-0pt} {r_{{\text{k}}}^{{{\max}}} }}$$
(24)

It is significant to mention that, the Max-EBR \(r_{{\text{k}}}^{{{\max}}}\) maintains a nonlinear relationship with the initial external load \(P_{0}\) when \(r_{k}^{e}\) is defined by Eq. (19) since the GYF defined by Eq. (12) is non-homogeneous. Hence, the 2nd order HGYF in Eq. (16) is used to define \(r_{k}^{e}\) for the tower members. Repeat the above iterative process until the stability ultimate capacity of the two adjacent steps meets the convergence criterion:

$$\left| {\frac{{P_{{\text{k}}}^{L} - P_{{\text{k}} - 1}^{L} }}{{P_{{\text{k}} - 1}^{L} }}} \right| \le \varepsilon ,\quad k \ge 2$$
(25)

Where \(\varepsilon\) is the convergence tolerance, generally taken as 0.001 ~ 0.01.

Illustrative examples

A single span angle steel beam with analytical and traditional incremental nonlinear finite element methods (i.e. INFEM) and a tower with INFEM are adopted as benchmarks in this section to demonstrate the accuracy and efficiency of the HGYF and the linear elastic iterative method. ANSYS software is employed for constructing finite element models and computation in the benchmarks. The convergence tolerance ε is set to 0.005. The computations are performed on a PC with a CPU running at 2.50 GHz and 8 GB of RAM.

Stability ultimate capacity of single span beam under uniformly distributed load and axial force

A single-span equal-leg angle beam with dimensions of ∠150 × 8 and a span of 4 m, supported at one end and fixed at the other end, under uniform and axial force, as shown in Fig. 5a and c. The initial load q is 1 kN/m. The yield strength is 420 MPa with an initial elastic modulus of 200 GPa. The angle beam will be discretized by beam189 element, which has 3 nodes and 7 degrees of freedom per node. The following steps will provide a detailed process for calculating the stability ultimate capacity of the beam using the linear elastic iterative method based on the proposed HGYF.

Fig. 5
figure 5

Single span beam and element divisions.

Full size image

The various parameters as follows are prepared for the linear elastic iterative method:

$$\begin{aligned} & A = T\left( {2B - T} \right) = 2336\;{\text{mm}},\;\;b = B - \frac{T}{2} = 146\;{\text{mm}} \\ & I_{z} = 2.07 \times 10^{6} \;{\text{mm}}^{4} ,\;\;I_{y} = 8.30 \times 10^{6} \;{\text{mm}}^{4} ,\;\;k_{c} = \frac{{6\left( {1 - \nu } \right)}}{{{\uppi }^{{2}} }} = 0.43,\;\; f_{{{\text{cr}}}} = \frac{{k_{c}\uppi ^{{2}} E}}{{12(1 - \nu^{2} )}}\left( \frac{T}{b} \right)^{2} = 233.37\;{\text{MPa}}, \\ & f_{eZ} = \frac{{\pi^{2} E}}{{\lambda_{z}^{2} }} = 109.325\;{\text{MPa}},\;\; f_{eY} = \frac{{\pi^{2} E}}{{\lambda_{y}^{2} }} = 438.342\;{\text{MPa}}, \\ & \lambda_{cY} = \sqrt {\frac{{f_{y} }}{{f_{eY} }}} = \sqrt {\frac{420}{{438.342}}} = 0.979 \le 1.5,\;\;f_{yY}^{\prime} = 0.658^{{\lambda_{cY}^{2} }} f_{y} = 0.658^{{0.979^{2} }} \times 420 = 281.209\;{\text{MPa}}, \\ & \lambda_{cZ} = \sqrt {\frac{{f_{y} }}{{f_{eZ} }}} = \sqrt {\frac{420}{{109.325}}} = 1.960 > 1.5,\;\;f_{yZ}^{\prime} = \frac{0.877}{{\lambda_{cZ}^{2} }}f_{y} = \frac{0.877}{{1.960^{2} }} \times 420 = 95.882\;{\text{MPa}}, \\ & {\text{so}},\;\;f_{y}^{\prime} = \min \left( {f_{yY}^{\prime} ,f_{yZ}^{\prime} } \right) = 95.882\;{\text{MPa }} \\ & \lambda = \sqrt {\frac{{f_{y}^{\prime} }}{{f_{{{\text{cr}}}} }}} = \sqrt {\frac{95.882}{{233.37}}} = 0.641 \le 0.673,\;\;{\text{so}}\;\;\rho = 1, \\ & N_{{\text{P}}} = \rho Af_{y}^{\prime} = {{2\rho bTf_{y}^{\prime} } \mathord{\left/ {\vphantom {{2\rho bTf_{y}^{\prime} } {1.1}}} \right. \kern-0pt} {1.1}} = 2.04 \times 10^{5} \,{\text{N}},\;\;M_{{{\text{P}}y}} = \frac{\sqrt 2 }{2}f_{y0} b^{2} T = 4.6 \times 10^{7} \,{\text{N}}\,{\text{mm}}, \\ & M_{{{\text{P}}z}} = \frac{\sqrt 2 }{4}f_{y0} b^{2} T = 2.3 \times 10^{7} \,{\text{N}}\,{\text{mm,}} \\ & N_{{{\text{E}}y}} = \frac{{\pi^{2} EA}}{{\lambda_{y}^{2} }} = 1.59 \times 0.64 \times 10^{6} { = 1}{\text{.02}} \times 10^{6} \;{\text{N}},\;\;N_{{{\text{E}}z}} = \frac{{\pi^{2} EA}}{{\lambda_{z}^{2} }} = 4.0 \times 0.64 \times 10^{5} { = 2}{\text{.56}} \times 10^{5} \;{\text{N}}, \\ \end{aligned}$$
$$\begin{aligned} & \lambda_{{\text{p}}} = \sqrt {\frac{{f_{y} }}{{f_{{{\text{cr}}}} }}} = \sqrt {\frac{420}{{233.37}}} = 1.34 > 1.22,\;\;{\text{so}}\;\;e_{y} = \frac{5B}{{16\sqrt 2 }} \cdot \frac{{\lambda_{{\text{p}}} - 1.22}}{{\lambda_{{\text{p}}} - 0.22}} = 3.55\,{\text{mm}},\;\;e_{z} = 0, \\ & a_{{\text{E}}} = a_{{{\text{E}}y}} = \frac{{N_{{\text{P}}} }}{{N_{{{\text{E}}y}} }} = \frac{{2.03 \times 10^{5} \,{\text{N}}}}{{1.02 \times 10^{6} \,{\text{N}}}} = 0.199,\;\;b_{{\text{E}}} = b_{{{\text{E}}y}} = \frac{{e_{y} N_{{{\text{E}}y}} }}{{M_{{{\text{P}}y}} }} = \frac{{3.55\,{\text{mm}} \times 1.02 \times 10^{6} \,{\text{N}}}}{{4.6 \times 10^{7} \,{\text{N}}\,{\text{mm}}}} = 0.079 \\ \end{aligned}$$

The first iteration of the linear elastic iterative method

The angle beam is discretized into four elements, each with a length of 1 m, as shown in Fig. 5b. The internal forces in each element (i.e., elements ①–④) can be extracted from the finite element model for the first iteration step, as shown in Table 4.

FI and FJ represent the axial force in each element at the I and J ends, respectively. MyI and MyJ represent the strong axial bending (y-axis) at the I and J ends of each element, respectively. MzI and MzJ represent the weak axial bending (z-axis) at the I and J ends of each element, respectively. All these values are taken from the applied load values.

Table 4 Internal forces of each element in the first iteration.
Full size table

For I-end of element ①, the dimensionless internal forces and HGYF from Eq. (16) are calculated as follows:

$$n_{I}^{{\textcircled{\large1}}} = \frac{N}{{N_{P} }} = \frac{40}{{204}} = 0.196,\;\;m_{yI}^{\textcircled{\large1}} = \frac{{M_{yI} }}{{M_{Py} }} = \frac{1.3}{{46}} = 0.028,\;\;m_{zI}^{\textcircled{\large1}} = \frac{{M_{zI} }}{{M_{Pz} }} = \frac{1.3}{{23}} = 0.056$$
(26)
$$\begin{aligned} \overline{f}_{2I} & = 0.028^{2} + \left( { - 0.329 - 2.051a_{{\text{E}}} } \right)\left( { - 5.519 - 0.719b_{{\text{E}}} } \right) \times 0.056 \times 0.028 + 0.056^{2} \\ & \quad + \left( { - 3.193 + 0.970a_{{\text{E}}} } \right)\left( { - 0.640 + 0.028b_{{\text{E}}} } \right) \times 0.196 \times 0.028 \\ & \quad + \left( {0.811 + 1.736a_{{\text{E}}} } \right)\left( {2.238 + 0.526b_{{\text{E}}} } \right) \times 0.196 \times 0.056 + 0.196^{2} = 0.089 \\ \end{aligned}$$
(27)

Similarly, for J-end of element ①:

$$n_{{\text{J}}}^{\textcircled{\large1}} = \frac{N}{{N_{P} }} = \frac{40}{{204}} = 0.196,\;\;m_{{y{\text{J}}}}^{\textcircled{\large1}} = \frac{{M_{yJ} }}{{M_{Py} }} = \frac{0.10}{{46}} = 0.002,\;\;m_{{z{\text{J}}}}^{\textcircled{\large1}} = \frac{{M_{{z{\text{J}}}} }}{{M_{Pz} }} = \frac{0.10}{{23}} = 0.004$$
(28)
$$\begin{aligned} \overline{f}_{2J} & = 0.002^{2} + \left( { - 0.329 - 2.051a_{{\text{E}}} } \right)\left( { - 5.519 - 0.719b_{{\text{E}}} } \right) \times 0.004 \times 0.002 + 0.004^{2} \\ & \quad + \left( { - 3.193 + 0.970a_{{\text{E}}} } \right)\left( { - 0.640 + 0.028b_{{\text{E}}} } \right) \times 0.196 \times 0.002 \\ & \quad + \left( {0.811 + 1.736a_{{\text{E}}} } \right)\left( {2.238 + 0.526b_{{\text{E}}} } \right) \times 0.196 \times 0.004 + 0.196^{2} = 0.042 \\ \end{aligned}$$
(29)

The EBRs based on Eq. (20) for element ① in the first iteration are calculated as follows:

$$r_{{\text{I}}}^{\textcircled{\large1}} = \sqrt {\overline{f}_{{{\text{2I}}}} } = 0.298,\;\;r_{{\text{J}}}^{\textcircled{\large1}} = \sqrt {\overline{f}_{{{\text{2J}}}} } = 0.204,\;\;r^{\textcircled{\large1}} = \max \left( {r_{{\text{I}}}^{\textcircled{\large1}} ,r_{{\text{J}}}^{\textcircled{\large1}} } \right) = 0.298 \,$$
(30)

The calculation process for elements ② to ④ is the same as above. The results of the calculations for elements ① to ④ in the first iteration are summarized in Table 5, where element ① is identified as the high-load element. The calculation of the reference EBR is as follows:

$$\overline{r}_{k} = \frac{1}{{N_{e} }}\sum\limits_{e - 1}^{{N_{e} }} {r_{k}^{e} } = \frac{0.298 + 0.259 + 0.258 + 0.257}{4} = 0.268$$
(31)
$$r_{k}^{\min } = 0.257;\;\;r_{k}^{\max } = 0.298;\;\;d_{k} = \frac{{\overline{r}_{k} + r_{k}^{\min } }}{{\overline{r}_{k} + r_{k}^{\max } }} = \frac{0.268 + 0.257}{{0.268 + 0.298}} = 0.928$$
(32)
$$r_{k}^{0} = r_{k}^{{{\max}}} - \left( {r_{k}^{{{\max}}} - r_{k}^{{{\min}}} } \right)d_{k} = 0.298 - \left( {0.298 - 0.257} \right) \times 0.928 = 0.260$$
(33)
Table 5 Results of each element in the first iteration.
Full size table

The Max-EBR of the single span angle steel beam in the first iteration is \(r_{1}^{\max } = r^{\textcircled{\large1}} = 0.298\) and the reference EBR is \(r^{0} = 0.260\). Obviously, all the EBRs are less than \(r^{0}\) except \(r^{\textcircled{\large1}}\). Hence, the elastic modulus of element ① should be reduced, while the elastic moduli of elements ② to ④ should remain unchanged based on the elastic modulus reduction strategy:

$$\left\{ {\begin{array}{*{20}l} {E_{2}^{\textcircled{\large1}} = E_{1}^{\textcircled{\large1}} \frac{{2\left( {r_{1}^{0} } \right)^{2} }}{{\left( {r_{1}^{\textcircled{\large1}} } \right)^{2} + \left( {r_{1}^{0} } \right)^{2} }} = 200 \times 10^{3} \times \frac{{2 \times 0.26^{2} }}{{0.298^{2} + 0.26^{2} }} = 173 \times 10^{3} \;{\text{MPa}}} \hfill \\ {E_{2}^{\textcircled{\large2}} = E_{1}^{\textcircled{\large2}} ,\;\;E_{2}^{\textcircled{\large3}} = E_{1}^{\textcircled{\large3}} ,\;\;E_{2}^{\textcircled{\large4}} = E_{1}^{\textcircled{\large4}} } \hfill \\ \end{array} } \right.$$
(34)

Where \(E_{1}^{\textcircled{\large1}} ,E_{1}^{\textcircled{\large2}} ,E_{1}^{\textcircled{\large3}}\) and \(E_{1}^{\textcircled{\large4}}\) represent the elastic moduli of elements ① to ④ in the first iteration (i.e., current step), respectively. Similarly, \(E_{2}^{\textcircled{\large1}} ,E_{2}^{\textcircled{\large2}} ,E_{2}^{\textcircled{\large3}}\) and \(E_{2}^{\textcircled{\large4}}\) represent respectively the elastic moduli of Elements ① to ④ in the second iteration (i.e., the next step), which are the initial elastic moduli for the second iteration.

The stability ultimate capacity of the beam for the first iteration can be obtained from Eq. (24):

$$q_{1}^{s} = \frac{{q_{0} }}{{r_{1}^{\max } }} = \frac{1}{0.298} = 3.36\,{\text{kN/m}}$$
(35)

The second iteration of the linear elastic iterative method

The new element stiffness equations are formed using the elastic moduli determined by Eq. (34) for the second iteration, and the overall stiffness equation is integrated to obtain the internal forces in each element. Consequently, the EBRs for Elements ① to ④ and the Max EBR in the second iteration for the beam can be calculated:

$$r_{2}^{\textcircled{\large1}} = 0.293,\;\;r_{2}^{\textcircled{\large2}} = 0.261,\;\; \, r_{2}^{\textcircled{\large3}} = 0.261,\;\;r_{2}^{\textcircled{\large4}} = 0.258,\;\;r_{2}^{\max } = r_{2}^{\textcircled{\large1}} = 0.293$$
(36)

Then, the stability capacity of the beam for the second iteration can be obtained:

$$q_{2}^{s} = 3.42\;{\text{kN/m}}$$
(37)

The convergence criterion is satisfied when the absolute difference between the stability ultimate capacities in the two steps is less than or equal to the convergence tolerance \(\varepsilon\). The judgment on whether the two iterations converge is as follows:

$$\frac{{\left| {q_{2}^{s} - q_{1}^{s} } \right|}}{{q_{1}^{s} }} = 0.0179 \ge 0.005$$
(38)

The above equation does not meet the convergence, and it is necessary to further reduce the elastic modulus of the high-bearing element for the next iteration.

Stability ultimate capacity in the linear elastic iterative method

The iterative process is repeated as described above, and the EBRs (\(r\)), the elastic moduli (E, unit: MPa) of element ① to element ④, the reference EBR (\(r^{0}\)), and the stability ultimate capacity for each iteration are listed in Table 6. The high-load elements are marked in gray backgrounds. The variation of the EBRs of the four elements with the iteration is shown in Fig. 5.

Table 6 Results of each iteration.
Full size table

It can be observed that the EBR of element ① is consistently higher than the reference EBR \({r^0}\) at every iteration indicating that element ① is a high-load element. Similarly, the EBRs of elements ② and ③ are initially lower than \({r^0}\) in the first iteration, but they gradually increase and eventually become higher than \({r^0}\) in other iterations, also qualifying them as high-load elements. On the other hand, element ④ consistently has the EBR lower than \({r^0}\) at every iteration, making it a low-load element. It should be noted that, elements ② and ③ may start as low-load elements in the early stages of iteration, but as the internal forces redistribute, they eventually evolve into high-load elements (Fig. 6).

Fig. 6
figure 6

Iterative process of EBR.

Full size image

The stability ultimate capacity of the linear elastic iterative method satisfies convergence until the 8th iteration:

$$\frac{{\left| {q_{8}^{s} - q_{7}^{s} } \right|}}{{q_{7}^{s} }} = 0.0028 < 0.005$$
(39)

The stability ultimate capacity obtained at the end of the iteration is considered as the final stability ultimate capacity of the beam:

$$q_{L} = q_{8}^{s} = 3.60\,{\text{kN/m}}$$
(40)

Different methods of stability ultimate capacity

The analytical solution for the stability ultimate capacity of the single span beam is q = 3.71 kN/m based on the plastic limit analysis method in Eq. (1), see Appendix C for details. Results corresponding to different methods are listed in Table 7. The linear elastic iteration method proposed in this paper is recorded as EMRM. The iteration processes of EMRM are illustrated in Fig. 7 for the legend ‘HGYF’ when the EBR is defined by the HGYF in Eq. (16). It can be observed that the results of the EMRM and the INFEM are nearly identical and both show a small deviation from the analytical solution.

Table 7 Comparison of stability ultimate capacity for different methods.
Full size table
Fig. 7
figure 7

Iterative process of the stability ultimate capacity for the single-span beam.

Full size image

The necessity for homogenization

The iteration processes of the linear elastic iterative method are illustrated in Fig. 7. for the legend ‘GYF’ when the EBR is defined by the GYF in Eq. (12). It is obvious that the results based on the nonhomogeneous GYF are dependent on the value of the initial external load P0, resulting in unstable and inaccurate stability ultimate capacities. In contrast, stability ultimate capacities based on the HGYF are independent of P0, keeping constant under different initial external loads and agreeing well with the analytical solution and the INFEM, which demonstrate the accuracy and applicability of the proposed HGYF in Eq. (16).

Stability ultimate capacity of a 6-m tower

A 6-m equal-leg angle tower is composed of 64 nodes and 136 members, with all intersections assumed to be rigid connections, as shown in Fig. 8. The main legs, diagonal bracings, and redundant members of the tower are ∠200 × 20, ∠100 × 10, and∠80 × 8, respectively. The elastic modulus (E) is set to 210 GPa and the yield strength of steel (fy) is 235 MPa. At the four vertices of the tower, three concentrated loads are applied to each vertex in the horizontal, vertical, and lateral directions, and the self-weight of the tower is neglected. The stability ultimate capacity analysis of the tower is performed using the EMRM. The result of the INFEM can be used as a reference.

Fig. 8
figure 8

Schematic drawing of the 6 m tower.

Full size image

Convergence analysis of discrete elements

Results corresponding to different numbers of discrete elements are listed in Table 8. The stability ultimate capacities from the two methods tend to converge when the members are discretized into 4 elements, with only a minor difference between them. Simultaneously, it can be concluded that the EMRM achieves much higher efficiency than the INFEM, based on the CPU time.

Table 8 Results of different methods.
Full size table

The necessity for homogenization

The iteration processes of the linear elastic iterative method are illustrated in Fig. 9 for the legend ‘GYF’ when the EBR is defined by the GYF in Eq. (12). It is obvious that the results based on the non-homogeneous GYF are dependent on the value of the initial external load P0 (i.e., P0 = 10, 50, 100 kN), resulting in unstable and inaccurate stability ultimate capacities. In contrast, stability ultimate capacities based on the HGYF are independent of P0, remaining constant under different initial external loads and agreeing well with the INFEM, which is consistent with the conclusion on the single-span beam case.

Fig. 9
figure 9

Iterative process of the stability ultimate capacity for the tower.

Full size image

Influence of stability on ultimate capacity

The INFEM is also used to calculate the strength ultimate capacity (i.e., no stability)2 of the 6 m tower by closing large deformations and ignoring defects. Results of the strength ultimate capacity and the stability ultimate capacity calculated by the INFEM and the EMRM are listed in Table 9. For the INFEM, it can be seen that the stability ultimate capacity is 17.12% lower than the strength ultimate capacity, while the stability ultimate capacity of the EMRM is 13.32%. This indicates that stability has a significant impact on the ultimate capacity of the tower, and it is essential to consider stability for an accurate assessment of the ultimate capacity.

Table 9 Influence of stability on ultimate capacity.
Full size table

Conclusion

The stability generalized yield criteria (GYC) considering both normal force and bi-axial bending from AS/NZS 4600 is selected for equal-leg angle members, and a homogeneous generalized yield function (HGYF) is proposed using non-dimensionalization and homogenization techniques. A linear elastic iterative method is presented for estimating the stability ultimate capacity of equal-leg angle towers. A single-span beam with the analytical and traditional numerical methods and a tower with the traditional numerical method are adopted as benchmarks to demonstrate the accuracy and efficiency of the HGYF and the linear elastic iterative method. The following conclusions can be drawn:

  1. (1)

    The impact of stability on the ultimate capacity of the equal-leg angle towers may exceed 15%, and it is necessary to select stability GYCs to obtain the ultimate capacity.

  2. (2)

    The proposed HGYF is accurate for the stability ultimate capacity analysis of equal-leg angle towers through the EMRM, overcoming the deficiencies of current GYCs.

  3. (3)

    The proposed linear elastic iterative method achieves much higher accuracy and efficiency for stability ultimate capacity of equal-leg angle towers.