Abstract
A highly efficient and multi-functional butterfly polarization conversion metasurface is proposed for the Ku-Ka frequency range, designed to reduce the radar cross-section. The suggested converter enables dual frequency bands linear-to-cross (LX) and linear-to-circular (LC) polarization transformations. The efficiency of cross-polarization conversion exceeds 90% over the frequency ranges of 14.57–16.30 GHz and 25.70–37.03 GHz, with relative bandwidths of 11% and 36%, respectively. Reflections of left-hand (LHCP) and right-hand circularly polarized (RHCP) waves are realized within the frequency ranges of 17.78–25.31 GHz and 37.38–37.73 GHz, with relative bandwidths of 35% and 0.9%. The oblique incidence significantly affects the metasurface conversion performance, and the proposed model manifests angular robustness up to 60°. Additionally, the butterfly metasurfaces are deployed in a triangular chessboard configuration to achieve radar cross section (RCS) reduction spanning the frequency bands of 14–15.17 GHz, 24.60–35.20 GHz, and 36.30–38 GHz. Drawing from simulation results and test-based validation data, the proposed converter holds promising applications in wireless communication, antenna engineering, and radar stealth.
Similar content being viewed by others
Introduction
Metasurfaces with unique electromagnetic properties have significant potential in the field of communications. Through flexible design, they can achieve polarization conversion(PC) of electromagnetic waves in various forms, thus improving the polarization state of signals and enhancing the communication capability and efficiency of communication systems in complex electromagnetic environments1. In radar systems, metasurfaces are utilized to control polarization scattering characteristics, thereby enhancing the accuracy of target detection and identification2. Therefore, precise control over the polarization state of electromagnetic waves is indispensable. However, conventional polarization control devices suffer from issues such as high energy consumption, complex structures, and high costs3,4, significantly diminishing their conversion performance. Hence, metasurfaces with outstanding characteristics remain of great research value.
The polarization types of metasurfaces include three types of polarization conversion: linear–linear polarization5,6,7,8,9, linear-circular polarization10,11,12, and circular polarization13. Due to the efficient electromagnetic polarization control capability of metasurfaces, various polarization conversion devices have been proposed successively. For instance, in reference14,15, Liu et al. introduced a broadband LX polarization conversion metasurface composed of tilted end-loaded H-shaped resonators, achieving conversion efficiency exceeding 0.9 across the 9.83–29.37 GHz frequency range. Additionally, they presented a LC polarization conversion metasurface consisting of an open loop and a square patch, achieving less than 3 dB conversion loss in the 29–41.5 GHz and 52.5–61.5 GHz frequency bands, demonstrating excellent conversion characteristics. In16,17, Kamal et al. and Lin et al. proposed metasurfaces for PC across multiple frequency bands. Kamal’s design, featuring two square split-ring resonators with a unit cell period of 7 mm, and Lin’s design, utilizing reflective resonators with a period of 8 mm, both achieve polarization conversion over various frequency ranges. In18,19, Zhang et al. and Nguyen et al. introduced metasurfaces based on curved square rings with diagonal split strips, and double-angled square patches, respectively. Zhang’s metasurface demonstrates various types of polarization conversion across multiple frequency bands within the 2–16 GHz range, while Nguyen’s metasurface achieves LX and LC polarization conversion in the 8–12 GHz, 7.42–7.6 GHz, and 13–13.56 GHz frequency bands. Although these devices have excellent polarization conversion capabilities, their large unit cell period20, dielectric substrate thickness21, and the limitation to single-band22 or single type of polarization conversion , such as LX polarization or circular polarization (CP)23,24, greatly restrict their application in the microwave frequency band. Only a few conversion devices simultaneously exhibit cross-polarization and circular polarization conversion characteristics25,26,27. Furthermore, based on the polarization conversion characteristics of metasurfaces, extensive research has been conducted on reducing radar cross section. In28, Coskun et al. introduced a broadband polarization conversion metasurface. They studied the unit cell characteristics using equivalent circuit analysis and achieved RCS reduction through a checkerboard arrangement. In29, Liu et al. proposed a cross-polarization conversion unit composed of two tilted asymmetric triangular split-ring resonators. They arranged the resonators in a triangular chessboard pattern to achieve RCS reduction in the cross-polarization frequency band, demonstrating good electromagnetic stealth performance.
Currently, significant progress has been made in the research of RCS reduction based on the electromagnetic properties of metasurfaces30,31,32,33,34,35. However, devices that simultaneously achieve polarization conversion and RCS reduction have not received sufficient research attention. The limitation of single-type polarization conversion also restricts the versatility of these devices36. In37, Khan et al. proposed a multifunctional and efficient polarization converter capable of achieving LX polarization conversion in three bands and LC polarization conversion in four bands, suitable for C-K bands. Additionally, in38, Tahir et al. introduced a fish-like metasurface operating in the X-band. This metasurface achieves LX polarization conversion in the 8–11 GHz range and LC polarization conversion in two frequency bands: 7.5–7.7 GHz and 11.5–11.9 GHz. However, the focus of these studies remains on achieving polarization conversion, with the proposed units not addressing RCS reduction. Therefore, in increasingly complex electromagnetic environments, designing metasurfaces that are efficient, dual-band, capable of multiple polarization conversion types, and also reduce RCS remains a key research focus.
This paper presents an anisotropic butterfly metasurface polarization converter operating in the Ku-Ka bands, which addresses the challenge of simultaneously achieving dual-band LX polarization conversion and dual-band LC polarization conversion, while also reducing RCS. The proposed design features small unit cell periods and thin dielectric substrates. Within the frequency range of the Ku-Ka band, it not only converts incident LP waves into cross-polarized waves within the frequency ranges of 14.57–16.30 GHz and 25.70–37.03 GHz (PCR > 90%), but also reflects LHCP waves and RHCP waves within the frequency bands of 17.78–25.31 GHz and 37.38–37.73 GHz, respectively (AR < 3 dB). The designs were validated for sensitivity to PCR and AR across various incident angles, demonstrating polarization conversion capability even at a steep 60° angle of incidence. Additionally, leveraging the phase cancellation principle, the formula for calculating radar RCS reduction was analyzed. Subsequently, a 1-bit coding approach was applied to metasurfaces arranged in a triangular chessboard configuration to achieve RCS reduction, thereby enabling electromagnetic stealth capabilities.
Stepwise evaluation of the model design
As depicted in Fig. 1, the butterfly metasurface proposed in this study and its corresponding functionalities are demonstrated. Under linear polarization electromagnetic wave incidence, efficient multi-functional polarization transformation is obtained spanning the frequency bands of 14–38 GHz. Based on the polarization characteristics of the model, at least 10 dB reduction in RCS is achieved with optimal array arrangement. Fig. 1a illustrates the conversion process of the resonant unit performing LX polarization and LC polarization, along with representations of incident (reflected) LP waves, LHCP, and RHCP representing left-hand and right-hand circular polarization (CP) waves, respectively. Fig. 1b presents the triangular chessboard configuration based on the phase cancellation principle used for RCS reduction. Fig. 1c depicts the polarization conversion model of the butterfly metasurface, where yellow represents copper metal and purple represents the dielectric substrate polytetrafluoroethylene (PTFE).
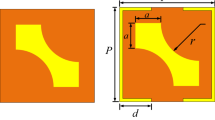
Resonant metasurface model design and evolution are predicated on the anisotropic nature of the electromagnetic structure, progressively achieving optimal metasurface structural design through parameter simulation and optimization. The proposed butterfly resonator undergoes optimization through four critical steps, as illustrated in Fig. 2. Table 1 presents the variations in key parameters during the evolution from Unit-1 to Unit-4. Fig. 3 shows the corresponding simulation results throughout the model’s evolution.Under y-polarized electromagnetic wave incidence, it’s observed that the resonator in Unit-1 achieves only linear-cross polarization conversion within a narrow low-frequency range. Additionally, as the frequency shifts to higher values, it is found that the co-polarized coefficient approaches 0 dB, while the cross-polarized coefficient becomes excessively large, indicating no polarization conversion occurs. This is attributed to the strong isotropy of Unit-1, as illustrated in Fig. 3a. In Unit-2, by adjusting the length of the rectangle in the upper right corner of resonant Unit-1 from l = 0.9 mm to l = 0.44 mm, an enhancement in the effective frequency band for polarization conversion is observed. This improvement is particularly significant in the Ka-band frequency range, as depicted in Fig. 3b.
Unit-3 extends the outer ring from Unit-2 and retains openings with an arc length b = 1.98 mm in the first and third quadrants. It was observed that the polarization conversion capability significantly improves within the 14–38 GHz frequency range. This enhancement is attributed to the reduced length of the rectangle in the upper right corner and the extension of the outer ring, which enhance the resonator’s anisotropy and thus improving its polarization conversion capability, as depicted in Fig. 3(c).In Unit-4, increasing the arc length of the outer ring openings in Unit-3 to b = 2.17 mm further enhances the anisotropy. This modification enables the butterfly metasurface to achieve dual-band, high-efficiency polarization conversion across the entire Ku-Ka frequency band, as illustrated in Fig. 3d.
Design and analysis of units
Configuration of the butterfly metasurface unit structure
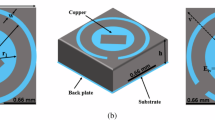
The proposed polarization conversion unit, as illustrated in Fig. 4, adopts a three-layer sandwich structure. The upper layer comprises an anisotropic butterfly resonator, while the intermediate layer consists of a dielectric substrate, and the lowermost layer is metallic ground. Both the upper layer and the metallic ground employ copper with a thickness of \(t = 0.017mm\) and a conductivity of \(5.8 \times 10^{7} S/m\) as the model material. The dielectric substrate in the middle isolates the butterfly resonator from the bottom. The dielectric layer is filled with PTFE, with a relative electric permittivity denoted as \(\varepsilon {}_{r} = 2.1\) and a loss tangent represented by \(\tan \delta = 0.0002\), and has a thickness of \(h = 1.6mm\). The tilted rectangular unit is sloped at 45° relative to the horizontal orientation and coincides with the origin of the coordinates. To achieve optimal simulation results, we conducted size optimization of the model structure using CST simulation software. Fig. 4a illustrates the simulation conditions of the model, while Fig. 4b displays the optimized parameters of the unit. Fig. 4c provides a side view of the designed model. In Table 2, the optimized parameters of the resonant unit model are shown, with the initial coordinates of b set to (− 0.59, − 0.59, 1.634).
When a beam of electromagnetic waves is vertically incident on the resonator along the z-axis, the relationship between the electric field components of the incident and reflected waves on the x- and y-axis can be represented by the Jones matrix36:
where \(\mathop {E_{x}^{r} }\limits^{ \to }\) and \(\mathop {E_{y}^{r} }\limits^{ \to }\) represent the electric field intensity vectors of the reflected waves on the x- and y-axis, respectively; \(\mathop {E_{x}^{i} }\limits^{ \to }\) and \(\mathop {E_{y}^{i} }\limits^{ \to }\) represent the electric field intensity vectors of the incident waves on the x- and y-axis, respectively; \(i\) and \(r\) represent the incident electromagnetic waves and reflected electromagnetic waves, respectively. The co-polarized reflection coefficients \(R_{xx} = \left| {E_{x}^{r} } \right|/\left| {E_{x}^{i} } \right|\) and \(R_{yy} = \left| {E_{y}^{r} } \right|/\left| {E_{y}^{i} } \right|\) represent the reflections from x to x and y to y, respectively, while the cross-polarized reflection coefficients \(R_{xy} = \left| {E_{x}^{r} } \right|/\left| {E_{y}^{i} } \right|\) and \(R_{yx} = \left| {E_{y}^{r} } \right|/\left| {E_{x}^{i} } \right|\) represent the reflections from y to x and x to y, respectively. With the reflection coefficients in Eq. (1), the PCR for y-polarized incident waves can be expressed as37:
At the same time, under y-polarized wave incidence conditions, the co-polarized and cross-polarized reflection amplitudes generating circularly polarized reflected waves should satisfy \(\left| {R_{xy} } \right| = \left| {R_{yy} } \right|\), with the phase difference meeting \(\Delta \varphi = \varphi_{yy} - \varphi_{xy} = \pm {\pi \mathord{\left/ {\vphantom {\pi {2 \pm }}} \right. \kern-0pt} {2 \pm }}2k\pi\) (where k is an integer), where \(\varphi_{yy}\) and \(\varphi_{xy}\) are the phases corresponding to the co- and cross-polarization coefficients. To evaluate the conversion efficiency of circularly polarized reflected waves, the axial ratio is used for characterization, defined by the formula25:
where \(\xi\) is denoted as25:
Additionally, the conversion performance of circularly polarized reflected waves is evaluated using Stokes parameters. Introducing parameters I, V, Q and U, under y-polarized incident electromagnetic waves, I, V, Q and U, can be respectively described as11:
The conversion performance of circular polarization is quantified using the ellipticity E, defined as \(E = V/I\), where \(\Delta \varphi = \varphi_{yy} - \varphi_{xy}\). According to this equation, the ellipticity E varies between − 1 and 1. When \(\left| {R_{xy} } \right| = \left| {R_{yy} } \right|\) and \(\Delta \varphi = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} + 2k\pi\) (where k is an integer), the ellipticity value E is − 1, indicating the reflected wave is converted to left-hand circular polarization . Conversely, when \(\Delta \varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} + 2k\pi\) (where k is an integer), the ellipticity E value is 1, indicating the reflected wave is converted to right-hand circular polarization. The energy conversion efficiency of circular polarization is given by Eq. (9) 11:
Equivalent circuit and working principle of the butterfly metasurface unit
To further investigate the polarization conversion principle of the proposed metasurface, we developed an equivalent circuit using ADS software. Based on the simulation results shown in Fig. 3d, we performed a layer-by-layer analysis of the physical interactions among the top layer, dielectric layer, and bottom layer of the metasurface. The analysis indicates that the surface currents on the top-layer resonators induce inductance, while the gaps between different parts of the resonant units and the edge charge accumulation around the units form capacitance. Consequently, the top layer of the resonant unit can be equivalently modeled as two series RLC branches and one LR branch. Additionally, each of the interfaces between the top layer, dielectric layer, and bottom layer can be represented by an equivalent RLC branch. By optimizing the simulations and combining the equivalent circuits of the top layer with those of the other components, we obtained the overall equivalent circuit model of the metasurface unit, as shown in Fig. 5a. The optimized circuit parameters for each part of the equivalent circuit are as follows: \(R_{1} = 9.206\Omega\),\(R_{2} = 1.603\Omega\),\(R_{3} = 11.715\Omega\),\(R_{4} = 6.745\Omega\),\(R_{5} = 78.264\Omega\),\(C_{gap} = 0.047pF\),\(C_{1} = 0.001pF\),\(C_{2} = 0.004pF\),\(C_{3} = 0.005pF\), \(L_{1} = 36.148nH\), \(L_{2} = 1.962nH\), \(L_{3} = 24.220nH\), \(L_{4} = 6.835nH\), \(L_{5} = 46.169nH\).
Meanwhile, we decompose the y-axis incident polarized electromagnetic waves, generating u and v components while maintaining them perpendicular to each other, laying the foundation for a thorough analysis and understanding of the polarization conversion mechanism of the butterfly resonator. The polarization principle is illustrated in Fig. 5b, where the u- and v-axes are obtained by counterclockwise rotation of the coordinate axes by 45°. Through this decomposition, the two different forms of waves (incident and reflected), \(E_{i}\) and \(E_{r}\) can be represented by the formulas:
In which, \(r_{u}\) and \(r_{v}\) are the reflection components on the u- and v-axes, respectively, and \(\mathop u\limits^{ \wedge }\) and \(\mathop v\limits^{ \wedge }\) are unit polarization vectors. In the u-v coordinate system, the co-polarization coefficients are denoted by \(R_{uu} = {{E_{ru} } \mathord{\left/ {\vphantom {{E_{ru} } {E{}_{iu}}}} \right. \kern-0pt} {E{}_{iu}}}\) and \(R_{vv} = {{E_{rv} } \mathord{\left/ {\vphantom {{E_{rv} } {E{}_{iv}}}} \right. \kern-0pt} {E{}_{iv}}}\), and the cross-polarization coefficients are denoted by \(R_{uv} = {{E_{ru} } \mathord{\left/ {\vphantom {{E_{ru} } {E{}_{iv}}}} \right. \kern-0pt} {E{}_{iv}}}\) and \(R_{vu} = {{E_{rv} } \mathord{\left/ {\vphantom {{E_{rv} } {E{}_{iu}}}} \right. \kern-0pt} {E{}_{iu}}}\). The co-polarization phases are represented by \(\varphi_{uu}\) and \(\varphi_{vv}\), meanwhile, the phase difference is indicated by \(\Delta \varphi = \varphi_{uu} - \varphi_{vv}\). According to the polarization conversion principle, when the phase difference satisfies \(\Delta \varphi = \varphi_{uu} - \varphi_{vv} = \pm 180^\circ\) under the conditions \(\left| {R_{uu} } \right| = \left| {R_{vv} } \right| \cong 1\) and \(\left| {R_{uv} } \right| = \left| {R_{vu} } \right| \cong 0\), cross-polarization conversion can be achieved. When the phase difference \(\Delta \varphi = \pm 90^\circ\), the resonator achieves circular polarization conversion. Furthermore, when \(\Delta \varphi = + 90^\circ\), the reflected wave will be altered to RHCP wave, and when \(\Delta \varphi = - 90^\circ\) , the reflected wave will be morphed into LHCP wave. In essence, the electromagnetic polarization conversion generated by metasurfaces is due to their anisotropy and strong electromagnetic response. The relationship between the uppermost layer current and lowermost layer current of the resonant model and the electric and magnetic fields can be expressed as37:
where, J and M are current density and magnetic flux density respectively, \(\alpha_{ee}\) and \(\alpha_{mm}\) are self-coupled electronic polarization and magnetic polarization, \(\alpha_{em}\) and \(\alpha_{me}\) are mutual coupling electromagnetic polarization, E and H represent the electric field and the magnetic field intensity.
Simulation results of metasurface unit
Under the premise of frequency ___domain analysis, floquet port boundary conditions are set for the resonator unit, and various parameters of the model are simulated and evaluated within the frequency range of 14–38 GHz. From the simulation data in Fig. 6, the following information can be obtained: Firstly, under y-polarized electromagnetic wave incidence, the cross-polarization amplitude is near to 0 within the frequency band of 14.57–16.30 GHz and 25.70–37.03 GHz, while the co-polarization amplitude is below − 10 dB. Within the frequency range of 17.78–25.31 GHz and 37.38–37.73 GHz, the co-polarization amplitude and the cross-polarization amplitude are approximately equal, with resonant points located at 15.33 GHz, 26.15 GHz, 27.36 GHz, and 33.73 GHz, respectively. Their co-polarization peaks are − 50 dB, − 43 dB, − 51 dB and − 60 dB, as shown in Fig. 6(a). Secondly, within the frequency span of 17.78–25.31 GHz, the phase difference between co- and cross-polarization is \(\Delta \varphi = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\), while within the frequency range of 37.38–37.73 GHz, the phase difference is \(\Delta \varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\). These phase differences assess the conditions for circular polarization (CP) conversion, as depicted in Fig. 6(b). To evaluate the effectiveness of the butterfly resonator in achieving LX polarization and LC polarization transformation, simulations for PCR, AR and E were conducted, and the data are showcased in Fig. 6c, d. Several aspects can be observed from Fig. 6c: firstly, within the frequency ranges of 14.57–16.30 GHz and 25.70–37.03 GHz, cross-polarization conversion occurred, with relative bandwidths of 11% and 36% respectively. The conversion efficiency PCR exceeded 90% in both ranges and remained above 97% within the frequency ranges of 14.96–15.78 GHz and 25.92–36.64 GHz. Moreover, at the resonant points located at 15.33 GHz, 26.15 GHz, 27.36 GHz, and 33.73 GHz, the polarization conversion efficiency approached 100%. In addition, the conversion efficiency for left-hand circular polarization (LHCP) and right-hand circular polarization (RHCP) exceeds 95%, indicating that the proposed butterfly metasurface has a highly efficient energy conversion efficiency.As depicted in Fig. 6d ,it can be observed that within the frequency ranges of 17.78–25.31 GHz and 37.38–37.73 GHz, the AR values were below 3 dB, indicating successful linear-to-circular polarization conversion, with fractional bandwidths of 35% and 0.9%. Meanwhile, within the frequency range of 17.78–25.31 GHz, the normalized ellipticity E approached -1, indicating that the reflected wave was transformed into LHCP wave; within the frequency range of 37.38–37.73 GHz, the normalized ellipticity E approached 1, manifesting that the reflected wave was transformed into RHCP wave.
In the u- and v-axis, in accordance with the simulated data depicted in Fig. 7, the following phenomena can be observed: The co- and cross-polarized coefficient satisfy \(\left| {R_{uu} } \right| = \left| {R_{vv} } \right| \cong 1\) and \(\left| {R_{uv} } \right| = \left| {R_{vu} } \right| \cong 0\), as shown in Fig. 7a. In the frequency band of 14.57–16.30 GHz and 25.70–37.03 GHz, the phase difference \(\Delta \varphi \cong 180^\circ\) is achieved, realizing cross-polarization. While in the frequency interval of 17.78–25.31 GHz, the phase difference \(\Delta \varphi \cong - 90^\circ ,\,270^\circ ( - 90^\circ )\), resulting in the reflection wave transformed into LHCP wave. In the frequency range of 37.38–37.73 GHz, the.
phase difference \(\Delta \varphi \cong - {270}^\circ {(90}^\circ {)}\), generating RHCP wave, as depicted in Fig. 7b.
Surface current analysis of the metasurface unit
To gain deeper insights into the physical mechanism responsible for the linear-to-circular polarization conversion in the proposed design, as illustrated in Fig. 8, we selected two frequency points: 21.14 GHz from the LC polarization band (17.78–25.31 GHz) and 33.62 GHz from the LX polarization band (25.70–37.03 GHz). The current flow directions at 0°, 90°, 180°, and 270° phases were then simulated for both frequency points. Furthermore, with the overall surface current directions represented by vector arrows. At the frequency of 21.14 GHz, as shown in Fig. 8a, the surface current on the resonant unit at a phase of 0° primarily flows towards the upper left. When the phase shifts to 90°, the current direction reverses towards the lower left, as depicted in Fig. 8b. At 180°, the overall current flow is opposite to that at 0°, now directed towards the lower right, as depicted in Fig. 8c. However, when the phase shifts to 270°, the current flows towards the upper right, as shown in Fig. 8d. In contrast, at 33.62 GHz within the LX polarized band, the surface current at phases of 0° and 270° both point towards the upper right, as shown in Fig. 8e, g. Similarly, at 90° and 180°, the current flows consistently towards the lower left, as depicted in Fig. 8f, h. The vector arrows clearly indicate that within the LC polarized band, the surface current at 21.14 GHz undergoes a rotational behavior as the phase changes from 0° to 270°. This controlled rotation of the surface current as a function of phase is the key mechanism enabling the linear-to-circular polarization conversion. However, at 33.62 GHz in the LX polarized band, the surface current does not exhibit such rotational behavior as the phase changes.
Fig. 9 demonstrates the allocation of surface currents induced on the uppermost and lowermost surfaces of the resonator unit at resonance frequency of 15.33 GHz, 26.18 GHz, 27.36 GHz and 33.73 GHz. Simulation reveals that at the resonance frequency of 15.33 GHz, the surface electric currents induced on the uppermost and lowermost surfaces of the butterfly resonator are parallel but in opposite directions, thus forming a strong magnetic resonance effect. However, at the resonance frequencies of 26.18 GHz, 27.36 GHz and 33.73 GHz, the surface currents induced on the top and lower surfaces of the butterfly resonator are parallel-aligned and in the same direction, resulting in a strong electric resonance effect. The generation of this effect also partially reveals the mechanism of polarization conversion.
Angular stability under oblique incidence
Under ideal conditions, electromagnetic waves act on the metasurface in a vertical incidence manner. However, when the incident angle becomes oblique, the sensitivity of conversion efficiency and bandwidth to the incident angle becomes more critical. Therefore, the relationships between PCR and AR with the incidence angle and frequency were simulated separately.The following information can be observed from Fig. 10: Firstly, in the frequency band of 14.57–16.30 GHz, with the growth of the oblique incident angle, the conversion bandwidth slightly narrows and shifts towards higher frequencies. However, the conversion efficiency remains above 90% throughout and exhibits excellent performance in linear polarization transformation. In the frequency band of 25.92–36.64 GHz, for incident angles between 0° and 15°, good broadband polarization conversion can be maintained. Between 15° and 30°, the reflected wave achieves polarization conversion in both a broadband and a narrowband range. However, between 30° and 60°, polarization conversion is limited to a narrowband range, as shown in Fig. 10a. This can be anticipated as the proposed butterfly metasurface serves as a polarization converter based on multiple plasmon resonances, thereby reducing sensitivity to incident angles. Secondly, during the variation of the incident angle spanning from 0° to 52°, the conversion bandwidth of AR gradually decreases with increasing angle, leading to a slight reduction in conversion efficiency, but remains below 3 dB overall. Meanwhile, a narrowband of circular polarization appears in the range of 45° to 60°, as demonstrated in Fig. 10b.
RCS reduction of butterfly metasurface
The proposed metamaterial surface follows the principle of phase cancellation to achieve the reduction of radar cross section. When the resonant unit itself and the mirror unit are exposed to the same electromagnetic wave, the amplitudes of co-polarized reflections and cross-polarized reflections are approximately equal, and the phase difference of the cross-polarized coefficients falls within the range of \(\pm 180^\circ \pm 36^\circ\), while the phase difference of the co-polarized reflection coefficients is \(0^\circ\). This satisfies the prerequisite for RCS reduction. Fig. 11a illustrates the schematic structure of the resonant unit and the mirror unit, denoted as ‘1’ and ‘0’ respectively. The reflection amplitudes are represented by \(A_{1}\) and \(A_{0}\), and the co-polarized phases and cross-polarized phases of the resonant unit and the mirror unit are denoted as \(\varphi_{1\_co}\), \(\varphi_{1\_cro}\), \(\varphi_{0\_co}\), and \(\varphi_{0\_cro}\). The cross polarized coefficients and co-polarized coefficients are depicted as \(R_{xy}\) and \(R_{yy}\) respectively. These conditions can be expressed by the following formulas:
Meanwhile, the reflected electric field of individual unit in the array can be formulated as:
From Fig. 12(a, b), it can be noticed that, under the incidence of y-polarized electromagnetic waves, the cross-polarized amplitude and co-polarized amplitude of unit ‘1’ and its mirror unit ‘0’ are nearly equal. Additionally, the phase difference corresponding to the co-polarized reflection coefficient between the resonant model and the mirror unit is \(0^\circ\), while the phase difference corresponding to the cross-polarized reflection coefficient is \(\pm 180^\circ\).
Based on the designed model, a checkerboard configuration is adopted with a triangular arrangement, and transient analysis is conducted using CST Microwave Studio. The supercell is rotated clockwise by 90° as a step to achieve optimized arrangement. When electromagnetic waves are vertically incident, due to energy conservation, the electromagnetic energy reflected in the normal direction is dispersed to four different directions, thereby reducing the concentration of energy reflected in a single direction. Fig. 11(b) illustrates the checkerboard array with a triangular arrangement. The performance of RCS reduction after the special arrangement can be quantified by the formula35:
Under the same scale of PEC, the RCS reduction of the array with triangular chessboard configuration can be approximated as follows35:
By deriving Eq. (22), it can be concluded that the arrangement of the metasurface array to achieve RCS reduction of 10 dB or more is closely related to the PCR of the resonant units. When the amplitude of the cross-polarization approaches 0 dB and the amplitude of the co-polarization is higher than − 10 dB, higher cross-polarization conversion efficiency can be obtained in the corresponding frequency range, thus achieving at least 10 dB of RCS reduction. Fig. 13a, b respectively illustrate the PCR of the resonant units and the RCS reduction under the arrangement of the triangular array. From Fig. 13a, b, it can be observed that: Firstly, the proposed resonant unit and its mirror image exhibit similar PCR, achieving over 90% conversion efficiency in the frequency ranges of 14.57–16.30 GHz and 25.70–37.03 GHz. Secondly, the array configuration of the triangular array enables the proposed metasurface to achieve radar cross section reduction of 10 dB or more in the frequency ranges of 14–15.17 GHz, 24.60–35.20 GHz, and 36.30–38 GHz, with fractional bandwidths of 8.1%, 35%, and 4.6%, and the maximum reduction peak is 25 dB. The triangular array arrangement induces mutual coupling between resonant units, which is the reason why the metasurface achieves RCS reduction of 10 dB or more in frequency bands where PCR is less than 90%. Table 3 presents a comparison between the performance of our research work and existing polarization conversion devices. From Table 3, it is evident that our research work demonstrates superior performance compared to other metasurfaces, with advantages including smaller periods, lower profiles, higher angular robustness, and multifunctional polarization. This highlights the excellent performance of our design.
Experimental validation and simulation verification
To validate the effectiveness of the butterfly resonant unit, we made two samples for experiments. The top layer of the sample adopts the butterfly resonance unit printed from 0.017 mm thick copper, and the dielectric layer is composed of 1.6 mm polytetrafluoroethylene, with 0.017 mm thick copper attached on the back. Each sample is composed of 26 × 26 units, with a total size of 156 × 156 mm2. All tests were conducted in a microwave anechoic chamber. Fig. 14a, b respectively depict the two fabricated test samples (RCS test sample and reflection coefficient test sample). Fig. 14(c) illustrates the measurement setup in the microwave anechoic chamber.We used three sets of horn antennas, which were HB-0118-SMAF, HB-SGA-42–25 and HB-SGA-28–25 (horizontally placed as the transmitting antenna, vertically placed as the receiving antenna) for testing, and the frequency ranges of these horn antennas covered the broadband 1–18 GHz, 18–26.5 GHz and 26.5–40 GHz, respectively. The horn antenna was fixed on the scanning frame and joined to the German N5225A Vector Network Analyzer (VNA) through a Coaxial Line. To guarantee the accuracy of the test, the sample was placed directly in front of the horn antenna, and kept the same horizontal height with the center of the horn antenna. During the measurement, the calibration plate of the same size was first used for normalization processing, and then the signals were collected when the two horn antennas were kept horizontal (HH), and the collected signals were processed by the vector network analyzer to obtain the test data of co-polarization coefficient. For the cross-polarization coefficient test, the emitting antenna was kept horizontal and the receiving antenna was rotated 90° vertically (HV) to collect cross-polarization measurement data. Fig. 14d, e are the contrast between the simulation data and the measured data of the butterfly metasurface reflection coefficient and RCS, respectively. It can be observed that the overall trend of the measured data is in close accordance with the simulation results, which fully displays that the suggested model is effective and feasible. However, the measured results show obvious deviations around the resonance point. On the one hand, the deviations are caused by the processing errors during the production of the real object, and on the other hand, the deviations caused by the calibration and test environment between the horn antenna and the sample.
Conclusion
The paper presents and investigates a butterfly metasurface operating in the Ku-Ka band to achieve multifunctional polarization conversion and reduce radar cross section. Through simulation and experimental verification, its conversion efficiency and RCS reduction performance are evaluated within the frequency range of 14–38 GHz. The converter not only performs dual-band linear-cross polarization conversion (PCR > 90%), but also efficiently converts linearly polarized (LP) incident waves into LHCP waves and RHCP waves (AR < 3). Additionally, the PCR and AR exhibit robust performance against oblique incidence angles. The polarization conversion characteristics of the resonant unit and mirror unit are derived and theoretically analyzed. Based on 1-bit coded triangular chessboard configuration, over 10 dB RCS reduction is achieved in the frequency ranges of 14–15.17 GHz, 24.60–35.20 GHz, and 36.30–38 GHz. Furthermore, the proposed design offers advantages such as low profile, miniaturization, and relative inexpensive of the dielectric substrate (PTFE). Given these features, the proposed butterfly metasurface holds great potential for applications including wireless communication and electromagnetic stealth.
Data availability
The data that support the fndings of this study are available from the authors upon reasonable request. For details, please contact corresponding author Lijian Zhang.
References
Fahad, A. K., Ruan, C., Nazir, R. & Raza, M. T. Multifunctional multi-band metasurface for linear to circular polarization conversion in transmission and reflection modes. Results Phys. 50, 106595 (2023).
Zheng, C. et al. Terahertz metasurface polarization detection employing vortex pattern recognition. Photon. Res. 11, 2256–2263 (2023).
Yu, Y., Xiao, F., He, C., Jin, R. & Zhu, W. Double-arrow metasurface for dual-band and dual-mode polarization conversion. Opt. Express 28, 11797–11805 (2020).
Li, F. et al. Design and implementation of metamaterial polarization converter with the reflection and transmission polarization conversion simultaneously. J. Opt. 21, 045102 (2019).
Xu, J., Li, R., Qin, J., Wang, S. & Han, T. Ultra-broadband wide-angle linear polarization converter based on H-shaped metasurface. Opt. Express 26, 20913–20919 (2018).
Zhao, Y., Hou, Z., Yan, B., Su, B. & Zhang, C. Metasurface-based terahertz wideband linear polarization converter. Res. Opt. 13, 100523 (2023).
Xu, P., Jiang, W. X., Wang, S. Y. & Cui, T. J. An ultrathin cross-polarization converter with near unity efficiency for transmitted waves. IEEE Trans. Antenn. Propag. 66, 4370–4373 (2018).
Wu, J. L., Lin, B. Q. & Da, X. Y. Ultra-wideband reflective polarization converter based on anisotropic metasurface. Chin. Phys. B 25, 088101 (2016).
Yang, Z. et al. Ultrathin tri-band reflective cross-polarization artificial electromagnetic metasurface. J. Electromag. Wave 34, 1491–1501 (2020).
Lin, B. et al. An ultra-wideband reflective linear-to-circular polarization converter based on anisotropic metasurface. IEEE Access 8, 82732–82740 (2020).
Jiang, Y., Wang, L., Wang, J., Akwuruoha, C. N. & Cao, W. Ultra-wideband high-efficiency reflective linear-to-circular polarization converter based on metasurface at terahertz frequencies. Opt. Express 25, 27616–27623 (2017).
Wang, H. B., Cheng, Y. J. & Chen, Z. N. Wideband and wide-angle single-layered-substrate linear-to-circular polarization metasurface converter. IEEE Trans. Antenn. Propag. 68, 1186–1191 (2019).
Lin, B. Q. et al. Ultra-wideband circular polarization-maintaining reflection realized by an anisotropic metasurface. J. Electromag. Wave 34, 1420–1429 (2020).
Zhang, B. et al. Ultra-broadband angular-stable reflective linear to cross polarization converter. Electronics 11, 3487 (2022).
Liu, X. et al. Dual-band dual-rotational-direction angular stable linear-to-circular polarization converter. IEEE Trans. Antenn. Propag. 70, 6054–6059 (2022).
Kamal, B. et al. Design and experimental analysis of dual-band polarization converting metasurface. IEEE Antenn. Wirel. Pr. 20, 1409–1413 (2021).
Lin, B. et al. Dual-band linear-to-circular and circular-to-linear polarization converter based on reflective metasurface. Appl. Phys. A 128, 1011 (2022).
Dutta, R., Ghosh, J., Yang, Z. & Zhang, X. Multi-band multi-functional metasurface-based reflective polarization converter for linear and circular polarizations. IEEE Access 9, 152738–152748 (2021).
Nguyen, T. K. T. et al. Simple design of efficient broadband multifunctional polarization converter for X-band applications. Sci. Rep. 11, 2032 (2021).
Wu, Y. et al. Dual-band linear polarization converter based on multi-mode metasurface. Results Phys. 40, 105859 (2022).
Fu, C., Sun, Z., Han, L. & Liu, C. Dual-bandwidth linear polarization converter based on anisotropic metasurface. IEEE Photon. J. 12, 1–11 (2020).
Majeed, A. et al. An ultra-wideband linear-to-circular polarization converter based on a circular, pie-shaped reflective metasurface. Electronics 11, 1681 (2022).
Yadav, V. S., Kundu, D., Kaushik, B. K. & Patnaik, A. Metasurface-based conformal linear-to-circular polarization converter for emerging wireless applications. Optik 296, 171553 (2024).
Pouyanfar, N., Nourinia, J. & Ghobadi, C. Multiband and multifunctional polarization converter using an asymmetric metasurface. Sci. Rep. 11, 9306 (2021).
Ozturk, G. & Corapsiz, M. F. Ultra-thin reflective linear and circular polarization converter for Ku band applications. Opt. Commun. 516, 128268 (2022).
Liao, K. et al. A polarization converter with single-band linear-to-linear and dual-band linear-to-circular based on single-layer reflective metasurface. Int. J. RF Microw. Comput. Aided Eng. 32, e22955 (2022).
Coskun, A., Hasar, U. C., Ozmen, A. & Ertugrul, M. Easy-to-implement ultra-thin, wide-band, and multi-functional polarization converter for K and Ka band applications. Adv. Theor. Simul. 5, 2100543 (2022).
Liu, J., Li, J. Y. & Chen, Z. N. Broadband polarization conversion metasurface for antenna RCS reduction. IEEE Trans. Antenn. Propag. 70, 3834–3839 (2021).
Zheng, Q., Guo, C., Li, H. & Ding, J. Broadband radar cross-section reduction using polarization conversion metasurface. Int. J. Microw. Wirel. Technol. 10, 197–206 (2018).
Lu, Y. et al. Ultrawideband monostatic and bistatic RCS reductions for both copolarization and cross polarization based on polarization conversion and destructive interference. IEEE Trans. Antenn. Propag. 67, 4936–4941 (2019).
Fu, C., Han, L., Liu, C., Sun, Z. & Lu, X. Dual-band polarization conversion metasurface for RCS reduction. IEEE Trans. Antenn. Propag. 69, 3044–3049 (2020).
Chen, H. et al. X-Band and Low-RCS Flexible Wideband Antenna Array Based on Metasurface. IEEE Antenn. Wirel. Pr. 1-5 (2024)
Zhang, L. et al. Efficient polarization conversion metasurface for scattered beam control and RCS reduction. Sci. Rep. 14, 26260 (2024).
Trost, P. & Eder, M. An analytical performance approach for RCS/RS with one robot serving multiple stack heights under a one-path relocation strategy. Sci. Rep. 14, 3593 (2024).
Jia, Y., Liu, Y., Guo, Y. J., Li, K. & Gong, S. A dual-patch polarization rotation reflective surface and its application to ultra-wideband RCS reduction. IEEE Trans. Antenn. Propag. 65, 3291–3295 (2017).
Wu, L. P., Fang, Q. H., Pan, W. K., Li, M. H. & Dong, J. F. Realizing of cross-polarization conversion for linearly polarized waves in multiband by orthotropic metasurface. J. Electromag. Wave 36, 101–114 (2022).
Ahmed, F., Khan, M. I. & Tahir, F. A. A multifunctional polarization transforming metasurface for C-, X-, and K-band applications. IEEE Antenn. Wirel. Propag. 20, 2186–2190 (2021).
Khan, M. I., Khalid, Z. & Tahir, F. A. Linear and circular-polarization conversion in X-band using anisotropic metasurface. Sci. Rep. 9, 4552 (2019).
Acknowledgements
This work is supported by the Natural Science Basic Research Program of Shaanxi Province, (2024JC-YBQN-0312) and the Key Projects of Natural Science Basic Research Program of Shaanxi Province (2022JZ-35).
Author information
Authors and Affiliations
Contributions
Haoyu Zhang: conceptualization, methodology, software, writing—original draft, visualization. Lijian Zhang: conceptualization, formal analysis, resources. Peng Song: formal analysis, data curation. Yunhong Li: investigation, methodology. Chuang Gao: validation, investigation. Penghui Xin: resources, investigation. Tian Liu: supervision, investigation, project administration. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhang, H., Zhang, L., Song, P. et al. A butterfly metasurface with efficient multi-functional polarization conversion operating in the Ku-Ka band. Sci Rep 14, 30161 (2024). https://doi.org/10.1038/s41598-024-81357-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-81357-3