Abstract
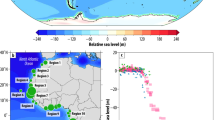
Coastal populations are susceptible to relative sea-level (RSL) rise and accurate local projections are necessary for coastal adaptation. Local RSL rise may deviate from global mean sea-level rise because of processes such as geoid change, glacial isostatic adjustment (GIA), and vertical land motion (VLM). Amongst all factors, the VLM is often inadequately estimated. Here, we estimated the VLM for the Oka estuary, northern Spain and compared it to the VLM component of sea-level projections in the Intergovernmental Panel on Climate Change (IPCC) Sixth Assessment Report (AR6) and the Spanish National Climate Change Adaptation Plan (NCCAP). To estimate VLM, we updated Holocene RSL data from the Atlantic coast of Europe and compared it with two 3D GIA models. Both models fit well with RSL data except in the Oka estuary. We derived a VLM rate of − 0.88 ± 0.03 mm/yr for the Oka estuary using the residuals of GIA misfits. Comparable VLM rates of − 0.85 ± 0.14 mm/yr and − 0.80 ± 0.32 mm/yr are estimated based on a nearby Global Navigation Satellite Systems station and differenced altimetry-tide gauge technique, respectively. Incorporating the updated late Holocene estimate of VLM in IPCC AR6 RSL projections under a moderate emissions scenario increased the rate of RSL rise by 15% by 2030, 11% by 2050, and 9% by 2150 compared to the original IPCC AR6 projections, and also increased the magnitude of RSL rise by over 40% by 2035 and 2090 compared with projections from the Spanish NCCAP. Our study demonstrates the importance of accurate VLM estimates for local sea-level projections.
Similar content being viewed by others
Introduction
More than 600 million people live in low-elevation coastal zones and this population is likely to increase to 1.4 billion people under the highest-end growth assumption by 20601,2. Coastal populations are susceptible to relative sea-level (RSL) rise and accurate local sea-level projections are necessary for relevant adaptation and mitigation strategies2,3,4,5,6. Currently, rising global mean sea level (GMSL) is primarily driven by thermal expansion of ocean water7 and ice mass loss from glaciers, ice caps and the Greenland and Antarctica Ice Sheets8,9,10. However, local RSL rise can deviate from GMSL3,11,12 because of processes such as vertical land motion (VLM)13,14,15,16,17,18,19.
VLM is caused by a wide range of natural and anthropogenic processes, such as glacial isostatic adjustment (GIA)12, tectonics20, sediment loading and compaction21,22, and subsidence from resource (e.g., ground water) extraction23. Short-term (annual to decadal) VLM signals have been estimated from instrumental measurements such as tide gauge data24 and Global Navigation Satellite Systems (GNSS) data25,26. Tide gauges measure changes in sea level relative to the land where they are located, including changes in both sea surface height and land height. Tide gauges have been used to derive the VLM signal in the Intergovernmental Panel on Climate Change (IPCC) Sixth Assessment Report (AR6) RSL projections3 but given that many gauges are located in port facilities where wharf removal, development, and/or extensions occur, the datum history of the tide gauge can be problematic27,28. GNSS data have been widely used to estimate the VLM signal29,30,31, however they are limited by the station spatial coverage and temporal time span32, especially along coastal regions26. Short-term VLM signals can also be estimated from a differenced altimetry-tide gauge technique using satellite altimetry data and tide gauge data14, but the processing techniques are still developing and are limited by the broad spectrum of error sources15,33,34. As an alternative, long-term (multi-centennial to millennial scale) rates of VLM can be derived using late Holocene (~ 4 ka to present) RSL data supported by GIA models35,36. Late Holocene RSL data from the U.K.37, Atlantic38,39 and Pacific40 coasts of the U.S., Oceania36, Eastern Mediterranean41, and Adriatic coast of Croatia42, have been used to deduce VLM from subsiding and uplifting coastlines.
Here, we estimated VLM in the Oka estuary, northern Spain using an updated Holocene RSL database from the Atlantic coast of Europe (Fig. 1A and B). The Oka estuary is renowned for its well-preserved natural conditions and biodiversity, and its densely populated municipalities like Gernika-Lumo are vulnerable to sea-level rise43. We compared Holocene RSL data44 with two GIA models using two ice models ICE-6G_C45,46 and ANU-ICE47,48,49 and a singular 3D Earth model HetML14050. Both GIA models fit the RSL data along the Atlantic coast of Europe except the Oka estuary, where significant misfits arise implying potential long-term VLM (Figs. 2, 3). The RSL database is standardized following the HOLSEA protocol51 and radiocarbon ages are recalibrated with the latest calibration curve52. We derived the long-term VLM rate via linear regression using the residuals between the GIA prediction and late Holocene RSL data with the consideration of geoid variation as uncertainty in derived VLM rate. Then we compared the estimated long-term VLM rate with nearby GNSS data and differenced altimetry-tide gauge data (Fig. 4). We applied the long-term VLM rate in the Oka estuary to produce new RSL projections. We then compared the likely (17–83rd percentiles) and very likely (5–95th percentiles) ranges of new RSL projections with projections from IPCC AR63 and Spanish National Climate Change Adaptation Plan (NCCAP)53 (Fig. 5). We show the VLM component is underestimated in current RSL projections for the Oka estuary and the projected RSL will exceed 0.5 m and 1 m thresholds earlier.
Atlantic coast of Europe study region and ___location of relative sea-level (RSL) databases. (A) The Atlantic coast of Europe and (B) the updated deglacial RSL database modified after ref.44 showing regions 1–13 and (C) region 8, Oka estuary and ___location of SOPU Global Navigation Satellite Systems (GNSS) and Bilbao tide gauge (TG) stations. The gray-shaded areas in panel A and B represent the ice coverage at Last Glacial Maximum (LGM, 26 ka BP) of ICE-6G_C45,46. The figure is generated using Generic Mapping Tools software version 5.4.554.
Holocene relative sea-level (RSL) data compared with predictions from 3D glacial isostatic adjustment (GIA) model ICE-6G_C (HetML140). Holocene RSL data showing sea-level index points (SLIP) are plotted as boxes with 2\(\sigma \) vertical and temporal uncertainties and terrestrial and marine limiting data providing upper and lower constraints on RSL, respectively. The RSL comparison plot of 3D GIA model ANU-ICE (HetML140) and RSL data at 13 regions are shown in Fig. S1.
Summary of the late Holocene relative sea-level (RSL) misfit \(\chi \)-statistic. (A) Late Holocene RSL misfit \(\chi \)-statistic with the two glacial isostatic adjustment models ICE-6G_C (HetML140) and ANU-ICE (HetML140) at 13 regions along the Atlantic coast of Europe. (B) The inset shows the derived vertical land motion (VLM) rate of − 0.88 ± 0.03 mm/yr via linear regression using late Holocene RSL residuals with ICE-6G_C model at region 8 and considering the geoid contribution from ICE-6G_C (HetML140) as uncertainty in VLM rate derivation. The shaded boxes in the inset indicate the upper and lower bounds of the RSL residual. The misfit \(\chi \)-statistics after late Holocene RSL data correction of a VLM rate of − 0.88 ± 0.03 mm/yr at region 8 are indicated by bars with dashed outlines. After the VLM correction, the misfit \(\chi \)-statistics for ICE-6G_C at region 8 (Oka estuary) declined by ~ 80% from 4.7 to 0.9.
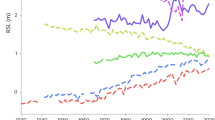
Estimated vertical land motion (VLM) rates from instrumental records and VLM rate used in IPCC AR6 projections. (A) The Global Satellite Navigation Systems (GNSS) vertical positions at SOPU station produced by the Nevada Geodetic Laboratory30 and the derived linear rate and its associated uncertainty (1σ) of − 0.85 ± 0.14 mm/yr. (B) The calculated VLM from differencing satellite altimetric sea-level anomalies and tide gauge records at Bilbao tide gauge station, and the derived VLM rate and its associated uncertainty (1σ) of − 0.80 ± 0.32 mm/yr. For more details see the text. (C) Comparison of the VLM rates of − 0.88 ± 0.03 mm/yr derived from late Holocene RSL data (red solid line with pink envelope, Fig. 3 inset), GNSS data, differenced altimetry-tide gauge data and VLM rate used in IPCC AR6. The blue bars with black lines indicate the derived VLM rates with 1σ uncertainties. The grey-dashed line indicates the 0 value line.
Comparison of projections of relative sea-level (RSL) rise from the Spanish National Climate Change Adaptation Plan (NCCAP) and IPCC AR6. Projected likely (17–83rd percentiles) and very likely (5–95th percentiles) RSL rise from the NCCAP under RCP4.5 and RCP8.5 scenarios by 2026–2045 and by 2081–2100, compared with the IPCC AR6 sea-level projections under SSP2-4.5 and SSP5-8.5 scenarios by (A) 2035 and (B) 2090, respectively. The IPCC AR6 projections with the updated VLM rate of − 0.88 ± 0.03 mm/yr are also presented. The difference in the projected magnitude of sea-level rise (50th percentile value) are summarized in Table 2. We have standardized the Spanish NCCAP projection to the same baseline as IPCC AR6 of 1995–2014 following ref.55.
Results
Late Holocene RSL and GIA model performance along the Atlantic coast of Europe
RSL data along the Atlantic coast of Europe show similar patterns of sea-level change, with a monotonic RSL rise from lower than − 40 m at rates > 5 mm/yr in the early Holocene. Rising RSL subsequently decelerates during the mid-Holocene to a nearly constant rate of rise of < 1 mm/yr during the late Holocene44 (Fig. 2).
Coupled with the 3D Earth model HetML14050, both GIA models ICE-6G_C and ANU-ICE fit well with the RSL data in most regions (Figs. 2, S1–S3) with the late Holocene RSL misfit \(\chi \)-statistic < 1.5. The exception is in region 8 (Oka estuary), which has a misfit \(\chi \)-statistic > 4.5 for both GIA models (Fig. 3). In the Oka estuary, late Holocene sea-level index points (SLIPs) are consistently lower than the GIA predictions by ~ 2.1 m to ~ 3.3 m.
Vertical land motion in the Oka estuary
We derived a VLM rate of − 0.88 ± 0.03 mm/yr via linear regression using the residuals between the late Holocene RSL data and RSL predictions from GIA model ICE-6G_C in the Oka estuary as ICE-6G_C fits better than ANU-ICE. We corrected the late Holocene RSL data in the Oka estuary using the VLM rate of − 0.88 ± 0.03 mm/yr, which reduced the ICE-6G_C misfit \(\chi \)-statistic by ~ 80% from 4.7 to 0.9 (Fig. 3).
Importantly, the derived VLM rate is consistent with the VLM rate of − 0.85 ± 0.14 mm/yr calculated based on nearby GNSS station SOPU with 15 years long measurements. Similarly, we estimated a VLM rate of − 0.80 ± 0.32 mm/yr using the differenced altimetry-tide gauge technique with ~ 30 years measurements of satellite altimetry and Bilbao tide gauge data (Fig. 4).
The VLM rate applied in IPCC AR6 projections at the Bilbao tide gauge station close to the Oka estuary (Fig. 1C) is − 0.20 mm/yr (50th percentile)3, which is an underestimate of ~ 77% compared to the long-term VLM rate of − 0.88 ± 0.03 mm/yr estimated from late Holocene RSL data (Fig. 4).
The VLM rate applied in the Spanish NCCAP is from IPCC AR556 and was estimated with a GIA model using the mean of the ICE-5G57 and ANU-ICE48 as the input ice model. For the Oka estuary this is estimated to be − 0.14 mm/yr, which is an underestimate of ~ 84% compared to the long-term VLM rate of − 0.88 ± 0.03 mm/yr.
Sea-level projections in the Oka estuary
We produced RSL projections and likely ranges (17–83rd percentile) for Bilbao tide gauge station near (~ 25 km) the Oka estuary using the original and updated VLM for IPCC AR6 Shared Socioeconomic Pathway (SSP) SSP2-4.5 for three time horizons (2030, 2050, 2150; Fig. S4, Table S1). Projections for SSP1-1.9 and SSP5-8.5 are provided in the Supplementary Text S1 and Table S1.
Using the derived long-term VLM under the SSP2-4.5 scenario, the projected rate of RSL rise increased by 15.1% by 2030, 10.6% by 2050, and 9.0% by 2150 compared to IPCC AR6 using the original VLM estimate. Similarly, the magnitude of RSL rise increased by ~ 0.02 m (14.9%) by 2030, ~ 0.03 m (13.3%) by 2050, and ~ 0.10 m (10.7%) by 2150 using the updated VLM. The likely range is 0.08–0.19 m at 2030, 0.18–0.36 m at 2050, and 0.68–1.50 m at 2150. The timing of exceedance of 0.5 m and 1.0 m thresholds are earlier using the updated VLM: 10 years from 2090 to 2080 and 15 years from 2161 to 2146, respectively (Fig. S4, Table 1).
Because the VLM component in IPCC AR6 projections is scenario independent3, using the updated VLM increased the projected rate of RSL rise continuously by ~ 0.7 mm/yr.
The Spanish NCCAP RSL projections for Representative Concentration Pathway (RCP) 4.5 in the Oka estuary show RSL rising 0.10 m (50th percentile value) by 2026–2045 and 0.36 m by 2081–2100 (Table 2, Fig. 5). The projected RSL from the IPCC AR6 for SSP2-4.5 using the long-term VLM in the Oka estuary will increase to 0.16 m by 2035 and 0.57 m by 2090. Comparing the corresponding RCP4.5 and SSP2-4.5 scenarios, IPCC AR6 projected magnitudes of RSL rise using the long-term VLM increase by 59% by 2035 and by 58% by 2090 (Table 2, Fig. 5).
Discussion and conclusions
Late Holocene subsidence in the Oka estuary
Similar late Holocene subsidence and lowering of RSL has been identified in areas such as along the Atlantic coast of the U.S.35,39, Mekong River Delta58,59, Oceania36, and Eastern Mediterranean41. In these studies, the late Holocene subsidence was attributed to a variety of processes including forebulge collapse35,39, mantle dynamics19, tectonics41, sediment compaction58, and (fluvial) sediment/coral/volcanic loading36,60. For example, ref.42 compared late Holocene RSL data with GIA model ICE-7G_NA (VM7) predictions from the central-eastern Adriatic coast of Croatia showing a subsidence rate of 0.45 ± 0.60 mm/yr driven by tectonics in the Adriatic microplate. Reference60 compared Holocene RSL data from Bohai Bay, China with ICE-6G_C and ANU-ICE models and revealed subsidence rates of 1.25 mm/yr driven by a combination of tectonic subsidence and fluvial sediment loading.
The Oka estuary is located at the periphery of the former ice margins of the British-Irish and Fennoscandian Ice Sheets and is affected by forebulge collapse44,61,62 (Fig. 1A). Forebulge collapse is a bending-related subsidence of the lithosphere outside previously glaciated areas involving elastic lithosphere and beneath viscoelastic mantle63. The ICE-6G_C, coupled with the 3D Earth model HetML140, shows a subsidence rate of 0.25 ± 0.16 mm/yr (uncertainty from ref.64) in the Oka estuary, which is consistent with the subsidence rate of 0.21 mm/yr from the 1D model ICE-6G_C (VM5a)46 and the results from ref.65. Similarly, the Atlantic and Pacific coasts of the U.S. are located at the periphery of the Laurentide Ice Sheet38,39. The magnitude of RSL rise caused by forebulge collapse of the Laurentide Ice Sheet, however, is larger (up to 1.6 mm/yr, ref.35) due to a shorter distance from the former ice margin and larger size of the Laurentide Ice Sheet compared to the British-Irish and Fennoscandian Ice Sheets46,49,66.
The ICE-6G_C GIA model can explain ~ 28% (i.e., 0.25 ± 0.16 mm/yr) of the estimated long-term subsidence rate of Oka estuary of 0.88 ± 0.03 mm/yr. Other studies have revealed subsidence in northern Spain67,68. Reference16 showed low to moderate subsidence with a mean rate of ~ 0.6 mm/yr along the Iberian Atlantic coast, but with significant spatial variations and up to 2.2 mm/yr subsidence along the northern Spain coast that reflects more localised effects (e.g., local tectonic, anthropogenetic influence)69. More importantly, the Oka estuary is in the Basque-Cantabrian Basin that formed with the opening of the North Atlantic Ocean and the Bay of Biscay70. This basin developed in the Mesozoic and was inverted during the Pyrenean orogeny71. It is characterized by Upper Triassic evaporites (Keuper facies) between the Paleozoic basement and the sedimentary cover72,73. These evaporites have been subjected to halokinetic processes, at times associated with folds and faults74,75,76. It is possible that salt migration contributed to the enhanced subsidence (the non-GIA component) during the late Holocene in the Oka estuary.
The long-term subsidence derived from late Holocene sea-level reconstructions assumes minimal influence from local processes such as paleotidal range change and sediment compaction36,77. Paleotidal range has been estimated for the North Atlantic region and shows the strongest amplification occurred during the early Holocene78 with minimal changes in the late Holocene, even at the estuary scale79. We applied the paleotidal model from ref.80 to the region of the Oka estuary, which shows nearly no change in tidal range during the last 4 ka and would, therefore, not influence the elevation of the SLIPs (Fig. S5; ref.80).
Sediment compaction of intertidal sediments can result in post-depositional lowering81,82, which can lead to an overestimation of the magnitude and rate of RSL rise83. For example, ref.84 showed the maximum contribution of sediment compaction to the sea-level reconstruction in North Carolina was up to ~ 12%. The susceptibility of intertidal sediments to compaction varies with sediment composition85 and depth of overburden81. Sediments rich in organic matter (e.g., peats) are generally more compressible than minerogenic sediments (e.g., sands, silts and clays)85. In northern Spain, salt-marsh sediments exhibit a much lower organic matter content, compared to their eastern North American counterparts22, and typically are below 10%, which diminishes with depth due to degradation at the surface86,87,88,89. Furthermore, the coarse minerogenic nature of sands in the intertidal sediments beneath the SLIPs minimizes further compaction90. The depth of overburden81 where the greater thickness above generates higher compressive stresses to reduce the thickness of sediment strata beneath81,91. In the Oka estuary, the depth of overburden in the late Holocene sea-level reconstructions is less than ~ 6 m. Nonetheless, sediment compaction has been revealed in other Spanish coastal areas despite the presence of sands in sediments92,93. For example, ref.94 estimated a subsidence rate of ~ 1.75 mm/yr in sediment sequences comprised of sandy delta-front facies from the mid to late Holocene in the Ebro delta, northeastern Spain. Reference93 also inferred increasing subsidence rates from the mid to late Holocene in the Ebro delta, which are likely linked to the transition from estuarine to deltaic environments.
While we are currently unable to precisely quantify the contribution of sediment compaction to the late Holocene RSL reconstructions in the Oka estuary, it is important to note the derived subsidence rate (− 0.88 ± 0.03 mm/yr) is consistent with local GNSS data (− 0.85 ± 0.14 mm/yr) and differenced altimetry-tide gauge results (− 0.80 ± 0.32 mm/yr).
This study demonstrates that late Holocene RSL data, supported by GIA modelling, has the potential and capability to constrain the VLM component of future sea-level projections.
Influences of the underestimated VLM component on sea-level projections in the Oka estuary
The updated VLM rate of − 0.88 ± 0.03 mm/yr in the Oka estuary is much greater than the VLM rate of − 0.20 mm/yr used in IPCC AR6 at Bilbao tide gauge station close to the Oka estuary (Fig. 4). The VLM signal in IPCC AR6 is solely derived from tide gauge records11, which measure changes in both land height and sea surface height. The latter includes the sea-level contributions from non-VLM signals, such as thermal expansion of ocean water, melting input from ice sheets and glaciers, and land water storage change7,95. Where possible, the tide gauge records should be subtracted by satellite altimetry data to separate the VLM component14,15. Furthermore, the trend derived from tide gauge records varies using different time periods96, especially in the context of sea-level rise acceleration27.
We show that incorporation of the updated local VLM rate increases future sea-level rise up to tens of centimetres and exceeds the timing of 0.5 m and 1.0 m thresholds earlier by 7–18 years and 6–15 years, respectively. Furthermore, rates of RSL rise exceeding the ability of salt-marsh ecosystems to vertically accrete (7.1 mm/yr97) will also be reached as early as ~ 2050 (50th percentile) compared with ~ 2104 in IPCC AR6 under the SSP2-4.5 scenario (Table S1), leaving much shorter time for coastal adaptation. The difference of projected magnitudes of RSL rise for the Oka estuary between the Spanish NCCAP under RCP4.5 scenario by 2081–2100 (0.36 m, 50th percentile value) and IPCC AR6 using the updated VLM rate under SSP2-4.5 scenario by 2090 (0.57 m) is 0.21 m (Table 2, Fig. 5). This will significantly increase the coastal flood risk98. For example, ref.99 showed that the extreme sea-level rise would render the Bay of Biscay exposed biennially under RCP4.5 scenario to the present-day 100-year event by 2100. But this is also underestimated because the updated long-term subsidence rate was not accounted for. We suggest that the sea-level rise adaptation and mitigation policies and strategies based on the Spanish NCCAP need to be updated accordingly with the new sea-level projections from IPCC AR6 that incorporate accurate VLM estimates as presented here100,101.
The Oka estuary, situated within the Urdaibai Biosphere Reserve in northern Spain, is recognized as a wetland of international importance under the Ramsar Convention in 1993, the estuary receives additional protection for its environmental values. This wetland area spans across 10 municipalities with a combined population of over 24,000 residents, predominantly concentrated in Gernika-Lumo, located in the upper estuary43. Despite considerable human impact, especially from dredging activities to maintain navigation routes from the mid-twentieth century to 2003102,103, the estuary remains a critical habitat, supporting extensive mudflats and seagrass meadows essential for local biodiversity104,105. Economically, the Oka estuary offers vital ecosystem services, including ecotourism and recreation, which are significant economic drivers for the region106. Although the results in this study are illustrative of the Oka estuary, the methodology can be used for wider regions and it raises a significant potential problem of utilizing generalized sea-level projections without an understanding of local conditions.
Methods
Late Holocene RSL database along the Atlantic coast of Europe
We updated the Holocene RSL database along the Atlantic coast of Europe44 with new SLIPs for the Oka estuary90. The updated database has 210 SLIPs, which define the elevation of RSL at a given point in space and time with corresponding spatial and temporal uncertainties, 91 marine limiting data points and 35 terrestrial limiting data points (Figs. 1, 2), which provide lower and upper limits on the position of RSL, respectively. There are 77 SLIPs and 15 marine limiting data points in the late Holocene period.
To generate SLIPs, samples from salt-marshes, estuaries, and lagoons were utilized. Conversion of these samples into SLIPs involved measuring the present-day elevation of these environments and analyzing their microfossil (e.g., foraminifera, pollen, diatoms, and ostracoda) and plant macrofossil content. Modern indicator zonation was then employed to interpret the core samples (i.e., the indicative meaning), where the indicative range denotes a vertical span wherein the coastal sample may be situated, and the reference water level (RWL) represents the midpoint of that vertical range with reference to a specific water level (e.g., Mean Tide Level, MTL). Marine limiting dates were established using estuarine and lagoonal sediments not meeting the criteria for classification as index points. Detailed RWL and indicative range values for each sample type are available in the original database paper44.
In the case of the Oka estuary, SLIPs were derived from three cores: two from the middle estuary (AN2 and AN3) and one from the upper estuary (GK9)44,90. In the Anbeko area (AN2 and AN3), the sedimentary sequence comprises 3.3 m of fluvial gravels, 8.1 m of brackish intertidal muds, 9.6 m of near-marine intertidal sands, 6.9 m of salt-marsh sandy muds, and 0.3 m of anthropogenic infill. Conversely, in Gernika (GK9), the sedimentary sequence consists of 1.1 m of supratidal paleosol muds, 1.8 m of brackish intertidal sandy muds, 2 m of salt-marsh sandy muds, and 6.1 m of anthropogenic infill.
Notably, post-depositional lowering resulting from sediment compaction and changes in paleotidal range were not factored into the analysis.
We recalibrated all data using CALIB 8.2107 with IntCal2052 and Marine20108 for terrestrial and marine materials, respectively. We estimated the local marine reservoir correction (ΔR) values from the Marine Radiocarbon Reservoir Correction database (http://calib.org/marine/) or recalculated published ΔR values using deltar109. The ΔR varied between − 330 ± 91 14C yr and 107 ± 114 14C yr (see the supplementary Text S2 for further details).
Glacial isostatic adjustment models
The 3D GIA models were computed using the Coupled Laplace-Finite Element (CLFE) method110 with 0.5 \(\times \) 0.5° horizontal resolution near the surface, decreasing with depth to 2.0 \(\times \) 2.0° in the lower mantle to reduce computational resources. More details about the 3D GIA description can be found in ref.111.
We compared the Holocene RSL database with two GIA models to validate their performance along the Atlantic coast of Europe. The two GIA models apply distinct ice models ICE-6G_C45,46 and ANU-ICE47,48,49, which are developed independently and have different ice-equivalent sea-level histories. For both GIA models, we apply the same 3D Earth model HetML14050. The use of 3D Earth models is supported by the ANU-ICE model47,48,49 and ICE-6G_C ice model111. The HetML140 model provides better fit with RSL data from Laurentia and Fennoscandia than the 1D model VM5a when coupled with the ICE-6G_C ice model50,112. Moreover, the lithospheric thickness (60–140 km) and upper mantle viscosity (~ 4 \(\times \) 1020 Pa s beneath Fennoscandia) of HetML140 model are within the preferred parameter ranges of ANU-ICE47,66 and thus it is compatible to be coupled with the ANU-ICE model.
For a quantitative evaluation of the model fit, we generated GIA predictions at the unique ___location of each late Holocene RSL data point (Figs. 1, 2) and compared the predictions to each SLIP to calculate the misfit \(\chi \)-statistic in each region (Fig. 3):
where \(N\) represents the number of data in the \(k\)th region, \({o}_{i}\) indicates \(i\)th observation with 2\(\sigma \) vertical uncertainty \(\Delta {o}_{i}\) and temporal uncertainty \(\Delta {\varvec{t}}\), and \({p}_{i}({m}_{j})\) are the \(i\)th prediction for model \({m}_{j}\). Following ref.113, we account for the uncertainty \(\Delta t\) in the observation age by considering GIA predictions at three times \(t\) and \(t\pm \Delta t\) and choosing the value minimizing \({\left[\left[\frac{{o}_{i}-{p}_{i}({m}_{j})}{{\Delta o}_{i}}\right](t)\right]}^{2}\). The smaller the \(\chi \)-statistic, the better the RSL predictions fit the deglacial RSL data.
Estimating VLM in the Oka estuary
We estimated both long-term and short-term VLM for the Oka estuary. In ICE-6G_C ice model, deglaciation of the Antarctica Ice Sheet ended at 4 ka BP. To minimise the influence of ice melting signal in deriving the long-term VLM, we only applied the residuals between the late Holocene (since 4 ka BP) RSL data and GIA model predictions via linear regression to estimate the long-term VLM rate for the Oka estuary (Fig. 3). The linear rate assumption has been widely used in late Holocene RSL studies36,39,42,60. However, apart from the VLM contribution, the residuals also contain contributions from geoid change114. Then we treat the geoid change during the late Holocene from the ICE-6G_C (HetML140) model as uncertainty in estimating long-term VLM rate (Fig. 3). We applied the estimated VLM rate to correct the late Holocene RSL data and recalculate the RSL misfit \(\chi \)-statistic in region 8 (Oka estuary, Fig. 3).
We also conducted the exponential fit for the residuals between the late Holocene RSL data and GIA model predictions (Fig. S6), which does show a better fit than linear fit. The exponential fit has a R value of 0.79, while the linear fit has a R value of 0.64. However, for this exponential fit, the rate of post depositional lowering in the last 15 years would be 2.63 mm/yr, far in excess of the GNSS rates of − 0.85 ± 0.14 mm/yr. It would be 2.61 mm/yr during the last 27 years, which is three times larger compared to the differenced altimetry-tide gauge technique (− 0.80 ± 0.32 mm/yr).
We further estimated the short-term VLM rates using GNSS data and satellite altimetry and tide gauge data (Fig. 4). We used the GNSS vertical positions at SOPU station (2007–2022) produced by the Nevada Geodetic Laboratory30 and corrected an offset of 3.4 mm in the GNSS time series due to change of antenna on 20th March 2012. Assuming that satellite altimetry and tide gauges capture the same changes in sea surface height, differencing observations from the two observing systems can generate VLM changes at tide gauge sites14. We used reprocessed multi-mission altimetric sea-level anomalies with daily temporal resolution and spatial sampling of 0.25 degree produced by the Copernicus Climate Change Service115 and monthly tide gauge data at 1806 site Bilbao from the archives of the Permanent Service for Mean Sea Level. Due to data gap in year 2021, we only used tide gauge data from year 1993 to year 2020. We calculated VLM from satellite altimetry and tide-gauge observations at the Bilbao tide gauge station. Details of how we derived VLM from satellite altimetry and tide gauge observations can be found in ref.116. We calculated linear rates and their associated uncertainties (1σ) of the edited GNSS time series and VLM time series using SARI software117 and a combination of a power-law and a white noise model.
We estimated the VLM rate used in the Spanish NCCAP by taking the mean of VLM rate predictions from ICE-5G57 and ANU-ICE48 in the Oka estuary.
Sea-level projections in the Oka estuary
We extracted the most up to date sea-level projections in the Oka estuary for the Bilbao tide gauge station from the IPCC AR6 projections (relative to a baseline of 1995–2014) under three medium confidence SSP scenarios (SSP1-1.9, SSP2-4.5, SSP5-8.5) that include the lowest and highest emissions scenarios, respectively3. We investigated the influence of the VLM component in sea-level projections, both for rates and magnitude, by 2030, 2050 and 2150 (Fig. 5, Table S1), and projected timing of sea-level rise exceedance of 0.5 m and 1.0 m thresholds (Table 1), under three SSP scenarios. The full decadal values for rates and magnitudes of sea-level projections for Bilbao tide gauge station using the original and updated VLM for IPCC AR6 are provided in Table S1. We follow the theory of propagation of errors when updating the VLM component for IPCC AR6 sea-level projections.
The Spanish NCCAP projected magnitudes of sea-level rise under RCP4.5 and RCP8.5 scenarios by 2026–2045 and 2081–2100 (relative to a baseline of 1985–2005). We standardized the Spanish NCCAP projection to the same baseline as IPCC AR6 of 1995–2014 following ref.55. SSP2-4.5 and SSP5-8.5 are the moderate and highest emissions scenarios and analogous to RCP4.5 and RCP8.5, respectively11,118. We quantitatively compared the magnitude of sea-level rise from IPCC AR6 using the original and updated VLM by 2035 and 2090 with the sea-level projections from the Spanish NCCAP by 2026–2045 and by 2080–2100 under moderate and highest emissions scenarios (Fig. 5, Table 2).
Data availability
The instrumental sea-level data for Bilbao tide gauge station are available from https://www.psmsl.org/data/obtaining/. The satellite altimetry data are available from https://climate.copernicus.eu/. The ICE-6G_C ice model data profiles are available from https://www.atmosp.physics.utoronto.ca/~peltier/data.php. The sea-level projections developed by the IPCC AR6 report are available from https://sealevel.nasa.gov/ipcc-ar6-sea-level-projection-tool and the raw data files are available from https://doi.org/https://doi.org/10.5281/zenodo.5914709.
References
Neumann, B., Vafeidis, A. T., Zimmermann, J. & Nicholls, R. J. Future coastal population growth and exposure to sea-level rise and coastal flooding-a global assessment. PLoS ONE 10, e0118571 (2015).
Hauer, M. E. et al. Sea-level rise and human migration. Nat. Rev. Earth Environ. 1, 28–39 (2020).
Fox-Kemper, B. et al. Ocean, cryosphere, and sea level change. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change 1211–1361 (Cambridge University Press, 2021).
Kulp, S. A. & Strauss, B. H. New elevation data triple estimates of global vulnerability to sea-level rise and coastal flooding. Nat. Commun. 10, 1–12 (2019).
Hinkel, J. et al. Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc. Natl. Acad. Sci. 111, 3292–3297 (2014).
Nicholls, R. J. & Cazenave, A. Sea-level rise and its impact on coastal zones. Science 328, 1517–1520 (2010).
Frederikse, T. et al. The causes of sea-level rise since 1900. Nature 584, 393–397 (2020).
Shepherd, A. et al. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 558, 219–222 (2018).
Shepherd, A. et al. Mass balance of the Greenland Ice Sheet from 1992 to 2018. Nature 579, 233–239 (2020).
Mercer, J. H. West Antarctic ice sheet and CO2 greenhouse effect: A threat of disaster. Nature 271, 321–325 (1978).
Kopp, R. E. et al. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earths Future 2, 383–406 (2014).
Peltier, W. R., Wu, P. P. C., Argus, D., Li, T. & Velay-Vitow, J. Glacial isostatic adjustment: Physical models and observational constraints. Rep. Prog. Phys. (2022).
Tay, C. et al. Sea-level rise from land subsidence in major coastal cities. Nat. Sustain. 1–9 (2022).
Wöppelmann, G. & Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 54, 64–92 (2016).
Pfeffer, J. & Allemand, P. The key role of vertical land motions in coastal sea level variations: A global synthesis of multisatellite altimetry, tide gauge data and GPS measurements. Earth Planet Sci. Lett. 439, 39–47 (2016).
Mendes, V. B., Barbosa, S. M. & Carinhas, D. Vertical land motion in the Iberian Atlantic coast and its implications for sea level change evaluation. J. Appl. Geod. 14, 361–378 (2020).
Milne, G. A. & Mitrovica, J. X. Searching for eustasy in deglacial sea-level histories. Quat. Sci. Rev. 27, 2292–2302 (2008).
Naish, T. et al. The significance of interseismic vertical land movement at convergent plate boundaries in probabilistic sea-level projections for AR6 scenarios: The New Zealand case. Earths Future 12, e2023EF004165 (2024).
Shirzaei, M. et al. Measuring, modelling and projecting coastal land subsidence. Nat. Rev. Earth Environ. 2, 40–58 (2021).
Wang, K., Hu, Y. & He, J. Deformation cycles of subduction earthquakes in a viscoelastic Earth. Nature 484, 327–332 (2012).
Ivins, E. R., Dokka, R. K. & Blom, R. G. Post-glacial sediment load and subsidence in coastal Louisiana. Geophys. Res. Lett. https://doi.org/10.1029/2007GL030003 (2007).
Walker, J. S. et al. A 5000-year record of relative sea-level change in New Jersey, USA. Holocene 33, 167–180 (2023).
Chaussard, E., Amelung, F., Abidin, H. & Hong, S. Remote Sensing of Environment Sinking cities in Indonesia: ALOS PALSAR detects rapid subsidence due to groundwater and gas extraction. Remote Sens. Environ. 128, 150–161 (2013).
Zervas, C., Gill, S. & Sweet, W. Estimating vertical land motion from long-term tide gauge records. NOAA Technical Report NOS CO-OPS 65, (2013).
Dow, J. M., Neilan, R. E. & Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geod. 83, 191–198 (2009).
Hammond, W. C., Blewitt, G., Kreemer, C. & Nerem, R. S. GPS imaging of global vertical land motion for studies of sea level rise. J. Geophys. Res. Solid Earth 126, e2021JB022355 (2021).
Wöppelmann, G., Pouvreau, N. & Simon, B. Brest sea level record: A time series construction back to the early eighteenth century. Ocean Dyn. 56, 487–497 (2006).
Horton, B. P. et al. Mapping sea-level change in time, space, and probability. Annu. Rev. Environ. Resour. 43, 481–521 (2018).
Sella, G. F. et al. Observation of glacial isostatic adjustment in ``stable’’ North America with GPS. Geophys. Res. Lett. https://doi.org/10.1029/2006GL027081 (2007).
Blewitt, G., Hammond, W. C. & Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 99, 485 (2018).
Kaplan, E. D. & Hegarty, C. Understanding GPS/GNSS: Principles and Applications (Artech House, 2017).
Li, X. et al. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 89, 607–635 (2015).
Watson, P. J. An assessment of the utility of satellite altimetry and tide gauge data (ALT-TG) as a proxy for estimating vertical land motion. J. Coast Res. 35, 1131–1144 (2019).
Oelsmann, J. et al. The zone of influence: Matching sea level variability from coastal altimetry and tide gauges for vertical land motion estimation. Ocean Sci. 17, 35–57 (2021).
Walker, J. S. et al. Common Era sea-level budgets along the US Atlantic coast. Nat. Commun. 12, 1841 (2021).
Sefton, J. P. et al. Implications of anomalous relative sea-level rise for the peopling of Remote Oceania. Proc. Natl. Acad. Sci. 119, e2210863119 (2022).
Shennan, I. & Horton, B. P. Relative sea-level changes and crustal movements of the UK. J. Quat. Sci. 16, 511–526 (2002).
Nikitina, D. et al. Sea-level change and subsidence in the Delaware Estuary during the last ∼ 2200 years. Estuar. Coast Shelf Sci. 164, 506–519 (2015).
Engelhart, S. E., Horton, B. P., Douglas, B. C., Peltier, W. R. & Törnqvist, T. E. Spatial variability of late Holocene and 20th century sea-level rise along the Atlantic coast of the United States. Geology 37, 1115–1118 (2009).
Simms, A. et al. Tectonic subsidence of California estuaries increases forecasts of relative sea-level rise. Estuar. Coasts 39, 1571–1581 (2016).
Liberatore, M. et al. Vertical velocity fields along the Eastern Mediterranean coast as revealed by late Holocene sea-level markers. Earth Sci. Rev. 234, 104199 (2022).
Shaw, T. A. et al. Tectonic influences on late Holocene relative sea levels from the central-eastern Adriatic coast of Croatia. Quat. Sci. Rev. 200, 262–275 (2018).
Euskal Estatistika Erakundea, Instituto Vasco de Estadística. Población con actividad laboral PRA (2022).
García-Artola, A. et al. Holocene sea-level database from the Atlantic coast of Europe. Quat. Sci. Rev. 196, 177–192 (2018).
Argus, D. F., Peltier, W. R., Drummond, R. & Moore, A. W. The Antarctica component of postglacial rebound model ICE-6G_C (VM5a) based on GPS positioning, exposure age dating of ice thicknesses, and relative sea level histories. Geophys. J. Int. 198, 537–563 (2014).
Peltier, W. R., Argus, D. F. & Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 120, 450–487 (2015).
Lambeck, K., Purcell, A., Zhao, J. & Svensson, N.-O. The Scandinavian ice sheet: from MIS 4 to the end of the Last Glacial Maximum. Boreas 39, 410–435 (2010).
Lambeck, K., Rouby, H., Purcell, A., Sun, Y. & Sambridge, M. Sea level and global ice volumes from the Last Glacial Maximum to the Holocene. Proc. Natl. Acad. Sci. 111, 15296–15303 (2014).
Lambeck, K., Purcell, A. & Zhao, S. The North American Late Wisconsin ice sheet and mantle viscosity from glacial rebound analyses. Quat. Sci. Rev. 158, 172–210 (2017).
Li, T. & Wu, P. Laterally heterogeneous lithosphere, asthenosphere and sub-lithospheric properties under Laurentia and Fennoscandia from Glacial Isostatic Adjustment. Geophys. J. Int. 216, 1633–1647 (2019).
Khan, N. S. et al. Inception of a global atlas of sea levels since the Last Glacial Maximum. Quat. Sci. Rev. 220, 359–371 (2019).
Reimer, P. J. et al. The IntCal20 Northern Hemisphere radiocarbon age calibration curve (0–55 cal kBP). Radiocarbon 62, 725–757 (2020).
Gobierno de España. National Climate Change Adaptation Plan 2021–2030 (2020).
Wessel, P., Smith, W. H. F., Scharroo, R., Luis, J. & Wobbe, F. Generic mapping tools: Improved version released. Eos Trans. Am. Geophys. Union 94, 409–410 (2013).
Garner, A. J. et al. Evolution of 21st century sea level rise projections. Earths Future 6, 1603–1615 (2018).
Church, J. A. et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (2013).
Peltier, W. R. Global glacial isostasy and the surface of the ice-age Earth: The ICE-5G (VM2) model and GRACE. Annu. Rev. Earth Planet. Sci. 32, 111–149 (2004).
Zoccarato, C., Minderhoud, P. S. J. & Teatini, P. The role of sedimentation and natural compaction in a prograding delta: Insights from the mega Mekong delta, Vietnam. Sci. Rep. 8, 1–12 (2018).
Stattegger, K. et al. Mid to late Holocene sea-level reconstruction of Southeast Vietnam using beachrock and beach-ridge deposits. Glob. Planet Change 110, 214–222 (2013).
Wang, F. et al. Holocene sea-level change on the central coast of Bohai Bay, China. Earth Surf. Dyn. 8, 679–693 (2020).
Vink, A., Steffen, H., Reinhardt, L. & Kaufmann, G. Holocene relative sea-level change, isostatic subsidence and the radial viscosity structure of the mantle of northwest Europe (Belgium, the Netherlands, Germany, southern North Sea). Quat. Sci. Rev. 26, 3249–3275 (2007).
Fjeldskaar, W. The amplitude and decay of the glacial forebulge in Fennoscandia. Norsk Geologisk Tidsskrift 74, 2–8 (1994).
Walcott, R. I. Past sea levels, eustasy and deformation of the earth. Quat. Res. 2, 1–14 (1972).
Li, T. et al. Uncertainties of Glacial Isostatic Adjustment model predictions in North America associated with 3D structure. Geophys. Res. Lett. 47, e2020GL087944 (2020).
Spada, G. & Melini, D. New estimates of ongoing sea level change and land movements caused by Glacial Isostatic Adjustment in the Mediterranean region. Geophys. J. Int. 229, 984–998 (2022).
Lambeck, K., Smither, C. & Johnston, P. Sea-level change, glacial rebound and mantle viscosity for northern Europe. Geophys. J. Int. 134, 102–144 (1998).
Casas-Sainz, A. M. & Gil-Imaz, A. Extensional subsidence, contractional folding and thrust inversion of the eastern Cameros basin, northern Spain. Geologische Rundsch. 86, 802–818 (1998).
Rubio, J. C. & Simon, J. L. Tectonic subsidence v. erosional lowering in a controversial intramontane depression: The Jiloca basin (Iberian Chain, Spain). Geol. Mag. 144, 127–141 (2007).
Wöppelmann, G. & Marcos, M. Coastal sea level rise in southern Europe and the nonclimate contribution of vertical land motion. J. Geophys. Res. Oceans https://doi.org/10.1029/2011JC007469 (2012).
García-Mondéjar, J. Plate reconstruction of the Bay of Biscay. Geology 24, 635–638 (1996).
Roca, E., Muñoz, J. A., Ferrer, O. & Ellouz, N. The role of the Bay of Biscay Mesozoic extensional structure in the configuration of the Pyrenean orogen: Constraints from the MARCONI deep seismic reflection survey. Tectonics https://doi.org/10.1029/2010TC002735 (2011).
Ábalos, B. Geologic map of the Basque-Cantabrian Basin and a new tectonic interpretation of the Basque Arc. Int. J. Earth Sci. 105, 2327–2354 (2016).
Ortí, F., Pérez-López, A. & Salvany, J. M. Triassic evaporites of Iberia: Sedimentological and palaeogeographical implications for the western Neotethys evolution during the Middle Triassic-Earliest Jurassic. Palaeogeogr. Palaeoclimatol. Palaeoecol. 471, 157–180 (2017).
Cuevas, J. & Tubía, J. M. Estructuras diapíricas asociadas al sinclinorio de Vizcaya. Munibe 37, 1–4 (1985).
Camara, P. Inverted turtle salt anticlines in the Eastern Basque-Cantabrian basin, Spain. Mar. Pet. Geol. 117, 104358 (2020).
Roca, E. et al. Salt tectonics and controls on halokinetic-sequence development of an exposed deepwater diapir: The Bakio Diapir, Basque-Cantabrian Basin, Pyrenees. Mar. Pet. Geol. 123, 104770 (2021).
King, D. J., Newnham, R. M., Gehrels, W. R. & Clark, K. J. Late Holocene sea-level changes and vertical land movements in New Zealand. N. Z. J. Geol. Geophys. 64, 21–36 (2021).
Hill, D. F., Griffiths, S. D., Peltier, W. R., Horton, B. P. & Törnqvist, T. E. High-resolution numerical modeling of tides in the western Atlantic, Gulf of Mexico, and Caribbean Sea during the Holocene. J. Geophys. Res. Oceans https://doi.org/10.1029/2010JC006896 (2011).
Shennan, I. et al. Integration of shelf evolution and river basin models to simulate Holocene sediment dynamics of the Humber Estuary during periods of sea-level change and variations in catchment sediment supply. Sci. Total Environ. 314, 737–754 (2003).
Sulzbach, R. et al. Evolution of global ocean tide levels since the Last Glacial Maximum. Paleoceanogr. Paleoclimatol. 38, e2022PA004556 (2023).
Brain, M. J. Past, present and future perspectives of sediment compaction as a driver of relative sea level and coastal change. Curr. Clim. Change Rep. 2, 75–85 (2016).
Törnqvist, T. E. et al. Mississippi Delta subsidence primarily caused by compaction of Holocene strata. Nat. Geosci. 1, 173–176 (2008).
Horton, B. P. & Shennan, I. Compaction of Holocene strata and the implications for relative sealevel change on the east coast of England. Geology 37, 1083–1086 (2009).
Brain, M. J. et al. Quantifying the contribution of sediment compaction to late Holocene salt-marsh sea-level reconstructions, North Carolina, USA. Quat. Res. 83, 41–51 (2015).
Brain, M. J. et al. The contribution of mechanical compression and biodegradation to compaction of salt-marsh sediments and relative sealevel reconstructions. Quat. Sci. Rev. 167, 96–111 (2017).
Cearreta, A. et al. Recent salt marsh development and natural regeneration of reclaimed areas in the Plentzia estuary N. Spain. Estuar. Coast Shelf Sci. 54, 863–886 (2002).
Cearreta, A., García-Artola, A., Leorri, E., Irabien, M. J. & Masque, P. Recent environmental evolution of regenerated salt marshes in the southern Bay of Biscay: Anthropogenic evidences in their sedimentary record. J. Mar. Syst. 109, S203–S212 (2013).
Santín, C. et al. Effects of reclamation and regeneration processes on organic matter from estuarine soils and sediments. Org. Geochem. 40, 931–941 (2009).
Fernández, S., Santín, C., Marquínez, J. & Álvarez, M. A. Saltmarsh soil evolution after land reclamation in Atlantic estuaries (Bay of Biscay, North coast of Spain). Geomorphology 114, 497–507 (2010).
García-Artola, A. et al. Holocene environmental evolution and relative sea-level change in the Oka estuary (Urdaibai Biosphere Reserve, northern Spain). Estuar. Coast Shelf Sci. 286, 108310 (2023).
Horton, B. P. et al. Influence of tidal-range change and sediment compaction on Holocene relative sea-level change in New Jersey, USA. J. Quat. Sci. 28, 403–411 (2013).
Brisset, E., Burjachs, F., Navarro, B. J. B. & de Pablo, J.F.-L. Socio-ecological adaptation to Early-Holocene sea-level rise in the western Mediterranean. Glob. Planet Change 169, 156–167 (2018).
Vacchi, M. et al. Multiproxy assessment of Holocene relative sea-level changes in the western Mediterranean: Sea-level variability and improvements in the definition of the isostatic signal. Earth Sci. Rev. 155, 172–197 (2016).
Somoza, L. et al. Architectural stacking patterns of the Ebro delta controlled by Holocene high-frequency eustatic fluctuations, delta-lobe switching and subsidence processes. Sediment. Geol. 117, 11–32 (1998).
Douglas, B. C. Sea level change in the era of the recording tide gauge. Int. Geophys. 75, 37–64 (2001).
Breili, K. Evolution of sea-level trends along the Norwegian coast from 1960 to 2100. Ocean Dyn. 72, 115–136 (2022).
Horton, B. P. et al. Predicting marsh vulnerability to sea-level rise using Holocene relative sea-level data. Nat. Commun. 9, 1–7 (2018).
Taherkhani, M. et al. Sea-level rise exponentially increases coastal flood frequency. Sci. Rep. 10, 1–17 (2020).
Vousdoukas, M. I., Mentaschi, L., Voukouvalas, E., Verlaan, M. & Feyen, L. Extreme sea levels on the rise along Europe’s coasts. Earths Future 5, 304–323 (2017).
Arns, A. et al. Sea-level rise induced amplification of coastal protection design heights. Sci. Rep. 7, 40171 (2017).
Nicholls, R. J. et al. Integrating new sea-level scenarios into coastal risk and adaptation assessments: An ongoing process. Wiley Interdiscip. Rev. Clim. Change 12, e706 (2021).
Monge Ganuzas, M., Cearreta, A. & Iriarte Avilés, E. Consequences of estuarine sand dredging and dumping on the Urdaibai Reserve of the Biosphere (Bay of Biscay): The case of the “Mundaka left wave”. J. Iber. Geol. 34, 215–234 (2008).
Cearreta, A., Irabien, M. J. & Pascual, A. Human activities along the Basque coast during the last two centuries: Geological perspective of recent anthropogenic impact on the coast and its environmental consequences. In Oceanography and Marine Environment of the Basque Country. Elsevier Oceanography Series Vol. 70 27–50 (Elsevier, 2004).
Borja, Á. et al. Benthic communities, biogeography and resources management. In Oceanography and marine environment of the Basque Country. Elsevier Oceanography Series, Vol. 70. 455–492 (Elsevier, 2004).
Garmendia, J. M., Valle, M., Borja, Á., Chust, G. & Franco, J. Cartografía de Zostera noltii en la costa vasca: Cambios recientes en su distribución (2008–2012). Rev. Invest. Mar 20, 1–22 (2013).
Castillo-Eguskitza, N., Rescia, A. J. & Onaindia, M. Urdaibai biosphere reserve (Biscay, Spain): Conservation against development?. Sci. Total Environ. 592, 124–133 (2017).
Stuiver, M., Reimer, P. J. & Reimer, R. W. CALIB 8.2. CALIB Radiocarbon Calibration. http://calib.org/calib/ (дaтa oбpaщeния 15 Feb 2021) (2021).
Heaton, T. J. et al. Marine20—the marine radiocarbon age calibration curve (0–55,000 cal BP). Radiocarbon 62, 779–820 (2020).
Reimer, R. W. & Reimer, P. J. An online application for ΔR calculation. Radiocarbon 59, 1623–1627 (2017).
Wu, P. Using commercial finite element packages for the study of earth deformations, sea levels and the state of stress. Geophys. J. Int. 158, 401–408 (2004).
Li, T. et al. Influence of 3D earth structure on glacial isostatic adjustment in the Russian Arctic. J. Geophys. Res. Solid Earth 127, e2021JB023631 (2022).
Li, T., Wu, P., Steffen, H. & Wang, H. In search of laterally heterogeneous viscosity models of glacial isostatic adjustment with the ICE-6G_C global ice history model. Geophys. J. Int. 214, 1191–1205 (2018).
Tushingham, A. & Peltier, W. R. Ice-3G: A new global model of late Pleistocene deglaciation based upon geophysical predictions of post-glacial relative sea level change. J. Geophys. Res. Solid Earth 96, 4497–4523 (1991).
Mitrovica, J. X. & Milne, G. A. On post-glacial sea level: I General theory. Geophys. J. Int. 154, 253–267 (2003).
Taburet, G. et al. DUACS DT2018: 25 years of reprocessed sea level altimetry products. Ocean Sci. 15, 1207–1224 (2019).
Peng, D., Ng, G., Feng, L., Cazenave, A. & Hill, E. M. Coastal vertical land motion across Southeast Asia derived from combining tide gauge and satellite altimetry observations. Sci. Remote Sens. 10, 100176. https://doi.org/10.1016/j.srs.2024.100176 (2024).
Santamaría-Gómez, A. SARI: Interactive GNSS position time series analysis software. GPS Solut. 23, 52 (2019).
O’Neill, B. C. et al. A new scenario framework for climate change research: The concept of shared socioeconomic pathways. Clim. Change 122, 387–400 (2014).
Acknowledgements
We thank W. Richard Peltier for providing the ICE-6G_C ice model and Kurt Lambeck and Anthony Purcell for providing the ANU-ICE ice model. The global ANU-ICE combination model used in this study was kindly provided by Holger Steffen. We thank Patrick Wu for the helpful discussion on this work. This research is supported by the Ministry of Education, Singapore, under its MOE AcRF Tier 3 Award MOE2019-T3-1-004, and Tier 2 Award MOE-T2EP50120-0007. Ane García-Artola and Alejandro Cearreta are supported by the projects Harea-Coastal Geology Group (Basque Government, IT1616-22), Antropicosta-2 (RTI2018-095678-B-C21, MCIN/AEI/10.13039/501100011033 and ERDF A way of making Europe and European Union) and Sea-level changes and vertical land motion on the Basque coast: The Urdaibai Biosphere Reserve as a case study (University of the Basque Country UPV/EHU, EHU-N23/16). We thank the projection authors for developing and making the sea-level rise projections available, multiple funding agencies for supporting the development of the projections, and the NASA Sea Level Change Team for developing and hosting the IPCC AR6 Sea Level Projection Tool. This research is conducted in part using the research computing facilities and/or advisory services offered by Information Technology Services, the University of Hong Kong. We express our gratitude to Muhammad Hadi Ikhsan for his support with the graphics. This work is Earth Observatory of Singapore contribution number 539 and Geo-Q Zentroa Research Unit (Joaquín Gómez de Llarena Laboratory) contribution number 64.
Author information
Authors and Affiliations
Contributions
T.L and B.P.H designed the whole study. T.L led the GIA modelling and analyses, writing of the first draft and following versions of the manuscript and plotting of figures. A.G updated the Holocene RSL database along the Atlantic coast of Europe. D.P processed the GNSS data, satellite altimetry and tide gauge data. A.G, J.S.W, D.P, T.A.S, A.C, and B.P.H provided feedback on the data analyses and interpretation of results. All authors contributed to the improvement of the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Li, T., García-Artola, A., Shaw, T.A. et al. Vertical land motion is underestimated in sea-level projections from the Oka estuary, northern Spain. Sci Rep 14, 31302 (2024). https://doi.org/10.1038/s41598-024-82692-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-82692-1