Introduction

Currently, a series of threats such as resource shortage, climate change, environmental pollution and energy poverty challenges the world, which is caused by over-reliance on fossil energy. In response, establishing a renewable energy system has become a critical global strategic objective. For instance, the United States has committed to achieving carbon neutrality by 20501, while China has proposed ambitious goals to reach carbon peak and carbon neutrality. In light of this, the rapid adoption of NEVs has gained significant momentum due to their reduced environmental impact, particularly in lowering carbon emissions2. Governments and industries worldwide are actively supporting this transition. For example, the UK government has announced a ban on the sale of new gasoline and diesel vehicles by 20303, while major automotive manufacturers such as Volkswagen and Audi have pledged to phase out internal combustion engine vehicles by 2035 and 2033, respectively4. The rapid growth of NEV ownership has created an urgent need for efficient battery recycling solutions.

It is widely recognized that NEVs are instrumental in mitigating emissions. However, they also present a latent environmental challenge: the issue of retired power battery disposal. Therefore, low-carbon transition of the EVs’ supply chain has become critical to carbon neutrality in the NEV diffusion, especially the production process of power batteries5. According to the McKinsey report, carbon emissions from the production phase of the entire electric vehicle industry chain are estimated to account for 45% of total vehicle lifecycle emissions by 2025 and it will reach about 85% by 2040. The European Commission published the new Battery Regulation, which requires for the EOL management of EV batteries6. Meanwhile, China also issued the management measures for the NEV power batteries recycle, encouraging battery manufacturers to participate in the recycling and utilization of decommissioned batteries7.

While global policies have driven the adoption of NEVs, significant technological challenges remain, particularly in battery recycling. However, solutions to technological challenges depend not only on technological innovation, but also require a shift in social behavior. Pro-social behaviors, such as cooperation, trust and sharing, are recognized as key factors in promoting sustainable development and addressing global challenges. In that context batteries recycle become more mainstream while technical challenges remain8. Generally, there are mainly two ways to address the NEVs battery remanufacturing process: directly re-use or dismantling to re-build. Consequently, manufacturers and recyclers face significant pressure to manage the large-scale recycling and disposal of decommissioned NEV batteries9. Indeed, many retired batteries retain utility and can be repurposed across various applications, including energy storage, photovoltaic power generation, residential electricity, and low-speed electric vehicles10,11. Besides, collected wasted batteries are subjected to a series of tests and can be reused or dismantled to extract and recover the precious metal materials12.

Technological innovation by NEV manufacturers and recyclers is essential for enterprise competitiveness. For enterprises, the key to reducing carbon emissions lies in the adoption of new technologies, materials and processes13. Vigorously develop the circular economy, focus on enhancing energy efficiency and using renewable resources is one important way to promote the achievement of peak carbon neutrality. In brief, technological innovation facilitates to accelerate the circular economy and improve the recycling rate of key materials. Hence, in order to achieve a greener, low-carbon and circular economy in NEV battery recycling technological innovations must be developed. Furthermore, it is essential to advance policy frameworks that guide the development of power battery recycling standards. There is a need to explore the establishment of a comprehensive standard system that accounts for the full life cycle carbon emissions of power batteries14.

Prosocial behavior refers to actions taken by individuals or organizations that benefit others or society as a whole for the benefit of the whole of society15. While prosocial is often associated with altruism and environmental concern, emphasizing the social and environmental motivations behind the individual’s behavior16. In this regard, emotions such as guilt and shame can motivate pro-social behaviors that can reduce food waste and promote sustainable behavior change17. As some other studies have indicated that pro-social attributes can positively contribute to consumer adoption of electric vehicles18. In terms of power battery recycling, when consumers are more concerned about the environment and social interests, thereby generating prosocial behavior. Therefore, manufacturers and recyclers actively implement technological innovations in recycling, which will promote consumers to actively purchase NEVs and actively recycle retired power batteries. Due to consumers’ prosocial behavior, NEV manufacturers and recyclers, take the initiative to establish recycling networks and provide services due to environmental protection and social responsibility. Indeed, a positive correlation exists between investment in research and development (R&D) and the performance of innovation19.

The effects of the prosocial behavior in NEVs battery technological innovation for CLSC rarely been studied so far. This study investigates the payoffs of NEV manufacture and battery recyclers for potential technological innovation in EV batteries reverse supply chain. The following questions are addressed: (1) How does prosocial behavior influence the technological innovation decisions of NEV manufacturers and recyclers? What role does it play in the dynamic evolution of the CLSC? (2) To what extent can prosocial behavior incentivize manufacturers and recyclers to adopt technological innovation? How can its mechanisms be strengthened through policy design and market practices? (3) How can policy makers design subsidy mechanisms based on consumers’ pro-social behaviors to influence NEV manufacturers’ and recyclers’ technological innovation strategies for power battery recycling?

Power battery recycling is an important initiative to deal with environmental problems and resource shortage, and pro-social behavior plays a key role in this process. The public, enterprises and the government have embodied the core value of pro-social behavior by taking the initiative to assume social responsibility and actively participate in the construction and promotion of battery recycling system. Meanwhile, technological innovation is the core driving force to promote the development of the power battery recycling industry. Pro-social behavior in technological innovation is manifested in the fact that researchers and enterprises are oriented to solving social problems and are committed to developing more environmentally friendly and efficient battery recycling technologies. This kind of innovative behavior aiming at social well-being not only promotes technological progress, but also injects new vitality into the industry, realizing the dual goals of environmental protection and resource utilization. In addition, the pro-social behavior also promotes the formation of social consensus, promotes the synergistic development of power battery recycling and technological innovation, and also provides a sustained impetus for technological innovation, which ultimately lays a solid foundation for the realization of resource conservation and environmentally sustainable development.

In the field of power battery recycling, the policies, industry practices, and individual behaviors jointly drive technological innovation through dynamic interactions. For instance, regulations and trade-in subsidy policies directly incentivize manufacturers and recyclers to increase investment in technological R&D. Specifically, technological innovations by manufacturers and recyclers include advanced material recovery technologies, artificial intelligence-driven sorting systems, and blockchain-based traceability solutions. At the consumer level, prosocial behaviors, such as active participation in recycling programs and preferences for green and sustainable products, further encourage enterprises to enhance their battery recycling technologies. Thus, it is evident that the behavioral preferences of micro-level consumers serve not only as the foundational basis for the effectiveness of policy implementation but also as a critical driver for industrial innovation. In summary, through the analytical lens of evolutionary game theory, the dynamic balance among policies, industry practices, and individual behaviors can be revealed. This multi-level interaction mechanism provides systematic support for technological innovation and prosocial behavior in the field of power battery recycling, while also laying a theoretical and practical foundation for achieving sustainable development goals.

The main contributions of this paper are as follows: (1) Introducing the concept of pro-social behavior into the study of power battery recycling breaks through the technical and economic perspectives of the traditional study and provides a novel dimension of analysis. (2) Adopting the evolutionary game method, it can dynamically simulate the behavioral strategy evolution of different social subjects in the battery recycling process, and reveal the decision-making principle between cooperation and competition. (3) It provides scientific references for enterprises to formulate sustainable development strategies and the government to formulate incentive policies by exploring the influence of pro-social behaviors on the technological innovation of enterprises.

Literature review

Power battery recycle

With the NEV market experiencing rapid growth, the recycling of used power batteries has garnered significant social concerns, highlighting a persistent challenge within the NEV sector. Previous literature mostly focused on environmental sustainability20, value creation21, and resource conservation22. Therefore, we provide a brief review of relevant literatures from three levels: macro-policy, mid-industrial and micro-behavioral.

At the macro-policy level, Liu and Wang23 found that the government’s subsidy policy to NEV manufacturers in the power battery recycling process was beneficial to improve company profits and social welfare. A positive correlation was established between a manufacturer’s electric vehicle (EV) production and EV battery recycling grants24. Similarly, research has demonstrated that providing subsidies to service providers, rather than directly to consumers, for the swapping of EV batteries is more effective. This approach is more likely to optimize social welfare25. Zhao et al.26 analyzed how subsidy policy promotes NEVs diffusion in China, based on a three-stage model. Yet, to avoid NEVs manufacturer over-reliance on subsidies, the Chinese government has been gradually cutting production subsidies since 201027. In contrast, China’s NEVs industry diffusion still requires policy incentives to avoid manufacturers of NEVs being at a cost disadvantage in the automotive market28. Besides, in the context of circular economy, European Union (EU) introduced a battery regulation and renewed its pledge to increase the collection and recycling of waste EV batteries in European countries29.

At the meso-industrial level, end-of-life batteries’ recycling process is complex, there are six main methods for recycling and processing lithium batteries refers to different technical characteristics and each with its advantages and shortcomings30. Different NEV battery manufacturers produce different types, performance and sizes of power batteries, resulting in a complex recycling process for used batteries9. Traceability of the EV batteries throughout its life cycle is essential for waste management, which could avoid chemicals leakage minimizing economic loss2. As a result, some manufacturers have started to add tags, QR codes or RFID labels on key modules and sub-components to facilitate recycling31. Recently, there has been a pressing call for power battery lifecycle traceability, utilizing blockchain technology to record data used to evaluate battery usage and condition32. Furthermore, some companies are also planning to adopt blockchain technology to enable entire life-cycle tracking of battery modules33,34.

At the micro-mechanism level, Gu et al.35 take into account the echelon utilization rate of the used batteries collected by recyclers, and to improve the efficiency of power battery CLSC, governments should subsidize recyclers when the utilization rate is low; conversely, it is not necessary not to subsidize.

Zhao, et al.36 made a supplement for carbon emission regulation from micro perspective through analyzing the association with capital allocation efficiency NEVs enterprise and the vehicle carbon emissions. Zhao and Liu37 studied behavioral strategies of the governments and enterprises in the issue of carbon capture and storage(CCS) adoption, further found that the governments can adopt a carbon tax mechanism to ease the financial pressure. Feng, et al.38 formulated a tri-level model including governments, NEV manufacturers and customers to explore the decision-making process in new energy vehicles. Liu et al.39 conducted an analysis of NEV patents in six countries spanning from 1988 to 2018. Their findings suggest that government policies significantly influence technological advancements in China. However, the research also indicates that there is considerable room for improvement if China is to establish a leading position in NEVs technology.

Considering the technological innovation strategy of batteries recycle regarding NEV manufactures, recyclers and governments, this paper further discuss NEV batteries recycle from three levels, namely macro (subsidy policy), meso (technology innovation activities) and micro (decision-making behaviors). This multi-tiered approach offers a novel perspective for understanding the drivers of technological innovation in the reverse supply chain of power battery recycling.

Consumer behavior

Individual self-identity affects their behavioral intentions to a certain extent40. Therefore, people with pro-environmental awareness in power battery recycling is reflected in choosing greener recycling ways41. Ge42 indicates that consumers’ environmental awareness are positively correlated with the willingness to recycle power batteries. Liu, et al.43 examined the mechanisms by which target framing influences consumers to exhibit altruistic behavior in tourism-related marketing. Consumers’ expectations and attitudes towards tourism and the expression of prosocial behaviors in the tourism industry also could drive them to achieve satisfaction in the tourism44.

Prosocial behavior

Eisenberg and Miller45 described prosocial behavior as voluntary behavior that results in benefits for another, at the same time, two conditions must be met: motive46 and altruistic47. Despite altruism as a subset of prosocial behavior, whether the ultimate motivation of altruism is self-benefit is still controversial in academics48. Fehr and Fischbacher49 discussed the nature of human altruism formation from the perspective of evolutionary origins, to explain why humans exhibit large-scale cooperation.

Moreover, altruism and prosocial behavior are another framework for evaluating pro-environmental behavior. In line with others, Otto et al.50 proposed pro-environmental behaviors is a type of prosocial behavior, and then they examined the media role of nature as a link between prosocial and pro-environmental behaviors. In addition, Onwezen, et al.51 investigated the roles of anticipated pride and guilt as motivators for pro-environmental behavior. Kollmuss and Agyeman52 explored factors that have some influence on pro-environmental behavior based on the altruism and prosocial behavior model. Likewise, climate change might evoke individuals moral intuition to support for environmental policies and behavior53. Some scholars supported that psychological motives could affect individuals’ choice on their low-carbon consumption habits54. Tan and Lin55 believed that people are willing to pay more for the new energy bus if they certainly know that would contributes to improve air quality. Meanwhile, Gao, et al.56 noted that individual’s energy saving intention is one of prosocial behaviors. Recently, study also found the low-carbon attributions of NEVs are significant to consumers’ willingness to pay57.

Existing research employs a variety of theories and methodologies to analyze NEV battery recycling issues from multiple perspectives, offering a scientific approach and guidance for this study. However, scant research has delved into the role of prosocial behavior and its impact on NEV production, with even fewer studies addressing the intersection of battery recycling and prosocial behavior.

To fill this gap, an EGT method is be used to examine the dynamic interaction between NEV manufactures and battery recyclers on technological innovation. Moreover, innovative incorporation of prosocial behavior in the model as an impact factor for technological innovation decisions in power battery recycling, which can shed a light on how incentive subsidies and prosocial behavior affect NEV battery recycling.

Problem description and assumptions

Currently, China, the European Union (EU), and the U.S. have implemented various policies to promote battery recycling. For instance, China’s Extended Producer Responsibility (EPR) and the EU’s Battery Regulation emphasize corporate responsibility and set recycling rate targets. Both manufacturers and recyclers are actively involved in NEV power battery recycling, investing in recycling centers and closed-loop channels.

On the manufacturing side, Tesla uses automatic dismantling robots to efficiently break down battery packs and predicts battery decommissioning time through its vehicle remote diagnostic system. BYD has developed a battery laddering utilization and material recycling system. Meanwhile, the battery company CATL, through its subsidiary Brunp Recycling, employs physical crushing and hydrometallurgy technologies, achieving a recycling rate of over 95%. Third-party recyclers like GEM recover metal materials from used batteries, ensuring a stable resource supply and reducing costs, thereby closing the industry loop. However, the power battery recycling industry still faces challenges such as imperfect regulations and insufficient incentives. Further optimization of policy design is needed to drive technological innovation and sustainable development.

Pro-social consumers, driven by environmental awareness and social responsibility, are more likely to return used batteries to designated recycling points and purchase products made from recycled materials. This behavior can further encourage technological advancements and policy improvements, fostering a more sustainable industry.

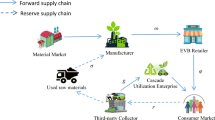
In this section, we present an overview of the research issues addressed and the hypotheses formulated for this study. Further we build the replicator dynamics equations to find the equilibrium strategies by solving the equations. Finally, concepts of EGT are introduced to facilitate the understanding of the subsequent analysis. Evolutionary game modeling for NEVs technology innovation behavior. Figure 1 illustrates NEVs battery recycling process.

Fig. 1
figure 1

NEVs battery recycling process.

Full size image

Problem description

Considering that the NEVs’ power battery recycling market consists of NEV manufacturers and recyclers, where players are the large and finite populations, respectively27. All NEV manufacturers and recyclers in the population have the technological innovation capability to improve the utilization rate and reduce carbon emissions. Both face the choice of two innovation strategies, namely positive technological innovation and negative technological innovation, which are noted as \(I\) strategy and \(IN\) strategy, respectively. NEV manufacturers with strategy \(I\) will strengthen renewable clean energy research and development efforts, producing longer life, more energy-efficient, and environmentally friendly power battery. On the other hand, technological innovations help recyclers to accurately classify and dispose of used power batteries, increase the echelon utilization of retired batteries and recycle metals in them, which will help reduce production costs58. In addition to the potential economic benefits, recycling retired power batteries can also reduce the number of waste batteries to be buried, thereby reducing soil and groundwater pollution. The strategic choices of manufacturers and recyclers will lead to differences in the level of innovation in closed-loop technology for power battery recycling, while consumer prosocial behavior and government innovation subsidies will have an impact on the decision-making of innovation entities. This paper, divides the power battery recycling population into two groups, NEV manufacturers and recyclers, with heterogeneity between the groups, and investigates a two-population model.

Basic assumptions

During the initial stage of NEV power battery green recycling, it is difficult for participants to pursue a well-balanced development of their own interests and social responsibilities. Therefore, it is necessary to develop innovative strategies according to their own needs in the continuous game process, so that the participants can explore each other and optimize their choices in the dynamic game process. In order to develop an effective multi-agent evolutionary game, some assumptions are given as follows. To address the problem described above, there are some assumptions59,60:

Assumption 1

Players. There are two types of companies that consider technology innovation in the closed-loop supply chain of power battery recycling: manufacturers and recyclers. Manufacturers improve recycling efficiency and extend battery life through innovative technologies such as battery health prediction, cascade utilization and modular design; recyclers invest in the research and development of advanced physical or chemical methods to recycle metal resources and intelligent environmentally friendly processing technologies to achieve efficient resource recycling and sustainable development of the industry.

Assumption 2

Bounded rational. EGT is derived from traditional game theory and biological evolutionary theory. Different traditional game theory, which posits that participants are fully rational and possess complete information, EGT operates under the premise of bounded rationality61. In the case of repetitive dynamic game players in the NEV battery recycling market, bounded rationality consistent with the actual situation62. Implementing technological innovation strategies usually does not find the optimal strategy at the outset, whereas the game players gradually seek the optimal strategy by continuously acquiring information63.

Assumption 3

Strategy. In our model, it is assumed that both NEV manufacturers and recyclers have two sets of strategies, namely positive technological innovation and negative technological innovation. Specifically, manufacturers’ technological innovations mainly include automated disassembly64, battery health prediction65, echelon utilization and modular design66, aiming to improve recycling efficiency and extend battery life cycle. Recyclers, on the other hand, use advanced hydrometallurgy, intelligent sorting67 and environmentally friendly processing technologies to achieve efficient resource recycling and sustainable development of the industry. Recent practices demonstrate that, through innovative recycling processes for end-of-life EV batteries, recovering critical metals for use in new batteries can reduce greenhouse gas emissions by up to 74% and cut costs by 20%68.

Model construction

Based on the assumptions of the model, parameters related to NEV manufacturers and recyclers are showed in Table 1.

Table 1 Model parameters and implications.
Full size table

Supposing the initial income of NEVs manufacturers and recyclers are \(\Pi_{P}\) and \(\Pi_{R}\) respectively, and the additional benefits obtained after implementing technological innovation strategies between each parties are \(\gamma \Pi_{P}\) and \(\theta \Pi_{R}\). \(\delta_{P}\) and \(\delta_{R}\) indicates the benefits of synergistic innovation for NEV manufacturers and recyclers. \(\beta\) and \(\alpha\) free-riding income increase rate of NEV manufacturers and recyclers. Because of the existence of free-riding behavior, there is \(\beta \Pi_{P} > \delta_{P}\) and \(\alpha \Pi_{R} > \delta_{R}\). Among them \(\gamma\) is unit revenue increase rate for NEV manufacturers, \(\theta\) is unit revenue increase rate for recyclers. Once the power batteries have reached the end of their life cycle and collected, they will be tested and assessed by the recyclers. Then the batteries will be sorted to echelon utilization, which is the phase of reasonable utilization of the remaining capacity of the power battery10. At that point, the recyclers will additionally obtain the benefits from the echelon utilization, which is expressed as \(E\). When recyclers actively engage in technological innovation to adequately utilize and dismantle used power batteries, it further saves energy and mitigate the environmental impact of used batteries. Therefore, recyclers earned the recycler a social reputation \(K_{0}\) and rewards from the governments60. Besides, we consider that the existence of consumer prosocial behavior increases the recycler’s revenue \(\mu_{i} T(i = 1,2)\). Among them, \(T\) represents the increase in the recycler’s revenue when the consumer has prosocial behavior, \(\mu_{1}\) and \(\mu_{2} (0 < \mu_{1} ,\mu_{2} < 1)\) denotes the probability of the occurrence of consumer pro-social behavior in the case of the recycler’s positive technological innovation and negative technological innovation, there is \(\mu_{1} > \mu_{2}\).

\(x(0 \le x \le 1)\) denotes the proportion of NEV manufacturers with positive technological innovation while NEV manufacturers negative technology innovation proportion is \(1 - x\). Then, \(y(0 \le y \le 1)\) and \(1 - y\) indicates the proportion of recyclers with a choice positive technological innovation (\(I\)) and negative technology innovation (\(IN\)), respectively. The game payoff matrix as can be seen in Table 2.

Table 2 Technology innovation payoff matrix of players.
Full size table

Evolutionary game analysis

Evolutionary game without government technology subsidies

Analysis of NEV manufacturer’s stability strategy

The payoff matrix of the NEVs battery manufacturers is defined as \({\mathbf{H}}\):

$${\mathbf{H}} = \left( {\begin{array}{*{20}c} {(1 + \gamma )\Pi_{P} - C_{P} + \delta_{P} { + }d} & {(1 + \gamma )\Pi_{P} - C_{P} { + }d} \\ {(1 + \beta )\Pi_{P} } & {\Pi_{P} } \\ \end{array} } \right)$$
(1)

When NEVs battery manufacturers expected utility for strategy \(I\), is defined:

$$\begin{gathered} U_{MI} = {\mathbf{eH}}^{{\mathbf{T}}} {\mathbf{y}} = (\begin{array}{*{20}c} 1 & 0 \\ \end{array} )\left( {\begin{array}{*{20}c} {(1 + \gamma )\Pi_{P} - C_{P} + \delta_{P} { + }d} & {(1 + \beta )\Pi_{P} } \\ {(1 + \gamma )\Pi_{P} - C_{P} { + }d} & {\Pi_{P} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} y \\ {1 - y} \\ \end{array} } \right) \hfill \\ = y[(1 + \gamma )\Pi_{P} - C_{P} + d + \delta_{P} ] + (1 - y)[(1 + \gamma )\Pi_{P} + d - C_{P} ] \hfill \\ \end{gathered}$$
(2)

The NEVs battery manufacturers’ expected utility is as follows:

$$\begin{gathered} \overline{U}_{M} = {\mathbf{x}}^{{\mathbf{T}}} {\mathbf{H}}^{{\mathbf{T}}} {\mathbf{y}} = \left( {\begin{array}{*{20}c} x & {1 - x} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {(1 + \gamma )\Pi_{P} - C_{P} + \delta_{P} { + }d} & {(1 + \beta )\Pi_{P} } \\ {(1 + \gamma )\Pi_{P} - C_{P} { + }d} & {\Pi_{P} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} y \\ {1 - y} \\ \end{array} } \right) \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} = x\left[ {y[(1 + \gamma )\Pi_{P} - C_{P} + d + \delta_{P} ] + (1 - y)[(1 + \gamma )\Pi_{P} + d - C_{P} ]} \right] + (1 - x)\left[ {y(1 + \beta )\Pi_{P} + (1 - y)\Pi_{P} } \right] \hfill \\ \end{gathered}$$
(3)

In the context of evolutionary game theory, the replicator dynamic equation, which is derived from the Malthusian growth model, can be articulated as follows:

$$F(x,y) = \frac{dx}{{dt}} = x[{\mathbf{eH}}^{{\mathbf{T}}} {\mathbf{y}} - {\mathbf{x}}^{{\mathbf{T}}} {\mathbf{H}}^{{\mathbf{T}}} {\mathbf{y}}] = x(1 - x)[\gamma \Pi_{P} - C_{P} + d + (\delta_{P} - \beta \Pi_{P} )y]$$
(4)

The first derivative of \(F(x,y)\) is as follows:

$$\frac{\partial F(x,y)}{{\partial x}} = (1 - 2x)[\gamma \Pi_{P} - C_{P} + d + (\delta_{P} - \beta \Pi_{P} )y]$$
(5)

Observing Eq. (4), let \(F(x,y) = 0\), \(x = 0,x = 1\) and \(y = y_{D} = \frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\) are the solutions.

According to the stability theorem, when \(F(x,y) = 0\), \(\frac{\partial F(x,y)}{{\partial x}} \le 0\), \(x\) is the evolutionary stability strategy (ESS). Because \(\frac{\partial F(x,y)}{{\partial x}} < 0\) means that the increase in \(x\) inhibits its own growth, so the system tends to be stable.

If \(\frac{\partial F(x,y)}{{\partial x}} > 0\) it means that the increase in \(x\) promotes its own growth, and the system tends to be unstable.

If \(y \ne \frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\), then for any \(x\), then NEV manufacturer’s behavioral strategy is analyzed in three scenarios.

Case 1 If \(\gamma \Pi_{P} - C_{P} + d < 0\), then \(y > \frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\), for two solutions \(x = 0,x = 1\) of Eq. (4), \(\frac{\partial F(x,y)}{{\partial x}}\left| {_{x = 0} < 0} \right.,\frac{\partial F(x,y)}{{\partial x}}\left| {_{x = 1} > 0} \right.\), based on the stability theorem \(F(x,y) = 0\), \(\frac{\partial F(x,y)}{{\partial x}} \le 0\), it can be deduced that \(x = 0\) is the only ESS.. When the probability of recyclers innovation reaches \(\frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\) and continue to increase, the probability of NEV manufacturers performing technological innovation activities gradually weaken, and then NEVs manufacturers will adopt an non-technological innovations strategy anyway, as shown in (a), Fig. 2.

Fig. 2
figure 2

Dynamic evolution diagram of NEV manufacturers’ decision-making.

Full size image

Case 2 If \(0 < \gamma \Pi_{P} - C_{P} + d < \beta \Pi_{P} - \delta_{P}\), following two scenarios are to be addressed.

When \(y > \frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\), \(\frac{\partial F(x,y)}{{\partial x}}\left| {_{x = 0} < 0} \right.,\frac{\partial F(x,y)}{{\partial x}}\left| {_{x = 1} > 0} \right.\), similarly, it can be deduced that \(x = 0\) is the only ESS. Otherwise, when \(y < \frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\), \(\frac{\partial F(x,y)}{{\partial x}}\left| {_{x = 0} > 0} \right.,\frac{\partial F(x,y)}{{\partial x}}\left| {_{x = 1} < 0} \right.\), \(x = 1\) is the only ESS, as shown in (b), Fig. 2.

Case 3 If \(\gamma \Pi_{P} - C_{P} + d > \beta \Pi_{P} - \delta_{P}\), then \(y < \frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\), for two solutions \(x = 0,x = 1\) of Eq. (4), \(\frac{\partial F(x,y)}{{\partial x}}\left| {_{x = 0} > 0} \right.,\frac{\partial F(x,y)}{{\partial x}}\left| {_{x = 1} < 0} \right.\), it can be deduced that \(x = 1\) is the ESS. Therefore, when the technological innovation probability of recyclers below \(\frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\) and continues to weaken, the probability of NEVs manufacturers implementing technological innovation strategies increases, and finally regarding innovation as its best strategy, as shown in (c), Fig. 2.

Analysis of NEV recycler’s stability strategy

Similarly, from Table 2 we define the payoff matrix for recyclers as \({\mathbf{B}}\), as shown below:

$${\mathbf{B}} = \left( {\begin{array}{*{20}c} {(1 + \theta )\Pi_{R} - C_{R} + \delta_{R} + E + K_{0} + \mu_{1} T} & {(1 + \alpha )\Pi_{R} + K_{0} + \mu_{2} T} \\ {(1 + \theta )\Pi_{R} - C_{R} + E + K_{0} + \mu_{1} T} & {\Pi_{R} + K_{0} + \mu_{2} T} \\ \end{array} } \right)$$
(6)

Then, the expected utility of recyclers technological innovation is denoted \(U_{RI}\):

$$\begin{gathered} U_{RI} = {\mathbf{eBx}} = (\begin{array}{*{20}c} 1 & 0 \\ \end{array} )\left( {\begin{array}{*{20}c} {(1 + \theta )\Pi_{R} - C_{R} + \delta_{R} + E + K_{0} + \mu_{1} T} & {(1 + \alpha )\Pi_{R} + K_{0} + \mu_{2} T} \\ {(1 + \theta )\Pi_{R} - C_{R} + E + K_{0} + \mu_{1} T} & {\Pi_{R} + K_{0} + \mu_{2} T} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} x \\ {1 - x} \\ \end{array} } \right) \hfill \\ = x[(1 + \theta )\Pi_{R} - C_{R} + \delta_{R} + E + K_{0} + \mu_{1} T] + (1 - x)[(1 + \theta )\Pi_{R} - C_{R} + E + K_{0} + \mu_{1} T] \hfill \\ \end{gathered}$$
(7)

The recyclers’ average expected utility denotes \(\overline{U}_{R}\):

$$\begin{gathered} \overline{U}_{R} = {\mathbf{y}}^{{\mathbf{T}}} {\mathbf{H}}^{{\mathbf{T}}} {\mathbf{x}} = \left( {\begin{array}{*{20}c} y & {1 - y} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {(1 + \theta )\Pi_{R} - C_{R} + \delta_{R} + E + K_{0} + \mu_{1} T} & {(1 + \alpha )\Pi_{R} + K_{0} + \mu_{2} T} \\ {(1 + \theta )\Pi_{R} - C_{R} + E + K_{0} + \mu_{1} T} & {\Pi_{R} + K_{0} + \mu_{2} T} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} x \\ {1 - x} \\ \end{array} } \right) \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} = y\left[ {x[(1 + \theta )\Pi_{R} - C_{R} + \delta_{R} + E + K_{0} + \mu_{1} T] + (1 - x)[(1 + \theta )\Pi_{R} - C_{R} + E + K_{0} + \mu_{1} T]} \right] \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} + (1 - y)\left[ {x[(1 + \alpha )\Pi_{R} + K_{0} + \mu_{2} T] + (1 - x)(\Pi_{R} + K_{0} + \mu_{2} T)} \right] \hfill \\ \end{gathered}$$
(8)

Similarly, the replicator dynamic equation is as follows:

$$G(x,y) = \frac{dy}{{dt}} = y\left[ {{\mathbf{eBx - y}}^{{\mathbf{T}}} {\mathbf{Bx}}} \right] = y(1 - y)[E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} + (\delta_{R} - \alpha \Pi_{R} )x]$$
(9)

The first derivative of \(G(x,y)\) is as follows:

$$\frac{\partial G(x,y)}{{\partial y}} = (1 - 2y)[E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} + (\delta_{R} - \alpha \Pi_{R} )x]$$
(10)

It could be derived that \(y = 0,y = 1\) and \(x = x_{D} = \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\) are the solutions of dynamic replication Eq. (9). Similarly, when \(G(x,y) = 0\),\(\frac{\partial G(x,y)}{{\partial y}} < 0\), \(y\) is the evolutionary stability strategy.

If \(x = \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\), \(G(x,y) \equiv 0\) is valid, then axis \(y\) is in a stable state. When the possibility of NEV manufactures implementing technology innovation strategy reaches \(x = \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\), the possibility of recyclers’ innovation behavior is stable.

If \(x \ne \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\), then further discussion is provided below.

Case 4 If \(E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} < 0\), then \(x > \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\), for two solutions \(y = 0,y = 1\) of Eq. (9), \(\frac{\partial G(x,y)}{{\partial y}}|_{y = 0} < 0,\frac{\partial G(x,y)}{{\partial y}}|_{y = 1} > 0\), so \(y = 0\) is the ESS; when the ratio of manufactures actively performing technology innovation strategy reaches \(x = \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\) and remains to growth, the probability of recyclers’ innovation behavior decreases, and regarding non-innovation as it best strategy after a period of evolution, as shown in (a) in Fig. 3.

Fig. 3
figure 3

Dynamic evolution diagram of recyclers’ decision-making.

Full size image

Case 5 If \(0 < E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} < \alpha \Pi_{R} - \delta_{R}\), following two scenarios are to be addressed.

When \(x > \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\), \(\frac{\partial G(x,y)}{{\partial y}}|_{y = 0} < 0,\frac{\partial G(x,y)}{{\partial y}}|_{y = 1} > 0\), \(y = 0\) is the only ESS. Otherwise, when \(x < \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\), \(\frac{\partial G(x,y)}{{\partial y}}|_{y = 0} > 0,\frac{\partial G(x,y)}{{\partial y}}|_{y = 1} < 0\), then \(y = 1\) is the ESS, as shown in (b) in Fig. 3.

Case 6 If \(E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} > \alpha \Pi_{R} - \delta_{R}\), then \(x < \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\), for two solutions \(y = 0,y = 1\) of Eq. (9), \(\frac{\partial G(x,y)}{{\partial y}}|_{y = 0} > 0,\frac{\partial G(x,y)}{{\partial y}}|_{y = 1} < 0\), then \(y = 1\) is the ESS; when the ratio of NEV manufactures negatively performing technology innovation strategy is below \(x = \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\) and remain to decreases, the probability of recyclers’ innovation behavior increases, and regarding innovation as it best strategy after a period of evolution, as shown in (c) in Fig. 3.

Stability analysis of equilibrium points

According to the analysis above, NEV manufacturers and recyclers have three stability strategies with different circumstances. Given the current landscape of China’s NEV industry, this study focuses on two specific scenarios: Case 1, which examines the technological capabilities of NEV manufacturers, and Case 4, which explores the recycling scale of recyclers and the emergence of consumers’ prosocial behavior. Conversely, Case 3 and Case 6 extend beyond the boundaries of this research, as they do not align with the present investigation’s objectives and available resources. Accordingly, this section further develops the dynamic evolutionary processes of system under case 2 and 5. According to Eq. (4) and Eq. (9) a two-dimensional nonlinear dynamic system (\(S\)) for NEV manufacturers and recyclers as follows:

$$\left\{ \begin{gathered} F(x,y) = x[U_{MI} - \overline{U}_{M} ] = x(1 - x)[\gamma \Pi_{P} - C_{P} + d + (\delta_{P} - \beta \Pi_{P} )y] \hfill \\ G(x,y) = y(U_{RI} - \overline{U}_{R} ) = y(1 - y)[E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} + (\delta_{R} - \alpha \Pi_{R} )x] \hfill \\ \end{gathered} \right.$$
(11)

Equilibrium points of system (\(S\)) can be derived under the condition: \(0 < \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }} < 1,0 < \frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }} < 1\).

Proposition 1

The equilibrium points of the replicator dynamic system (\(S\)) are \((0,0)\),\((0,1)\),\((1,0)\),\((1,1)\) and \((x_{D} ,y_{D} )\),\(x_{D} \in [0,1]\),\(y_{D} \in [0,1][0,1]\).

\(x_{D} = \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} }}{{\alpha \Pi_{R} - \delta_{R} }}\), \(y_{D} = \frac{{\gamma \Pi_{P} - C_{P} + d}}{{\beta \Pi_{P} - \delta_{P} }}\).

For the convenience of calculation, let \(x_{D}\) equal to 0 and 1, have \(\gamma_{1} = \frac{{C_{P} - d}}{{\Pi_{P} }}\),\(\gamma_{2} = \frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }}\), respectively. The same \(\theta_{1} = \frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\), \(\theta_{2} = \frac{{\alpha \Pi_{R} - \delta_{R} + C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\).

According to Jacobian matrix \(J\), the evolutionary stable conditions for stability of fixed points are: (i)\(DetJ = a_{11} a_{22} - a_{12} a_{21} > 0\), and (ii)\(trJ = a_{11} + a_{22} < 0\).

$$J = \left[ \begin{gathered} \frac{\partial F(x,y)}{{\partial x}} \, \frac{\partial F(x,y)}{{\partial y}} \hfill \\ \frac{\partial G(x,y)}{{\partial x}} \, \frac{\partial G(x,y)}{{\partial y}} \hfill \\ \end{gathered} \right]{ = }\left[ \begin{gathered} a_{11} \, a_{12} \hfill \\ a_{21} \, a_{22} \hfill \\ \end{gathered} \right]$$
(12)

The expressions for each factor in the Jacobian matrix as shown in Eq. (12 )are presented in Table 3.

Table 3 The expression of each factor of Jacobian matrix.
Full size table

The values of the Jacobian matrix factors at different equilibrium points are showed in Table 4.

Table 4 Parameter values at different equilibrium points.
Full size table

\(M = \frac{{(\gamma \Pi_{P} - C_{P} + d)(\beta \Pi_{P} - \gamma \Pi_{P} + C_{P} - d - \delta_{P} )}}{{\delta_{P} - \beta \Pi_{P} }}\) and \(N = \frac{{[\theta \Pi_{R} + E - C_{R} - (\mu_{2} - \mu_{1} )T][\alpha \Pi_{R} - \delta_{R} - E + C_{R} + (\mu_{2} - \mu_{1} )T - \theta \Pi_{R} ]}}{{\delta_{R} - \alpha \Pi_{R} }}\).

Proposition 2

When \(0 < \gamma_{{}} < \frac{{C_{P} - d}}{{\Pi_{P} }}\) and \(0 < \theta_{{}} < \frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\), then \((0,0)\) is an ESS of the replicator dynamic system (\(S\)). The behavior strategy is (IN, IN).

Proposition 3

When \(\frac{{C_{P} - d}}{{\Pi_{P} }} < \gamma < \frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }}\) and, \(0 < \theta < \frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\)\(\frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }} < \gamma < 1\) and \(0 < \theta < \frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\) or \(\frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }} < \gamma < 1\) and \(\frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }} < \theta < \frac{{\alpha \Pi_{R} - \delta_{R} + C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\), then \((1,0)\) is an ESS of the replicator dynamic system \((S)\). The behavior strategy is (Innovation, Not innovation).

Proposition 4

When \(0 < \gamma < \frac{{C_{P} - d}}{{\Pi_{P} }}\) and \(\frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }} < \theta < \frac{{\alpha \Pi_{R} - \delta_{R} + C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\),\(0 < \gamma < \frac{{C_{P} - d}}{{\Pi_{P} }}\) and \(\frac{{\alpha \Pi_{R} - \delta_{R} + C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }} < \theta < 1\) or \(\frac{{C_{P} - d}}{{\Pi_{P} }} < \gamma < \frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }}\) and \(\frac{{\alpha \Pi_{R} - \delta_{R} + C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }} < \theta < 1\), then \((0,1)\) is an ESS of the replicator dynamic system \((S)\). The behavior strategy is (Not innovation, Innovation).

Proposition 5

When \(\frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }} < \gamma < 1\) and \(\frac{{\alpha \Pi_{R} - \delta_{R} + C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }} < \theta < 1\), then \((1,1)\) is an ESS of the replicator dynamic system (I). The behavior strategy is (Innovation, Innovation).

Proposition 6

When \(\frac{{C_{P} - d}}{{\Pi_{P} }} < \gamma < \frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }}\) and \(\frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }} < \theta < \frac{{\alpha \Pi_{R} - \delta_{R} + C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\), then both \((1,0)\) and \((0,1)\) is an ESS of the replicator dynamic system \((S)\). The behavior strategy is (I, IN) and (IN, I).

The Jacobian matrix of the replicator dynamics is computed and analyzed for eigenvalues; if the real part of all eigenvalues are negative, the equilibrium is locally stable, thus supporting the identification of ESS, i.e. the equilibrium is locally stable when conditions \(DetJ > 0\) and \(trJ < 0\) are satisfied. See the appendix A.2 for the detailed proof.

For instance, strategy \((0,0)\) which means none of the NEV manufacturers and recyclers adopt technological innovation strategy. It is clear that the behavior of the individuals in adopting the technological innovation strategy is determined by average increase in market demand per unit with technological innovation of the both NEV manufacturers and recyclers. Notwithstanding technological innovation process increases consumers’ demand, it costs enterprises much on innovation activities.

Evolutionary game with government technological innovation subsidy

According to the analysis above, enterprises may discourage their active technological innovation due to the innovation cost, in this section the government subsidy \(K_{G}\) be introduced to offset technology cost by rewarding the agents who active performing technological innovation. In other words, the government through giving grants to incentivize enterprises to actively adopt innovative technologies.

According to the above relationship between the NEV manufacturers and the recyclers, a subsidy mechanism be created to construct novel evolutionary game model, as shown in Table 5.

Table 5 Technology innovation payoff matrix with subsidy mechanism.
Full size table

According to Table 5, the replicator dynamic \(S\) of “\(I\)” chosen by NEV manufacturers \(F_{1}(x,y)\) and the replicator dynamic \(S\) of “\(I\)” chosen by recyclers \(G_{1}(x,y)\) are as follows:

$$F_{1}(x,y) = \frac{dx}{{dt}} = x(1 - x)[\gamma \Pi_{P} - C_{P} + d + K_{G} + (\delta_{P} - \beta \Pi_{P} )y]$$
(13)
$$G_{1}(x,y) = \frac{dy}{{dt}} = y(1 - y)[E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} + K_{G} + (\delta_{R} - \alpha \Pi_{R} )x]$$
(14)
$$J_{1} = \left[ \begin{gathered} \frac{{\partial F_{1}(x,y)}}{\partial x} \, \frac{{\partial F_{1}(x,y)}}{\partial y} \hfill \\ \frac{{\partial G_{1}(x,y)}}{\partial x} \, \frac{{\partial G_{1}(x,y)}}{\partial y} \hfill \\ \end{gathered} \right]$$
$${ = }\left[ {\begin{array}{*{20}c} {(1 - 2x)[\gamma \Pi_{P} - C_{P} + d + K_{G} + (\delta_{P} - \beta \Pi_{P} )y]} & {x(1 - x)(\delta_{P} - \beta \Pi_{P} )} \\ {y(1 - y)(\delta_{R} - \alpha \Pi_{R} )} & {(1 - 2y)[E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} + K_{G} + (\delta_{R} - \alpha \Pi_{R} )x]} \\ \end{array} } \right]$$

Proposition 7

The equilibrium points of Eq. (13) and Eq. (14) are \((0,0),(0,1),(1,0),(1,1)\), and.

\(x_{1D} = \frac{{E - C_{R} - (\mu_{2} - \mu_{1} )T + \theta \Pi_{R} + K_{G} }}{{\alpha \Pi_{R} - \delta_{R} }},y_{1D} = \frac{{\gamma \Pi_{P} - C_{P} + d + K_{G} }}{{\beta \Pi_{P} - \delta_{P} }}\) is also the equilibrium point of the system, only if it satisfies following inequality \(\max (\tau_{1} ,\tau_{2} ) < K_{G} < \min (\tau_{3} ,\tau_{4} )\), where

$$\begin{gathered} \tau_{1} = C_{R} - E + (\mu_{2} - \mu_{1} )T - \theta \Pi_{R} ,\tau_{2} = C_{P} - \gamma \Pi_{P} - d \hfill \\ \tau_{3} = C_{R} - E + (\mu_{2} - \mu_{1} )T - \theta \Pi_{R} + \alpha \Pi_{R} - \delta_{R} ,\tau_{4} = C_{P} - \gamma \Pi_{P} - d + \beta \Pi_{P} - \delta_{P} \hfill \\ \end{gathered}$$

Proposition 8

\((1,1)\) is the only stable equilibrium point of the system(13) and (14), i.e., the stable strategy of the system when both the NEV manufacturer and the recycler choose to adopt the technological innovation strategy, then the sufficient condition to reach is as below:

$$K_{G} > \max (\beta \Pi_{P} - \gamma \Pi_{P} - \delta_{P} - d + C_{P} ,\alpha \Pi_{R} - \theta \Pi_{R} - \delta_{R} + C_{R} + (\mu_{2} - \mu_{1} )T - E)$$

Proposition 8 shows that when the benefits of technological innovation by NEV manufacturers and recyclers in the CLSC of NEVs battery are relatively small, i.e., \(0 < \gamma < \gamma_{1} ,0 < \theta < \theta_{1}\). However, NEV manufacturers and recyclers will tend to choose innovation if government subsidies compensate for the costs of innovation by NEV manufacturers and recyclers and the amount of subsidies is large enough to make the benefits of "free-riding" behavior by NEV manufacturers and recyclers smaller than the benefits of technological innovation.

Simulation analysis

In order to analyze the evolutionary pattern between manufacturers and recyclers more intuitively, the parameter settings in this chapter refer to the previous research literature69,70,71, and the key variable assignments are adjusted by consulting experts in the related fields.

Verification of evolutionary stability strategy situation

MATLAB software was utilized to solve and analyze the aforementioned models with their initial parameters. To enhance the scientific validity and objectivity of the simulation outcomes, a set of parameter values were randomly determined based on the presupposed conditions. It is crucial to clarify that these values are not reflective of the actual financial figures for payments or earnings within the sector of new energy vehicle battery manufacturers and recyclers.

Proposition 1.

Let \(\gamma = 0.2\), \(\theta = 0.2\), which satisfies the conditions of \(0 < \gamma < \frac{{C_{P} - d}}{{\Pi_{P} }}\) and \(0 < \theta_{{}} < \frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\). The evolutionary path of the new energy vehicle battery manufacturers and recyclers is solved as shown in Fig. 4.

Fig. 4
figure 4

Evolutionary path in situation 1.

Full size image

The results obtained from the Matlab simulation are shown in Fig. 4. With different initial ratios of \(x\) and \(y\), a large proportion of new energy vehicle battery manufacturers initially choose the “Technological innovation” strategy, but the increased revenue is less than the cost of choosing that strategy, and the lack of government subsidies for the " Technological innovation " strategy. The net benefits of choosing the “Technological innovation” strategy is smaller than which choosing the "Non-technological innovation " strategy. In the end, battery manufacturers are driven by their own interests and those of their shareholders to maximize their profits from “Technological innovation” to "Non-technological innovation". However, since the cost of technological innovation is higher than the increased in revenue, and the government’s subsidy for technology innovation is smaller, the net revenue of technology innovation is smaller than that of no technology innovation. In the end, recyclers tend to switch from “technological innovation” to "Non-technological innovation" driven by their own interests. The interaction behavior of both sides evolves to the worst equilibrium point \((0,0)\), at which the innovation level of new energy vehicle electric recycling market is the lowest and the overall social utility is the smallest. If this “ineffective” state continues, it will lead to waste of resources and aggravation environmental pollution.

Proposition 10

Let , \(\gamma = 0.28\),\(\theta = 0.2\), \(\gamma = 0.6\),\(\theta = 0.2\) and \(\gamma = 0.6\),\(\theta = 0.4\) which satisfies the conditions of \(\frac{{C_{P} - d}}{{\Pi_{P} }} < \gamma < \frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }}\) and \(0 < \theta < \frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\), \(\frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }} < \gamma < 1\) and \(0 < \theta < \frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\),\(\frac{{\beta \Pi_{P} - \delta_{P} + C_{P} - d}}{{\Pi_{P} }} < \gamma < 1\) and \(\frac{{C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }} < \theta < \frac{{\alpha \Pi_{R} - \delta_{R} + C_{R} - E + (\mu_{2} - \mu_{1} )T}}{{\Pi_{R} }}\), respectively.

As depicted in Fig. 5, the trajectory of evolution for new energy vehicle battery manufacturers and recyclers is addressed. A considerable segment of manufacturers opts for the “Technological innovation” strategy from the outset, despite minimal government subsidies for innovation. This preference stems from the fact that the net benefits of pursuing innovation surpass the expenses associated with the "Non-technological innovation" approach. The advantages of embracing the “Technological innovation” strategy are more pronounced compared to those of the "Non-technological innovation" strategy. Ultimately, manufacturers tend to switch from "Non-technological innovation" to “Technological innovation” driven by pursuing their own and shareholders’ interests. While recyclers initially choose “technology innovation” strategy in order to maximize social interests, a higher proportion of them choose “technology innovation” strategy. "But since the cost of innovation is higher than the increase in revenue, recyclers eventually tend to move from “Technological innovation” to "Non-technological innovation". The interactive behavior of both players evolves to the inferior equilibrium point \((1,0)\), at which the innovation mechanism of recyclers is in a poor state, and if recyclers do not innovate technology for a long time, it may lead to low efficiency of power battery recycling and insufficient recycling of used batteries, which may cause energy waste.

Fig. 5
figure 5

Evolutionary path in situation 2.

Full size image

Proposition 10

Let ,\(\gamma = 0.2,\theta = 0.4\), \(\gamma = 0.2,\theta = 0.6\),\(\gamma = 0.28,\theta = 0.6\), which satisfies the conditions of \(0 < \gamma < \gamma_{1} ,\theta_{1} < \theta < \theta_{2}\),\(0 < \gamma < \gamma_{1} ,\theta_{2} < \theta < 1\) and \(\gamma_{1} < \gamma < \gamma_{2} ,\theta_{2} < \theta < 1\), respectively. The evolutionary path of the battery manufacturers and recyclers is solved as shown in Fig. 6. With different initial ratios of \(x\) and \(y\), manufacturers initially have a higher share of choosing the “Technological innovation” strategy, but the costs of that option greater than the increased benefits, also governments lack incentives for manufacturers to innovating technology, so the net benefits of choosing the “Technological innovation” strategy less than those of choosing the "Non-technological innovation" strategy. Eventually, manufacturers tend to switch from “Technological innovation” to "Non-technological innovation" driven by their and shareholders’ interests. In addition, recyclers are initially limited by the level of innovation and choose the "Non-technological innovation" strategy in a higher proportion. As the proportion of manufacturers choosing "Non-technological innovation" increases, the market demand for recyclers’ technological innovation becomes urgent, so that recyclers’ technological innovation profits are increased. Due to recyclers pursuing their own interests while seeking to maximize social benefits, eventually they move from "Non-technological innovation" to “Technological innovation”. The interactive behavior of the two parties evolves to the inferior equilibrium point \((0,1)\). Currently, the absence of governmental incentives hampers manufacturers’ drive to innovate, primarily due to budgetary limitations. Consequently, they struggle to enhance the recycling processes for electric vehicle batteries in their production cycle.

Fig. 6
figure 6

Evolutionary path in situation 3.

Full size image

Proposition 11

Let \(\gamma = 0.6,\theta = 0.6\), which satisfies the conditions of \(\gamma_{2} < \gamma < 1,\theta_{2} < \theta < 1\). The evolutionary path of the NEVs manufacturers and recyclers is solved as shown in Fig. 7. With different initial proportions of \(x\) and \(y\), manufacturers initially have a higher share of the "Non-technological innovation" strategy. The net benefit of choosing the “Technological innovation” is greater than that of choosing the "Non-technological innovation". Eventually, manufacturers move from the "Non-technological innovation" to the “Technological innovation”, while a higher proportion of recyclers initially choose the "Non-technological innovation" strategy. With the price of technological innovation increases, the net benefit of “technological innovation” for recyclers is smaller than it of "Non-technological innovation", so eventually recyclers pursue their own interests when maximizing social benefits in the context of pro-social behavior of consumers, from "Non-technological innovation" to “Technological innovation”. Which indicates that the manufacturer’s technological innovation benefits increase as the same time technological innovation subsidy mechanism for recyclers takes effect, so recyclers actively innovate under the influence of consumers’ pro-social behavior, finally, interaction evolves to a virtuous equilibrium point \((1,1)\). At this point, the technological innovation mechanism of power battery recycling has reached the “ideal” state, and both manufacturers and recyclers are highly motivated to consciously innovate technologies to give full play to the advantages of resources, maximize social benefits, and achieve sustainable and high-quality development of power battery recycling process.

Fig. 7
figure 7

Evolutionary path in situation 4.

Full size image

Proposition 12

Let \(\gamma = 0.28,\theta = 0.4\), which satisfies the conditions of \(\gamma_{1} < \gamma < \gamma_{2} ,\theta_{1} < \theta < \theta_{2}\). The ESS of the replication dynamic system is \((0,1)\) and \((1,0)\). The evolutionary path of manufacturers and recyclers is solved as shown in Fig. 8.

Fig. 8
figure 8

Evolutionary path in situation 5.

Full size image

Parameter sensitivity analysis

The sensitivity analysis with respect to pro-social behavior intensity (\(\mu_{1} ,\mu_{2}\)) for recyclers is presented in Fig. 6. By increasing \(\mu_{1}\) in the models, increased intensity of pro-social behavior leads to in the recyclers’ profits rising. As shown in Fig. 9, with lower value \(\mu_{1}\) it is not profitable for recyclers while if \(\mu_{1}\) increases it will profitable for the recyclers to perform technological innovation strategies. The long-term behavior of the recyclers is shown in Fig. 6. As it is seen, as the level of consumer pro-social behavior increases, evolutionary trajectories of recyclers converge to technological innovation. Great level of pro-social behavior of consumers (\(\mu_{1}\)) means they are sensitive to the recyclers technology innovation. In such cases, consumers prefer to hand over end-of-life batteries to the recycler who is actively innovating disposal technology than the others. Therefore, with higher \(\mu_{1}\) recyclers use less time to reach the ESS. Generally, the evolution of the recycler’s strategy eventually tends towards technological innovation when \(\mu_{1} > \mu_{2}\) and, conversely, towards non-technological innovation when \(\mu_{1} < \mu_{2}\). However, when \(\mu_{1}\) is lower than \(\mu_{2}\) then recyclers eventually evolve into a non-technical innovation.

Fig. 9
figure 9

The effect of consumer prosocial behavior on technological innovation of recyclers.

Full size image

In the two-dimensional dynamic system \(S\), setting the probability of NEVs manufacturers providing less pollution and easy to recycle batteries is \(x = 0.6\), and the probability that the recyclers will adopt technological innovation is \(y = 0.6\). The contrast of \(K_{G}\) taking different values the evolutionary path between the manufacturers and the recyclers is showed in Fig. 10. and Fig. 11, respectively.

Fig. 10
figure 10

The effect of \(K_{G}\) on the manufacturers’ long-term behavior.

Full size image
Fig. 11
figure 11

The effect of \(K_{G}\) on the recyclers’ long-term behavior.

Full size image

As it is seen in Fig. 9, for manufacturers when technology innovation subsidies \(K_{G} = 0\), manufacturers are tend to not adopt technology innovation strategy in the long term. However, when governments giving incentives to enterprises, manufacturers evolve towards technological innovation. Furthermore, it can be derived that the stronger the government subsidy more rapid manufacturer evolves to a stable strategy.

As can be seen from Fig. 8, when \(K_{G} = 0\), the proportion of technological innovation of the recyclers decreases at the first and then increases until it evolves to 1. The evolutionary path of the recyclers always tends to 1 when \(K_{G} > 0\), and the higher the \(K_{G}\) is the shorter the time to reach the ESS.

Conclusions and managerial implications

Main conclusions

This study reveals the key role of technological innovation and policy subsidies in battery recycling through an evolutionary game model, introduces the psychological concept of prosocial behavior into the research on power battery recycling, and enriches the research results on power battery recycling. The main conclusions are as follows:

  1. (1)

    Prosocial behavior plays a crucial role in driving technological innovation in power battery recycling. By influencing consumers’ participation and support for green initiatives, it motivates manufacturers and recyclers to pursue innovations like battery health management, disassembly, metal recovery, and harmless treatment, thereby enhancing recycling rates. Consumers’ active involvement in recycling and their support for remanufactured products reduce costs and signal market demand for sustainability, encouraging manufacturers and recyclers to invest in innovation to improve efficiency and competitiveness. Additionally, prosocial behavior fosters a positive social environment, lowering transaction costs for recyclers and further optimizing the recycling system. The study highlights that strengthened prosocial behavior, guided by policies and market incentives, can translate into innovation motivation for enterprises.

  2. (2)

    In the realm of technological innovation, new energy vehicle manufacturers and recyclers often exhibit free-riding behavior, which undermines innovation enthusiasm. Higher free-riding benefits lead firms to reduce their own innovation investments and instead capitalize on the benefits, cost reductions, and risk minimization resulting from others’ achievements. This behavior not only stifles individual firms’ innovation motivation but also hinders industry-wide technological progress and the sustainable development of the recycling system by diminishing spillover effects. Notably, between manufacturers and recyclers, the positive externalities of innovation results exacerbate free-riding, further weakening innovation incentives.

  3. (3)

    The government can significantly shape the innovation strategies of manufacturers and recyclers by designing subsidy mechanisms based on consumer prosocial behavior. Increased subsidies effectively promote innovation among both manufacturers and recyclers. However, manufacturers are more responsive to subsidies than recyclers, suggesting that differentiated policy tools should be employed to address their distinct needs. Manufacturers, with longer R&D cycles and higher costs, rely more on subsidies, whereas recyclers, focused on process optimization, respond more consistently to incentives. Policymakers should prioritize manufacturers’ needs to unlock their innovation potential. Furthermore, dynamic adjustments and precise design of subsidy policies are essential for maximizing effectiveness.

Managerial implications

  1. (1)

    Manufacturers, as the core entities driving technological innovation in new energy vehicle production, should prioritize increasing their investment in research and development (R&D), particularly in areas such as battery health management and intelligent technologies. Such investments are essential for enhancing product competitiveness and improving recycling efficiency. Furthermore, as consumers’ pro-social behaviors, including environmental awareness and social responsibility, continue to grow, a market demand for sustainable development is gradually taking shape. To align with this trend, manufacturers should focus on designing green products and enhancing user experience. Crucially, manufacturers should actively respond to and leverage government subsidy policies to alleviate the financial pressures associated with R&D, especially given the long cycles and high costs typically associated with technological advancements. These subsidy policies serve as a critical tool for stimulating manufacturers’ innovation motivation and fostering their commitment to sustainable practices.

  2. (2)

    Recyclers serve as critical stakeholders in promoting the recycling of power batteries and should prioritize investments in R&D, particularly focusing on the optimization of recycling processes and the implementation of closed-loop systems to enhance resource efficiency and sustainability. This focus on innovation is crucial for improving recycling efficiency and processing capacity. Notably, consumers are increasingly inclined to deliver retired power batteries to low-carbon, green recyclers, a behavior driven by pro-social motivations. This not only provides recyclers with a stable supply of resources and reduces recycling costs but also conveys green market signals, encouraging recyclers to increase their technological innovation efforts. Additionally, the willingness of consumers to support green initiatives creates a larger market space and competitive advantage for recyclers. While recyclers’ response to government subsidies has been relatively stable, they must remain attentive to policy changes and ensure the stability and continuity of their technological innovation investments.

  3. (3)

    The government plays a key role in guiding market behavior and mitigating the free-rider phenomenon through precise policy design. Policymakers should develop differentiated subsidy policies tailored to the distinct technological innovation focuses of manufacturers and recyclers. For manufacturers, subsidies should be increased to compensate for their high R&D costs, particularly in areas such as technological breakthroughs in battery performance and battery materials. For recyclers, subsidy policies should prioritize technological innovation in key areas, including the extraction efficiency of valuable metals from retired batteries, the development of advanced battery processing equipment, and the improvement of environmentally friendly processes.

To further promote sustainable development, the government should enhance public awareness campaigns to strengthen consumers’ environmental consciousness and social responsibility, thereby encouraging greater participation in the recycling of used batteries. Additionally, the government can address the negative externalities of technological innovation and mitigate the inhibitory effects of the free-rider phenomenon by improving intellectual property (IP) protection mechanisms. Which includes promoting the establishment of technological innovation alliances and cooperation platforms to reduce the risks of innovation spillover and foster collaborative development across the industry.