Introduction

The study of non-Newtonian fluids presents a fascinating divergence from classical fluid dynamics, where fluids exhibit shear stress behavior that does not follow the simple proportionality described by Newton’s law of viscosity. Unlike Newtonian fluids, where viscosity remains constant under steady conditions, non-Newtonian fluids exhibit a more complex relationship between shear stress and shear strain, which can vary with factors such as temperature, pressure, and applied force. These unique characteristics not only set non-Newtonian fluids apart but also significantly broaden their practical applications in industries ranging from biomedicine to materials processing.

At the core of non-Newtonian fluid dynamics lies the need to modify traditional momentum conservation equations, with models such as viscoelastic fluids, power-law fluids, and Bingham plastics among the many frameworks used to describe their behavior. One particularly influential model is the Jeffreys fluid model, which offers a highly effective representation of viscoelastic fluids exhibiting shear-thinning and yield stress properties. Originally developed to address geophysical phenomena, the Jeffreys model has found applications in various fields, including the study of complex biological fluids like blood, as well as in industrial systems like foams, syrups, and coatings. Recent advancements in nanofluid dynamics have added further complexity and opportunity. Nanofluids, which consist of nanoscale particles suspended in a base fluid, demonstrate enhanced thermal and flow properties compared to traditional fluids. Their behavior in micro- and nanoscale systems, particularly in porous media with converging-diverging channels, is crucial for the development of advanced cooling systems, energy-efficient devices, and biomedical applications. This research explores the intricate dynamics of non-Newtonian Jeffreys nanofluids in such channels, with a focus on key phenomena like slip velocity, magnetohydrodynamics (MHD), and entropy generation. By addressing gaps in the current literature-particularly concerning the influence of multiple slip mechanisms and MHD effects on heat transfer. This work seeks to contribute valuable insights into optimizing fluid flow, thermal management, and energy efficiency in various practical applications. Among these modifications are viscoelastic fluid models1, power-law fluids2, differential Walters-B short memory models3,4, Oldroyd-B models5, Reiner-Rivlin models6, Bingham plastics7, tangent hyperbolic models8, Eyring-Powell models9, nano non-Newtonian fluid models10, and Maxwell models11. Similar to other rheological models that have been created, the Jeffreys model has shown to be highly effective. The original purpose of this straightforward yet sophisticated rheological model was to model crustal flow issues on Earth12. It depicts a viscoelastic fluid model with high shear viscosity, yield stress, and shear-thinning properties13. Similarly for more applications of non-Newtonian fluid one can seed the series of papers14,15,16,17. Notably, the Jeffreys fluid model transitions to a Newtonian fluid at very high wall shear stress, where the wall stress significantly exceeds the yield stress. This fluid model also provides a reasonable approximation of the rheological behavior of various other liquids, including physiological suspensions, foams, geological materials, cosmetics, syrups, and more.

In fluid dynamics, the velocity differential between a fluid and a solid boundary submerged in the fluid is referred to as “slip velocity”. It shows the velocity of the solid border itself as well as the velocity differential between the fluid particles immediately adjacent to the barrier (commonly called the no-slip circumstance). The concept of slip velocity is fundamental to the study of fluid flow near solid obstacles, especially in micro- and nanoscale channels, small-scale fluid movement scenarios, and interactions with patterned surfaces. Several aspects of fluid dynamics’ slip velocity have been studied in several studies. Khan et al.18 examined squeezed flow in nanofluids while accounting for viscous dissipation and velocity slip. Second-order velocity slip and nanoparticle migration were used in Zhu et al.‘s study19 to study nonfluid performance between two spinning plates. Zheng et al.20 investigate the radiative heat transfer in nanofluid flow across a stretchable sheet with temperature jump and velocity slip within the porous material. By combining slip effects and magnetohydrodynamics (MHD), Amer et al.21 carried out a comprehensive study of the characteristics of Tangent hyperbolic nanofluid flow across a stretched sheet in a porous environment. Hussain et al.17 looked at the effects of slip on three-dimensional rotating dual-phase nanofluid flow on an exponentially stretched sheet with varying viscosity22,23,24,25,26,27. 

The intriguing and complex behavior of nanofluid flow in porous convergent-divergent channels has garnered a lot of attention recently. This research area spans the boundaries of nanotechnology, fluid dynamics, and porous media, offering numerous chances to enhance heat transfer and fluid movement in a broad range of technical applications. There are physical processes and practical implications to the unique arrangement of nanoscale particles suspended in a base fluid flowing through intricately designed tubes with varying cross-sectional geometries. A thorough understanding and optimization of nanofluid flow in porous convergent-divergent channels are crucial for engineers, scientists, and industries seeking innovative solutions to challenges such as enhanced energy efficiency, advanced cooling systems, and more effective filtration. Hashim et al.28 have achieved dual solutions for the temperature and velocity profiles in the convergent channel, whereas Saleem et al.29 have conducted theoretical research on heat transfer in Ellis NF flow through diverging channels. Mishra et al.30 investigated the impact of radiative heat on nanofluid (NF) flow through the wavy walls of a tapering channel. Boujelbene et al.31 employed an inclined channel configuration to enhance thermal characteristics and minimize entropy decay in NF flow. Dogonchi and Ganji32 studied the effects of thermal radiation on NF flow and heat transfer in expanding and contracting convergent-divergent channels by incorporating the effects of thermal radiation. Nazari and Toghraie33 used numerical simulations to investigate heat transmission in sinusoidal channels with porous media. Furthermore, for medical purposes. Alnahdi et al.34 investigated the behavior of ternary Casson hybrid nanofluids in divergent and convergent channels. In order to examine entropy formation in nanofluid flow within convergent and divergent channels under the effect of the Lorentz force, Zada et al.35 carried out a computational and thermal case study. In a follow-up study, hybrid nanoparticles were added to convergent and divergent channels in engine oil to improve heat transfer performance and energy efficiency by Zada et al.35.

The irreversibility that has place during thermal activities is measured by entropy production36. Understanding fluid flow dynamics requires an understanding of entropy production, a measure of disorder in a system and its surroundings. Efficient heating and cooling are essential in many industrial domains and design procedures, particularly in digital and electronic energy systems. Apart from utilizing active techniques such as geometric alterations and nanofluid applications to enhance convective heat transfer, it is vital to assess thermal performance from a second law of thermodynamics standpoint to reduce entropy creation37.

The entropy generation ratio of PGGNP/nanofluid in three different converging channels—exponential, linear, and Bessel was investigated by Owojori et al.38. In contrast to smooth pipes, they discovered that convergent pipes had less thermal entropy formation. Entropy production in non-Newtonian flow over a stretched surface and Eyring–Powell nanofluid was examined by Rehman et al.39 and Bhatti et al.40. A thorough solution was provided by Rana et al.41, who looked into entropy creation in time-dependent electro-magnetohydrodynamic Hiemenz stationary flow across a stretched surface. Using the homotopy analysis method (HAM), Shukla et al.22 conducted a second law analysis on transient non-Newtonian nanofluid flow across a stretched sheet.

Despite extensive literature addressing classical Jeffery-Hamel flow (JHF) for non-Newtonian fluids, including considerations for no-slip conditions, heat and mass transport, thermal radiation, heat generation/absorption, and slip-boundary conditions, significant gaps remain. While flow through divergent and convergent channels is often modeled using Carreau fluids as analogs for blood, research on entropy optimization in Jeffery flow involving non-Newtonian nanofluids with multiple slip mechanisms is still lacking. When shear forces are applied, human blood, a prime example of a shear-thinning fluid, shows decreased apparent viscosity. Slip at the artery wall is regarded as a type of partial blockage in this context. With the significance of these computations and the various uses of nanofluids in thermal engineering and biological domains, including blood flow via arteries and veins, this work attempts to close this gap. The following are the novel aspects of this work:

  • How does slip velocity affect velocity profiles and pressure distributions in non-Newtonian Jeffrey nano-fluids within convergent/divergent channels?

  • What is the impact of magnetohydrodynamic (MHD) effects, characterized by Hartmann numbers, on fluid flow and thermal dynamics?

  • How do slip velocity and MHD effects collectively enhance heat transfer in Jeffrey nano-fluids?

  • What role does viscous dissipation play in the heat transport dynamics of Jeffrey nano-fluid flows modeled with the Buongiorno framework?

  • How can entropy generation in porous systems be optimized using the second law of thermodynamics and Jeffrey constitutive relations?

Physical model and problem description

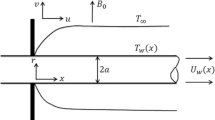
Consider the laminar, two-dimensional steady and incompressible MHD flow of non-Newtonian nano-fluid from a sink/source between two stretchable/shrinkable convergent /divergent channels, which make an angle \(\:2\alpha\:\) (See Fig. 1). Further assumptions are\({\text{V}}=[u(r,\theta ),0,0]\), is the velocity field. The channels are assumed to be divergent if \(\alpha >0\) and convergent if \(\alpha <0\). The magnetic field along \(\:z\)-direction is zero. Heat source and viscous dissipation are taking into consideration. Velocity slip condition is also considered in the boundary conditions.

Fig. 1
figure 1

Geometry of the model.

Full size image

Dimensional formulation of the problem

The continuity, momentum, concentration, and energy equations for the non-Newtonian nanofluid flow under the specified conditions23.

Mass conservation expression

Thus, with the above assumption, the basic conservation Laws are:

$$\nabla .{\text{V}}=0,$$
(1)

using the assumption, Eq. (1) reduced into the following form,

$$\frac{\rho }{r}\frac{\partial }{{\partial r}}\left( {ru} \right)=0.$$
(2)

Momentum expression

$$\rho \frac{{D{\text{V}}}}{{Dt}}= - \nabla P+\nabla S+\rho {f^*}.$$
(3)

Here \(\rho\)is the density of fluid of fluid. \(\nabla p\), represent a gradient of pressure. S is share stress and \(\:{f}^{*}\) is the body forces. For Jeffery flow, S is defined as,

$$S=\frac{\mu }{{\left( {1+{\lambda _1}} \right)}}\left\{ {{{\text{A}}_{\text{1}}}+{\lambda _2}\frac{d}{{dt}}{{\text{A}}_1}} \right\}$$
(4)

.

In Eq. (2),\(\:{\lambda\:}_{1}\),\(\:\:{\lambda\:}_{2}\) are time relaxation and retardation parameters. \({{\text{A}}_{\text{1}}}\), represent the kinematic tensor defined through,

$${{\text{A}}_{\text{1}}}=\left( {\nabla L} \right)+{\left( {\nabla L} \right)^T}$$
(5)

Since \(\:\nabla\:\text{L}\) denotes the gradient of velocity. The Eq. (3) can be written in components form as,

$$\:\widehat{r:}\:\:\:{\uprho\:}\left(\frac{\partial\:u}{\partial\:t}+u\frac{\partial\:u}{\partial\:r}+\frac{v}{\theta\:}\frac{\partial\:u}{\partial\:\theta\:}+w\frac{\partial\:u}{\partial\:z}-\frac{{v}^{2}}{r}\right)=-\frac{\partial\:p}{\partial\:r}+\frac{1}{r}\frac{\partial\:}{\partial\:r}\left(r{S}_{rr}\right)+\frac{1}{r}\frac{\partial\:}{\partial\:\theta\:}\left(r{S}_{r\theta\:}\right)-\frac{{S}_{\theta\:\theta\:}}{r}+\frac{\partial\:}{\partial\:z}\left({S}_{rz}\right)$$
(6)
$$\:\widehat{\theta\::}\:\:\:{\uprho\:}\left(\frac{\partial\:v}{\partial\:t}+u\frac{\partial\:v}{\partial\:r}+\frac{v}{\theta\:}\frac{\partial\:v}{\partial\:\theta\:}+w\frac{\partial\:v}{\partial\:z}\right)=-\frac{1}{r}\frac{\partial\:p}{\partial\:\theta\:}+\frac{1}{{r}^{2}}\frac{\partial\:}{\partial\:r}\left({r}^{2}{S}_{r\theta\:}\right)+\frac{1}{r}\frac{\partial\:}{\partial\:\theta\:}\left({S}_{\theta\:\theta\:}\right)$$
(7)
$$\:\widehat{z:}\:\:\:{\uprho\:}\left(\frac{\partial\:w}{\partial\:t}+u\frac{\partial\:w}{\partial\:r}+\frac{v}{\theta\:}\frac{\partial\:w}{\partial\:\theta\:}+w\frac{\partial\:w}{\partial\:z}\right)=-\frac{\partial\:p}{\partial\:z}+\frac{1}{r}\frac{\partial\:}{\partial\:r}\left(r{S}_{rz}\right)+\frac{1}{r}\frac{\partial\:}{\partial\:\theta\:}\left(r{S}_{rz}\right).$$
(8)

Using the assumptions, Eqs. (6–8) reduced into the following form:

$$\:\widehat{r:}\:\:\:\:\:\:\:\:\:\:{\uprho\:}u\frac{\partial\:u}{\partial\:r}=-\frac{\partial\:p}{\partial\:r}+\frac{1}{r}\frac{\partial\:}{\partial\:r}\left(r{S}_{rr}\right)+\frac{1}{r}\frac{\partial\:}{\partial\:\theta\:}\left(r{S}_{r\theta\:}\right)-\frac{{S}_{\theta\:\theta\:}}{r}$$
(9)
$$\:\widehat{\theta\::}\:\:\:\:\:\:\:\:\:0=-\frac{1}{r}\frac{\partial\:p}{\partial\:\theta\:}+\frac{1}{{r}^{2}}\frac{\partial\:}{\partial\:r}\left({r}^{2}{S}_{r\theta\:}\right)+\frac{1}{r}\frac{\partial\:}{\partial\:\theta\:}\left({S}_{\theta\:\theta\:}\right)$$
(10)

From Eq. (4), the stress tensor components are:

$$\begin{gathered} {S_{rr}}=\frac{\mu }{{\left( {1+{\lambda _1}} \right)}}\left( {2\frac{{\partial u}}{{\partial r}}+2{\lambda _2}u\frac{{{\partial ^2}u}}{{\partial {r^2}}}} \right),\,\,{S_{r\theta }}=\frac{\mu }{{\left( {1+{\lambda _1}} \right)}}\left( {\frac{1}{r}\frac{{\partial u}}{{\partial \theta }}+{\lambda _2}\frac{u}{r}\frac{{{\partial ^2}u}}{{\partial r\partial \theta }} - {\lambda _2}\frac{u}{{{r^2}}}\frac{{\partial u}}{{\partial \theta }}} \right), \hfill \\ {S_{\theta \theta }}=\frac{\mu }{{\left( {1+{\lambda _1}} \right)}}\left( {\frac{2}{r}\frac{u}{r}+2{\lambda _2}\frac{u}{r}\frac{{\partial u}}{{\partial r}} - 2{\lambda _2}\frac{{{u^2}}}{{{r^2}}}} \right), \hfill \\ \end{gathered}$$
(11)

After substitution Eq. (11) into Eqs. (9–10), it gives.

$$u\frac{{\partial u}}{{\partial r}}= - \frac{{\partial p}}{{\rho \partial r}} - \frac{1}{\rho }\left( {\frac{{\sigma B_{0}^{2}}}{{{r^2}}} - \frac{\mu }{K}} \right)u+\frac{\mu }{{\rho \left( {1+{\lambda _1}} \right)}}\left[ \begin{gathered} \frac{{2{\partial ^2}u}}{{\partial {r^2}}}+\frac{{2\partial u}}{{r\partial r}}+\frac{{{\partial ^2}u}}{{{r^2}\partial {\theta ^2}}} - \frac{{2u}}{{{r^2}}}+2{\lambda _2}\frac{u}{r}\frac{{{\partial ^2}u}}{{\partial {r^2}}}+ \hfill \\ 2{\lambda _2}u\frac{{{\partial ^3}u}}{{\partial {r^3}}}+\frac{{{\lambda _2}}}{{{r^2}}}\frac{{\partial u}}{{\partial \theta }}\frac{{{\partial ^2}u}}{{\partial r\partial \theta }}++\frac{{{\lambda _2}}}{{{r^2}}}u\frac{{{\partial ^3}u}}{{\partial r\partial {\theta ^2}}} - \hfill \\ \frac{{{\lambda _2}}}{{{r^3}}}\frac{{\partial u}}{{\partial \theta }}\frac{{\partial u}}{{\partial \theta }} - {\lambda _2}\frac{u}{{{r^2}}}\frac{{{\partial ^2}u}}{{\partial {\theta ^2}}} - 2{\lambda _2}\frac{u}{{{r^2}}}\frac{{\partial u}}{{\partial r}}+2{\lambda _2}\frac{{{u^3}}}{{{r^3}}} \hfill \\ \end{gathered} \right]$$
(12)
$$0= - \frac{1}{{\rho r}}\frac{{\partial p}}{{\partial \theta }}+\frac{\mu }{{\rho \left( {1+{\lambda _1}} \right)}}\left[ \begin{gathered} \frac{1}{{{r^2}}}\frac{{\partial u}}{{\partial \theta }}+\frac{1}{{{r^2}}}\frac{{\partial u}}{{\partial \theta }}+\frac{1}{r}\frac{{{\partial ^2}u}}{{\partial r\partial \theta }}+{\lambda _2}\frac{1}{r}\frac{{\partial u}}{{\partial r}}\frac{{{\partial ^2}u}}{{\partial r\partial \theta }}+{\lambda _2}\frac{1}{r}u\frac{{{\partial ^3}u}}{{\partial {r^2}\partial \theta }} - \hfill \\ {\lambda _2}\frac{1}{{{r^2}}}\frac{{\partial u}}{{\partial r}}\frac{{\partial u}}{{\partial \theta }}+2{\lambda _2}\frac{1}{{{r^2}}}\frac{{\partial u}}{{\partial \theta }}\frac{{\partial u}}{{\partial r}}+2{\lambda _2}\frac{1}{{{r^2}}}u\frac{{{\partial ^2}u}}{{\partial \theta \partial r}} - 4{\lambda _2}\frac{1}{{{r^3}}}u\frac{{\partial u}}{{\partial \theta }} \hfill \\ \end{gathered} \right]$$
(13)

Taking the derivative of Eq. (12) concerning \(\theta\) and Eq. (13) concerning r eliminating the pressure term from Eqs. (12–13):

Energy expression

The energy equation in the vector form is23:

$$\rho Cp\left( {\frac{{\partial T}}{{\partial t}}+V.\nabla T} \right)=k{\nabla ^2}+{Q_t}^{*}$$
(14)

.

In Eq. (14), \({Q_t}^{*}\) represents the extra effects like heat source, viscous dissipation terms. Using the assumptions, Eq. (14) reduced to the following form:

$$\begin{gathered} u\frac{{\partial T}}{{\partial r}}=\frac{k}{{\left( {\rho Cp} \right)}}\left( {\frac{{{\partial ^2}T}}{{\partial {r^2}}}+\frac{1}{r}\frac{{\partial T}}{{\partial r}}+\frac{1}{{{r^2}}}\frac{{{\partial ^2}T}}{{\partial {\theta ^2}}}} \right)+\frac{1}{{\left( {\rho Cp} \right)}}\frac{{{Q_0}T}}{{{r^2}}}+\frac{{{D_{kT}}}}{{{C_s}}}\left( {\frac{{{\partial ^2}C}}{{\partial {r^2}}}+\frac{1}{r}\frac{{\partial C}}{{\partial r}}+\frac{1}{{{r^2}}}\frac{{{\partial ^2}C}}{{\partial {\theta ^2}}}} \right) \hfill \\ +\beta _{1}^{*}K_{r}^{2}C{\left( {\frac{T}{{{T_0}}}} \right)^m}\exp \left( {\frac{{ - {E_a}}}{{{K_1}^{*}T}}} \right)+{\text{\varvec{\upvarphi}}} \hfill \\ \end{gathered}$$
(15)

,

where \(\varphi\) is the viscous dissipation term and given by the following expression,

$${{\varvec{\upvarphi}}}=\frac{\mu }{{\left( {1+{\lambda _1}} \right)}}\left[ {2{{\left( {\frac{{\partial u}}{{\partial r}}} \right)}^2}+\frac{1}{{{r^2}}}{{\left( {\frac{{\partial u}}{{\partial \theta }}} \right)}^2}+2\frac{u}{r}+2{\lambda _2}u\frac{{\partial u}}{{\partial r}}\frac{{{\partial ^2}u}}{{\partial {r^2}}}+{\lambda _2}\frac{u}{{{r^2}}}\frac{{\partial u}}{{\partial \theta }}\frac{{{\partial ^2}u}}{{\partial r\partial \theta }} - {\lambda _2}\frac{u}{{{r^3}}}{{\left( {\frac{{\partial u}}{{\partial \theta }}} \right)}^2}+2{\lambda _2}\frac{u}{r}\frac{{\partial u}}{{\partial r}} - 2{\lambda _2}\frac{{{u^2}}}{{{r^2}}}} \right].$$

Concentration equation

The concentration equation is23,

$$u\frac{{\partial C}}{{\partial r}}={D_B}\left( {\frac{{{\partial ^2}C}}{{\partial {r^2}}}+\frac{1}{r}\frac{{\partial C}}{{\partial r}}+\frac{1}{{{r^2}}}\frac{{{\partial ^2}C}}{{\partial {\theta ^2}}}} \right)+\frac{{{D_T}}}{{{T_0}}}\left( {\frac{{{\partial ^2}T}}{{\partial {r^2}}}+\frac{1}{r}\frac{{\partial T}}{{\partial r}}+\frac{1}{{{r^2}}}\frac{{{\partial ^2}T}}{{\partial {\theta ^2}}}} \right) - K_{r}^{2}C{\left( {\frac{T}{{{T_0}}}} \right)^m}\exp \left( {\frac{{ - {E_a}}}{{K_{1}^{*}T}}} \right)$$
(16)

The boundary conditions for the problem are:

$$\begin{gathered} u={u_c},\,\frac{{\partial u}}{{\partial \theta }}\,\,=\frac{{\partial T}}{{\partial \theta }}=\frac{{\partial C}}{{\partial r}}=0,\,\,\,\, \hfill \\ u= - \gamma \frac{{\partial u}}{{\partial \theta }},\,\,\,T=\frac{{{T_w}}}{{{r^2}}},\,\,C=\frac{{{C_w}}}{{{r^2}}}\,\, \hfill \\ \end{gathered}$$
(17)

Let us consider the radial flow and the, Eq. (1) is expressed:

$$F(\theta )=ru(r,\theta )$$
(18)

.

Non-dimensional parameters

To transform the PDEs (13–16) in ODEs, the following suitable transformation is used23:

$$f(\xi )=\frac{{F(\theta )}}{{{u_c}}},\,\,\,\,\,\Theta (\xi )={r^2}\frac{T}{{{T_w}}},\,\,\,\,\phi (\xi )={r^2}\frac{C}{{{C_w}}},\,\,\,\,\,\,\xi =\frac{\theta }{\alpha }$$
(19)

The variables of temperature, thermal conductivity, pressure, wall temperature, kinematic viscosity, central line displacement, and specific heat at constant pressure are symbolized by \(T,k,{T_w},\nu ,{u_c}\) respectively. The parameters of mass diffusivity coefficient, concentration susceptibility, wall concentration, and average flow temperature are denoted as \(D,C,{C_w}\), and \({T_m}\). Through the utilization of the similarity transformation outlined in Eq. (19), a set of ordinary differential equations governing the velocity, temperature, and concentration profiles is derived.

$$\begin{aligned}& f^{\prime\prime\prime} - 2{\beta _1}ff^{\prime\prime\prime} - 32{\alpha ^2}{\beta _1}ff^{\prime} - 6{\beta _1}f^{\prime}f^{\prime\prime}+2(1+{\lambda _1}){\alpha ^2}\operatorname{Re} ff^{\prime} \hfill \\ &\quad + Ha{\alpha ^2}(1+{\lambda _1})f^{\prime}+{K_1}{\alpha ^2}(1+{\lambda _1})f^{\prime}=0 \hfill \\ \end{aligned}$$
(20)

.

$$\begin{aligned} &\Theta ^{\prime\prime}+2{\alpha ^2}\left( {\Pr f+2+\frac{1}{2}Q} \right)\Theta +\Pr Du\left( {4{\alpha ^2}\phi +\phi ^{\prime\prime}} \right) - \frac{{Ec\Pr }}{{\left( {1+{\lambda _1}} \right)\operatorname{Re} }}\left( {4{\alpha ^2}{f^2}+{{f^{\prime}}^2}} \right)\\ &\quad + \frac{{{\beta _1}Ec\Pr }}{{\left( {1+{\lambda _1}} \right)\operatorname{Re} }}\left( {6{\alpha ^2}{f^3}+2f{{f^{\prime}}^2}} \right)+{\lambda ^ * }{\left( {\delta \Theta } \right)^m}\phi \exp \left( { - \frac{E}{{\delta \Theta }}} \right)=0 \end{aligned}$$
(21)
$$\phi ^{\prime\prime}+2{\alpha ^2}\left( {2+{S_c}f} \right)\phi +{S_c}{S_r}\left( {2{\alpha ^2}\Theta +\Theta ^{\prime\prime}} \right)\phi ^{\prime\prime} - {S_c}{\gamma _1}{\alpha ^2}{\left( {\delta \Theta } \right)^m}\phi \exp \left( {\frac{{ - E}}{{\delta \Theta }}} \right)=0$$
(22)

The transformed boundary conditions are:

$$\begin{gathered} f\left( 0 \right)=1,\,\,\,f^{\prime}\left( 0 \right)=0,\,\,\,\,\,\Theta ^{\prime}\left( 0 \right)=0,\,\,\,\,\,\phi ^{\prime}\left( 0 \right)=0 \hfill \\ f\left( 1 \right)+\gamma f^{\prime}\left( 1 \right)=0,\,\,\,\,\Theta \left( 1 \right)=1,\,\,\,\,\,\,\phi \left( 1 \right)=1 \hfill \\ \end{gathered}$$
(23)

The dimensionless physical quantities arising in system of ODEs (20–22).

\({\gamma _1}=\frac{{{r^2}{k_r}^{2}}}{{{u_c}}},\Pr =\frac{{{u_c}\left( {\rho Cp} \right)}}{k},\,Ec=\frac{{\alpha {u_c}^{2}}}{{{T_w}\left( {Cp} \right)}},\,\operatorname{Re} =\frac{{\alpha {u_c}}}{\nu },\,{S_c}=\frac{{{u_c}}}{D},\,{S_r}=\frac{{D{k_T}{T_w}}}{{{u_c}{T_m}{C_w}}},{\beta _1}=\frac{{{\lambda ^2}}}{{{r^2}}}\)

are Prandtl number, Eckert, Reynolds’s, Soret, Schmidt’s, and Deborah’s numbers respectively.

Engineering parameters

Physical parameters of scientific and engineering importance include the Nusselt number, Sherwood number, and coefficient of skin friction. These specifications are expressed as follows35:

$${C_f}={\left( {\frac{{{S_{r\theta }}}}{{{\rho _f}{u_c}^{2}}}} \right)_{\xi =1}},\,\,\,\,Ns={\left( {\frac{{r{q_w}}}{{{k_f}{T_w}}}} \right)_{\xi =\alpha }},\,\,\,\,\,Sh={\left( {\frac{{r{q_m}}}{{{k_f}{C_w}}}} \right)_{\xi =\alpha }},$$
(24)

Where,

$$\left\{ \begin{gathered} {S_{r\theta }}=\frac{\mu }{{\left( {1+{\lambda _1}} \right)}}\left( {\frac{1}{r}\frac{{\partial u}}{{\partial \theta }}+{\lambda _2}\frac{u}{r}\frac{{{\partial ^2}u}}{{\partial r\partial \theta }} - {\lambda _2}\frac{u}{{{r^2}}}\frac{{\partial u}}{{\partial \theta }}} \right), \hfill \\ \,{q_w}=\frac{{ - {k_f}}}{r}{\left( {\frac{{\partial u}}{{\partial \theta }}} \right)_{\xi =\alpha }},\,\,\,\,{q_m}= - {D_B}{\left( {\frac{{\partial C}}{{\partial r}}} \right)_{\xi =\alpha }}. \hfill \\ \end{gathered} \right.$$
(25)

Using Eq. (19) the Eq. (24) reduce to the following form:

$$\operatorname{Re} {C_f}=\frac{1}{{1+{\lambda _1}}}\left[ {f^{\prime}(1)+2{\beta _1}f(1)f^{\prime}(1)} \right],\,\,\,\,\,{\alpha ^2}{r^2}Nu= - \Theta ^{\prime}(1),\,\,\,\,\,\,\,{\alpha ^2}{r^2}Sh= - \phi ^{\prime}(1)$$
(26)

.

Entropy analysis

Entropy formation can be decreased by improving heat transmission characteristics. Convection processes involving a nanofluid liquid layer flow, however, are irreversible by nature. Entanglement is a constant result of non-equilibrium conditions brought about by momentum and energy exchange at solid-fluid borders and inside the nanofluid itself. Contributions from fluid friction, porosity effects, and heat transfer across finite temperature gradients are included in this entropy synthesis.

$$\begin{gathered} {S_{gen}}=\underbrace {{\frac{{k{r^4}}}{{T_{w}^{2}}}\left[ {{{\left( {\frac{{\partial T}}{{\partial r}}} \right)}^2}+\frac{1}{{{r^2}}}{{\left( {\frac{{\partial T}}{{\partial \theta }}} \right)}^2}} \right]}}_{{Heat\,transfer}}+\underbrace {{\frac{{\mu {r^2}}}{{{T_w}}}\left( \varphi \right)}}_{{Viscous\,dissipation}}+\underbrace {{\frac{\mu }{{k{T_w}}}\left( {{u^2}} \right)}}_{{Porous\,medium}}+\underbrace {{\frac{{\sigma {B_0}^{2}}}{{{T_w}}}\left( {{u^2}} \right)}}_{{Megnetic}} \hfill \\ +\underbrace {{\frac{{{D_B}}}{{{C_w}}}\left[ {{{\left( {\frac{{\partial C}}{{\partial r}}} \right)}^2}+\frac{1}{{{r^2}}}{{\left( {\frac{{\partial C}}{{\partial \theta }}} \right)}^2}} \right]+\frac{{{D_B}}}{{{T_w}}}\left[ {\left( {\frac{{\partial T}}{{\partial r}}} \right)\left( {\frac{{\partial C}}{{\partial r}}} \right)+\frac{1}{{{r^2}}}\left( {\frac{{\partial C}}{{\partial \theta }}} \right)\left( {\frac{{\partial C}}{{\partial \theta }}} \right)} \right]}}_{{Diffusive}} \hfill \\ \end{gathered}$$
(27)

Using the similarity transformation. The Entropy generation number \({N_g}\) becomes:

$$\begin{gathered} {N_g}=\frac{{{\alpha ^2}{r^4}}}{{{k_f}}}{S_{gen}}=4{\alpha ^2}{\Theta ^2}+{{\Theta ^{\prime}}^2}+\frac{{Br}}{{\left( {1+{\lambda _1}} \right)\operatorname{Re} }}\left( {4{\alpha ^2}{f^2}+{{f^{\prime}}^2}} \right) - \frac{{{\beta _1}Br}}{{\left( {1+{\lambda _1}} \right)\operatorname{Re} }}\left( {6{\alpha ^2}{f^3}+2f{{f^{\prime}}^2}} \right) \hfill \\ +Md\left( {{\phi ^2}+\Theta \phi } \right)+Br\left( {{K_1}+{M^2}} \right){f^2} \hfill \\ \end{gathered}$$
(28)

In Eq. (27), the \(Br\)is the Brinkman number, \(\operatorname{Re}\) is the local Reynolds number, and \({K_1}\) is the porosity parameter and \(Md=\frac{{{D_B}{C_w}}}{{{k_f}}}\)

Analysis of homotropy perturbation method

Consider the general nonlinear differential equation in the form of:

$${\text{A}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)} \right) - {f^*}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } \in \Omega \,\,\,\,\,\,\,$$
(29)

In Eq. (28) \({\text{A}}\)is the differential operator, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)\) is unknown function which can be determined, \({f^*}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)\)is the source term and \(\Omega \,\)is the ___domain of the problem. The differential operator \({\text{A}}\)can be divided into two parts:

$${\text{A}}\,{\text{=}}\,L\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)+N\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right),\,$$
(30)

Put Eq. (29) into Eq. (28), we get the following expression,

$$L\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)+N\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right) - {f^*}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } \in \Omega \,\,\,\,\,\,\,$$
(31)

Construct the Homotopy:

$$H\left[ {\Psi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } ;q} \right)} \right]=\left( {1 - q} \right)L\left[ {\Psi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } ;q} \right)} \right] - L\left[ {{f^*}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)} \right]+q{\text{A}}\left[ {\Psi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } ;q} \right)} \right] - {f^*}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)=0,$$
(32)

where q is a small parameter that is varies from 0 to 1.

Remark 1

When \(q=0\)then Eq. (31) becomes:

$$H\left[ {\Psi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } ;0} \right),0} \right]=L\left[ {\Psi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } ;0} \right)} \right] - L\left[ {{f_0}^{*}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)} \right]=0,$$
(33)

Remark 2

When \(q=1\)then Eq. (31) becomes:

$$H\left[ {\Psi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } ;1} \right),1} \right]={\text{A}}\left[ {\Psi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } ;1} \right)} \right] - {f^*}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)=0,$$
(34)

Remark 3

The changing process of q from 0 to 1, the solution approaches form \({\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} _0}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)\) to \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)\) which is the exact solution. That is why, we consider the solution in power series form such that,

$$\Psi \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } ,q} \right)={\Psi _0}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)+{\Psi _1}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)q+{\Psi _2}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right){q^2}+\cdots +\sum\limits_{{i=0}}^{n} {{\Psi _i}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\xi } } \right)} {q^i}$$
(35)

The flow chart for the homotopy perturbation technique is shown in Fig. 2.

Fig. 2
figure 2

Diagram for the HPM scheme.

Full size image

Advantages of HPM

The HPM offers several advantages for solving nonlinear differential equations and other complex mathematical models:

  • Simple and efficient: HPM combines homotopy (a deformation approach) with perturbation techniques, providing straightforward calculations without the need for small parameters (unlike classical perturbation methods).

  • Wide applicability: It is applicable to a broad range of problems, including linear, nonlinear, and fractional differential equations, making it versatile for different fields.

  • Rapid convergence: The series solution obtained via HPM converges quickly, often requiring fewer iterations to achieve accurate results.

  • No linearization needed: Unlike some other methods, HPM does not require linearization or discretization, preserving the original nonlinear properties of the problem.

  • High accuracy: It provides highly accurate analytical approximations that often agree closely with numerical or exact solutions.

  • Flexible framework: The homotopy structure allows for adjustable choices in the initial guess and auxiliary parameter, enhancing adaptability to specific problems.

Code validation

In this section the skin friction \(f^{\prime}(1)\) and \(- \Theta ^{\prime}(1)\) for diverse value of \(\lambda\)are compared with results obtained by30 for Newtonian case when we take \({\lambda _2}=0\)in our model. An excellent agreement has been observed in Table 1.

Table 1 Numerical values of skin friction and Nusselt number for different value of \(\alpha\) when re = 50, \({\lambda _1}={\lambda _2}=0\)
Full size table

Graphical results and discussion

This section is dedicated to examining the impact of various physical parameters on the velocity, temperature, concentration, and entropy fields in both convergent and divergent channels. For this purpose, the section is divided into four sections: velocity field, temperature field, concentration field, and entropy field. Furthermore, the numerical values of different parameters arising from the model are fixed,

\(\Pr =1.8,\,Ec=0.3,\,\alpha ={5^0},\,\operatorname{Re} =50,\,Ha=100,\,\beta =0.1,Sc=0.1,\,Sr=1,\,{K_1}=0.1,\,{\lambda _1}=0.1,\,Q=0.01\)

Discussion on velocity

Figure 3 in the study provides 2D plots illustrating the relationship between the velocity profile of a fluid and the Hartmann number, which is a dimensionless number characterizing the influence of a magnetic field on the flow. Solid lines show the divergent case while the dashed lines show the convergent case. The key observation from the plots is that, for both types of channels, the velocity of the fluid increases as the Hartmann number increases. This indicates that the presence of a stronger magnetic field (reflected by a higher Hartmann number) enhances the velocity of the fluid flow in both convergent and divergent channels, albeit in potentially different ways due to their geometric differences. Figure 4 illustrates how the slip parameter affects velocity. The graph uses solid lines to represent the scenario where the flow is divergent and dashed lines to depict the case where the flow is convergent. In both scenarios, the velocity increases as the slip parameter increases. This indicates that higher slip at the boundary leads to a higher flow velocity, regardless of whether the flow is diverging or converging. Figure 5 illustrates the effect of the porosity parameter (\({K_1}\)) on the velocity profile. Solid lines represent the scenario where the channels are divergent, while dashed lines depict the scenario where the channels are convergent. In both cases, an increase in the porosity parameter leads to a decrease in velocity. Physically, this means that as the porosity of the medium increases, the flow resistance also increases, which slows down the fluid movement. Higher porosity indicates more void spaces within the material, causing the fluid to encounter more resistance as it passes through these spaces. This effect is consistent regardless of whether the channels are diverging or converging, showing that increased porosity universally impedes the flow velocity.

Fig. 3
figure 3

Solid lines show the velocity profile against Ha for divergent case and Dashed lines.

Full size image
Fig. 4
figure 4

Solid figure shows the velocity profile against for divergent case and Dashed figure shows.

Full size image
Fig. 5
figure 5

Solid figure shows the velocity profile against Ha for divergent case and Dashed figure shows.

Full size image

Discussion on temperature

Figure 6 illustrates the behavior of temperature with respect to the Hartmann number. Solid lines represent the divergent case, where the temperature increases, while dashed lines depict the convergent case, where the temperature also increases. Physically, this means that as the Hartmann number increases, the temperature rises in both divergent and convergent scenarios. The Hartmann number is a dimensionless quantity representing the influence of a magnetic field on the fluid flow. An increase in the Hartmann number suggests a stronger magnetic field effect, which likely induces greater thermal energy in the fluid, thereby raising the temperature regardless of whether the flow is diverging or converging. Figure 7 illustrates the temperature profile in relation to heat generation (Q). In both cases depicted in the figure, the temperature increases as Qincreases. Physically, this means that as more heat is generated within the system, the temperature rises correspondingly. Heat generation adds thermal energy to the system, which results in an overall increase in temperature. This trend holds true regardless of other varying conditions within the system. The concentration profile in relation to the Schmidt number (\(Sc\)) is illustrated in Fig. 8. There are solid and dashed lines for the divergent and convergent cases. The concentration of the fluid increases with the \(Sc\)in both cases. As the \(Sc\)increases, which is a dimensionless number representing the ratio of momentum diffusivity to mass diffusivity, the fluid’s concentration rises. There is a greater retention and accumulation of the substance within the fluid when the Schmidt numbers are higher. Divergent and convergent flow conditions show this trend. Figure 9 illustrates the impact of the Soret effect (\(Sr\)) on concentration for both divergent and convergent cases. The solid lines represent the divergent case, while the dashed lines represent the convergent case. In both scenarios, the concentration decreases as the Soret number increases. Physically, this means that as the Soret number, which quantifies the strength of the thermal diffusion effect, increases, the concentration of the fluid decreases. The Soret effect causes particles to move from hotter regions to cooler regions in response to a temperature gradient. A higher Soret number intensifies this movement, leading to a more significant reduction in concentration in both divergent and convergent flows.

Fig. 6
figure 6

Solid figure shows the velocity profile against Ha for divergent case and Dashed figure shows the velocity profile against Ha for convergent case.

Full size image
Fig. 7
figure 7

Solid figure shows the velocity profile against Ha for divergent case and Dashed figure shows the velocity profile against Ha for convergent case.

Full size image
Fig. 8
figure 8

Solid figure shows the velocity profile against Ha for divergent case and Dashed figure shows the velocity profile against Ha for convergent case.

Full size image
Fig. 9
figure 9

Solid figure shows the velocity profile against Ha for divergent case and Dashed figure shows the velocity profile against Ha for convergent case.

Full size image

Discussion on entropy

Figure 10 illustrates the entropy generation against the magnetic parameter (M) for both convergent and divergent channels. In both cases, entropy generation increases as M increases. Physically, this means that as the strength of the magnetic field, represented by the magnetic parameter, M increases, the disorder or randomness in the system, quantified by entropy generation, also increases. The magnetic field influences the fluid flow, leading to greater energy dissipation and thus higher entropy generation. This trend is observed in both convergent and divergent flow scenarios Table 2.

Fig. 10
figure 10

Solid figure shows the velocity profile against Ha for divergent case and Dashed figure shows the velocity profile against Ha for convergent case.

Full size image
Table 2 HPM analysis of velocity, temperature, and concentration at different \(\xi\) values with constant parameters \({\beta _1}=0.1,\,\,\alpha ={5^0},\,\,{K_1}=0.1,\,\,Ec=0.3\),\({\lambda _1}=0.1,\,\,Sc=0.3,\,\,Sr=1,\,\,Ha=100,\,\,\)
Full size table

Conclusion

This study has successfully developed and analyzed a comprehensive mathematical model to investigate the behavior of non-Newtonian nano-fluids in convergent and divergent channels, incorporating the effects of slip velocity and magnetohydrodynamics (MHD). Utilizing the homotopy perturbation method (HPM), we derived analytical solutions to describe the velocity profiles, pressure distributions, and heat transfer characteristics under these complex conditions. Our findings highlight significant alterations in velocity profiles and pressure.

The key observations of this research are given as follows:

  • Slip velocity effects: Slip velocity significantly alters velocity profiles and pressure distributions in convergent/divergent channels. Increased slip results in higher flow velocities across both channel types.

  • Magnetohydrodynamic effects: Stronger magnetic fields, as indicated by higher Hartmann numbers, lead to enhanced fluid velocities and increased temperatures. The MHD effects are pronounced in both convergent and divergent channels.

  • Heat transfer enhancement: The presence of slip velocity and MHD effects collectively improves heat transfer rates within the channels, suggesting potential improvements in thermal management systems.

  • Entropy generation: The research highlights that higher magnetic parameters contribute to increased entropy generation, indicating greater energy dissipation and disorder within the system.

  • Engineering applications: The study’s results can optimize the design and performance of fluid systems in various engineering applications, such as microfluidics and industrial heat exchangers, by providing a deeper understanding of non-Newtonian nano-fluid behavior in complex channel geometries.

In the upcoming, the current scheme might be used to a number of physical and technical obstacles24,42,43,44,45,46.

Future work direction

This study provides a comprehensive analysis of non-Newtonian nanofluid flow in convergent and divergent channels, incorporating slip velocity, magnetohydrodynamics (MHD), and entropy generation. However, several aspects warrant further investigation:

  • Experimental validation: Future studies should include experimental analysis to validate the theoretical and numerical results obtained in this work.

  • Extension to three-dimensional flow: Extending the current model to three-dimensional geometries can provide deeper insights into the behavior of nanofluids in complex structures.

  • Fractional-order models: Incorporating fractional calculus can improve the accuracy of the model in describing memory and hereditary effects in non-Newtonian fluids.

  • Hybrid nanofluids: Studying the impact of hybrid nanofluids, which involve multiple types of nanoparticles, can enhance thermal performance and entropy optimization.

  • Unsteady and transient effects: Investigating time-dependent flow scenarios will provide a better understanding of fluid behavior under dynamic conditions.