Introduction

Inner Mongolia is a key ecological zone in northern China. Its deserts cover nearly 25% of the country’s total desert area. In recent years, the extensive cultivation of xerophytic shrubs, such as sand willows, has effectively mitigated the ongoing threat of desertification in these regions1. However, the vastness of the desert presents challenges, as the equipment used for planting sand willows predominantly includes suspended drilling machines, handheld drilling machines, and water jet drilling machines—methods that are both inefficient and labor-intensive. To promote the mechanized planting of xerophytic shrubs in Inner Mongolia’s desert regions, it is essential to develop suitable mechanical equipment. The foremost task in this endeavor is to conduct a comprehensive study of the sandy soil characteristics in Inner Mongolia where xerophytic shrubs are planted. This research will provide critical insights for establishing efficient planting technologies and equipment tailored to these shrubs.

As technology rapidly advances, soil contact parameters can be obtained using the Discrete Element Method (DEM), which has found widespread application in the study of contact parameters for granular materials2,3,4. This method not only facilitates the optimization of mechanical devices in terms of structural and operational parameters but also enhances development efficiency and reduces costs. In material property research, DEM parameter calibration is an essential technique for accurately determining material contact parameters. The objective of parameter calibration is to ensure that the behavior of the simulated particle group closely resembles that of the physical particle group. The accuracy of this calibration is influenced not only by the physical properties of the particles, boundary conditions, and contact models but also by the particles’ shapes, their positions, and the design methodology of the experiments5,6,7. Dai et al. employed the soil angle of repose as a key indicator to calibrate soil contact parameters through experimental design and optimization8. Yang et al. selected the soil angle of repose, cohesion, and internal friction angle as response variables, utilizing the Plackett-Burman method to identify significant factors and applying the Box-Behnken test to refine the parameters9. Du et al. utilized the Hertz–Mindlin with JKR contact model within EDEM to calibrate the relevant model parameters for ginseng soil, focusing on the contact parameters between soil particles in soft soil after tillage and between the soil and Q235 steel10. Qi et al. combined physical experiments with simulations to accurately obtain the contact parameters for sandy soil used in tiger fruit cultivation in the desert region of Xinjiang, employing nonlinear tools, the Plackett-Burman design, and Response Surface Methodology (RSM)11. Zhang et al. performed parameter calibration using various spherical shapes, discovering that non-standard shapes exhibited smaller relative errors than standard shapes when achieving the same angle of repose12. Si et al. considered the particle size distribution of soil during particle generation and adjusted the parameters of the soil EEPA model to maintain an average accuracy level of 80%13. Liu et al. sought to derive simulation parameters for discrete element simulations of soil, employing actual soil direct shear tests and compaction tests to determine the soil’s Poisson’s ratio and various contact parameters14. Sun et al. established the contact parameters between the soil on the Loess Plateau and the rotary tillage components using the Box-Behnken test15. Chen et al. conducted research on the calibration of cohesive particle and aggregate parameters using discrete element software16. However, existing research is primarily focused on parameter calibration for conventional agricultural soils or clayey soils. Inner Mongolia, one of the driest regions in China, has soils with distinctive physical properties: the particle size distribution is predominantly between 0.075 and 0.30 mm (comprising up to 90%), and the moisture content during the planting season is less than 3%17,18,19. These physical characteristics are substantially lower than those found in typical agricultural soils. The main challenge in developing mechanized planting systems lies in the insufficient understanding of the interaction between desert soils and machinery. This lack of knowledge often leads to soil backflow during operation, causing an increased backfill rate for planting holes. Additionally, discrepancies in contact parameters result in greater simulation errors, which, in turn, contribute to a higher tool failure rate during real-world use.

In summary, although extensive research has been conducted on the calibration of soil and contact component parameters, most of these studies focus on conventional agricultural soils or cohesive soils. In contrast, research on calibrating parameters for sandy soils in desert regions—characterized by extreme aridity, looseness, and a concentrated particle size—is relatively scarce. Building upon existing research, this study concentrates on the sandy soil utilized for planting xerophytic shrubs in the desert region of Inner Mongolia. By integrating nonlinear tools with EDEM software, we optimize and fit the key parameters identified, ultimately determining the contact parameters and validating them through drilling tests. These calibrated parameters provide a theoretical foundation for designing mechanized desert shrub planters. They also address critical issues like desert region economic development and desertification control. Moreover, it offers valuable insights for the optimization of planting machinery in other sandy regions.

Materials and methods

Experimental materials

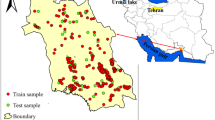
The sand samples were collected from the Kubuqi Desert in Inner Mongolia, which spans an area of 1.4 square kilometers. This desert is located in the central part of Inner Mongolia, bordered to the north by the Yinshan Mountains, to the south by the Loess Plateau, and to the west by the Maowusu Desert. The Kubuqi Desert features an arid climate, characterized by low annual precipitation of approximately less than 100 millimeters. Summer temperatures can exceed 40 °C, while winter temperatures may drop to around − 30 °C. The geographical coordinates of the desert range approximately from 38° 30ʹ to 40° 30ʹ N and 108° 30ʹ to 110° 30ʹ E, as illustrated in Fig. 1 According to the soil testing method standards (GB/T 50123-2019), the density of the sandy soil was determined using the ring knife method, yielding a result of 2.664 g/cm3. The particle size was assessed using the sieve method, as shown in Fig. 2, and the moisture content of the sandy soil was measured using the drying method, resulting in a value of 0.53%.

Fig. 1
figure 1

Soil sampling ___location.

Full size image
Fig. 2
figure 2

Basic Information of particle size.

Full size image

Experimental methods

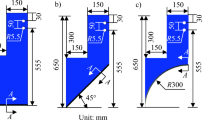
As an inherent characteristic of bulk materials, the angle of repose captures essential factors such as surface contact, friction, and flow. It is utilized to calibrate various parameters, including the recovery coefficient, static friction coefficient, and rolling friction coefficient between soil particles and between soil and steel20,21. The calibration of contact parameters for sandy soil is achieved by combining the actual angle of repose with a simulated angle of repose. The physical model used to determine the actual angle of repose is grounded in relevant research from the literature, employing the GB 11986-89/ISO 4324-1977 injection method for measurement. The funnel itself is constructed from steel, featuring an inclination angle of 60°, an outlet diameter of 17 mm, and a height of 105 mm above the ground, as illustrated in Fig. 3.

The sandy soil was allowed to flow freely from the funnel to form a pile and is left to settle for 1 min. The accumulation of the sandy soil is then recorded using a horizontally positioned high-speed camera. This experiment is repeated five times. Once all accumulation tests are completed, the captured images are analyzed. Using MATLAB software, the images of the sandy soil pile are converted to grayscale and binarized. Edge detection is performed using the Canny and Sobel algorithms to obtain the boundary image22. The boundary image files are imported into Origin software, where the image digitization tool is employed to extract the coordinate values of the boundary image. Linear fitting is conducted on the one-sided coordinate values to create a scatter plot, fitted line, and linear fitting equation. By applying the inverse trigonometric function to the slope of the fitted equation and converting it to degrees, the angle of repose value is determined23, as shown in Fig. 4. Ultimately, the average angle of repose is calculated to be 34.85°.

Fig. 3
figure 3

Angle of repose test for nonlinear tools.

Full size image
Fig. 4
figure 4

Process of obtaining the actual angle of repose.

Full size image

The simulated angle of repose is calibrated through an experimental design approach, with the actual angle of repose serving as the target value. Before starting simulation experiments, selecting the right experimental methods is crucial. The Plackett–Burman (PB) method is ideal for quickly identifying the key factors that affect results. It enables rapid identification of the most important contact parameters with fewer experimental points, saving both time and costs. It progressively narrows the parameter space. This helps identify the exact contact parameter combination24,25. The steepest ascent experiment, in turn, quickly converges toward the center of the response surface analysis26. For response surface experimental design, there are various methods available, including Central Composite Design (CCD), Box-Behnken Design (BBD), Koshal Design, Hybrid Design, and A-Optimality criteria27. Of these, CCD and BBD are the most commonly used. CCD is particularly useful for capturing complex quadratic effects and interactions, though it requires a larger number of experimental points, making it suitable for high-precision model fitting28. However, it can be costly and computationally intensive. On the other hand, BBD design involves fewer experimental points and is better suited for multi-factor experiments, especially when dealing with a smaller number of factors or moderate complexity28. For sand soil parameter calibration, the PB method and steepest ascent experiment are chosen to quickly identify the trends of key factors, minimizing the number of required experiments. The BBD experiment strikes an effective balance between efficiency and complexity while capturing interaction effects between factors. As such, these three experimental approaches are highly suitable for simulation in sand soil parameter calibration.

First, a Plackett–Burman design is implemented using Design-Expert 13.0 to perform multi-factor significance screening and analysis, identifying the parameters that most significantly affect the angle of repose. Next, the range of significant factors is narrowed using the steepest ascent test. Following this, a Box-Behnken response surface experiment is conducted, and the regression model is refined. The regression model is further used to determine the optimal combination of key parameters. Finally, simulations are carried out using these optimal parameters, and the simulated values are compared with the actual values to validate the accuracy and effectiveness of the calibrated parameters.

Triaxial compression test

During the simulation of the accumulation angle test, the sand’s Poisson’s ratio and elastic modulus were unavailable. Therefore, the elastic modulus was measured using the TSZ-2 automatic triaxial apparatus, and Poisson’s ratio was subsequently determined, as shown in Fig. 5. The test was performed using a drainage method, and to ensure the accuracy and reliability of the results, the experiment was repeated five times.

The curve illustrating the relationship between the principal stress difference and axial strain is presented in Fig. 6.The ratio of the principal stress difference to the axial strain, which reflects the slope of the linear section, represents the soil’s elastic modulus E. The formulas for calculating the elastic modulus E and Poisson’s ratio v are provided as (1) and (2), respectively. The soil’s elastic modulus is 3.67 MPa, and Poisson’s ratio is 0.36.

$$E=\frac{{\Delta {\sigma _\partial }}}{{\Delta {\varepsilon _\partial }}}$$
(1)
$$v=\frac{1}{2}\left( {1 - \frac{{\Delta {\varepsilon _v}}}{{\Delta {\varepsilon _a}}}} \right)$$
(2)

where, \(\Delta {\sigma _a}\)signifies the principal stress;\(\Delta {\varepsilon _a}\) refers to the axial strain; \(\Delta {\varepsilon _v}\)represents the volumetric strain.

Fig. 5
figure 5

Triaxial compression testing.

Full size image
Fig. 6
figure 6

Principal stress difference–axial strain relationship curve.

Full size image

In the plane of shear strength versus principal stress difference, shear strength is represented on the vertical axis, while the principal stress difference is plotted on the horizontal axis. The center of the Mohr’s circle is located at half the sum of the major principal stress and the minor principal stress at failure, with the radius defined as half the difference between the major and minor principal stresses. Mohr’s stress circles are constructed in this plane, along with the envelopes of these circles at various confining pressures12. From these representations, the internal cohesion c and internal friction angle ϕ of the specimen can be derived, as illustrated in Fig. 7. The internal cohesion is 2.5 kPa and internal friction angle is 30.6°.

Fig. 7
figure 7

Mohr’s stress circles.

Full size image

Parameter selection and experimental design

Granular contact models

The most commonly used particle models include Hertz-Mindlin with JKR, Hertz-Mindlin with Bonding, and Hertz-Mindlin (no-slip). The Hertz-Mindlin with JKR model accounts for surface adhesion forces and is ideal for fine particles or gel-like materials29,30. The Hertz-Mindlin with Bonding model is used when strong chemical or physical bonds exist between particles12. The Hertz-Mindlin (no-slip) model, on the other hand, is applied when elastic contact is the dominant interaction, especially in scenarios with no slip, minimal friction between particles, or where friction effects can be neglected31. The planting season for sand shrubs typically occurs from April to May. During this period, desert soils, with their low moisture content, result in weaker particle adhesion and relatively minor friction effects. Consequently, particle interactions are primarily driven by elastic forces. For this reason, the Hertz-Mindlin (no-slip) model, which effectively simulates elastic contact behavior between particles, is chosen to simulate the soil particle accumulation angle test in such low-adhesion, low-friction conditions32,33. The net force acting on each particle is the sum of the contact forces arising from particle interactions and the gravitational force.

$$m_{i} \frac{{du_{i} }}{{dt}} = m_{i} g + F_{i}^{c}$$
(3)

where, mi is the mass of particle i, g is the acceleration due to gravity, \(F_{i}^{c}\) is the contact force on particle i.

$$F_{{ij}}^{{ne}} = \frac{4}{3}E^{ * } (R^{ * } )^{{\frac{1}{2}}} \delta_{{ij}}^{n{\frac{3}{2}}}$$
(4)
$$F_{{ij}}^{{nv}} = C_{n} \left( {8m^{ * } E^{ * } \left( {R^{ * } \delta _{{ij}}^{n} } \right)^{{\frac{1}{2}}} } \right)^{{\frac{1}{2}}} v_{{ij}}^{n}$$
(5)

where, the contact force \(F_{{ij}}^{c}\)between particles i and j can be divided into normal component \(F_{{ij}}^{n}\)and tangential component \(F_{{ij}}^{t}\). The normal force \(F_{{ij}}^{n}\) is composed of Hertz elastic force \(F_{{ij}}^{{ne}}\) and viscous force \(F_{{ij}}^{{nv}}\).\(\delta _{{ij}}^{n}\) is the overlap of particles in the normal direction, \(C_{n}\) is the normal damping coefficient, \(v_{{ij}}^{n}\) represents the normal relative velocity.

The equivalent mass \({m^{*}}\) was shown in Eqs. (6)–(8).

$$\frac{1}{{{E^{*}}}}=\frac{{1 - v_{i}^{2}}}{{{E_i}}}+\frac{{1 - v_{j}^{2}}}{{{E_j}}}$$
(6)
$$\frac{1}{{{R^{*}}}}=\frac{1}{{{R_i}}}+\frac{1}{{{R_j}}}$$
(7)
$$\frac{1}{{{m^{*}}}}=\frac{1}{{{m_i}}}+\frac{1}{{{m_j}}}$$
(8)

where, \({E^{*}}\)is equivalent elastic modulus,\({R^{*}}\) is equivalent radius.

The tangential force between particles is based on the Mindlin theory of Mohr Coulomb’s law. Therefore, the tangential force \(F_{{ij}}^{t}\) is composed of viscous force \(F_{{ij}}^{{tv}}\) and elastic force \(F_{{ij}}^{{te}}\), which are determined by the following formula:

$$F_{{ij}}^{{tv}}={C_t}\left( {6\mu {m^{*}}\left| {\left. {F_{{ij}}^{{ne}}} \right|} \right.\sqrt {\frac{{1 - \hbox{min} \left( {{\delta_t},{\delta_{t,\hbox{max}}}} \right)}}{{{\delta_{t,\hbox{max}}}}}} } \right)$$
(9)
$$F_{{ij}}^{{te}}=\mu \left. {\left| {F_{{ij}}^{{ne}}} \right.} \right|\left( {1 - \frac{{1 - \hbox{min} \left( {{\delta _t},{\delta_{t,\hbox{max} }}} \right)}}{{{\delta_{t,\hbox{max} }}}}} \right)$$
(10)

where, \(\mu\) is rolling friction coefficient, \({C_t}\) is tangential damping coefficient, \({C_t}\) is the displacement in the tangent direction, \(v_{{ij}}^{t}\) is the relative velocity in the tangent direction.

Among them,

$${\delta _{t,\hbox{max} }}=\mu \frac{{\left( {2 - v} \right)}}{{2\left( {1 - v} \right)}}\delta _{{ij}}^{n}$$
(11)

where, ν is poisson’s ratio.

Establishment of geometric models

To establish a suitable particle model, the mass distribution of sandy soil particles within the range of 0.1–0.4 mm was investigated. It was found that these particles comprise 95.92% of the total mass of the selected test samples, making them representative of the entire sandy soil sample. Given the laboratory conditions and the physical properties of the sand particles, spherical particles with a diameter of 0.25 mm were chosen. It is important to note that both the particle size and shape of the sand influence the computational results and efficiency. While using non-spherical particles could enhance computational precision, spherical particles were selected to improve efficiency. This decision simplifies the model and sacrifices a degree of accuracy. However, the loss in precision has minimal impact on the final outcomes, making this trade-off justifiable12. Based on the physical testing model, a model was created in UG software, and using the Hertz-Mindlin (no slip) contact model, it was integrated into EDEM as a simulation model for the funnel device. Figures 8 and 9 present the particle model and the funnel model, respectively.

Fig. 8
figure 8

Particle model.

Full size image
Fig. 9
figure 9

Funnel model.

Full size image

During the simulation process, the initial radius of the particles was established at 0.125 mm, with the particles being generated randomly. A virtual particle factory positioned above the funnel was employed to facilitate the dynamic generation of particles within the funnel. The total production weight was set at 0.3 kg, with a generation rate of 0.15 kg/s. The data storage time interval was configured to 0.01 s, and the fixed time step was set to 20% of the Rayleigh time step. Additional parameter values are provided in Table 1.

Table 1 Material parameters.
Full size table

Plackett–Burman experimental design

As the impact of soil–soil and soil–steel contact parameters on the angle of repose remains undetermined, a series of screening experiments were conducted to assess these parameters, which include the soil-soil recovery coefficient, soil–soil static friction coefficient, soil-soil rolling friction coefficient, soil–steel recovery coefficient, soil–steel static friction coefficient, and soil–steel rolling friction coefficient. A total of 12 experimental groups were performed. Each group was conditioned according to the factor levels specified in the Plackett–Burman experimental matrix, as illustrated in Table 2, and the response values for the angle of repose were recorded.

Table 2 Plackett–Burman design factor levels and coding values.
Full size table

Steepest ascent experimental design

Utilizing the Plackett–Burman experimental design, three factors that significantly affect the angle of repose were identified. A steepest ascent experiment was conducted on these selected factors to further refine their value ranges. Throughout the experiments, the simulated response values of the angle of repose were recorded and compared to the results obtained from physical measurements. By analyzing the trends in the errors, the optimal working region was gradually approached.

Box–Behnken experimental design

Using the optimal ranges identified for the significant factors, Box–Behnken experimental design and regression analysis were employed to systematically optimize the parameters and the response variable, leading to the best experimental results.

Analysis of results from Plackett–Burman experiments

Using the Plackett–Burman method, a significance screening analysis was conducted on six test factors. The Plackett–Burman experimental design and the corresponding response values for the angle of repose are illustrated in Table 3, while the significance analysis of the parameters is detailed in Table 4.

As shown in Table 4, the model’s P-value is 0.0018, which is less than 0.05, indicating a significant effect and confirming the reliability of the model for the angle of repose. The model fits well across the entire regression region studied. Additionally, the P-values for factors N2, N3, and N5 are all below 0.05, establishing them as significant influencing factors. Specifically, the significant factors identified are the soil–soil static friction coefficient (N2), the soil–soil rolling friction coefficient (N3), and the soil–steel static friction coefficient (N5). After performing multiple regression fitting on the data, the resulting regression equation is provided in (12).

$$Y=36.56+0.0825{N_1}+2.30{N_2}+7.36{N_3} - 0.0458N_{4}+1.87{N_5}+1.65{N_6}$$
(12)
Table 3 Scheme and results of Plackett–Burman experimental.
Full size table
Table 4 Plackett–Burman experimental results.
Full size table

Analysis of results from steepest ascent trialsc

According to the regression Eq. (12), the partial regression coefficient for factor N3 is 7.36, indicating it is the most significant factor. Therefore, using N3 as the climbing unit, the significant factor step lengths are calculated accordingly, as detailed in formulas (13) to (15)38. Although the effects of factors N1, N4, and N5 on the angle of repose are not significant, they must still be considered during the simulation process. Based on the data in Table 2, the midpoint values for the numerical ranges are set at 0.45, 0.40, and 0.50, respectively. The design and results of the steepest ascent trialsc are summarized in Table 5.

$${N_3}step_{{}}^{{}}size=\frac{{2.30}}{{7.36}} \times \frac{{\left( {0.68 - 0.44} \right)}}{2} \approx 0.04$$
(13)
$${N_3}step_{{}}^{{}}size=\frac{{7.36}}{{7.36}} \times \frac{{\left( {0.4 - 0.01} \right)}}{2} \approx 0.195$$
(14)
$${N_5}step_{{}}^{{}}size=\frac{{1.87}}{{7.36}} \times \frac{{\left( {0.7 - 0.3} \right)}}{2} \approx 0.05$$
(15)
Table 5 Scheme and results of steepest slope experiment.
Full size table

According to the results of the steep slope experiments, the response value of the angle of repose for sample 2 is closest to the actual angle of repose. Thus, sample 2 is selected as the central value for the response surface experiments.

Analysis of Results from Box–Behnken Experiments.

The results of the Box–Behnken test and variance analysis are shown in Tables 6 and 7.

From Table 7, it can be observed that the P value of the fitted model is less than 0.0001, indicating that the model is highly significant, while the omitted fitting terms are not significant (P > 0.05). The polynomial regression equation is presented in (16).

$$Y=39.99+0.67N_{2}+9.58N_{3}+0.65_{5}+0.71N_{2}N_{3}+0.13N_{2}N_{5}+1.16N_{3}N_{5} - 1.27N_{2}^{2} - 5.08N_{3}^{2}+0.41N_{5}^{2}$$
(16)
Table 6 Scheme and results of Box–Behnken experimental.
Full size table
Table 7 ANOVA results of Box–Behnken experimental.
Full size table

The model’s correlation coefficient (R2 = 0.9984) and adjusted coefficient (Radj2 =0.9962) indicate a good fit, explaining 99.62% of the variation in the response values. The predicted determination coefficient Rpre2=0.9925, which exceeds 0.9, demonstrates that the model accurately reflects real situations. This model can be utilized to analyze and predict the angle of repose (°). The key factors, N2, N3, and N5, significantly affect the angle of repose, with N3 emerging as the most influential. Its F-value of 3586.09 and P < 0.0001 highlight its particularly strong effect on the angle of repose. Interaction terms such as N2N3 and N3N5, along with secondary terms like N22 and N32, also show significant impact. Among these, N3 holds the highest influence, emphasizing that the soil-soil rolling friction coefficient (N3) plays a dominant role in the model, overshadowing the other factors. Further analysis reveals that changes in N3 directly influence the dynamic friction behavior between soil particles, likely linked to factors such as particle shape, size, rolling resistance, the flowability of desert sand, and other environmental conditions. It is important to note that the simulation in this experiment used spherical particles, which exhibit lower friction and resistance, resulting in greater flowability. However, if non-spherical particles, such as angular or irregularly shaped ones, were used, their irregular surfaces and larger contact areas would likely lead to a substantial increase in friction and rolling resistance, while decreasing their flowability. Therefore, non-spherical particles could alter the N3 values, affecting the dynamic friction behavior between the soil particles. Moreover, the influence ranking of the factors is N3 > N2 > N5, indicating that the soil-soil rolling friction coefficient is greater than the soil-soil static friction coefficient, which is in turn greater than the soil-steel static friction coefficient.

To gain a more thorough understanding of the model’s fit quality and residual distribution, regression diagnostic plots were employed to further validate the model’s assumptions and predictive ability, as shown in Fig. 10. Regression diagnostic plots are crucial tools for assessing the performance of a regression model. By examining the distribution of residuals, their relationship with predicted values, and the correlation between predicted and actual values, potential issues with the model can be effectively identified.

Fig. 10
figure 10

Regression diagnosis diagram of stacking angle.

Full size image

As shown in Fig. 10a, most of the residual points are close to the diagonal line, indicating that the residuals approximately follow a normal distribution, which supports the model’s assumptions. In Fig. 10b, the residuals are evenly distributed without any systematic bias, suggesting that the model’s fit is stable across various predicted values. In Fig. 10c, the majority of the data points are tightly clustered around the diagonal, indicating that the model’s predictions are very close to the actual observations, demonstrating an ideal fit.

Response surface methodology (RSM)

The response surface significantly influencing the angle of repose in the regression model is depicted in Fig. 11.

Fig. 11
figure 11

Response surface diagram.

Full size image

The variance analysis of the regression model indicates that the interactions N2N3 and N3N5 have significant effects on the angle of repose. The steepness of the response surface further confirms the substantial impact of these interactions. When N2 is held constant, N3 demonstrates a rapid increasing trend, followed by a more gradual increase. Conversely, when N3 is constant, N2 shows a gentle upward trend, as illustrated in Fig. 11a. Similarly, when N3 is constant, N5 exhibits a gentle upward trend, whereas when N5 is constant, N3 displays a rapid increasing trend, as shown in Fig. 11b.

Comparison test of angle of repose

The constraint solver tool in Design Expert software was used with a target value of 34.85°, which represents the measured value. The resulting solution (soil–soil static friction coefficient = 0.442, soil–soil rolling friction coefficient = 0.140, soil–steel static friction coefficient = 0.305) was subsequently optimized.

Fig. 12
figure 12

Comparison between physical and simulation experiments of stacking angle.

Full size image

To further validate the accuracy of the optimal solution, a method combining physical measurements with soil angle of repose simulations was employed. The optimal solution was tested through three repeated simulation experiments, with an average of 34.74° obtained from the three measurements. The relative error between this result and the physical measurement was only 0.3%, indicating that the calibrated soil contact parameters are highly accurate. The comparison between the best soil angle of repose simulation and the physical experiment is shown in Fig. 12.

Pore-forming planting trials for sandy shrubs

Surface contact parameters were designed to simulate the drilling machine’s planting process in sandy regions more accurately. This approach not only aims to improve operational parameters but also to meet planting requirements, thus achieving energy efficiency. To validate the accuracy and feasibility of the calibrated contact parameters, both simulation and physical drilling experiments were conducted.

Physical pore-forming test

The physical pore-forming tests were conducted in the Kubuqi Desert, Inner Mongolia. On the day of the test, the temperature ranged from 8℃ to 16 °C, the weather was cloudy, the northwest wind was blowing at level 2, ultraviolet radiation was weak, and the air humidity was 22%. To ensure consistent environmental conditions across multiple trials, two relatively flat sand areas in the Kubuqi Desert were chosen for the experiment. The longitudinal distance between the two holes was 1000 mm. The intrinsic parameters of the soil were as measured previously.

The test prototype of the drilling device is illustrated in Fig. 13a. The drilling device exerts a traction force of 48.5 kW. The operational parameters are as follows: the drill rod motor speed is set at 400 r/min, the hydraulic cylinder lifting speed is 20 mm/s, the stroke length is 1 m, the drilling depth is 600 mm, and the drilling width is 60 mm. The physical tests were conducted in 5 groups, totaling 10 holes, with each individual drilling test lasting 1 min. The opening diameter and effective depth of each pore-forming test were measured and recorded as data results, while the average values from the 10 physical pore-forming tests were compiled as the final numerical results.

Simulated pore-forming test

The UG software constructs the drilling device used for physical testing at a 1:1 scale and integrates it into the EDEM environment. The drilling device is made of steel, with intrinsic parameters of a density of 7.85 g/cm3, an elastic modulus of 2.1 × 1011 Pa, and a Poisson’s ratio of 0.3.

Within the EDEM software, a soil bin measuring 600 mm × 600 mm × 750 mm is created, corresponding to the dimensions of the physical test site. The specific parameters are identical to the previously measured actual values. The initial state of the EDEM simulation model is depicted in Fig. 13b, with the drilling device situated directly above the soil bin. The device is set to rotate clockwise at 400 r/min, with a feed rate of 20 mm/s. Through 10 simulated pore-forming tests, the opening diameter and effective depth of the holes were measured. The average values from the 10 tests were compiled as the final test results, and the relative error was calculated.

Fig. 13
figure 13

Prototype for experiments and simulation testing platform.

Full size image

Analysis of the results from simulation and physical experiments

Accurate soil parameter calibration is vital for drilling optimization. It helps us understand how soil type affects bit resistance. It becomes possible to select the right drill bit, adjust drilling speed, and modify feed force to reduce resistance and energy consumption during the drilling process. This not only prevents bit wear but also enhances drilling efficiency. Furthermore, accurate soil parameters help anticipate challenges that may arise during drilling, ensuring a smoother and more stable process, which ultimately leads to a significant boost in operational efficiency.

The simulated drilling test is illustrated in Fig. 14a, while the physical drilling test is shown in Fig. 14b.

Fig. 14
figure 14

Pore formation test.

Full size image

The results and errors from both the physical drilling tests and the simulated tests are summarized in Table 8, with the relative error calculation formula shown in (17). The findings indicate that, based on the Hertz-Mindlin (no slip) model, and by combining the recommended contact parameter ranges from the literature with the GEMM database in the EDEM software, the contact parameters between the soil and agricultural machinery components were calibrated and optimized using a surrogate model. The relative errors for the opening diameter and effective depth of the holes were 2.9% and 0.4%, respectively. The discrepancy primarily arose because physical drilling tests were conducted in different areas, and slight errors occurred due to variations in sandy soil composition. Additionally, as the drilling depth increases, the drill rod may experience slight deflection, leading to some errors in the results. However, the overall test results demonstrate that the method for calibrating desert soil parameters is both accurate and feasible. It is also crucial to note that the optimized soil parameters are effective during the growing season but not in winter and early spring, when temperatures can reach − 35 °C in winter and − 25 °C in early spring, and the ground below the surface is predominantly frozen. Therefore, the soil parameter calibration developed in this study is not applicable to winter and early spring conditions.

$${\text{relative error}}=\frac{{\left| {{a_1} - {a_2}} \right|}}{{{a_2}}} \times 100\%$$
(17)

where, \({a_1}\) is simulation value, \({a_2}\) is actual measured value.

Table 8 Results of physical and simulation experiments.
Full size table

Conclusion

  1. (1)

    A brief overview of the collection site for sandy soil is provided, including details on its density, moisture content, and particle size distribution. A hybrid approach combining physical experiments and simulations was used to calibrate the contact parameters of the sandy soil. A nonlinear tool was employed to perform the angle of repose test, with MATLAB and Origin utilized to ascertain the actual angle of repose at 34.85°. Additionally, the triaxial compression test was conducted to determine the elastic modulus, Poisson’s ratio, internal friction angle, and cohesion of the sandy soil.

  2. (2)

    The Plackett–Burman experiment demonstrates that the contact parameters of the soil-soil static friction coefficient, soil–soil rolling friction coefficient, and soil–steel static friction coefficient have a significant impact on the angle of repose of the soil. Using the steepest ascent test, the range of contact parameter values that significantly influence the angle of repose was refined, with the non-significant factors identified as a soil–soil restitution coefficient of 0.45, a soil–steel restitution coefficient of 0.40, and a soil–steel rolling friction coefficient of 0.50. The Box–Behnken experiment indicated that the main, interaction, and secondary terms of the significant contact parameters considerably affect the angle of repose. By solving the second-order regression model, optimal values for the simulated contact parameters were determined: a soil–soil static friction coefficient of 0.442, a soil–soil rolling friction coefficient of 0.140, and a soil–steel static friction coefficient of 0.305. The relative error between the physical and simulated angle of repose tests using these optimal parameters was 0.3%.

  3. (3)

    The comparative results of physical pore-forming experiments and simulation tests reveal that, following the optimization of discrete element parameters for sandy soil using a surrogate model, the motion behavior of the drilling apparatus in the soil simulation model exhibits a smaller deviation compared to the physical experiments. The relative errors in the physical dimensions of the formed pores are 2.9% and 0.4%, respectively, and the physical and mechanical properties of the simulated soil closely align with those of the actual soil.